Multi-Task Vehicle Platoon Control: A Deep Deterministic Policy Gradient Approach
Abstract
1. Introduction
2. Related Work
- This study constructs a multi-task approach based on a DDPG framework to control vehicles in a platoon. The main contribution of this work is defining a reward function that allows the implementation of such control tasks.
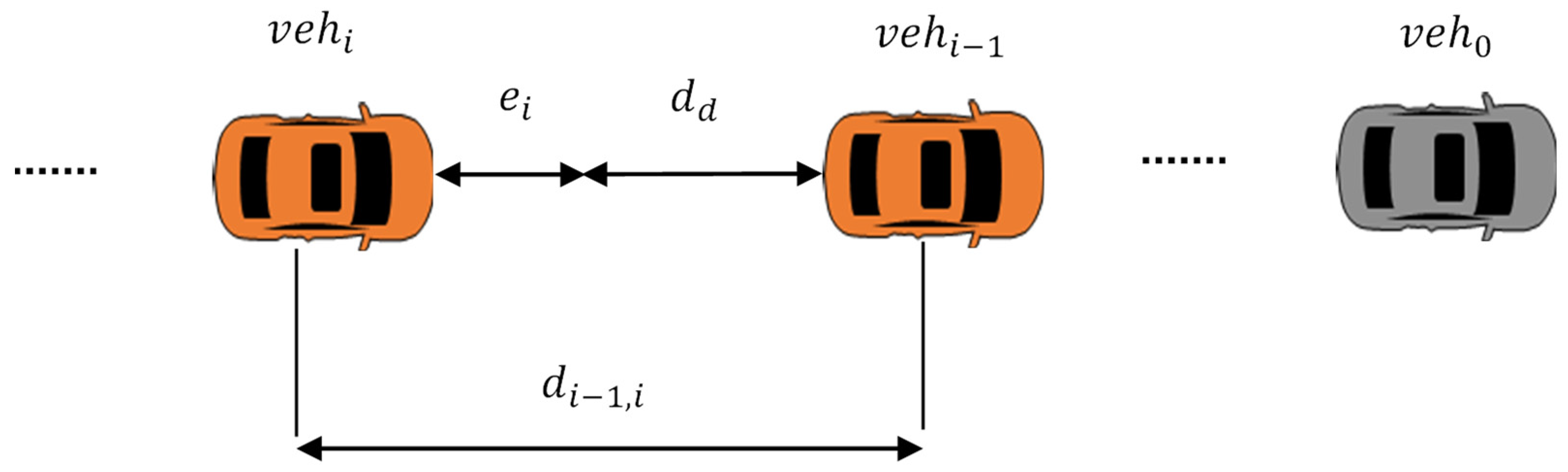
- Introduction of an effective inter-vehicle distance based on the actual longitudinal distance of two consecutive vehicles and their speed;
- Imposing a specific constraint on a variation in the ego-vehicle’s relative speed with respect to its predecessor and including that in the developed single reward function; as a result, the speed chattering of the ego-vehicle during the gap-closing/opening manoeuvres, or in the speed-tracking of the leading vehicle, is reduced.
3. Vehicular Platoon Architecture and Control Problem Statement
4. Deep Reinforcement Learning Algorithm
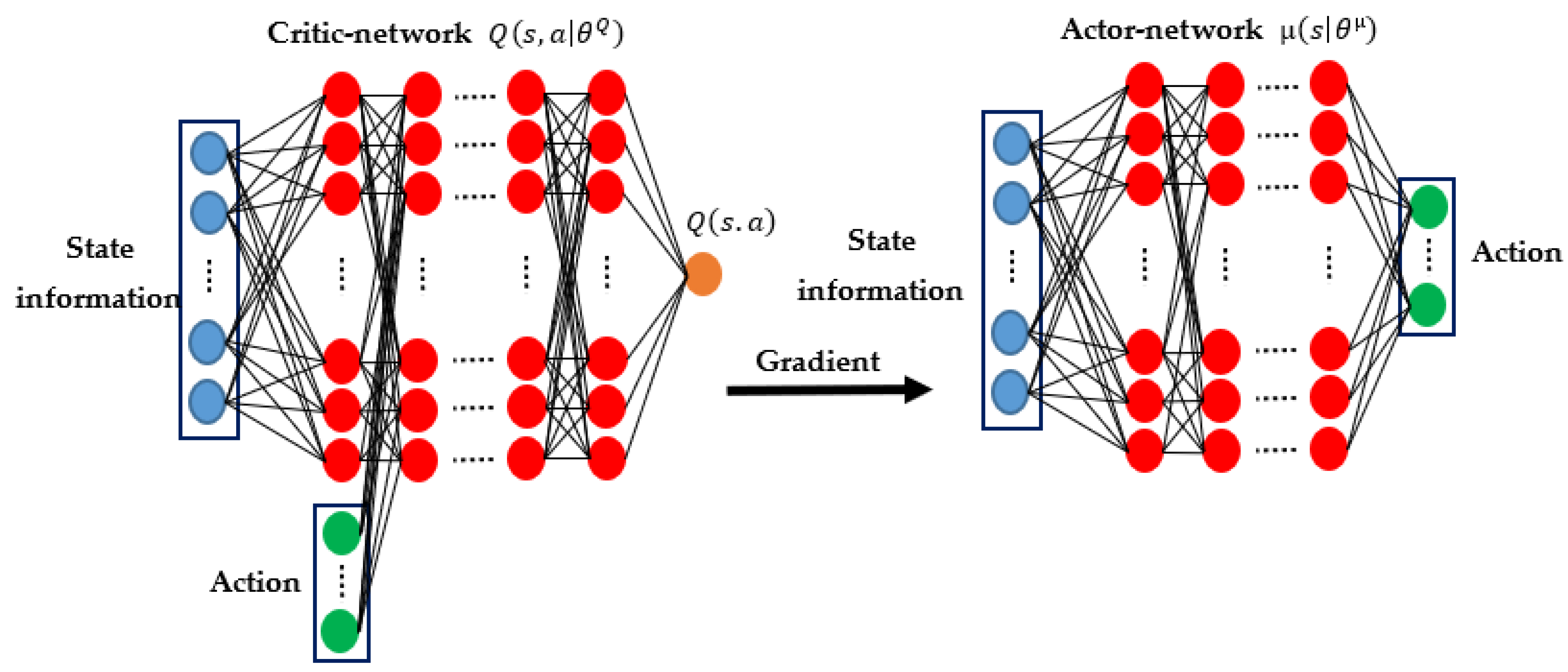
4.1. DDPG Algorithm
4.2. Definition of DDPG State Space
4.3. Proposed Reward Function
5. Results and Discussion
5.1. Simulation Setup
5.2. Simulation Results
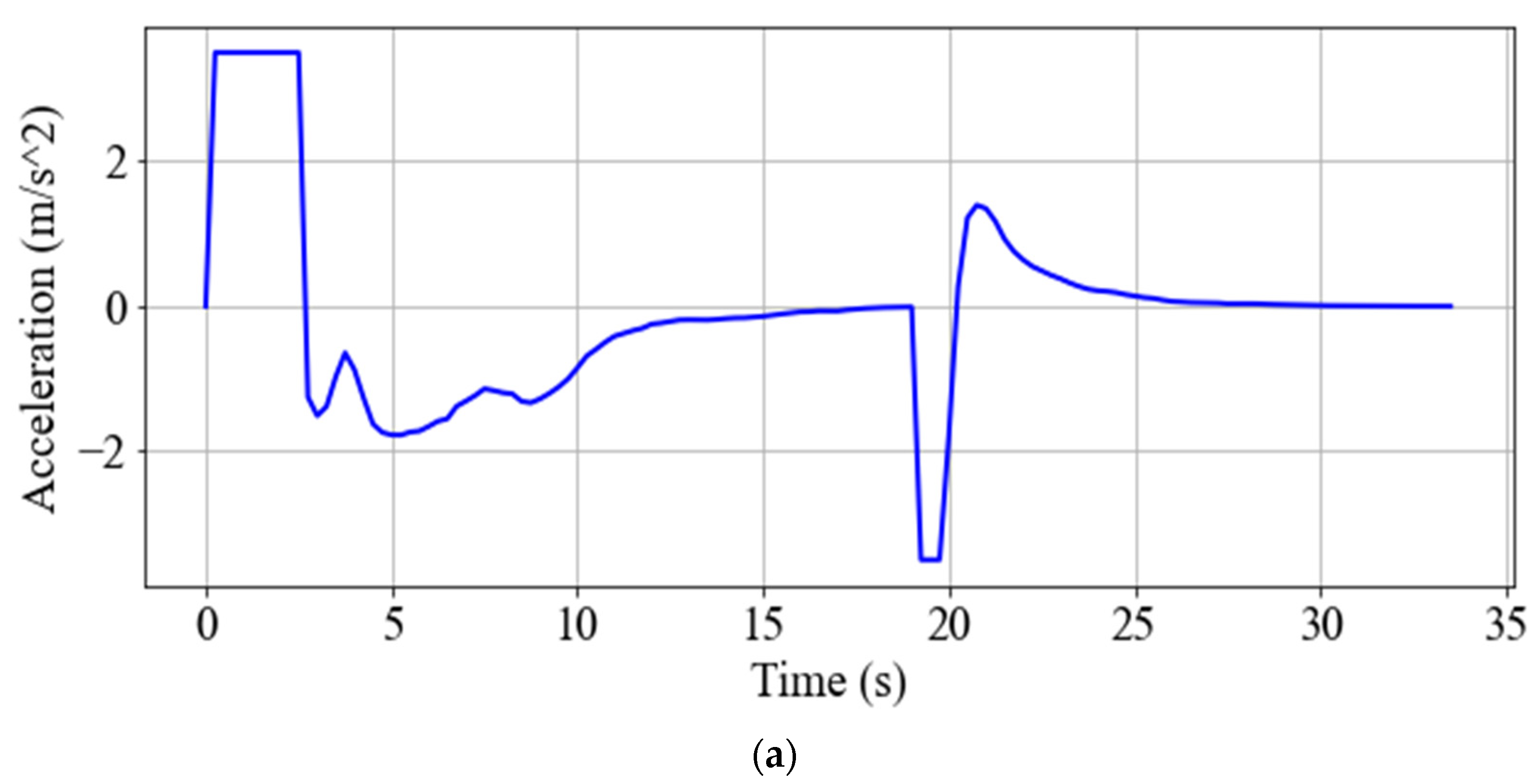
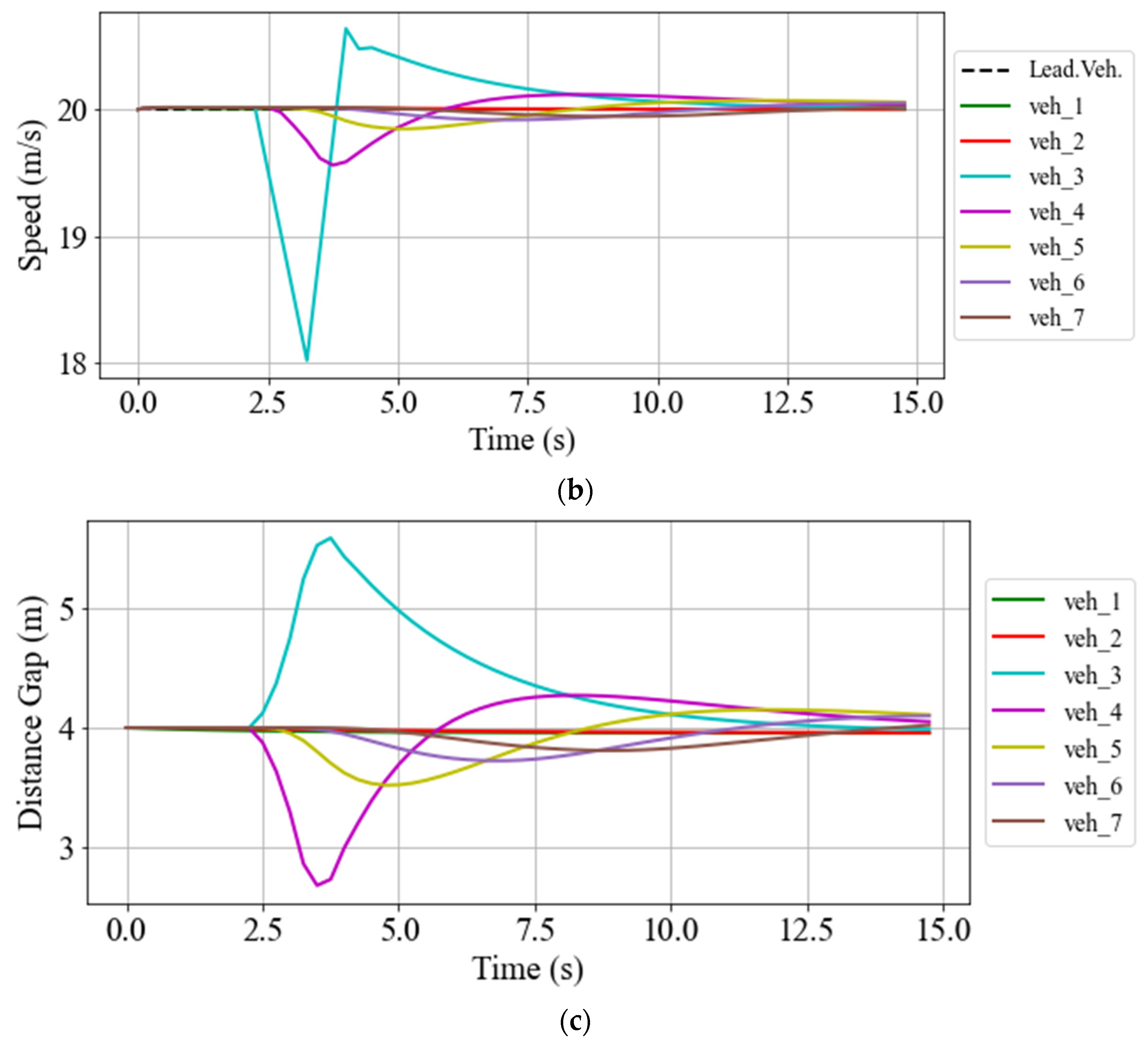
5.2.1. Gap-Closing/Opening
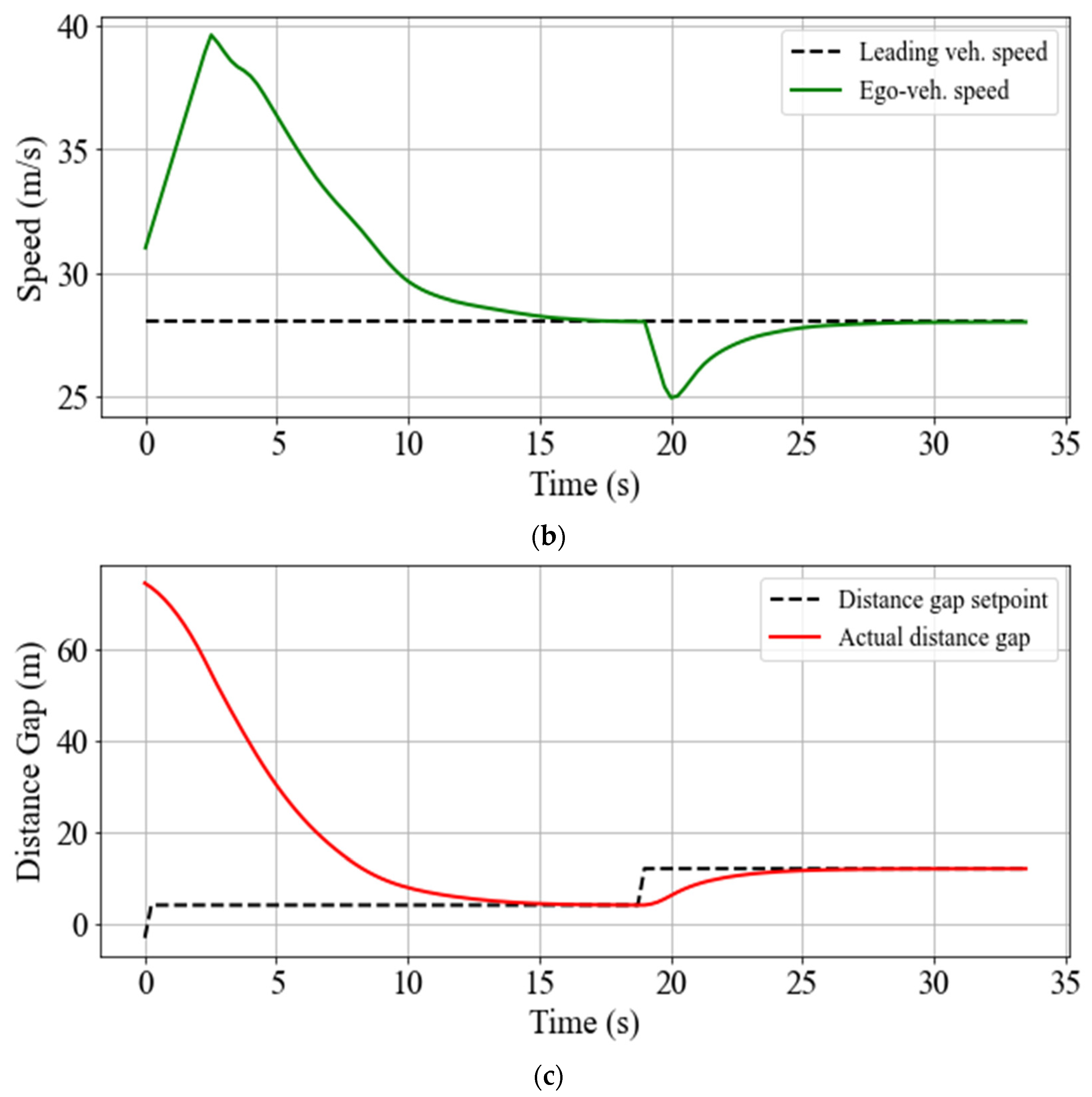
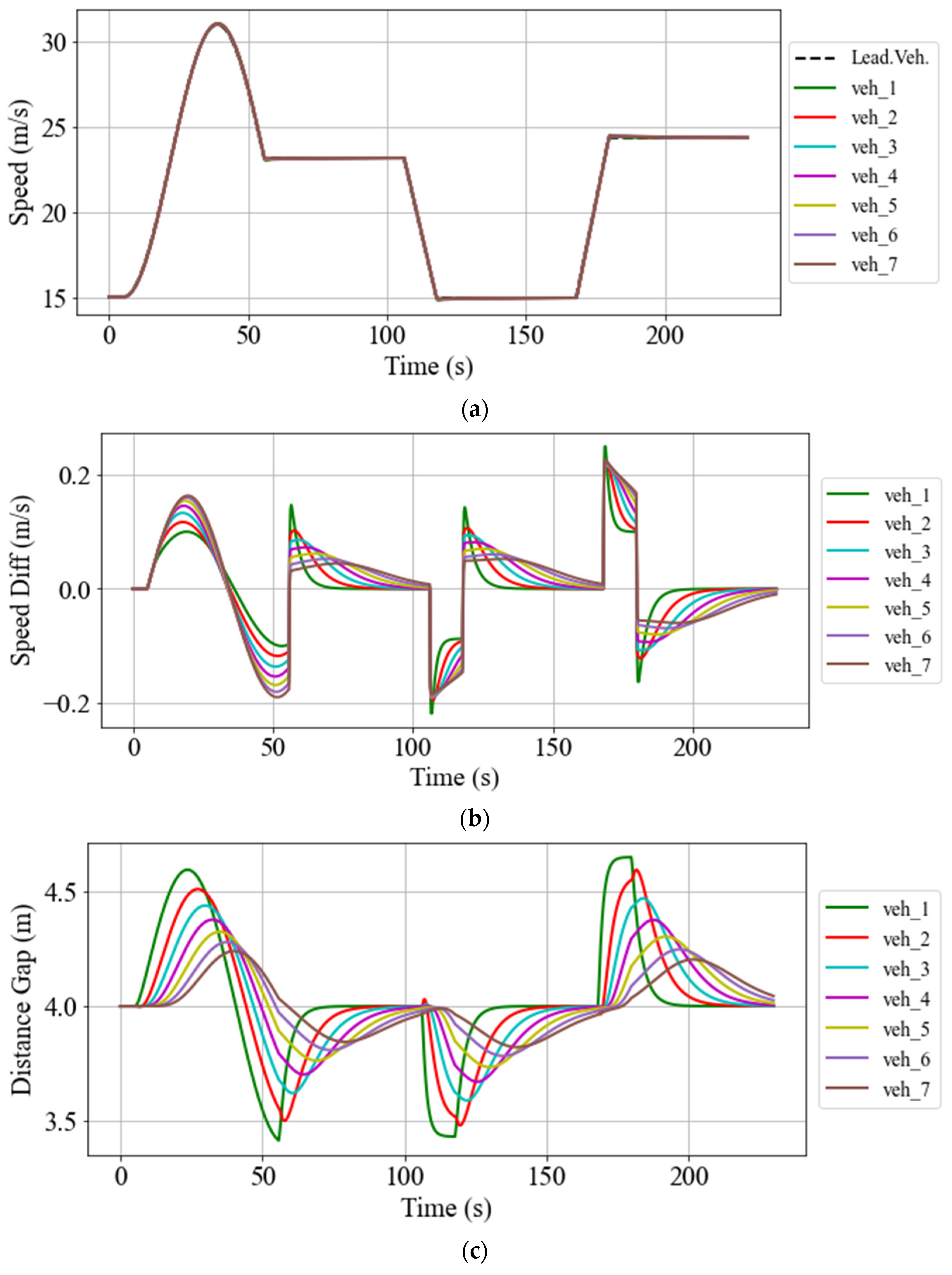
5.2.2. Speed and Space Gap Control
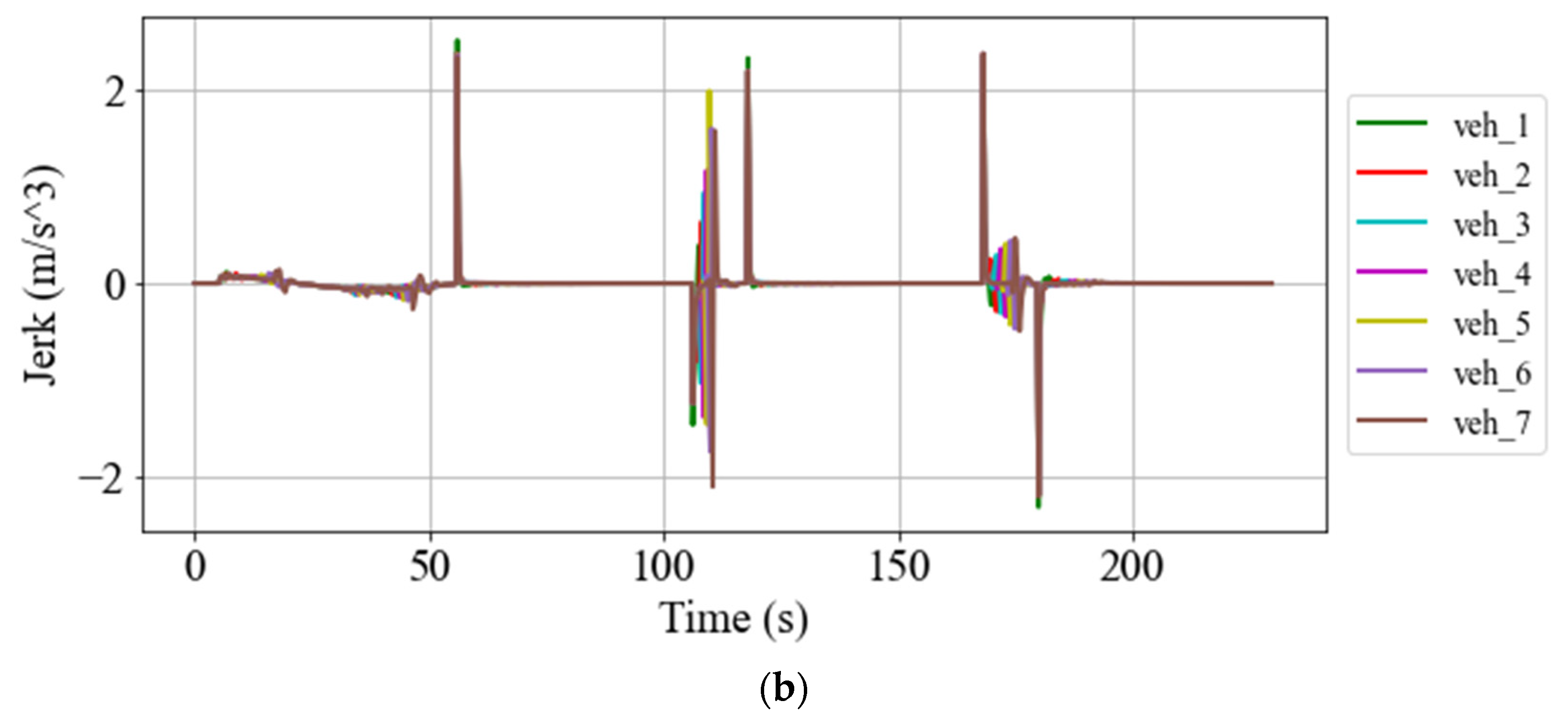
5.2.3. String Stability Assessment
5.2.4. Comparison Between the Proposed DDPG Method and CACC
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhang, J.; Wang, F.Y.; Wang, K.; Lin, W.H.; Xu, X.; Chen, C. Data-driven intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- Horowitz, R.; Varaiya, P. Control design of an automated highway system. Proc. IEEE 2000, 88, 913–925. [Google Scholar] [CrossRef]
- Rostami-Shahrbabaki, M.; Haghbayan, S.A.; Akbarzadeh, M.; Bogenberger, K. On the Technical Feasibility of Vehicle to Vehicle Charging for Electric Vehicles via Platooning on Freeways. In Proceedings of the 2022 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2022; pp. 530–537. [Google Scholar] [CrossRef]
- Johansson, I.; Jin, J.; Ma, X.; Pettersson, H. Look-ahead speed planning for heavy-duty vehicle platoons using traffic information. Transp. Res. Procedia 2017, 22, 561–569. [Google Scholar] [CrossRef]
- Wang, M.; van Maarseveen, S.; Happee, R.; Tool, O.; van Arem, B. Benefits and Risks of Truck Platooning on Freeway Operations Near Entrance Ramp. Transp. Res. Rec. 2019, 2673, 588–602. [Google Scholar] [CrossRef]
- VanderWerf, J.; Shladover, S.; Kourjanskaia, N.; Miller, M.; Krishnan, H. Modeling Effects of Driver Control Assistance Systems on Traffic. Transp. Res. Rec. 2001, 1748, 167–174. [Google Scholar] [CrossRef]
- Chehardoli, H.; Homaeinezhad, M.R. Third-order leader-following consensus protocol of traffic flow formed by cooperative vehicular platoons by considering time delay: Constant spacing strategy. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 285–298. [Google Scholar] [CrossRef]
- Gao, F.; Li, S.E.; Zheng, Y.; Kum, D. Robust control of heterogeneous vehicular platoon with uncertain dynamics and communication delay. IET Intell. Transp. Syst. 2016, 10, 503–513. [Google Scholar] [CrossRef]
- Fardad, M.; Lin, F.; Jovanović, M.R. Sparsity-promoting optimal control for a class of distributed systems. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 2050–2055. [Google Scholar] [CrossRef]
- Dunbar, W.B.; Caveney, D.S. Distributed receding horizon control of vehicle platoons: Stability and string stability. IEEE Trans. Automat. Contr. 2012, 57, 620–633. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.E.; Zheng, Y.; Hedrick, J.K. Distributed sliding mode control for multi-vehicle systems with positive definite topologies. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 5213–5219. [Google Scholar] [CrossRef]
- Aradi, S. Survey of Deep Reinforcement Learning for Motion Planning of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 740–759. [Google Scholar] [CrossRef]
- Lin, Y.; McPhee, J.; Azad, N.L. Comparison of Deep Reinforcement Learning and Model Predictive Control for Adaptive Cruise Control. IEEE Trans. Intell. Veh. 2021, 6, 221–231. [Google Scholar] [CrossRef]
- Zhou, Y.; Fu, R.; Wang, C. Learning the Car-following Behavior of Drivers Using Maximum Entropy Deep Inverse Reinforcement Learning. J. Adv. Transp. 2020, 2020, 4752651. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flotterod, Y.P.; Hilbrich, R.; Lucken, L.; Rummel, J.; Wagner, P.; Wiebner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar] [CrossRef]
- Haydari, A.; Yilmaz, Y. Deep Reinforcement Learning for Intelligent Transportation Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11–32. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. Part C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Li, M.; Li, Z.; Xu, C.; Liu, T. Deep Reinforcement Learning-Based Vehicle Driving Strategy to Reduce Crash Risks in Traffic Oscillations. Transp. Res. Rec. 2020, 2674, 42–54. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2018, 97, 348–368. [Google Scholar] [CrossRef]
- Zhou, M.; Yu, Y.; Qu, X. Development of an Efficient Driving Strategy for Connected and Automated Vehicles at Signalized Intersections: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 433–443. [Google Scholar] [CrossRef]
- Isele, D.; Rahimi, R.; Cosgun, A.; Subramanian, K.; Fujimura, K. Navigating Occluded Intersections with Autonomous Vehicles Using Deep Reinforcement Learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Kim, M.; Lee, S.; Lim, J.; Choi, J.; Kang, S.G. Unexpected collision avoidance driving strategy using deep reinforcement learning. IEEE Access 2020, 8, 17243–17252. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Secure Distributed Adaptive Platooning Control of Automated Vehicles Over Vehicular Ad-Hoc Networks Under Denial-of-Service Attacks. IEEE Trans. Cybern. 2021, 52, 12003–12015. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Secure and collision-free multi-platoon control of automated vehicles under data falsification attacks. Automatica 2022, 145, 110531. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Perez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Wei, S.; Zou, Y.; Zhang, T.; Zhang, X.; Wang, W. Design and Experimental Validation of a Cooperative Adaptive Cruise Control System Based on Supervised Reinforcement Learning. Appl. Sci. 2018, 8, 1014. [Google Scholar] [CrossRef]
- Yan, R.; Jiang, R.; Jia, B.; Huang, J.; Yang, D. Hybrid Car-Following Strategy Based on Deep Deterministic Policy Gradient and Cooperative Adaptive Cruise Control. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2816–2824. [Google Scholar] [CrossRef]
- Berahman, M.; Rostmai-Shahrbabaki, M.; Bogenberger, K. Driving Strategy for Vehicles in Lane-Free Traffic Environment Based on Deep Deterministic Policy Gradient and Artificial Forces. IFAC-PapersOnLine 2022, 55, 14–21. [Google Scholar] [CrossRef]
- Luo, X.; Chen, T.; Li, M.; Li, S. Platoon Control of Automatic Vehicles Based on Deep Deterministic Policy Gradient. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; Volume 2021, pp. 6154–6159. [Google Scholar] [CrossRef]
- Semsar-Kazerooni, E.; Verhaegh, J.; Ploeg, J.; Alirezaei, M. Cooperative adaptive cruise control: An artificial potential field approach. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016. [Google Scholar]
- Li, S.E.; Zheng, Y.; Li, K.; Wang, J. An overview of vehicular platoon control under the four-component framework. IEEE Intell. Veh. Symp. Proc. 2015, 2015, 286–291. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Chien, C.C.; Ioannou, P. A Comparision of Spacing and Headway Control Laws for Automatically Controlled Vehicles1. Veh. Syst. Dyn. 2007, 23, 597–625. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Wegener, A.; Piórkowski, M.; Raya, M.; Hellbrück, H.; Fischer, S.; Hubaux, J.P. TraCI: An interface for coupling road traffic and network simulators. In Proceedings of the 11th Communications and Networking Simulation Symposium, Ottawa, ON, Canada, 14–17 April 2008; pp. 155–163. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the NIPS 2017 Autodiff Workshop: The Future of Gradient-based Machine Learning Software and Techniques, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Xiao, L.; Gao, F. Practical string stability of platoon of adaptive cruise control vehicles. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1184–1194. [Google Scholar] [CrossRef]
- Li, S.E.; Zheng, Y.; Li, K.; Wu, Y.; Hedrick, J.K.; Gao, F.; Zhang, H. Dynamical Modeling and Distributed Control of Connected and Automated Vehicles: Challenges and Opportunities. IEEE Intell. Transp. Syst. Mag. 2017, 9, 46–58. [Google Scholar] [CrossRef]
- Shaout, A.K.; Jarrah, M.A. Cruise control technology review. Comput. Electr. Eng. 1997, 23, 259–271. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Actor & Critic learning rates | 10−4 (10−2) | Highway length (width) | 5 km (3.2 m) |
| 0.99 | Vehicle length (width) | 3.2 m (1.6 m) | |
| τ | 0.005 | 0.25 s | |
| Batch size | 256 | Initial vehicle speed | [10, 50] m/s |
| Experience replay buffer size | 1,000,000 | ) | 4 s (2 s) |
| Maximum acceleration (deceleration) | 3.5 (−3.5) m/s2 | dd | 4 m |
| 0.1 | Maximum simulation step at each episode | 100 |
| Parameter | ||||
|---|---|---|---|---|
| Value | 0.15 | 0.01 | 0.02 | 0.9 |
| KPI | CACC | DDPG |
|---|---|---|
| 25,846 m | 25,627 m | |
| 369.31 m/s | 334.13 m/s | |
| 171.08 m/s2 | 226.62 m/s2 | |
| Max_gap_error | 65 cm | 40 cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berahman, M.; Rostami-Shahrbabaki, M.; Bogenberger, K. Multi-Task Vehicle Platoon Control: A Deep Deterministic Policy Gradient Approach. Future Transp. 2022, 2, 1028-1046. https://doi.org/10.3390/futuretransp2040057
Berahman M, Rostami-Shahrbabaki M, Bogenberger K. Multi-Task Vehicle Platoon Control: A Deep Deterministic Policy Gradient Approach. Future Transportation. 2022; 2(4):1028-1046. https://doi.org/10.3390/futuretransp2040057
Chicago/Turabian StyleBerahman, Mehran, Majid Rostami-Shahrbabaki, and Klaus Bogenberger. 2022. "Multi-Task Vehicle Platoon Control: A Deep Deterministic Policy Gradient Approach" Future Transportation 2, no. 4: 1028-1046. https://doi.org/10.3390/futuretransp2040057
APA StyleBerahman, M., Rostami-Shahrbabaki, M., & Bogenberger, K. (2022). Multi-Task Vehicle Platoon Control: A Deep Deterministic Policy Gradient Approach. Future Transportation, 2(4), 1028-1046. https://doi.org/10.3390/futuretransp2040057






