Abstract
Jute is a bio-degradable, agro-renewable, and widely available lingo cellulosic fiber having high tensile strength and initial modulus, moisture regain, good sound, and heat insulation properties. For these unique properties and eco-friendly nature of jute fibers, jute-based products are now widely used in many sectors such as packaging, home textiles, agro textiles, build textiles, and so forth. The diversified applications of jute products create an excellent opportunity to mitigate the negative environmental effect of petroleum-based products. For producing the best quality jute products, the main prerequisite is to ensure the jute yarn quality that can be defined by the load at break (L.B), strain at break (S.B), tenacity at break (T.B), and tensile modulus (T.M). However, good quality yarn production by considering these parameters is quite difficult because these parameters follow a non-linear relationship. Therefore, it is essential to build up a model that can cover this entire inconsistent pattern and forecast the yarn quality accurately. That is why, in this study, a laboratory-based research work was performed to develop a fuzzy model to predict the quality of jute yarn considering L.B, S.B, T.B, and T.M as input parameters. For this purpose, 173 tex (5 lb/spindle) and 241 tex (7 lb/spindle) were produced, and then L.B, S.B, T.B and T.M values were measured. Using this measured value, a fuzzy model was developed to determine the optimum L.B, S.B, T.B, and T.M to produce the best quality jute yarn. In our proposed fuzzy model, for 173 tex and 241 tex yarn count, the mean relative error was found to be 1.46% (Triangular membership) and 1.48% (Gaussian membership), respectively, and the correlation coefficient was 0.93 for both triangular and gaussian membership function. This result validated the effectiveness of the proposed fuzzy model for an industrial application. The developed fuzzy model may help a spinner to produce the best quality jute yarn.
Keywords:
triangular membership; gaussian membership; jute spinning; tex; quality ratio; fuzzy logic 1. Introduction
The excessive use of plastic products has led to a massive increase in environmental pollution. Therefore, government, industry, and consumers pay more attention to natural and biodegradable resources that are less hazardous to the environment as well as to human and animal health. For this reason, the uses of natural fiber-based products are increasing extensively in many applications such as automobiles, furniture, building materials, cosmetics, medicine, packaging and so on due to their biodegradable, widely available, and environment-friendly features [1]. Among the natural fibers, jute is the second most widely used biodegradable, and environmentally friendly fiber [2]. Therefore, scientists are using jute to develop commercial products such as packaging [3], home textile products [4], geo-textiles [5,6], low-weight and flexible composites [7,8,9], and so on to reduce the uses of synthetic products to protect the environment. To use jute in these applications, the quality of jute yarn production is the most important factor. Jute yarn quality can be defined by its L.B, S.B, T.B, and T.M values. To produce the best quality yarn by maintaining these properties is very tough due to the non-linear behavior among L.B, S.B, T.B, and T.M. In this case, modeling the yarn qualities by identifying yarn properties is the most enthralling issue in textile research. Various prediction approaches have been exercised to forecast the different yarn qualities. The quality characteristics of the yarn depend on various parameters. Sometimes, it is difficult for scientists and researchers to control the required quality for specific purposes. Therefore, the modeling of the yarn quality characteristics based on different physical parameters will be the solution of this problem that meets the consumer’s requirements. With this regard, numerous modeling methods are being used nowadays to determine yarn performance under different considerations viz. strength, elongation, evenness, hairiness, quality ratio, etc. But the procedure of controlling the process parameters at the time of yarn production is vital to obtaining end products that fulfill the consumer’s necessity [10]. In addition, all of these factors execute in a non-linear manner and interact with one another. Therefore, it is quite difficult for researchers to manage the process parameters for yarn production.
Hence, the development of a precise model that relates the process parameters and quality features may help textile engineers to forecast the required yarn production in advance which will reduce the total cost and the production time [11]. For this reason, for forecasting yarn qualities, there are three well-known modelling methods: mathematical model, statistical analysis model, and soft computing methods are becoming popularity day-by-day. Hunter [12], Mogahzy [13], Hafez [14] and Smith & Waters [15] provided statistical regression models and the beta co-efficient analysis to show the relative impact of various inputs on yarn strength. Bogdan [16,17], Frydrych [18], Zurek, Frydrych, & Zakrzewski [19], Subramanian, Ganesh, & Bandyopadhyay [20] and Abhijit & Anindya [21] have developed mathematical models that are incredibly attractive since they are based on core ideas of basic sciences and provide a good knowledge of the process procedure. But the forecast precision of the mathematical model is not particularly promising owing to the guesses used when developing this model, because mathematical and statistical modeling is inadequate to represent the non-linear interaction between inputs and outcomes.
To solve this problem, the introduction of artificial intelligence (A.I) has given a precise additional drive to study yarn property modeling. Ramesh, Rajamanickam and Jayaraman, [22], Cheng and Adams [23], Zhu and Ethridge [24,25], Guha, Majumdar, and Majumdar [26] and Guha, Chattopadhyay and Jayadeva [27] were able to predict several properties of spun yarns using neural-fuzzy approaches and an artificial neural network (ANN). However, due to the significant waste of time and resources, a traditional trial-and-error experimental technique failed in this regard [28]. Furthermore, constructing a forecast model employing an artificial neural network (ANN) and adaptive neuro-inference system (ANFIS) is likewise a complex and lingering task owing to an enormous number of trial results [29,30]. Under this situation, a fuzzy inference system (FIS) is the scientific and technical option for quality modeling, as it executes very well through limited amounts of trial data in a non-linear, trial-and-error, and intricate textile area [21,31]. Furthermore, compared to other models, a fuzzy logic model is more reasonable, less expensive to design and generally easier to implement [32,33].
In this work, a fuzzy model was built to predict the quality ratio of the jute yarn. The quality ratio is one of the properties of jute yarn that indicates the breaking load. It is the percentage ratio of single yarn strength in pound (lb) and yarn count in lb/spyndle (1 spyndle = 14,400 yards). Yarn with a better-quality ratio demonstrates greater yarn strength [34,35]. Therefore, an attempt has been made in the current study to build a fuzzy logic expert model using the Mamdani method for predicting of the strength of jute yarn that has not been mentioned in the past studies so far. This fuzzy prediction model can be used to modify spinning process parameters to achieve the desired yarn strength, i.e., quality ratio, as a decision-making support tool for jute spinners before the process is started to generate a better-quality yarn as per the buyer’s requirements.
2. Materials and Methods
2.1. Materials
The jute plants of variety C-145, Bangle white-B (BWB) (Corchorus capsularis) were collected from Bangladesh Jute Research Institute (BJRI), Dhaka and retted for 14 days under fresh water. The fibers were extracted and dried at room temperature. The consequent fibers were used as fibrous raw materials for producing of yarn counts 173 (5 lb/spyndle) and 241 (7 lb/spyndle) tex, respectively (count in tex system = lb/spyndle × 34.45).
2.2. Yarn Preparation
The yarn samples were developed at the Textile-Jute spinning mills, Daulatpur, Khulna, Bangladesh. For processing the raw jute, the fibers were passed through a jute softener machine with a 25% emulsion by weight of the fiber. To soften the fibers, a mixture of 79% water, 1.5% emulsifier, and 19.5% JBO was added for this purpose. The soft jute fibers were stored in a bin for conditioning of 48 h as generally performed in jute spinning mills and these pilled fibers were processed using a traditional sequence of the jute processing system [36]. Figure 1a,b shows the raw jute fiber and jute sliver, respectively. To produce 173 and 241 tex yarns, the finisher draw frame sliver was spun using a jute flyer spinning frame. The machine was operated to assess its performance using a variety of factors such as draft, twist, spindle speed, and so on. The yarn was spun in the flyer spinning frame using draft16, spindle speed 4200 rpm, and twist 354 tpm for the 173 tex and draft16, spindle speed 4500 rpm, and twist 354 tpm for the 241 tex.

Figure 1.
Experimental image; (a) raw jute fiber, (b) jute yarn sliver before spinning, (c) Testing of jute yarn using UTM machine and tearing of jute yarn after applying force (d).
2.3. Measurement of Quality Ratio (QR)
The properties of the produced yarn like tensile strength, extension at break and quality ratio were measured using the Universal Strength Tester (Titan2, UK) guided by ASTM, D2256, as shown in Figure 1c,d. ASTM D1907 was used to determine the linear density of the yarn. The twist per meter of the yarn was determined using a mechanical Shirley Twist Tester. The strength of the yarn was calculated using the following equation, which is also known as the quality ratio (equation1) [37,38]. All tests were evaluated at a standard testing atmosphere i.e., 65 ± 2% RH and 20 ± 2 °C temperature for 48 h [39].
Quality ratio% = (Single yarn strength in lb)/(Jute yarn count in lb/spyndle) × 100
2.4. Development of Fuzzy Modelling for Jute Yarn Quality Ratio
In this study, two different yarn counts (173 and 241 tex) were modeled using the MATLAB R2017a (9.2.0.538062) fuzzy logic toolbox to determine the quality ratio based on the four input parameters, viz. L.B, S.B, T.B and T.M. For modeling, the fuzzy ‘AND’ operator, the implication operator (min), the aggregation method (max) and the defuzzification method (centroid) were applied. Although there are various choices for the membership function in MATLAB, only Gaussian and Triangular membership functions were selected, as demonstrated in Figure 2 and Figure 3. Three and five linguistic values were chosen, respectively, for the input and output parameters, as shown in Table 1. As there are four input parameters and each input parameter has three linguistic values, a total of 81 (3C1 × 3C1 × 3C1 × 3C1) rules are created. The linguistic variables and 81 rules were created based on the knowledge of the expert system, experimental data, and previous experience. For simplification, here only 27 rules are mentioned in matrix form, as shown in Table 2. Here, Table 1 shows the input and output ranges for modeling of jute yarn quality ratio.
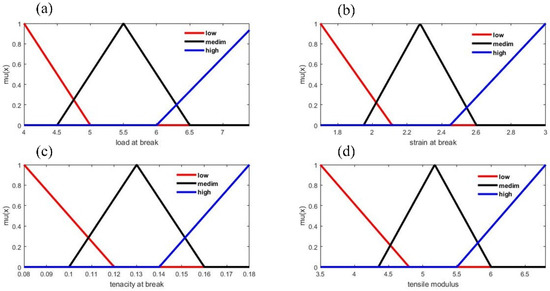
Figure 2.
Triangular membership function for the input parameters; (a) load at break, (b) strain at break, (c) tenacity at break, and (d) tensile modulus.
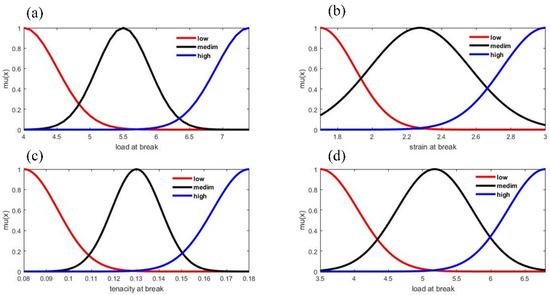
Figure 3.
Gaussian membership function for the input parameters; (a) load at break, (b) strain at break, (c) tenacity at break, and (d) tensile modulus.

Table 1.
Fuzzy Inference System (FIS) properties.

Table 2.
Fuzzy Inference rules for input and output parameters.
3. Results and Discussion
3.1. Operation of Fuzzy Prediction Model
In the fuzzy logic toolbox, we input the non-fuzzy value and receive the output as a non-fuzzy form. However, the internal processing is performed by a fuzzy inference system. It is called the heart of fuzzy logic system which performs from fuzzification through defuzzification. Figure 4 illustrates the operation of the fuzzy inference system. The fuzzy inference system works into five parts: (i) fuzzify the non-fuzzy input by determining the degree of membership function; (ii) application of fuzzy if-then rules; (iii) determine the fuzzy output of each rule by implication method; (iv) aggregating the outputs of each rule to convert a single fuzzy output and (v) defuzzify the final output into a non-fuzzy value.
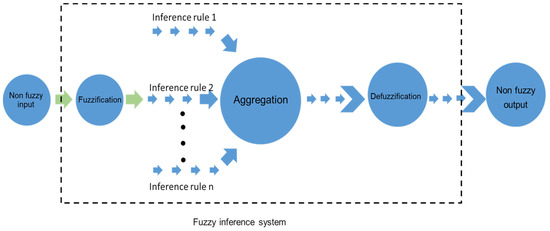
Figure 4.
Fuzzy inference system.
Figure 5 and Figure 6 represent the schematic diagram of the fuzzy inference process and the MATLAB rule viewer of the quality ratio of the jute yarn. The MATLAB rule viewer is a graphical representation that shows the final result against the input values. In the rule viewer, if we input any value within the range that was assigned to the four inputs, all 81 rules will be evaluated simultaneously and finally give the output quality ratio within the range (81–104). According to Figure 6, it can be said that if the load at break is 5.5, strain at break is 2.27, tenacity at break is 0.107 and tensile modulus is 5.77 then all rules will be reviewed and finally the jute yarn quality ratio is shown to be 92.40.
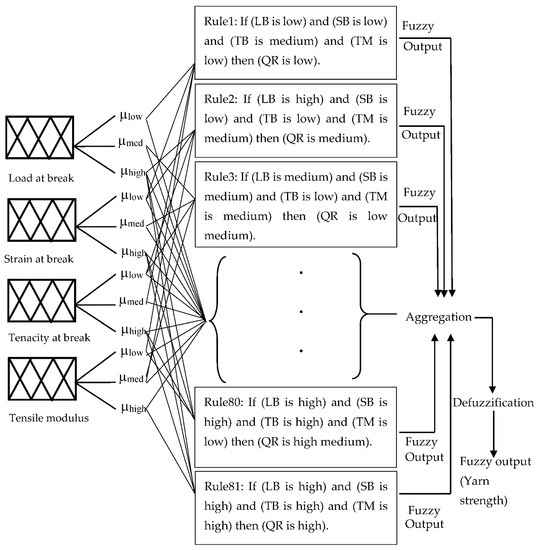
Figure 5.
Construction of FIS Model.
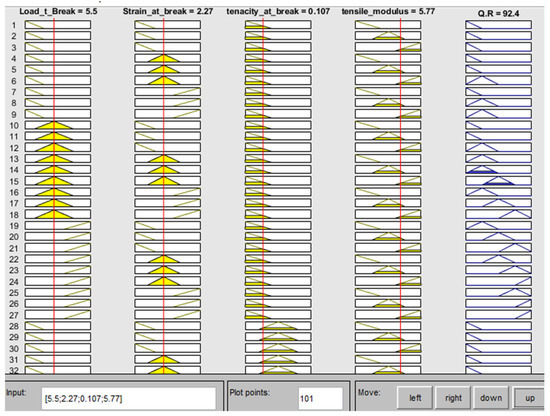
Figure 6.
MATLAB rule viewer of quality ratio.
To illustrate the fuzzy operation process, here only 14 and 15 number rules are discussed in the case of triangular membership function for the input values 5.5, 2.27, 0.107, 5.77 due to avoiding complexity.
- (i)
- Fuzzification process or determine membership degrees
The degrees of membership of the triangular membership function can be determined by the following equations for the given input ranges (Table 1).
For input values 5.5, 2.27, 0.107, 5.77; membership degrees are μL(LB) = 0, μM(LB) = 1, μH(LB) = 0; μL(SB) = 0, μM(SB) = 0.98, μH(SB) = 0; μL(TB) = 0.33, μM(TB) = 0.233, μH(TB) = 0, μL(TM) = 0, μM(TM) = 0.28, μH(TM) = 0.21.
- (ii)
- Fuzzy if-then rules
Rule 14: If the load at break is medium and the strain at break is medium and the tenacity at break is low and the tensile modulus is medium then the quality ratio is low medium.
μM(LB) and μM(SB) and μL(TB) and μM(TM)µLM(QR)
Rule 15: If the load at break is medium and the strain at break is medium and the tenacity at break is low and the tensile modulus is high, then the quality ratio is medium.
μM(LB) and μM(SB) and μL(TB) and μH(TM)µM(QR)
- (iii)
- Determine fuzzy output by implication method (min)
For rule 14: min(μM(LB) and μM(SB) and μL(TB) and μM(TM))µLM(QR)
= min(μM(5.5), μM(2.27), μL(0.107), μM(5.77))µLM(QR)
= min (1, 0.98, 0.33, 0.28)µLM(QR)
= 0.28 µLM(QR)
For rule 15: min(μM(LB) and μM(SB) and μL(TB) and μH(TM))µM(QR)
= min(μM(5.5), μM(2.27), μL(0.107), μH(5.77))µM(QR)
= min (1, 0.98, 0.33, 0.21)µM(QR)
= 0.21 µM(QR)
- (iv)
- Aggregation(max) of 14 and 15 rules only
Max(min(μM(5.5), μM(2.27), μL(0.107), μM(5.77)), min(μM(5.5), μM(2.27), μL(0.107), μH(5.77))
= Max (min (1, 0.98, 0.33, 0.28), min (1, 0.98, 0.33, 0.21)
= Max (0.28, 0.21)
= 0.28
- (v)
- Defuzzification (centroid)
This aggregated fuzzy output was finally defuzzified by the centroid method and provided the final result. The defuzzified value can be calculated by the following equation:
Here, bi belongs to the ith universe and μi is the firing strength of truth values of rule i (i = 1, 2 … n and n = number of observations) [40].
3.2. Influence of Input Parameters on Jute Yarn Quality Ratio
Figure 7, Figure 8, Figure 9 and Figure 10 demonstrate the impact of the physical properties of the jute yarn on the quality ratio. From Figure 7, for both the triangular and gaussian membership functions, it can be perceived that the quality ratio of the jute increases with the increase of LB, and SB and the quality ratio touches the highest peak when both input values reach their optimum level.
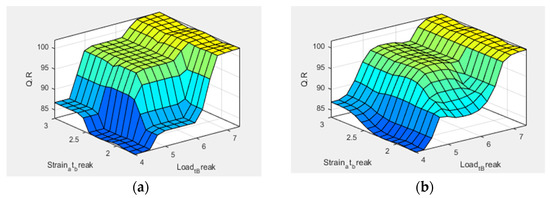
Figure 7.
Surface view of load at break (X-axis) and strain at break (Y-axis) effect on jute yarn quality (Z-axis); (a) for triangular membership function and (b) gaussian membership function.
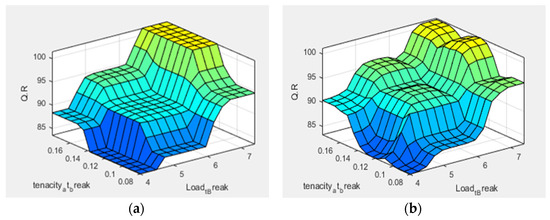
Figure 8.
Surface view of load at break (X-axis) and tenacity at break (Y-axis) effect of jute yarn quality (Z-axis); (a) for triangular membership function and (b) gaussian membership function.
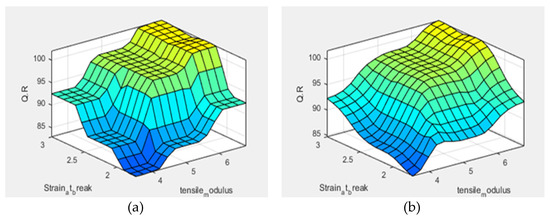
Figure 9.
Surface view of tensile modulus (X-axis) and strain at break (Y-axis) effect on jute yarn quality (Z-axis); (a) for triangular membership function and (b) gaussian membership function.
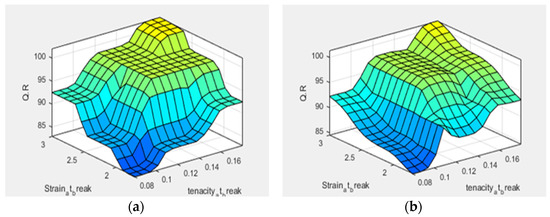
Figure 10.
Surface view of tenacity at break (X-axis) and strain at break (Y-axis) effect on jute yarn quality (Z-axis); (a) for triangular membership function and (b) gaussian membership function.
However, the individual effect of LB and SB on the quality ratio is different. For both triangular and Gaussian membership functions, the jute yarn quality remains at 85 to 90 when strain at break reaches the highest value which elucidated the lower impact of strain at break on the quality of the jute yarn. On the other hand, jute yarn quality reaches its highest value, when load at break is at its optimum level which has proved that the load at break has a greater impact on the quality of the jute yarn.
Figure 8 illustrates that the quality ratio remains low when LB and TB are at their minimum values for both the triangular and gaussian membership functions. However, the quality ratio increases significantly with the increase in load at break compared to the tenacity at break. For triangular and gaussian membership functions, quality ratio increases from 83.40 to 94.5 and 84 to 95.40 for raising the value of LB from 4.40 to 6.75, respectively.
From Figure 9 it can be said that tensile modulus and strain at break have almost a similar effect on yarn quality ratio for both triangular and gaussian membership functions. The quality ratio fluctuates between 90 and 95, when the tensile modulus or the strain at break reaches its maximum value. The quality ratio increases concomitantly and reaches its highest peak when TM and SB reach their maximum value.
From Figure 10, it can be concluded that tenacity at break and strain at break have approximately a similar effect on the quality ratio of the jute yarn for the triangular and gaussian membership functions. Moreover, when TB and SB are at their maximum value, the quality ratio also reaches the peak point.
3.3. Model Validation
The authors developed the prediction model of the quality ratio of the jute, which is based on two yarn counts: 173 tex and 241 tex. These prediction models were carried out by comparing the actual value, which is determined in the laboratory, and the fuzzy value. During the laboratory experiment, the draft (16) and the TPM (354) were kept constant for both counts of yarn. The model accuracy of the fuzzy expert system is calculated by the coefficient (R2) correlation and the mean absolute error% of the real and forecast consistency ratio of the yarn. The results are provided in Table 3 and are also shown in Figure 11. It is noted that correlation coefficients (R2) are found to be 0.93 for both triangular membership and gaussian membership. That means that the proposed fuzzy model can be explained up to 93% by the triangular membership and gaussian membership function for both yarn counts. In the case of 173 tex and 241 tex, Table 3 shows that the mean absolute error for triangular and gaussian membership functions is 1.46 and 1.48, respectively. This error% is less than acceptable limits (5%). Therefore, the validation of our developed fuzzy model will be applicable in the industrial scale for predicting the quality of the jute yarn.

Table 3.
Prediction of jute yarn strength.
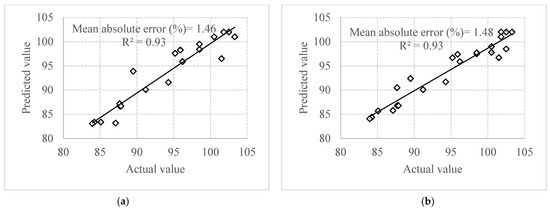
Figure 11.
Correlation between actual and predicted yarn quality ratio using triangular membership function (a) and gaussian membership function (b).
4. Conclusions
A fuzzy modeling system has been built to model the quality ratio of the jute yarn. For the fuzzy model, the load at break, the strain at break, the tenacity at break and the tensile modulus of the jute yarn were used as input parameters and the quality ratio (%) was selected as the output parameter.
- The proposed model shows that the load at break greatly affects the jute yarn quality such as strain at break, tenacity at break, and tensile modulus. Although the proposed fuzzy model showed that (S.B and T.M), and (S.B and T.B) together account for the highest value of yarn quality. Therefore, the presented fuzzy model gives clear explanations of the interaction between the input variables and their effect on the jute yarn quality.
- For both the triangular and the gaussian membership function, the correlation coefficient was 0.93. This means that the developed fuzzy model can predict up to 93% of total jute yarn quality.
- In the case of varying spindle speed, for both yarn counts, the mean relative error was found to be 1.46% (triangular membership) and 1.48% (gaussian membership), respectively, which validates the model’s relative effectiveness for an industrial application, although triangular membership functions show a slight good result in terms of prediction error% than gaussian membership function.
- It can therefore be entirely assumed that the established intelligent fuzzy model can be applied as an effective tool for satisfactorily predicting the quality ratio of jute yarns before bulk production which can minimize the time, costs, and wastage of jute yarn production. The proposed fuzzy model will be very useful for spinners and textile researchers in the field of yarn engineering, particularly for jute yarn manufacturing.
Author Contributions
Conceptualization, T.K.P., M.S.P. and M.A.J.; methodology, T.K.P. and T.I.J.; software, T.K.P., T.I.J. and I.H.; validation, M.S.P., M.A.A. and T.I.; formal analysis, T.K.P., M.R.R. and M.A.J.; investigation, T.K.P., M.S.P. and M.R.R.; resources, M.R.R., M.A.A. and I.H.; data curation, T.K.P., M.S.P. and T.I.; writing—original draft preparation, T.K.P., M.R.R. and M.A.A.; writing—review and editing, M.R.R., I.H., M.A.A. and T.I; visualization, T.K.P., M.R.R. and M.A.J.; supervision, M.R.R. and M.A.J.; project administration, M.R.R. and M.A.J.; funding acquisition, M.A.J. All authors have read and agreed to the published version of the manuscript.
Funding
The authors received no financial support for the research, authorship, and/or publication of this article.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Technical supports from the “ZR Research Institute for Advanced Materials”, Sherpur-2100, Bangladesh, are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
Load at Break: LB; Strain at Break: SB; Tenacity at Break: TB; Tensile Modulus: TM; Artificial Intelligence: AI; Artificial neural network: ANN; Adaptive neuro-inference system: ANFIS; Fuzzy inference system: FIS; Quality ratio: QR.
References
- Karimah, A.; Ridho, M.R.; Munawar, S.S.; Adi, D.S.; Damayanti, R.; Subiyanto, B.; Fatriasari, W.; Fudholi, A. A review on natural fibers for development of eco-friendly bio-composite: Characteristics, and utilizations. J. Mater. Res. Technol. 2021, 13, 2442–2458. [Google Scholar] [CrossRef]
- Wang, H.; Memon, H.; Hassan, E.A.M.; Miah, M.S.; Ali, M.A. Effect of Jute Fiber Modification on Mechanical Properties of Jute Fiber Composite. Materials 2019, 12, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cejudo-Bastante, C.; Arjona-Mudarra, P.; Fernández-Ponce, M.T.; Casas, L.; Mantell, C.; Martínez de la Ossa, E.J.; Pereyra, C. Application of a Natural Antioxidant from Grape Pomace Extract in the Development of Bioactive Jute Fibers for Food Packaging. Antioxidants 2021, 10, 2. [Google Scholar] [CrossRef] [PubMed]
- Saikia, M.; Gogoi, N.; Bhuyan, S.; Babu, V.R.; Ariharasudhan, S. Evaluation of Physical and Mechanical Properties of Bhindi Jute- Blended Fabric and Development of Eco Friendly Products. J. Nat. Fibers. 1978, 48, 701–705. [Google Scholar] [CrossRef]
- Midha, V.K.; Joshi, S.; Kumar, S.S. Performance of Chemically Treated Jute Geotextile in Unpaved Roads at Different in situ Conditions. J. Inst. Eng. 2017, 98, 47–54. [Google Scholar] [CrossRef]
- Gupta, S.; GuhaRay, A.; Kar, A.; Komaravolu, V.P. Performance of alkali-activated binder-treated jute geotextile as reinforcement for subgrade stabilization. Int. J. Geotech. Eng. 2021, 15, 299–312. [Google Scholar] [CrossRef]
- Mlýnek, J.; Petrů, M.; Martinec, T.; Koloor, S.S.R. Fabrication of high-quality polymer composite frame by a new method of fiber winding process. Polymers 2020, 12, 5. [Google Scholar] [CrossRef]
- Mlýnek, J.; Koloor, S.S.R.; Martinec, T.; Petrů, M. Fabrication of high-quality straight-line polymer composite frame with different radius parts using fiber winding process. Polymers 2021, 13, 1–17. [Google Scholar] [CrossRef]
- Shahinur, S.; Sayeed, M.M.A.; Hasan, M.; Sayem, A.S.M.; Haider, J.; Ura, S. Current Development and Future Perspective on Natural Jute Fibers and Their Biocomposites. Polymers 2022, 14, 1445. [Google Scholar] [CrossRef]
- Murugesh, B.K.; Selvadass, M. Influence of wet processing on properties of single jersey knitted fabrics. Int. J. Fiber Text. Res. 2013, 3, 18–30. [Google Scholar]
- Jamshaid, H.; Hussain, T.; Malik, Z.A. Comparison of regression and adaptive neuro-fuzzy models for predicting the burst-ing strength of plain knitted fabrics. Fibers Polym. 2013, 14, 1203–1207. [Google Scholar] [CrossRef]
- Hunter, L. Prediction of cotton processing performance and yarn properties from HVI test results. Melliand Textilber. 1988, 69, E123–E124. [Google Scholar]
- Mogahzy, Y.E.E. Selecting Cotton Fiber Properties for Fitting Reliable Equations to HVI Data. Text. Res. J. 1988, 58, 392–397. [Google Scholar] [CrossRef]
- Hafez, O.M.A. Yarn-strength prediction of American cottons. Text. Res. J. 1978, 48, 701–705. [Google Scholar] [CrossRef]
- Smith, B.; Waters, B. Extending Applicable Ranges of Regression Equations for Yarn Strength Forecasting. Text. Res. J. 1985, 55, 713–717. [Google Scholar] [CrossRef]
- Bogdan, J.F. The Characterization of Spinning Quality. Text. Res. J. 1956, 26, 720–730. [Google Scholar] [CrossRef]
- Bogdan, J.F. The Prediction of Cotton Yarn Strengths. Text. Res. J. 1967, 37, 536–537. [Google Scholar] [CrossRef]
- Frydrych, I. A New Approach for Predicting Strength Properties of Yarn. Text. Res. J. 1992, 62, 340–348. [Google Scholar] [CrossRef]
- Zurek, W.; Frydrych, I.; Zakrzewski, S. A Method of Predicting the Strength and Breaking Strain of Cotton Yarn. Text. Res. J. 1987, 57, 439–444. [Google Scholar] [CrossRef]
- Subramanian, T.A.; Ganesh, K.; Bandyopadhyay, S. A generalized equation for predicting the lea strength of ring-spun cot-ton yarns. J. Text. Inst. 1974, 65, 307–313. [Google Scholar] [CrossRef]
- Majumdar, A.; Ghosh, A. Yarn strength modelling using fuzzy expert system. J. Eng. Fiber. Fabr. 2008, 3, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, M.C.; Rajamanickam, R.; Jayaraman, S. The prediction of yarn tensile properties by using artificial neural net-works. J. Text. Inst. 1995, 86, 459–469. [Google Scholar] [CrossRef]
- Cheng, L.; Adams, D.L. Yarn Strength Prediction Using Neural Networks: Part I: Fiber Properties and Yarn Strength Rela-tionship. Text. Res. J. 1995, 65, 495–500. [Google Scholar] [CrossRef]
- Zhu, R.; Ethridge, M.D. The prediction of cotton yarn irregularity based on the ‘AFIS’ measurement. J. Text. Inst. 1996, 87, 509–512. [Google Scholar] [CrossRef]
- Zhu, R.; Ethridge, M.D. Predicting Hairiness for Ring and Rotor Spun Yarns and Analyzing the Impact of Fiber Properties. Text. Res. J. 1997, 67, 694–698. [Google Scholar] [CrossRef]
- Majumdar, A.; Majumdar, P.K.; Sarkar, B. Application of an adaptive neuro-fuzzy system for the prediction of cotton yarn strength from HVI fibre properties. J. Text. Inst. 2005, 96, 55–60. [Google Scholar] [CrossRef]
- Guha, A.; Chattopadhyay, R.; Jayadeva. Predicting Yarn Tenacity: A Comparison of Mechanistic, Statistical, and Neural Network Models. J. Text. Inst. 2001, 92, 139–145. [Google Scholar] [CrossRef]
- Hussain, T.; Safdar, F.; Nazir, A.; Iqbal, K. Optimizing the shrinkage and bursting strength of knitted fabrics after resin fin-ishing. J. Chem. Soc. Pakistan 2013, 35, 1451–1456. [Google Scholar]
- Hossain, I.; Hossain, A.; Choudhury, I.A. Color strength modeling of viscose/Lycra blended fabrics using a fuzzy logic approach. J. Eng. Fiber. Fabr. 2015, 10, 158–168. [Google Scholar] [CrossRef]
- Hossain, I.; Hossain, A.; Choudhury, I.A.; Mamun, A.A. Fuzzy knowledge based expert system for prediction of color strength of cotton knitted fabrics. J. Eng. Fiber. Fabr. 2016, 11, 33–44. [Google Scholar]
- Hossain, I.; Choudhury, I.A.; Mamat, A.B.; Shahid, A.; Khan, A.N.; Hossain, A. Predicting the Mechanical Properties of Vis-cose/Lycra Knitted Fabrics Using Fuzzy Technique. Adv. Fuzzy Syst. 2016, 2016, 3632895. [Google Scholar]
- Vadood, M. Predicting the color index of acrylic fiber using fuzzy-genetic approach. J. Text. Inst. 2014, 105, 779–788. [Google Scholar] [CrossRef]
- Hatua, P.; Majumdar, A.; Das, A. Modeling ultraviolet protection factor of polyester-cotton blended woven fabrics using soft computing approaches. J. Eng. Fiber. Fabr. 2014, 9, 99–106. [Google Scholar] [CrossRef]
- Jalil, M.A.; Sinha, R.C.; Islam, M.K. Analysis of jute yarn quality by the change of drafting zone of third drawing frame. J. Innov. Dev. Strateg. 2010, 4, 18–22. [Google Scholar]
- Jalil, M.A.; Sinha, R.C.; Mahabubuzzaman, A.K.M.; Rokonuzzaman, M. A comparative study on the quality control of fine jute yarn conventional drawing method vs modified drawing method. Int. J. Text. Fash. Technol. 2011, 1, 1–10. [Google Scholar]
- Jalil, M.A.; Sinha, R.C.; Mahabubuzzaman, A.K.M.; Hossain, M.M.; Idris, M.A. Study on Physical and Structural Properties of Jute-Palf Blended Yarn Spun by Apron Draft Spinning. Res. J. Text. Appar. 2015, 19, 9–15. [Google Scholar] [CrossRef]
- Jalil, M.A.; Parvez, M.S.; Siddika, A.; Rahman, M.M. Characterization and Spinning Performance of Pineapple Leaf Fibers: An Economic and Sustainable Approach for Bangladesh. J. Nat. Fibers 2021, 18, 1128–1139. [Google Scholar] [CrossRef]
- Jalil, M.A.; Moniruzzaman, M.; Parvez, M.S.; Siddika, A.; Gafur, M.A.; Repon, M.R.; Hossain, M.T. A novel approach for pineapple leaf fiber processing as an ultimate fiber using existing machines. Heliyon 2021, 7, e07861. [Google Scholar] [CrossRef] [PubMed]
- Booth, J.E. Principle of Textile Testing; CBS Publishers & Distributers: New Delhi, India, 1996. [Google Scholar]
- Hossain, I.; Uddin, H.; Hossain, A.; Jalil, M.A.; Uddin, Z. Modelling the effect of resin-finishing process variables on the di-mensional stability and bursting strength of viscose plain knitted fabric using a fuzzy expert system. Tekstilec 2021, 64, 119–135. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).