Abstract
In some cases, the water content in granular soil increases to the extent that it becomes saturated, which noticeably alters its responses. For example, the pore water pressure within saturated granular soil would increase rapidly under sudden external loading, which is equivalent to undrained or constant volume conditions. This reduces the effective stress in soil dramatically and may result in catastrophic failure. There have been different numerical approaches to analyse such a failure mechanism of soil to provide a deeper understanding of soil behaviour at the microscopic level. One of the most common numerical tools for such analysis is the discrete element method (DEM) due to its advantage in obtaining microscopic properties (e.g., statistics on particle contacts and fabric), reproducibility and simple feedback control. However, most DEM studies ignore the fluid phase and merely consider the solid particles while the fluid pressure is indirectly calculated by mimicking undrained condition to a constant volume condition. Note that fluid’s influence does not limit to the change of pore water pressure. For example, the external loading would induce the movement of fluid, and the fluid-solid interaction could subsequently drag the solid particles to shift within the system. In addition, the state of soil could change from solid to suspension under an excess hydraulic gradient. Therefore, the study of the fluid-solid mixture is essential as it is a typical scenario in geotechnical practice, and the simulations of saturated sand should be conducted in numerical forms in which both the solid and fluid phases can be modelled.
1. Introduction
Soil is composed of discrete particles, and the effective stress in the soil is governed by the forces transferred internally through inter-particle contacts. The contact forces form the contact force network or internal structure, i.e., soil fabric. Traditionally, soil failure assessment has emerged in the literature including liquefaction analysis [1,2,3,4,5]. Been, et al. [6] emphasised that soil fabric could considerably influence the observed soil behaviour. However, the traditional applications of critical state theory do not capture the effect of soil fabric and other micromechanical parameters properly. Some previous works used the optical microscope to determine the orientation and distribution of grain particles on a small portion of the testing specimens [7]. Arthur and Dunstan [8] proposed that the particle packing (fabric) could be studied using radiography measurements to track the particle packing. These approaches can be expensive and may not satisfy the requirements in both quantity and quality because of difficulties with continuous measurement of the fabric. Furthermore, Arthur and Menzies [9] stated that the differences between radiographs can be hard to identify.
Microscopic information, including fabric, can be assessed using a numerical simulation and it can be an effective and economical tool for investigating soil behaviour [10,11,12,13,14,15]. The capability of eliminating additional variables and focusing on important factors makes the numerical solution scheme ideal [16]. Gong [17] stated that compared to physical models, the boundary conditions in numerical models could be better controlled and boundary effects could be almost eliminated. The modelling data could be assessed at any stage of the test [18]. Due to such advantages, an increasing number of studies on soil behaviour are undertaken by numerical simulations [18,19,20,21,22].
The Discrete Element Method (DEM) proposed by Cundall and Strack [18] is such a numerical tool and has been widely used for simulating discontinuous materials and the dynamic movement of particles for sands, sand with fines, etc. [10,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Dinesh, et al. [41] stated DEM has the advantages of collecting micromechanical and statistical information (e.g., internal stress, contact behaviour) in addition to the macroscopic properties, and the simulation results are reproducible. Sitharam, et al. [42] used 3D DEM simulations for spherical particles to investigate post-liquefaction undrained behaviour. Kuhn, et al. [43] discovered the influence of Hertz-Mindlin contact model parameters during cyclic simple shear simulation of an assembly of 3D angular particles and suggested that DEM is suitable for cyclic liquefaction studies and offers certain advantages over laboratory experiments. Huang, et al. [44] investigated the qualitative behaviour of 2D angular particles under monotonic and cyclic direct shear.
One of the contributors to the failure of geomaterials is the development of excess pore water pressure between the particles. However, the majority of conventional DEM studies did not consider any physical fluid between the discrete particles and only used mathematical relationships for effective stress calculations to estimate the excess pore water pressure [42,45,46,47]. This may not always be ideal for capturing the representative behaviour of geomaterials, as the interaction between fluid and solid at their interface is more complicated. Since the conventional DEM lacks the capacity to simulate physical fluids, achieving a more realistic representation of behavior requires coupling DEM with another computational tool, such as Computational Fluid Dynamics (CFD), capable of accounting for fluid effects.
Therefore, there have been some developments in the coupling methods for DEM and CFD [21,28,48,49,50,51]. In CFD, an individual solid is divided into boundary nodes by the fluid grids and the hydrodynamic force is calculated by the movements of the boundary nodes. The coupling process of CFD and DEM depends on the interaction between fluids and particles, and particles and particles. Norouzi, et al. [52] mentioned there are four different methods of coupling, namely, one-way (effect of fluids on particles), two-way (effect of fluids on particles and vice versa), three-way (effect of fluids on particles and vice versa, and disturbance of fluids on particles) and four-way coupling (effect of fluids on particles and vice versa, disturbance of fluids on particles, and interparticle reactions). The details of these methods can be found in the following sections. However, CFD has the challenge of finding the appropriate drag coefficient for the drag forces in the system, as there are different variations of drag coefficients in the literature [53,54,55,56,57,58]. So, a comparative study should be conducted to evaluate the efficiency of these methods, and it requires a new calculation algorithm for this problem.
Due to some shortcomings of the current DEM studies in geotechnics and the challenges of implementing physical fluids into the DEM model, this literature review paper would like to revisit some important studies in CFD and DEM to explore a new technique to solve this problem.
2. Traditional Discrete Element Method (DEM)
The DEM approach was originally developed by Cundall and Strack [18] to use for analysing rock. But later, this tool has been widely used in granular materials [40,45,59,60,61,62,63]. DEM can reproduce a grain size distribution, illustrate force chain networks, access micromechanical properties of particle contacts, and trace the evolution of the contacts. A contact is defined as the interaction between two components that comply with Newton’s laws of motion, and it is dynamically created and destroyed throughout the simulation [64]. Cundall and Hart [65] pointed out that the representation of contacts and the determination of contacts are significant when utilising the DEM program. The DEM model follows an explicit numerical scheme, particles and contacts are tracked individually at each timestep [18]. The particle movement follows Newton’s second law of motion, and contact is generated when the particles overlap [41]. The magnitude of contact force is calculated using the force-displacement law [18]. The contact model in DEM can be illustrated as shown in Figure 1.
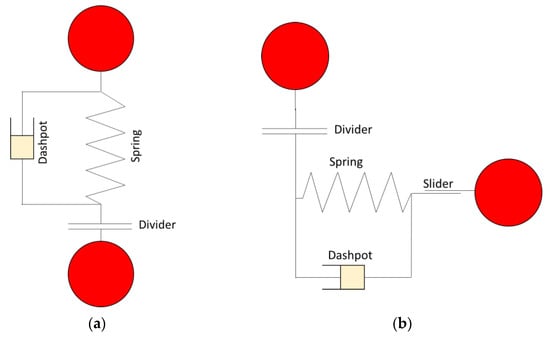
Figure 1.
A typical DEM contact model: (a) normal and (b) tangential contacts.
In DEM, there are two different methods to calculate the contact forces, linear and non-linear [40,45,59,60,61,62,63]. Linear model considers linear relationship between contact overlap/deformation and contact force, whereas non-linear model adopts non-linear calculations for contact forces. It worths noting that neither linear nor non-linear contact models can be able to perfectly capture the complexity of soil behaviour. Therefore, the selection of contact model mostly depends on research interest and computational time.
There are extensive DEM studies on the behaviour of granular soils in the past decades [17,18,66,67,68,69,70,71,72,73,74,75]. Dinesh, Thallak and Vinod [41] assessed the dynamic properties and liquefaction behaviour of granular soils under undrained conditions. Their study showed the shear modulus tends to reduce, and the damping ratio would increase under large shear strain. In addition, they explained soil particles were reoriented under cyclic loading, and the loss in average coordination number during that process caused the later liquefaction. Gu, Huang and Qian [67] modified the initial densities and confining pressures in the drained and undrained triaxial tests and captured the evolution of micromechanical properties such as coordination number, contact force, and anisotropic behaviour of contacts. Their model showed state-dependent behaviour of granular soil under shear loading, including contractive and dilative behaviour and phase transformation, which verify the representative of the DEM approach. Nguyen, Rahman and Fourie [68] analysed the effect of isotropic and -consolidation paths on granular soil considering the constant volume triaxial compression simulations. The authors considered a wide range of and and found a unique critical state line for different consolidation conditions. Moreover, they examined the normalised anisotropic fabric variable () and the trace of the joint stress-fabric tensor (), and then stated the critical state value could be achieved for those micromechanical parameters as shearing continues. Therefore, DEM can be a suitable tool for the study of soil stress-strain behaviour and fabric evolution. An example of the constant volume triaxial test of soil in DEM is represented in Figure 2. In such a test, the incremental strain is applied in the vertical direction, and the strains in lateral directions are adjusted to keep the volume constant. The arrows showed the directions of strains.
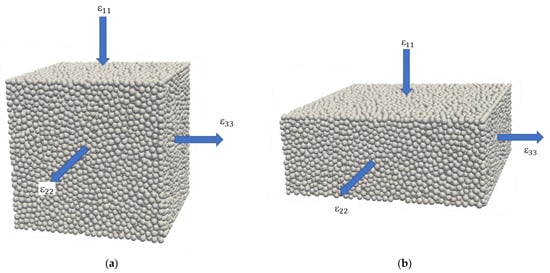
Figure 2.
Triaxial test in DEM: (a) before shearing and (b) after shearing.
Apart from simulating the element test, DEM has been also used to replicate the field test such as CPT [23,76,77,78]. Jiang, Dai, Cui, Shen and Wang [77] applied various friction coefficients between the cone and particles. Additionally, CPT penetrations were performed under different insertion angles instead of the standard downward direction. The authors then explored the CPT responses such as the velocity and displacement of particles and the evolution of principal stress orientation during the penetration process. Ciantia, et al. [79] examined the effect of grain crushing on the cone tip resistance during CPT by using crushable microporous granular material. The specimens were set to different densities and various confining stresses were applied. The authors investigated the micromechanical behaviour and found that the difference between the contact force networks of the crushable and non-crushable loose specimens is unnoticeable; however, for denser specimens, a significantly larger cluster of high-stress particles could be observed in the non-crushable specimens. Furthermore, they pointed out that the buttressing effect on the cone was influenced due to particle’s sudden breakdown. It should be noted the sand is assumed as uncrushable in this project. Khosravi, Martinez and DeJong [23] examined the effect of several modelling parameters by conducting CPT in a virtual calibration chamber (VCC), and microscopic parameters including interparticle force, particle orientation, and force chain were analysed. The authors emphasised the importance of interparticle contacts, chamber boundary conditions and sample void ratio as these features would significantly influence the CPT response. The above studies showed DEM could provide promising results and interpretations at both macro and micro levels when applied to CPT. However, none of the above research followed the CSSM framework to evaluate the liquefaction protentional of tested soil, which remains the current research gap. In addition, the studies above did not consider physical fluid inside the specimen, and the pore water pressure was calculated based on the theoretical effective stress calculation. Therefore, this framework is controversial as particles could be affected by forces such as drag force and buoyancy force when they are immersed in the fluid field.
3. Computational Fluid Dynamics (CFD) in DEM
3.1. Background of Fluid in Soil
The solid-fluid interactions could alter soil behaviour. For example, in the upward seepage flow problem, a critical flow velocity or hydraulic gradient could cause a quick condition or liquefaction [80]. Liquefaction occurs when the pore water pressure significantly increases within a short period due to external loading and results in a sudden drop of soil effective stress. Quicksand condition happens when the granular deposit is subjected to an upward pore fluid flow. Both conditions could trigger ground failure. Additionally, the pore fluid in a saturated granular will potentially fluctuate or flow under external loading and convey the soil particles into movement [81]. El Shamy and Zeghal [82] pointed out a considerable hydraulic gradient may transit the state of soil from solid to suspension, which will lower the soil strength.
3.2. History of Coupling Methods
Continuum theories of porous media, which include the interactions between pore fluids and particles, are commonly used. However, the interrelation at the microscopic level remains unclear [81]. The traditional analysis frequently uses macroscopic constitutive models and parameters, including soil weight and shear strength to address the microscopic interactions without direct interpretations of microscopic behaviour [83]. It should be noted this approach is limited to quasi-static cases in which the presence of the fluid is stabilised. Other analytical investigations containing solving governing equations have faced difficulties due to nonlinearities and complex boundary conditions. As for the cases that involve high hydrodynamic forces, a more advanced scheme that considers the skeleton deformation is needed [83]. It is widely accepted that the interparticle interactions along with solid-fluid interactions dominate the macroscopic mechanism of the compound [84]. From a micro-scale point of view, the energy is mainly dissipated through interparticle and particle-wall friction and collision in the ‘dry case’ (without the presence of fluid), on the other hand, there is a significant kinetic energy or momentum transfer between particles and fluid [85,86]. Moreover, for a partially drained saturated soil, pore water pressure increases as granular porosity reduce while it could simultaneously decrease due to pore drainage [87]. A numerical analysis scheme that allows access to microparameters and solid-fluid interaction is much needed for analysing solid-fluid mixture. The following sections will discuss some common approaches and formulations used in the solid-fluid mixture model.
It is also worth noting that in some approaches, the fluid is modeled either by smoothed-particle hydrodynamics (SPH) or Lattice Boltzmann method (LBM). SPH [88,89] is a computational technique in fluid dynamics, astrophysics, geophysics, and engineering simulations. SPH represents a continuous medium as discrete particle. SPH is a versatile numerical method that handles large deformations, fluid-solid interactions, and free surface flows. It is valuable for scientific and engineering applications because it can handle irregular geometries and adapt to resolution requirements. SPH uses particles to represent material properties like density, pressure, and velocity. Adaptive resolution improves accuracy and detail. Boundary modelling in SPH is challenging. Ghost or boundary particles can be used to handle boundary conditions. SPH uses smoothing kernels to interpolate particle properties from neighbouring particles. The choice of kernel affects accuracy and stability [88,89]. The coupling in DEM-SPH primarily relies on two methods, namely:
- -
- Direct Numerical Simulation (DNS): In this approach, the hydrodynamic forces acting on solid particles are determined by directly solving the Navier-Stokes (N-S) equations. One notable drawback of DNS is its demand for an exceedingly fine particle resolution, making it less practical for large-scale particle systems. Typically, empirical models are used to calculate hydrodynamic forces in this method [90,91].
- -
- Local Averaging Approach [92]: This method involves defining a smoothing operator like that used in Smoothed Particle Hydrodynamics (SPH). This operator is employed to calculate smoothing variables and local porosity fields. It does not define the interaction between DEM particles and SPH particles but relies on local averaging of liquid-to-solid particles and widely used.
On the other hand, LBM is a particle-based computational technique for simulating fluid dynamics. It simplifies Boltzmann’s kinetic theory of gases by discretising velocity space into a lattice structure and modelling particle interactions using collision rules. This makes it an efficient and accurate alternative to traditional CFD methods. LBM simulates both single-phase and multiphase flows, including interfaces and phase transitions. Various methods have been proposed to model the fluid-solid interactions using DEM-LBM. They included the drag force model [93], momentum exchange model [94], or Stokes drag force model [95] and immerse boundary method (IBM). The IBM is commonly used [96,97]. The momentum exchange of fluid density distribution function near the boundary is applied to calculate the coupling force and torque. It should be noted that this particle-based method is at the mesoscale. So it may not be representative of element soil test in geotechnical engineering.
3.2.1. Eulerian and Lagrangian Approach in Fluid Dynamics
The Eulerian-Eulerian and Eulerian-Lagrangian approaches are the two most commonly used methods for the solid-fluid mixture model. The representative of the solid-fluid modelling is particularly dependent on the estimation of interaction forces and the momentum transfer between solid and fluid phases. These two phases are considered as either continuous or discrete in the coupling scheme.
The purely Eulerian approach (Eulerian-Eulerian) considers both solid and fluid as continuous flow phases. To average the flow variables of the solid phase and fluid phase, the volume averaging method is commonly used. van Deemter and van der Laan [98] proposed the following relationship for fluid momentum using flow averaging:
where is the volume fraction of the solid particles, is the fluid density, is the velocity of the fluid, is the gravitational acceleration, is the pressure acting on the fluid, is the Kronecker delta, is the shear stress tensor, and is the force per unit volume acting on the fluid from the solid phase. Ibrahim and Meguid [83] pointed out the flow volume size could significantly affect the fluid velocity, , and the force acting on the fluid, , which could lead to unstable and unreliable results. Furthermore, they emphasised that for the cases involving turbulent flow, a single fluid velocity is not representative of the overall fluid flow.
As previously discussed, the micromechanical behaviour governs the overall soil behaviour. Tsuji, et al. [99] pointed out that despite the Eulerian-Eulerian approach requiring less computational time, the solid phase is oversimplified and has lost its discrete nature. On the other hand, the Eulerian-Lagrangian approach treats the solid phase as discrete particles and the fluid phase as a continuous flow. This feature increases the accuracy of the modelling due to the consideration of interparticle and particle-wall collisions [100]. The governing equations for the Eulerian-Lagrangian approach are different from the purely Eulerian approach as the solid particles are represented by discrete grains. The equation of continuity proposed by Anderson and Jackson [92] is given below:
where is the porosity of the granular packing, is the fluid density, is the time, and is the average velocity of a fluid cell. Navier-Stokes momentum equation is solved along with the continuity equation and is shown below [101]:
where is the stress tensor of the fluid field, is the gravitational acceleration, and is the volumetric fluid-particle interaction force. For laminar flow [101], the could be calculated as:
where is the fluid dynamic viscosity.
3.2.2. Coupling Scheme
One of the following numerical schemes can be applied in performing coupling depending on the different conditions of the solid-fluid mixture [52]. Figure 3 also demonstrated these coupling methods.
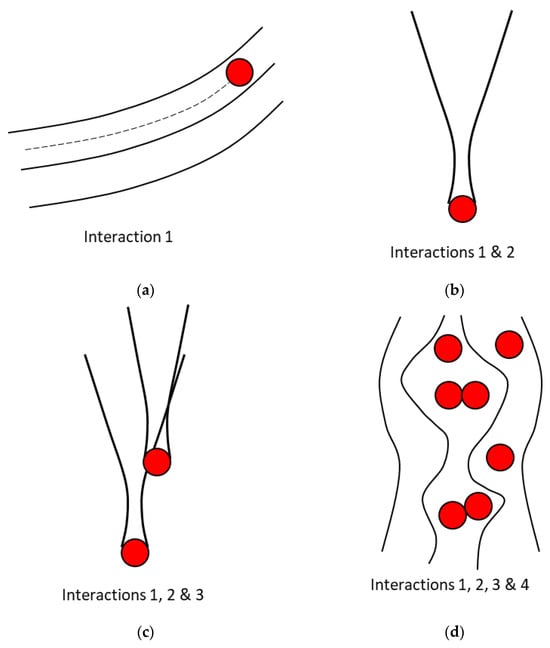
Figure 3.
Coupling methods in CFD-DEM: (a) One-way, (b) Two-way, (c) Three-way and (d) Four-way. Note: Interaction 1 is fluid affecting particle’s motion. Interaction 2 is particle motion affecting fluid’s motion. Interaction 3 is particle disturbance of the fluid affects another particle’s motion. Interaction 4 is interaction between particles.
One-way coupling: For a solid-fluid mixture with an insignificant portion of solid particles, the solid phase could be easily governed by the fluid phase while the inverse influence is negligible. This is referred to as one-way coupling in literature. In practice, the volume fraction of the solid particles in each fluid computational cell is first calculated based on their locations. The fluid flow is then resolved using the averaged Navier-Stokes equations and the continuity equations to compute the fluid forces acting on the solid particles. Afterward, the motion of the solid particle is computed under the Newtonian laws of motion. Lastly, the positions of the particles are updated, and a new iteration of the volume fraction is initiated. This loop continues until the predefined simulation time is achieved.
Two-way coupling: For a solid-fluid mixture with a denser solid concentration, the solid particles could alter flow behaviour and must be included in the coupling system. This is known as the two-way coupling. To execute the effect of particle motion on the fluid phase, the fluid flow is resolved once more before moving to the next iteration.
Three-way coupling: This method is similar to two-way coupling, but it considers the particle disturbance of the fluid locally affecting another particle’s movement.
Four-way coupling: For a solid-fluid mixture that contains a considerably high concentration of solid particles, the particle-particle interactions are required to be computed in addition to the correlative effects between solid and fluid phases. This is named four-way coupling and is one of the most common approaches to solving geotechnical problems given the typical high proportion of solid particles.
3.2.3. Particle/Mesh Size Ratio and Fluid Properties
The ‘resolved method’ and ‘unresolved method’ are the two standard techniques to solve solid-fluid coupling problems when using the Eulerian-Lagrangian approach. The resolved method assumes the particle size is significantly larger than the fluid mesh size, while the unresolved method represents the system containing a large number of particles inside each fluid element in the FEM mesh [102]. A graphic illustration is shown in Figure 4. In the resolved models, the solid-fluid interactions are evaluated by integrating the shear stresses over the surface of the solid [103]. Ibrahim and Meguid [83] pointed out that the resolved method could improve the model accuracy and determine the precise interaction force since the volume averaging method would not be utilized. However, the excessive computational demand would weaken its applicability in a denser particulate system. On the other hand, the fluid phase forces are averaged over the particles in unresolved cases. In addition, a critical ratio is required to reduce data fluctuation from determining solid volume fraction, as a single particle could be located across more than one fluid cell instead of fully immersed in one [104]. The volume fraction estimation is critical in the solid-fluid coupling as it determines the force impact from each phase. Kloss, et al. [105] recommended the size ratio of fluid mesh over particle should be over 10. A later study conducted by Zhao, Houlsby and Utili [53] suggested that the ratio could be reduced to 5 while obtaining a realistic particle settling velocity. For geotechnical problems, the unresolved method is commonly used as they often contain a high number of grains i.e., 18,000 particles [25,106,107,108].
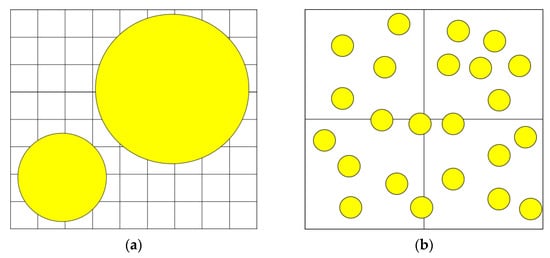
Figure 4.
Resolved (a) and unresolved (b) methods.
El Shamy and Zeghal [82] addressed that the pore fluid in the granular soils could be viewed as incompressible because the volumetric change of fluid is extremely small in comparison to soil. Furthermore, the fluid viscous shear stress could be ignored since the energy dissipation mainly occurs at fluid-particle interfaces [87].
3.2.4. Interaction Forces
The interaction forces between the solid phase and fluid phase could be categorised into two groups, namely hydrostatic force, and hydrodynamic force. The hydrostatic force includes the pressure gradient force, which is caused by the difference in pressure across a solid particle and implemented over the volume of the particle. According to Zhao, et al. [109], it can be calculated using the following equation
where is the volume of the particle, and is the pressure of the fluid flow. The buoyancy force is one of the primary forces of pressure gradient force, it can be calculated using [110]:
where is the diameter of the particle. It should be noted for an engineering-scale study, such as dam erosion or landslide, the gravitational force exists hence the consideration of buoyancy force, however, for simulations of laboratory studies such as triaxial tests, a zero-gravity environment is often implemented in the numerical study. As for the hydrodynamic force, the drag force is generally considered. This force is a result of viscous shearing and it is caused by the velocity differences between solid particles and the fluid field [83]. Theoretically, the drag force should be applied to the surface of the particle, however, it is a general practice that this force is assumed to act at the centre of the particle. Zhao, Houlsby and Utili [53] stated the orientation of the drag force is the same as the flow motion direction. The drag force could be expressed as [111]:
where and are the velocities of fluid and particle, respectively, and is the solid-fluid moment transfer coefficient. This parameter is derived from the experimental correlations by Ergun [56] and Wen and Yu [57], and could be expressed as:
Multiple expressions of drag force coefficient () have been proposed in the literature, and they are summarised in Table 1.

Table 1.
Summary of drag force coefficient in the literature.
is the Reynolds number which is used to predict the flow patterns in the fluid. It could be expressed as:
Kafui, et al. [112] stated the formulations proposed by Ergun [56] and Wen and Yu [57] are commonly followed depending on the solid concentration of the fluidised bed, and a void fraction of 0.8 is the border to determine whether the regime should be categorised as dense or dilute. The authors examined the superficial slip velocities of a sphere particle using the above two formulations and stated the step change inherent was not properly computed. They then claimed the formulation provided by Di Felice [113] could offer continuous results and therefore is suitable when applied to numerical analysis. Many recent CFD-DEM coupling studies have adopted this correlation in the geotechnical field [53,81,114], and the formulation is expressed:
The porosity correction function considers the presence of other particles. The expression of the term is:
Other hydrodynamic forces such as virtual mass force, Basset history force, and lift force are considerably neglectable compared to the drag force when the flow is relatively steady [115]. The illustration for hydrostatic (Buoyancy) and hydrodynamic (drag) forces are shown in Figure 5.
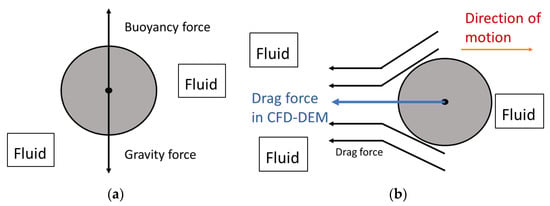
Figure 5.
(a) Hydrostatic force and (b) Hydrodynamic force.
3.2.5. Computing Interaction Force
The assigning of solid-fluid interaction forces is particularly dependent on the estimation of particle volume fraction and the location of the particles within a fluid cell. For the unresolved method which is applied to the majority of the geotechnical studies, the fluid cell is considerably larger than the solid particles and, commonly, the particles are located at the mesh boundary. To address this effect, the Centre Void Fraction method and the Divided Void Fraction method are the two most widely used methods [81]. For the Centre Void Fraction method, when the centre of one particle is in a fluid cell region, the whole volume of that particle will be considered within that specific cell. Although this method is straightforward and requires less computational effort, such an assumption will either overestimate or underestimate the void fraction within one cell and the variation could be severe depending on the cases. As for the Divided Void Fraction method, the precise volume of one particle immersed in the fluid cell would be calculated. Zhao and Shan [81] stated this method could provide more accurate results compared to the Centre Void Fraction method. However, the simulation efficiency would be dramatically reduced because of the extra calculation on immersed volume within each cell especially if it is a solid-fluid mixture with high solid concentration.
4. Coupling Technique for CFD and DEM
Anderson [116] stated the Computational Fluid Dynamic (CFD) could provide insights into the behaviour of the fluid flow and easily solve the flow problem if it is combined with appropriate governing flow equations. In addition, the author emphasised CFD is a computer program that is transportable and can be easily accessed remotely compared to the physical models. The CFD approach discretises the fluid domain into individual meshes and a locally average method is applied to determine the fluid properties including density, velocity, and pressure within a single cell [81]. It should be noted the fluid is assumed to be identical across all places within each mesh [53]. Zhu, Zhou, Yang and Yu [115] stated the CFD approach combined with DEM requires less computational resource and effort numerical-wise compared to its counterparts (e.g., Lattice-Boltzmann (LB) coupled DEM, Direct Numerical Simulation (DNS) coupled DEM). The CFD-DEM approach could fulfil the requirements of this project, which is to analyse the solid-fluid mixture following the Eulerian-Lagrangian approach, applying four-way coupling, and using the unresolved method. Furthermore, the microscopic parameters of both solid and fluid phases could be examined. The coupling CFD-DEM was first proposed by Tsuji, Kawaguchi and Tanaka [99] to solve a two-dimensional gas-fluidized bed problem. The interactions between gas and particle were considered and both the fluid phase and solid phase were analysed. Hager, Kloss, Pirker and Goniva [102] explained when applying CFD-DEM, the fluid movement is evaluated by the CFD solver and the motion of the immersed particle is determined by the DEM solver, respectively. Zhao and Shan [81] added that particle movement follows Newton’s equation, and the fluid flow complies with the Navier-Stokes equation. Furthermore, the interactions between the fluid phase and solid phase are tracked.
The CFD-DEM approach has been widely applied in the geotechnical field. Zeghal and El Shamy [87] investigated the liquefaction response of loose and cemented granular soils induced by dynamic base excitation in a saturated condition. The authors stated the numerical results were representative and showed qualitative mechanisms that are in line with the experimental data. The microscopic coordination numbers were examined and it was concluded the liquefaction started from the surface and then spread to the deeper ground. Zhao and Shan [81] used coupled CFD-DEM to investigate the formation of the sand heap in water that poured from a hopper and the effect of rolling resistance and polydispersity. The microscopic behaviour including contact force and fabric anisotropy were analysed in their study. It was found that the presence of water has led to different behaviour compared to the cases without water, that the pressure dip was reduced, the contact force chains were more vertically aligned, and the critical contact force was lower in magnitude. A similar study was conducted by Zhao, Houlsby and Utili [53] to investigate the batch sedimentation of granular particles in water. It was found the coarse grains tend to settle first and form the bottom part of the deposit. Zhang, Jiang and Thornton [108] considered the pore fluid as compressible and conducted undrained triaxial tests on granular soil using both the constant volume method and CFD-DEM coupling. In their study, the pore water pressure was calculated as the difference between the current effective confining stress and the initial effective confining stress at the start of triaxial shearing. The results from the same sample were compared between two approaches and it was found the novel CFD-DEM coupling method showed comparable qualitative behaviours. The authors also stated that under the assumption of constant fluid compressibility, the undrained behaviour of granular soil remained the same despite various initial pore pressures. Moreover, a unique relationship between the microscopic coordination numbers and excess pore pressure was identified. The undrained triaxial tests were also performed by Foroutan and Mirghasemi [25] on granular soil using the CFDEM program, which is a CFD-DEM solver introduced by Goniva, Kloss, Deen, Kuipers and Pirker [104]. Based on the CFDEM framework, they developed a new solver that incorporates fluid compressibility and mesh movement and then explored the effect of the intermediate stress ratio, at both macroscopic (e.g., excess pore water pressure) and microscopic (e.g., fabric anisotropy, contact force anisotropy tensor) levels. The numerical results were compared to the experimental data. With the support of numerical modelling, three-dimensional histograms were used to illustrate the contact forces in the granular assembly at the initial state, peak state, and residual state. In addition, the authors stated as increases from 0 to 1, the deviatoric coefficient of fabric anisotropy increases yet the same parameter for contact force anisotropy shows opposite behaviour. To conclude, it could be agreed that the CFD-DEM approach is a powerful tool to investigate solid-fluid mixtures and researchers are able to access valuable microscopic parameters. However, all the reviewed studies above do not analyse the liquefaction potential of granular soil under the CSSM framework. Additionally, limited literature was found on applying CFD-DEM in CPT. This remains the research gap in the current study hence the topic of this research project.
Ibrahim and Meguid [83] conducted an extensive literature review on the different approaches to reproducing solid-fluid mixtures in the geotechnical engineering field. They pointed out that the CFD-DEM approach is outstanding in providing microscopic information on solids, fluids, and their interactions; however, this merit requires the simulation of numerous individual elements, and the number could sometimes go up to billions in an engineering-scale application. It is hence unachievable or infeasible to comply with the excess computational demands of common researchers or engineers, and it remains one of the disadvantages of applying CFD-DEM in geotechnical problems. Nevertheless, this limitation primarily comes from the DEM part, and it has been frequently identified in the previous DEM studies. The widely utilised solutions are adopting particle size upscaling and increasing gravitational acceleration. It is worth noting unlike the purely DEM models, the CFD-DEM modelling contains the solid-fluid interaction forces which could be significantly affected by the particle dimensions. Therefore, sensitivity analysis is required when applying the size-upscale method. Moreover, Zeghal and El Shamy [87] specified a relationship between the pore fluid viscosity () and particle diameter () under an amplified gravitational field as shown in the following equation:
where N is the level of the applied gravitational field, superscript denotes the prototype, and superscript denotes the model. Hence, the viscosity is also upscaled when the gravitational field is increased, and sensitivity checks should be performed to ensure numerical stability.
Hirche, Birkholz and Hinrichsen [100] applied a hybrid Eulerian-Eulerian-Lagrangian model for gas-solid mixtures where the gas phase was treated as the usual continuous media, while the solid phase was simulated by both continuous and discrete media. The authors emphasized the difficulties in assigning the fluid-particle interaction forces because the discrete particles are not always perfectly located inside the fluid cell. Furthermore, Hager, Kloss, Pirker and Goniva [102] stated the positions of the solids need to be correctly determined before calculating the fluid field. Details of the computing and the two commonly used methods in unresolved cases, the Centre Void Fraction method and the Divided Void Fraction method. It is important to note both methods sacrifice either accuracy or efficiency, therefore, a more advanced approach is required. Hager, Kloss, Pirker and Goniva [102] adopted a stair step method that falls under the resolved method category, where the particle is represented by individual cells as shown in Figure 2. This method provides a quicker distinction between fluid cells and solid cells and could count the particle volume more precisely. The mesh dimension needs to be at least eight times smaller than the particle diameter to obtain accurate outcomes, which could be easily achieved by dividing the domain into smaller meshes. Another issue was raised that some cells between the two contacted particles were considered solid cells where it was a fluid region. This error connected two solid particles and led to numerical instabilities. The authors explained, unlike the original smooth circular particle, the new mesh-represented solid has sharp edges and hence causes the misrepresentative of the cells at the solid-fluid interface. Therefore, this method requires further improvement to accurately represent the solids and fluids. Further analysis could also be performed to examine the possibility of combining this stair step method and the general unresolved method, in which the solid particles are refined into smaller meshes, and the fluid meshes are still considerably larger than the solid particles. As for the largely increased cell number from refinement, Hager, Kloss, Pirker and Goniva [102] applied dynamic meshing to eliminate unnecessary refinement and an example is displayed in Figure 6. The dynamic meshing approach was also implemented by Mondal, Wu and Sharma [84] and they specified the Courant-Friedrichs-Lewy (CFL) condition, which restrains the ratio of fluid velocity and mesh length over timestep, needs to be met to maintain numerical stability. This means the refinement should be over a critical value, however, the authors stated for solid-fluid mixtures with a high particle concentration, this condition is often violated because a large number of small meshes are regularly generated at the interface between two particles. Thus, studies are required when applying the dynamic meshing approach to the geotechnical applications which usually contain dense particle concentrations.
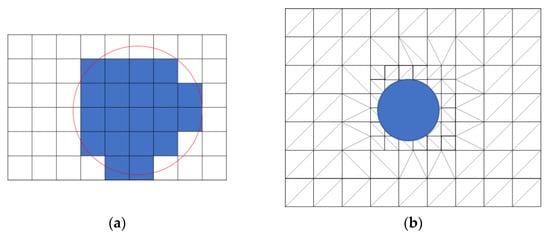
Figure 6.
(a) Stair step representation of particle (b) Dynamic local mesh refinement.
It is important to highlight that one of the most prominent computational fluid dynamics (CFD) tools at present is OpenFOAM. This CFD software is noteworthy for being open-source and has been primarily developed by OpenCFD Ltd, Bracknell, UK. Within this software, researchers have the capability to utilize a range of pre-defined solvers to simulate diverse scenarios. In specific instances, such as when conducting elemental tests on soil, certain solvers tailored to those scenarios might not be readily available, which need to be developed. Additionally, there are some available open-source discrete element method (DEM) packages that can be coupled with CFD, such as PFC3D from Itasca, LIGGGHTS, and YADE. As mentioned earlier, these software packages can be integrated using one-way, two-way, three-way, or four-way coupling methods. The four-way coupling method offers a more comprehensive representation, yet it comes with higher computational demands. Consequently, researchers should wisely select the coupling method that aligns most effectively with their research purposes. The flow chart for the coupling scheme can be found in Figure 7. However, for specific problems, the contact model and controlling feedback within DEM and CFD will be different. Some potential applications of coupling CFD and DEM in geotechnical problems in which fluids play an important role are landslides, in-situ tests (CPT or SPT), laboratory testing (permeability, triaxial, etc.), etc.
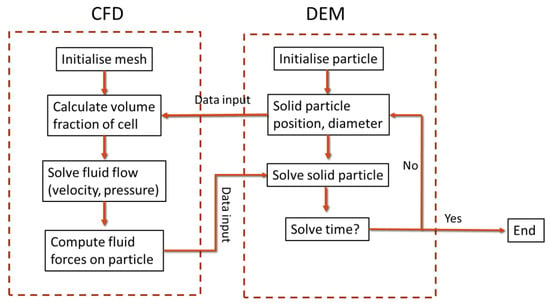
Figure 7.
The flow chart for CFD and DEM coupling scheme.
5. Conclusions
The CFD-DEM approach has been adopted in many geotechnical problems to explore interactions between physical fluids and solid materials. Early studies using CFD-DEM focused on analyzing stress-strain relationships and pore water pressure in saturated granular materials. However, these studies merely compared numerical models to experimental data without delving into the influence of the fluid phase. Specifically, they failed to compare CFD-DEM determined pore water pressure to the theoretically derived pore water pressure from purely DEM models employing the constant volume method.
More recent research has addressed this gap by comparing pore water pressure obtained through the constant volume method and CFD-DEM in undrained triaxial tests. The determination of fluid pressures in these studies was based on the current effective confining stress and the initial effective confining stress. It is important to note that the constant volume method assumes the pore water pressure can be calculated by the difference between stress paths under drained and undrained conditions, with total stress considered equivalent to effective stress in drained conditions. Nevertheless, a missing link between effective stress and axial strain in their research calls for further investigation. Therefore, more comprehensive studies are still needed to explore the impact of the fluid phase and assess soil response when conducting triaxial tests using CFD-DEM modelling.
One of the main problems when coupling CFD with DEM is to define the appropriate drag force formula. As mentioned, there have been various calculations for drag force. However, there is limited research on evaluating the efficiency of each calculation method for a specific problem, especially for element tests in geotechnical engineering. Therefore, further study on this drag force calculation is required in the future.
Author Contributions
Conceptualization, Y.C. and H.B.K.N.; literature review, Y.C., D.A. and H.B.K.N.; formal analysis, Y.C. and D.A.; investigation, Y.C., H.B.K.N. and M.M.R.; writing—original draft preparation, Y.C. and H.B.K.N.; writing—review and editing, H.B.K.N. and M.R.K.; visualization, M.M.R.; supervision, H.B.K.N., M.M.R. and M.R.K.; project administration, Y.C. and H.B.K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to restrictions.
Acknowledgments
This first author in this paper would like to acknowledge the University of South Australia President’s Scholarship for his PhD study to pursue this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouckovalas, G.D.; Andrianopoulos, K.I.; Papadimitriou, A.G. A critical state interpretation for the cyclic liquefaction resistance of silty sands. Soil Dyn. Earthq. Eng. 2003, 23, 115–125. [Google Scholar] [CrossRef]
- Huang, A.-B.; Chuang, S.-Y. Correlating cyclic strength with fines contents through state parameters. Soils Found. 2011, 51, 991–1001. [Google Scholar] [CrossRef]
- Baki, M.A.L.; Rahman, M.M.; Lo, S.R. Predicting onset of cyclic instability of loose sand with fines using instability curves. Soil Dyn. Earthq. Eng. 2014, 61–62, 140–151. [Google Scholar] [CrossRef]
- Jefferies, M.; Been, K. Soil Liquefaction: A Critical State Approach; Taylor & Francis: London, UK, 2006. [Google Scholar]
- Rahman, M.M.; Sitharam, T.G. Cyclic liquefaction screening of sand with non-plastic fines: Critical state approach. Geosci. Front. 2018, 11, 429–438. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G.; Hachey, J. The critical state of sands. Géotechnique 1991, 41, 365–381. [Google Scholar] [CrossRef]
- Oda, M. Initial fabrics and their relations to mechanical properties of granular material. Soils Found. 1972, 12, 17–36. [Google Scholar] [CrossRef]
- Arthur, J.R.F.; Dunstan, T. Radiography measurements of particle packing. Nature 1969, 223, 464–468. [Google Scholar] [CrossRef]
- Arthur, J.R.F.; Menzies, B.K. Inherent anisotropy in a sand. Géotechnique 1972, 22, 115–128. [Google Scholar] [CrossRef]
- Hu, X.; He, C.; Lai, X.; Walton, G.; Fu, W.; Fang, Y. A DEM-based study of the disturbance in dry sandy ground caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 2020, 101, 103410. [Google Scholar] [CrossRef]
- Cao, Y.; Nguyen, H.B.K.; Rahman, M.M.; Karim, M.R.; Cheng, W.-C. The Effects of Fines on the Response of Granular Soil during Earth Pressure Balance (EPB) Shield Tunneling. In Proceedings of the Geo-Congress 2023, Los Angeles, CA, USA, 26–29 March 2023; pp. 249–257. [Google Scholar]
- Aikins, D.; Rahman, M.M.; Karim, M.R.; Nguyen, H.B.K. Effect of Interparticle Friction and Particle Elasticity on Behavior of Granular Materials. In Proceedings of the Geo-Congress 2023, Los Angeles, CA, USA, 26–29 March 2023; pp. 258–268. [Google Scholar]
- Feng, Y. Thirty years of developments in contact modelling of non-spherical particles in DEM: A selective review. Acta Mech. Sin. 2023, 39, 1–41. [Google Scholar] [CrossRef]
- Zhao, T.; Ye, J. 3D DEM Simulation on the Reliquefaction Behavior of Sand Considering the Effect of Reconsolidation Degree. J. Earthq. Eng. 2022, 27, 2919–2941. [Google Scholar] [CrossRef]
- Nie, J.-Y.; Zhao, J.; Cui, Y.-F.; Li, D.-Q. Correlation between grain shape and critical state characteristics of uniformly graded sands: A 3D DEM study. Acta Geotech. 2022, 17, 2783–2798. [Google Scholar] [CrossRef]
- Qu, T.; Wang, S.; Hu, Q. Coupled discrete element-finite difference method for analysing effects of cohesionless soil conditioning on tunneling behaviour of EPB shield. KSCE J. Civ. Eng. 2019, 23, 4538–4552. [Google Scholar] [CrossRef]
- Gong, G. DEM Simulations of Drained and Undrained Behaviour; University of Birmingham: Birmingham, UK, 2008. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Fourie, A.B.; Luo, X.D.; Tang, X.; Yang, J. Discussion on How particle shape affects the critical state, triggering of instability and dilatancy of granular materials results from a DEM study. Géotechnique 2023. [Google Scholar] [CrossRef]
- Guo, N.; Yang, F.; Yang, Z.X.; Zhao, S. Deformation characteristics of inherently anisotropic granular media under repeated traffic loading: A DEM study. Acta Geotech. 2022, 17, 3377–3395. [Google Scholar] [CrossRef]
- Kuhn, M.R.; Daouadji, A. Simulation of undrained quasi-saturated soil with pore pressure measurements using a discrete element (DEM) algorithm. Soils Found. 2020, 60, 1097–1111. [Google Scholar] [CrossRef]
- Kuhn, M.R. The critical state of granular media: Convergence, stationarity and disorder. Géotechnique 2016, 66, 902–909. [Google Scholar] [CrossRef]
- Khosravi, A.; Martinez, A.; DeJong, J.T. Discrete element model (DEM) simulations of cone penetration test (CPT) measurements and soil classification. Can. Geotech. J. 2020, 57, 1369–1387. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, J.; Huang, X. DEM analysis of monotonic and cyclic behaviors of sand based on critical state soil mechanics framework. Comput. Geotech. 2020, 128, 103787. [Google Scholar] [CrossRef]
- Foroutan, T.; Mirghasemi, A.A. CFD-DEM model to assess stress-induced anisotropy in undrained granular material. Comput. Geotech. 2020, 119, 103318. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Cameron, D. Undrained Behavior of Sand by DEM Study. In Geo-Congress 2015; Iskander, M., Suleiman, M.T., Anderson, J.B., Laefer, D.F., Eds.; Geotechnical Special Publication; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 182–191. [Google Scholar]
- Ng, T.-T.; Zhou, W.; Ma, G.; Chang, X.-L. Damping and Particle Mass in DEM Simulations under Gravity. J. Eng. Mech. 2015, 141, 04014167. [Google Scholar] [CrossRef]
- Liu, G.; Rong, G.; Peng, J.; Zhou, C. Numerical simulation on undrained triaxial behavior of saturated soil by a fluid coupled-DEM model. Eng. Geol. 2015, 193, 256–266. [Google Scholar] [CrossRef]
- Huang, X.; Hanley, K.J.; O’Sullivan, C.; Kwok, C.Y. Exploring the influence of interparticle friction on critical state behaviour using DEM. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1276–1297. [Google Scholar] [CrossRef]
- Kwok, C.Y.; Bolton, M.D. DEM simulations of soil creep due to particle crushing. Géotechnique 2013, 63, 1365–1376. [Google Scholar] [CrossRef]
- Bolton, M.D.; Nakata, Y.; Cheng, Y.P. Micro- and macro-mechanical behaviour of DEM crushable materials. Géotechnique 2008, 58, 471–480. [Google Scholar] [CrossRef]
- Zhao, S.; Evans, T.M.; Zhou, X. Shear-induced anisotropy of granular materials with rolling resistance and particle shape effects. Int. J. Solids Struct. 2018, 150, 268–281. [Google Scholar] [CrossRef]
- Zhang, L.; Evans, T.M. Boundary effects in discrete element method modeling of undrained cyclic triaxial and simple shear element tests. Granul. Matter 2018, 20, 60. [Google Scholar] [CrossRef]
- Zhao, X.; Evans, T.M. Numerical analysis of critical state behaviors of granular soils under different loading conditions. Granul. Matter 2011, 13, 751–764. [Google Scholar] [CrossRef]
- Cao, Y.; Nguyen, H.B.K.; Rahman, M.M.; Cheng, W.-C. Soil Behavior in the Earth Pressure Balance (EPB) Shield Tunnelling—A DEM Study. In Geo-Congress 2022; American Society of Civil Engineers: Reston, VA, USA, 2022; pp. 690–698. [Google Scholar]
- Wang, R.; Cao, W.; Xue, L.; Zhang, J.-M. An anisotropic plasticity model incorporating fabric evolution for monotonic and cyclic behavior of sand. Acta Geotech. 2021, 16, 43–65. [Google Scholar] [CrossRef]
- Huang, X.; Kwok, C.-y.; Hanley, K.J.; Zhang, Z. DEM analysis of the onset of flow deformation of sands: Linking monotonic and cyclic undrained behaviours. Acta Geotech. 2018, 13, 1061–1074. [Google Scholar] [CrossRef]
- Kuhn, M.R.; Suzuki, K.; Daouadji, A. Linear-frictional contact model for 3D discrete element simulations of granular systems. Int. J. Numer. Methods Eng. 2020, 121, 560–569. [Google Scholar] [CrossRef]
- Kuhn, M. Smooth Convex Three-Dimensional Particle for the Discrete-Element Method. J. Eng. Mech. 2003, 129, 539–547. [Google Scholar] [CrossRef]
- Kuhn, M.R. A flexible boundary for three-dimensional DEM particle assemblies. Eng. Comput. 1995, 12, 175–183. [Google Scholar] [CrossRef]
- Dinesh, S.; Thallak, S.; Vinod, J.S. Dynamic properties and liquefaction behavior of granular materials using discrete element method. Curr. Sci. 2004, 87, 1379–1387. [Google Scholar]
- Sitharam, T.; Vinod, J.; Ravishankar, B. Post-liquefaction undrained monotonic behaviour of sands: Experiments and DEM simulations. Géotechnique 2009, 59, 739–749. [Google Scholar] [CrossRef]
- Kuhn, M.; Renken, H.; Mixsell, A.; Kramer, S. Investigation of Cyclic Liquefaction with Discrete Element Simulations. J. Geotech. Geoenviron. Eng. 2014, 140, 04014075. [Google Scholar] [CrossRef]
- Huang, M.; Chen, Y.; Gu, X. Discrete element modeling of soil-structure interface behavior under cyclic loading. Comput. Geotech. 2019, 107, 14–24. [Google Scholar] [CrossRef]
- Sitharam, T.; Vinod, J.S.; Ravishankar, B. Evaluation of undrained response from drained triaxial shear tests: DEM simulations and experiments. Geotechnique 2008, 58, 605–608. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Cameron, D.A.; Fourie, A.B. The effect of consolidation path on undrained behaviour of sand—A DEM approach. In Computer Methods and Recent Advances in Geomechanics; CRC Press: Boca Raton, FL, USA, 2015; pp. 175–180. [Google Scholar]
- Nguyen, H.B.K.; Rahman, M.M. The role of micro-mechanics on the consolidation history of granular materials. Aust. Geomech. 2017, 52, 27–36. [Google Scholar]
- Shamy, U.E.; Zeghal, M. Coupled Continuum-Discrete Model for Saturated Granular Soils. J. Eng. Mech. 2005, 131, 413–426. [Google Scholar] [CrossRef]
- Shamy, U.E.; Zeghal, M.; Dobry, R.; Thevanayagam, S.; Elgamal, A.; Abdoun, T.; Medina, C.; Bethapudi, R.; Bennett, V. Micromechanical Aspects of Liquefaction-Induced Lateral Spreading. Int. J. Geomech. 2010, 10, 190–201. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Hong, Y.; Zhao, J.; Yin, Z.-Y. A coupled CFD-DEM investigation of suffusion of gap graded soil: Coupling effect of confining pressure and fines content. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 2473–2500. [Google Scholar] [CrossRef]
- Wang, M.; Feng, Y.T.; Owen, D.R.J.; Qu, T.M. A novel algorithm of immersed moving boundary scheme for fluid–particle interactions in DEM–LBM. Comput. Methods Appl. Mech. Eng. 2019, 346, 109–125. [Google Scholar] [CrossRef]
- Norouzi, H.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Zhao, T.; Houlsby, G.T.; Utili, S. Investigation of granular batch sedimentation via DEM–CFD coupling. Granul. Matter 2014, 16, 921–932. [Google Scholar] [CrossRef]
- Stokes, G.G.; Larmor, J.; Rayleigh, J.W.S. Mathematical and Physical Papers; University Press: Cambridge, UK, 1880. [Google Scholar]
- DallaValle, J.M. Micromeritics: The Technology of Fine Particles; Pitman Publishing Limited: New York, NY, USA, 1948. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Wen, C.Y.; Yu, Y.H. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Brown, P.P.; Lawler, D.F. Sphere drag and settling velocity revisited. J. Environ. Eng. 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Sazzad, M.M.; Suzuki, K. Effect of interparticle friction on the cyclic behavior of granular materials using 2D DEM. J. Geotech. Geoenviron. Eng. 2011, 137, 545–549. [Google Scholar] [CrossRef]
- Kwok, C.; Bolton, M. DEM simulations of thermally activated creep in soils. Geotechnique 2010, 60, 425–433. [Google Scholar] [CrossRef]
- Utili, S.; Nova, R. DEM analysis of bonded granular geomaterials. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1997–2031. [Google Scholar] [CrossRef]
- Ferellec, J.-F.; McDowell, G. A simple method to create complex particle shapes for DEM. Geomech. Geoengin. Int. J. 2008, 3, 211–216. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Itasca Particle Flow Code, 5.0; Itasca Consulting Group Incorporated: Minneapolis, MN, USA, 2014.
- Cundall, P.A.; Hart, R.D. Numerical modelling of discountinua. Eng. Comput. 1992, 9, 101–113. [Google Scholar] [CrossRef]
- Barnett, N.; Rahman, M.M.; Karim, M.R.; Nguyen, H.B.K.; Carraro, J.A.H. Equivalent state theory for mixtures of sand with non-plastic fines: A DEM investigation. Géotechnique 2021, 71, 423–440. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Qian, J. DEM investigation on the evolution of microstructure in granular soils under shearing. Granul. Matter 2014, 16, 91–106. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Fourie, A.B. Undrained behaviour of granular material and the role of fabric in isotropic and K0 consolidations: DEM approach. Géotechnique 2017, 67, 153–167. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.M.; Fourie, A.B. How particle shape affects the critical state, triggering of instability and dilatancy of granular materials—Results from a DEM study. Géotechnique 2021, 71, 749–764. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Vinod, J.S. Critical state behaviour of granular materials from isotropic and rebounded paths: DEM simulations. Granul. Matter 2009, 11, 33–42. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, J.; Chang, X. Three-dimensional DEM investigation of critical state and dilatancy behaviors of granular materials. Acta Geotech. 2017, 12, 527–540. [Google Scholar] [CrossRef]
- Dobry, R.; Ng, T.T. Discrete modelling of stress-strain behaviour of granular media at small and large strains. Eng. Comput. 1992, 9, 129–143. [Google Scholar] [CrossRef]
- Kolapalli, R.; Rahman, M.M.; Karim, M.R.; Nguyen, H.B.K. A DEM investigation on the influence of cyclic and static stress ratios and state variables on the pore water pressure generation in granular materials. J. Geotech. Geoenviron. Eng. 2023, 149, 04023043. [Google Scholar] [CrossRef]
- Kolapalli, R.; Rahman, M.M.; Karim, M.R.; Nguyen, H.B.K. The failure modes of granular material in undrained cyclic loading: A critical state approach using DEM. Acta Geotech. 2023, 18, 2945–2970. [Google Scholar] [CrossRef]
- Nguyen, H.B.K.; Rahman, M.; Karim, R. An Investigation of Instability on Constant Shear Drained (CSD) Path under the CSSM Framework: A DEM Study. Geosciences 2022, 12, 449. [Google Scholar] [CrossRef]
- Butlanska, J.; Arroyo, M.; Gens, A. Homogeneity and symmetry in DEM models of cone penetration. AIP Conf. Proc. 2009, 1145, 425–428. [Google Scholar] [CrossRef]
- Jiang, M.; Dai, Y.; Cui, L.; Shen, Z.; Wang, X. Investigating mechanism of inclined CPT in granular ground using DEM. Granul. Matter 2014, 16, 785–796. [Google Scholar] [CrossRef]
- Arroyo, M.; Butlanska, J.; Gens, A.; Calvetti, F.; Jamiolkowski, M. Cone penetration tests in a virtual calibration chamber. Géotechnique 2011, 61, 525–531. [Google Scholar] [CrossRef]
- Ciantia, M.O.; Arroyo, M.; Butlanska, J.; Gens, A. DEM modelling of cone penetration tests in a double-porosity crushable granular material. Comput. Geotech. 2016, 73, 109–127. [Google Scholar] [CrossRef]
- Chen, F.; Drumm, E.C.; Guiochon, G. Coupled discrete element and finite volume solution of two classical soil mechanics problems. Comput. Geotech. 2011, 38, 638–647. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD–DEM simulation of fluid–particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- El Shamy, U.; Zeghal, M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils. Soil Dyn. Earthq. Eng. 2007, 27, 712–729. [Google Scholar] [CrossRef]
- Ibrahim, A.; Meguid, M.A. Coupled flow modelling in geotechnical and ground engineering: An overview. Int. J. Geosynth. Ground Eng. 2020, 6, 39. [Google Scholar] [CrossRef]
- Mondal, S.; Wu, C.-H.; Sharma, M.M. Coupled CFD-DEM simulation of hydrodynamic bridging at constrictions. Int. J. Multiph. Flow. 2016, 84, 245–263. [Google Scholar] [CrossRef]
- Climent, N.; Arroyo, M.; O’Sullivan, C.; Gens, A. Sand production simulation coupling DEM with CFD. Eur. J. Environ. Civ. Eng. 2014, 18, 983–1008. [Google Scholar] [CrossRef]
- Shan, T.; Zhao, J. A coupled CFD-DEM analysis of granular flow impacting on a water reservoir. Acta Mech. 2014, 225, 2449–2470. [Google Scholar] [CrossRef]
- Zeghal, M.; El Shamy, U. Liquefaction of saturated loose and cemented granular soils. Powder Technol. 2008, 184, 254–265. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH and Riemann solvers. J. Comput. Phys. 1997, 136, 298–307. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Huppert, H.E.; Worster, M.G. Solidification using smoothed particle hydrodynamics. J. Comput. Phys. 2005, 206, 684–705. [Google Scholar] [CrossRef]
- Gotoh, H.; Sakai, T. Key issues in the particle method for computation of wave breaking. Coast. Eng. 2006, 53, 171–179. [Google Scholar] [CrossRef]
- Potapov, A.V.; Hunt, M.L.; Campbell, C.S. Liquid–solid flows using smoothed particle hydrodynamics and the discrete element method. Powder Technol. 2001, 116, 204–213. [Google Scholar] [CrossRef]
- Anderson, T.; Jackson, R. A Fluid Mechanical Description of Fluidized Beds. Ind. Eng. Chem. Fundam. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, B.; Wang, X.; Ge, W.; Li, J. Lattice Boltzmann based discrete simulation for gas–solid fluidization. Chem. Eng. Sci. 2013, 101, 228–239. [Google Scholar] [CrossRef][Green Version]
- Zhang, H.; Trias, F.X.; Oliva, A.; Yang, D.; Tan, Y.; Shu, S.; Sheng, Y. PIBM: Particulate immersed boundary method for fluid–particle interaction problems. Powder Technol. 2015, 272, 1–13. [Google Scholar] [CrossRef]
- Habte, M.A.; Wu, C. Particle sedimentation using hybrid Lattice Boltzmann-immersed boundary method scheme. Powder Technol. 2017, 315, 486–498. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311–339. [Google Scholar] [CrossRef]
- van Deemter, J.J.; van der Laan, E.T. Momentum and energy balances for dispersed two-phase flow. Appl. Sci. Res. 1961, 10, 102–108. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Hirche, D.; Birkholz, F.; Hinrichsen, O. A hybrid Eulerian-Eulerian-Lagrangian model for gas-solid simulations. Chem. Eng. J. 2019, 377, 119743. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, X. Comparison of the implementation of three common types of coupled CFD-DEM model for simulating soil surface erosion. Int. J. Multiph. Flow 2017, 91, 89–100. [Google Scholar] [CrossRef]
- Hager, A.; Kloss, C.; Pirker, S.; Goniva, C. Parallel resolved open source CFD-DEM: Method, validation and application. J. Comput. Multiph. Flows 2014, 6, 13–27. [Google Scholar] [CrossRef]
- Catalano, E.; Chareyre, B.; Barthélémy, E. Pore-scale modeling of fluid-particles interaction and emerging poromechanical effects. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 51–71. [Google Scholar] [CrossRef]
- Goniva, C.; Kloss, C.; Deen, N.G.; Kuipers, J.A.M.; Pirker, S. Influence of rolling friction on single spout fluidized bed simulation. Particuology 2012, 10, 582–591. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid. Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, T. A coupled CFD–DEM simulation of slurry infiltration and filter cake formation during slurry shield tunneling. Infrastructures 2018, 3, 15. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Gao, C.-P.; Yin, Z.-Y. CFD-DEM modeling of seepage erosion around shield tunnels. Tunn. Undergr. Space Technol. 2019, 83, 60–72. [Google Scholar] [CrossRef]
- Zhang, A.; Jiang, M.; Thornton, C. A coupled CFD-DEM method with moving mesh for simulating undrained triaxial tests on granular soils. Granul. Matter 2020, 22, 13. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, F.; Xu, N.-W. Coupled DEM-CFD investigation on the formation of landslide dams in narrow rivers. Landslides 2016, 14, 189–201. [Google Scholar] [CrossRef]
- O’Sullivan, C. Particle-based discrete element modeling: Geomechanics perspective. Int. J. Geomech. 2011, 11, 449–464. [Google Scholar] [CrossRef]
- Zhao, T. Coupled DEM-CFD Analyses of Landslide-Induced Debris Flows; Springer: Singapore, 2017. [Google Scholar]
- Kafui, K.D.; Thornton, C.; Adams, M.J. Discrete particle-continuum fluid modelling of gas–solid fluidised beds. Chem. Eng. Sci. 2002, 57, 2395–2410. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y.; Ren, N.; Shi, W. A coupled CFD-DEM simulation of upward seepage flow in coarse sands. Mar. Georesour. Geotechnol. 2019, 37, 589–598. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).