Concurrent Validity of Depth-Sensor-Based Quantification of Compensatory Movements during the Swing Phase of Gait in Healthy Individuals
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Procedure
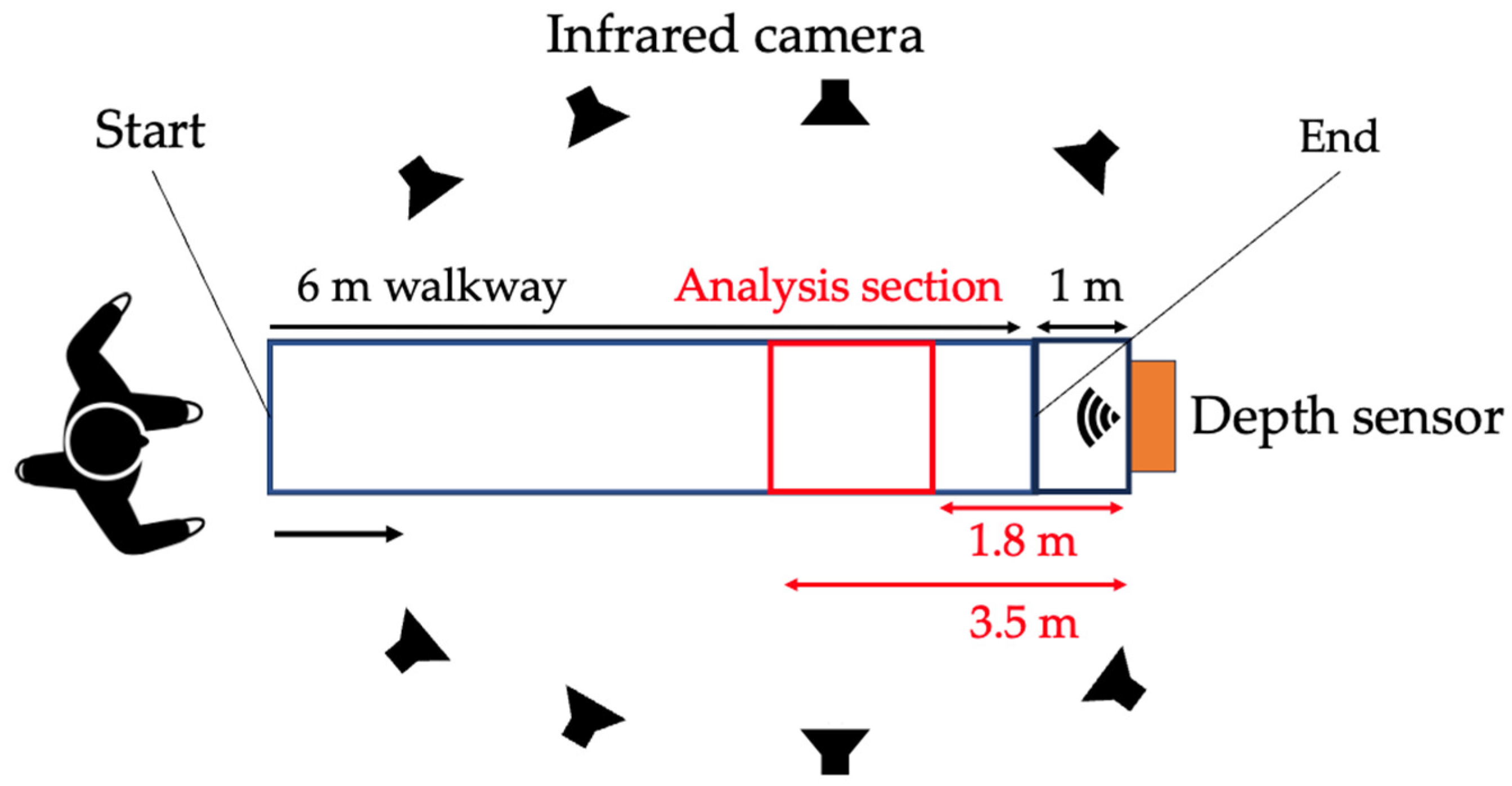
2.3. Data Collection
2.4. Failed Trial of Gait Analysis Using Depth-Sensor-Based 3DMA
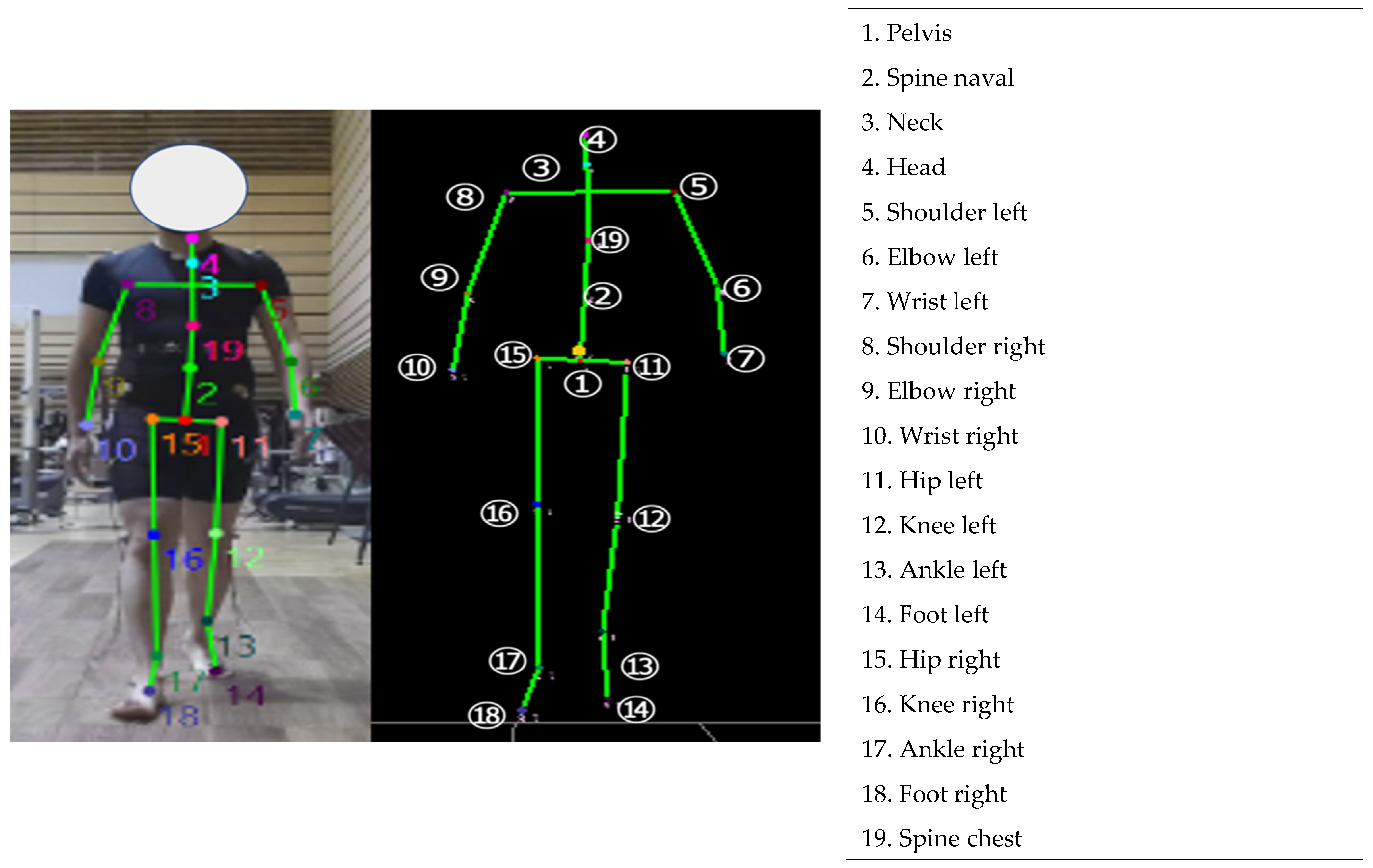
2.5. Data Reduction and Analysis
2.6. Spatiotemporal Variables
2.7. Trunk and Lower Limb Kinematics
2.8. Whole-Body Kinematics
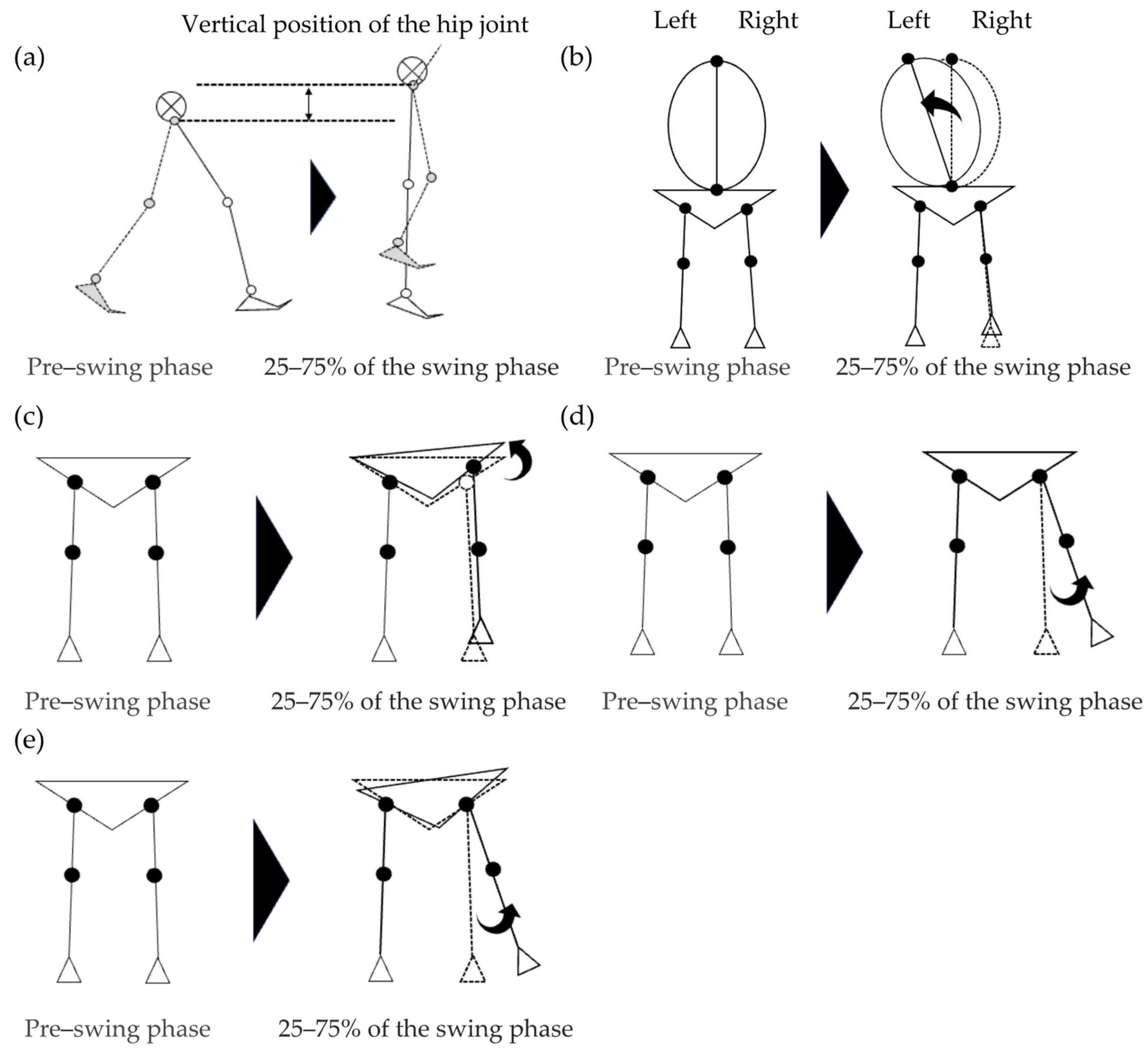
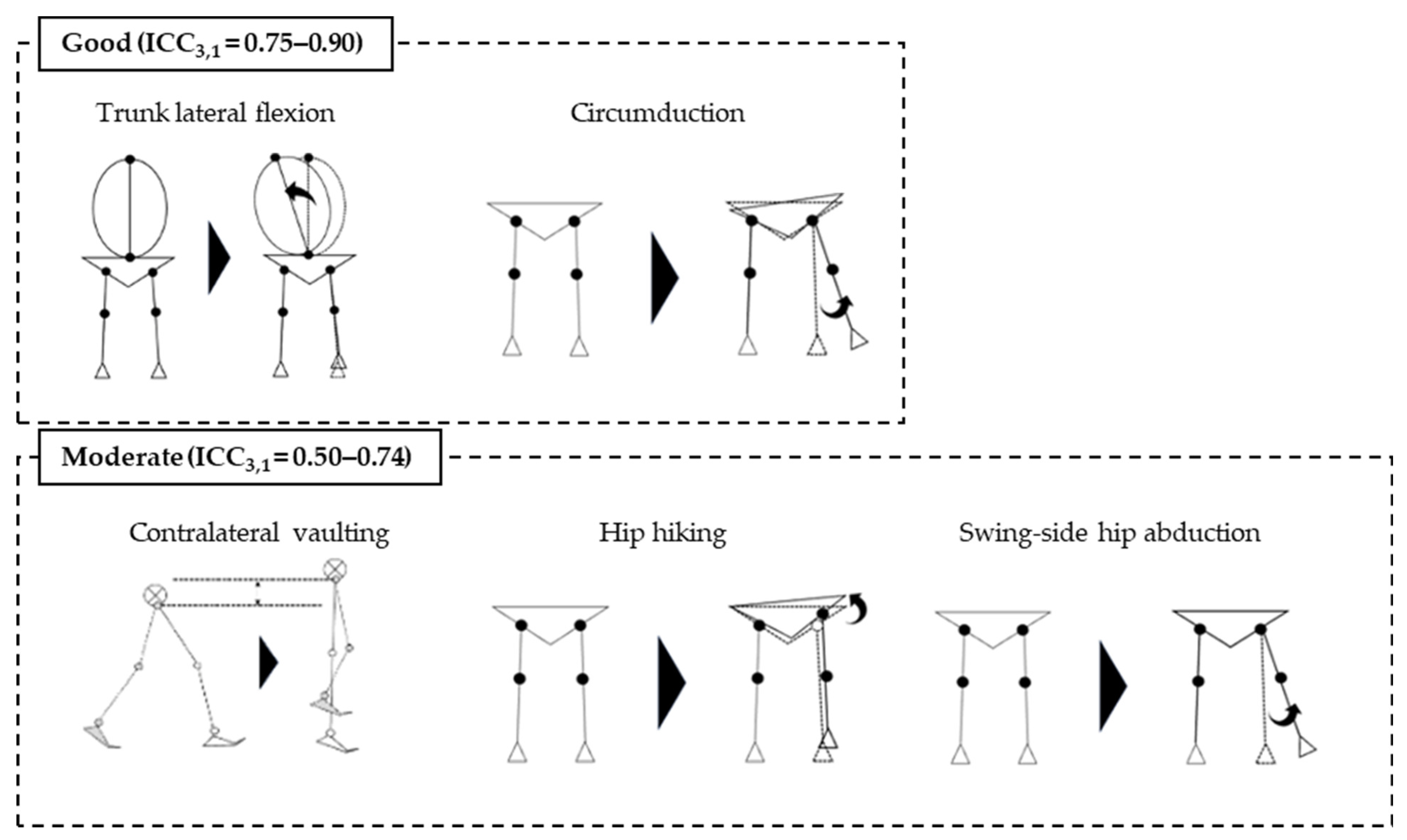
2.9. Definition of Abnormal Gait Patterns
2.10. Statistical Analysis
3. Results
3.1. Walking Speed in Each Condition
3.2. Concurrent Validity of Abnormal Gait Patterns
3.3. Concurrent Validity of Spatiotemporal Variables
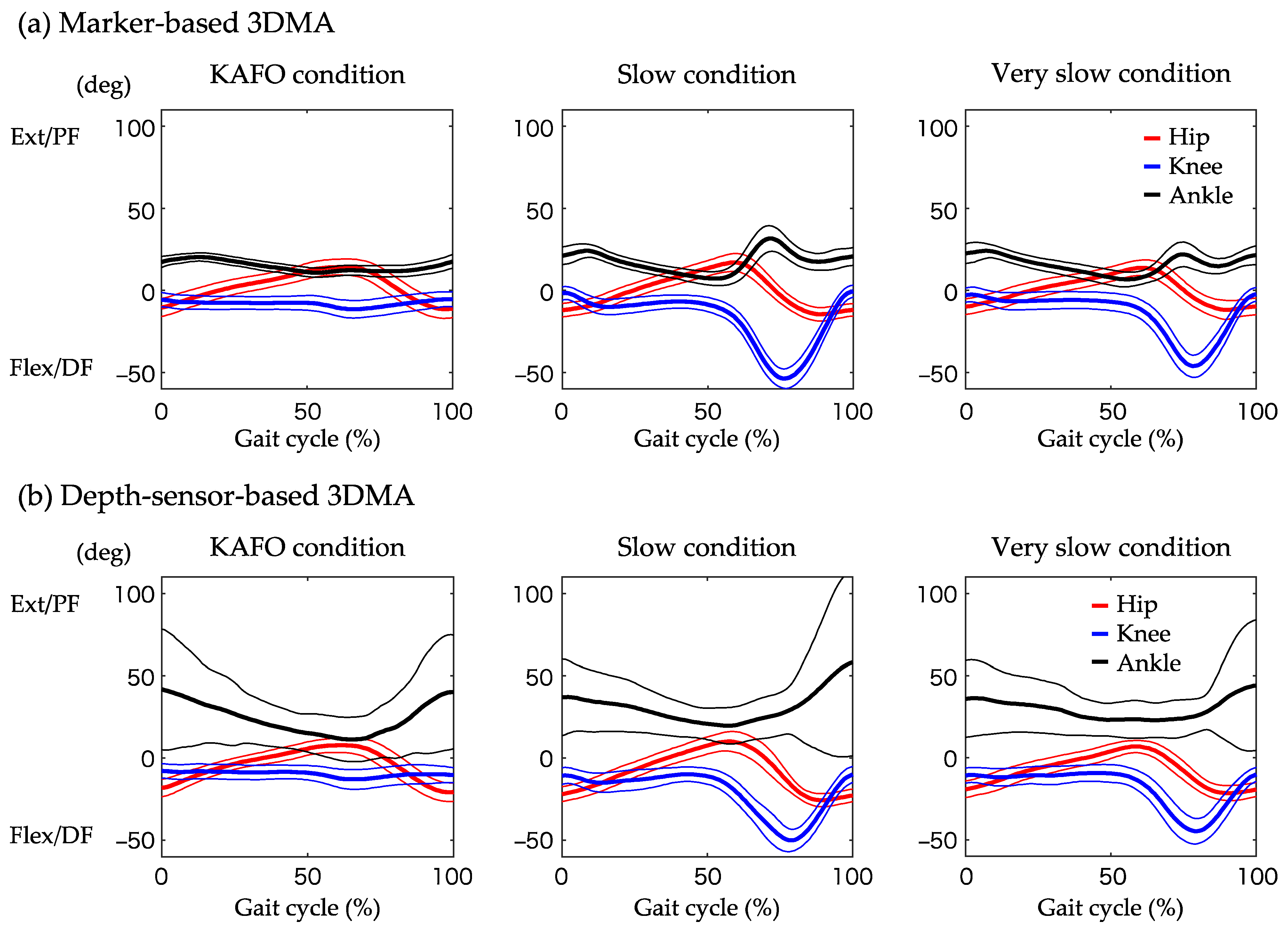
3.4. Concurrent Validity of Trunk and Lower Limb Kinematics
3.5. Concurrent Validity of Whole-Body Kinematics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van de Port, I.G.; Kwakkel, G.; Lindeman, E. Community ambulation in patients with chronic stroke: How is it related to gait speed? J. Rehabil. Med. 2008, 40, 23–27. [Google Scholar] [CrossRef] [PubMed]
- Thilarajah, S.; Mentiplay, B.F.; Bower, K.J.; Tan, D.; Pua, Y.H.; Williams, G.; Koh, G.; Clark, R.A. Factors associated with post-stroke physical activity: A systematic review and meta-analysis. Arch. Phys. Med. Rehabil. 2018, 99, 1876–1889. [Google Scholar] [CrossRef] [PubMed]
- Weerdesteyn, V.; de Niet, M.; van Duijnhoven, H.J.; Geurts, A.C. Falls in individuals with stroke. J. Rehabil. Res. Dev. 2008, 45, 1195–1213. [Google Scholar] [CrossRef] [PubMed]
- Michael, K.M.; Allen, J.K.; Macko, R.F. Reduced ambulatory activity after stroke: The role of balance, gait, and cardiovascular fitness. Arch. Phys. Med. Rehabil. 2005, 86, 1552–1556. [Google Scholar] [CrossRef] [PubMed]
- Perry, J.; Garrett, M.; Gronley, J.K.; Mulroy, S.J. Classification of walking handicap in the stroke population. Stroke 1995, 26, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Fulk, G.D.; He, Y.; Boyne, P.; Dunning, K. Predicting home and community walking activity poststroke. Stroke 2017, 48, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, H.; Awad, L.N.; Palmer, J.A.; Higginson, J.S.; Binder-Macleod, S.A. Contribution of paretic and nonparetic limb peak propulsive forces to changes in walking speed in individuals poststroke. Neurorehabil. Neural Repair 2016, 30, 743–752. [Google Scholar] [CrossRef] [PubMed]
- Patterson, K.K.; Mansfield, A.; Biasin, L.; Brunton, K.; Inness, E.L.; McIlroy, W.E. Longitudinal changes in poststroke spatiotemporal gait asymmetry over inpatient rehabilitation. Neurorehabil. Neural Repair 2015, 29, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Awad, L.N.; Palmer, J.A.; Pohlig, R.T.; Binder-Macleod, S.A.; Reisman, D.S. Walking speed and step length asymmetry modify the energy cost of walking after stroke. Neurorehabil. Neural Repair 2015, 29, 416–423. [Google Scholar] [CrossRef]
- Jørgensen, L.; Crabtree, N.J.; Reeve, J.; Jacobsen, B.K. Ambulatory level and asymmetrical weight bearing after stroke affects bone loss in the upper and lower part of the femoral neck differently: Bone adaptation after decreased mechanical loading. Bone 2000, 27, 701–707. [Google Scholar] [CrossRef]
- Kerrigan, D.C.; Frates, E.P.; Rogan, S.; Riley, P.O. Hip hiking and circumduction: Quantitative definitions. Am. J. Phys. Med. Rehabil. 2000, 79, 247–252. [Google Scholar] [CrossRef]
- Stanhope, V.A.; Knarr, B.A.; Reisman, D.S.; Higginson, J.S. Frontal plane compensatory strategies associated with self-selected walking speed in individuals post-stroke. Clin. Biomech. 2014, 29, 518–522. [Google Scholar] [CrossRef]
- Tyrell, C.M.; Roos, M.A.; Rudolph, K.S.; Reisman, D.S. Influence of systematic increases in treadmill walking speed on gait kinematics after stroke. Phys. Ther. 2011, 91, 392–403. [Google Scholar] [CrossRef] [PubMed]
- Mukaino, M.; Ohtsuka, K.; Tanikawa, H.; Matsuda, F.; Yamada, J.; Itoh, N.; Saitoh, E. Clinical-oriented three-dimensional gait analysis method for evaluating gait disorder. J. Vis. Exp. 2018, 133, e57063. [Google Scholar] [CrossRef]
- Clark, R.A.; Vernon, S.; Mentiplay, B.F.; Miller, K.J.; McGinley, J.L.; Pua, Y.H.; Paterson, K.; Bower, K.J. Instrumenting gait assessment using the Kinect in people living with stroke: Reliability and association with balance tests. J. Neuroeng. Rehabil. 2015, 12, 15. [Google Scholar] [CrossRef] [PubMed]
- Latorre, J.; Colomer, C.; Alcañiz, M.; Llorens, R. Gait analysis with the Kinect v2: Normative study with healthy individuals and comprehensive study of its sensitivity, validity, and reliability in individuals with stroke. J. Neuroeng. Rehabil. 2019, 16, 97. [Google Scholar] [CrossRef]
- Lachat, E.; Macher, H.; Landes, T.; Grussenmeyer, P. Assessment and calibration of a RGB-D camera (Kinect v2 Sensor) towards a potential use for close-range 3D modeling. Remote Sens. 2015, 7, 13070–13097. [Google Scholar] [CrossRef]
- Usami, T.; Nishida, K.; Iguchi, H.; Okumura, T.; Sakai, H.; Ida, R.; Horiba, M.; Kashima, S.; Sahashi, K.; Asai, H.; et al. Evaluation of lower extremity gait analysis using Kinect V2® tracking system. SICOT J. 2022, 8, 27. [Google Scholar] [CrossRef]
- Eltoukhy, M.; Oh, J.; Kuenze, C.; Signorile, J. Improved kinect-based spatiotemporal and kinematic treadmill gait assessment. Gait Posture 2017, 51, 77–83. [Google Scholar] [CrossRef]
- Matsuda, F.; Mukaino, M.; Ohtsuka, K.; Tanikawa, H.; Tsuchiyama, K.; Teranishi, T.; Kanada, Y.; Kagaya, H.; Saitoh, E. Biomechanical factors behind toe clearance during the swing phase in hemiparetic patients. Top. Stroke Rehabil. 2017, 24, 177–182. [Google Scholar] [CrossRef]
- Zissimopoulos, A.; Fatone, S.; Gard, S.A. Biomechanical and energetic effects of a stance-control orthotic knee joint. J. Rehabil. Res. Dev. 2007, 44, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Akbas, T.; Prajapati, S.; Ziemnicki, D.; Tamma, P.; Gross, S.; Sulzer, J. Hip circumduction is not a compensation for reduced knee flexion angle during gait. J. Biomech. 2019, 87, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Mukaino, M.; Ohtsuka, K.; Otaka, Y.; Tanikawa, H.; Matsuda, F.; Tsuchiyama, K.; Yamada, J.; Saitoh, E. Gait characteristics of post-stroke hemiparetic patients with different walking speeds. Int. J. Rehabil. Res. 2020, 43, 69–75. [Google Scholar] [CrossRef]
- Ferraris, C.; Cimolin, V.; Vismara, L.; Votta, V.; Amprimo, G.; Cremascoli, R.; Galli, M.; Nerino, R.; Mauro, A.; Priano, L. Monitoring of gait parameters in post-stroke individuals: A feasibility study using RGB-D sensors. Sensors 2021, 21, 5945. [Google Scholar] [CrossRef] [PubMed]
- Learn Microsoft. Available online: https://learn.microsoft.com/ja-jp/azure/kinect-dk/body-joints (accessed on 14 May 2024).
- Kurabayashi, J.; Mochimaru, M.; Kouchi, M. Validation of the estimation methods for the hip joint center. J. Soc. Biomech. 2003, 27, 28–36. [Google Scholar] [CrossRef]
- Tokuda, K.; Anan, M.; Takahashi, M.; Sawada, T.; Tanimoto, K.; Kito, N.; Shinkoda, K. Biomechanical mechanism of lateral trunk lean gait for knee osteoarthritis patients. J. Biomech. 2018, 66, 10–17. [Google Scholar] [CrossRef]
- Kagami, S.; Mochimaru, M.; Ehara, Y.; Miyata, N.; Nishiwaki, K.; Kanade, T.; Inoue, H. Measurement and comparison of humanoid H7 walking with human being. Robot. Auton. Syst. 2004, 48, 177–187. [Google Scholar] [CrossRef]
- Mizuta, N.; Hasui, N.; Kai, T.; Inui, Y.; Sato, M.; Ohnishi, S.; Taguchi, J.; Nakatani, T. Characteristics of limb kinematics in the gait disorders of post-stroke patients. Sci. Rep. 2024, 14, 3082. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A.; Quanbury, A.O.; Hobson, D.A.; Sidwall, H.G.; Reimer, G.; Trenholm, B.G.; Steinke, T.; Shlosser, H. Kinematics of normal locomotion—A statistical study based on T.V. data. J. Biomech. 1974, 7, 479–486. [Google Scholar] [CrossRef]
- Clark, R.A.; Bower, K.J.; Mentiplay, B.F.; Paterson, K.; Pua, Y.H. Concurrent validity of the Microsoft Kinect for assessment of spatiotemporal gait variables. J. Biomech. 2013, 46, 2722–2725. [Google Scholar] [CrossRef]
- Mentiplay, B.F.; Perraton, L.G.; Bower, K.J.; Pua, Y.H.; McGaw, R.; Heywood, S.; Clark, R.A. Gait assessment using the Microsoft Xbox One Kinect: Concurrent validity and inter-day reliability of spatiotemporal and kinematic variables. J. Biomech. 2015, 48, 2166–2170. [Google Scholar] [CrossRef] [PubMed]
- French, M.A.; Koller, C.; Arch, E.S. Comparison of three kinematic gait event detection methods during overground and treadmill walking for individuals post stroke. J. Biomech. 2020, 99, 109481. [Google Scholar] [CrossRef] [PubMed]
- Zeni, J.A., Jr.; Richards, J.G.; Higginson, J.S. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [PubMed]
- Matsuzawa, Y.; Miyazaki, T.; Takeshita, Y.; Higashi, N.; Hayashi, H.; Araki, S.; Nakatsuji, S.; Fukunaga, S.; Kawada, M.; Kiyama, R. Effect of leg extension angle on knee flexion angle during swing phase in post-stroke gait. Medicina 2021, 57, 1222. [Google Scholar] [CrossRef] [PubMed]
- Hof, A.L.; Gazendam, M.G.; Sinke, W.E. The condition for dynamic stability. J. Biomech. 2005, 38, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Tanikawa, H.; Ohtsuka, K.; Mukaino, M.; Inagaki, K.; Matsuda, F.; Teranishi, T.; Kanada, Y.; Kagaya, H.; Saitoh, E. Quantitative assessment of retropulsion of the hip, excessive hip external rotation, and excessive lateral shift of the trunk over the unaffected side in hemiplegia using three-dimensional treadmill gait analysis. Top. Stroke Rehabil. 2016, 23, 311–317. [Google Scholar] [CrossRef]
- Itoh, N.; Kagaya, H.; Saitoh, E.; Ohtsuka, K.; Yamada, J.; Tanikawa, H.; Tanabe, S.; Itoh, N.; Aoki, T.; Kanada, Y. Quantitative assessment of circumduction, hip hiking, and forefoot contact gait using lissajous figures. Jpn. J. Compr. Rehabil. Sci. 2012, 3, 78–84. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Pfister, A.; West, A.M.; Bronner, S.; Noah, J.A. Comparative abilities of Microsoft Kinect and Vicon 3D motion capture for gait analysis. J. Med. Eng. Technol. 2014, 38, 274–280. [Google Scholar] [CrossRef]
- Xu, X.; McGorry, R.W.; Chou, L.S.; Lin, J.H.; Chang, C.C. Accuracy of the Microsoft Kinect for measuring gait parameters during treadmill walking. Gait Posture 2015, 42, 145–151. [Google Scholar] [CrossRef]
- Ma, Y.; Mithraratne, K.; Wilson, N.C.; Wang, X.; Ma, Y.; Zhang, Y. The validity and reliability of a kinect v2-based gait analysis system for children with cerebral palsy. Sensors 2019, 19, 1660. [Google Scholar] [CrossRef]
- Tamura, H.; Tanaka, R.; Kawanishi, H. Reliability of a markerless motion capture system to measure the trunk, hip and knee angle during walking on a flatland and a treadmill. J. Biomech. 2020, 109, 109929. [Google Scholar] [CrossRef]
- Stratford, P.W.; Goldsmith, C.H. Use of the standard error as a reliability index of interest: An applied example using elbow flexor strength data. Phys. Ther. 1997, 77, 745–750. [Google Scholar] [CrossRef] [PubMed]
- Akbas, T.; Neptune, R.R.; Sulzer, J. Neuromusculoskeletal simulation reveals abnormal rectus femoris-gluteus medius coupling in post-stroke gait. Front. Neurol. 2019, 10, 301. [Google Scholar] [CrossRef] [PubMed]
- Hall, A.L.; Peterson, C.L.; Kautz, S.A.; Neptune, R.R. Relationships between muscle contributions to walking subtasks and functional walking status in persons with post-stroke hemiparesis. Clin. Biomech. 2011, 26, 509–515. [Google Scholar] [CrossRef] [PubMed]

| Study | Participants | Indicators of Compensatory Movements during Swing Phase | Equipment |
|---|---|---|---|
| Kerrigan et al. [11] | Post-stroke patients (n = 23), healthy people (n = 23) | Peak values during paretic swing phase (coronal pelvic angle, transverse pelvic rotation, hip adduction, hip abduction, thigh adduction, and thigh abduction), values at mid-swing (coronal pelvic angle, transverse pelvic angle, bilateral coronal hip angle, and affected thigh angle) | Marker-based 3DMA |
| Stanhope et al. [12] | Post-stroke patients (n = 21) | Peak paretic pelvic tilt angle, peak paretic hip abduction angle, toe displacement | Marker-based 3DMA |
| Tyrell et al. [13] | Post-stroke patients (n = 22) | Hip hiking (the angle in the frontal plane between the pelvis position in static standing and the maximum deviation from that position in the swing phase), circumduction (maximum lateral difference between the position of the heel marker in the stance phase and the same heel marker position in the swing phase immediately following the stance phase) | Marker-based 3DMA |
| Sex (male, female) a | 32 (19/13) |
| Age (years) b | 2.0 |
| Height (cm) b | 9.8 |
| Weight (kg) b | 9.3 |
| Variables | Marker-Based 3DMA | Depth-Sensor-Based 3DMA | p-Value | ICC2,1 (95% CI) | ICC3,1 (95% CI) | RMSE |
|---|---|---|---|---|---|---|
| Combined sample | ||||||
| Contralateral vaulting (m) | 0.01 | 0.01 | 0.827 | 0.57 (0.37–0.72) | 0.57 (0.37–0.71) | 0.01 |
| Trunk lateral flexion to stance side (deg) | 2.42 | 2.06 | 0.624 | 0.80 (0.55–0.90) | 0.85 (0.77–0.90) | 1.30 |
| Hip hiking (deg) | 4.87 | 2.45 | 0.103 | 0.59 (0.39–0.72) | 0.64 (0.47–0.77) | 1.99 |
| Swing-side hip abduction (deg) | 3.13 | 1.92 | 0.498 | 0.59 (0.40–0.73) | 0.59 (0.40–0.73) | 2.37 |
| Circumduction (deg) | 2.68 | 2.57 | 0.001 a | 0.61 (0.26–0.78) | 0.76 (0.63–0.84) | 1.53 |
| KAFO condition | ||||||
| Contralateral vaulting (m) | 0.01 | 0.01 | 0.644 | 0.51 (0.08–0.79) | 0.56 (0.12–0.82) | 0.01 |
| Trunk lateral flexion to stance side (deg) | 2.31 | 1.95 | 0.001 a | 0.66 (0.04–0.89) | 0.79 (0.51–0.92) | 1.43 |
| Hip hiking (deg) | 1.90 | 2.25 | 0.047 a | 0.09–0.75) | 0.11–0.72) | 1.77 |
| Swing-side hip abduction (deg) | 1.90 | 2.17 | 0.083 | 0.09–0.84) | 0.83 (0.60–0.94) | 2.67 |
| Circumduction (deg) | 2.77 | 3.29 | 0.016 a | 0.03–0.89) | 0.72 (0.38–0.89) | 0.96 |
| Variables | Marker-Based 3DMA | Depth-Sensor-Based 3DMA | p-Value | ICC2,1 (95% CI) | ICC3,1 (95% CI) | RMSE | |
|---|---|---|---|---|---|---|---|
| Combined sample | |||||||
| Step width (m) | 0.04 | 0.04 | 0.213 | 0.89 (0.79–0.91) | 0.87 (0.78–0.91) | 0.02 | |
| Step length (m) | Right | 0.08 | 0.08 | 0.001 a | 0.93 (0.51–0.98) | 0.96 (0.95–0.98) | 0.03 |
| Left | 0.08 | 0.08 | 0.001 a | 0.93 (0.56–0.97) | 0.96 (0.94–0.98) | 0.03 | |
| Stride length (m) | 0.19 | 0.19 | 0.001 a | 0.98 (0.96–0.99) | 0.98 (0.98–0.99) | 0.04 | |
| Cadence (steps/min) | 9.93 | 10.20 | 0.146 | 0.97 (0.95–0.98) | 0.97 (0.95–0.98) | 2.40 | |
| Gait velocity (m/s) | 0.17 | 0.17 | 0.013 a | 0.99 (0.99–1.00) | 0.99 (0.99–1.00) | 0.01 | |
| Stance time (s) | 0.15 | 0.15 | 0.222 | 0.93 (0.88–0.96) | 0.94 (0.90–0.96) | 0.05 | |
| Swing time (s) | 0.05 | 0.05 | 0.477 | 0.80 (0.67–0.88) | 0.82 (0.73–0.83) | 0.03 | |
| Gait cycle time (s) | 0.19 | 0.19 | 0.217 | 0.97 (0.96–0.98) | 0.97 (0.95–0.98) | 0.04 | |
| (%) | 2.44 | 2.33 | 0.001 a | 0.58 (0.34–0.74) | 0.63 (0.45–0.76) | 2.27 | |
| (%) | 2.46 | 2.37 | 0.001 a | 0.58 (0.34–0.74) | 0.63 (0.43–0.76) | 2.27 | |
| Step length ratio | 0.12 | 0.15 | 0.705 | 0.71 (0.56–0.82) | 0.71 (0.55–0.81) | 0.10 | |
| Swing time ratio | 0.09 | 0.10 | 0.021 a | 0.71 (0.42–0.85) | 0.77 (0.65–0.86) | 0.08 | |
| KAFO condition | |||||||
| Step width (m) | 0.03 | 0.05 | 0.087 | 0.87(0.67–0.95) | 0.88 (0.71–0.96) | 0.02 | |
| Step length (m) | Right | 0.07 | 0.06 | 0.001 a | 0.85 (0.17–0.96) | 0.93 (0.81–0.97) | 0.04 |
| Left | 0.06 | 0.05 | 0.001 a | 0.93 (0.80–0.97) | 0.94 (0.84–0.98) | 0.03 | |
| Stride length (m) | 0.13 | 0.11 | 0.121 | 0.97 (0.92–0.99) | 0.97 (0.92–0.99) | 0.03 | |
| Cadence (steps/min) | 1.54 | 2.38 | 0.124 | 0.09–0.70) | 0.11–0.72) | 2.42 | |
| Gait velocity (m/s) | 0.07 | 0.06 | 0.063 | 0.94 (0.90–0.99) | 0.97 (0.92–0.99) | 0.02 | |
| Stance time (s) | 0.05 | 0.06 | 0.251 | 0.10–0.71) | 0.12–0.71) | 0.06 | |
| Swing time (s) | 0.05 | 0.04 | 0.930 | 0.72 (0.38–0.89) | 0.72 (0.37–0.86) | 0.04 | |
| Gait cycle time (s) | 0.04 | 0.05 | 0.180 | 0.11–0.70) | 0.13–0.71) | 0.04 | |
| (%) | 2.60 | 2.40 | 0.518 | 0.63 (0.22–0.84) | 0.62 (0.21–0.84) | 2.26 | |
| (%) | 2.60 | 2.40 | 0.518 | 0.63 (0.22–0.85) | 0.62 (0.21–0.84) | 2.26 | |
| Step length ratio | 0.15 | 0.16 | 0.027 a | 0.75 (0.38–0.91) | 0.79 (0.52–0.92) | 0.12 | |
| Swing time ratio | 0.11 | 0.11 | 0.061 | 0.66 (0.28–0.86) | 0.69 (0.35–0.88) | 0.10 | |
| Variables | Marker-Based 3DMA | Depth-Sensor-Based 3DMA | p-Value | ICC2,1 (95% CI) | ICC3,1 (95% CI) | RMSE |
|---|---|---|---|---|---|---|
| Combined sample | ||||||
| Trunk angle (deg) | ||||||
| Peak-to-peak | ||||||
| Flexion–extension | 1.77 | 1.85 | 0.001 a | 0.74 (0.22–0.90) | 0.85 (0.75–0.90) | 1.49 |
| Lateral flexion | 3.37 | 2.13 | 0.099 | 0.76 (0.63–0.86) | 0.76 (0.63–0.84) | 1.89 |
| Rotation | 3.45 | 4.30 | 0.001 a | 0.79 (0.01–0.85) | 0.79 (0.68–0.87) | 3.77 |
| Mean | ||||||
| Flexion–extension | 3.20 | 2.43 | 0.086 | 0.03–0.65) | 0.85 (0.76–0.91) | 6.10 |
| Lateral flexion | 1.41 | 1.06 | 0.001 a | 0.65 (0.44–0.77) | 0.69 (0.53–0.80) | 1.08 |
| Rotation | 3.87 | 3.17 | 0.386 | 0.73 (0.58–0.83) | 0.72 (0.58–0.83) | 2.63 |
| Hip joint angle [+extension/−flexion] (deg) | ||||||
| Maximum | 4.81 | 4.63 | 0.001 a | 0.40 (0.07–0.75) | 0.80 (0.69–0.87) | 7.42 |
| Minimum | 4.94 | 4.46 | 0.001 a | 0.23 (0.03–0.60) | 0.80 (0.70–0.88) | 11.00 |
| Peak-to-peak | 5.33 | 6.23 | 0.092 | 0.72 (0.06–0.93) | 0.93 (0.89–0.96) | 4.45 |
| Knee joint angle [+extension/−flexion] (deg) | ||||||
| Maximum | 4.18 | 2.75 | 0.001 a | 0.07–0.86) | 0.75 (0.69–0.80) | 6.24 |
| Minimum | 18.63 | 15.90 | 0.522 | 0.93 (0.83–0.95) | 0.92 (0.88–0.95) | 5.93 |
| Peak-to-peak | 20.53 | 15.10 | 0.001 a | 0.87 (0.70–0.93) | 0.90 (0.84–0.94) | 8.52 |
| Ankle joint angle [+plantar flexion/−dorsal flexion] (deg) | ||||||
| Maximum | 7.09 | 33.10 | 0.001 a | 0.03 (–0.12–0.15) | 0.05 (–0.30–0.20) | 49.67 |
| Minimum | 3.87 | 8.56 | 0.001 a | 0.05(–0.12–0.10) | 0.27 (–0.49–0.03) | 10.81 |
| Peak-to-peak | 8.06 | 36.56 | 0.001 a | 0.43 (0.02–0.67) | 0.57 (–0.37–0.71) | 49.63 |
| Maximum leg extension angle (deg) | 3.89 | 3.74 | 0.001 a | 0.81 (0.03–0.93) | 0.92 (0.87–0.95) | 2.56 |
| KAFO condition | ||||||
| Trunk angle (deg) | ||||||
| Peak-to-peak | ||||||
| Flexion–extension | 1.94 | 1.48 | 0.001 a | 0.71 (0.03–0.91) | 0.85 (0.64–0.94) | 1.47 |
| Lateral flexion | 2.50 | 1.65 | 0.001 a | 0.07–0.81) | 0.69 (0.32–0.87) | 1.89 |
| Rotation | 3.84 | 4.43 | 0.001 a | 0.69 (0.08–0.90) | 0.81 (0.54–0.93) | 3.77 |
| Mean | ||||||
| Flexion–extension | 3.40 | 0.93 | 0.043 a | 0.04–0.70) | 0.83 (0.59–0.93) | 6.02 |
| Lateral flexion | 1.76 | 1.30 | 0.048 a | 0.67 (0.30–0.87) | 0.71 (0.36–0.88) | 1.34 |
| Rotation | 3.91 | 3.13 | 0.213 | 0.90 (0.74–0.96) | 0.90 (0.74–0.96) | 1.68 |
| Hip joint angle [+extension/−flexion] (deg) | ||||||
| Maximum | 4.55 | 3.79 | 0.001 a | 0.08–0.75) | 0.75 (0.43–0.90) | 6.99 |
| Minimum | 5.13 | 4.55 | 0.001 a | 0.05–0.68) | 0.76 (0.46–0.91) | 10.24 |
| Peak-to-peak | 3.75 | 4.41 | 0.027 a | 0.08–0.92) | 0.90 (0.04–0.96) | 3.84 |
| Knee joint angle [+extension/−flexion] (deg) | ||||||
| Maximum | 4.14 | 3.21 | 0.001 a | 0.02–0.76) | 0.02–0.75) | 3.95 |
| Minimum | 4.94 | 4.29 | 0.001 a | 0.08–0.68) | 0.02–0.76) | 6.34 |
| Peak-to-peak | 1.69 | 2.83 | 0.001 a | 0.02–0.34) | 0.41–0.52) | 4.67 |
| Ankle joint angle [+plantar flexion/−dorsal flexion] (deg) | ||||||
| Maximum | 2.09 | 25.50 | 0.033 a | 0.12–0.28) | 0.42–0.51) | 49.46 |
| Minimum | 1.84 | 7.69 | 0.021 a | 0.09–0.16) | 0.52–0.41) | 9.52 |
| Peak-to-peak | 1.99 | 29.52 | 0.001 a | 0.47–0.49) | 0.45–0.46) | 55.88 |
| Maximum leg extension angle (deg) | 2.85 | 3.74 | 0.001 a | 0.09–0.90) | 0.85 (0.62–0.94) | 2.70 |
| Variables | Marker-Based 3DMA | Depth-Sensor-Based 3DMA | p-Value | ICC2,1 (95% CI) | ICC3,1 (95% CI) | RMSE |
|---|---|---|---|---|---|---|
| Combined sample | ||||||
| Peak-to-peak value of center of mass movement (m) | ||||||
| Mediolateral | 0.03 | 0.02 | 0.063 | 0.94 (0.91–0.97) | 0.95 (0.91–0.97) | 0.01 |
| Vertical | 0.02 | 0.01 | 0.001 a | 0.15–0.17) | 0.26–0.26) | 0.03 |
| Mediolateral margin of stability (m) | 0.02 | 0.03 | 0.001 a | 0.10–0.76) | 0.77 (0.64–0.86) | 0.04 |
| Anteroposterior margin of stability (m) | 0.03 | 0.05 | 0.001 a | 0.04–0.56) | 0.75 (0.61–0.84) | 0.10 |
| KAFO condition | ||||||
| Peak-to-peak value of center of mass movement (m) | ||||||
| Mediolateral | 0.02 | 0.02 | 0.392 | 0.84 (0.55–0.94) | 0.87 (0.70–0.94) | 0.01 |
| Vertical | 0.02 | 0.01 | 0.013 a | 0.38–0.30) | 0.57–0.35) | 0.03 |
| Mediolateral margin of stability (m) | 0.03 | 0.03 | 0.001 a | 0.11–0.80) | 0.72 (0.38–0.89) | 0.04 |
| Anteroposterior margin of stability (m) | 0.02 | 0.03 | 0.001 a | 0.04–0.31) | 0.07–0.74) | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusuda, K.; Matsubara, S.; Noguchi, D.; Kuwahara, M.; Hamasaki, H.; Miwa, T.; Maeda, T.; Nakanishi, T.; Ninomiya, S.; Honda, K. Concurrent Validity of Depth-Sensor-Based Quantification of Compensatory Movements during the Swing Phase of Gait in Healthy Individuals. Biomechanics 2024, 4, 411-427. https://doi.org/10.3390/biomechanics4030028
Kusuda K, Matsubara S, Noguchi D, Kuwahara M, Hamasaki H, Miwa T, Maeda T, Nakanishi T, Ninomiya S, Honda K. Concurrent Validity of Depth-Sensor-Based Quantification of Compensatory Movements during the Swing Phase of Gait in Healthy Individuals. Biomechanics. 2024; 4(3):411-427. https://doi.org/10.3390/biomechanics4030028
Chicago/Turabian StyleKusuda, Kento, Shigehito Matsubara, Daisuke Noguchi, Moe Kuwahara, Hiroomi Hamasaki, Toshihiro Miwa, Toru Maeda, Toshihito Nakanishi, Shogo Ninomiya, and Keita Honda. 2024. "Concurrent Validity of Depth-Sensor-Based Quantification of Compensatory Movements during the Swing Phase of Gait in Healthy Individuals" Biomechanics 4, no. 3: 411-427. https://doi.org/10.3390/biomechanics4030028
APA StyleKusuda, K., Matsubara, S., Noguchi, D., Kuwahara, M., Hamasaki, H., Miwa, T., Maeda, T., Nakanishi, T., Ninomiya, S., & Honda, K. (2024). Concurrent Validity of Depth-Sensor-Based Quantification of Compensatory Movements during the Swing Phase of Gait in Healthy Individuals. Biomechanics, 4(3), 411-427. https://doi.org/10.3390/biomechanics4030028








