Effects of Gait Speed and Sole Adjustment on Shoe–Floor Angles: Measurement Using Shoe-Type Sensor

Abstract

Background: Assessment of walking with shoes is important for understanding different types of walking in various environments. Methods: In this study, a shoe-type sensor was used to demonstrate the shoe–floor angle in fifteen participants who walked on a treadmill under varying gait speed and sole adjustments, lifting one side of the sole. The shoe–floor angle in the sagittal; the angle of toe-up (θTup) and toe-down (θTdown) and frontal planes; and the angle of pronation (θPro) and supination (θSup) were calculated, and angles at the initial contact and maximum angles were extracted. Results: The results showed that most angles significantly increased with an increase in the gait speed (θTup and θTdown; p < 0.01 both, θPro and θSup; p < 0.02 and 0.04). Conversely, only the supination angle at the initial contact changed significantly, owing to the tilt of the sole (p < 0.01). Conclusion: Shoe movements were more strongly affected by gait speed than by sole adjustment.

1. Introduction

Individuals wear shoes for a significant amount of time. Hence, the evaluation of walking in shoes is essential for understanding the different types of walking in various environments. Previous studies reported differences between barefoot and shoe-wearing gaits [1]. An increase in stride length [2] and a decrease in cadence [3] have been reported when wearing shoes. Furthermore, an increase in the anteroposterior center of pressure displacement has been reported [4]. The range of motion of the ankle joint is significantly increased by wearing shoes [4], and differences in the plantar flexion moment [5] and the propulsive ground reaction force [6] have also been observed. Shoes may increase the forefoot stiffness by decreasing the spread of the forefoot and providing support against the increased plantar flexion moment during the late stance phase. However, the effects of the gait conditions on shoe movements remain unclear. Therefore, clarifying the kinematic changes in gait conditions is needed for designing shoes in various environments.

Although various gait analysis methods have been reported, the simplest and easiest method is the use of an accelerometer. In particular, lumbar-mounted accelerometers are widely used for the quantification of gait [7]. Menz et al. [8] calculated the root mean square range of motion values of acceleration data measured using a lumbar accelerometer to evaluate the sway of the center of gravity. To show the periodicity of gait, Moe-Nilssen et al. [9] calculated the similarity of the acceleration waveforms between each gait cycle. Other methods that indicate the harmony and stationarity of gait, such as the harmonic ratio [10] and entropy [11], have also been reported. Subsequently, lower leg-mounted accelerometers were used to demonstrate gait events, such as heel contact, and the previous study showed the gait instability using the variability of stride time [12].

A method for measuring foot movements using a foot-mounted accelerometer has also been reported [13]. Previous studies have used the foot–floor angle (FFA), which is the angle between the foot and floor. FFAs in the sagittal plane are clinically important for gait speed [14], slip accidents [15], and falls [16]. The pronation angle in the frontal plane has been shown to be associated with low back pain [17] and injuries during running [18]. Although the characteristics of FFAs have been reported, the angle between the shoe and floor (shoe–floor angle; SFA) has not been clear. Furthermore, it requires the sensors to be placed inside the shoes to clarify the SFA directly.

In this study, the ORPHE, a shoe-type sensor with a built-in accelerometer, was used. The validity of the method using this sensor was clarified in a previous study [19]. ORPHE can directly measure and demonstrate the details of SFAs in real time. In this study, we evaluated the changes in the parameters measured using this sensor under various gait speed and sole adjustment conditions. The purpose of this study is to clarify the change in the SFA due to gait speed and sole adjustment. We hypothesized that changes in gait speed and shoe adjustment cause the change in the SFA in the sagittal plane and frontal plane, respectively. The results of this study are expected to provide basic data for gait analyses in diverse environments.

2. Materials and Methods

2.1. Participants

A total of 15 healthy young adults (11 males and 4 females) participated in the study (mean ± standard deviation: age 27.3 ± 9.1 years; height 172.0 ± 8.0 cm; weight 67.9 ± 12.1 kg). The sample size was calculated by G*Power 3.1 (effect size was set at 0.5, significance level at 5%, and power at 0.8) with reference to a previous study [20]. The exclusion criteria were that they had been diagnosed with a musculoskeletal or neurological disease within 2 months of the measurement and current treatment. Furthermore, the inclusion criterion was the absence of pain or instability during walking. The participants were faculty and students affiliated with medical universities who had a general standard of physical activity without excessive or special training.

2.2. Procedure

Gait measurements were performed while the participants wore shoes (SHIBUYA 2.0, ORPHE Inc., Tokyo, Japan) on a treadmill (AUTO RUNNER AR-200; MINATO MERDICAL SCIENCE Co., Osaka, Japan). The shoe-type sensor ORPHE TRACK (ORPHE Inc., Tokyo, Japan; size: 45 mm × 29 mm × 14 mm; weight: 20 g, sampling frequency: 200 Hz; Figure 1) measured the three-axial accelerations and angular velocities using a built-in sensor. Shoe sizes were selected from a range of 23 to 28 cm in 1 cm increments. Five walking conditions were performed: two conditions of gait speed change, two conditions of change in sole adjustments, and the normal condition. The treadmill was set at an inclined angle of 0°, and the walking speed for each condition was set before the measurement. The starting speed was set to 0 km/h and was gradually increased until the set speed was reached after a few seconds; after the set speed was reached, a constant speed was maintained. During the measurements, the participants walked for 1 min under each condition, and the data for the following 15 s were measured.

For the normal condition (Normal), the walking speed was set to 4 km/h; for the other two conditions, the walking speed was set to 3 km/h (Slow) and 5 km/h (Fast). The average speed during overground walking was 4.5–4.8 km/h [21]. However, a comfortable gait speed on a treadmill has been reported to be slower than that of overground walking [22]. To examine changes in speed, the other two conditions were set to ±1 km/h from the walking speed set for the Normal condition. For the sole adjustment condition, 2 cm wide and 6 mm thick ethylene-vinyl acetate hard sponges were cut from the calcaneus to the thenar and attached under the shoe insert with double-sided tape. In each condition, the sponges were inserted in the medial (Medial) and lateral (Lateral) positions to lift one side of the sole. Each condition was performed in a random order to minimize learning effects.

2.3. Data Analysis

The data obtained were analyzed using ORPHE ANALYTICS (ORPHE Inc.) [19]. Euler angles were calculated using a Madgwick filter [23] from the obtained acceleration and angular velocity. The SFAs were demonstrated on the sagittal and frontal planes. Data from five gait cycles were extracted and normalized to a 100% gait cycle, and the average waveform was calculated. As shown in Figure 2, the angle of toe-up (θTup) and toe-down (θTdown) in the sagittal plane, and the angle of supination (θSup) and pronation (θPro) in the frontal plane were demonstrated.

For outcomes, θTup and θSup at the initial contact and the maximum θTdown and θPro were extracted as the magnitude of the SFA relating to important events during gait. The waveform obtained was expressed as 100% for each gait cycle and standardized across the participants. This approach enabled calculating the timing within the gait cycles, and the timing of maximum θTdown and θPro were evaluated as the timing of the SFA. The average and median values of parameters were calculated for each condition as a representative value.

2.4. Statistical Analysis

Statistical analyses were performed using the SPSS software (version 28; IBM, Armonk, NY, USA). The measured data were tested for normality using the Shapiro–Wilk test. The test showed that some of the data were not normally distributed.

Table 1. The average and median values of parameters among each condition and results of the Shapiro–Wilk test.

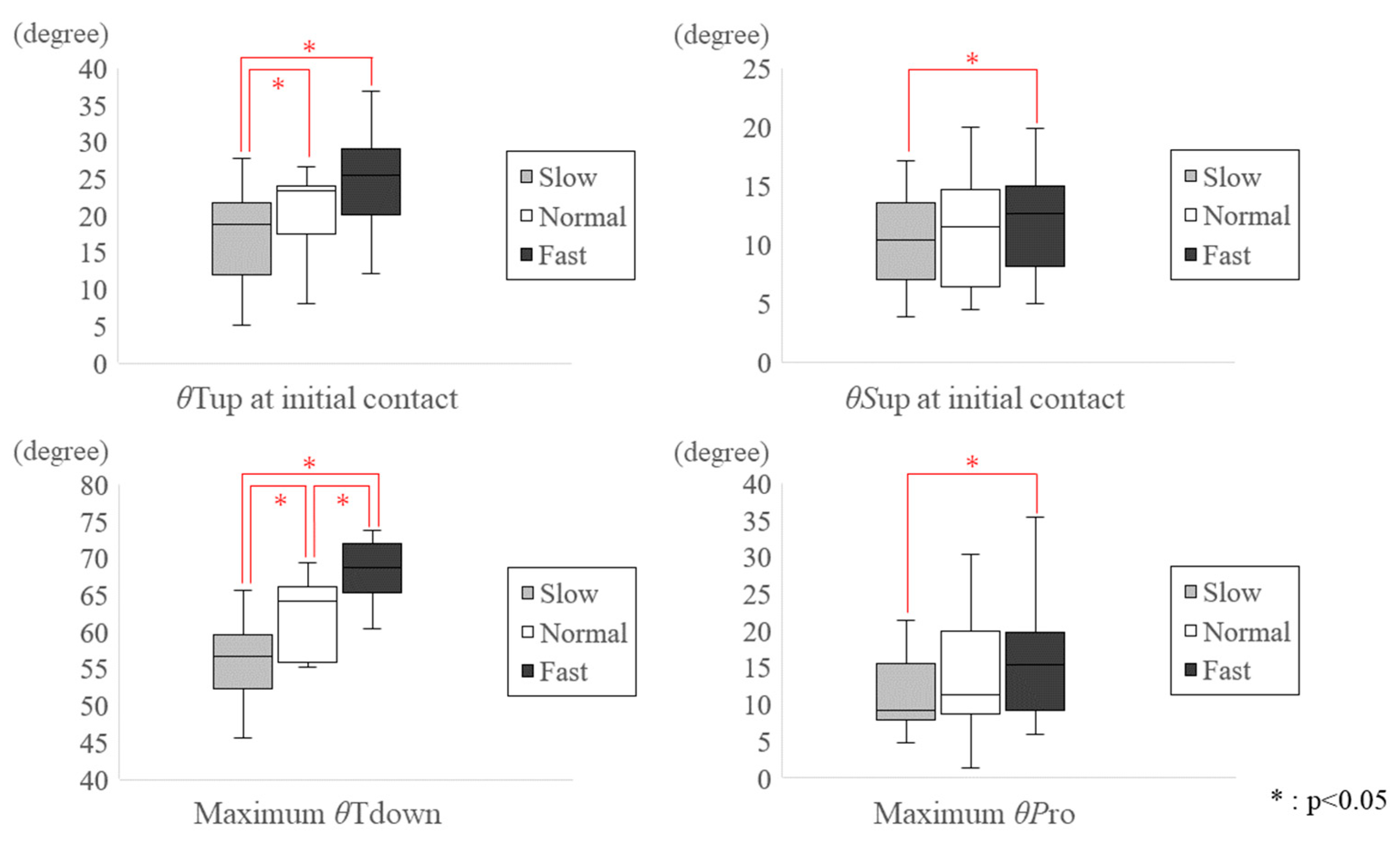
Parameters	Condition	Average (SD)	Median (IQR)	p-Value of Shapiro–Wilk Test
θTup at Initial contact
	Normal	21.4 (6.3)	23.3 (18.6–23.9)	0.49
	Slow	17.3 (6.0)	18.8 (14.3–21.3)	0.54
	Fast	25.3 (6.3)	25.4 (20.8–28.9)	0.97
	Medial	21.4 (6.7)	24.0 (16.9–26.2)	0.10
	Lateral	19.1 (5.9)	21.8 (15.5–22.9)	0.04 *
θSup at Initial contact
	Normal	11.1 (4.2)	11.5 (7.7–13.8)	0.57
	Slow	10.2 (3.7)	10.4 (7.6–12.9)	0.92
	Fast	12.0 (4.3)	12.6 (8.2–14.5)	0.71
	Medial	9.4 (3.5)	9.6 (6.5–11.9)	0.98
	Lateral	12.6 (4.1)	11.6 (10.4–14.6)	0.20
Maximum θTdown
	Normal	61.9 (5.1)	64.2 (56.5–65.8)	0.06
	Slow	56.0 (5.1)	56.6 (52.2–59.4)	1.00
	Fast	68.5 (4.0)	68.7 (66.0–71.8)	0.29
	Medial	61.4 (3.9)	62.2 (58.5–64.2)	0.75
	Lateral	60.9 (3.8)	58.9 (58.4–63.9)	0.09
Maximum θPro
	Normal	14.2 (7.7)	11.3 (9.1–18.8)	0.33
	Slow	11.2 (4.7)	9.2 (8.4–13.2)	0.02 *
	Fast	17.1 (9.5)	15.3 (9.8–19.1)	0.04 *
	Medial	12.5 (6.1)	11.4 (8.7–14.2)	0.21
	Lateral	13.5 (7.9)	10.8 (7.7–18.8)	0.52
Timing of maximum θTdown
	Normal	70.1 (2.0)	70 (68–71.5)	0.03 *
	Slow	71.3 (1.4)	71 (70–72.5)	0.32
	Fast	67.9 (1.8)	67 (67–69.5)	0.29
	Medial	69.7 (1.8)	69 (68.5–70.5)	0.10
	Lateral	69.8 (1.4)	70 (69–71)	0.45
Timing of maximum θPro
	Normal	74.7 (4.9)	72 (71–76)	<0.01 *
	Slow	76.8 (3.4)	77 (74.5–78)	0.31
	Fast	71.9 (3.9)	71 (69–73)	0.03 *
	Medial	75.8 (4.1)	74 (73–77)	0.03 *
	Lateral	75.3 (4.7)	75 (72–76.5)	0.12

SD: standard deviation. IQR: interquartile range. *: p < 0.05.

shows the average and median value of parameters and the results of the Shapiro–Wilk test in each condition. To compare the parameters using a consistent method, we used the Friedman test for all parameters to examine the differences due to changes in gait speed and sole adjustment. In addition, a post-hoc analysis with the Bonferroni correction was performed to compare the conditions. The statistical significance was set at 5%.

Written informed consent was obtained from all the participants. This study was approved by the Institutional Ethics Review Committee (PAZ21-31; 27 October 2021), and measurements were obtained with the participants’ free and voluntary consent.

3. Results

The average angular changes during the five gait cycles are shown in Figure 3. And the data of each participant are shown in Table S1.

3.1. Change in Magnitude of SFA with Gait Speed

Figure 4 shows the changes in the magnitude of the SFA with changes in speed. In the sagittal plane, the median θTup values at initial contact were 18.8°, 23.3°, and 25.4° in the Slow (3 km/h), Normal (4 km/h), and Fast (5 km/h) speed, respectively, and a significant effect of gait speed was found (p < 0.01). Significant differences were observed between the Slow and Normal speed (p = 0.01) and the Slow and Fast speed (p < 0.01); however, no significant difference between the Normal and Fast speed (p = 0.05) was noted.

The maximum θTdown values were 56.6°, 64.2°, and 68.7° under the Slow, Normal, and Fast speed, respectively, indicating a significant increase at higher speed (p < 0.01). Significant differences were observed between all speeds (Slow-Normal, p = 0.02; Normal-Fast, p = 0.02; Slow-Fast, p < 0.01).

In the frontal plane, the θSup values at initial contact were 10.4°, 11.5°, and 12.6° for the Slow, Normal, and Fast speed, respectively, and a significant effect of gait speed was demonstrated (p = 0.04). However, a statistically significant difference was observed only between the Slow and Fast speed (p = 0.03); there was no significant difference between the Slow and Normal (p = 0.60) or Normal and Fast speed (p = 0.60). Finally, the maximum θPro values were 9.2°, 11.3°, and 15.3° for the Slow, Normal, and Fast speed, respectively, and a significant effect of gait speed was found (p = 0.02). A statistically significant difference was observed only between the Slow and Fast speed (p = 0.02), and no significant difference was found between the Slow and Normal (p = 0.30) and Normal and Fast speed (p = 0.82).

3.2. Change in Magnitude of SFA with Sole Adjustment

The changes in the magnitude of the SFA due to the lift of one side of the sole are shown in Figure 5. A significant difference was observed only in the θSup at the initial contact (p < 0.01). Specifically, the increase in the θSup values were 11.5°, 9.6°, and 11.6° for the Normal, Medial, and Lateral conditions, respectively. Significant differences were observed only between the Medial and Lateral conditions (p < 0.01); however, there were no significant differences between the Normal and Medial (p = 0.82) or Normal and Lateral conditions (p = 0.08).

3.3. Change in Timing of SFA with Gait Speed and Sole Adjustment

The results for the timing of the SFA are listed in

Table 2. Change in timing of SFA with gait speed and sole adjustment.

% Gait Cycle (% GC)	Normal	Slow	Fast	Medial	Lateral
Toe down	70	71	67 *	69	70
Pronation	72	77	71 *	74	75

The data are expressed as 100% for each gait cycle (% gait cycle; % GC). The timing of the maximum toe-down and pronation were evaluated as timing of SFA. *: Significant difference compared with Normal.

. The timing is expressed as a percentage of the gait cycle with the gait cycle set as 100% (%gait cycle; %GC). The timing of the maximum θTdown were 71% GC, 70% GC, and 67% GC for the Slow, Normal, and Fast speed, respectively, and the timing significantly changed with gait speed (p < 0.01). Significant differences were observed between the Normal and Fast speed (p < 0.01), and between the Slow and Fast speed (p < 0.01).

The timing of maximum θPro were 77% GC, 72% GC, and 71% GC for the Slow, Normal, and Fast speed, respectively, and the timing significantly changed as speed increased (p < 0.01). Significant differences were observed between the Normal and Fast speed (p = 0.02) and between the Slow and Fast speed (p < 0.01).

No significant difference was observed in the effect of the sole adjustment on the timing of maximum θTdown and θPro (p = 0.35 and 0.19, respectively).

4. Discussion

The results of this study showed that a significant effect of gait speed was confirmed for several parameters relating to the magnitude of the SFA. Changes of sole adjustment affected only the supination angle at initial contact.

As shown in Figure 3, the shoe was grounded in the toe-up position, and the SFA changed to a toe-down position during the late stance. Additionally, the shoe was grounded in the supination position, in the loading response, it was in the intermediate position owing to shoe stiffness, and finally, it exhibited a maximum pronation position with the toe-off. Huang et al. [24] investigated the shoe–floor angle using a method similar to our study. The average waveform shown in this previous study is consistent with the waveform shown in this study (Figure 3), and the range of motion also shows similar values between both figures. Therefore, it is considered that the measurement used in this study is appropriate for indicating the shoe–floor angle.

The timing of the SFA demonstrated that the maximum pronation and toe-down occurred simultaneously during the toe-off in the late stance phase. In this phase, the center of pressure may move medially and forward from the heel because of the weight transfer to the opposite lower limb. Hence, it is suggested that the shoe pronation in the late stance phase is important for moving the center of foot pressure medially and guiding it to the thenar region during toe-off.

For the angle in the sagittal plane, both the toe-up and toe-down angles significantly increased with increasing gait speed. A previous study showed that dorsiflexion at the loading response, plantar flexion at the toe-off, and pronation and supination angles changed according to gait speed in the barefoot condition [20]. The results of this study showed similar changes in the SFA. These changes in angle may have occurred because of the increase in stride length. An increase in stride length may lead to an increase in the plantar flexion moment related to an increase in the angle of the toe-down. In a previous study, the foot angle in the late stance was related to forward propulsion [25]. An increase in the plantar flexion moment and forward propulsion may assist the swinging of the lower limb, resulting in a difference in the toe-up angle. A previous study showed that the foot angle in the sagittal plane was more strongly related to gait speed than to gait efficiency [14], which supports the results of this study. These results indicate that increased gait speed may expand the range of motion in the sagittal plane during fast walking. It is suggested that the contact area is reduced at initial contact and the toe-off phase. Therefore, higher balance ability and shoe flexibility may be needed for stability during fast walking. Furthermore, the results of this study suggested that shoes may contact the floor surface at the upper (proximal) positions of the toe and heel. When designing shoes for sports, it is important to adjust the flexibility of the forefoot and heel areas, and the choice of materials for the contact area with the floor.

Previous studies have reported changes in gait caused by sole adjustments in barefoot conditions. A previous study reported a reduction in the supination angle caused by a medial wedge insole [26]. Similarly, in this study, the supination angle tended to decrease in the Medial condition and slightly increase in the Lateral condition compared to that in the Normal condition, and a significant difference was found between the Medial and Lateral conditions. These results suggest that a change in the supination angle occurred to maintain a constant angle between the foot sole and floor surfaces. A previous study also showed the compensatory change to adapt to road conditions and shoe materials to prevent falls [27]. This result also suggested that the medial wedge insole may cause the displacement of the center of pressure toward a lateral position. The lateral area of the shoes needs to be robust and flexible. Furthermore, the results of this study showed that the lift of the lateral side of the sole increased the supination angle, suggesting that clinicians and designers should consider the possibility of an increased risk of inversion sprains when adjusting the shape of the sole surface.

This study has some limitations. First, the age range of the participants was narrow. The results may differ for older people and children because of differences in gait patterns compared to that for adults. However, these results need to be verified in a variety of participants, including patients and athletes. Second, the study was conducted in a laboratory setting, and the measurements were performed on a treadmill. A previous study showed a difference in gait between overground and treadmill walking [22]; therefore, future studies are required to investigate overground walking under outdoor conditions. Third, the relationship between the foot–floor angle and shoe–floor angle was not demonstrated. It is not clear to what extent a sole adjustment induces pronation and supination of the foot. To solve this problem, it is necessary to measure foot motion inside shoes during gait; however, this is currently difficult owing to the limitations of the measurement equipment. In the present study, the change in shoe movement was due to the gait conditions, but the reason of the results was unclear. In future studies, it will be necessary to consider a setting that allows simultaneous measurement of foot and shoe movements. Finally, for clinical applications, it is necessary to clarify the relationship among data measured using shoe-type sensors, motor function, and functional disorders. In the future, it will be necessary to clarify the correlation between the shoe–floor angle and the parameters used in medical and sports settings.

Shoe-type sensors do not require procedures such as attaching and fixing an accelerometer, allowing for simple measurements. Accelerometers are widely used in laboratory settings; however, in clinical settings, it is important to simplify the measurements to provide immediate feedback. The results of this study clarified the changes in the shoe–floor angle, and we believe that it has the potential for use in several clinical settings. A previous study showed that this sensor could be attached to commercially available shoes and to a patient’s own shoes [19]. Thus, it may be possible to use this sensor repeatedly to adjust trial products and to assess gait function. In particular, the results of this study indicate that the contact area may differ depending on the walking speed and sole adjustment, which is an important issue for shoemakers to consider when maintaining the robustness and flexibility of shoes.

5. Conclusions

The results of this study demonstrated the SFA in response to changes in gait speed and showed that compensatory changes occurred in response to changes in the sole adjustment. These results suggest that the magnitude of the SFA measured using ORPHE change according to gait speed, and the indices in the frontal plane can be indicators that reflect adaptive behavior. Shoe designers need to consider the change in the SFA to design shoes to prevent injuries and ensure durability. Thus, designing shoes according to the walking conditions is needed. Further studies are required to verify the SFA during various movements and activities of daily living. It is important to note that the ORPHE has potential as an assessment tool in gait analysis, shoemaking, and adjustment.