Evaluating Phonon Characteristics by Varying the Layer and Interfacial Thickness in Novel Carbon-Based Strained-Layer Superlattices
Abstract
:1. Introduction
2. Theoretical Background
2.1. Lattice Dynamics
2.2. Raman Scattering
Raman Intensity Profiles
2.3. Rigid-Ion-Model for Bulk Binary Materials
2.3.1. Rigid-Ion Model for (SiC)m/(GeC)n Superlattices
2.3.2. Coulomb Interactions in Superlattices
3. Numerical Computation Results and Discussions
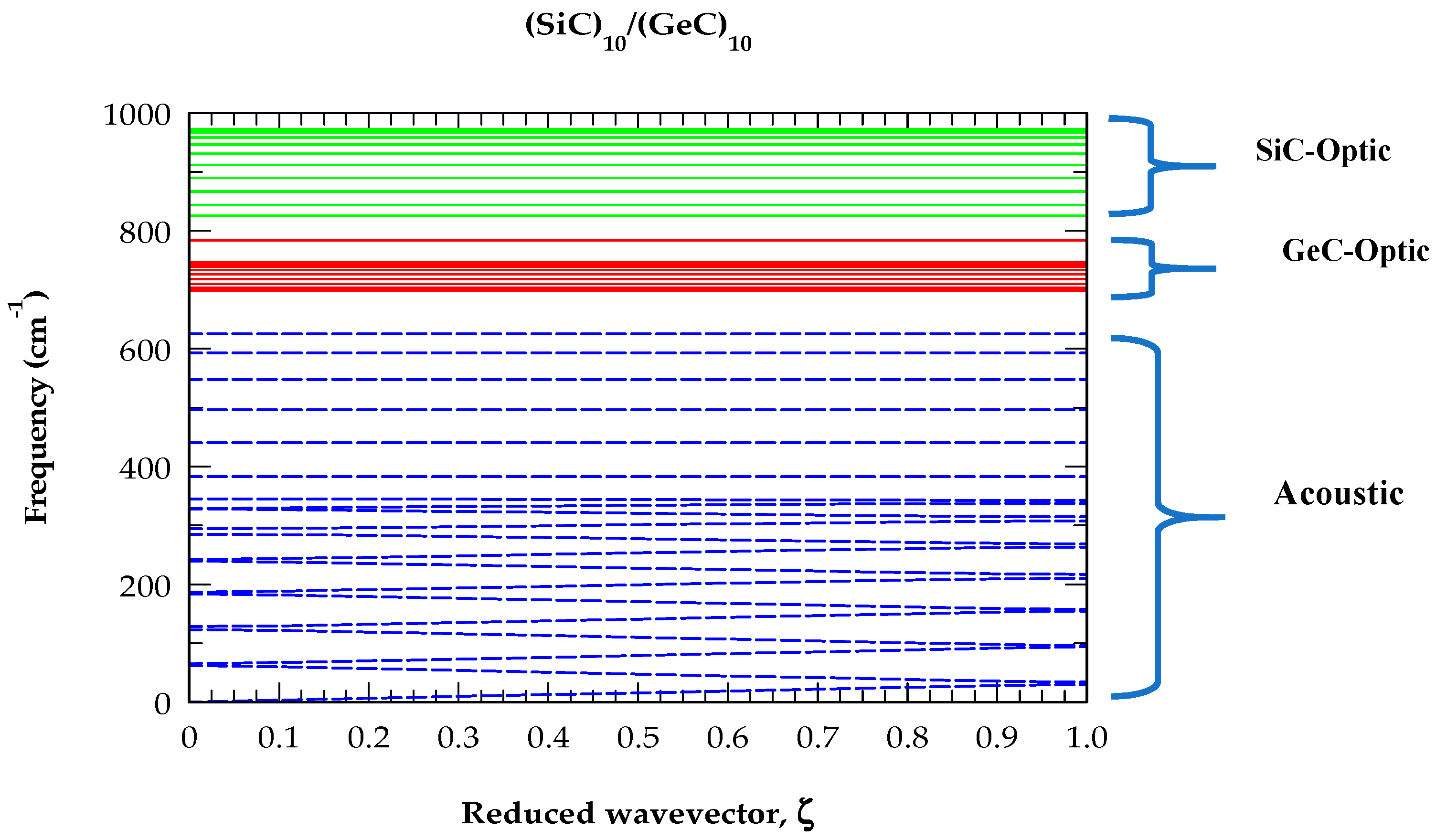
3.1. M-LCM Phonon Dispersions of (SiC)m/(GeC)n
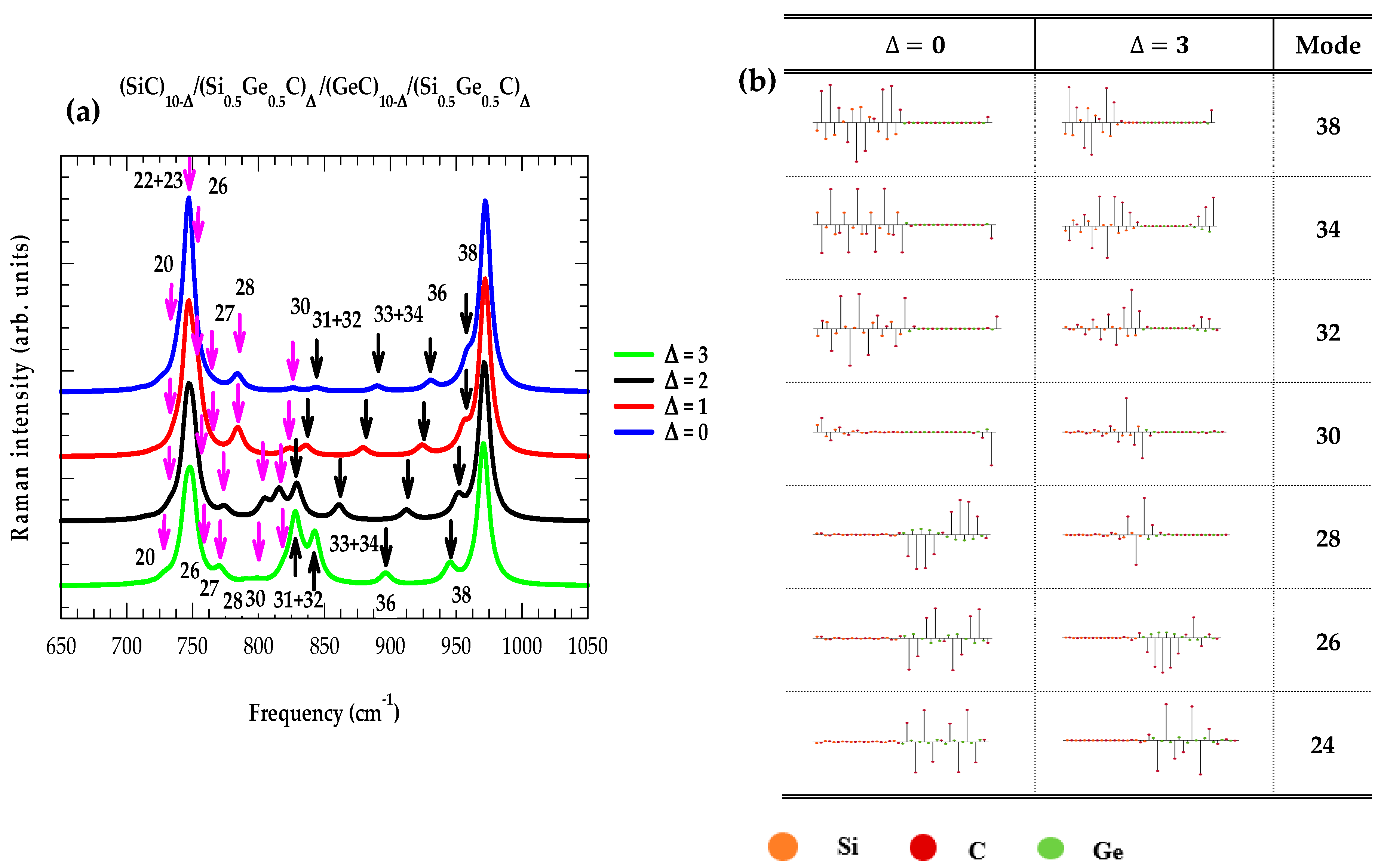
3.2. Raman Scattering Profiles in SLs
3.3. Atomic Displacements in Superlattices
3.4. RIM Calculations of Bulk zb SiC and zb GeC
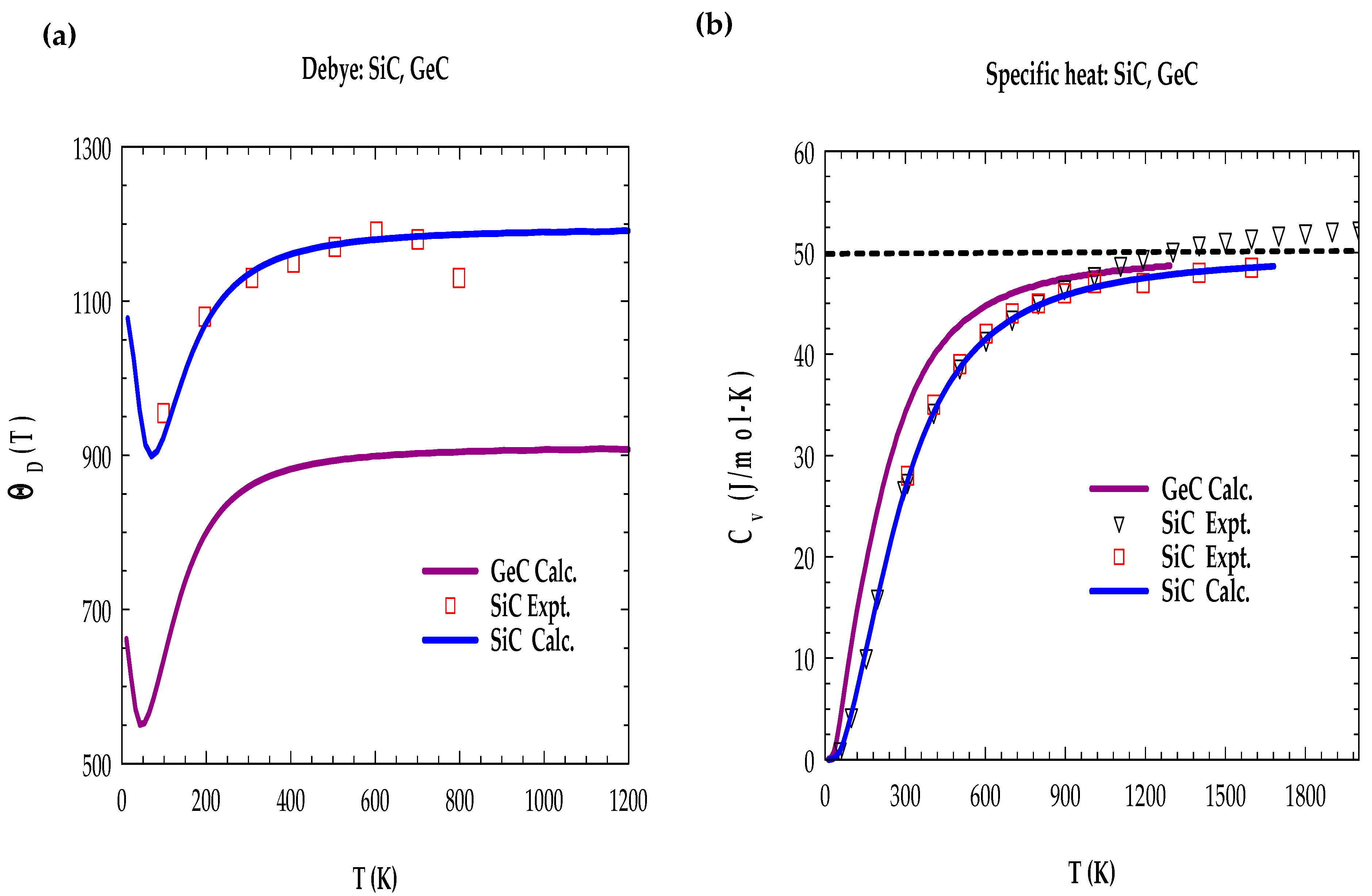
3.4.1. Debye Temperature and Specific Heat of Bulk zb SiC and zb GeC
3.5. RIM Calculations of (SiC)m/(GeC)n SLs
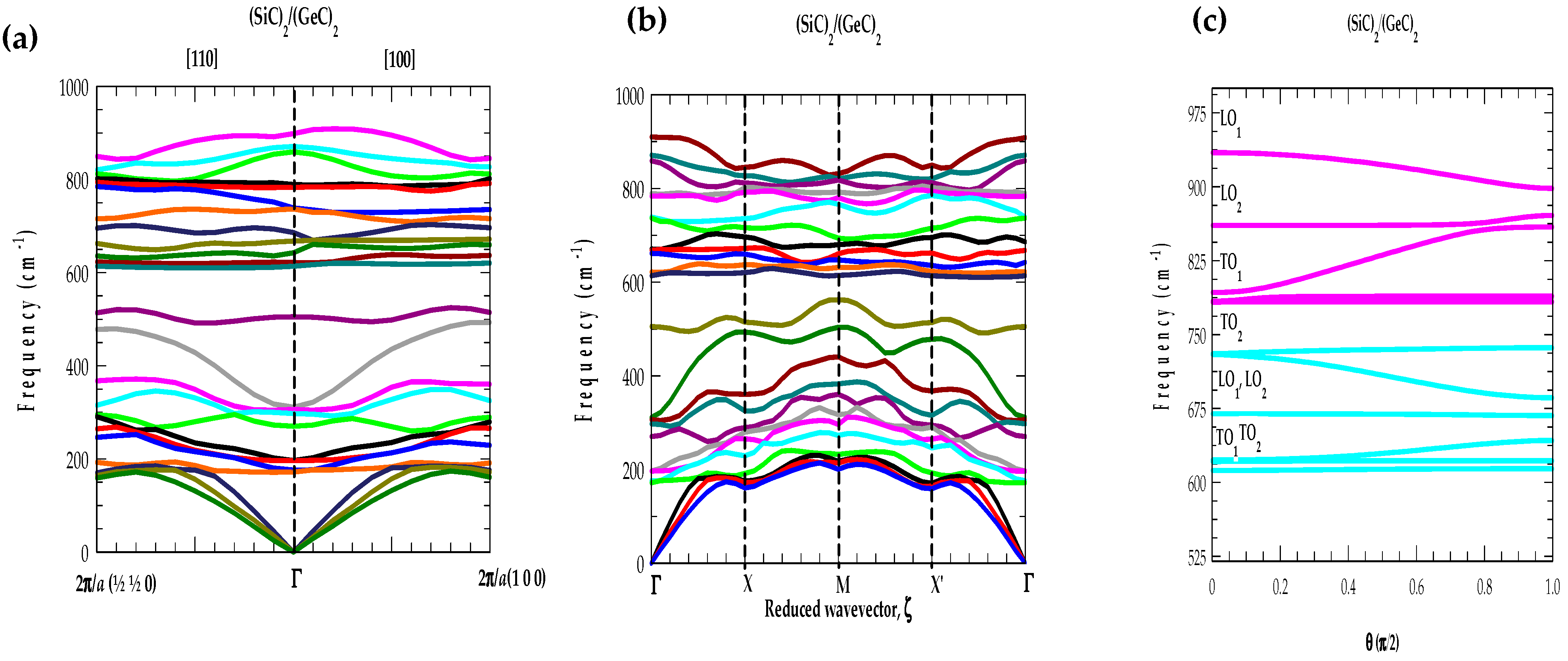
3.5.1. Phonons of SLs along the Growth Direction
3.5.2. Phonons of SLs Perpendicular to the Growth Direction
3.5.3. Angular Dependence of Optical Phonons in SLs
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbas, A.S. Ultrawide-bandgap semiconductor of carbon-based materials for meta-photonics-heterostructure, lasers, and holographic displays. AAPPS Bull. 2023, 33, 4. [Google Scholar] [CrossRef]
- Xing, F.; Ji, G.; Li, Z.; Zhong, W.; Wang, F.; Liu, Z.; Xin, W.; Tian, J. Preparation, properties and applications of two-dimensional superlattices. Mater. Horizons 2022, 10, 722–744. [Google Scholar] [CrossRef] [PubMed]
- Jmerik, V. Special Issue: Semiconductor Heterostructures (with Quantum Wells, Quantum Dots and Superlattices). Nanomaterials 2022, 12, 1685. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Gao, Y.; Zhang, X.; Li, L.; Tang, D. The in-depth description of phonon transport mechanisms for XC (X = Si, Ge) under hydrostatic pressure: Considering pressure-induced phase transitions. Int. J. Heat Mass Transf. 2022, 191, 122851. [Google Scholar] [CrossRef]
- Guo, Y.; Wei, X.; Gao, S.; Yue, W.; Li, Y.; Shen, G. Recent advances in carbon-based multi-functional sensors and their applications in electronic skin systems. Adv. Funct. Mater. 2021, 31, 2104288. [Google Scholar] [CrossRef]
- Si, Z.; Chai, C.; Zhang, W.; Song, Y.; Yang, Y. Theoretical investigation of group-IV binary compounds in the P4/ncc phase. Results Phys. 2021, 26, 104349. [Google Scholar] [CrossRef]
- Zultak, J.; Magorrian, S.J.; Koperski, M.; Garner, A.; Hamer, M.J.; Tóvári, E.; Novoselov, K.S.; Zhukov, A.A.; Zou, Y.; Wilson, N.R.; et al. Ultra-thin van der Waals crystals as semiconductor quantum wells. Nat. Commun. 2020, 11, 125. [Google Scholar] [CrossRef]
- Pike, N.A.; Løvvik, O.M. Calculation of the anisotropic coefficients of thermal expansion: A first-principles approach. Comput. Mater. Sci. 2019, 167, 257–263. [Google Scholar] [CrossRef]
- Luo, M.; Yu, B.; Xu, Y.-E. Tuning Electronic Properties of the SiC-GeC Bilayer by External Electric Field: A First-Principles Study. Micromachines 2019, 10, 309. [Google Scholar] [CrossRef]
- Davydov, V.; Roginskii, E.; Kitaev, Y.; Smirnov, A.; Eliseyev, I.; Nechaev, D.; Jmerik, V.; Smirnov, M. Phonons in Short-Period GaN/AlN Superlattices: Group-Theoretical Analysis, Ab initio Calculations, and Raman Spectra. Nanomaterials 2021, 11, 286. [Google Scholar] [CrossRef]
- Baslaev, Y.M.; Malysheva, E.N. Electronic structure of single-layer superlattices (GeC)1/(SiC)1, (SnC)1/(SiC)1, and (SnC)1/GeC)1. Semiconductors 2017, 51, 617. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Liu, Z. Controlling electronic and optical properties of layered SiC and GeC sheets by strain engineering. Mater. Des. 2016, 108, 333–342. [Google Scholar] [CrossRef]
- Gupta, N.; Veettil, B.P.; Xia, H.; Karuturi, S.K.; Conibeer, G.; Shrestha, S. Synthesis of nano-crystalline germanium carbide using radio frequency magnetron sputtering. Thin Solid Films 2015, 592, 162–166. [Google Scholar] [CrossRef]
- Serrano, J.; Strempfer, J.; Cardona, M.; Schwoerer-Böhning, M.; Requardt, H.; Lorenzen, M.; Stojetz, B.; Pavone, P.; Choyke, W.J. Determination of the phonon dispersion of zincblende (3C) silicon carbide by inelastic x-ray scattering. Appl. Phys. Lett. 2002, 80, 4360. [Google Scholar] [CrossRef]
- Zhang, X.; Quan, S.; Ying, C.; Li, Z. Theoretical investigations on the structural, lattice dynamical and thermodynamical properties of XC (X = Si, Ge and Sn). Sol. State Commun. 2011, 151, 1545. [Google Scholar] [CrossRef]
- Souadkia, M.; Bennecern, B.; Kalarasse, F. Elastic, vibrational and thermodynamic properties of αSn based group IV semiconductors and GeC under pressure. J. Phys. Chem. Solids 2013, 74, 1615–1625. [Google Scholar] [CrossRef]
- Liu, Q.-J.; Liu, Z.-T.; Che, X.-S.; Feng, L.-P.; Tian, H. First-principles calculations of the structural, elastic, electronic, chemical bonding and optical properties of zinc-blende and rock salt GeC. Solid State Sci. 2011, 13, 2177–2184. [Google Scholar] [CrossRef]
- Sahnoun, M.; Khenata, R.; Baltache, H.; Rérat, M.; Driz, M.; Bouhafs, B.; Abbar, B. First-principles calculations of optical properties of GeC, SnC and GeSn under hydrostatic pressure. Phys. B Condens. Matter 2005, 355, 392–400. [Google Scholar] [CrossRef]
- Silva, M.A.A.; Ribeiro, E.; Schulz, P.A.; Cerdeira, F.; Bean, J.C. Linear-chain-model interpretation of resonant Raman scattering in GenSim microstructures. Phs. Rev. B 1996, 53, 15871. [Google Scholar] [CrossRef]
- Sekkal, W.; Zaoui, A. Predictive study of thermodynamic properties of GeC. New J. Phys. 2002, 4, 9. [Google Scholar] [CrossRef]
- Kisielowski, C.; Weber, Z.L.; Nakamura, S. Atomic scale indium distribution in a GaN/In0.43Ga0.57N/Al0.1Ga0.9N quantum well structure. Jpn. J. Phys. 1997, 36, 6932. [Google Scholar] [CrossRef]
- Behr, D.; Niebuhr, R.; Wagner, J.; Bachem, K.-H.; Kaufman, U. Resonant Raman scattering in GaN/(AlGa)N single quantum wells. Appl. Phys. Lett. 1997, 70, 363. [Google Scholar] [CrossRef]
- Pezoldt, J.; Cimalla, V.; Masri, P.; Schröter, B. The Influence of Surface Preparation on the Properties of SiC on Si(111). Phys. Status Solidi (a) 2001, 185, 159–166. [Google Scholar] [CrossRef]
- Tsai, G.; Wang, D.-L.; Wu, C.-E.; Wu, C.-J.; Lin, Y.-T.; Lin, H.-H. InAsPSb quaternary alloy grown by gas source molecular beam epitaxy. J. Cryst. Growth 2007, 301–302, 134–138. [Google Scholar] [CrossRef]
- Goldberg, Y.; Levinshtein, M.E.; Rumyantsev, S.L.; Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. (Eds.) Properties of Advanced Semiconductor Materials GaN, AlN, SiC, BN, SiC, SiGe; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 93–148. [Google Scholar]
- Kern, E.L.; Hamill, D.W.; Deem, H.W.; Sheets, H.D. Thermal properties of β-silicon carbide from 20 to 2000 °C. Mater. Res. Bull. 1969, 4, 25. [Google Scholar]
- Seong, T.-Y.; Booker, G.R.; Norman, A.G.; Stringfellow, G.B. Modulated Structures and Atomic Ordering in InPySb1-y Layers Grown by Organometallic Vapor Phase Epitaxy. Jpn. J. Appl. Phys. 2008, 47, 2209–2212. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Part V Defects: Optical Properties of Defects. In Semiconductor Physics, 2nd ed.; Springer Nature: Cham, Switzerland, 2023; p. 703. [Google Scholar]
- Romanov, V.V.; Ermakov, B.S.; Kozhevnikov, V.A.; Stelmakh, K.F.; Vologzhanina, S.A. Lanthanide doping of AIIIBV crystals. In Proceedings of the 9th International Conference “Refrigeration and Food Technologies in the 21st Century”, St. Petersburg, Russia, 13–15 November 2019; Volume 826, p. 012010. [Google Scholar]
- Smołka, T.; Motyka, M.; Romanov, V.V.; Moiseev, K.D. Photoluminescence Spectroscopy of the InAsSb-Based p-i-n Heterostructure, Heterostructure. Materials 2022, 15, 1419. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Song, T.; Zou, M.; Lu, D.; Chen, H.; Wang, B.; Wang, S.; Xu, F. Probing Surface Information of Alloy by Time of Flight-Secondary Ion Mass Spectrometer. Crystals 2021, 11, 1465. [Google Scholar] [CrossRef]
- MacLaren, I.; Annand, K.J.; Black, C.; Craven, A.J. EELS at very high energy losses. Microscopy 2017, 67, i78–i85. [Google Scholar] [CrossRef]
- Varshni, Y. Temperature dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Fang, Z.M.; Ma, K.Y.; Jaw, D.H.; Cohen, R.M.; Stringfellow, G.B. Photoluminescence of InSb, InAs, and InAsSb grown by organometallic vapor phase epitaxy. J. Appl. Phys. 1990, 67, 7034–7039. [Google Scholar] [CrossRef]
- Williams, F.E.; Hebb, M.H. Theoretical Spectra of Luminescent Solids. Phys. Rev. 1951, 84, 1181–1183. [Google Scholar] [CrossRef]
- Shionoya, S.; Koda, T.; Era, K.; Fujiwara, H. Nature of luminescence Transitions in ZnS crystals. J. Phys. Soc. Jpn. 1964, 19, 1157–1167. [Google Scholar] [CrossRef]
- Mastelaro, V.; Flank, A.M.; Fantini, M.C.A.; Bittencourt, D.R.S.; Carren, M.N.P.; Pereyra, O.I. On the structural properties of a-Si1-xCx:H thin films. J. Appl. Phys. 1996, 79, 1324–1329. [Google Scholar] [CrossRef]
- Zheng, H.W.; Wang, Z.Q.; Liu, X.Y.; Diao, C.L.; Zhang, H.R.; Gu, Y.Z. Local structure and magnetic properties of Mn-doped 3C-SiC nanoparticles. Appl. Phys. Lett. 2011, 99, 222512. [Google Scholar] [CrossRef]
- An, Y.; Duan, L.; Li, X.; Wu, Z.; Liu, J. Investigation of microstructures and optical properties in Mn-doped SiC films. Appl. Surf. Sci. 2012, 258, 7070–7074. [Google Scholar] [CrossRef]
- Jin, C.; Wu, X.; Zhuge, L. The structure and photoluminescence properties of Cr-doped SiC films. Appl. Surf. Sci. 2009, 255, 4711–4715. [Google Scholar] [CrossRef]
- Lagarde, P.; Flank, A. Analysis of Si-K edge EXAFS in the low k domain. J. Phys. 1986, 47, 1389–1394. [Google Scholar] [CrossRef]
- Monguchi, T.; Fujioka, H.; Uragami, T.; Ohuchi, H.; Ono, K.; Baba, Y.; Oshimaa, M. X-ray absorption studies of anodized monocrystalline 3C-SiCX-ray absorption studies of anodized monocrystalline 3C-SiC. J. Electrochem. Soc. 2000, 147, 741–743. [Google Scholar] [CrossRef]
- Liu, L.; Yiu, Y.M.; Sham, T.K.; Zhang, L.; Zhang, Y. Electronic structures and optical properties of 6H- and 3C-SiC microstructures and nanostructures from X-ray absorption fine structures, X-ray excited optical luminescence, and theoretical studies. J. Phys. Chem. C 2010, 114, 6966–6975. [Google Scholar] [CrossRef]
- Geurts, J. Raman spectroscopy from buried semiconductor interfaces: Structural and electronic properties. Phys. Status Solidi B 2015, 252, 19–29. [Google Scholar] [CrossRef]
- Wu, J.-B.; Lin, M.-L.; Cong, X.; Liu, H.-N.; Tan, P.-H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822. [Google Scholar] [CrossRef] [PubMed]
- Cong, X.; Lin, M.; Tan, P.-H. Lattice vibration and Raman scattering of two-dimensional van der Waals heterostructure. J. Semicond. 2019, 40, 091001. [Google Scholar] [CrossRef]
- Wang, C.; Omanakuttan, G.; Xu, L.; Liu, T.; Huang, Z.; Lourdudoss, S.; Xie, C.; Sun, Y.-T. Optical and interfacial properties of epitaxially fused GaInP/Si heterojunction. J. Appl. Phys. 2020, 128, 055308. [Google Scholar] [CrossRef]
- Cong, X.; Liu, X.-L.; Lin, M.-L.; Tan, P.-H. Application of Raman spectroscopy to probe fundamental properties of two-dimensional materials. npj 2D Mater. Appl. 2020, 4, 13. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Song, Y.; Liu, T.; Dong, B.; Liu, J.; Wang, H. Interfacial stress characterization of GaN epitaxial layer with sapphire substrate by confocal Raman spectroscopy. Nanotechnol. Precis. Eng. 2021, 4, 023002. [Google Scholar] [CrossRef]
- Rahaman, M.; Zahn, D.R.T. Plasmon-enhanced Raman spectroscopy of two-dimensional semiconductors. J. Phys. Condens. Matter 2022, 34, 333001. [Google Scholar] [CrossRef]
- Garg, S.; Fix, J.P.; Krayev, A.V.; Flanery, C.; Colgrove, M.; Sulkanen, A.R.; Wang, M.; Liu, G.-Y.; Borys, N.J.; Kung, P. Nanoscale Raman Characterization of a 2D Semiconductor Lateral Heterostructure Interface. ACS Nano 2021, 16, 340–350. [Google Scholar] [CrossRef]
- Van Velson, N.; Zobeiri, H.; Wang, X. Thickness-Dependent Raman Scattering from Thin-Film Systems. J. Phys. Chem. C 2023, 127, 2995–3004. [Google Scholar] [CrossRef]
- Kunc, K. Dynamique de réseau de composés ANB8-N présentant la structure de la blende. Ann. Phys. 1974, 48, 319. [Google Scholar] [CrossRef]
- Bevk, J.; Mannaerts, J.P.; Feldman, L.C.; Davidson, B.A.; Ourmazd, A. Ge-Si layered structures: Artificial crystals and complex cell ordered superlattices. Appl. Phys. Lett. 1986, 49, 286–288. [Google Scholar] [CrossRef]
- Kasper, E.; Herzog, H.-J.; Dambkes, H.; Abstreiter, G. Layered Structures and Epitaxy. In Materials Research Society Proceedings; Gibson, J.M., Osbourn, G.C., Tromp, R.M., Eds.; MRS: Pittsburgh, PA, USA, 1986; Volume 56. [Google Scholar]
- Zhu, B.; Chao, K.A. Phonon modes and Raman scattering in GaAs/Ga1-xAlxAs. Phys. Rev. B 1987, 36, 4906. [Google Scholar] [CrossRef]
- Jusserand, B.; Cardona, M. Light Scattering in Solids V. In Topics in Applied Physics; Cardona, M., Güntherodt, G., Eds.; Springer: Heidelberg, Germany, 1989; Volume 66, p. 49. [Google Scholar]
- Dharma-Wardana, M.W.C.; Aers, G.C.; Lockwood, D.J.; Baribeau, J.M. Interpretation of Raman spectra of Ge/Si ultrathin superlattices. Phys. Rev. B 1990, 41, 5319. [Google Scholar] [CrossRef]
- Wang, H.; Farias, G.A.; Freire, V.N. Interface related exciton-energy blueshift in GaN/AlxGa1-xN zinc-blende and wurtzite single quantum wells. Phys. Rev. B 1999, 60, 5705. [Google Scholar] [CrossRef]
- Talwar, D.N.; Lin, H.-H. Assessing thermo-dynamical properties of Al1−xGaxSb alloys and optical modes for Al1−xGaxSb/GaAs epifilms and (AlSb)m/(GaSb)n superlattices. J. Vac. Sci. Technol. A 2022, 40, 032801. [Google Scholar] [CrossRef]
- Talwar, D.N.; Becla, P. Assessment of optical phonons in BeTe, BexZn1−xTe, p-BeTe epilayers and BeTe/ZnTe/GaAs (001) superlattics. Appl. Phys. A 2022, 128, 702. [Google Scholar] [CrossRef]
- Talwar, D.N.; Becla, P. Interfacial strain-dependent localization of phonons in (CdS)m/(CdTe)n superlattices. Phys. B 2023, 650, 414500. [Google Scholar] [CrossRef]
- Talwar, D.N. Dilute III-V Nitride Semiconductors and Material Systems. In Materials Science; Physics and Technology Series; Erol, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 105, Chapter 9; p. 222. [Google Scholar]
- Plumelle, P.; Vandevyver, M. Lattice Dynamics of ZnTe and CdTe. Phys. Status Solidi B 1976, 73, 271–281. [Google Scholar] [CrossRef]
- Molinari, E.; Baroni, S.; Giannozzi, P.; de Gironcoli, S. Effects of disorder on the Raman spectra of GaAs/AlAs superlattices. Phys. Rev. B 1992, 45, 4280–4288. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.-F.; Chu, H.; Chang, Y.-C. Anisotropy of optical phonons and interface modes in GaAs-AlAs superlattices. Phys. Rev. B 1988, 37, 8899. [Google Scholar] [CrossRef] [PubMed]
- Kanellis, G. New approach to the problem of lattice dynamics of modulated structures: Application to superlattices. Phys. Rev. B 1987, 35, 746. [Google Scholar] [CrossRef] [PubMed]
- Davydov, V.Y.; Roginskii, E.M.; Kitaev, Y.E.; Smirnov, A.N.; Eliseyev, I.A.; Rodin, S.N.; Zavarin, E.E.; Lundin, W.V.; Nechaev, D.V.; Jmerik, V.N.; et al. Analysis of the sharpness of interfaces in short-period GaN/AlN superlattices using Raman spectroscopy data. In Proceedings of the International Conference PhysicA.SPb/2021, Saint Petersburg, Russia, 18–22 October 2021; Volume 2103, p. 012147. [Google Scholar]
- Hurley, D.C.; Tamura, S.; Wolfe, J.P.; Morkoç, H. Imaging of acoustic phonon stop bands in superlattices. Phys. Rev. Lett. 1987, 58, 2446–2449. [Google Scholar] [CrossRef] [PubMed]
- Tamura, S.; Wolfe, J.P. Coupled-mode stop bands of acoustic phonons in semiconductor superlattices. Phys. Rev. B 1987, 35, 2528–2531. [Google Scholar] [CrossRef] [PubMed]

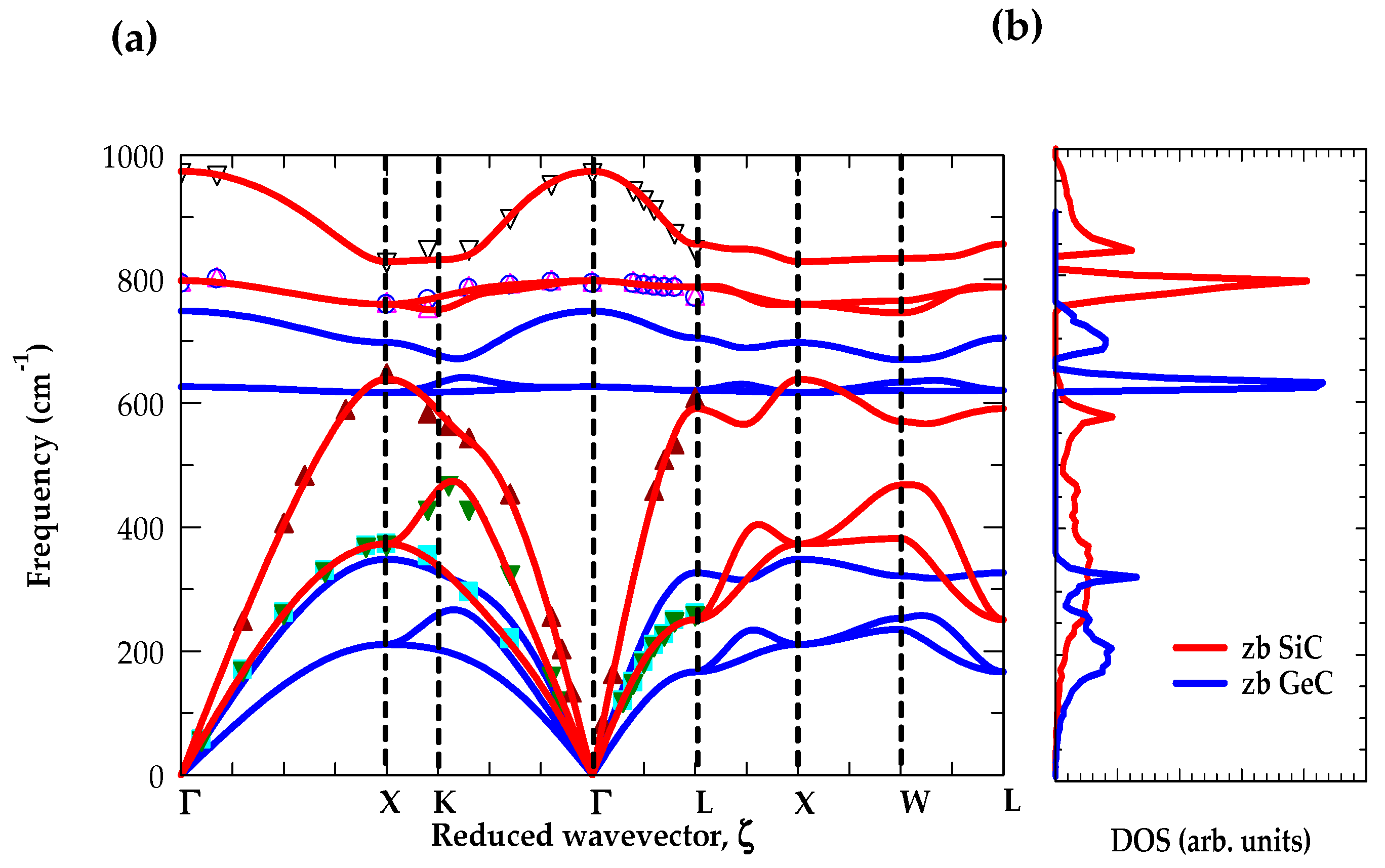

| Physical Parameter | Expt. | SiC Theory | Our | GeC Theory | Our |
|---|---|---|---|---|---|
| c11 | 39.0 (a) | 38.5–39.0 (e) | 38.7 (f) | 31.8 (e) | 31.9 (f) |
| c12 | 14.2 (a) | 13.2–14.2 (e) | 14.3 (f) | 10.4 (e) | 10.7 (f) |
| c44 | 25.6 (a) | 24.3–25.6 (e) | 25.8 (f) | 19.2 (e) | 17.6 (f) |
| a0 | 4.36 (a) | 4.28–4.40 (e) | 4.36 (f) | 4.59 (e) | 4.59 (f) |
| LO(Γ) | 972 (b) | 945–956 (e) | 974 (f) | 748 (e) | 749 (f) |
| TO(Γ) | 796 (b) | 774–783 (e) | 797 (f) | 626 (e) | 626 (f) |
| LO(X) | 829 (b) | 807–829 (e) | 828 (f) | 697 (e) | 698 (f) |
| TO(X) | 761 (b) | 741–755 (e) | 760 (f) | 617 (e) | 617 (f) |
| LA(X) | 640 (b) | 622–629 (e) | 639 (f) | 348 (e) | 348 (f) |
| TA(X) | 373 (b) | 361–366 (e) | 373 (f) | 214 (e) | 210 (f) |
| LO(L) | 838 (b) | 817–838 (e) | 857 (f) | 705 (e) | 705 (f) |
| TO(L) | 766 (b) | 747–766 (e) | 787 (f) | 612 (e) | 621 (f) |
| LA(L) | 610 (b) | 601–610 (e) | 591 (f) | 331 (e) | 326 (f) |
| TA(L) | 266 (b) | 257–261 (e) | 251 (f) | 162 (e) | 166 (f) |
| 1080 (c) | 1080 (f) | 670 (f) | |||
| 1270 (d) | 1186 (f) | 904 (f) | |||
| 26.84 (d) | 26.24 (f) | 34.3 (f) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talwar, D.N.; Becla, P. Evaluating Phonon Characteristics by Varying the Layer and Interfacial Thickness in Novel Carbon-Based Strained-Layer Superlattices. Solids 2023, 4, 287-303. https://doi.org/10.3390/solids4040018
Talwar DN, Becla P. Evaluating Phonon Characteristics by Varying the Layer and Interfacial Thickness in Novel Carbon-Based Strained-Layer Superlattices. Solids. 2023; 4(4):287-303. https://doi.org/10.3390/solids4040018
Chicago/Turabian StyleTalwar, Devki N., and Piotr Becla. 2023. "Evaluating Phonon Characteristics by Varying the Layer and Interfacial Thickness in Novel Carbon-Based Strained-Layer Superlattices" Solids 4, no. 4: 287-303. https://doi.org/10.3390/solids4040018
APA StyleTalwar, D. N., & Becla, P. (2023). Evaluating Phonon Characteristics by Varying the Layer and Interfacial Thickness in Novel Carbon-Based Strained-Layer Superlattices. Solids, 4(4), 287-303. https://doi.org/10.3390/solids4040018







