A Theory of Dynamical Responses for Metal Films: Surface Roughness Effects
Abstract
1. Introduction
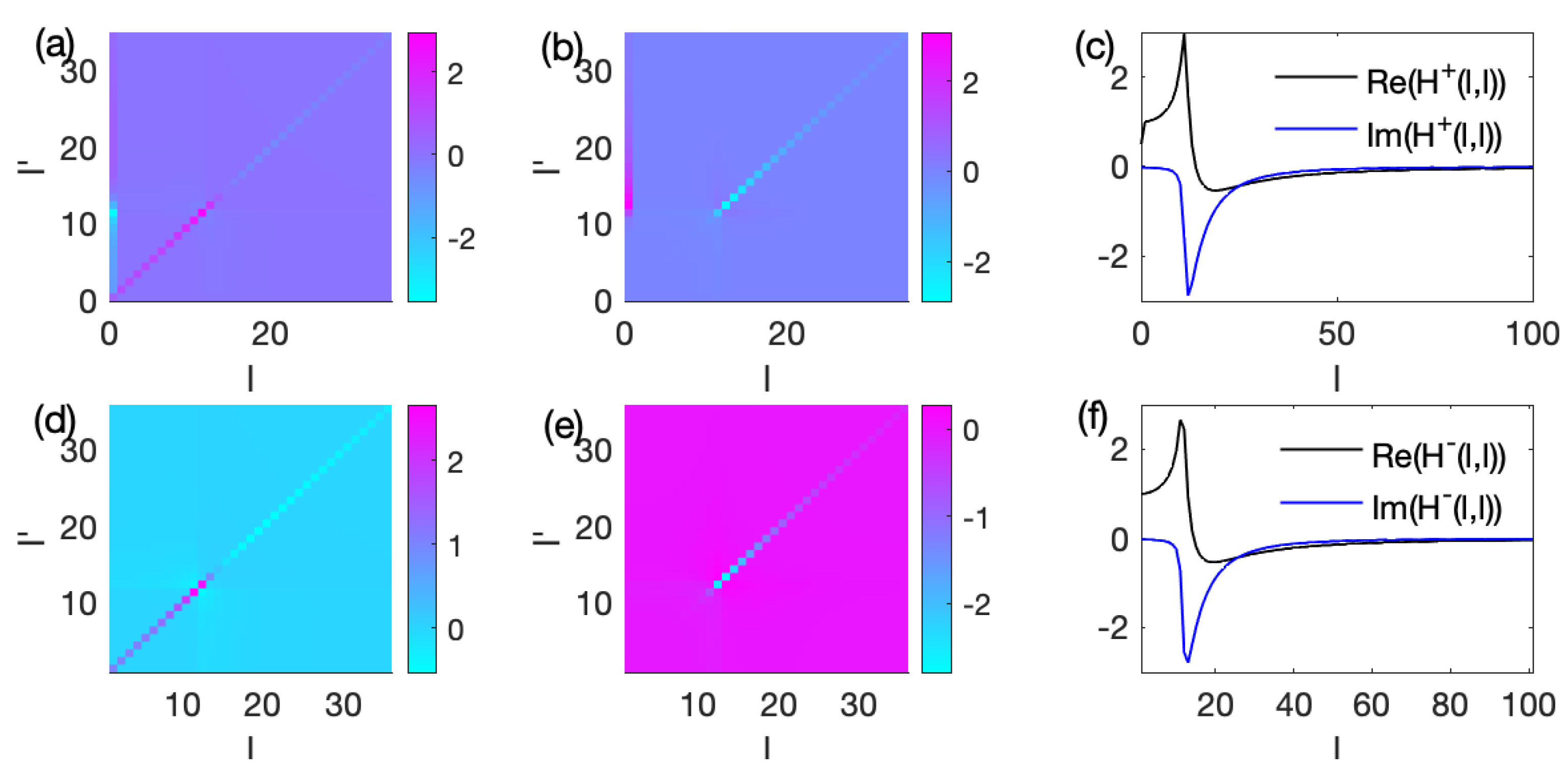
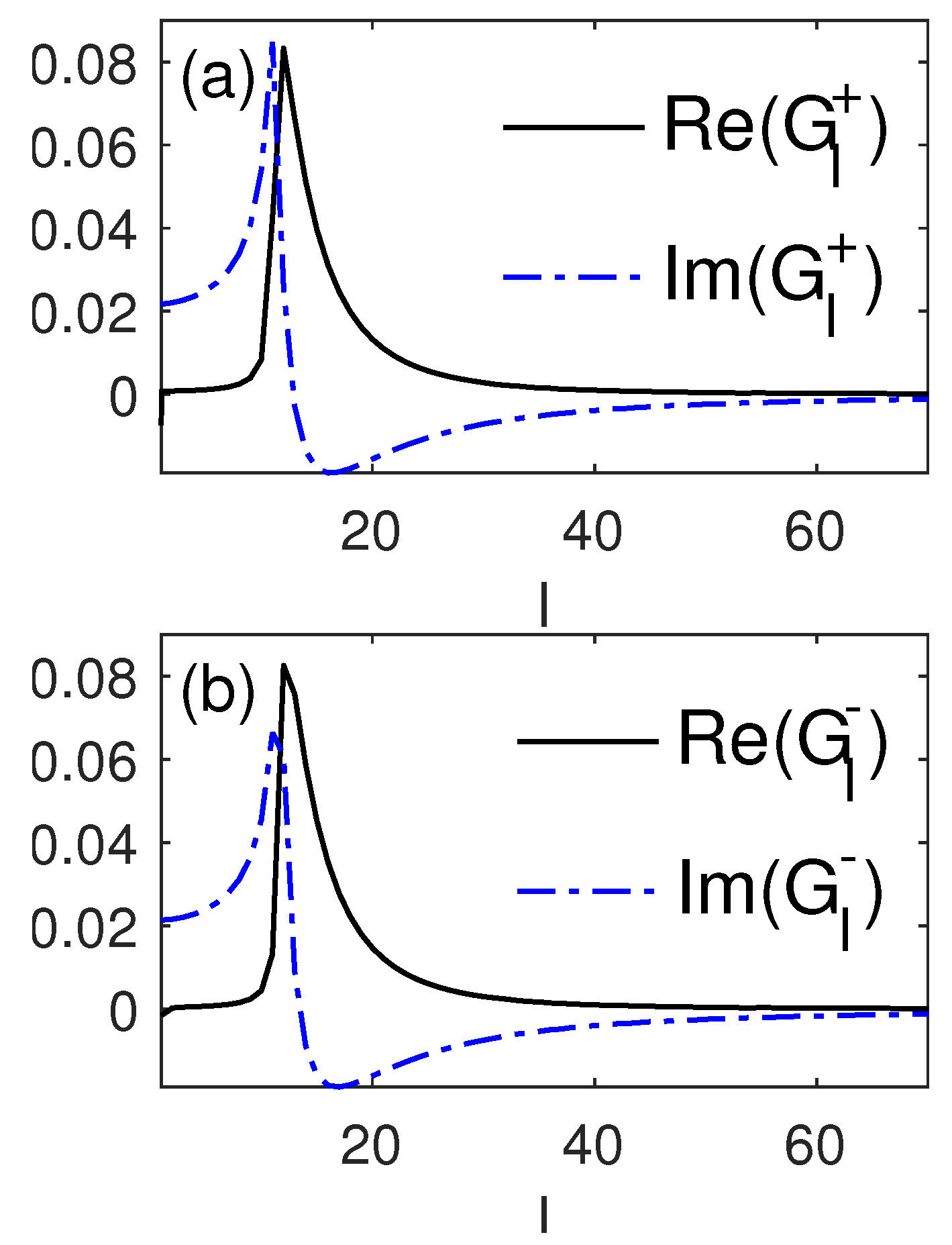
2. Analytical Expressions for the Dynamical Response Function
2.1. Generic Formalism
2.2. Macroscopic Limit
2.3. Kinetic Theory
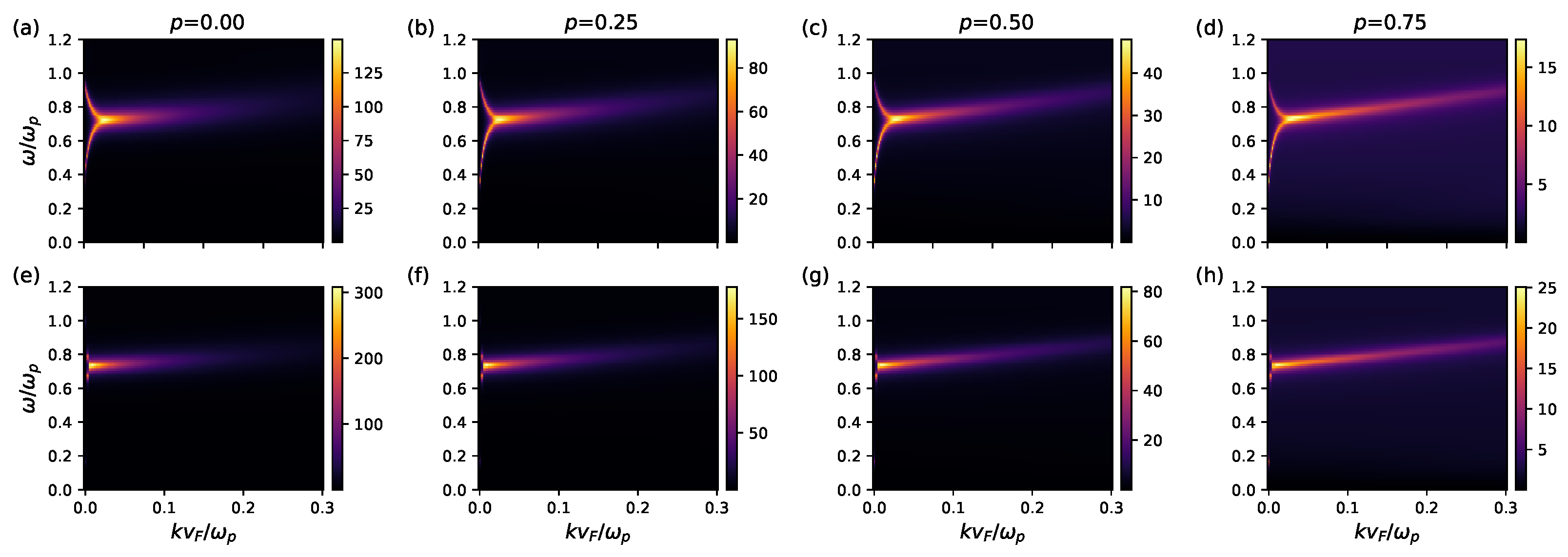
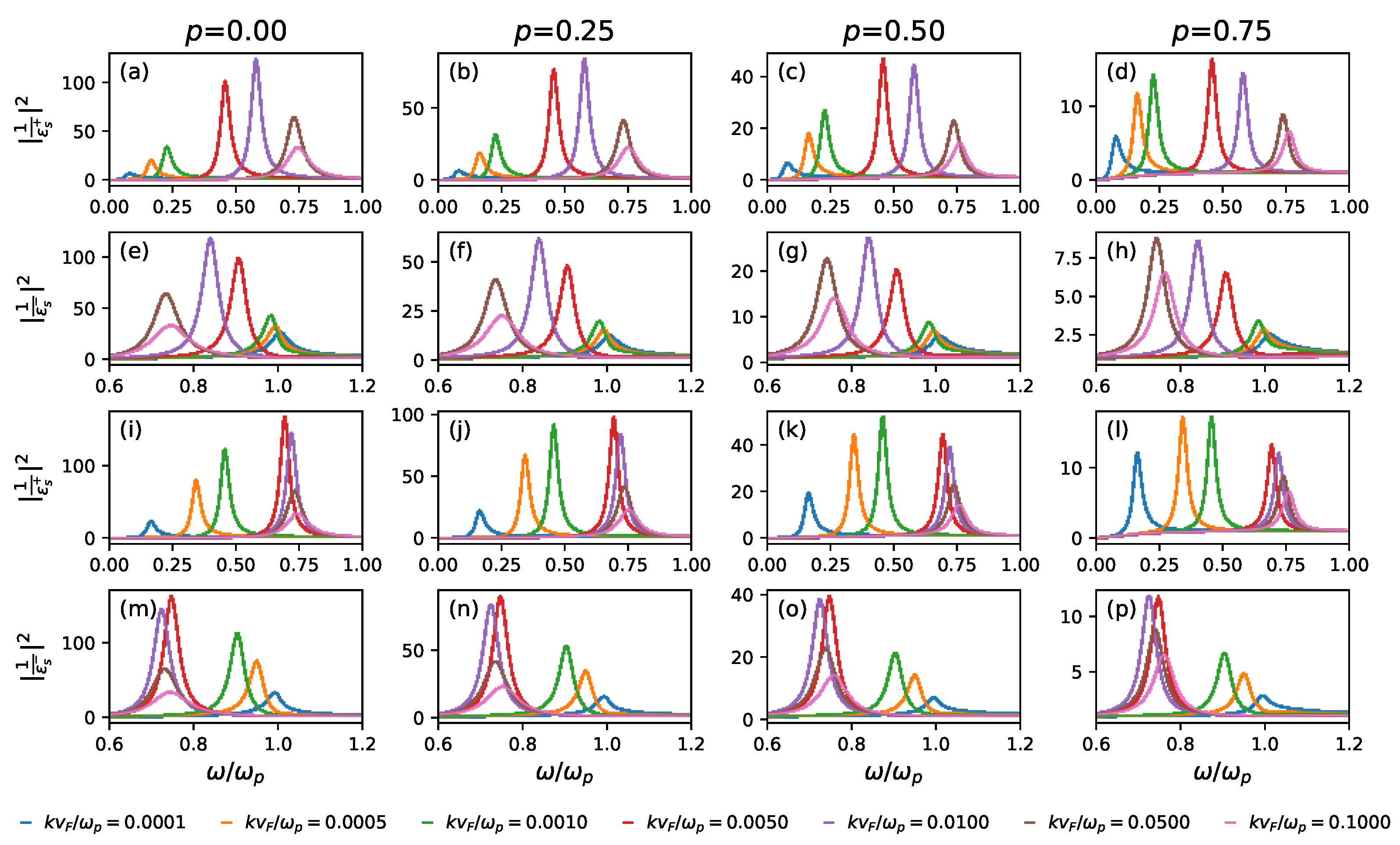
3. Application to Plasma Waves
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kulik, I.O. Thomas–Fermi screening of a moving surface charge. Low Temp. Phys. 1997, 23, 650. [Google Scholar] [CrossRef]
- Silkin, V.M.; Kazansky, A.K.; Chulkov, E.V.; Echenique, P.M. Time-dependent screening of a point charge at a metal surface. J. Phys. Condens. Matter 2010, 22, 304013. [Google Scholar] [CrossRef]
- Muino, R.D.; Sanchez-Portal, D.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Time-dependent electron phenomena at surfaces. Proc. Natl. Acad. Sci. USA 2011, 108, 971. [Google Scholar] [CrossRef]
- Mizielinski, M.S.; Bird, D.M.; Persson, M.; Holloway, S. Spectrum of electronic excitations due to the adsorption of atoms on metal surfaces. J. Chem. Phys. 2005, 122, 084710. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, K.-D.; Plummer, E.W.; Liebsch, A.; Pehlke, E.; Kempa, K.; Bakshi, P. The normal modes at the surface of simple metals. Surf. Sci. 1991, 247, 302. [Google Scholar] [CrossRef]
- Ibach, H.; Mills, D.L. Electron Energy Loss Spectroscopy and Surface Vibrations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Nazarov, V.U.; Silkin, V.M.; Krasovskii, E.E. Role of the kinematics of probing electrons in electron energy-loss spectroscopy of solid surfaces. Phys. Rev. B 2016, 93, 035403. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: London, UK, 1960. [Google Scholar]
- Despoja, V.; Echenique, P.M.; Sunjic, M. Nonlocal microscopic theory of quantum friction between parallel metallic slabs. Phys. Rev. B 2011, 83, 205424. [Google Scholar] [CrossRef]
- Remy, M. Theory concerning the interaction of an alkali atom and a metallic surface. J. Chem. Phys. 1970, 53, 2487. [Google Scholar] [CrossRef]
- Alducin, M.; Muino, R.D.; Juaristi, J.I. Non-adiabatic effects in elementary reaction processes at metal surfaces. Prog. Surf. Sci. 2017, 92, 317. [Google Scholar] [CrossRef]
- Moskovits, M. Surface roughness and the enhanced intensity of Raman scattering by molecules adsorbed on metals. J. Chem. Phys. 1978, 69, 4159. [Google Scholar] [CrossRef]
- Rother, A.I.C.J.; Gregor, I.; Janshoff, A.; Enderlein, J. Metal-induced energy transfer for live cell nanoscopy. Nat. Photonics 2014, 8, 124. [Google Scholar]
- Brown, D.; Deng, H.-Y. Hydrodynamic effects on the energy transfer from dipoles to metal slab. J. Chem. Phys. 2021, 155, 114109. [Google Scholar] [CrossRef]
- Monreal, R.C. Auger neutralization and ionization processes for charge exchange between slow noble gas atoms and solid surfaces. Prog. Surf. Sci. 2014, 89, 80. [Google Scholar] [CrossRef]
- Goldman, A.M. Electrostatic gating of ultrathin films. Annu. Rev. Mater. Res. 2014, 44, 45. [Google Scholar] [CrossRef]
- Niv, A.; Gharghi, M.; Gladden, C.; Miller, O.D.; Zhang, X. Near-field electromagnetic theory for thin solar cells. Phys. Rev. Lett. 2012, 109, 138701. [Google Scholar] [CrossRef]
- Li, Y.; Sun, L.; Liu, H.; Wang, Y.; Liu, Z. Preparation of single-crystal metal substrates for the growth of high-quality two-dimensional materials. Inorg. Chem. Front. 2021, 8, 182. [Google Scholar] [CrossRef]
- Chu, Y.T.; Warmack, R.J.; Ritchie, R.H.; Little, J.W.; Becker, R.S.; Ferrell, T.L. Contribution of the surface plasmon to energy losses by electrons in a cylindrical channel. Part. Accel. 1984, 16, 13. [Google Scholar]
- Bohm, D.; Pines, D. A collective description of electron interactions: III. Coulomb interactions in a degenerate electron gas. Phys. Rev. 1953, 92, 609. [Google Scholar] [CrossRef]
- Pines, D. A collective description of electron interactions: IV. Electron interaction in metals. Phys. Rev. 1953, 92, 625. [Google Scholar] [CrossRef]
- Hubbard, J. The dielectric theory of electronic interactions in solids. Proc. Phy. Soc. A 1955, 68, 976. [Google Scholar] [CrossRef]
- Eguiluz, A.G.; Fleszar, A.; Gaspar, J.A. On the ab initio evaluation of dynamical electronic response in metals and its comparison with experiment. Nucl. Instrum. Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 1995, 96, 550. [Google Scholar] [CrossRef]
- Feibelman, P.J. Surface electromagnetic fields. Prog. Surf. Sci. 1982, 12, 287. [Google Scholar] [CrossRef]
- Apell, P.; Ljungbert, A.; Lundgvist, S. Non-local optical effects at metal surfaces. Phys. Scripta 1984, 30, 367. [Google Scholar] [CrossRef]
- Horing, N.J.M.; Kamen, E.; Cui, H.-L. Inverse dielectric function of a bounded solid-state plasma. Phys. Rev. B 1985, 32, 2184. [Google Scholar] [CrossRef] [PubMed]
- Kawaji, J. Surface Science: The First Thirty Years; Duke, C.B., Ed.; North-Holland: New York, NY, USA, 1994. [Google Scholar]
- Ritchie, R.H. Plasma losses by fast electrons in thin films. Phys. Rev. 1957, 106, 874. [Google Scholar] [CrossRef]
- Powell, C.J.; Swan, J.B. Origin of the Characteristic Electron Energy Losses in Magnesium. Phys. Rev. 1959, 116, 81. [Google Scholar] [CrossRef]
- Powell, C.J.; Swan, J.B. Origin of the Characteristic Electron Energy Losses in Aluminum. Phys. Rev. 1959, 115, 869. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science & Businnes Media: New York, NY, USA, 2007. [Google Scholar]
- Zayats, A.V.; Igor, I.S.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 828. [Google Scholar] [CrossRef]
- Ritchie, R.H. On surface plasma oscillations in metal foils. Prog. Theoret. Phys. 1963, 29, 607. [Google Scholar] [CrossRef]
- Bennett, A.J. Influence of the electron charge distribution on surface-plasmon dispersion. Phys. Rev. B 1970, 1, 203. [Google Scholar] [CrossRef]
- Harris, J. Surface-plasmon dispersion: A comparison of microscopic and hydrodynamic theories. Phys. Rev. B 1971, 4, 1022. [Google Scholar] [CrossRef]
- Barton, G. Some surface effects in the hydrodynamic model of metals. Rep. Prog. Phys. 1979, 42, 65. [Google Scholar] [CrossRef]
- Nakamura, Y.O. Quantization of non-radiative surface plasma oscillations. Prog. Theoret. Phys. 1983, 70, 908. [Google Scholar] [CrossRef]
- Gradov, O.M.; Stenflo, L. Linear theory of a cold bounded plasma. Phys. Rep. 1983, 94, 111. [Google Scholar] [CrossRef]
- Cirací, C.; Pendry, J.B.; Smith, D.R. Hydrodynamic Model for Plasmonics: A Macroscopic Approach to a Microscopic Problem. ChemPhysChem 2013, 14, 1109. [Google Scholar]
- Luo, Y.; Zhao, R.; Pendry, J.B. Van der Waals interactions at the nanoscale: The effects of nonlocality. Proc. Natl. Acad. Sci. USA 2014, 111, 18422. [Google Scholar] [CrossRef]
- Luo, Y.; Fernandez-Dominguez, A.I.; Wiener, A.; Maier, S.A.; Pendry, J.B. Surface plasmons and nonlocality: A simple model. Phys. Rev. Lett. 2013, 111, 093901. [Google Scholar] [CrossRef] [PubMed]
- Kupresak, M.; Zheng, X.; Vandenbosch, G.A.E.; Moshschalkov, V.V. Comparison of hydrodynamic models for the electromagnetic nonlocal response of nanoparticles. Adv. Theory Simul. 2018, 2018, 1800076. [Google Scholar] [CrossRef]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon polaritons. Rep. Prog. Phys. 2007, 70, 1. [Google Scholar] [CrossRef]
- Newns, D.M. Dielectric response of a semi-infinite degenerate electron gas. Phys. Rev. B 1970, 1, 3304. [Google Scholar] [CrossRef]
- Beck, D.E. Quantum-mechanical random-phase-approximation calculation of the surface-plasmon dispersion relation for a semi-infinite electron gas. Phys. Rev. B 1971, 4, 1555. [Google Scholar] [CrossRef]
- Kempa, K.; Schaich, W.L. Surface-plasmon dispersion in the infinite-barrier model. Phys. Rev. B 1985, 32, 8375. [Google Scholar] [CrossRef]
- Toscano, G.; Straubel, J.; Kwiatkowski, A.; Rockstuhl, C.; Evers, F.; Xu, H.; Mortensen, N.A.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics. Nat. Commun. 2015, 6, 7132. [Google Scholar] [CrossRef] [PubMed]
- Yan, W. Hydrodynamic theory for quantum plasmonics: Linear-response dynamics of the inhomogeneous electron gas. Phys. Rev. B 2015, 91, 115416. [Google Scholar] [CrossRef]
- Cirací, C.; Della Sala, F. Quantum hydrodynamic theory for plasmonics: Impact of the electron density tail. Phys. Rev. B 2016, 93, 205405. [Google Scholar] [CrossRef]
- Christensen, T.; Yan, W.; Jauho, A.-P.; Solijacic, M.; Mortensen, N.A. Quantum corrections in nanoplasmonics: Shape, scale, and material. Phys. Rev. Lett. 2017, 118, 157402. [Google Scholar] [CrossRef] [PubMed]
- Liebsch, A. Surface plasmon dispersion of Ag. Phys. Rev. Lett. 1993, 71, 145. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Lekue, A.; Pitarke, J.M. Energy loss of charged particles interacting with simple metal surfaces. Phys. Rev. B 2001, 64, 035423. [Google Scholar] [CrossRef]
- Alducin, M.; Silkin, V.M.; Juaristi, J.I.; Chulkov, E.V. Energy loss of ions at metal surfaces: Band-structure effects. Phys. Rev. A 2003, 67, 032903. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Silkin, V.M.; Gurtubay, I.G.; Pitarke, J.M. Energy loss of charged particles moving parallel to a magnesium surface: Ab initio calculations. Phys. Rev. B 2008, 78, 155428. [Google Scholar] [CrossRef]
- Ullrich, C.A.; Vignale, G. Theory of the linewidth of intersubband plasmons in quantum wells. Phys. Rev. Lett. 2001, 87, 037402. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Moliner, F.; Flores, F. Introduction to the Theory of Solid Surfaces; Cambridge University Press: New York, NY, USA, 1979. [Google Scholar]
- Garcia-Moliner, F.; Flores, F. Classical electrodynamics of non-specular dielectric surfaces. J. Phys. 1977, 38, 851–862. [Google Scholar] [CrossRef]
- Flores, F.; Garcia-Moliner, F. Classical electrodynamics of non-specular conducting surfaces. J. Phys. 1977, 38, 863–870. [Google Scholar] [CrossRef][Green Version]
- Fuchs, K. The conductivity of thin metallic films according to the electron theory of metals. Proc. Camb. Phil. Soc. 1938, 34, 100. [Google Scholar] [CrossRef]
- Reuter, G.E.H.; Sondheimer, E.H. The theory of the anomalous skin effect in metals. Proc. R. Soc. Lond. A 1948, 195, 338. [Google Scholar] [CrossRef]
- Kliewer, K.L.; Fuchs, R. Anomalous skin effect for specular electron scattering and optical experiments at non-normal angles of incidence. Phys. Rev. 1968, 172, 607. [Google Scholar] [CrossRef]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Kaganov, M.I.; Lyubarskiy, G.Y.; Mitina, A.G. The theory and history of the anomalous skin effect in normal metals. Phys. Rep. 1997, 288, 291. [Google Scholar] [CrossRef]
- Deng, H.-Y. Electrostatic responses of anisotropic dielectric films. Euro. J. Phys. 2020, 41, 035203. [Google Scholar] [CrossRef]
- Deng, H.-Y. A theory of electrodynamic response for bounded metals: Surface capacitive effects. Ann. Phys. 2020, 418, 168204. [Google Scholar] [CrossRef]
- Deng, H.-Y. On the electrical conductivity of metals with a rough surface. Phil. Mag. 2021, 101, 729. [Google Scholar] [CrossRef]
- Deng, H.-Y.; Muljarov, E.A. Scattering solution to the problem of additional boundary conditions. Phys. Rev. B 2022, 106, 195301. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Physical Kinetics; Pergamon Press Ltd.: Oxford, UK, 1981. [Google Scholar]
- Deng, H.-Y. Possible instability of the Fermi sea against surface plasma oscillations. J. Phys. Condens. Matter 2017, 29, 455002. [Google Scholar] [CrossRef] [PubMed]
- Pekar, S.I. Dispersion of light in the exciton absorption region of crystals. Sov. Phys. 1958, 6, 785. [Google Scholar]
- Deng, H.-Y. A universal macroscopic theory of surface plasma waves and their losses. New J. Phys. 2019, 21, 043055. [Google Scholar] [CrossRef]
- Bishop, M.F.; Maradudin, A.A. Energy flow in a semi-infinite spatially dispersive absorbing dielectric. Phys. Rev. B 1976, 14, 3384. [Google Scholar] [CrossRef]
- Lucas, M.S.P. Electrical conductivity of thin metallic films with unlike surfaces. J. Appl. Phys. 1965, 36, 1632. [Google Scholar] [CrossRef]
- Utkin, A.I.; Yushkanov, A.A. Electric current distribution in a thin metal layer for various specular reflection coefficients of its surfaces. Tech. Phys. 2016, 61, 1457. [Google Scholar] [CrossRef]
- Landau, L.D. On the vibrations of the electronic plasma. J. Phys. 1946, 10, 25. [Google Scholar]
- Dawson, J. On landau damping. Phys. Fluids 1961, 4, 869. [Google Scholar] [CrossRef]
- Deng, H.-Y.; Wakabayashi, K.; Lam, C.-H. Universal self-amplification channel for surface plasma waves. Phys. Rev. B 2017, 95, 045428. [Google Scholar] [CrossRef]
- Deng, H.-Y. Theory of nonretarded ballistic surface plasma waves in metal films. Phys. Rev. B 2017, 95, 125442. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praill, S.; Lawton, C.; Balable, H.; Deng, H.-Y. A Theory of Dynamical Responses for Metal Films: Surface Roughness Effects. Solids 2023, 4, 268-286. https://doi.org/10.3390/solids4030017
Praill S, Lawton C, Balable H, Deng H-Y. A Theory of Dynamical Responses for Metal Films: Surface Roughness Effects. Solids. 2023; 4(3):268-286. https://doi.org/10.3390/solids4030017
Chicago/Turabian StylePraill, Sam, Charlotte Lawton, Hasan Balable, and Hai-Yao Deng. 2023. "A Theory of Dynamical Responses for Metal Films: Surface Roughness Effects" Solids 4, no. 3: 268-286. https://doi.org/10.3390/solids4030017
APA StylePraill, S., Lawton, C., Balable, H., & Deng, H.-Y. (2023). A Theory of Dynamical Responses for Metal Films: Surface Roughness Effects. Solids, 4(3), 268-286. https://doi.org/10.3390/solids4030017






