An Electron Waveguide Model for FDSOI Transistors

Abstract

We extend our previous semi-empirical model for quantum transport in a conventional nano-MOSFET to FDSOI transistors. In ultra-thin-body and -BOX (UTBB) FDSOI transistors, the electron channel can be treated as an electron waveguide. In the abrupt transition approximation, it is possible to derive an analytical approximation for the potential seen by the charge carriers. With these approximations we calculate the threshold voltage and the transfer characteristics, finding remarkably good agreement with experiments in the OFF-state given the relative simplicity of our model. In the ON-state, our theory fails because Coulomb interaction between the free charge carriers and the device heating is neglected in our approach.

1. Introduction

The notion of electron waveguide transport was used in the late 1980s and in the 1990s to discuss split-gate AlGaAs/GaAs devices [1,2]. The initiating observation in this field was the observation of quantized conduction in a point contact [3,4]. The electron waves in the waveguide are the quantum mechanical wave functions resulting from the Schrödinger equation, which are assumed to be coherent in the entire device. In a wave guide, transport is subjected to a two-dimensional potential perpendicular to the transport direction and leading to global transverse modes. Here we present a model for a FDSOI transistor in which its conduction channel is treated as an electron waveguide (FD—fully depleted, SOI—silicon-on insulator; for a review, see [5]). The model is formulated so that it can be generalized to other modern transistor architectures such as FinFETs, horizontal and vertical Nanowire transistors, and Nanosheet FETs in which the conduction channel takes a similar form [6].

For the transverse modes of an electron waveguide to be observable, essentially three conditions have to be fulfilled [2]: (i) The scale of the transverse confinement must be at most comparable to the Fermi wave length; (ii) The dimensions of the conduction channel have to be smaller than the elastic and inelastic scattering lengths; and (iii) The differences of the energies of the transverse modes must be larger than the thermal energy and larger than $e{U}_D$, where $U_D$ is the applied drain voltage.

In a series of studies [7,8,9,10], we developed a compact semi-empirical model for quantum transport in a conventional nano-MOSFET in which the experimental output characteristics could be described quantitatively. In this study, we extend this model to thin body transistors focusing on ultra-thin-body and -BOX (UTBB) FDSOI transistors with a back plane (BP) as a back gate [5,11,12,13,14,15,16,17,18,19]. Typically, in a UTBB FDSOI transistor the threshold voltage (VT) is adjusted by the work function of the metal gate, the polarity of the BP-doping, and the back gate bias allowing multi-VT operation [5,18]: High-VT (HVT) devices allow for low-leakage currents and low power dissipation whereas standard-VT (SVT) and low-VT (LVT) devices allow for fast operation. Because of the ultra-thin-body it is possible to define in the considered devices global transverse modes without mode coupling, thus simplifying more complex T-matrix type approaches with inherent mode coupling as in References [20,21,22,23,24,25].

In general, Coulomb interaction between the free charge carriers and device heating play an important role in thin film devices [26,27,28,29,30,31]. However, here we focus on the threshold- and sub-threshold regime which are of particular importance for CMOS-technology. Therefore, we may neglect these effects. It is thus possible to derive an analytical understanding of a number of the aspects of the transistor. Compared to experiments by [18], we find reasonable agreement. We also discuss to what extent the electron waveguide conditions i–iii are met in the considered UTBB FDSOI transistors.

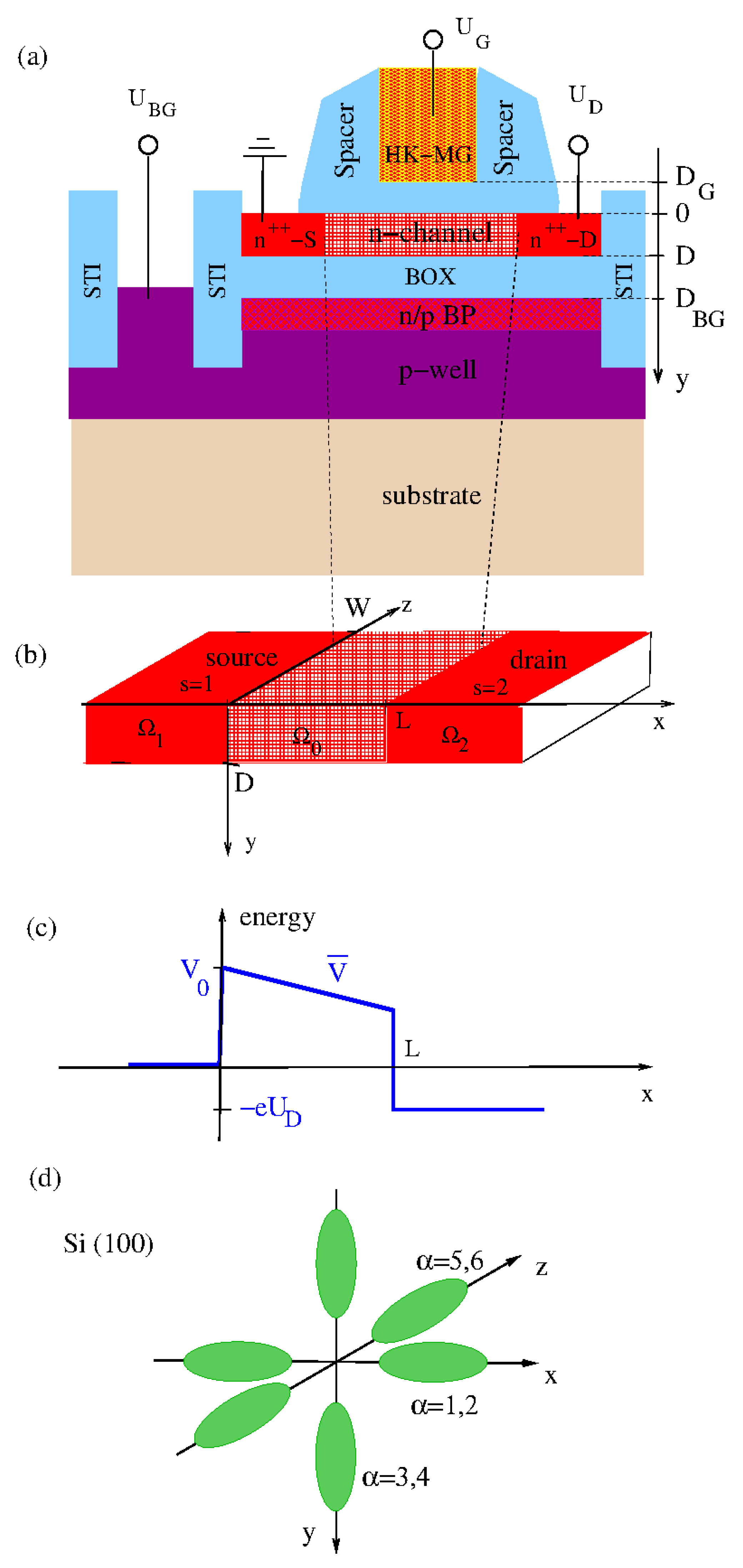
2. Materials and Methods

2.1. Quantum Transport Model

We consider a multiple VT, fully depleted SOI-transistor with a back plane (BP), as depicted in Figure 1. The n-conduction channel (waveguide) is located in a thin, nearly undoped active Si-layer of thickness D (’thin body’) and width W. The conduction channel is sandwiched between the source- and the drain contact, which are heavily n-doped. The bottom side of the active Si-layer is terminated by an insulating SiO₂-layer (BOX). Below lies the BP consisting either of a heavily p- or a heavily n-doped silicon layer. The back contact with voltage $U_{BG}$ is connected to the BP via a p-doped region (’p-well’). Further abbreviations are HK-MG for the high-k/metal gate stack and STI for shallow trench insulation. Outside the active Si-layer, the wave functions of the current carrying electrons vanish, leading to the boundary condition

$$\Psi (x,y=0,z,E)=\Psi (x,D,z,E)=\Psi (x,y,0,E)=\Psi (x,y,W,E)=0$$

(1)

Figure 1. (a) N-channel multiple VT, fully depleted SOI-transistor with a back plane (BP) (see text). (b) Active Si-layer for the conduction channel taking the form of a waveguide. (c) One-dimensional effective potential $\overline{V}$ after Equation (22). (d) The (100)-orientation of the active Si-layer with the six constant energy ellipsoids $\alpha =1\dots 6$.

(Definition of the coordinates. Figure 1b.) In the active layer with $\left(100\right)$-orientation (Figure 1d), we start from the single particle Schrödinger equation

$$\left[-\frac{{\hslash }^2}{2m_x^{\alpha }}\frac{{\partial }^2}{\partial x^2}-\frac{{\hslash }^2}{2m_y^{\alpha }}\frac{{\partial }^2}{\partial y^2}-\frac{{\hslash }^2}{2m_z^{\alpha }}\frac{{\partial }^2}{\partial z^2}+V(x,y)-E\right]\Psi (\overrightarrow{r},E)=0.$$

(2)

Here we assume isotropy in the z-direction (width direction). In the bulk semiconductor there are six equivalent valleys $\alpha =1\dots 6$, which in the finite Si-layers are split into three classes (Figure 1): First $\alpha =1,2$ with $m_x^{1,2}=m_{\Vert }$, $m_y^{1,2}=m_z^{1,2}=m_{\perp }$, second, $\alpha =3,4$ with $m_x^{3,4}=m_z^{3,4}=m_{\perp }$, $m_y^{3,4}=m_{\Vert }$, and, third, $\alpha =5,6$ with $m_x^{5,6}=m_y^{5,6}=m_{\perp }$, $m_z^{5,6}=m_{\Vert }$. Here $m_{\Vert }=0.91m_0$ is the large effective mass and $m_{\perp }=0.19m_0$ is the small effective mass associated with the constant energy ellipsoids of the valleys.

If the thickness of the Si-layer is small, one can approximate $V(x,y)$ by its average $\overline{V}\left(x\right)$ defined by

$$V(x,y)\to \overline{V}\left(x\right)=\frac{1}{D}{\int }_0^{D}dyV(x,y)$$

(3)

so that

$$\left[-\frac{{\hslash }^2}{2m_x^{\alpha }}\frac{{\partial }^2}{\partial x^2}-\frac{{\hslash }^2}{2m_y^{\alpha }}\frac{{\partial }^2}{\partial y^2}-\frac{{\hslash }^2}{2m_z^{\alpha }}\frac{{\partial }^2}{\partial z^2}+\overline{V}\left(x\right)-E\right]\Psi (\overrightarrow{r},E)=0$$

(4)

(see Figure 2b,c). Because of good screening in the contacts we can write $V(x<0,y)=0$ and $V(x\ge L,y)=-e{U}_D$ leading to

$$\overline{V}(x>L)=0\mathrm{and}\overline{V}(x\ge L)=-e{U}_D.$$

(5)

Figure 2. For the theoretical parameter set listed at the beginning of Section 3: (a) Energy diagrams of the isolated contacts. (b) Transverse confinement potential $V_T\left(y\right)$ for an n-BP at $U_{BG}=0$ (SVT(i)) for $U_G$ = 0.0 (black), 0.1 V (red), 0.2 V (green), 0.3 V (blue), 0.4 V (orange), 0.5 V (brown), 0.6 V (grey), 0.7 V (violet), 0.8 V (cyan), and 0.9 V (magenta). (c) In circles: Effective barrier height $V_0$ resulting from Equation (33), color coding as in part (b). Marked by an arrow: Threshold gate voltage $U_G^{th}$ determined by condition (39).

The effective potential in the scattering area $\overline{V}(0\le x\le L)$ will be discussed in Section 2.2. The independence of the potential (4) of the transverse coordinates allows for a product ansatz

$$\Psi (\overrightarrow{r},E)=\psi (x,E^x){\Phi }_n(y,z)$$

(6)

for the wave functions which correspond to electron states in an electron wave guide. Here the global transverse modes are given by

$${\Phi }_n={\Phi }_{n_y{n}_z}=\frac{2}{\sqrt{DW}}sin\left(n_y\frac{\pi }{D}y\right)sin\left(n_z\frac{\pi }{W}z\right).$$

(7)

The factor $\psi (x,E^x)$ describes the propagation of a charge carrier in this mode since the total energy E is split in a transverse energy of the motion in the y-z-direction

$$E_n^{\perp }=E_{n_y{n}_z}^{\perp }=\frac{{\hslash }^2}{2m_y^{\alpha }}{\left(n_y\frac{\pi }{D}\right)}^2+\frac{{\hslash }^2}{2m_z^{\alpha }}{\left(n_z\frac{\pi }{W}\right)}^2$$

(8)

and a longitudinal energy

$$E^x=E-E_n^{\perp }$$

(9)

of the motion in the x-direction. Insertion of (6) into (4) leads to the one-dimensional scattering problem

$$\left[-\frac{{\hslash }^2}{2m_x^{\alpha }}\frac{d^2}{d{x}^2}+\overline{V}\left(x\right)-E^x\right]\psi (x,E^x)=0.$$

(10)

The source-incident scattering solutions ${\psi }^1(x,E^x)$ exhibit the asymptotic

$${\psi }^{1\alpha }(x\le 0,E^x)=e^{i{k}_{1\alpha }x}+r^{1\alpha }\left(E^x\right)e^{-i{k}_{1\alpha }x}$$

(11)

and

$${\psi }^{1\alpha }(x\ge L,E^x)=t^{1\alpha }\left(E^x\right)e^{i{k}_{2\alpha }(x-L)}.$$

(12)

Here the wave number is given by

$$k_{ns\alpha }\left(E\right)=\sqrt[+]{\frac{2m_x^{\alpha }}{{\hslash }^2}(E-E_{\perp }^n+e{U}_s)}=\sqrt[+]{\frac{2m_x^{\alpha }}{{\hslash }^2}(E^x+e{U}_s)}\equiv k_{s\alpha }\left(E^x\right)$$

(13)

with $s=1$ for the source and $s=2$ for the drain as well as $U_1=0$ and $U_2=U_D$. Our method for the numerical evaluation of the transmission coefficients $t^{1\alpha }$ is described in detail in Appendix E of [10].

The drain current results from the contributions of the six valleys according to $I_D={\sum }_{\alpha }{I}_D^{\alpha }$ given by the Landauer–Büttiker formula. As we discuss in detail in Appendix A:

$$I_D^{\alpha }=\frac{2e}{h}{\int }_0^{\infty }d{E}^x\left[S_{\alpha }(E^x-\mu )-S_{\alpha }(E^x-\mu +e{U}_D)\right]{\tilde{T}}^{1d}\left(E^x\right).$$

(14)

Here the one-dimensional current transmission is given by

$${\tilde{T}}^{1d}\left(E^x\right)=k_{2\alpha }\left(E^x\right){\left|t^{1\alpha }\left(E^x\right)\right|}^2{k}_{1\alpha }{\left(E^x\right)}^{-1}.$$

(15)

In the limit of large W, the supply function is given by

$$S_{\alpha }\left(\beta \right)=W\sqrt{\frac{m_z^{\alpha }{k}_{B}T}{2\pi {\hslash }^2}}\sum _{n_y}{F}_{-1/2}\left[-\frac{1}{k_{B}T}\left(\beta +n_y^2\frac{{\pi }^2{\hslash }^2}{2m_y^{\alpha }{D}^2}\right)\right]$$

(16)

with the Fermi–Dirac integral

$$F_j\left(x\right)=\frac{1}{\Gamma (j+1)}{\int }_0^{\infty }dy\frac{y^j}{1+e^{y-x}}.$$

(17)

The calculation of the chemical potential $\mu$ is demonstrated in Appendix B. The total current per width is determined from (14) according to

$$J=\frac{I_D}{W}=\frac{1}{W}\sum _{\alpha }{I}_D^{\alpha }.$$

(18)

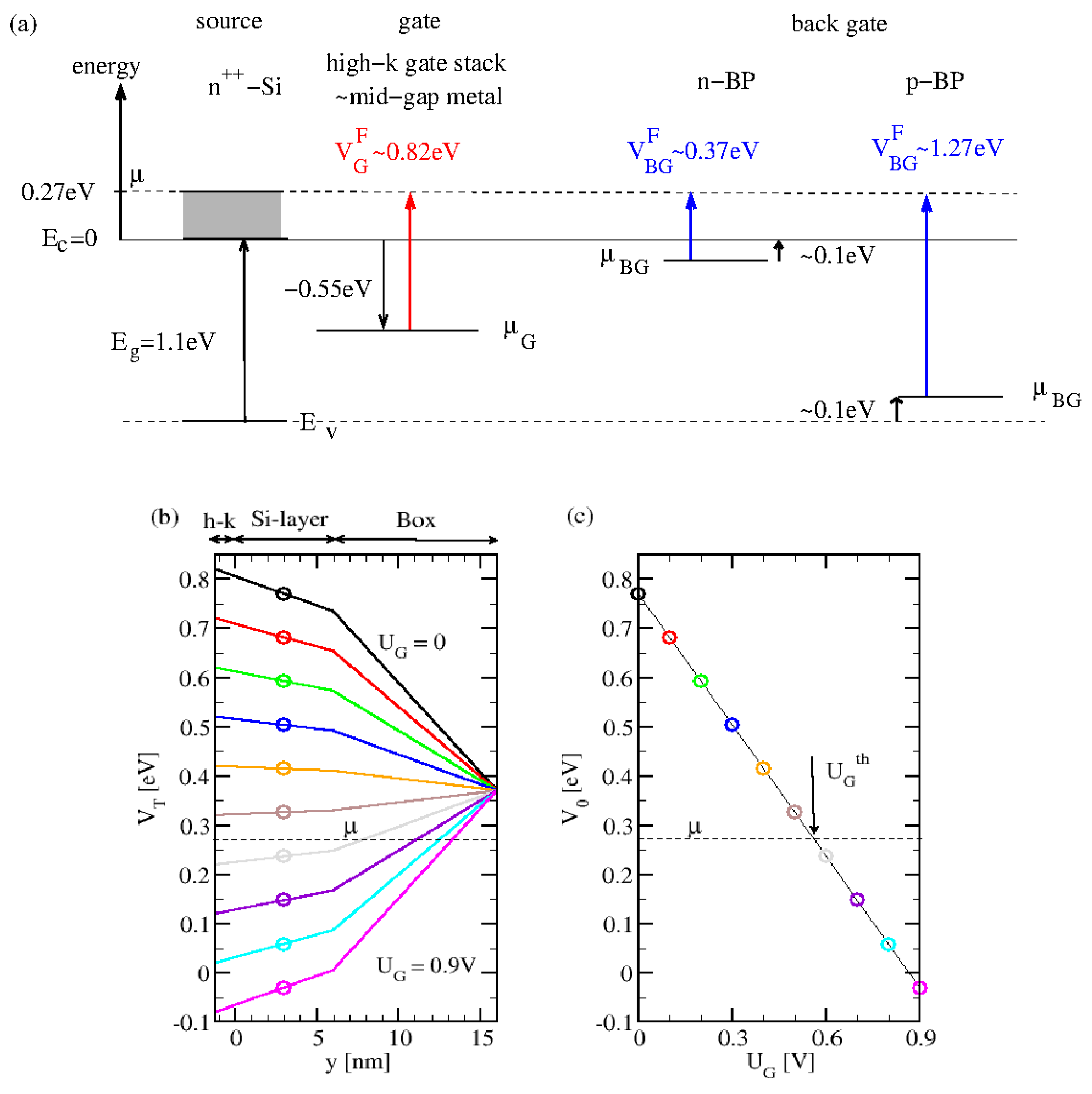
2.2. Potential in Abrupt Transition Approximation

For the potential in the Si-film entering into (2), we can write in the contacts $V(x<0,0\le y\le D)=0$ and $V(x>L,0\le y\le D)=-e{U}_D$. In the conduction channel, i.e., for $0\le x\le L$ it can be found from Poisson’s equation

$$\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)V(x,y)=\frac{e}{{\kappa }_0\kappa \left(y\right)}\rho (x,y)$$

(19)

with the charge density $\rho$ and appropriate boundary conditions. Here, ${\kappa }_0$ is the vacuum permitivity and $\kappa (-D_G<y<0)$ is given by the dielectric constant ${\kappa }_{HK}$ of the high-k-dielectric, $\kappa (0\le y\le D)$ is given by the dielectric constant ${\kappa }_{Si}$ of the Si-film, and $\kappa (D<y\le D_{BG})$ is given by the dielectric constant ${\kappa }_{Ox}$ in the BOX. As shown in Figure 1a, $y=-D_G$ marks the interface between top-gate insulation and top gate and $y=D_{BG}$ marks the interface between BOX and back gate (BP). For the conduction channel, we specialize Equation (19) to the threshold- and sub-threshold regime, which is important for technological applications. Here, we may neglect the contribution of the free charge carriers. In FDSOI technology, one assumes furthermore the full ionization of the impurities (depletion approximation) so that $\rho =-e{N}_A\Theta \left(y\right)\Theta (D-y)$ with the acceptor density $N_A$ in the Si-layer. One finds

$$\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)V(x,y)=-\frac{e^2}{{\kappa }_0\kappa \left(y\right)}{N}_A\Theta \left(y\right)\Theta (D-y)N_A.$$

(20)

This equation was studied, e.g., in References [32,33,34,35,36]. To construct a potential approximation of the form $\overline{V}\left(x\right)$ as assumed in Equation (4), we here apply the abrupt transition-approximation as described in References [9,10]. While in the contacts we have $V(x\le 0,y)=0$ and $V(x\ge L,y)=-e{U}_D$, there is an abrupt transition to the potential in the scattering area ($0<x<L$, conduction channel). In the scattering area, we seek a solution of (20) of the separable form

$$V(0\le x\le L,y)=-e{U}_D\frac{x}{L}+V_T\left(y\right)$$

(21)

and then construct according to (3)

$$\overline{V}\left(x\right)=\frac{1}{D}{\int }_0^{D}dy\left[-e{U}_D\frac{x}{L}+V_T\left(y\right)\right]=V_0-e{U}_D\frac{x}{L}.$$

(22)

In the latter expression we assume for a thin film that the quantization energy induced by the boundary condition $\Psi (x,y=0,z,E)=\Psi (x,D,z,E)$ is dominant over the potential variation of $V_T\left(y\right)$ so that we can replace $V_T\left(y\right)$ with its average, $V_0=(1/D){\int }_0^{D}dy{V}_T\left(y\right)$. Upon insertion of (21) into (20), one obtains

$$\frac{d^2}{d{y}^2}{V}_T\left(y\right)=-\frac{e}{{\kappa }_0\kappa \left(y\right)}{N}_A\Theta \left(y\right)\Theta (D-y).$$

(23)

We now impose Dirichlet boundary conditions

$$V_T(-D_G)=-e{U}_G^{\prime }=-e{U}_G+V_G^F\mathrm{and}{V}_T\left(D_{BG}\right)=-e{U}_{BG}^{\prime }=-e{U}_{BG}+V_{BG}^F.$$

(24)

As usual, the flat band energies

$$V_G^F=\mu -{\mu }_G\mathrm{and}{V}_{BG}^F=\mu -{\mu }_{BG}$$

(25)

are defined by the difference between the chemical potential in the grounded source $\mu$ and the chemical potential in the respective isolated contact, ${\mu }_G$ for the top gate and ${\mu }_{BG}$ for the back gate. Then, one has for the electro chemical potential in the top gate for $U_G=0$ the value ${\mu }_G+V_T(-D_G)={\mu }_G+V_G^F=\mu$ as required. Furthermore, we require at the two silicon-insulator interfaces at $y=0$ and $y=D$ the usual continuities of $V_T$ and $\kappa V_T^{\prime }$, resulting in

$$V_T\left(0^{-}\right)=V_T\left(0^{+}\right)\mathrm{and}\kappa \left(0^{-}\right)\frac{d}{dy}{V}_T{|}_{0^{-}}=\kappa \left(0^{+}\right)\frac{d}{dy}{V}_T{|}_{0^{+}}$$

(26)

plus corresponding relations at $y=D$. As is characteristic for the abrupt transition-approximation, the potential in (21) can be interpreted as the superposition of, first, a constant electric field in longitudinal direction, $E_x=-U_D/L$, induced by the drain voltage and, second, a transverse potential variation $V_T\left(y\right)$ describing an infinite conduction channel at $U_D=0$.

The reduced Poisson equation (23) with the boundary conditions (24) can be solved easily with the ansatz

$$V_T(y<0)=c_1(y+D_G)-e{U}_G^{\prime },$$

(27)

$$V_T(0\le y\le D)=-\frac{C}{2}{y}^2+\alpha y+\beta$$

(28)

with $C=e^2{N}_A/\left({\kappa }_0{\kappa }_{Si}\right)$, and

$$V_T(y>D)=c_2(y-D_{BG})-e{U}_{BG}^{\prime }.$$

(29)

In Appendix C we show

$$\alpha =\frac{C{D}^2/2+{\kappa }_{2}CD{D}_{Box}+e(U_G^{\prime }-U_{BG}^{\prime })}{D+{\kappa }_2{D}_{Box}+{\kappa }_1{D}_G}$$

(30)

as well as

$$\beta ={\kappa }_1\alpha D_G-e{U}_G^{\prime },$$

(31)

with ${\kappa }_1={\kappa }_{Si}/{\kappa }_{HK}$, ${\kappa }_2={\kappa }_{Si}/{\kappa }_{Ox}$, and $D_{Box}=D_{BG}-D$. Furthermore,

$$c_1={\kappa }_1\alpha \mathrm{and}nd{c}_2=-\frac{-C{D}^2/2+\alpha D+\beta +e{U}_{BG}^{\prime }}{D_{Box}}.$$

(32)

From Equations (3), (21) and (22) one finds for the barrier height

$$V_0=\frac{1}{D}{\int }_0^{D}dy\left[-\frac{C}{2}{y}^2+\alpha y+\beta \right]=-\frac{C}{6}{D}^2+\frac{\alpha }{2}D+\beta .$$

(33)

3. Results

Theoretical parameters: With the exception of Figure 3 where we vary the parameter $D_{Box}$, we use the parameters $D_G=1.2$ nm, $D=6$ nm, $D_{Box}=10$ nm, ${\kappa }_{Si}=12$, ${\kappa }_{Ox}=3.9$, ${\kappa }_{HK}=12$ ($D_G$ is the equivalent oxide thickness EOT), $L=30$ nm, $W\to \infty$, $T=298$ K, $N_D=5\times {10}^{20}{\mathrm{cm}}^{-3}$ ($n^{++}$-doping in source and drain), $N_A={10}^{15}{\mathrm{cm}}^{-3}$ (weak p-doping in conduction channel), and the operating voltage of $U_{DD}=0.9$ V. These parameters are compatible with the ones in Reference [18]. From Equation (A15), one obtains a value of $\mu \sim 0.27$ eV. As shown in the energy diagrams of the isolated contacts in Figure 2a, we take the bottom of the conduction band in the grounded $n^{++}$-source as the energy zero. For the chemical potential in the isolated gate metal, we choose ${\mu }_G=-0.55$ eV, which is the mid gap position in silicon. For the back gate one assumes a doping concentration markedly lower than that of the $n^{++}$-source ( $\sim {10}^{18}{\mathrm{cm}}^{-3}$ in Reference [18]) corresponding to ${\mu }_{BG}=-0.1$ eV for an n-BP and ${\mu }_{BG}=-1.0$ V for a p-BP. For the flat band voltages, it follows from (25)

$$V_G^F=0.82\mathrm{eV},V_{BG}^F=0.37\mathrm{eV}\left(\mathrm{n-BP}\right),\mathrm{and}{V}_{BG}^F=1.27\mathrm{eV}\left(\mathrm{p-BP}\right)$$

(34)

Figure 3. The threshold voltage versus thickness of the box: n-BP with $U_{BG}=0$ (orange), n-BP with $U_{BG}=U_{DD}$ (red), p-BP with $U_{BG}=0$ (blue), and p-BP with $U_{BG}=U_{DD}$ (green). Solid lines according to Equation (41) and dashed lines according to Equation (42). The circles mark the values for $D_{Box}=10$ nm which enter Table 1.

(See Figure 2a.) As an example, we consider in Figure 2 an n-channel transistor with an n-BP at $U_G=0$. In part (b), the transverse potential $V_T\left(y\right)$ is plotted as calculated from Equations (27)–(29). In the limit of small D, it is permissible to set $C\to 0$ (for discussion, see Equation (A30)) so that in (28) the curvature of the potential in the conduction channel can be neglected. In consequence, $V_T\left(y\right)$ is close to a piecewise linear function across the silicon layer. The transverse ideal box-confinement induced by the boundary condition $\Psi (x,y=0,z,E)=\Psi (x,D,z,E)$ in Equation (1) causes a typical quantization energy $\Delta E$ in the corresponding ideal box-confinement given by

$$\Delta E=\frac{{\hslash }^2}{2m\ast }{\left(\frac{\pi }{D}\right)}^2=32\mathrm{meV}.$$

(35)

at $D=6$ nm, were $m^{*}={(m_{\perp }\ast m_{\Vert }^2)}^{1/3}=0.32m_0$ is the effective band mass. We compare this energy to the absolute value of the total change $\Delta V$ of $V_T$ across the conduction channel as taken from Figure 2b. This change is maximum at $U_G=0$, taking the value $\Delta V\sim 80$ meV. Therefore, $\Delta V\lesssim \Delta E<3\Delta E$ holds, where $3\Delta E$ is the excitation energy from the first to the second lowest level of the quantization in the y-direction. This relation justifies the transition from Equation (2) to Equation (4). Comparing $\Delta E$ to $k_{B}T\sim 25$ meV at room temperature, it is seen that condition (iii) for the observability of the transverse modes listed in the introduction is fulfilled. Setting $\mu \sim E_F={\hslash }^2{k}_F^2/\left(2m^{*}\right)$ and ${\lambda }_F=2\pi /k_F$, one obtains ${\lambda }_F\sim 4$ nm. So condition (i) is almost fulfilled, especially if one takes smaller values for $N_D$. Condition (ii) probably requires shorter channels.

In Figure 2c, the effective barrier height $V_0$ according to Equation (33) is shown. In the limit $C\to 0$, one obtains a linear relation $V_0\left(U_G\right)$ given by

$$\begin{array}{c}\hfill V_0=V_0^0-(1-A)e{U}_G\end{array}$$

(36)

with

$$V_0^0=V_G^F+A(V_{BG}^F-V_G^F-e{U}_{BG})$$

(37)

and

$$A=\frac{D/2+{\kappa }_1{D}_G}{D+{\kappa }_2{D}_{Box}+{\kappa }_1{D}_G}$$

(38)

(see Appendix D). Because ${\kappa }_2{D}_{Box}\gg D,{\kappa }_1{D}_G$, the parameter A is small, for our system taking the value $A=0.12$, so that $d{V}_0/d{U}_G\sim -1$.

In Figure 2c, we also plot the threshold voltage $U_G^{th}$ (in text abbreviated with VT) as calculated from the condition

$$V_0\left(U_G^{th}\right)=\mu .$$

(39)

This condition was used in earlier studies for a conventional MOSFET (see, for example, Figure 4 of [9]).

An important feature of the FDSOI technology is the possibility to control the threshold gate voltage, first, by choosing either an n-BP or a p-BP, and, second, by applying a voltage $U_{BG}$ at the BP. Important VT-options are listed in Table 1 of [16]:

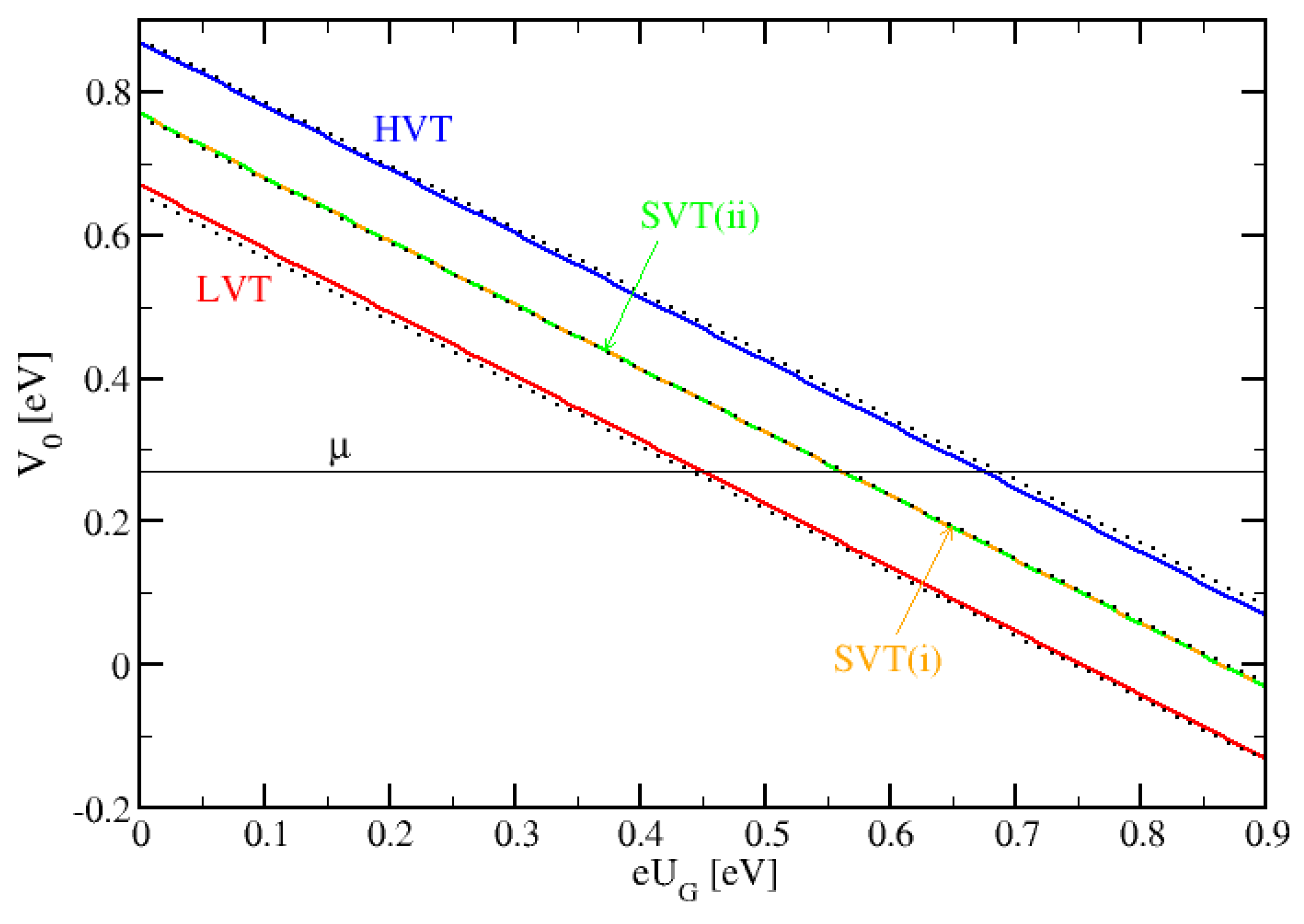
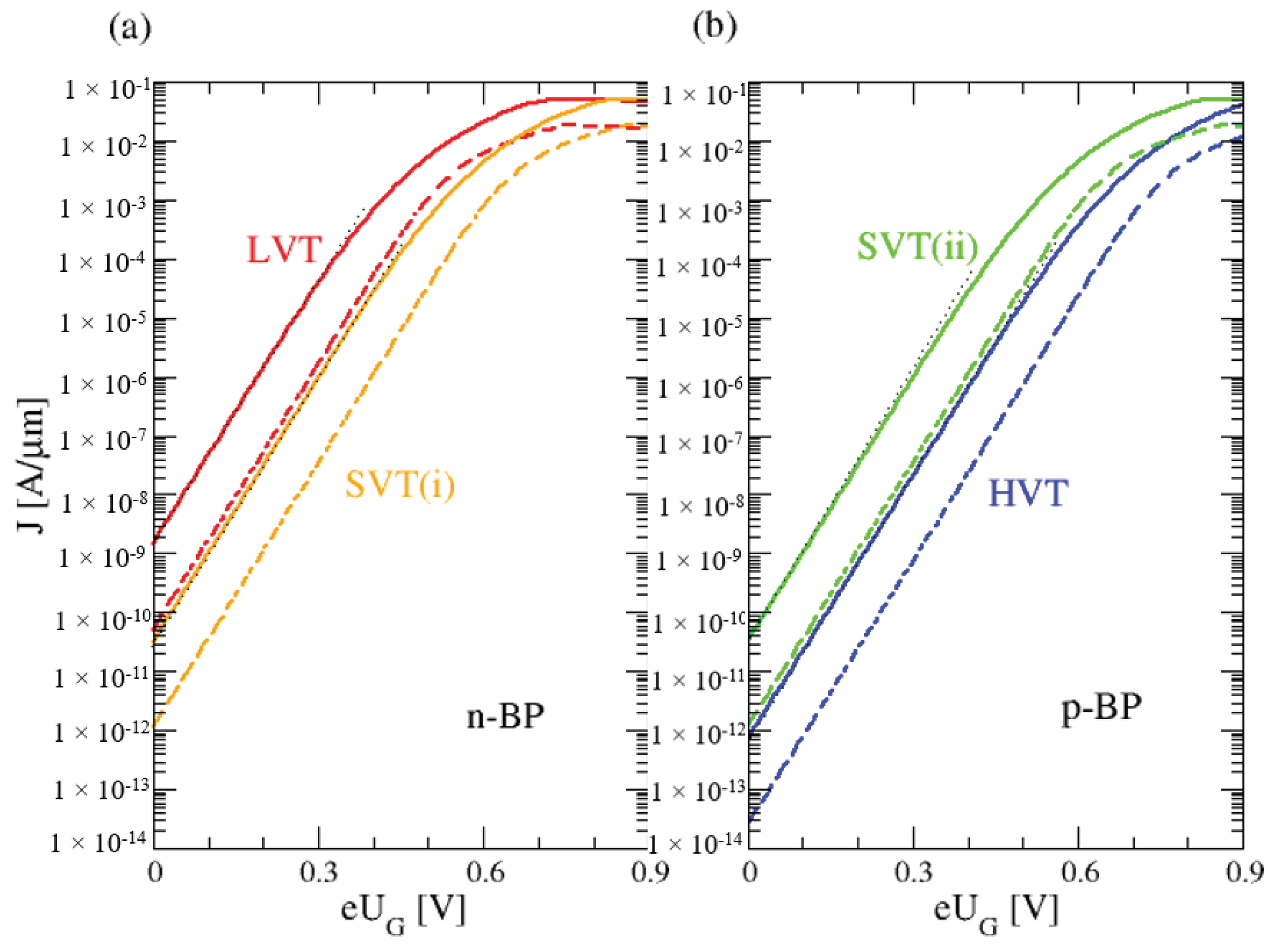
• n-BP with $U_{BG}=0$: standard-VT (SVT (i)), identical with Figure 2b;
• n-BP with $U_{BG}=U_{DD}$: low-VT (LVT);
• p-BP with $U_{BG}=0$: high-VT (HVT);
• p-BP with $U_{BG}=U_{DD}$ standard-VT (SVT (ii)).

The associated effective barrier heights $V_0$ are given in Figure 4. From Equation (36), one finds in all four cases a good linear approximation $V_0\left(U_G\right)$ with identical slopes $\sim -1$. A further inspection of Equation (36) reveals that equal barrier heights for SVT(ii) and SVT(i) result from the identical value $V_{BG}^F-e{U}_{BG}=0.5eV$. In the general case, one obtains identical results for SVT(i) and SVT(i) if

$$\Delta V_{BG}^F=e\Delta U_{BG}=U_{DD}$$

(40)

where $\Delta V_{BG}^F$ is the difference between the flat band energies in the p-BP and the n-BP.

Figure 4. For the system parameters, the barrier height $V_0\left(e{U}_G\right)$ from (33): n-BP with $U_{BG}=0$ (SVT(i), orange), n-BP with $U_{BG}=U_{DD}$ (LVT, red), p-BP with $U_{BG}=U_{DD}$ (SVT(ii), green), and p-BP with $U_{BG}=0$ (HVT, blue). In dotted black lines: Linear approximation to $V_0\left(e{U}_G\right)$ in Equation (36). The horizontal black solid line marks the chemical potential $\mu$ where the intersection points with $V_0\left(e{U}_G\right)$ give the threshold voltage $U_G^{th}$, according to (39).

In Figure 3, we plot the threshold voltage calculated from condition (39) with the linear approximation of $V_0\left(U_G\right)$, as given in Equation (36) so that

$$e{U}_G^{th}=\frac{V_0^0-\mu }{1-A}.$$

(41)

We find reasonable agreement with the experimental results in Figure 3 of [18]. In Appendix D, it is shown that (41) can be simplified to give

$$e{U}_G^{th}\sim -{\mu }_G+\frac{D/2+{\kappa }_1{D}_G}{{\kappa }_2{D}_{Box}}\left(-{\mu }_{BG}-e{U}_{BG}\right).$$

(42)

In Figure 3 it is demonstrated that the expressions (41) and (42) agree very closely. According to Equation (42), we find for $D_{Box}\to \infty$ the value for $U_G^{th,\infty }=-{\mu }_G=0.55$ corresponding to mid-gap position. From Figure 3 of [18], we read for $D_{Box}\to \infty$ the experimental value $U_G^{th,\infty }=400$ mV, which might indicate a shift of the experimental ${\mu }_G$ from mid-gap position. The formula (42) explains the finding $e{U}_G^{th}+{\mu }_G\propto 1/D_{Box}$, which is present in experiments as well. Note that in theory and experiments, the identical curves for SVT(i) and for SVT(ii) both bend up slightly.

In Figure 5 we plot the transfer characteristics resulting in the four VT-options. As documented in Table 1, we find for the threshold- and subthreshold regime a remarkable agreement between theory and experiment in view of the simplifications in our theory. The major simplifications are the use of the abrupt transition approximation, the neglect of Coulomb interaction of the free carriers, and the disregard of the x-dependence of $V_T$. It can be expected that without abrupt transition approximation, the transition between contacts and conduction channel is smoothed out and the maximum of the barrier is shifted from $x=0$ towards the interior of the conduction channel. Because of the longitudinal electric field in the conduction channel, the height of the barrier will then be reduced, leading to the well-known drain induced barrier lowering (DIBL). This effect can explain the higher theoretical values for $I_{OFF}$. As can be expected, in the ON-state our model fails. The first reason is the neglect of the free carriers in the charge density entering into the Poisson equation (20). Above threshold free carriers increasingly enter the conduction channel and alter the potential because of screening. The second reason is heating, which has been neglected in our approach but which becomes substantial above threshold. The third reason is the neglect of the linear drop of $V_T$, which becomes important in the ON-state when $V_0\sim 0$.

Figure 5. For theoretical parameters the transfer characteristics for $U_D=0.05$ V (dashed lines) and $U_D=0.9$ V (solid lines). (a) for a n-BP and (b) for a p-BP. Color coding as in Figure 3. In black: Traces taken to extract the SS.

Table 1. Electrical characteristics of multi-$V_T$ nMOS-transistors: above theoretical values taken from Figure 3 and Figure 5, below experimental values taken from TABLE 2 of Reference entering only experimental values as stated [18].

Type	${\mathit{U}}_{\mathit{G}}^{\mathbf{th}}$ [mV]	${\mathit{I}}_{\mathbf{ON}}[\mathsf{\mu }\mathbf{A}/\mathsf{\mu }\mathbf{m}]$	${\mathit{I}}_{\mathbf{OFF}}[\mathbf{pA}/\mathsf{\mu }\mathbf{m}]$	$\mathbf{SS}$ [mV/dec]
LVT	440	45,900	1474	70
SVT(i)	563	49,452	32	70
SVT(ii)	563	44,952	32	70
HVT(i)	686	39,385	0.7	70
LVT	278	480	2139	77
SVT(i)	429	332	16	76
SVT(ii)	430	333	17	77
HVT(i)	567	208	0.1	73

4. Discussion

The presented theoretical model for a FDSOI transistor has been designed on the one hand to be complex enough to enter all relevant physical parameters and on the other hand to be simple enough to allow for an analytical discussion as much as possible. It is designed for the threshold- and sub-threshold regime. Here, the theoretical results are remarkably close to the experimental ones. The model fails completely in the ON-state regime. Here, Coulomb interaction between the charge carriers and device heating becomes important [9] as well as the linear drop in $V_T$. These have been neglected in our model and have to be included in future work.