Surface Plasmons Excited by X-rays in the Surface Layers of Solids
Abstract
:1. Introduction
1.1. Total External Reflection of X-rays from the Surface of Solids
1.2. Ideas about the Excitation of Surface Plasmons in Solids by X-rays
1.2.1. Theoretical Concepts of Plasma Oscillations in Metals
1.2.2. Plasma Oscillations in Crystalline Semiconductors and Dielectrics
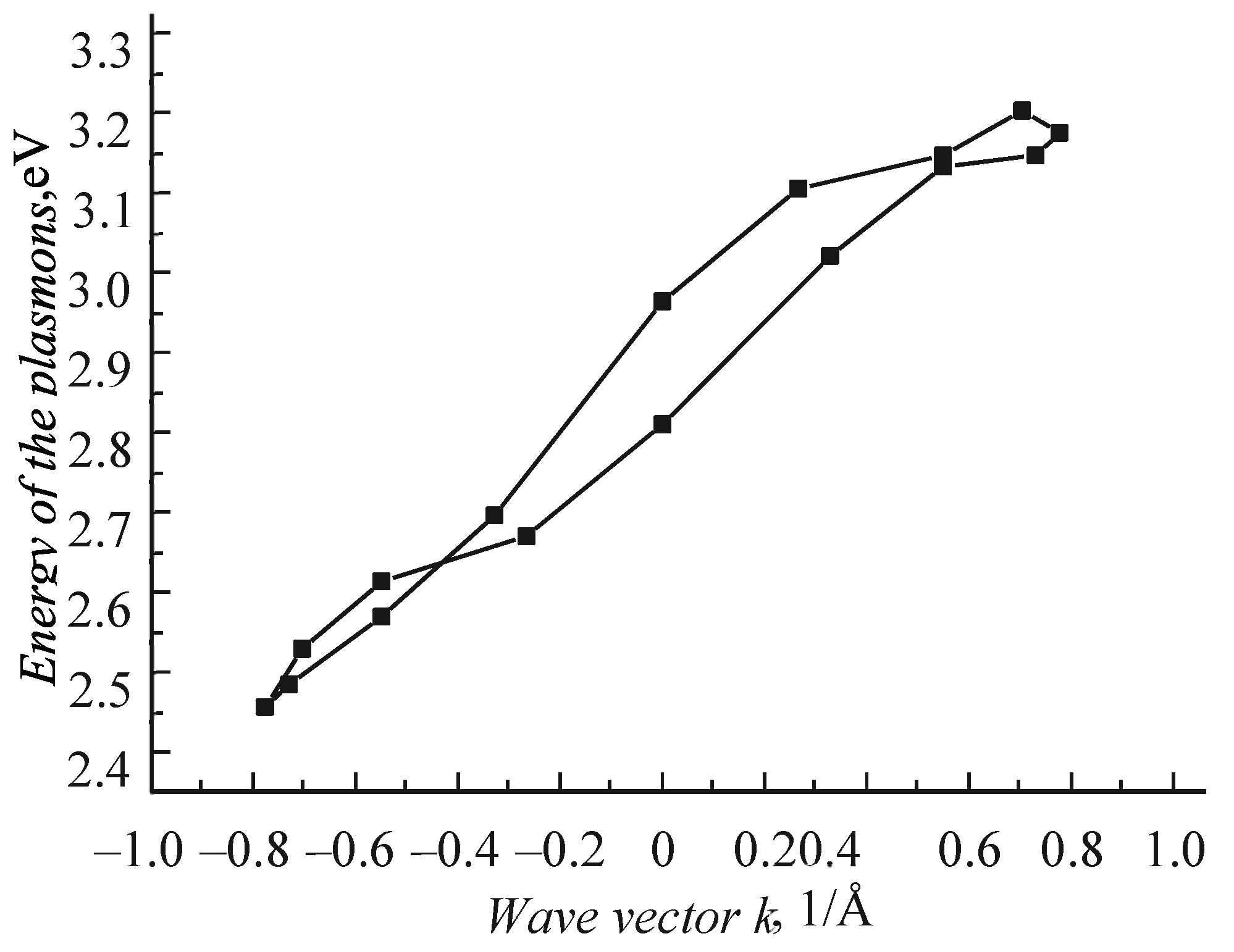
2. Dispersion of Surface Plasmons in Solids
2.1. Comparative Study of Plasmon Dispersion in Amorphous Fused Quartz and in a Single Crystal LiF
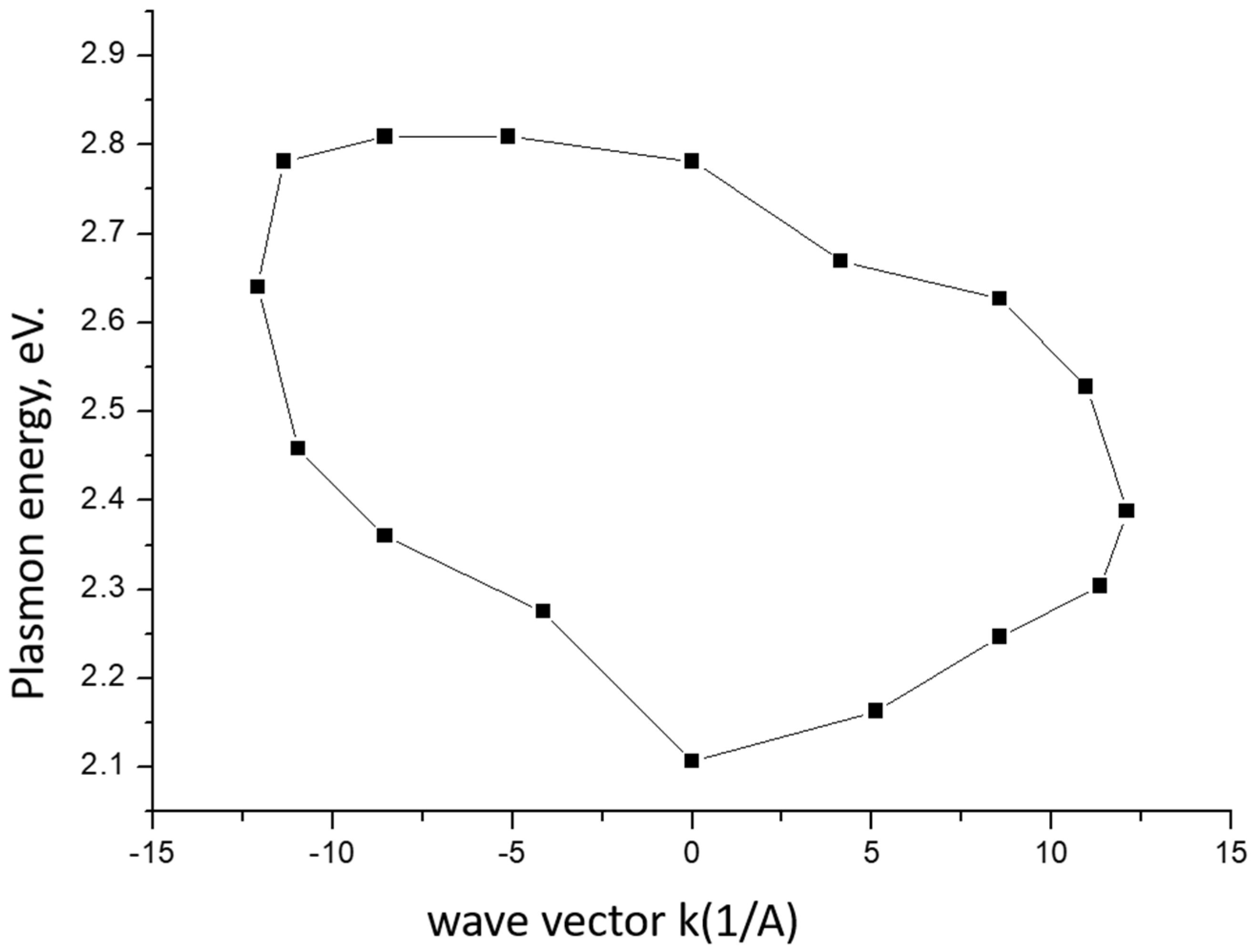
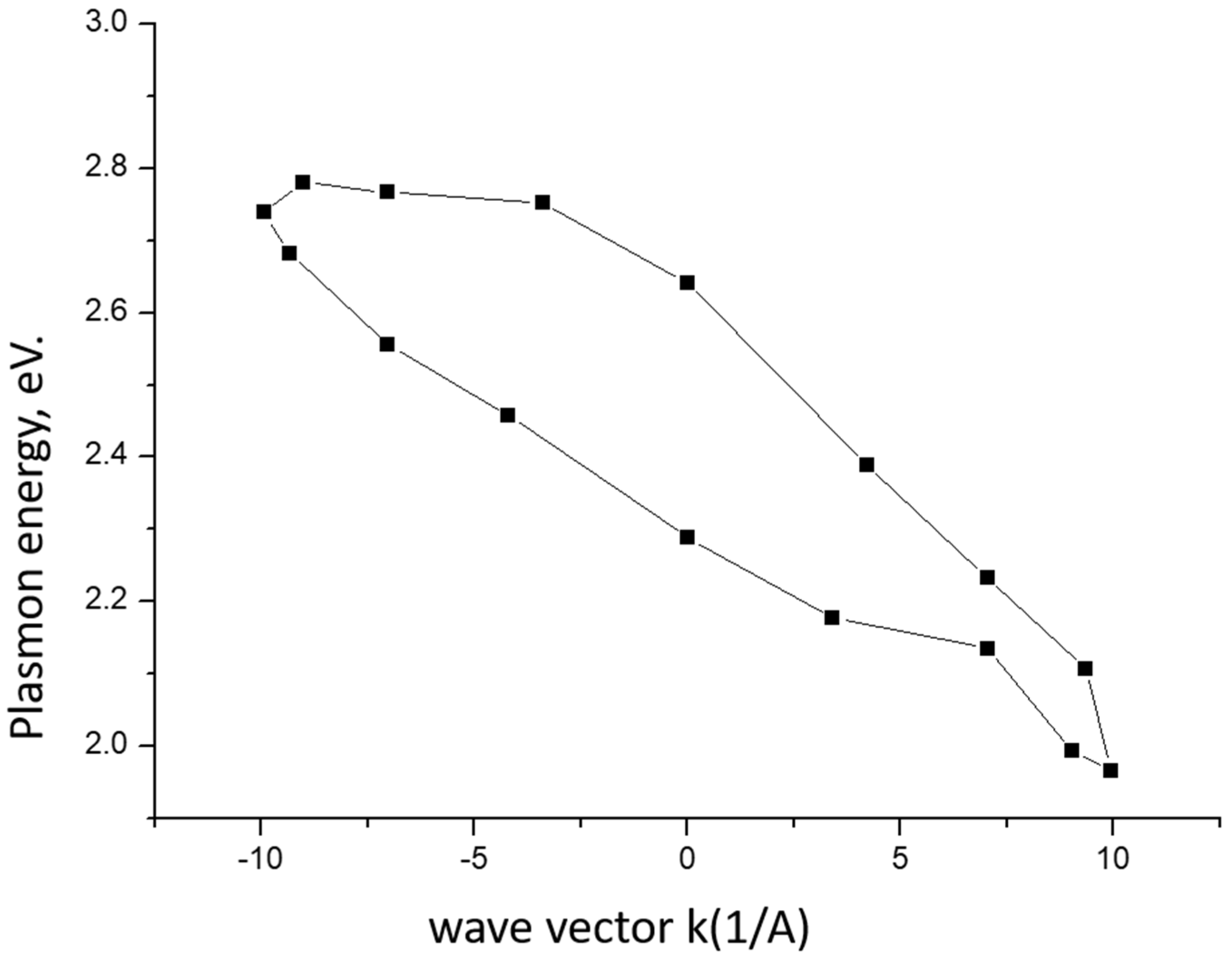
2.2. Plasmon Dispersion in Amorphous Vanadium Dioxide VO2 Films
2.2.1. Theoretical Calculations of Vanadium Dioxide
- (1)
- Calculation of the depth of the TSE X output.
- (2)
- Calculation of the depth x formation of TER X-rays.
- (3)
- Calculation of the number of electrons N involved in the excitation of plasmons in vanadium dioxide.
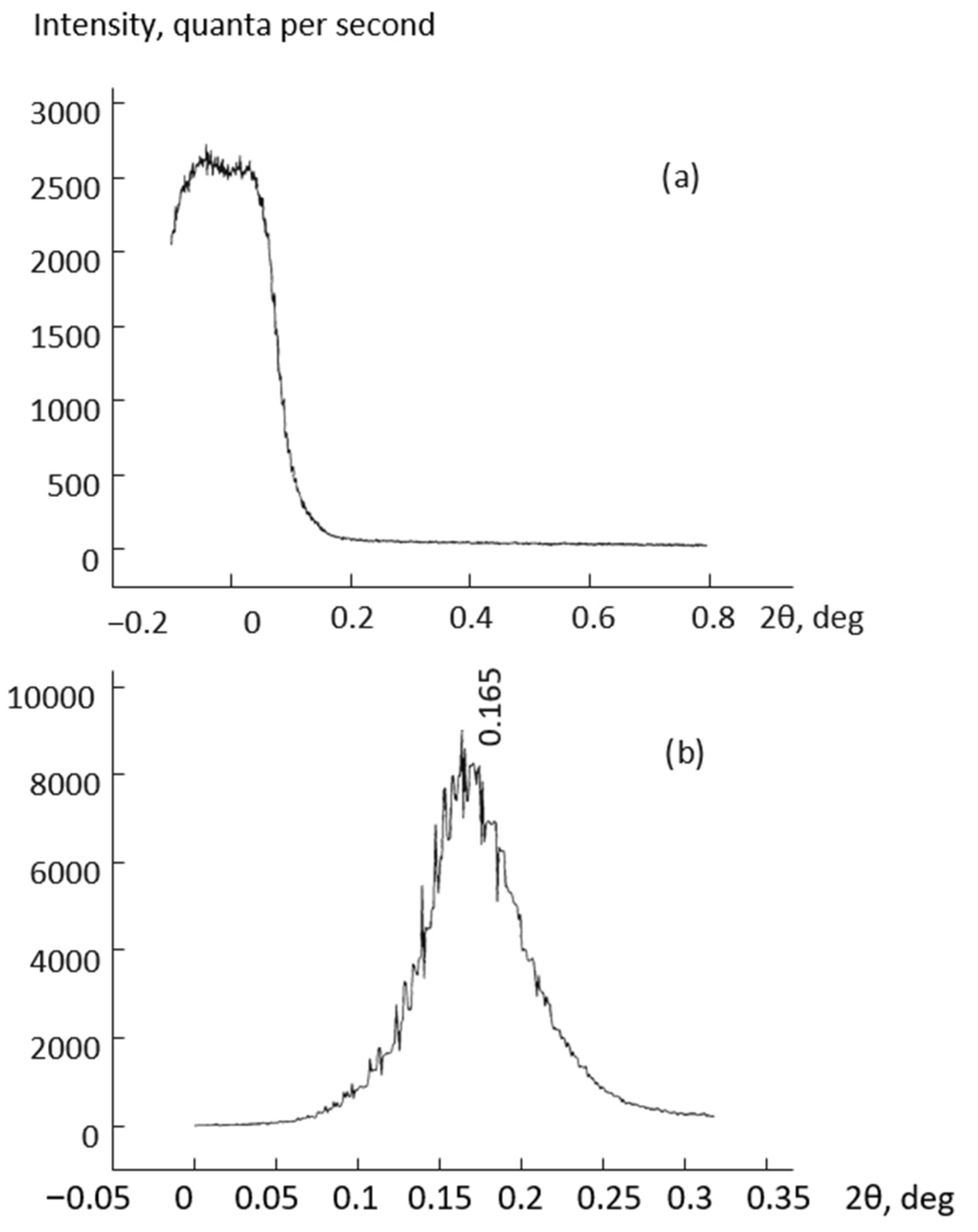
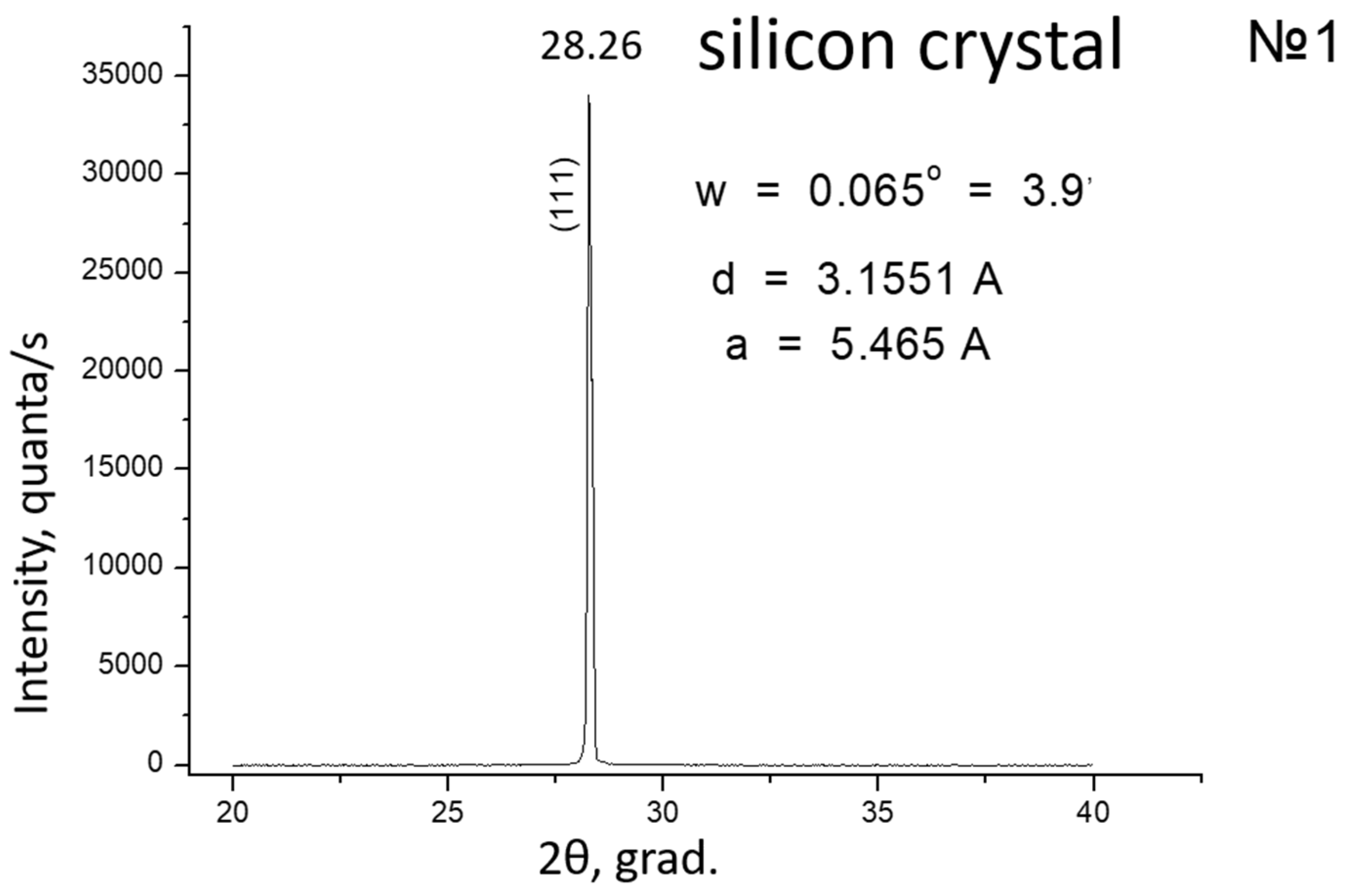
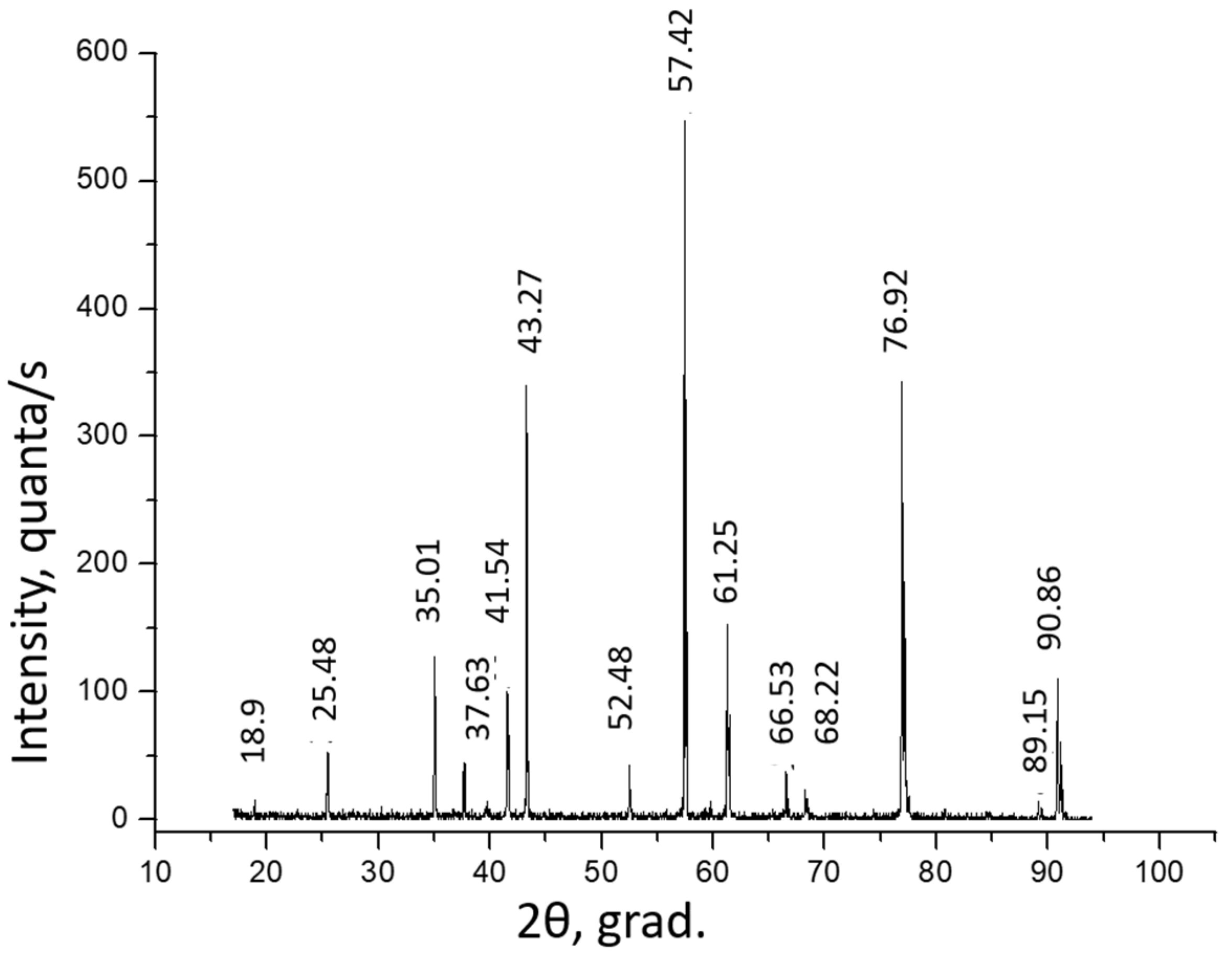
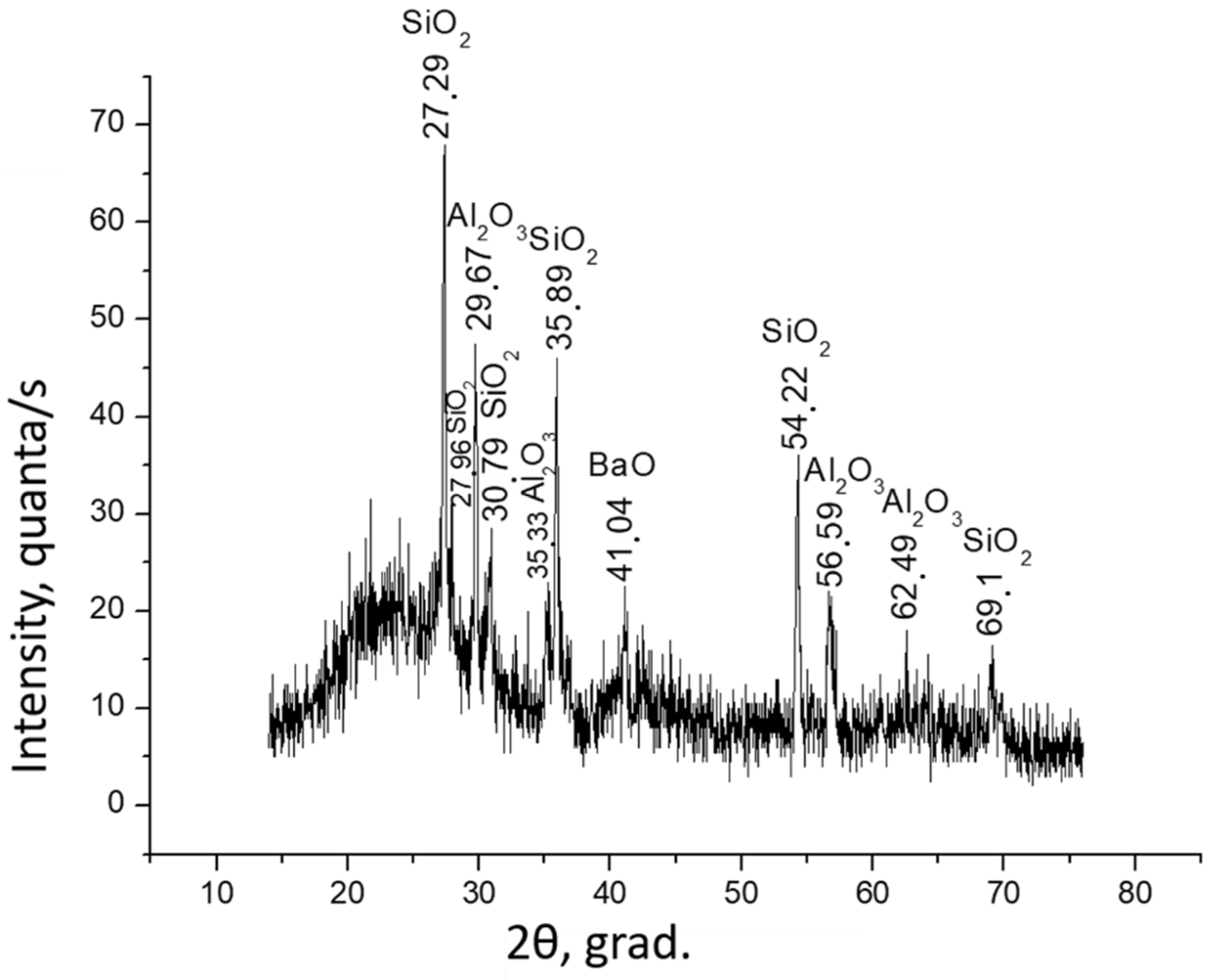
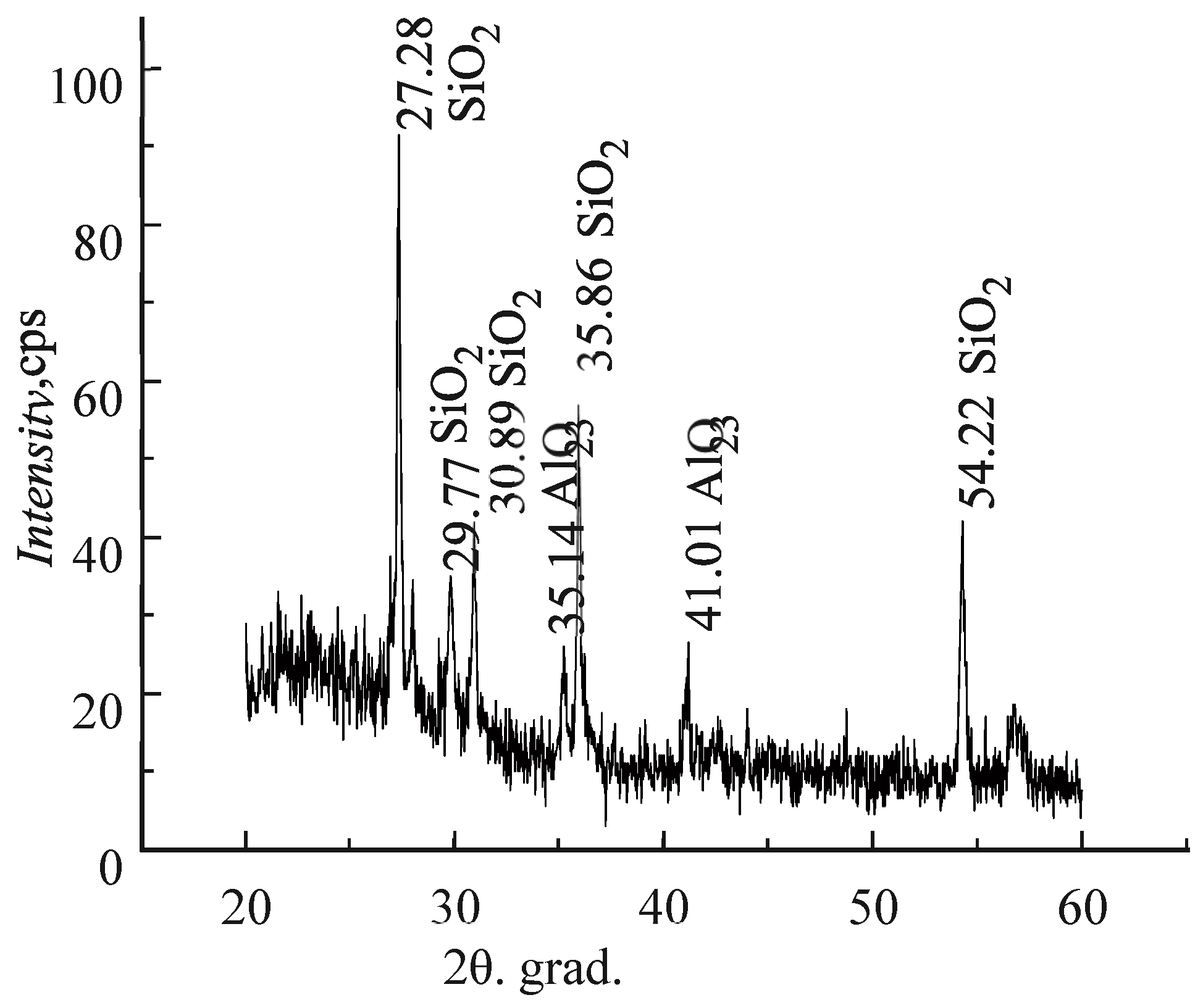
2.2.2. X-ray Diffraction Analysis of Samples of Vanadium Dioxide thin Films
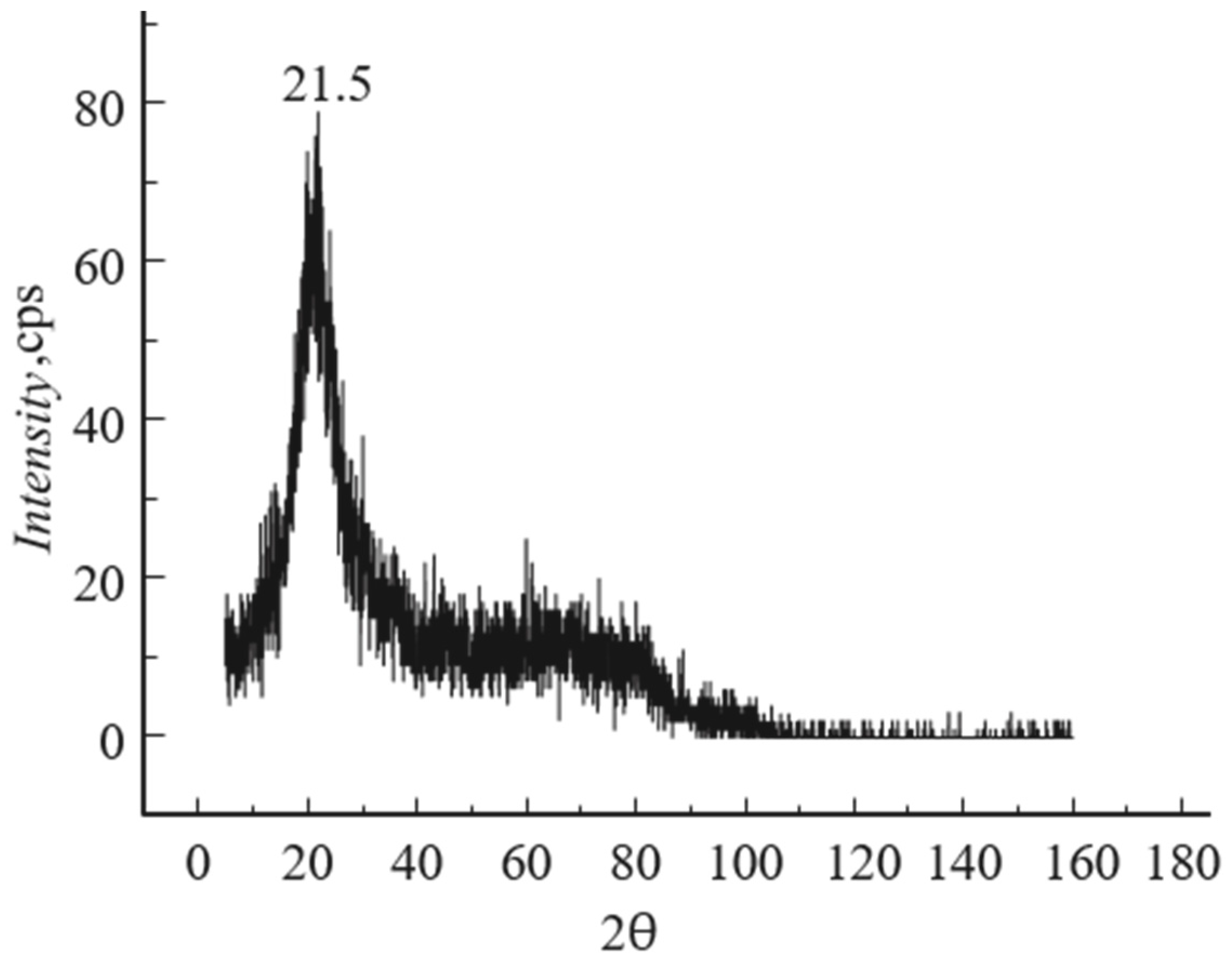
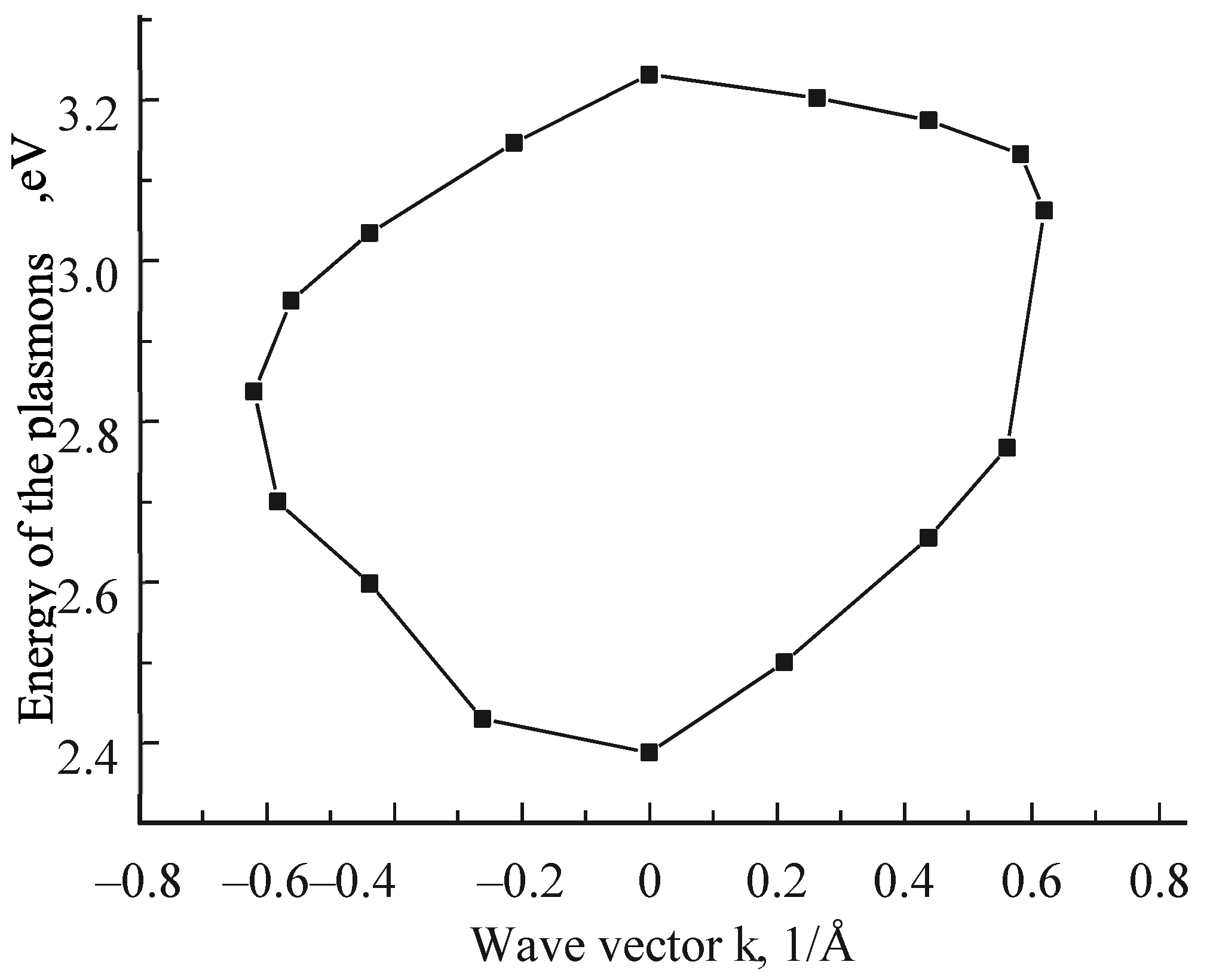
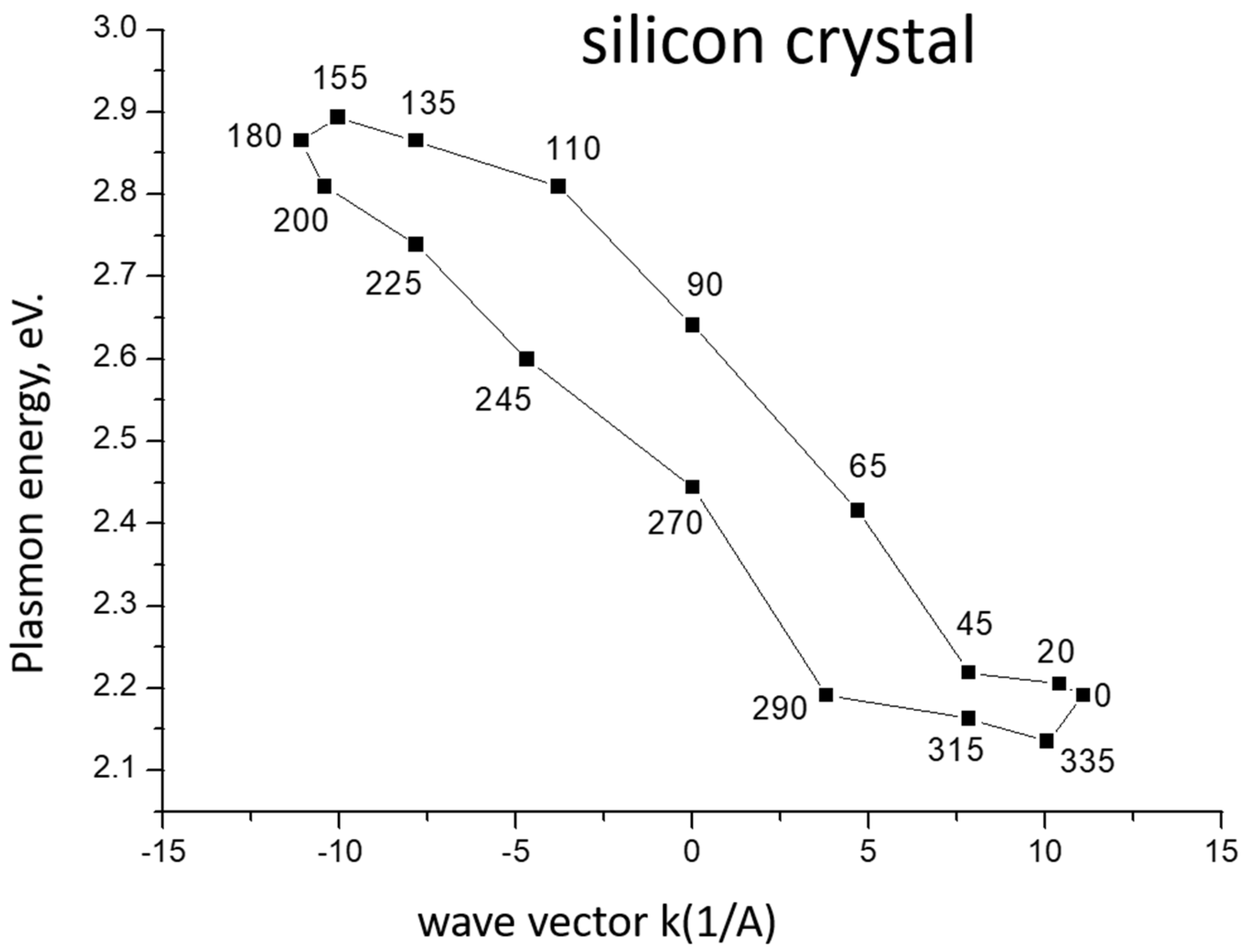
2.2.3. Investigation of the Dispersion of Surface Plasmons by the Method of Total External Reflection of X-rays from Samples of Vanadium Dioxide Thin Films
3. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Davydov, A.S. Solid State Theory; Nauka: Moscow, Russia, 1976; 405p. [Google Scholar]
- Ziman, J.M. Principles of the Theory of Solids; Cambridge University Press: Cambridge, UK, 1964; 405p. [Google Scholar]
- Pines, D. Elementary Excitations in Solids; CRC Press: New York, NY, USA, 1963. [Google Scholar]
- Bronstein, I.M.; Krainsky, I.L. Angular dependence of characteristic losses in magnesium and barium. Izv. USSR Acad. Sci. Phys. Ser. 1976, 40, 1956–1958. [Google Scholar]
- Komnik, Y.F. Physics of Metal Films; Atomizdat: Moscow, Russia, 1979; 263p. [Google Scholar]
- Petrov, Y.N. Physics of Small Particles; Science: Moscow, Russia, 1989; 358p. [Google Scholar]
- Klimov, V.V.; Fizmatgiz, M. Nanoplasmonics; Fizmatgiz: Moscow, Russia, 2009; 480p. [Google Scholar]
- Ramanavieius, H.; Herberg, F.W. Acta Med. Litnavica 2005, 12, 1–22. [CrossRef]
- Raether, H. Surface plasma oscillations and their application (A Review). Phys. Thin Film 1977, 12, 154. [Google Scholar]
- Kittel, C. Quantum Theory of Solids; John Wiley & Sons, Inc.: New York, NY, USA; London, UK, 1963; 485p. [Google Scholar]
- Gildenburg, V.B.; Kostin, V.A. Bulletin of the I.A. Lobachevsky Nizhny Novgorod Univ. 2011, 5, 314–322. [Google Scholar]
- Rumsh, M.A.; Shchemelev, V.N. The role of secondary emission processes in the X-ray photoelectric effect of metal cathodes. FTT 1963, 5, 71–75. [Google Scholar]
- Shchemelev, V.N.; Eliseenko, L.G.; Denisov, E.P.; Rumsh, M.A. On current and pulse measurements of X-ray photoemission of a massive cathode. FTT 1964, 6, 2574–2579. [Google Scholar]
- Stozharov, V.M.; Khinich, I.I. On the Mechanism of Excitation of Plasma Oscillations in Solids Investtigations with Total External Reflection of X-rays. Phys. Solid State 2021, 63, 794–796. [Google Scholar] [CrossRef]
- Compton, A.H. CXVII. The total reflexion of X-rays. Phil. Mag. 1923, 45, 1121. [Google Scholar] [CrossRef]
- Linnik, W.H.; Laschkarev, W. Determination of the Refractive Index of X-rays from the Phenomenon of Total Reflection. Z. Phys. 1926, 38, 659–671. [Google Scholar] [CrossRef]
- Raznomazov, V.M. Abstract of the Dissertation Microstructure and Elemental Analysis of Films Based on Oxides with the Structure of Perovskite According to X-ray Fluorescence Analysis with Full External Reflection; Southern Federal University: Rostov-Don, Russia, 2010; 52p. [Google Scholar]
- Stozharov, V.M. Total External Reflection of X-Rays from Solid Surfaces. Tech. Phys. 2017, 62, 152–156. [Google Scholar] [CrossRef]
- Parrat, L.G. Surface Studies by Total Reflection of X-Rays. Phys. Rev. 1954, 95, 359–369. [Google Scholar] [CrossRef]
- James, R.W. The Optical Principles of the Diffraction of X-rays; George Bell & Sons Ltd.: London, UK, 1950; 572p. [Google Scholar]
- Blokhin, M.A.; Schweitzer, I.E. X-ray Spectral Reference; Nauka: Moscow, Russia, 1982; pp. 94–99. [Google Scholar]
- Blokhin, M.A. Physics of X-rays; Publishing House of Technical and Theoretical Literature: Moscow, Russia, 1957; 511p. [Google Scholar]
- Katsnelson, A.A. Scattering of X-rays by Condensed Media; Moscow State University: Moscow, Russia, 1991; pp. 16–19. [Google Scholar]
- Katsnelson, A.A. Radiography. A Special Practice; Moscow State University: Moscow, Russia, 1986; pp. 24–33. [Google Scholar]
- Stozharov, V.M.; Pronin, V.P. On the mechanism of total external reflection of X-rays from the surface of polycrystalline solids. Tech. Phys. 2017, 62, 1899–1902. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saaunders College Publishing: New York, NY, USA; London, UK, 1976; Volume 1, 848p. [Google Scholar]
- Kay, D.; Labi, T. Handbook of an Experimental Physicist; IL: Moscow, Russia, 1969; 420p. [Google Scholar]
- Grosse, P. Free Electrons in Solids; Mir Publishers: Moscow, Russia, 1982; 260p. [Google Scholar]
- Stozharov, V.M. Determination of plasma oscillations in metals by the method of total external reflection of X-rays. Tech. Phys. 2019, 64, 977–979. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Electrodynamics of Continuous Media; State Publishing House of Technical and Theoretical Literature: Moscow, Russia, 1957; 509p. [Google Scholar]
- Levich, V.G.; Vdovin, Y.A.; Myamlin, V.A. Course of Theoretical Physics; Fizmatgiz: Moscow, Russia, 1962; Volume 2, 247p. [Google Scholar]
- Ridley, B.K. Quantum Processes in Semiconductors; Oxford University Press: Oxford, UK, 1982; 300p. [Google Scholar]
- Bronstein, I.M.; Freiman, B.S. Secondary Electronic Emission; Nauka: Moscow, Russia, 1969; pp. 244–245. [Google Scholar]
- Stozharov, V.M. Investigation of Plasma Oscillations in Glasslike Dielectric by Means of Total External Reflection of X-Rays. Tech. Phys. 2020, 65, 1071–1075. [Google Scholar] [CrossRef]
- Volkov, V.A. Plasmons and magnetoplasmons. In Influence on the Response of Semiconductor Structures in the Giga- and Terahertz Ranges; Kotelnikov Institute of Radioengineering and Electronics (IRE): Moscow, Russia, 2019; pp. 1–7. [Google Scholar]
- Lisitsa, V.S. Introduction to Nanooptics; Moscow Institute of Physics and Technology (MIPT): Moscow, Russia, 2012; pp. 104–112. [Google Scholar]
- Karalis, A.; Lidorikis, E.; Ibanesky, M.; Joannopoulos, J. Surface-Plasmon-Assisted Guiding of Broadband Slow and Subwafelength Light in Air. Phys. Rev. Lett. 2005, 95, 063901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eremin, M.V.; Kochergin, D.S. On the theory of plasmon dispersion in electronically dispersed cuprates. Lett. JETF 2018, 108, 119–123. [Google Scholar] [CrossRef]
- Davidovich, M.V. Dispersion of surface plasmons in structures with a conductive film. Opt. Spectrosc. 2019, 126, 360–369. [Google Scholar] [CrossRef]
- Baltar, H.; Drozdowicz, K.; Goldys, E.M. Propagating Surface Plasmons and Dispersion Relations for Nanoscale Multilayer Metall-Dielectric. In Plasmonics—Principles and Applications; Intechopen: London, UK, 2012; pp. 135–155. [Google Scholar]
- Lee, W.S.; Lee, J.J.; Nowadnick, E.A. Asymmetry of collective Excitations in electron and hole-doped cuprate. Nat. Phys. 2014, 10, 883–895. [Google Scholar] [CrossRef] [Green Version]
- Stozharov, V.M. Dispersion of Plasma Oscillations in Amorphous Chalcogenide Semiconductors. Tech. Phys. 2021, 66, 1035–1038. [Google Scholar] [CrossRef]
- Felts, A. Amorphous Glassy Solids; Mir Publishers: Moscow, Russia, 1882; 545p. [Google Scholar]
- Mott, N.; Devis, E. Electronic Processes in Non-Crystalline Materials; Oxford University Press: Oxford, UK, 1980; 350p. [Google Scholar] [CrossRef]
- Brytov, I.A.; Romashchenko, Y.N. X-ray spectral study of the electronic structure of silicon and aluminum oxides. Solid State Phys. 1978, 29, 664–672. [Google Scholar]
- Britov, I.A.; Gritsenko, V.A.; Romaschenko, Y.N. Short-range Order and Electronic structure of Amorphous SiNxOy. J. Exp. Theor. Phys. 1985, 62, 321–327. [Google Scholar]
- SNekrashevich, S.; Gritzenko, V.A. Electronic structure of Silicon dioxide (A REVIEW). Phys. Solid State 2014, 56, 207–222. [Google Scholar] [CrossRef]
- Klug, H.P.; Alexander, L.E. X-ray Diffraction Procedures; John Wiley and Sons, Inc.: New York, NY, USA; London, UK, 1954; 686p. [Google Scholar]
- Rabinovich, V.A.; Havin, Z.Y. A Brief Chemical Reference; Chemistry: Leningrad, Russia, 1970; 115p. [Google Scholar]
- Korsunsky, M.I. Physics of X-rays; ONTI: Moscow-Leningrad, Russia, 1936; 138p. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; John Wiley and Sons, Inc.: New York, NY, USA; London, UK, 1976; Volume 2, pp. 166–170. [Google Scholar]
- The Soviet Encyclopedia; Knuniants, I.L. (Ed.) Sovetskaya Entsiklopediya: Moscow, Russia, 1990; Volume 2, 671p. [Google Scholar]
- Ostroushko, Y.N. Lithium, Chemistry and Technology; Chemistry: Leningrad, Russia, 1960; 234p. [Google Scholar]
- Schultz, M.M.; Mazurin, O.V. Modern Understanding of the Structure of Glasses and Their Properties; Science: Leningrad, Russia, 1988; 488p. [Google Scholar]
- Eckertova, L. Physics of Thin Films; Springer: Boston, MA, USA, 1984; 340p. [Google Scholar]
- Anuryev, V.I. Handbook of a Mechanical Engineer Designer; Mechanical Engineering: Moscow, Russia, 2001. [Google Scholar]

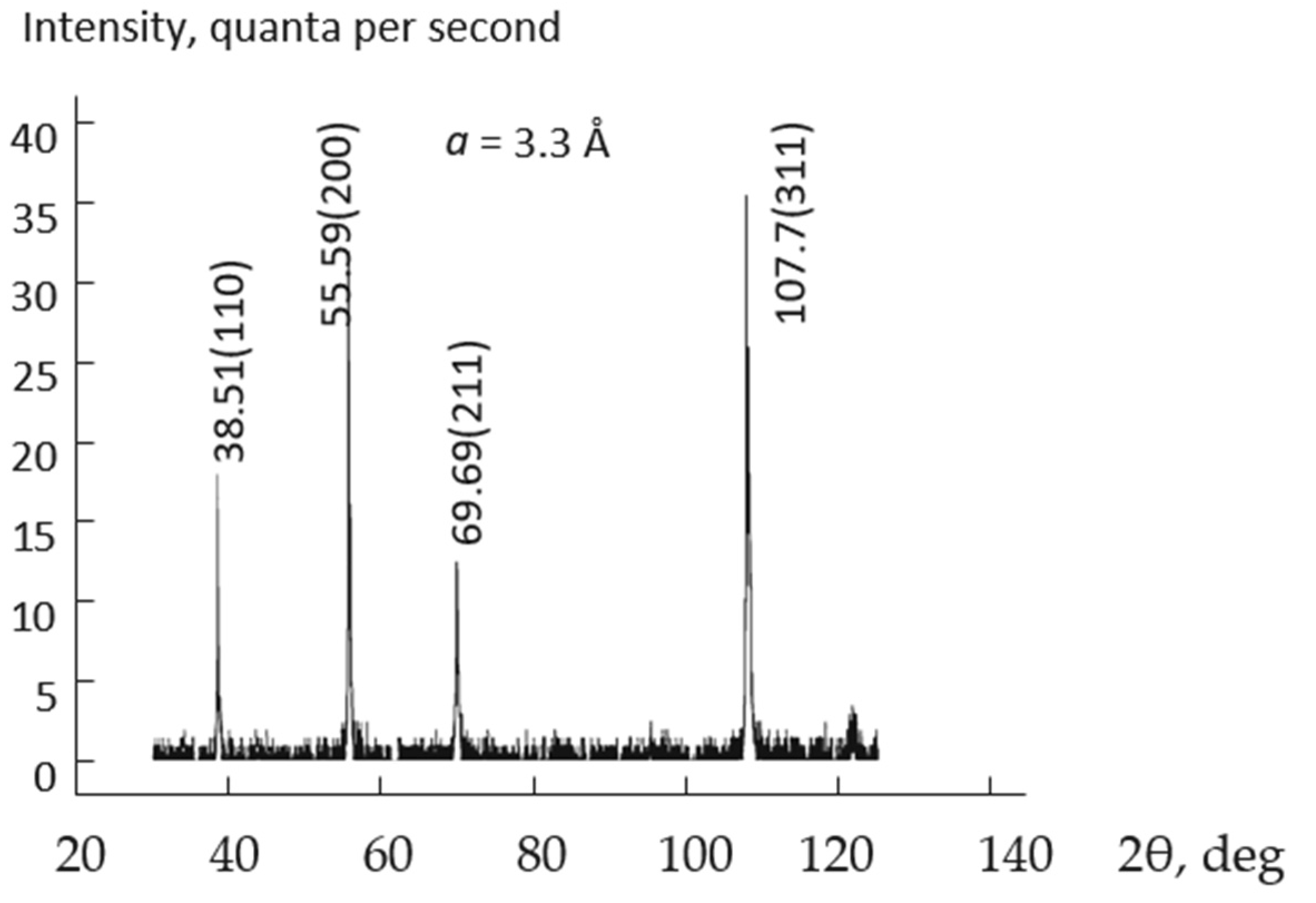

| Reflex Number | 2θ° | δ × 10−8 | |||||
|---|---|---|---|---|---|---|---|
| 1 | 38.5274 | 110 | 1.2273 | 5.2636 | 5.9057 | 2.3348 | |
| 2 | 55.6190 | 200 | 1.7355 | 29.329 | 3842.3 | 1.6511 | 23.1 |
| 3 | 69.6765 | 211 | 2.1251 | 3.0398 | 46.219 | 1.3484 | |
| 4 | 10.771 | 222 | 3.0052 | 2.1496 | 971.91 | 0.9535 | 13.3 |
| Metal | d, Å | ||||
|---|---|---|---|---|---|
| Ni | 21.1 | 1.7542 | 12 | 1 | 143.4 |
| Cu | 12.8 | 1.2786 | 10 | 3 | 52.5 |
| Ag | 26.3 | 2.0234 | 13 | 0 | 72.18 |
| Pt | 33.8 | 2.2537 | 15 | −2 | 17.90 |
| Bi | 54.2 | 3.9482 | 14 | −1 | 10.99 |
| Metal | |||||
|---|---|---|---|---|---|
| Cu | 0.0178 | 111 | 2.06 | 26 | 4.062 |
| 0.0261 | 200 | 4.06 | 52 | 8.707 | |
| Mo | 0.0776 | 200 | 10.9 | 42 | 7.723 |
| Ta | 0.0095 | 200 | 1.4 | 6.5 | 1.274 |
| 0.0785 | 222 | 11.0 | 50 | 7.865 | |
| Pt | 0.0141 | 111 | 1.98 | 5.35 | 2.548 |
| 0.0878 | 222 | 12.33 | 35.0 | 9.909 | |
| Ag | 0.0124 | 111 | 1.74 | 4.5 | 1.168 |
| Au | 0.0612 | 222 | 8.60 | 20.1 | 4.807 |
| Semiconductor Crystals | ||||
|---|---|---|---|---|
| Si | 2.146 | 90.5 | 1.120 | |
| Ge | 2.135 | 32 | 0.665 | |
| GaSb | 1.896 | 12 | 0.810 | |
| Dielectric Crystal | ||||
| LiF | 3.174 | 62.3 | 14.50 |
| Electron Asymmetry | |||||
|---|---|---|---|---|---|
| 0 | 0.0218 | 3.062 | 246 | 24 | N1(0)
/N1(180) = 1.26 N1(45) /N1(225) = 1.8 N1(90) /N1(270) = 2.54 N1(135) /N1(335) = 1.44 |
| 20 | 0.0223 | 3.132 | 252 | 26 | |
| 45 | 0.0226 | 3.174 | 256 | 27 | |
| 65 | 0.0228 | 3.202 | 258 | 28 | |
| 90 | 0.0230 | 3.231 | 260 | 28 | |
| 110 | 0.0224 | 3.146 | 253 | 26 | |
| 135 | 0.0126 | 3.034 | 244 | 23 | |
| 155 | 0.0210 | 2.950 | 238 | 22 | |
| 180 | 0.0202 | 2.837 | 228 | 19 | |
| 200 | 0.0192 | 2.700 | 217 | 16 | |
| 225 | 0.0185 | 2.598 | 209 | 15 | |
| 245 | 0.0173 | 2.430 | 196 | 12 | |
| 270 | 0.0170 | 2.388 | 192 | 11 | |
| 290 | 0.0178 | 2.500 | 201 | 13 | |
| 315 | 0.0189 | 2.655 | 214 | 16 | |
| 335 | 0.0197 | 2.767 | 223 | 18 |
| Substance | ||
|---|---|---|
| fused quartz | 0.574 | 3.129 |
| quartz glass | 0.395 | 2.153 |
| uviol glass | 0.412 | 2.246 |
| molybdenum glass | 0.432 | 2.354 |
| lithium fluoride | 0.0042 | 0 |
| sitall | 0.361 | 1.968 |
Electrons | N1(0)/N1(180) = 1.35 N1(45)/N(225) = 1.95 N1(90)/N1(270) = 2.3 N1(135)/N1(335) = 1.38 | ||||
| 0 | 0.0170 | 2.388 | 23.68 | 42.36 | |
| 20 | 0.0164 | 2.304 | 22.84 | 38.04 | |
| 45 | 0.0160 | 2.247 | 22.28 | 35.30 | |
| 65 | 0.0154 | 2.163 | 21.45 | 31.76 | |
| 90 | 0.0150 | 2.107 | 20.89 | 29.10 | |
| 110 | 0.0162 | 2.275 | 22.56 | 36.64 | |
| 135 | 0.0168 | 2.360 | 23.40 | 40.89 | |
| 155 | 0.0175 | 2.458 | 24.37 | 46.20 | |
| 180 | 0.0188 | 2.640 | 26.18 | 57.26 | |
| 200 | 0.0198 | 2.781 | 27.58 | 66.92 | |
| 225 | 0.0200 | 2.809 | 27.85 | 68.96 | |
| 245 | 0.0200 | 2.809 | 27.85 | 68.96 | |
| 270 | 0.0198 | 2.781 | 27.58 | 66.92 | |
| 290 | 0.0190 | 2.669 | 26.46 | 59.15 | |
| 315 | 0.0187 | 2.627 | 26.04 | 56.40 | |
| 335 | 0.0180 | 2.528 | 25.07 | 50.20 |
Electrons | N1(0)/N1(180) = 2.7 N1(45)/N1(225) = 1.5 N1(90)/N1(270) = 1.53 N1(135)/N1(335) = 2.18 | ||||
| 0 | 0.0140 | 1.966 | 19.50 | 19.21 | |
| 20 | 0.0150 | 2.107 | 20.89 | 22.64 | |
| 45 | 0.0159 | 2.233 | 22,14 | 28.14 | |
| 65 | 0.0170 | 2.388 | 23.68 | 34.42 | |
| 90 | 0.0188 | 2.641 | 26.18 | 46.55 | |
| 110 | 0.0196 | 2.753 | 27.30 | 52.73 | |
| 135 | 0.0197 | 2.767 | 27.48 | 53.54 | |
| 155 | 0.0198 | 2.781 | 27.58 | 54.36 | |
| 180 | 0.0195 | 2.739 | 27.16 | 51.96 | |
| 200 | 0.0191 | 2.683 | 26.60 | 48.81 | |
| 225 | 0.0182 | 2.556 | 25.35 | 42.21 | |
| 245 | 0.0175 | 2.458 | 24.37 | 37.53 | |
| 270 | 0.0163 | 2.289 | 22.70 | 30.32 | |
| 290 | 0.0155 | 2.177 | 21.59 | 26.08 | |
| 315 | 0.0152 | 2.135 | 21.17 | 24.60 | |
| 335 | 0.0142 | 1.994 | 19.78 | 20.04 |
| Vanadium Dioxide Films | ||||
|---|---|---|---|---|
| №1 | 1.745 | 0.517 | 3.386 | 27 |
| №2 | 1.980 | 0.230 | 1.506 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stozharov, V.M. Surface Plasmons Excited by X-rays in the Surface Layers of Solids. Solids 2022, 3, 122-146. https://doi.org/10.3390/solids3010009
Stozharov VM. Surface Plasmons Excited by X-rays in the Surface Layers of Solids. Solids. 2022; 3(1):122-146. https://doi.org/10.3390/solids3010009
Chicago/Turabian StyleStozharov, Valery M. 2022. "Surface Plasmons Excited by X-rays in the Surface Layers of Solids" Solids 3, no. 1: 122-146. https://doi.org/10.3390/solids3010009
APA StyleStozharov, V. M. (2022). Surface Plasmons Excited by X-rays in the Surface Layers of Solids. Solids, 3(1), 122-146. https://doi.org/10.3390/solids3010009





