A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain
Abstract
1. Introduction
2. Simulation Methods
3. Results and Discussion
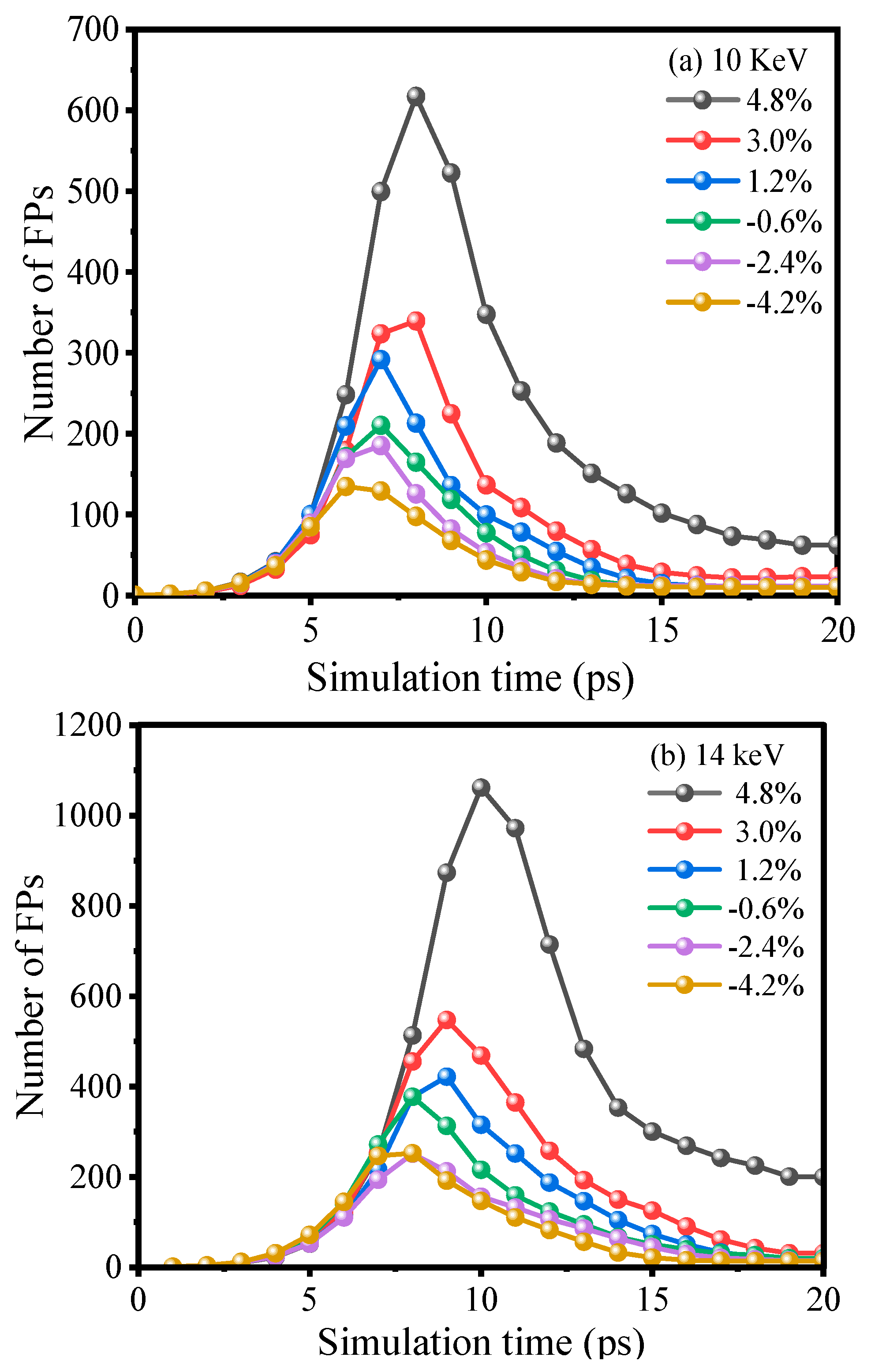
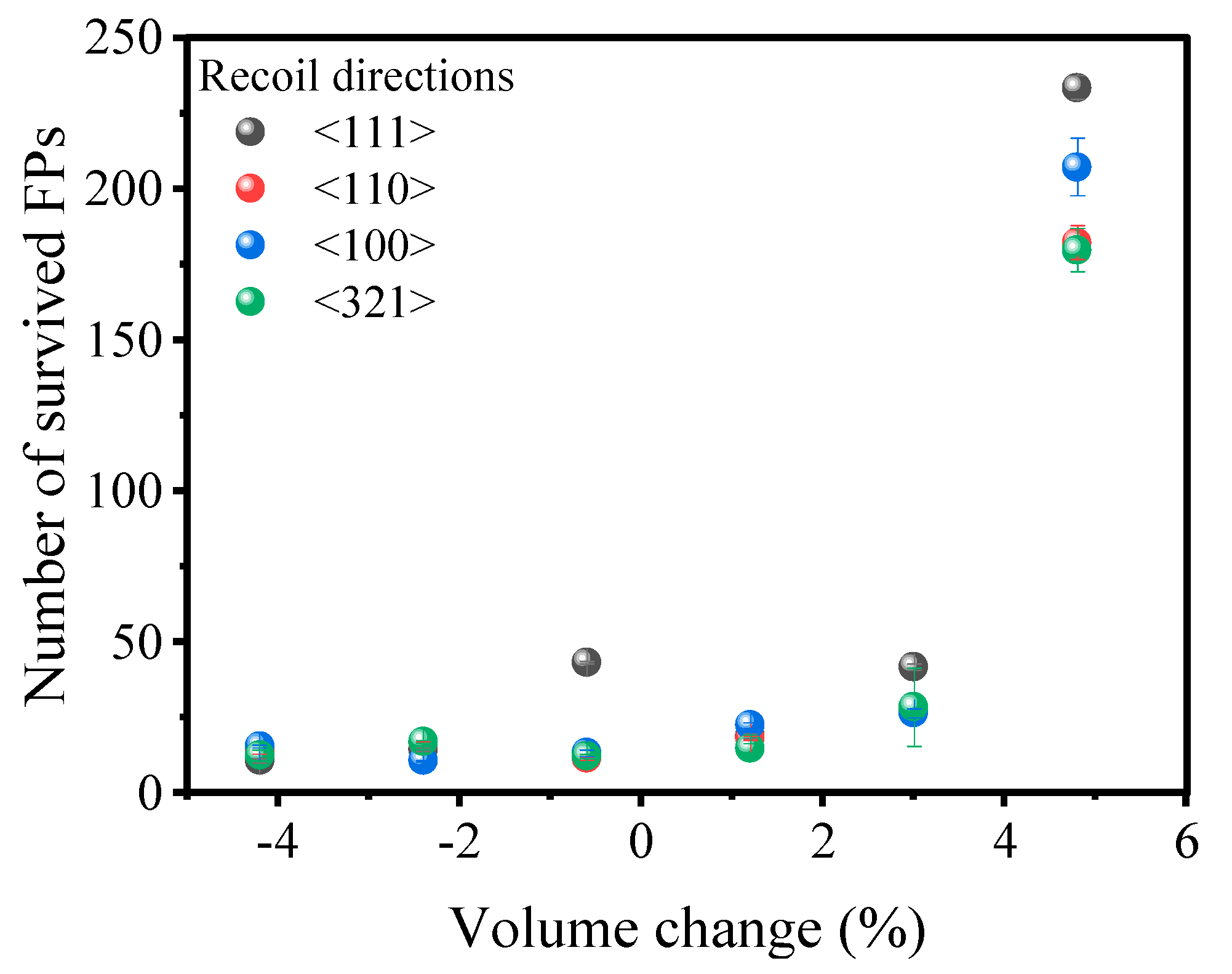
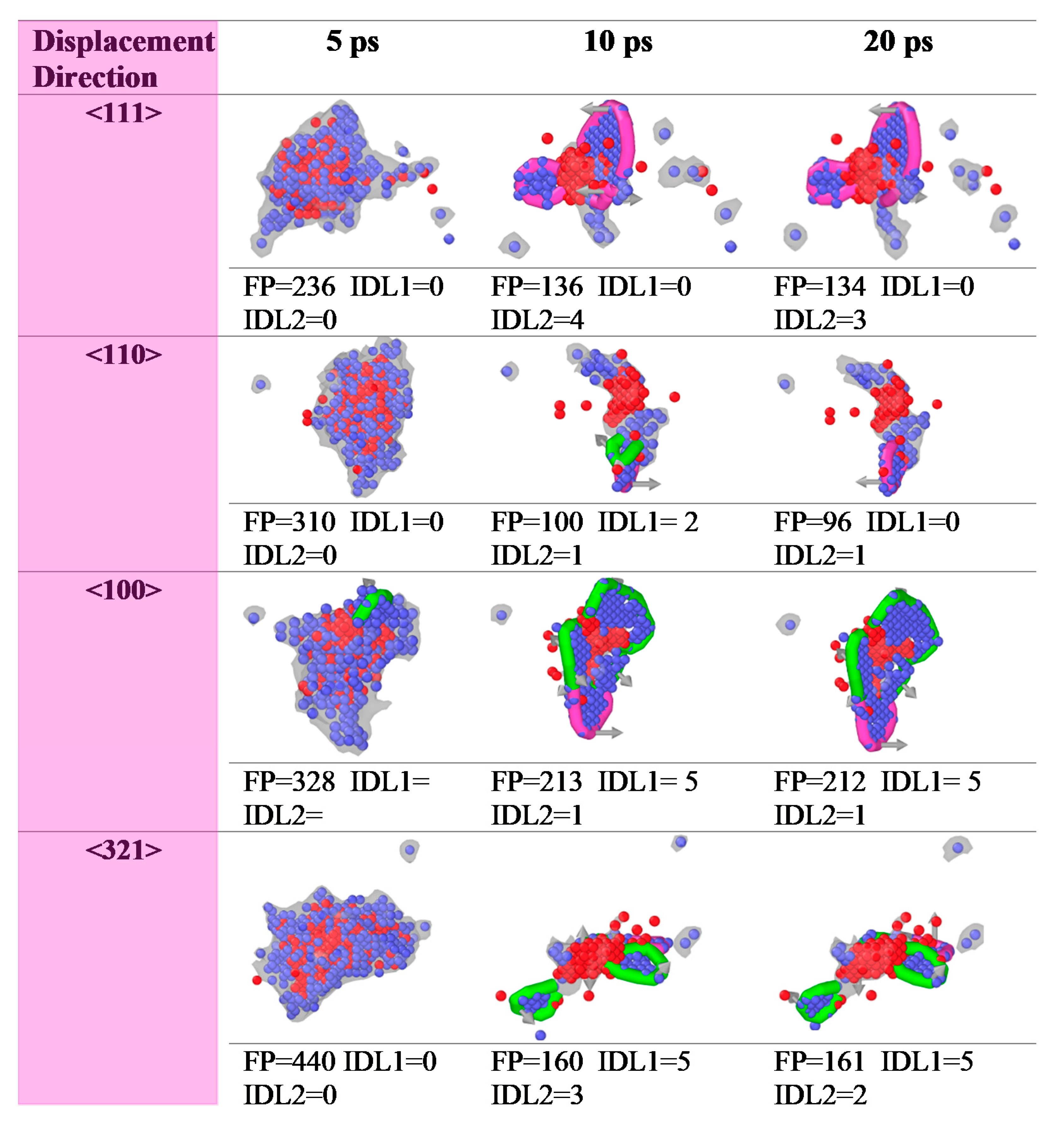
3.1. PKA Energy and Direction Effects
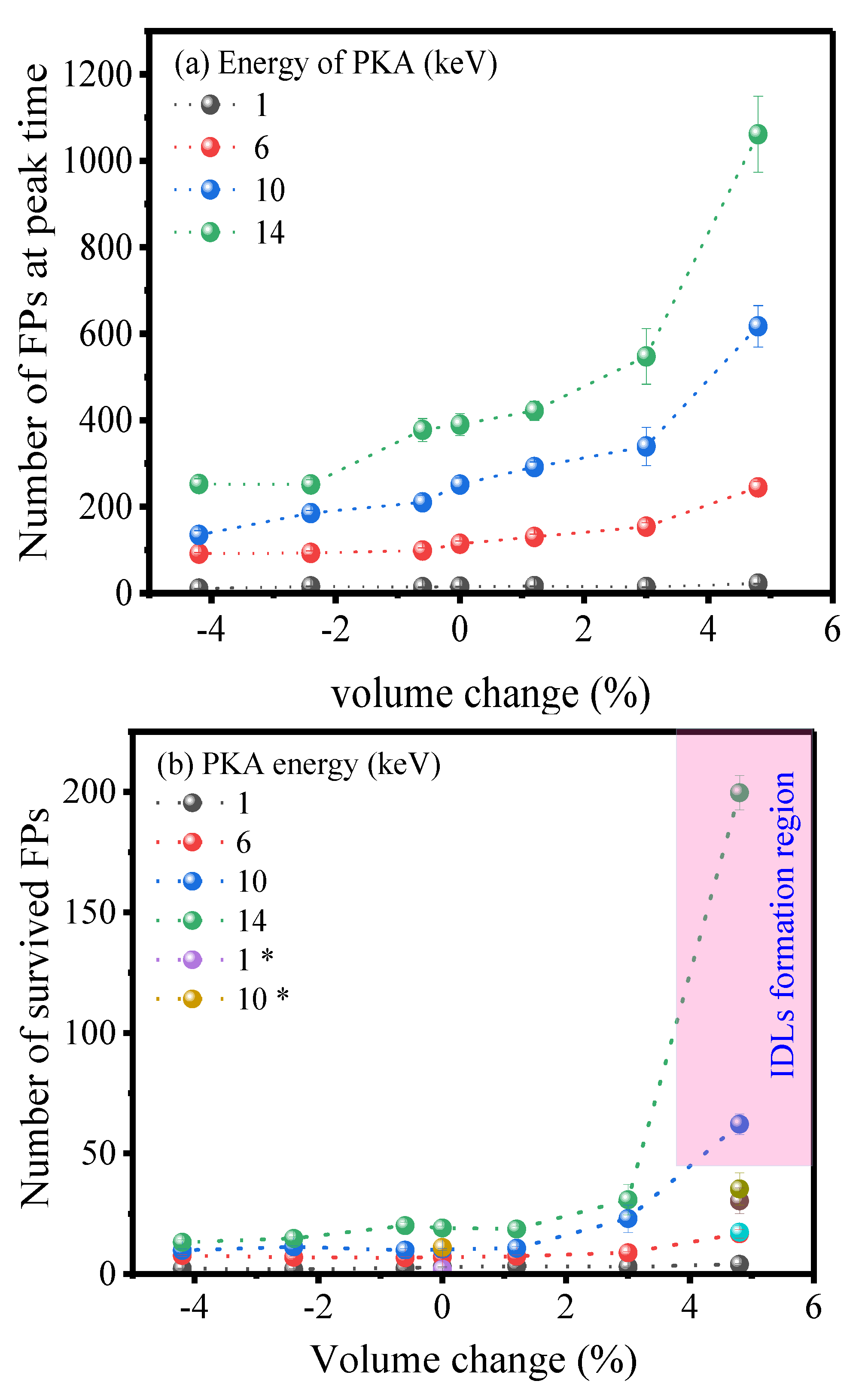
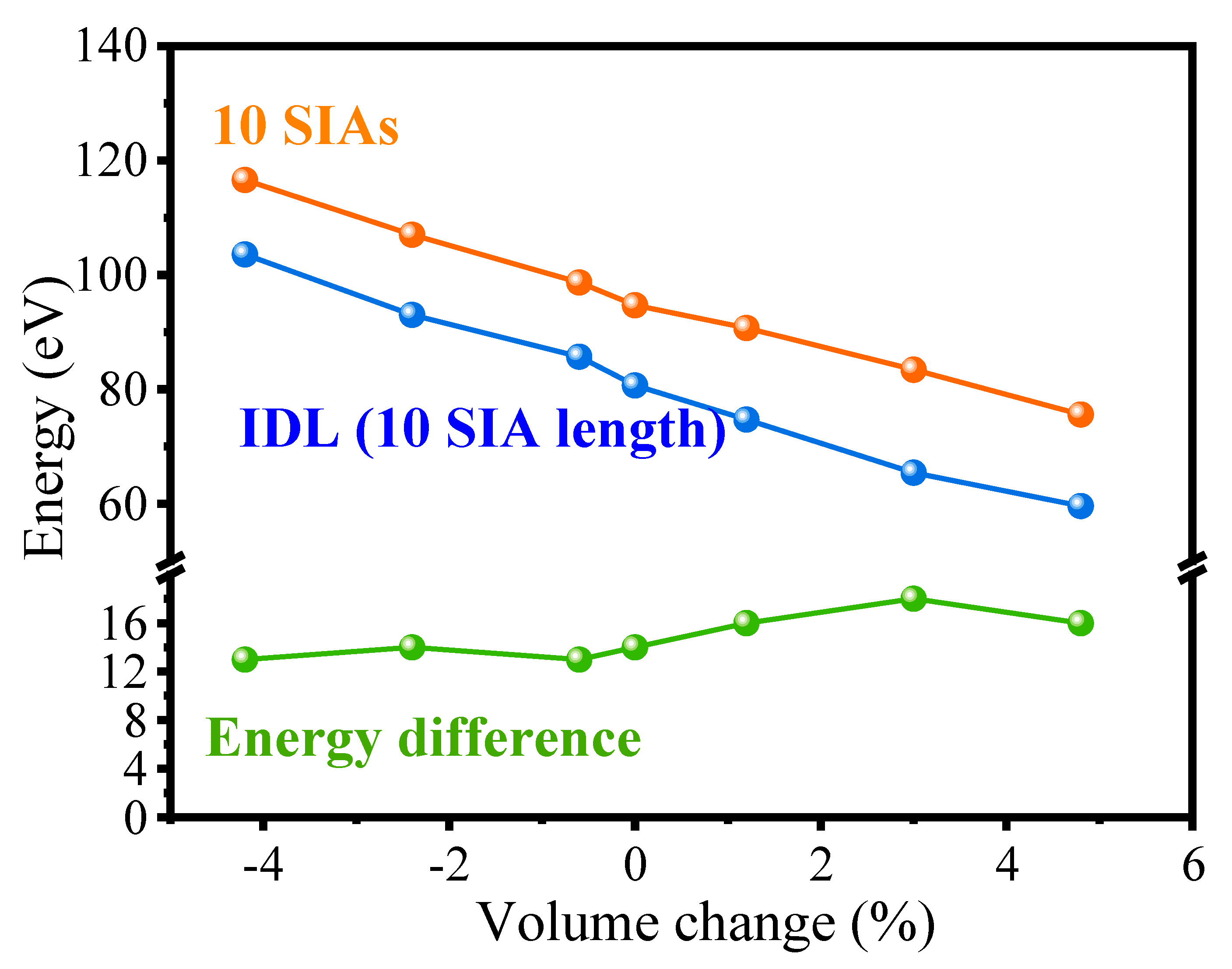
3.2. Strain Effects on Point Defects and IDLs
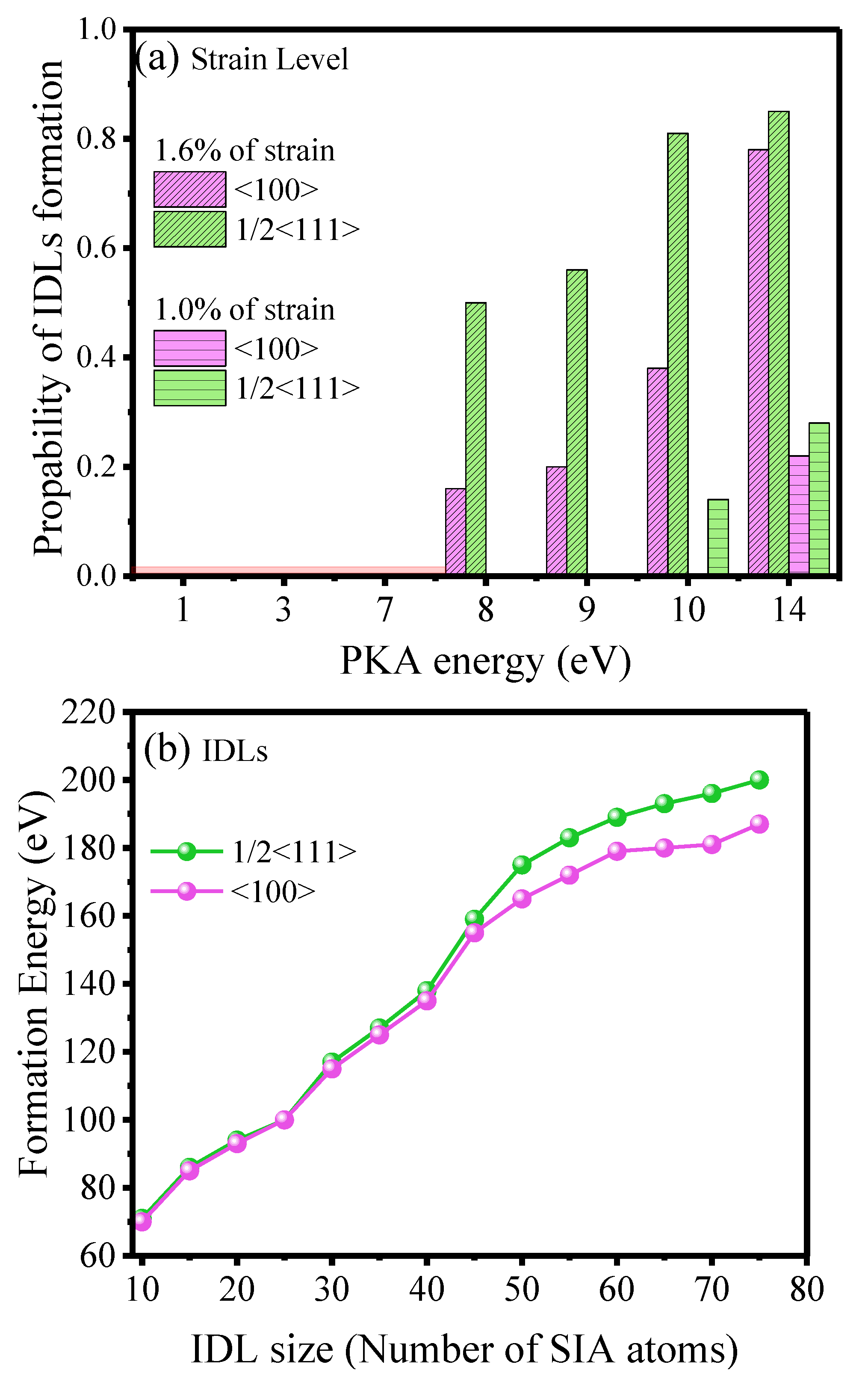
3.2.1. Point Defects and Dislocation Loop Formation
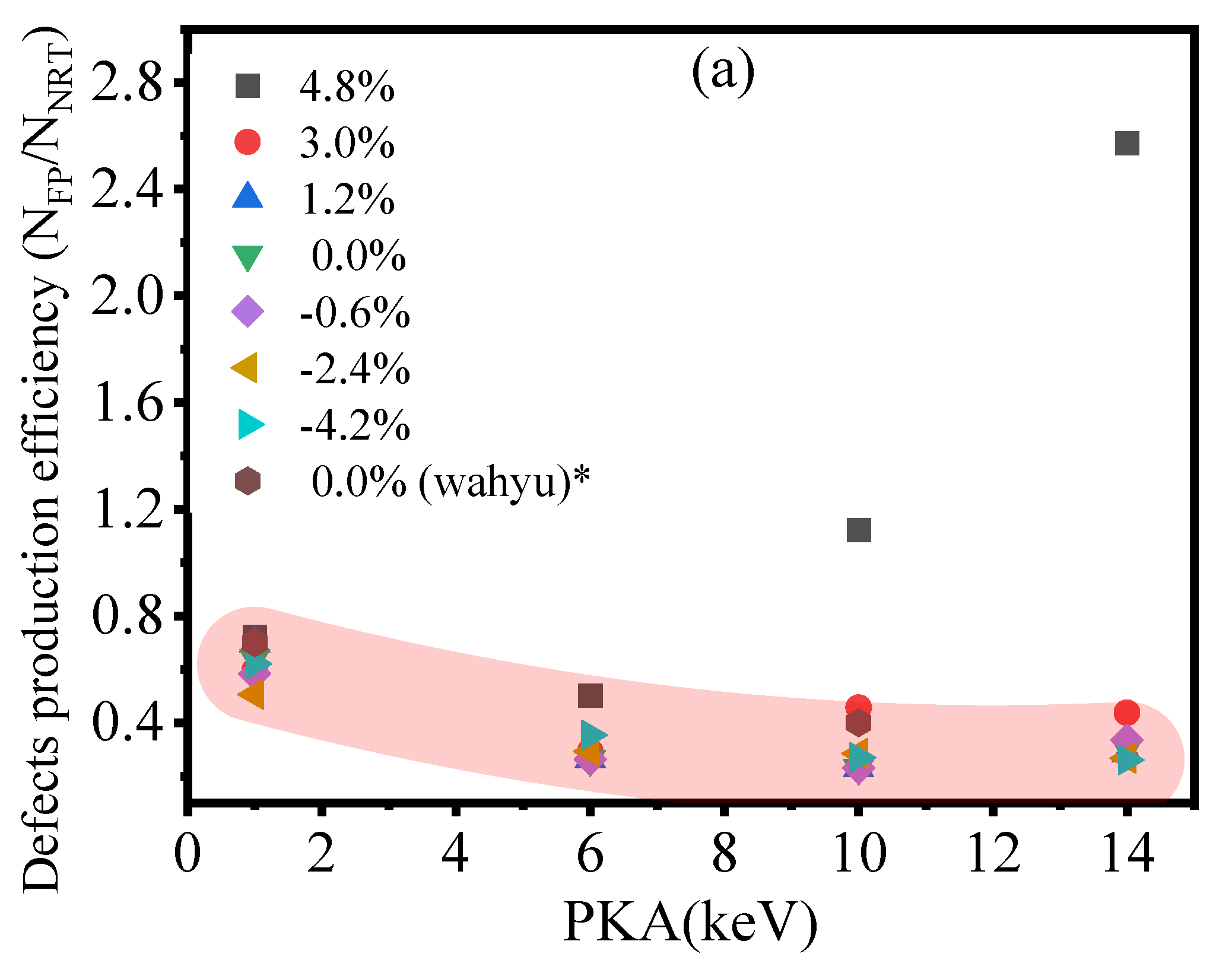
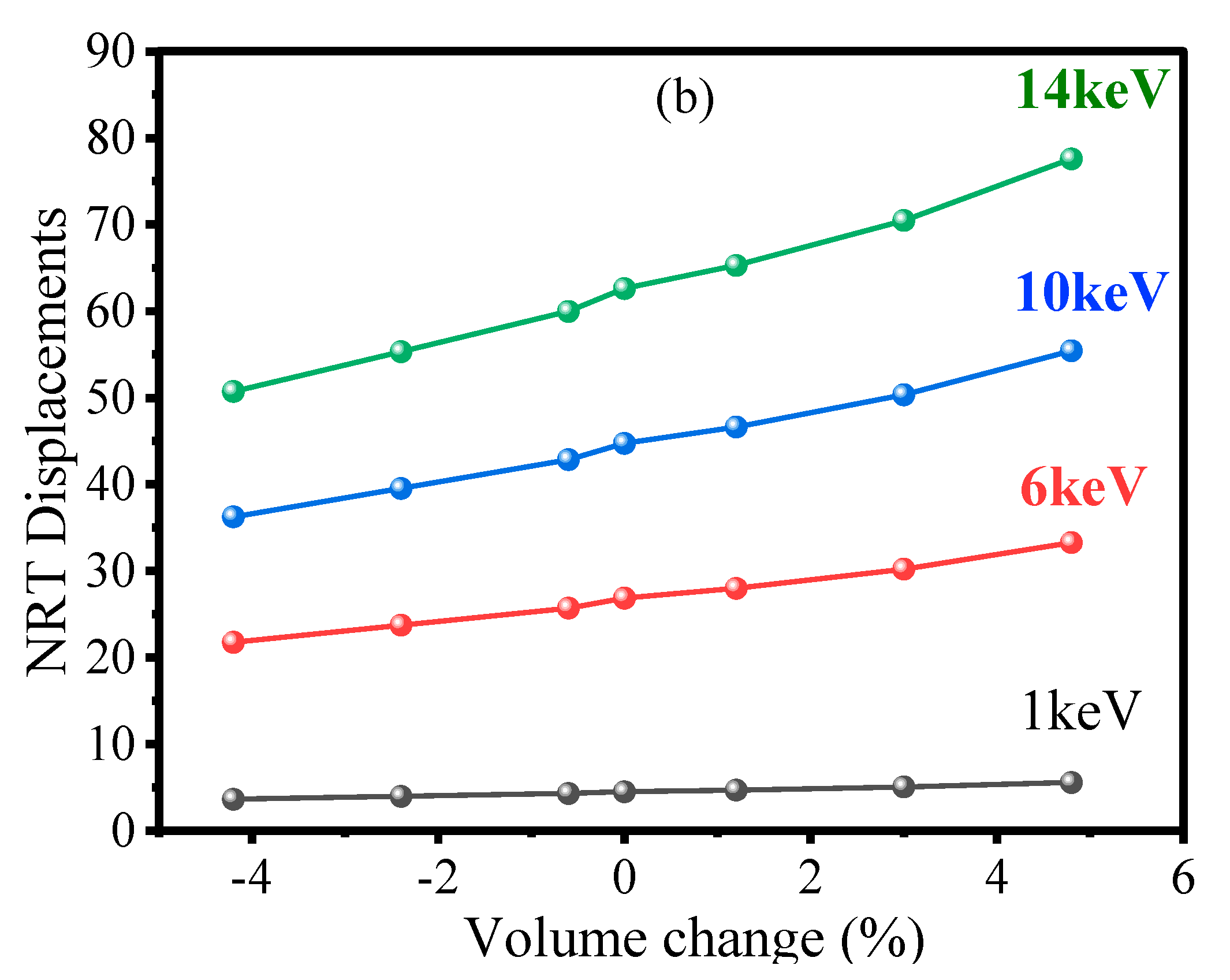
3.2.2. Extra Analysis for the Point Defects and Production Efficiency
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maisonnier, D.; Cook, I.; Pierre, S.; Lorenzo, B.; Luigi, D.P.; Luciano, G.; Prachai, N.; Aldo, P. DEMO and Fusion Power Plant Conceptual Studies in Europe. Fusion Eng. Des. 2006, 81, 1123–1130. [Google Scholar] [CrossRef]
- Nemoto, Y.; Hasegawa, A.; Satou, M.; Abe, K. Microstructural Development of Neutron Irradiated W-Re Alloys. J. Nucl. Mater. 2000, 283–287, 1144–1147. [Google Scholar] [CrossRef]
- Cottrell, G.A. Sigma Phase Formation in Irradiated Tungsten, Tantalum and Molybdenum in a Fusion Power Plant. J. Nucl. Mater. 2004, 334, 166–168. [Google Scholar] [CrossRef]
- López-Suárez, M.; Neri, I.; Rurali, R. Band Gap Engineering of MoS 2 upon Compression. J. Appl. Phys. 2016, 119, 165105. [Google Scholar] [CrossRef]
- Sun, M.; Ren, Q.; Wang, S.; Yu, J.; Tang, W. Electronic Properties of Janus Silicene: New Direct Band Gap Semiconductors. J. Phys. D. Appl. Phys. 2016, 49, 44. [Google Scholar] [CrossRef]
- Wang, S.K.; Wang, J. Spin and Valley Filter in Strain Engineered Silicene. Chinese Phys. B 2015, 24, 3. [Google Scholar] [CrossRef]
- Rurali, R. Colloquium: Structural, Electronic, and Transport Properties of Silicon Nanowires. Rev. Mod. Phys. 2010, 82, 427–449. [Google Scholar] [CrossRef]
- Frederiksen, T.; Brandbyge, M.; Lorente, N.; Jauho, A.P. Inelastic Scattering and Local Heating in Atomic Gold Wires. Phys. Rev. Lett. 2004, 93, 256601. [Google Scholar] [CrossRef]
- Bullough, R.; Eyre, B.L.; Perrin, R.C. The Growth and Stability of Voids in Irradiated Metals. Nucl. Appl. Technol. 1970, 9, 346–355. [Google Scholar] [CrossRef]
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Psakhie, S.G.; Zolnikov, K.P.; Kryzhevich, D.S.; Zheleznyakov, A.V.; Chernov, V.M. Evolution of Atomic Collision Cascades in Vanadium Crystal with Internal Structure. Crystallogr. Rep. 2009, 54, 1002. [Google Scholar] [CrossRef]
- Yi, X.; Jenkins, M.L.; Kirk, M.A.; Zhou, Z.; Roberts, S.G. In-Situ TEM Studies of 150 KeV W + Ion Irradiated W and W-Alloys: Damage Production and Microstructural Evolution. Acta Mater. 2016, 112, 105–120. [Google Scholar] [CrossRef]
- Yi, X.; Jenkins, M.L.; Hattar, K.; Edmondson, P.D.; Roberts, S.G. Characterisation of Radiation Damage in W and W-Based Alloys from 2MeV Self-Ion near-Bulk Implantations. Acta Mater. 2015, 92, 163–177. [Google Scholar] [CrossRef]
- Mason, D.R.; Yi, X.; Kirk, M.A.; Dudarev, S.L. Elastic Trapping of Dislocation Loops in Cascades in Ion-Irradiated Tungsten Foils. J. Phys. Condens. Matter 2014, 26, 375701. [Google Scholar] [CrossRef] [PubMed]
- Sand, A.E.; Dudarev, S.L.; Nordlund, K. High-Energy Collision Cascades in Tungsten: Dislocation Loops Structure and Clustering Scaling Laws. Epl 2013, 103, 4. [Google Scholar] [CrossRef]
- Fang, Z.Z.; Wang, X.; Ryu, T.; Hwang, K.S.; Sohn, H.Y. Synthesis, Sintering, and Mechanical Properties of Nanocrystalline Cemented Tungsten Carbide—A Review. Int. J. Refract. Met. Hard Mater. 2009, 27, 288–299. [Google Scholar] [CrossRef]
- Deb, S.K. Optical and Photoelectric Properties and Colour Centres in Thin Films of Tungsten Oxide. Philos. Mag. 1973, 27, 801–822. [Google Scholar] [CrossRef]
- Jansen, H.J.F.; Freeman, A.J. Total-Energy Full-Potential Linearized Augmented-Plane-Wave Method for Bulk Solids: Electronic and Structural Properties of Tungsten. Phys. Rev. B 1984, 30, 561–569. [Google Scholar] [CrossRef]
- Park, S.; Banisalman, M.J.; Oda, T. Characterization and Quantification of Numerical Errors in Threshold Displacement Energy Calculated by Molecular Dynamics in Bcc-Fe. Comput. Mater. Sci. 2019, 170, 109189. [Google Scholar] [CrossRef]
- Banisalman, M.; Oda, T. Molecular Dynamics Study for the Uniaxial Stress Effect on the Threshold Displacement Energy and Defect Formation Energies in Tungsten. In Proceedings of the KNS 2018—Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, 16–18 May 2018. [Google Scholar]
- Choi, S., II; Banisalman, M.J.; Lee, G.-G.; Kwon, J.; Yoon, E.; Kim, J.H. Using Rate Theory to Better Understand the Stress Effect of Irradiation Creep in Iron and Its Based Alloy. J. Nucl. Mater. 2020, 536, 152198. [Google Scholar] [CrossRef]
- Kaletta, D. The Role of Gases in Radiation Damage Patterns; Kernforschungszentrum Karlsruhe GmbH: Karlsruhe, Germany, 1979. [Google Scholar]
- Barrow, A.T.W.; Korinek, A.; Daymond, M.R. Evaluating Zirconium-Zirconium Hydride Interfacial Strains by Nano-Beam Electron Diffraction. J. Nucl. Mater. 2013, 432, 366–370. [Google Scholar] [CrossRef]
- Fu, B.Q.; Fitzgerald, S.P.; Hou, Q.; Wang, J.; Li, M. Effect of Collision Cascades on Dislocations in Tungsten: A Molecular Dynamics Study. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 2017, 393, 169–173. [Google Scholar] [CrossRef]
- Boev, A.O.; Zolnikov, K.P.; Nelasov, I.V.; Lipnitskii, A.G. Effect of Titanium on the Primary Radiation Damage and Swelling of Vanadium-Titanium Alloys. Lett. Mater. 2018, 8, 263–267. [Google Scholar] [CrossRef]
- Zhong, Y.; Nordlund, K.; Ghaly, M.; Averback, R. Defect Production in Tungsten: A Comparison between Field-Ion Microscopy and Molecular-Dynamics Simulations. Phys. Rev. B Condens. Matter Mater. Phys. 1998, 58, 2361–2364. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Virtual Lab. Inc. January 01 Materials Square (2017). Available online: https://www.materialssquare.com/ (accessed on 6 March 2022).
- Daw, M.S.; Baskes, M.I. Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and Other Defects in Metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Derlet, P.M.; Nguyen-Manh, D.; Dudarev, S.L. Multiscale Modeling of Crowdion and Vacancy Defects in Body-Centered-Cubic Transition Metals. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 54107. [Google Scholar] [CrossRef]
- Nordlund, K.; Dudarev, S. Modelling Radiation Effects Using the Ab-initio Based Tungs Potentials. Nucl. Instr. Meth. B 2010, 267, 3204. [Google Scholar]
- Byggmästar, J.; Granberg, F.; Nordlund, K. Effects of the Short-Range Repulsive Potential on Cascade Damage in Iron. J. Nucl. Mater. 2018, 508, 530–539. [Google Scholar] [CrossRef]
- Norgett, M.J.; Robinson, M.T.; Torrens, I.M. A Proposed Method of Calculating Displacement Dose Rates. Nucl. Eng. Des. 1975, 33, 50–54. [Google Scholar] [CrossRef]
- Salman, M.B.; Kilic, M.E.; Banisalman, M.J. Formation of Interstitial Dislocation Loops by Irradiation in Alpha-Iron under Strain: A Molecular Dynamics Study. Crystals 2021, 11, 317. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A Three-Dimensional Voronoi Cell Library in C++. ChaosInterdiscip. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- Wechsler, M.S.; Lin, C.; Sommer, W.F.; Daemen, L.U.L.; Feguson, P.D. Standard Practice for Neutron Radiation Damage Simulation by Charged-Particle Irradiation, E 521–96. Annu. B. ASTM Stand. 1996, 12.02, 1. [Google Scholar]
- Banisalman, M.J.; Park, S.; Oda, T. Evaluation of the Threshold Displacement Energy in Tungsten by Molecular Dynamics Calculations. J. Nucl. Mater. 2017, 495, 277–284. [Google Scholar] [CrossRef]
- Alexander, K.C.; Schuh, C.A. Visualization and Analysis of Atomistic Simulation Data with OVITO—The Open Visualization Tool. Model. Simul. Inmater. Sci. Eng. 2010, 18, 7. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated Identification and Indexing of Dislocations in Crystal Interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 5007. [Google Scholar] [CrossRef]
- Wang, D.; Gao, N.; Wang, Z.G.; Gao, X.; He, W.H.; Cui, M.H.; Pang, L.L.; Zhu, Y.B. Effect of Strain Field on Displacement Cascade in Tungsten Studied by Molecular Dynamics Simulation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 2016, 384, 68–75. [Google Scholar] [CrossRef]
- Calder, A.F.; Bacon, D.J.; Barashev, A.V.; Osetsky, Y.N. On the Origin of Large Interstitial Clusters in Displacement Cascades. Philos. Mag. 2010, 90, 863–884. [Google Scholar] [CrossRef]
- Setyawan, W.; Nandipati, G.; Roche, K.J.; Heinisch, H.L.; Wirth, B.D.; Kurtz, R.J. Displacement Cascades and Defects Annealing in Tungsten, Part I: Defect Database from Molecular Dynamics Simulations. J. Nucl. Mater. 2015, 462, 329–337. [Google Scholar] [CrossRef]
- Miyashiro, S.; Fujita, S.; Okita, T. MD Simulations to Evaluate the Influence of Applied Normal Stress or Deformation on Defect Production Rate and Size Distribution of Clusters in Cascade Process for Pure Cu. J. Nucl. Mater. 2011, 415, 1–4. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.H.; Gao, N.; Zhou, H.B.; Hu, W.; Lu, G.H.; Gao, F.; Deng, H. New Interatomic Potentials of W, Re and W-Re Alloy for Radiation Defects. J. Nucl. Mater. 2018, 502, 141–153. [Google Scholar] [CrossRef]
- Banisalman, M.J.; Oda, T. Atomistic Simulation for Strain Effects on Threshold Displacement Energies in Refractory Metals. Comput. Mater. Sci. 2019, 158, 346–352. [Google Scholar] [CrossRef]
- Stoller, R.E. Evaluation of Neutron Energy Spectrum Effects and RPV Thru-Wall Attenuation Based on Molecular Dynamics Cascade Simulations. Nucl. Eng. Des. 2000, 195, 129–136. [Google Scholar] [CrossRef][Green Version]
- Miyashiro, S.; Fujita, S.; Okita, T.; Okuda, H. MD Simulations to Evaluate Effects of Applied Tensile Strain on Irradiation-Induced Defect Production at Various PKA Energies. Fusion Eng. Des. 2012, 87, 1352–1355. [Google Scholar] [CrossRef]
| Strain Type | Cell Constants | Vol. Change Rate | ||
|---|---|---|---|---|
| x Axis | y Axis | z Axis | ||
| Hydrostatic | x0 (1 + ∆) | y0 (1 + ∆) | z0 (1 + ∆) | ~3∆ |
| PKA Energy (keV) | Number of Atoms in the System | Number of Simulations Set | NRT Displacements | Evolution Time (ps) |
|---|---|---|---|---|
| 1 | 54,000 | 16 | 5 | 20 |
| 6 | 182,250 | 16 | 28 | 20 |
| 10 | 432,000 | 16 | 47 | 30 |
| 14 | 432,000 | 16 | 62 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bany Salman, M.; Park, M.; Banisalman, M.J. A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain. Solids 2022, 3, 219-230. https://doi.org/10.3390/solids3020015
Bany Salman M, Park M, Banisalman MJ. A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain. Solids. 2022; 3(2):219-230. https://doi.org/10.3390/solids3020015
Chicago/Turabian StyleBany Salman, Mohammad, Minkyu Park, and Mosab Jaser Banisalman. 2022. "A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain" Solids 3, no. 2: 219-230. https://doi.org/10.3390/solids3020015
APA StyleBany Salman, M., Park, M., & Banisalman, M. J. (2022). A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain. Solids, 3(2), 219-230. https://doi.org/10.3390/solids3020015





