New Bayesian Posterior Approaches for Cytogenetic Partial Body Irradiation Inference

Simple Summary

In the event of a radiological emergency, it is crucial to quickly estimate how much radiation a person has been exposed to. One way to do this is by analyzing the changes in the chromosomes, which can be affected by radiation. This study compares two different mathematical methods for estimating the amount of radiation exposure. These methods are used in situations where only part of the body has been exposed to radiation, which is practical but makes the statistical analysis more complex. The first method is very accurate but slow, while the second, called Laplace’s approximation, is much faster but slightly less precise. The researchers tested both methods using real data from past experiments and found that the faster method still gives results that are good enough for most practical uses, such as deciding how to treat affected individuals in a timely manner. Although the slower method might offer more detail, its speed may limit its usefulness in emergencies. This research is valuable because it supports using quicker tools to help emergency teams make faster decisions, potentially improving care for people exposed to radiation.

Abstract

The number of chromosomal aberrations induced by a whole-body uniform exposure to ionizing radiation is typically assumed to follow a Poisson distribution. If this exposure is partial, the zero-inflated Poisson model is appropriate to describe the yield of chromosomal aberrations. In this work, two different Bayesian posterior approaches (numerical integration and Laplace’s approximation) for zero-inflated Poisson responses are studied for cytogenetic biodosimetry dose estimation purposes. They are evaluated using two experiments from the literature, both of which include data for dose–response calibration and the simulation of partial-body exposure. Laplace’s approximation demonstrates strong performance, delivering rapid results with a loss of precision that may not significantly impact clinical measurements compared to those obtained through the more computationally intensive numerical integration approach.

1. Introduction

The accurate estimation of the dose absorbed after exposure to partial-body ionizing radiation is essential in cytogenetic biodosimetry to assess potential health risks and guide medical interventions. Cytogenetic biomarkers, particularly the frequency of dicentric chromosomes in peripheral blood lymphocytes, are widely used to quantify the amount of dose absorbed in humans suspected of being overexposed to ionizing radiation. Partial body exposures, as opposed to whole-body exposures, combine the heterogeneous distribution of damage among exposed and unexposed cell populations.

Bayesian modeling (see [1], for instance) has gained traction in cytogenetic dose estimation due to its ability to incorporate prior knowledge and its good proficiency in quantifying uncertainty in calibration practice. In [2], a review of Bayesian methods applied to cytogenetic biodosimetry is presented. More recent Bayesian methods include the following works: (a) ref. [3], which proposes a dose estimation hierarchical model with random effects for accounting inter-individual variability; (b) refs. [4,5], which are mentioned below in this section; (c) refs. [6,7,8], which propose dose estimation models for mixed neutron and gamma radiation exposures; (d) ref. [9], which presents a Poisson finite mixture model for radiation dose estimation based on $\gamma$-H2AX protein data accounting for the time since exposure computed by the Laplace approximation method; and (e) ref. [10], which defines a bivariate zero-inflated model to compare the dicentric and translocation assays.

The amount of radiation-induced damage is quantified by cytogenetic dose–response curves. Homogeneous whole-body exposures are simulated by irradiating in vitro blood samples to different dose levels. At each of these levels, several blood cells are analyzed by counting the quantities of a specific chromosomal aberration among them. Typically, this incidence is assumed to follow a Poisson distribution with a quadratic effect for the absorbed dose, i.e.,

$$Y\sim \mathrm{Pois}\left({\beta }_0+{\beta }_{1}D+{\beta }_2{D}^2\right),$$

(1)

where D is the absorbed dose and $\mathit{\beta }=\{{\beta }_0,{\beta }_1,{\beta }_2\}$ is the set of dose–response parameters, usually fitted by maximum likelihood. There are other dose effects that can be assumed.

The distribution of chromosomal aberrations in partial-body exposures follows a different process than whole-body exposures, which, as mentioned before, is considered to be Poisson distributed in the most standardized case. The statistical interpretation of this process is based on a mixture of the non-irradiated cells (which can be assumed to be free of aberrations) and the irradiated ones (following a count data model as the Poisson distribution). This implies an extra population of zeros in comparison to the underlying whole-body distribution which is modeled by the so-called zero-inflated models, more specifically, the zero-inflated Poisson (ZIP) distribution for the most classical scenarios.

There are two classical methods for partial-body dose estimation in the cytogenetic biodosimetry literature, called the contaminated Poisson [11] and Qdr methods [12]. The former is the maximum likelihood estimation of the ZIP model with a correction for the effects of interphase death and miotic delay for estimating the fraction of the body irradiated (FBI). The latter is also based on the ZIP distribution, but it is specified for jointly using the yields of dicentrics plus rings and of excess of acentrics.

The fundamentals of cytogenetic biodosimetry, including aspects of the statistical analysis, can be found in [13].

In [5], a Bayesian version of the contaminated Poisson method is proposed. This method uses the Bayesian dose calibration defined in [4] and jointly provides the posterior distributions of the absorbed dose and the FBI. The posterior distribution is calculated by acceptance–rejection sampling, which may be computationally intensive. Here, two alternative posterior computations are explored. On the one hand, numerical integration is applied for accurate, but heavy as well, posterior computations. On the other hand, Laplace’s approximation is employed for quicker outcomes, although it is restricted by the Gaussian density.

2. Materials and Methods

Following [5], the inputs are a sample of chromosomal aberration counts in n blood cells, $\mathit{y}=\{y_1,\dots ,y_n\}$, and the maximum likelihood estimator (MLE) of the appropriate dose–response curve $\widehat{\mathit{\beta }}$ (for example, for the quadratic dose effect $\widehat{\mathit{\beta }}=\{{\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2\}$) with an estimated variance–covariance matrix ${\widehat{\Sigma }}_{\widehat{\mathit{\beta }}}$ (the inverse of the Hessian matrix of the model evaluated at $\widehat{\mathit{\beta }}$). Then, the joint posterior density of both the absorbed dose D and FBI F is

$${\displaystyle \pi (D,F|\mathit{y})=\frac{{\displaystyle \int L\left(\mathit{y}\right|D,F,d_0)\pi (D,F,d_0)\mathrm{d}{d}_0}}{{\displaystyle \int L\left(\mathit{y}\right|D,F,d_0)\pi (D,F,d_0)\mathrm{d}D\mathrm{d}F\mathrm{d}{d}_0}}.}$$

(2)

The parameter $d_0$ represents the 37% cell survival dose, useful for reconstructing the FBI accounting for cell death. The term $\pi (D,F,d_0)$ represents the density of the prior joint distribution of the parameters D, F, and $d_0$. The likelihood function of the parameters (D, F, and $d_0$) for the observed data $\mathit{y}$, $L\left(\mathit{y}\right|D,F,d_0)$, is derived in the following form from the dose–response MLE:

$${\displaystyle L\left(y\right|D,F,d_0)\propto {\left(F{\mathrm{e}}^{-D/d_0}-F+1\right)}^{-n}\sum _{j=1}^{n_0}\left(\genfrac{}{}{0pt}{}{n_0}{j}\right)\frac{F^{n-j}{(1-F)}^j}{{(n-j)}^s}P(X_j=s|D),}$$

(3)

where $X_j$ is a negative binomial random variable with the mean $(n-j)f(x,\widehat{\mathit{\beta }})$ and variance $(n-j)f(D,\widehat{\mathit{\beta }})+{(n-j)}^{2}v(D,\widehat{\mathit{\beta }})$, with $f(D,\widehat{\mathit{\beta }})$ being the fitted dose–response curve and $v(D,{\widehat{\Sigma }}_{\widehat{\mathit{\beta }}})=\nabla ·{\widehat{\Sigma }}_{\widehat{\mathit{\beta }}}·{\nabla }^T$ (∇ denotes the gradient of $f(D,\mathit{\beta })$ with respect to $\mathit{\beta }$) the variance of the fitted curve. In this work, the estimation of $d_0$ is not studied, although it may be interesting for biodosimetric purposes; for example, in [10,14], the survival index of irradiated cells, $\gamma =1/d_0$, is analyzed.

The joint prior distribution considered here is $(D,F,d_0)\sim {\mathcal{U}}_{\left[0,d_{\max }\right]}\times {\mathcal{U}}_{\left[0,1\right]}\times {\mathcal{U}}_{\left[2.7,3.5\right]}$, that is, three independent uniform distributions. For the Laplace approximation $d_{\max }=+\infty$ is set. Meanwhile, in order to make the numerical integration work more efficiently and accurately, $d_{\max }=\widehat{D}+6SE\left(\widehat{D}\right)$, where $\widehat{D}$ is the MLE under (3) of D and $SE\left(\widehat{D}\right)$ represents its standard error. The range $(2.7, 3.5)$ Gy for $d_0$ is experimentally supported [13].

In [5], the posterior computation of the model is drawn by the acceptance–rejection method because the density is non-tractable. This algorithm can be very inefficient and time consuming. However, numerical integration may be an interesting alternative, because it is accurate and not exorbitantly computationally intensive (there are only three parameters in the model).

Laplace’s approximation is another alternative for posterior calculation that does not present computational cost problems, albeit with a potential loss of precision. It returns the posterior distribution as a multivariate normal, as follows:

$$(D,F)|\mathit{y}\sim \mathcal{N}\left({\theta }^{*},{\Sigma }_{{\theta }^{*}}^{*}\right);$$

(4)

where ${\theta }^{*}=(D^{*},F^{*})$ is the mode of $\pi (D,F|\mathit{y})$, i.e.,

$${\theta }^{*}=\underset{(D,F)}{arg\; max}\int L\left(\mathit{y}\right|D,F,d_0)\pi (D,F,d_0)\mathrm{d}{d}_0,$$

(5)

and ${\Sigma }_{{\theta }^{*}}^{*}$ is the estimated variance–covariance matrix of the model evaluated at ${\theta }^{*}$. The integral concerning Equation (5) is computed by numerical integration; meanwhile, in the numerical integration approaches, all integrals involved in the posterior computations are numerically solved.

Laplace’s approximation is suitable for unimodal (at least, marginally) and nearly symmetric posterior densities. In this context, with uniform irradiation exposures, this may be reasonable for doses not close to 0 Gy and FBIs far from 0 and 1 (i.e., the method may not be appropriate if the mode of the posterior density is near a boundary of the model parameter space). Moreover, the asymptotic normality of the posterior distribution makes this method more suitable when analyzing large sample sizes.

In [5], the authors presented dicentric plus ring chromosome (D+R) data induced by gamma rays to construct a dose–response curve and to simulate two partial-body exposure schemes as follows: 10% to 2 Gy and 90% to 12 Gy. The calibration data range from 0 to 20.3 Gy. In [15], the authors also showed D+R but induced by X-rays, among other chromosomal aberrations induced by ionizing radiation, data for both the calibration of the dose effect (ranging from 0 to 5 Gy) and the in vitro simulation of whole- and partial-body irradiation test samples. These samples come from two different blood donors. For each donor, there is one control and assays with doses of 0.5, 1, 2, and 4 Gy in combination with 25, 50, and 100% body exposure, i.e., $2\mathrm{donors}\times (1\mathrm{control}+4\mathrm{dose}\mathrm{levels}\times 3\mathrm{FBI}\mathrm{levels})=26\mathrm{samples}$. Both calibration curves are fitted assuming the quadratic dose-effect Poisson model (1). In the next section, Section 3, the test samples referred to above are analyzed with the model (2) by both posterior approaches discussed in this work.

3. Results

This section presents the results of analyzing the data mentioned in Section 2 by applying numerical integration and the Laplace approximation. First, the posterior summaries applying both approaches are compared. Then, the graphical representation of the posterior densities of two samples are displayed.

3.1. Comparison of Approaches

Table 1. Results of the numerical integration approach for the test samples in [5].

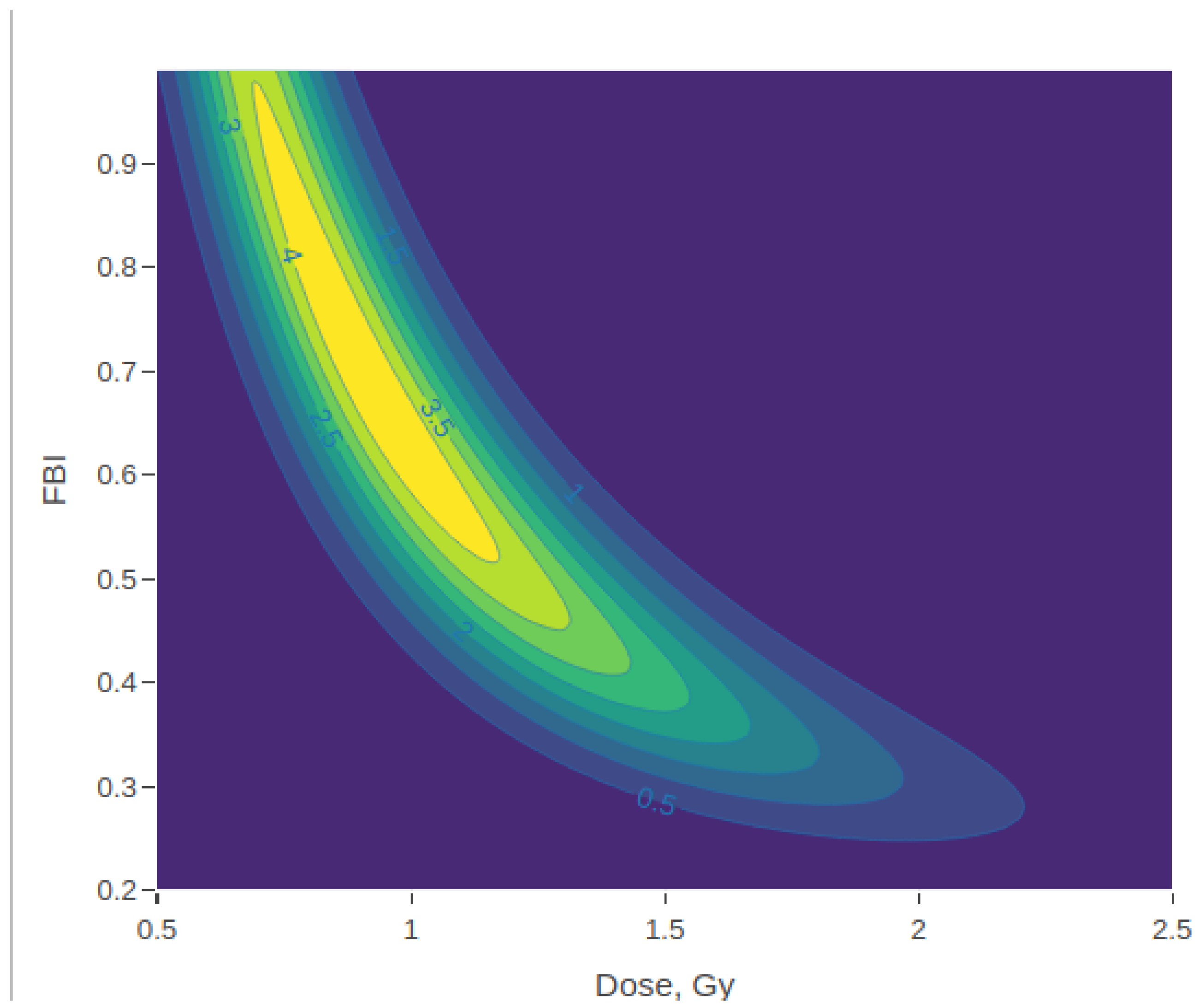
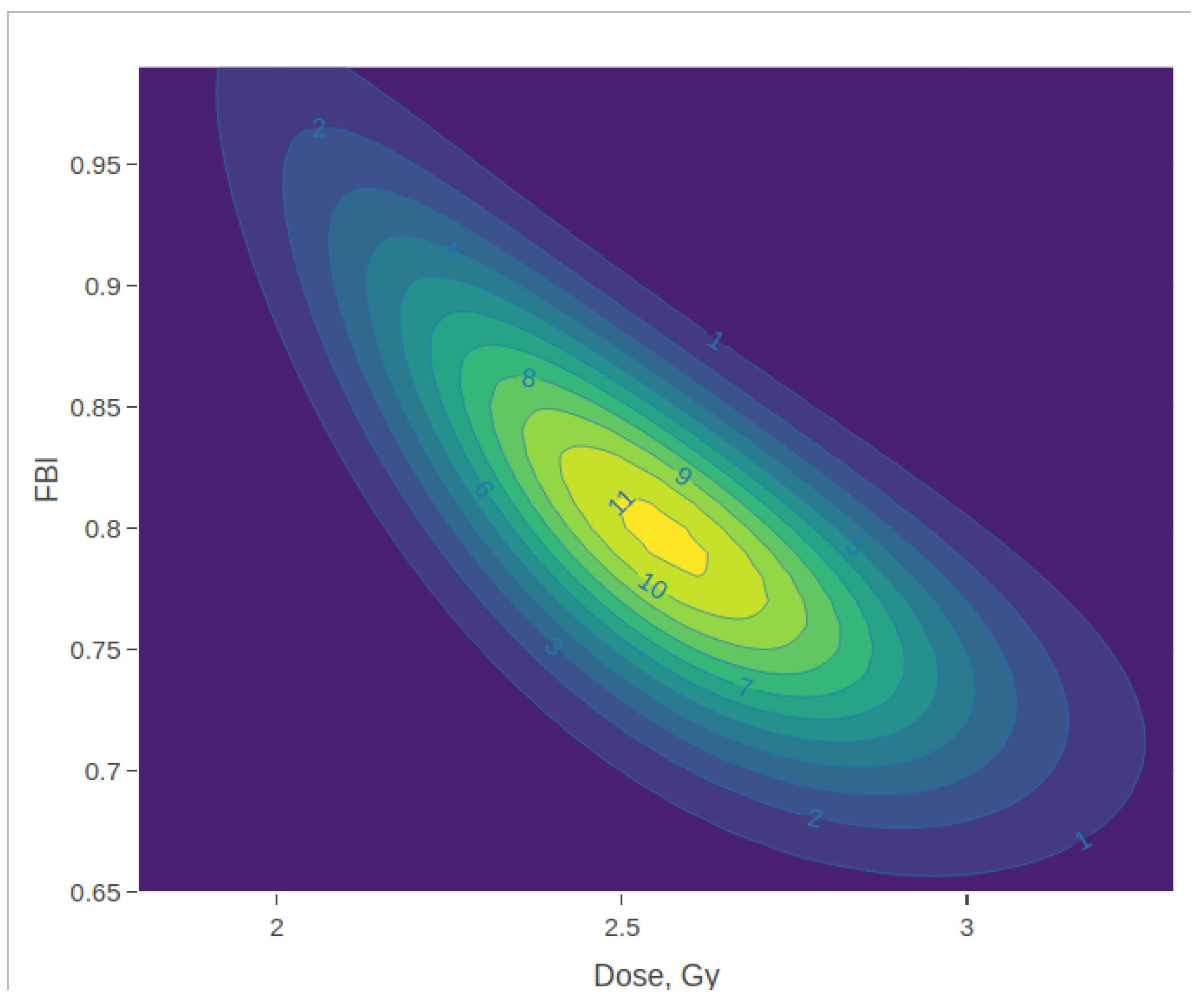
Dose	FBI	${\mathit{d}}_{\mathbf{max}}$	Marginal Dose Posterior: $\mathit{D}|\mathit{y}$					Marginal FBI Posterior: $\mathit{F}|\mathit{y}$
			Mode	Expected	Median	SD	95% HPDI	Mode	Expected	Median	SD	95% HPDI	Correlation
2.00	0.10	5.91	1.41	1.62	1.56	0.71	(0.34, 2.99)	0.11	0.14	0.12	0.07	(0.05, 0.28)	−0.63
12.00	0.90	13.12	10.71	10.72	10.71	0.39	(9.95, 11.49)	0.91	0.91	0.91	0.03	(0.86, 0.96)	0.38

and

Table 2. Results of Laplace’s approximation approach for the test samples in [5].

Dose	FBI	Marginal Dose Posterior: $\mathit{D}|\mathit{y}$			Marginal FBI Posterior: $\mathit{F}|\mathit{y}$
		Mode	SD	95% HPDI	Mode	SD	95% HPDI	Correlation
2.00	0.10	1.63	0.71	(0.24, 3.02)	0.11	0.04	(0.04, 0.19)	−0.75
12.00	0.90	10.73	0.40	(9.96, 11.51)	0.91	0.03	(0.84, 0.97)	0.28

show the posterior density summaries of the two above-mentioned test samples from [5], applying numerical integration and the Laplace approximation, respectively. Analogously,

Table 3. Results of the numerical integration approach for the test samples in [15].

Donor	Dose	FBI	${\mathit{d}}_{\mathbf{max}}$	Marginal Dose Posterior: $\mathit{D}|\mathit{y}$					Marginal FBI Posterior: $\mathit{F}|\mathit{y}$
				Mode	Expected	Median	SD	95% HPDI	Mode	Expected	Median	SD	95% HPDI	Correlation
1	0.00	1.00	10.12	0.03	0.68	0.23	1.10	(0.00, 3.10)	0.01	0.24	0.14	0.26	(0.00, 0.81)	−0.47
1	0.50	0.25	8.18	0.20	0.85	0.48	0.96	(0.00, 2.93)	0.05	0.34	0.25	0.28	(0.03, 1.00)	−0.61
1	0.50	0.50	7.27	0.25	0.75	0.50	0.72	(0.04, 2.30)	0.07	0.38	0.31	0.08	(0.05, 1.00)	−0.67
1	0.50	1.00	3.31	0.68	0.92	0.82	0.36	(0.41, 1.67)	0.60	0.63	0.63	0.05	(0.28, 1.00)	−0.83
1	1.00	0.25	6.17	0.63	1.29	1.16	0.68	(0.30, 2.63)	0.16	0.34	0.27	0.22	(0.07, 0.83)	−0.76
1	1.00	0.50	4.21	0.84	1.13	1.05	0.39	(0.55, 1.93)	0.48	0.61	0.59	0.20	(0.30, 1.00)	−0.84
1	1.00	1.00	2.90	1.19	1.29	1.25	0.20	(0.96, 1.70)	1.00	0.84	0.86	0.11	(0.63, 1.00)	−0.82
1	2.00	0.25	5.11	1.20	1.46	1.39	0.54	(0.57, 2.49)	0.29	0.43	0.39	0.19	(0.16, 0.85)	−0.81
1	2.00	0.50	3.48	1.47	1.61	1.57	0.25	(1.19, 2.11)	0.83	0.81	0.82	0.11	(0.62, 1.00)	−0.84
1	2.00	1.00	3.55	2.21	2.23	2.23	0.15	(1.95, 2.54)	1.00	0.96	0.97	0.03	(0.90, 1.00)	−0.49
1	4.00	0.25	4.27	1.82	1.88	1.86	0.38	(1.15, 2.61)	0.52	0.58	0.56	0.12	(0.37, 0.85)	−0.83
1	4.00	0.50	4.41	2.54	2.57	2.56	0.30	(2.00, 3.15)	0.79	0.80	0.80	0.07	(0.67, 0.95)	−0.75
1	4.00	1.00	5.27	3.74	3.75	3.75	0.22	(3.33, 4.19)	1.00	0.99	0.99	0.01	(0.97, 1.00)	−0.11
2	0.00	1.00	10.12	0.03	0.68	0.23	1.10	(0.00, 3.11)	0.01	0.25	0.14	0.26	(0.00, 0.82)	−0.47
2	0.50	0.25	9.49	0.26	0.95	0.58	0.98	(0.01, 3.09)	0.06	0.35	0.27	0.28	(0.01, 0.90)	−0.62
2	0.50	0.50	7.13	0.66	1.47	1.32	0.82	(0.26, 3.07)	0.12	0.28	0.20	0.21	(0.04, 0.76)	−0.72
2	0.50	1.00	3.07	0.73	0.93	0.85	0.31	(0.48, 1.58)	0.82	0.67	0.69	0.20	(0.34, 1.00)	−0.84
2	1.00	0.25	4.88	0.40	0.82	0.64	0.57	(0.15, 2.04)	0.15	0.45	0.41	0.26	(0.07, 0.94)	−0.75
2	1.00	0.50	3.26	0.70	0.93	0.84	0.35	(0.43, 1.65)	0.66	0.64	0.65	0.21	(0.30, 1.00)	−0.83
2	1.00	1.00	2.81	1.02	1.12	1.08	0.21	(0.77, 1.57)	1.00	0.82	0.84	0.13	(0.57, 1.00)	−0.81
2	2.00	0.25	3.07	0.79	0.97	0.90	0.30	(0.52, 1.60)	0.94	0.70	0.71	0.19	(0.37, 1.00)	−0.83
2	2.00	0.50	3.71	1.30	1.48	1.44	0.30	(0.99, 2.09)	0.70	0.73	0.73	0.14	(0.51, 1.00)	−0.85
2	2.00	1.00	3.81	2.21	2.28	2.26	0.23	(1.87, 2.72)	0.88	0.88	0.88	0.06	(0.77, 1.00)	−0.78
2	4.00	0.25	5.38	2.24	2.29	2.27	0.51	(1.29, 3.30)	0.31	0.35	0.33	0.09	(0.20, 0.53)	−0.70
2	4.00	0.50	4.74	2.95	2.96	2.95	0.30	(2.38, 3.54)	0.61	0.61	0.61	0.05	(0.51, 0.71)	−0.52
2	4.00	1.00	5.17	3.68	3.70	3.69	0.21	(3.28, 4.12)	1.00	0.99	0.99	0.01	(0.97, 1.00)	−0.09

and

Table 4. Results of Laplace’s approximation approach for the test samples in [15].

Donor	Dose	FBI	Marginal Dose Posterior: $\mathit{D}|\mathit{y}$			Marginal FBI Posterior: $\mathit{F}|\mathit{y}$
			Mode	SD	95% HPDI	Mode	SD	95% HPDI	Correlation
1	0.00	1.00	0.13	1.67	(−3.14, 3.40)	0.21	2.48	(−4.65, 5.07)	−1.00
1	0.50	0.25	0.13	0.95	(−1.73, 1.99)	0.95	6.44	(−11.66, 13.57)	−1.00
1	0.50	0.50	0.17	0.07	(0.02, 0.31)	1.00	0.04	(0.92, 1.08)	−0.09
1	0.50	1.00	0.56	0.09	(0.38, 0.74)	1.00	0.00	(1.00, 1.00)	0.00
1	1.00	0.25	1.39	0.79	(−0.16, 2.94)	0.21	0.14	(−0.07, 0.50)	−0.92
1	1.00	0.50	0.92	0.54	(−0.15, 1.99)	0.69	0.49	(−0.28, 1.65)	−0.97
1	1.00	1.00	1.09	0.09	(0.92, 1.27)	1.00	0.00	(1.00, 1.00)	0.00
1	2.00	0.25	1.50	0.60	(0.32, 2.67)	0.35	0.16	(0.04, 0.67)	−0.91
1	2.00	0.50	1.45	0.34	(0.79, 2.11)	0.89	0.22	(0.47, 1.31)	−0.94
1	2.00	1.00	2.15	0.12	(1.91, 2.38)	1.00	0.00	(1.00, 1.00)	0.00
1	4.00	0.25	1.89	0.39	(1.12, 2.66)	0.55	0.12	(0.32, 0.77)	−0.86
1	4.00	0.50	2.56	0.31	(1.96, 3.16)	0.80	0.07	(0.65, 0.94)	−0.77
1	4.00	1.00	3.71	0.21	(3.30, 4.13)	1.00	0.00	(1.00, 1.00)	0.00
2	0.00	1.00	0.13	1.68	(−3.16, 3.42)	0.22	2.56	(−4.80, 5.23)	−1.00
2	0.50	0.25	0.17	0.09	(−0.02, 0.35)	1.00	0.03	(0.94, 1.06)	−0.06
2	0.50	0.50	1.63	0.91	(−0.16, 3.42)	0.15	0.10	(−0.04, 0.34)	−0.88
2	0.50	1.00	0.62	0.09	(0.44, 0.80)	1.00	0.00	(1.00, 1.00)	0.00
2	1.00	0.25	0.30	0.09	(0.13, 0.47)	1.00	0.00	(0.99, 1.01)	−0.01
2	1.00	0.50	0.58	0.09	(0.40, 0.76)	1.00	0.00	(1.00, 1.00)	0.00
2	1.00	1.00	0.92	0.09	(0.74, 1.11)	1.00	0.00	(1.00, 1.00)	0.00
2	2.00	0.25	0.67	0.09	(0.49, 0.86)	1.00	0.00	(1.00, 1.00)	0.00
2	2.00	0.50	1.36	0.39	(0.60, 2.13)	0.78	0.24	(0.30, 1.25)	−0.95
2	2.00	1.00	2.22	0.26	(1.70, 2.73)	0.89	0.09	(0.72, 1.06)	−0.87
2	4.00	0.25	2.32	0.51	(1.32, 3.31)	0.32	0.07	(0.18, 0.46)	−0.70
2	4.00	0.50	2.95	0.30	(2.37, 3.53)	0.61	0.05	(0.51, 0.71)	−0.51
2	4.00	1.00	3.66	0.21	(3.25, 4.07)	1.00	0.00	(1.00, 1.00)	0.00

show the results for the 26 test samples of the D+R assay in [15]. They present the experimental levels of dose and FBI (for data from [15], the donor ID is also shown) along with measurements of central tendency and dispersion of the posterior marginal densities and their correlations.

On the one hand, the tables with the results of the numerical integration approach (i.e., Table 1 and Table 3) describe the marginal posterior densities with three measures of the central tendency (mode, expected value, and median), the standard deviation (SD), and the 95% highest posterior density interval (HPDI). They also show the $d_{\max }$ hyperparameter, i.e., the maximum of the uniform absorbed dose prior ranging from 0 ($D\sim {\mathcal{U}}_{\left[0,d_{\max }\right]}$). On the other hand, the tables with the results of the Laplace approximation approach (i.e., Table 2 and Table 4) report the mode, the SD, and the 95% HPDI of the marginal posteriors. Under the Gaussian assumption, the mean, mode, and median are identical and the 95% HPDI is indistinguishable within the range from the 5th to the 95th percentiles.

The comparison of the results in Table 1 and Table 2 shows that the central tendency measures for both approaches lead to an underestimation of the dose of radiation absorbed. Regarding the FBI, the posterior distribution measures exhibit competence in the estimation task. The 95% HPDIs can be considered comparable for both approaches; at the very least, they would lead to equivalent clinical conclusions.

The comparison of results in Table 3 and Table 4 shows an average discrepancy of 0.14, 0.25, and 0.16 Gy between the marginal posterior modal dose administered by the Laplace method, respectively, compared to the posterior modal, expected, and median doses obtained using the numerical integration method. The central tendency estimation of the Laplace method tends to be in closer agreement with the marginal posterior modal dose calculated by the numerical integration approach. Analogously, the posterior FBI central tendency estimation by the Laplace approximation method presents an average distance of 0.21, 0.19, and 0.19 units, respectively, compared to the posterior modal, expected, and median FBIs obtained by the numerical integration method.

In terms of uncertainty comparison, the coverage frequencies of cases in which both credibility intervals (for the marginal distributions of dose and FBI) contained the true values are computed. With the numerical integration approximation, the coverage percentage is ≈64%, whereas for the Laplace approximation it is ≈61% (≈72% among the cases where the numerical integration approximation achieves this coverage, and 40% among the cases where it does not). The similarity of the credibility intervals produced by both methods was also assessed using the intersection-over-union metric (the ratio of the lengths of the intersection to the union). Expressed as percentages, these metrics are ≈66% for the dose and ≈42% for the FBI (truncated in the Laplace approximation so that the dose is non-negative and the FBI lies between 0 and 1).

The results of the whole-body irradiation (FBI = 1, excluding the control samples for which the FBI value would be debatable) obtained using the Laplace approximation are noteworthy. Interestingly, they are highly accurate in estimating the true doses and FBI values, despite the fact that the 95% HPDIs of the posterior FBI slightly exceed a value of 1 and differ from those produced by the numerical integration method.

These results suggest that, in general terms, the outcomes associated with both methods are comparable. Therefore, it can be inferred that the choice between the Laplace approximation and the numerical integration methods for estimating radiation doses does not lead to significantly divergent conclusions in the vast majority of responses to radiation catastrophes.

3.2. Posterior Density Plots

Figure 1, Figure 2 and Figure 3 show some graphical results of the posterior densities that can be provided by the numerical integration approach. They cover the results of two test samples in [15]. First, the marginal dose and FBI posterior densities from the donor 1 sample irradiated to 1 Gy at a 50% fraction are shown at the top of Figure 1. Its joint posterior density is represented in Figure 2. Then, the bottom of Figure 1 and Figure 3 represent the corresponding posterior densities from the donor 1 sample irradiated by 4 Gy at a 50% fraction. The former sample is accurately estimated, and as shown in Table 3, the measures of the central tendency of both posterior densities are clustering around the real values and the HPDIs cover them properly. However, the latter do not meet these attributes. In both cases, the strong negative correlations ($-0.84$ and $-0.75$, respectively) between the absorbed and the FBI are manifested in Figure 2 and Figure 3.

4. Discussion

Radiological emergency situations require speed in all response processes, including the computation of statistical models. For this purpose, the Laplace approximation provides outcomes virtually instantaneously for the model in [5], which is of great relevance. Moreover, we note that loss of precision for this approach does not appear to lead to significant changes in the subsequent clinical actions, such as patient triage. However, the accuracy of the Laplace approximation may be substantially compromised due to the reduction in the sample size that can occur during a radiation emergency response [16].

The calculation of the posterior density through numerical integration is precise but far from able to provide immediate results. However, in this study, the calculations were performed using R-project [17], which is known for its slowness in executing such operations. In this regard, it is important to consider alternatives, such as using the C programming language [18], to execute these functions more quickly through an R-project front end. Nevertheless, improving the efficiency of the numerical integration alternative is beyond the scope of this work.

As mentioned above (Section 1), one of the main advantages of using Bayesian methods for cytogenetic dose estimation is the ability to incorporate available exposure information in the form of a prior distribution. The two approaches used here for the posterior density calculation do not impose restrictions on the prior distributions to be established, allowing great versatility in this concern. In addition, this model fits perfectly with any of the dose–response shapes that are usually applied in cytogenetic biodosimetry, beyond the usual quadratic effect of the dose that has been used in this work to illustrate the performance of the model and the two alternative posterior approaches. Consequently, this model is applicable to any radiation source that induces damage counts—pertaining to a specific type of chromosomal aberration—under the conditions of homogeneous whole-body exposure, provided that the resulting damage can be assumed to follow a Poisson distribution with an analytically expressible dose–response relationship.

5. Conclusions

In this study, two distinct Bayesian posterior estimation methods—numerical integration and Laplace’s approximation—in the context of a ZIP model, specifically applied to dose estimation in cytogenetic biodosimetry, are investigated and compared. These approaches were assessed using two previously published experimental datasets, both of which comprise information relevant to dose–response calibration, as well as the simulation of partial-body radiation exposure scenarios. The chosen datasets provided a robust framework for evaluating the performance and applicability of the two Bayesian methods under practically relevant conditions.

The findings indicate that Laplace’s approximation offers a computationally efficient alternative to full numerical integration, producing results at a substantially faster rate. While it entails a certain reduction in precision, this loss appears to have limited practical consequences for clinical or operational biodosimetry, where rapid dose estimation is often prioritized. In comparison, numerical integration remains the more accurate method but demands significantly greater computational resources. Overall, the results support the use of Laplace’s approximation as a viable and effective approach for routine applications where computational speed is critical and the minor decrease in accuracy is acceptable.