Abstract
The hydrodynamics of a river confluence generate significant vertical, lateral, and stream-wise gradients in the context of velocity, thereby forming a highly complex three-dimensional flow structure, including the development of large-scale turbulence structures. The above features affect the ecologically important underlying hyporheic zone, where surface and subsurface waters interact, and hence affect biological activity and result in highly varied habitats for organisms as well as the whole river environment. The influence of challenging conditions for in situ monitoring of hyporheic exchange—such as non-sinusoidal temperature signals, uncertainty in thermal parameters, and unsteady flows—have led to the development of hyporheic exchange detection methods that are based on the phase and amplitude changes in transient thermal signals. The use of heat as a tracer can require complex steps, including the isolation of the diurnal component of the temperature signal from other signals as well as stochastic variation. The focus of this study was to investigate a field campaign carried out between the Ninemile Creek and its tributary confluence, located in Marcellus, NY. Temperature data of the shallowest saturated sediment layers were measured from April to May 2019. Flux estimations were calculated using VFLUX 2, a MatLab based code, which performed data filtering and DHR (Dynamic Harmonic Regression). The patterns and rates of vertical flux exchange were then analyzed, and sampling of the temporal thermal profiles was performed. Furthermore, multiple analytical solutions of the one-dimensional heat transport model were analyzed and discussed in order to obtain the confluence hydrodynamic effect as well as the variations in the vertical flux estimation. This was achieved by utilizing different sensor pairs and porous medium characteristics, such as thermal diffusivity and conductivity. The predicted flow field shows that confluence topography—which includes the turbulent kinetic energy downstream of the junction, shear layer formations, bed stratigraphy and water table gradients—affects the magnitude and patterns of hyporheic exchange. The results of this study could help to advance the calibration of one-dimensional heat transport models in order to better understand the key hydrological, hydraulic, and ecological issues associated with river confluence.
1. Introduction
The riverine ecosystem is a continuum that includes the mixing zone of surface water and groundwater, and is called the hyporheic zone. This saturated zone contains many physical, biological, and chemical gradients that create highly varied habitats for aquatic and terrestrial species. Further, it supports several biogeochemical functions that are critical to aquatic and terrestrial systems [1].
The resulting fluxes are governed by spatial and temporal variations in channel features, including riverbed hydraulic conductivity, hydrodynamics and riverbed pressure distribution, groundwater pressure, grain roughness, and bedform topography. The latter induces a small-scale exchange via variation in the hydraulic head, i.e., streamline energy-per-unit weight around individual bedforms (i.e., dunes, ripples, and steps) as well as bars, bends, and riverbanks.
Identifying and characterizing hyporheic fluxes that are affected by a complex morphology, such as river confluences, becomes arduous and challenging when conducting in-field studies.
The scour and flow separation zone in a river confluence [2] regulates hydrodynamics. This affects bed pressure patterns and governs hyporheic upwelling and downwelling flux patterns during high and low flow conditions [3], to mention a few examples. The rapid increase in flow rates along transects from the upstream nodes to the downstream nodes of a confluence result in larger confluence angles and heterogeneous hyporheic exchange flux patterns and magnitudes. River confluences provide a rich set of hyporheic exchange drivers, and hence research on hyporheic water exchange in these nodal riverine systems has become an appealing topic in recent years [4].
Given the challenge of monitoring the zone beneath a riverbed [5], a variety of methods have been developed in order to help infer both the patterns and magnitude of hyporheic exchange. These have been used in previous studies to accurately assess hyporheic fluxes in situ, including tracer tests [6], seepage meters [7], mini wells [8], diffusive equilibrium in thin films [9], and thermal methods [10]. Thermal methods have been demonstrated as relatively low cost, rapid to deploy, and effective in monitoring pore water temperature.
In this study, the influence of challenging field conditions such as non-sinusoidal temperature signals, uncertainty in thermal parameters, and unsteady flows at the river confluence surface–subsurface water interface are shown through thermal-based detection model results. These are related to phase and amplitude changes in transient thermal signals. Secondly, the effects of long-time monitoring of deeper pore water sediments; heterogeneous porous medium characteristics that are dependent on thermal diffusivity and conductivity; and thermal dispersivity are all analyzed. In the end, the results highlight a combined method as a possible way to manage uncertainty, as they help to infer hyporheic downwelling and upwelling fluxes across river confluences under both low- and high-flow conditions.
2. Field Measurements
Study Area
This study of hyporheic exchange in a 90° angle junction river confluence was undertaken at Ninemile Creek (B = 12 m), as well as its unnamed tributary (B = 10 m). Both of these confluences are located southwest of the town of Marcellus, which is located in Onondaga County, New York state. Ninemile Creek is the major tributary of Onondaga Lake, and its watershed covers 158.50 km2 with a mean annual estimated runoff of 492.76 mm. In addition, the mean annual discharge of Ninemile Creek is 5 m3/s.
Its hydrodynamics are characterized by a flow separation and several shear layers that are caused by the presence of a riffle zone at the Ninemile Creek inlet. Indeed, a flow separation zone may be seen close to the erosional bank; further, the bankfull stage is approximately 2 m and the riparian zone is principally composed of woody vegetation with stretches of mainly shrubs and herbs.
The confluence bathymetry was surveyed by means of a total station Topcon GTS-250 (Topcon Positioning Systems, Inc., Livermore, CA, USA). This was used by taking a point density along the riverbed of 0.135/m2, and a natural neighbor gridding algorithm method was used for the purposes of the spatial interpolation of the surveyed point. The grain size analysis conducted on the collected samples showed a clear trend of coarser river sediment, mostly within the 1–2 mm range, at the main Ninemile Creek channel. Further, the unnamed tributary was predominantly sandy and flat, making it more easily regulated by the backwater from the bridge. This morphological configuration suggests an intensive erosional activity and momentum flow ratio dependence, with an evident mid-channel scour hole of approximately 20 m in length (Figure 1 and Figure 2).
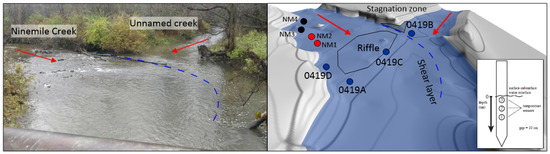
Figure 1.
Riverbed monitoring during field campaigns showing hydraulic conductivity test location (red circles), soil sample test locations (black circles), and temperature sediments (blue navy circles). Down-right window shows vertical thermistor array.
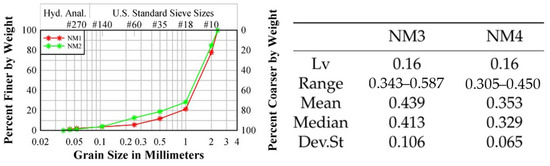
Figure 2.
Soil grain size distribution, showing a medium coarse of sand into the confluence zone (left) and statistical analysis of kv, developed by [11], during the 23 May 2019 field campaign at Ninemile Creek Confluence. Lv is the average length (m), while values are in m/d (right).
Hydraulic conductivity tests of the riverbed were conducted using the falling head method, herein after referred as kv, at Ninemile Creek site 1 (NM3) and site 2 (NM4). Both sites were in agreement with soil permeability rates.
3. Methodology
3.1. Temperature Measurements
Pore water temperature profiles were collected in situ by deploying four PVC pipes. Wooden stakes were inserted inside and slotted into the same gaps as the pipes, forming a vertical thermistor array, drilled at 5, 10, and 15 cm distances from the tip to create openings in order to hold the temperature thermistors. To secure and isolate the sensors, they were covered and sealed with a silicone glue [12]. Those pipes were driven into the riverbed in order to place one sensor in the river column just above the riverbed and the other sensors at depths of 5 cm and 10 cm, below the riverbed.
Three of the four sites were along a transect, which itself was along a riffle tail leading into the confluence. Further, the fourth was deployed in the unnamed tributary inlet. The thermistors were iButton temperature sensors (iButtonLink LLC, Whitewater, WI, USA). Each sensor had an accuracy of ±0.5 °C (from −10 °C to +65 °C) and a programmable resolution of 0.5 °C for 8-bit and 0.0625 °C for 11-bit data. Further, the vertical thermistor arrays had a sampling rate of 15 min.
3.2. Vertical Exchange Fluxes Estimated from Confluence Bed Temperature Profiles
Water sediments were monitored along the vertical transects from April 17 to May 23 2019; the thermal amplitude and phase analyses were conducted in VFLUX2, a MatLab-coded program, which calculated vertical flux rates using the temperature time series that was obtained from the pairs of temperature sensors [13]. The model computed one-dimensional vertical fluid flow based on the methods of [14,15,16,17]. The process involves formatting all time series records into one-dimensional vectors with coordinated time steps. Then, a low-pass filter is applied to extract 12 temperature readings per fundamental cycle, which, for this study, was diel. The fundamental signal was extracted using dynamic harmonic regression (DHR), which obtains isolated amplitude and phase shifts. The process concludes with contrasting pairs of sensors to infer flux directions and magnitudes that best explain the amplitude and phase shifts. The methods are based on an analytical solution to the one-dimensional conduction–advection–dispersion Equation [18]:
where T is temperature, z is the vertical coordinate, κe is effective thermal diffusivity, q is the fluid flux, Cw is the volumetric heat capacity of the saturated riverbed, and C is the volumetric heat capacity of the saturated sediment calculated as the mean of Cw and Cs; further, the volumetric heat capacity of the sediment grains is weighted by its total porosity [14,15]. The effective thermal diffusivity κe is expressed as follows:
where λ0 is the baseline thermal conductivity in the absence of fluid flow, which excludes the effects of dispersion, β is thermal dispersivity, c is specific heat of the sediment water, ρ is density of the sediment water, and vf is the linear particle velocity. The second term in Equation (2) represents the increase in effective thermal diffusivity caused by hydrodynamic dispersion and it is often assumed to have little influence in models with modest fluid flow rates. The methods in [14,15], which are included in VFLUX2, allow for the estimation of seepage rates using amplitude variations, Ar (amplitude method):
and phase variations, ∆ϕ (phase method):
Both (3) and (4) require a simultaneous solution, performed iteratively or via optimization, which depends on thermal sensitivity, estimated from empirical ranges (Table 1). VFLUX2 also uses a combined phase and amplitude method [16,17], which has the benefit of generating a time series of q and κe by using ∆ϕ and Ar simultaneously (the Luce method):
where ∆ϕr is the phase shift in radians, η = ln Ar/∆ϕr, and ω = 2π/P. This solution has another key advantage, which is detecting the flow direction beyond the κe.

Table 1.
The input parameters of VFLUX2 code for computing hyporheic flux, where β is dispersivity, KCal the thermal conductivity, CsCal the volumetric heat capacity of the sediment, and CwCal the volumetric heat capacity of the water.
4. Results and Discussion
4.1. Sediments’ Temporal Temperature
The sensors located at the scour hole mouth had a similar temperature distribution, while those placed at the tributary inlet showed a different trend, as well as those near the confluence bank. However, the sensors varied slightly from one another in their recording of lower values on April 29, followed by a general increasing trend during mid-May 2019. Temporal temperature exhibited a large difference between the interface and depths of 5 cm or 10 cm. It clearly appears that the temperature at the water–surface interface was related to the stream and air-fluctuating condition, while it also showed a lower difference in distribution in regard to depth.
Furthermore, the seasonal temperature variation was evident in all depths, demonstrating cooler values at 5 and 10 cm depths. This was shown in those that had narrower oscillations with minimum variations among the sensor pairs (minimum variation is understood as less than a °C grade difference). In addition to this, the highest temperature range was monitored near the stagnation zone (Figure 3, top right) at the end of May 2019, whereas, moving towards the riffle zone (Figure 3, down left and down right), the lowest values were instead noted.
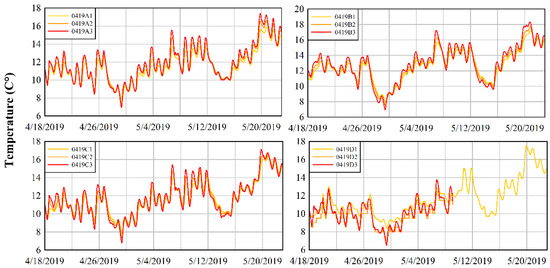
Figure 3.
Temperature time series at the sediment–water interface: top left figure represents 0419A, top right 0419B, down left 0419C, and down right 0419D. Yellow line is sediment water temperature at surface–subsurface interface. Further, orange and red lines are the 5 cm and 10 cm depths, respectively.
4.2. Estimated Hyporheic Flow Flux Using VFLUX2
4.2.1. Top Sensor Pairs
The largest down-welling flux rates (resulting depth of 0.025 m) mostly occurred at 0419C as well as 0419A, when considering the phase method results. On the other hand, the amplitude method yielded oscillating positive values, while the results from the combined method suggested a negative trend (upwelling) characterized by a cuspid during the field campaign.
At 0419D, near to 0419A, estimated fluxes were highly discordant among the three mentioned methods, highlighting flow separation zone effects on the shallowest pore water sediment yielding a fluctuating and uncertain down-welling pattern.
The results of the temperature sensors show that fluid flow is one-dimensional, due to 1D analytical methods, and the riverbed is homogeneous. These assumptions lead to uncertainty in the flux estimation, which were especially visible in the phase method used for the top sensor pairs (Figure 4). In fact, the amplitude method was shown to be stable and more accurate, particularly in regard to the non-steady flow conditions as compared to the phase and combined methods [13]. Examples of these can be found in the flow separation zone, [16,17] which allow for the estimated time series of effective thermal diffusivity, whose function is implemented in VFLUX2, which can be used as a reliability parameter of flux estimates.
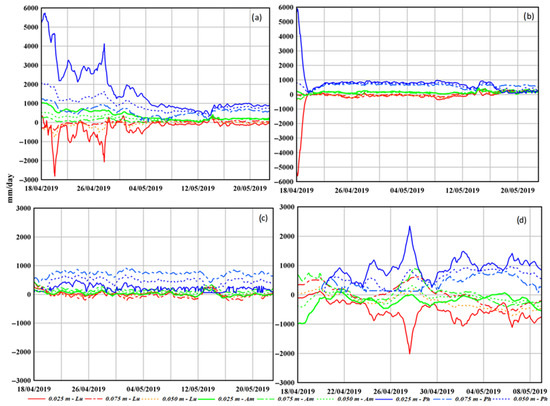
Figure 4.
Vertical flux results at the sediment–water interface: top left figure (a) represents 0419A, top right 0419C (b), down left 0419B (c), and downright 0419D (d). Lu, Am, and Ph are the Luce, amplitude, and phase method, respectively.
The study in [16] indicates that unreasonable variations in effective thermal diffusivity estimations lead to erroneous vertical flux assessments. Therefore, 0419A and 0419D demonstrated the largest out-of-range κe values, where temperature sensors were driven into two confluence locations and were subjected to typical hydrodynamic and topography influences where the water cycle between surface water interfaces were affected.
The probe located near the stagnation zone (0419B) instead demonstrated a close relation between the combined and amplitude methods (mean ± SD of 28.37 ± 73.97 mm/day, and mean ± SD of 23.95 ± 62.60 mm/day, respectively). However, the down-welling phase method results exhibited different means with a similar range (Mean ± SD of 233.98 ± 62.57 mm/day).
At the eastern riverbank, estimated fluxes based on top-pairs demonstrated a comparable trend and uncertainty flow direction (0419A and 0419D), which diminished within the western riverbank vicinity. This mainly refers to the vertical part of the exchange where it is well known that hyporheic magnitude and pattern vary on a three-dimensional scale [19]. Riverbed topography and the riverbanks’ vicinity are usually the responsible and main drivers of this effect [10,20]. However, the stream-wise velocity gradient visible at the eastern riverbank, which is typical of a flow separation zone, significantly impacted the hyporheic vertical flux pattern at 0419D and 0419A.
4.2.2. Sub and Extreme Sensor Pairs
The estimated hyporheic fluxes at the 0.075 and 0.05 m depths (grid distance of 5 and 10 cm, respectively) matched the overall well among all three methods, having relatively small variations. In fact, the fluxes at 0419A oscillated in a small range of down-welling values, especially considering the phase method. This observation suggested a great sensitivity at the first shallow sediments rather than in the deeper saturated sediment layers, which were enhanced by the water cycle of confluence hydrodynamics.
On the other hand, estimated vertical fluxes at 0419D demonstrated that neither the amplitude nor the phase method were in a small range of down-welling value variation in regard to 0419A, except for the combined one (mean ± SD of 23.33 ± 336.04 mm/day, and mean ± SD of −219.67 ± 243.77 mm/day, respectively). This latter result differs with regard to the couple of probes located in the middle and in the western region of the confluence, i.e., 0419C and 0419B, respectively.
Furthermore, temperature variations in 0419B were small (low flux velocity at the stagnation zone), demonstrating that the combined method is more reliable due to the removal of uncertainty in k0, which is not required as an input for the McCallum and Luce methods. Results showed that, on average, its approximation of calculated thermal diffusivity from the sediment sample was satisfactory (κe ≈ 6.0 × 10−7 m2/s). Further, this trend was visible on the sub and extreme pairs, as well. In fact, down-welling patterns were found [21] at the sub and extreme sensor pairs with a relative fair confidence as determined from the amplitude method calculations (Figure 5). The study in [13] demonstrated that it returns reliable results under transient flow conditions, as the shear layer may become induced due to helicoidal flow cells formation [22].
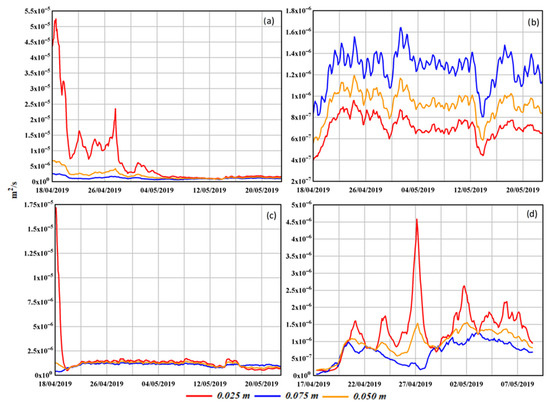
Figure 5.
Thermal diffusivity results at sediment–water interface: top left figure (a) represents 0419A, top right 0419C (b), down left 0419B (c), and down right 0419D (d).
At 0419C, down-welling fluxes were again predominant throughout the field campaign, matching with the shallowest sediment vertical fluxes’ estimation result. This probe was centered at the confluence and to the scour hole avalanche. It is known that downward vertical fluxes are mostly observed and the VFLUX2 results showed a clear pattern. Values from the amplitude and phase methods (0.05 depth) were within a narrow band even though they demonstrated contrary flux rates.
5. Conclusions
The hyporheic exchange was investigated at the Ninemile Creek river confluence in Marcellus (NY) in Spring 2019. Typical hydrodynamics, topographic, and stream bed characteristics were observed and visualized doing a field survey. The patterns and rates of the vertical flux exchange were analyzed, thereby sampling the temporal thermal profiles of the shallowest saturated sediments. Flux estimations were calculated using VFLUX 2, a MatLab-based code program, which performed data filtering and DHR. Based on the output values, downwelling patterns dominated the confluence area throughout the 34-day measurement dataset. The observed results suggested a clear connection with the common confluence morphological features, such as the scour hole, flow separation, and stagnation zone. The temperature amplitude method performed best among the other known analytical models (particularly at shallower depths) and in non-steady flow conditions. The greater distance between sensors was found to be sufficient at strong velocity gradient zones (shear layer) since they were subjected to fewer water cycle fluctuations at the surface water interface. Finally, saturated sediment thermal properties are sensitive to flux estimation and should be seriously taken into account when using a one-dimensional heat transport model.
Author Contributions
All the authors equally participated to this study. I.M. and T.A.E. conducted the field surveys while C.G. participated to the post-processing analysis. I.M., C.G., and T.A.E. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
This research was carried out during the “Civil System Engineering” PhD project of the first named author. He also shows his gratitude to SUNY for the hosting, support and instrumentation of this study. He gives his thanks to Guy Swenson for his assistance with all field campaigns. Collaboration with the staff of the Environmental Resources Engineering Department of the SUNY-ESF are also gratefully acknowledged. The second author acknowledges the financial support from the Exchange Program for Professors and Researchers of the University of Napoli Federico II in the year 2018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gualtieri, C.; Ianniruberto, M.; Filizola, N.; Santos, R.; Endreny, T. Hydraulic complexity at a large river confluence in the Amazon basin. Ecohydrology 2017, 10, e1863. [Google Scholar] [CrossRef]
- Best, J.L. Flow dynamics at river channel confluences: Implications for sediment transport and bed morphology. In Recent Developments in Fluvial Sedimentology; Society of Economic Palaeontologists and Mineralogists Special Publication: Tulsa, OK, USA, 1987; Volume 39. [Google Scholar]
- Martone, I.; Gualtieri, C.; Endreny, T.A. Characterization of Hyporheic Exchange Drivers and Patterns within a Low-Gradient, First-Order, River Confluence during Low and High Flow. Water 2020, 12, 649. [Google Scholar] [CrossRef]
- Movahedi, N.; Dehghani, A.A.; Schmidt, C.; Trauth, N.; Pasternack, G.B.; Stewardson, M.J.; Meftah Halghi, M. Hyporheic exchanges due to channel bed and width undulations. Adv. Water Resour. 2021, 149, 103857. [Google Scholar] [CrossRef]
- Endreny, T.A.; Lautz, L.K. Comment on ‘Munz M, Krause S, Tecklenburg, C., Binley, A. Reducing monitoring gaps at the aquifer–river interface by modelling groundwater–surfacewater exchange flow patterns’. Hydrol. Processes. 2012, 26, 1586–1588. [Google Scholar] [CrossRef]
- Knapp, J.L.A.; González-Pinzón, R.; Drummond, J.D.; Larsen, L.G.; Cirpka, O.A.; Harvey, J.W. Tracer-based characterization of hyporheic exchange and benthic biolayers in streams. Water Resour. Res. 2017, 53, 1575–1594. [Google Scholar] [CrossRef]
- Lee, C.; Kim, W.; Jeen, S.W. Measurement of Flux at Sediment–Water Interface Using a Seepage Meter under Controlled Flow Conditions. Water 2020, 12, 3071. [Google Scholar] [CrossRef]
- Song, J.; Zhang, G.; Wang, W.; Liu, Q.; Jiang, W.; Guo, W.; Tang, B.; Bai, H.; Dou, X. Variability in the vertical hyporheic water exchange affected by hydraulic conductivity and river morphology at a natural confluent meander bend. Hydrol. Processes 2017, 31, 3407–3420. [Google Scholar] [CrossRef]
- Byrne, P.; Zhang, H.; Ullah, S.; Binley, A.; Heathwaite, A.; Heppell, C.; Lansdown, K.; Trimmer, M. Diffusive equilibrium in thin films provides evidence of suppression of hyporheic exchange and large-scale nitrate transformation in a groundwater-fed river. Hydrol. Processes 2015, 29, 1385–1396. [Google Scholar] [CrossRef]
- Gariglio, F.P.; Tonina, D.; Luce, C.H. Spatiotemporal variability of hyporheic exchange through a pool-riffle-pool sequence. Water Resour. Res. 2013, 49, 7185–7204. [Google Scholar] [CrossRef]
- Chen, X. Measurement of streambed hydraulic conductivity and its anisotropy. Environ. Geol. 2000, 39, 1317–1324. [Google Scholar] [CrossRef]
- Lautz, L.K.; Kranes, N.T.; Siegel, D.I. Heat tracing of heterogeneous hyporheic exchange adjacent to in-stream geomorphic features. Hydrol. Processes 2010, 24, 3074–3086. [Google Scholar] [CrossRef]
- Irvine, D.J.; Lautz, L.K.; Briggs, M.A.; Gordon, R.P.; McKenzie, J.M. Experimental evaluation of the applicability of phase, amplitude, and combined methods to determine water flux and thermal diffusivity from temperature time series using VFLUX 2. J. Hydrol. 2015, 531, 728–737. [Google Scholar] [CrossRef]
- Hatch, C.E.; Fisher, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying surface water-groundwater interactions using time series analysis of streambed thermal records: Method development. Water Resour. Res. 2006, 42, W10410. [Google Scholar] [CrossRef]
- Keery, J.; Binley, A.; Crook, N.; Smith, J.W.N. Temporal and spatial variability of groundwater-surface water fluxes: Development and application of an analytical method using temperature time series. J. Hydrol. 2007, 336, 1–16. [Google Scholar] [CrossRef]
- McCallum, A.M.; Andersen, M.S.; Rau, G.C.; Acworth, R.I. A 1-D analytical method for estimating surface water–groundwater interactions and effective thermal diffusivity using temperature time series. Water Resour. Res. 2012, 48, W11532. [Google Scholar] [CrossRef]
- Luce, C.H.; Tonina, D.; Gariglio, F.; Applebee, R. Solutions for the diurnally forced advection-diffusion equation to estimate bulk fluid velocity and diffusivity in streambeds from temperature time series. Water Resour. Res. 2013, 49, 488–506. [Google Scholar] [CrossRef]
- Stallman, R.W. Steady one-dimensional fluid flow in a semi-infinite porous medium with sinusoidal surface temperature. J. Geophys. Res. 1965, 70, 2821–2827. [Google Scholar] [CrossRef]
- Tonina, D. Surface water and streambed sediment interaction: The hyporheic exchange. In Fluid Mechanics of the Environmental Interfaces; Taylor & Francis: Abingdon, UK, 2008; pp. 1–44. [Google Scholar]
- Song, J.; Jiang, W.; Xu, S.; Zhang, G.; Wang, L.; Wen, M.; Zhang, B.; Wang, Y.; Long, Y. Heterogeneity of hydraulic conductivity and Darcian flux in the submerged streambed and adjacent exposed stream bank of the Beiluo River, northwest China. Hydrogeol. J. 2016, 24, 2049–2062. [Google Scholar] [CrossRef]
- Cheng, D.; Song, J.; Wang, W.; Zhang, G. Influences of riverbed morphology on patterns and magnitudes of hyporheic water exchange within a natural river confluence. J. Hydrol. 2019, 574, 75–84. [Google Scholar] [CrossRef]
- Szupiany, R.N.; Amsler, M.L.; Parsons, D.R.; Best, J.L. Morphology, flow structure, and suspended bed sediment transport at two large braid-bar confluences. Water Resour. Res. 2009, 45, W05415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).