Abstract
Water distribution systems (WDSs) are considered inherently vulnerable to intentional and accidental contamination. The installation of a water quality sensor system (WQSS) represents a valid strategy for securing WDSs against contamination. This paper proposes a novel topological-based methodological approach for defining a suitable WQSS, by also addressing both the computational intractability of the problem as the size of the WDS increases and the assumption that sensors are wrongly modelled and positioned on WDS nodes, rather than along system pipes. The method is tested on the WDS of Parete (Italy) and the results demonstrate the significant detection efficiency of the defined WQSS.
1. Introduction
Water distribution systems (WDSs) represent critical infrastructure in cities and are considered inherently vulnerable to both intentional and accidental contamination due to their large size and large number of served users. In this regard, a widely used strategy for securing WDSs is represented by the installation of a water quality sensor system (WQSS) [] for quickly assessing water quality, enabling the early detection of potentially dangerous conditions and providing indications of contamination events []. To maximize the WQSS performance detection, water operators have to identify the most suitable locations where sensors can be placed by balancing technical and economic aspects [], also because, due to budget constraints, securing the entire network is not feasible in practice. Since 1991 [], researchers and practitioners have explored the optimal sensor placement problem in WDSs, and several methodologies have been proposed, even if there have not been any general optimality criteria found. In [], models and algorithms for solving the sensor placement problem were divided into two categories: (a) single-objective approaches [,,] and (b) multi-objective approaches [,,]. Extensive critical reviews of the topic can be found in [,]. Another issue related to the problem of the definition of an optimal WQSS layout is high computational costs, especially for large WDSs, due to the huge number of possible contamination scenarios and to the complexity of WDSs []. In this regard, continuous efforts have been made to develop ever more efficient numerical techniques and to increase the hydraulic modelling reliability in relation to the WQSS design []. Ref. [] maximized the demand coverage and the detection probability. Ref. [] discussed the impact of objective function selection on the optimal sensor placement problem. Ref. [] proposed a combined management strategy for monitoring WDSs based on water network sectorization and the installation of water quality sensors. Ref. [] proposed a topological approach that relied on the a priori clustering of the WDS and on the installation of water quality sensors at the topologically most central nodes of each cluster. Ref. [] proposed a multi-objective approach taking into account the risk levels of contamination events, while [] considered four contamination probability functions combined with a clustering-based post-processing method for a Pareto front analysis. Ref. [] adopted the Non-dominated Sorting Genetic Algorithm III (NSGA-III) algorithm and considered the effect of the contamination of important junctions in terms of social consequences. Finally, ref. [] developed a methodology to assess the cyber–physical attack resilience of WQSS.
The main novelty of this paper lies in that it considers, more realistically, the placement of sensors along pipes, rather than WDS nodes. In this regard, a novel method for defining the most suitable WQSS in a WDS is proposed by exploiting the algorithms of Complex Network Theory. The topologically most important pipes are defined on the graph of the WDS, and dummy nodes are inserted at their centre and considered as possible sensor locations for the optimization phase in which the detection likelihood is maximized. Economic and logistic site-specific conditions are further considered in order to identify the most efficient and effective monitoring system.
2. Materials and Methods
The methodology consists of four steps based on safety, logistic and economic criteria, and resulted in a tool for the decision-making process to choose the most suitable/appropriate WQSS layout.
(a) Topological step. The starting point of the method is modelling the WDS as an undirected, unweighted graph G = (V,E) [], where V is the set of n nodes (junctions, reservoirs and tanks) and E is the set of m links (pipes, valves and pumps). After that, the topologically most central links are defined through the edge betweenness bc(l) of a link l [], a centrality metric borrowed from complex network theory, which is defined as the sum of the ratios of the number σvi,vj(l) of shortest paths between pairs of nodes vi and vj that run through that link l and the total number σvi,vj of shortest paths connecting pairs of nodes vi and vj, as in Equation (1):
It can be used as a measure of the influence of a link over the information/water flow throughout the network. In this way, the search for the highest “edge betweenness” links will enable the topologically most central pipes to be identified, on which the following optimization step should be focused, reducing the solution space and, consequently, the computational burden of the entire process. After that, dummy nodes are inserted in the middle of the selected “major” pipes, making the proposed methodology closer to real-world applications, as sensors are installed along pipes and not at nodes. However, in this way, the computational simplicity of searching the optimal sensor locations in nodes is kept.
(b) Logistic step. Generally, the problem of water quality sensor placement is faced without considering practical aspects related to site-specific conditions and the spatial variability of logistic conditions, such as the accessibility of the area, as well as the presence of underground services, and all the locations are assumed to be equally good candidates for sensors [,]. In this regard, the analysis of a city map was performed to identify more/less desirable positions for placing sensors, and, consequently, the areas were classified as: (1) most-desirable locations (i.e., water company sites and public buildings); (2) least-desirable locations (i.e., highways, rivers and busy crossroads); and (3) neutral locations (those not belonging to the previous two classes). After this, the least desirable locations are eliminated from the suitable sensor locations, further reducing the solution space.
(c) Optimization step. The optimization run was carried out by using the Threat Ensemble Vulnerability Assessment and Sensor Placement Optimization Tool (TEVA-SPOT) [], and the Detection Likelihood Ps was used as an objective function:
where ds = 1 if contamination scenario s-th is detected, and ds = 0 otherwise; Ps represents the probability of detecting the contamination; and S is the total number of considered contamination scenarios. In particular, for the definition of S, all of the demand nodes and the reservoirs were, one-by-one, considered as potential locations for contaminant injection; the contamination starting time at the beginning of any of the 24 h of a day; 1 single value of the mass injection rate (100 gr/min); and 1 single value of the injection duration (60 min) (according to the procedure reported in []) for a total of S = 184 × 24 × 1 × 1 = 4416 contamination events. Ps is maximized so as to detect as many contamination scenarios as possible.
(d) Economic step. During the optimization step, 10 WQSS were defined with an increasing number of sensors (from 1 to 10 sensors). After that, a simple economic analysis was performed, and just the cost for buying the sensor Csens, or also for building the monitoring station (civil work cost Ccw), was attributed respectively to the most desirable and to the neutral locations. Consequently, the cost of a monitoring station is equal to:
The total cost Ctot of each WQSS is equal to the sum of the costs of all of the monitoring stations from which it is composed and the results are rearranged in terms of costs associated with the installation of sensors. Furthermore, a maximum available budget is assumed for selecting the most appropriate WQSS layout.
3. Results
The method was tested on the real WDS serving the city of Parete (Italy), with a population of around 11,000 inhabitants. The WDS of Parete had 182 demand nodes (with ground elevation between 53 m a.s.l. and 79 m a.s.l.), 282 pipes and 2 reservoirs with a fixed pressure head of 110 m a.s.l. In Figure 1, the map of the WDS serving the city of Parete is shown together with the location classification.
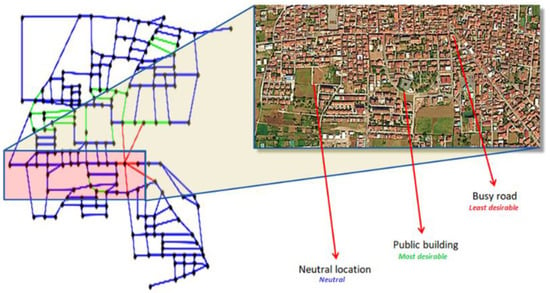
Figure 1.
Location classification: Most desirable (green); Least desirable (red); Neutral (blue).
The daily variation in the users’ demand was simulated through an hourly demand pattern, with multiplier values ranging from 0.2 to 3.1. The total demand at nodes ranged from 7.4 L/s at night to 113.9 L/s in the morning and midday peaks, with an average value of 54.6 L/s. The hydraulic and quality simulations were conducted using the hydraulic simulation software EPANET (EPANET 2, United States Environmental Protection Agency, Washington, DC, USA) [], assuming conservative contamination, a water quality time step of 5 min and a reporting time step of 5 min. The system was simulated for a total extended duration of 72 h, with a clock start time of 12 a.m.
Furthermore, preliminary financial analysis was carried out, assuming the cost of a multiple-parameter and continuous monitoring sensor to be Csens = 10,000 EUR and the civil work cost Ccw to be equal to the 30% of sensor costs Csens.
The simulation results are reported in Figure 2 in terms of cumulative benefit (%), which represents the increase in detection likelihood in comparison with the no-sensor scenario as a result of the installation of an increasing number of sensors (from 0 to 10).
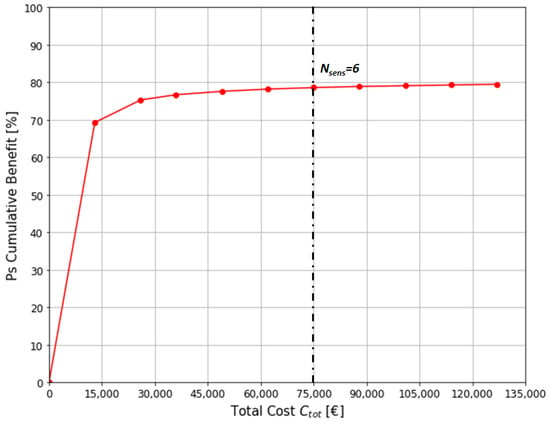
Figure 2.
Cumulative benefit of WQSS layouts as a function of the total cost Ctot.
Instead of the number of sensors, the x-axis reports the corresponding total cost Ctot of each WQSS, as defined above. It is evident that the additional benefit due to the installation of a further sensor, and consequently for an increasing total cost, progressively decreased.
This suggests the possibility to set a threshold of convenience for the choice of the most suitable number of sensors to install in the network, especially in the presence of budget constraints, according to the maximum available budget of the water utility, without the loss of generality; for this case study, it was assumed to be equal to 75,000 EUR (Figure 2).
Consequently, Nsens = 6 was chosen, and the corresponding WQSS layout was selected as the most feasible monitoring solution for the water system of Parete. The investment cost could be assumed acceptable for a medium-sized water utility, as the per-capita cost of this investment would correspond to roughly 7 EUR for each inhabitant. Furthermore, in Table 1, the performance of the selected solution is reported in terms of:

Table 1.
Quality performance for the selected solution (with a number of sensors Nsens = 6).
- -
- Detection likelihood (Ps), as defined in Equation (2);
- -
- Detection time (Tmean), which is the average, for all contamination events considered, of the time of the first contaminant detection;
- -
- Hit population (Pop), which is the average, for all the contamination events considered, of the number of contaminated people before the first detection.
The selected WQSS ensured a mean detection time Tmean of 214 min (with a reduction of 71.5% with respect to the no-sensor scenario), with a probability of detection Ps for the simulated contamination scenarios of 78.6% and a reduction in the hit population Pop of 84.4%.
The corresponding WQSS layout is superimposed on the map of the Parete WDS (coloured pipes according to the accessibility of the site) in Figure 3. The selected final solution yielded managerial and economic benefits and guaranteed an efficient monitoring and warning system.
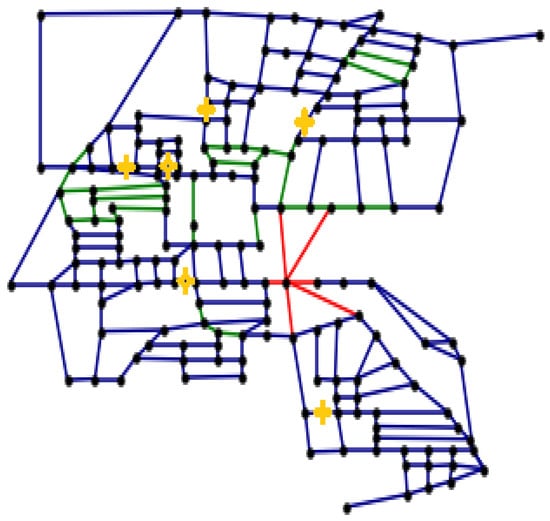
Figure 3.
Final selected solution of WQSS with Nsens = 6 (yellow stars) superimposed on a map of the Parete WDS with coloured pipes according to the accessibility of the site.
The major advantage of the proposed multi-criteria method, besides the progressive computational reduction due to the preliminary topological step (which allowed an almost 1/10,000 reduction of the solution space), is the possibility to select the most desirable solution for balancing the power of the heuristic tools (optimization step) with the opinion of experts (logistic and economic steps). Furthermore, the topological step allowed switching to a different perspective regarding the management and monitoring of water systems. Indeed, the problem of sensor placement was shifted from the nodes to the links (through the insertion of dummy nodes along the most central links), as, in reality, the devices are installed along pipes.
4. Conclusions
This paper proposes a multi-criteria methodology for the design of water quality sensor systems. The topological features of the water distribution system are exploited for the identification of the most central topological pipes and insertion of dummy nodes along them, leading to the reduction of the computational burden of the subsequent optimization step. A further reduction is also provided by disregarding, from the analysis, the areas characterized by low accessibility (least desirable locations). Subsequently, after the maximization of the detection likelihood as an objective function, logistic/economic criteria are included to definitively select the most desirable solution as a good compromise between economic/operational aspects and the aim of protecting populations.
Future work will investigate the possibility of including other urbanistic/logistic and managerial criteria, testing other objective functions and approaching the problem as multi-objective, and formalize an enriched decision-making tool that will also take into account the experts’ opinions for the selection of the optimal monitoring system.
Author Contributions
Conceptualization, C.G.; methodology, C.G.; validation, C.G. and R.G.; formal analysis, C.G.; data curation, C.G. and A.D.N.; writing—original draft preparation, C.G. and M.H.; writing—review and editing, C.G., A.D.N., E.C. and R.G.; visualization, C.G.; supervision, A.D.N., E.C. and R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data, models, and codes generated or used for this study are available from the corresponding author on request.
Acknowledgments
The research was conducted as part of the activities financed with the awarding of the V:ALERE:2019 project of the Università degli Studi della Campania ‘Luigi Vanvitelli’.
Conflicts of Interest
The authors declare no conflict of interest.
References
- AWWA. Contamination Warning Systems for Water: An Approach for Providing Actionable Information to Decision-Makers; AWWA: Denver, CO, USA, 2005. [Google Scholar]
- Janke, R.; Murray, R.; Uber, J.; Taxon, T. Comparison of Physical Sampling and Real-Time Monitoring Strategies for Designing a Contamination Warning System in a Drinking Water Distribution System. J. Water Resour. Plan. Manag. 2006, 132, 310–313. [Google Scholar] [CrossRef]
- Murray, R.; Baranowski, T.; Hart, W.E.; Janke, R. Risk Reduction and Sensor Network Design. In Water Distribution Systems Analysis; ASCE: Reston, VA, USA, 2008. [Google Scholar]
- Lee, B.H.; Deininger, R.A.; Clark, R.M. Locating monitoring stations in water distribution systems. J. Am. Water Works Assoc. 1991, 83, 60–66. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R.; Ormsbee, L. A review of sensor placement objective metrics for contamination detection in water distribution networks. Water Sci. Technol. Water Supply 2015, 15, 898–917. [Google Scholar] [CrossRef]
- Woo, H.M.; Yoon, J.H.; Choi, D.Y. Optimal monitoring sites based on water quality and quantity in water distribution systems. In Bridging the Gap: Meeting the World’s Water and Environmental Resources Challenges; ASCE: Orlando, FL, USA, 2001; pp. 1–9. [Google Scholar]
- Ostfeld, A.; Salomons, E. Securing water distribution systems using online contamination monitoring. J. Water Resour. Plan. Manag. 2005, 131, 402–405. [Google Scholar] [CrossRef]
- Berry, J.; Carr, R.D.; Hart, W.E.; Leung, V.J.; Phillips, C.A.; Watson, J.P. Designing contamination warning systems for municipal water networks using imperfect sensors. J. Water Resour. Plan. Manag. 2009, 135, 253–263. [Google Scholar] [CrossRef]
- Propato, M.; Piller, O. Battle of the water sensor networks. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Wu, Z.Y.; Walski, T. Multiobjective optimization of sensor placement in water distribution systems. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Dorini, G.; Jonkergouw, P.; Kapelan, Z.; Di Pierro, F.; Khu, S.T.; Savic, D. An efficient algorithm for sensor placement in water distribution systems. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–13. [Google Scholar]
- Hu, C.; Li, M.; Zeng, D.; Guo, S. A survey on sensor placement for contamination detection in water distribution systems. Wirel. Netw. 2018, 24, 647–661. [Google Scholar] [CrossRef]
- Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. A state-of-the-art review of an optimal sensor placement for contaminant warning system in a water distribution network. Urban Water J. 2019, 15, 985–1000. [Google Scholar] [CrossRef]
- Xu, X.; Lu, Y.; Huang, S.; Xiao, Y.; Wang, W. Incremental sensor placement optimization on water network. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Prague, Czech Republic, 23–27 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 467–482. [Google Scholar]
- Giudicianni, C.; Campisano, A.; Di Nardo, A.; Creaco, E. Pulsed demand modelling for the optimal placement of water quality sensors in water distribution networks. Water Resour. Res. 2022, 58, e2022WR033368. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Optimal sensor locations for contamination detection in pressure-deficient water distribution networks using genetic algorithm. Urban Water J. 2017, 14, 160–172. [Google Scholar] [CrossRef]
- Tinelli, S.; Creaco, E.; Ciaponi, C. Sampling significant contamination events for optimal sensor placement in water distribution systems. J. Water Resour. Plan. Manag. 2017, 143, 04017058. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing impacts of contamination in water distribution networks: A combined strategy based on network partitioning and installation of water quality sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Greco, R.; Creaco, E.; Scala, A. Topological placement of quality sensors in water-distribution networks without the recourse to hydraulic modeling. J. Water Resour. Plan. Manag. 2020, 146, 04020030. [Google Scholar] [CrossRef]
- He, G.; Zhang, T.; Zheng, F.; Zhang, Q. An efficient multi-objective optimization method for water quality sensor placement within water distribution systems considering contamination probability variations. Water Res. 2018, 143, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, S.M.; Barros, D.B.; Oliveira, E.; Brentan, B.; Ribeiro, L. Optimal sensor placement for contamination detection: A multi-objective and probabilistic approach. Environ. Model. Softw. 2020, 135, 104896. [Google Scholar] [CrossRef]
- Jafari, H.; Nazif, S.; Rajaee, T. A multi-objective optimization method based on NSGA-III for water quality sensor placement with the aim of reducing potential of important nodes contamination. Water Supply 2021, 22, 928–944. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Ostfeld, A.; Salomons, E.; Makropoulos, C. Resilience Assessment of Water Quality Sensor Designs under Cyber-Physical Attacks. Water 2021, 13, 647. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological taxonomy of water distribution networks. Water 2018, 10, 444. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Berry, J.; Hart, W.E.; Phillips, C.A.; Uber, J.G.; Walski, T.M. Water quality sensor placement in water networks with budget constraints. In Proceedings of the ASCE/EWRI (Environmental & Water Resources Institute) Conference, Anchorage, Alaska, 1 June 2005. [Google Scholar]
- Janke, R.; Murray, R.; Haxton, T.M.; Taxon, T.; Bahadur, R.; Samuels, W.; Uber, J. Threat Ensemble Vulnerability Assessment-Sensor Placement Optimization Tool (TEVA-SPOT) Graphical User Interface User’s Manual; US EPA National Homeland Security Research Center (NHSRC): Cincinnati, OH, USA, 2012; pp. 1–109.
- Rossman, L.A. EPANET2 Users Manual; EPA/600/R-00/057; US EPA: Washington, DC, USA, 2000.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).