Spatial Sensitivity of Navigation Using Signal-of-Opportunity (SoOP) from Starlink, Iridium-Next, GlobalStar, OneWeb, and Orbcomm Constellations ^†

Abstract

This paper presents a thorough investigation into the EKF-based SoOP navigation algorithm’s sensitivity to spatial parameters and receiver- and transmitter-related properties. Utilizing the innovative SoOPNE simulation platform, our study unveils significant insights. For instance, at high latitudes, Iridium-Next, and Oneweb show a ten-fold accuracy improvement over Orbcomm. Additionally, discrepancies between predicted and actual satellite trajectories, with a nominal drift of approximately 250 m, result in navigation errors of around 400 m. Our findings underscore the critical importance of addressing these factors to optimize SoOP navigation performance.

1. Introduction

The distinctive capabilities of the Global Navigation Satellite System (GNSS) for Positioning, Timing, and Navigation (PNT), along with their direct and indirect applications, constitute a fundamental component of numerous daily life services [1,2,3], industrial infrastructures [4,5], and military operations [6,7,8]. Their attributes, including nearly all-weather availability, precision, global coverage, and relatively high reliability, have propelled their market growth [9]. However, despite these advancements, GNSS-based services have not fully established their primary position in critical sectors such as aviation [10,11,12], where the reliability and interference-resistant characteristics of Inertial Navigation Systems consistently outperform GNSS-based PNT services [12,13,14]. Furthermore, GNSS satellites, constrained by limited resources, are unable to transmit more than a few tens of watts at allocated frequencies, resulting in weak signals in dense urban areas [15,16] and near-undetectable signals indoors [17,18]. Moreover, the open-source nature of GNSS services renders them susceptible to electronic warfare environments [16].

In recent years, significant advancements across various scientific domains, including the development of reusable launch systems [19,20] and efficient orbital thrusters [21], have ushered in a newfound role for low Earth orbit (LEO) in the communication satellite industry. Spacecraft operating in LEO can transmit more robust signals to receivers, offering reduced latency and increased bandwidth [22]. Among the pioneering LEO constellations providing positioning and timing services is Satelles, leveraging the Iridium-Next platform. Concurrently, substantial scientific endeavors have focused on justifying, conceptually designing, and delineating the characteristics and capabilities of a GNSS constellation in LEO, termed an LEO GNSS constellation [23,24].

A pivotal aspect of PNT services is their ability to remain accessible under any circumstances [25]. Historically, to mitigate service inadequacies and enhance reliability and accuracy, GNSS receivers were engineered to concurrently process navigation data received from multiple satellites or even different constellations [26]. While this strategy proves effective under normal conditions, it falters in electronic warfare environments, exposing a vulnerability. To address this vulnerability, researchers have proposed utilizing signals from alternative transmission sources. This initiative initially encompassed radio and television broadcast signals, later expanding to include signals from cellular networks [27,28,29,30]. However, terrestrial transmitters, not specifically intended for navigation purposes, operate at low altitudes, compromising their signal integrity for navigation. Moreover, many of these sources remain inaccessible in remote areas, with virtually none available for maritime applications. In contrast, satellites are meticulously designed to provide coverage over vast terrestrial expanses, or even global coverage in constellation configurations. Their signals operate within designated frequency bands, minimizing terrain-induced effects on signal reception. Although these signals were not originally intended for navigation, a tuned receiver can opportunistically capture them. While the conceptual groundwork for a navigation system utilizing Signals of Opportunity (SoOPs) from satellites emerged in the 1990s [31], the technological maturation of this field awaited approximately two decades to demonstrate its efficacy [32].

Previously, the majority of efforts in LEO-SoOP navigation (LEO-SoOP-Nav) have centered on the development of novel methods for data acquisition [33,34], estimation techniques [32,35], exploration of new navigational information carriers (i.e., [36]), and integration with Inertial Navigation Systems using an Inertial Measurement Unit [35]. However, certain critical factors have remained unexplored. Accordingly, the principal aim of this study is to examine the accuracy of an Extended Kalman Filter (EKF)-based LEO SoOP navigation model concerning various sources of errors, including the inherent errors of the Two-Line Element (TLE) [37,38], and spatial characteristics of the receiver. To achieve this goal, Section 2 will establish a set of assumptions and delineate Best-Case and Worst-Case Conditions to guide the design and development of the SoOP Navigation Engine (SoOPNE). The SoOPNE will serve as the simulation platform for evaluating the impact of multiple spatial parameters on navigation outcomes. Additionally, this section will outline the structure of the SoOPNE to elucidate the calculation methodologies. Subsequently, the following section will refine the simulation results into interpretable data by defining new parameters and aligning the acquired data for comparative analysis. Section 4 will present the primary novel findings of this paper, which delve into the spatial sensitivity of a representative SoOP-Nav algorithm, critical for satellite selection strategies. Finally, the paper will conclude with succinct summaries of the findings and suggestions for future development pathways.

2. Materials and Methods

2.1. Assumptions, BCCs, and WCCs

2.1.1. Dynamics of the Satellites

This paper will specifically examine satellite constellations in low Earth orbit, characterized by altitudes below 2000 km, with a maximum orbital period and eccentricity of 128 min and e = 0.25°, respectively [39]. Due to factors such as atmospheric drag, the non-uniform gravity of the Earth, the Earth’s oblateness effect on satellite altitude above the ground, and the high speed of space vehicles (SVs), the Simplified General Perturbations-4 (SGP-4) model, recognized as one of the most accurate Simplified Perturbations Models among five available, will be utilized to forecast SV dynamics [40]. Generally, the SGP-4 model necessitates two sets of parameters as input: time and orbital dynamic parameters. While the system can accept various types of sources as the time reference, such as Network Time Protocol (NTP) or Global Positioning System Pulse Per Second (GPS PPS) service, the SoOPNE maintains absolute time and is not sensitive to this error. Although this assumption does not compromise the generalizability of the study, temporal uncertainty presents a significant source of error in real-world SoOP-Nav applications. Two-Line Element (TLE) files encompass all required orbital dynamic parameters and typically exhibit an inherent error of 1 to 3 km at epoch [39]. Initially, this research assumes a TLE initial error of zero. Subsequently, a predefined deviation will be introduced to the output of the SGP-4 model to assess its impact on SoOPNE accuracy. Additionally, the SoOPNE will consistently utilize a valid and/or the latest version of the TLE file. Furthermore, considering the accumulative error of the SGP-4 model, which amounts to a few kilometers per day [38], the SoOPNE has been configured to initiate the processing of received navigational information carriers starting at t = t_s (where ts represents the Coordinated Universal Time of the receiver in its respective time zone) and continuing for a duration of Δt. Given the nonlinear increase rate of the SGP-4 accumulative error, Δt will be minimized to the greatest extent possible to render the effect of this error negligible.

2.1.2. Propagation Medium, Channel Properties, and Clock-Drift Consideration

The propagation medium has been presumed to be a uniform and homogeneous atmosphere of the Earth, with the propagation speed assumed to be v_p = 299,792,458 m/s. This assumption, representing a Best-Case Condition, guarantees the maximum possible transparency of the channel. Additionally, the channel is assumed to be a causal and time-invariant–linear medium, thereby allowing for the application of the superposition principle. Consequently, any desired equivalent value of additive white Gaussian noise can be incorporated at the input of the receiver. Also, to reduce the complexity of the simulation and to eliminate the effect of clock drift on overall simulation results, it has been assumed that the transmitters and receiver are equipped with well-disciplined clocks and the receiver has a priori knowledge of the transmitter clock drift, i.e., by using the 4th satellite from the same constellation. As this study considers the effect of the spatial sensitivity of navigation regarding the error of predicted satellite dynamics for different constellations, this assumption will not reduce the generality of the study.

2.2. SoOPNE Structure

SoOP navigation, in general, revolves around the processes of reception, processing, feature extraction, and utilization of acquired information for positioning, navigation, and timing. As previously outlined, the SoOP Navigation Engine (SoOPNE) primarily addresses the latter part of this sequence. Its focal point is to assess the characteristics, extract navigational features of the implemented algorithm(s), evaluate the effects of parameters and uncertainties, select suitable or desired satellite configurations, and so forth. To ensure compatibility for future development, the model has been devised using independent modules. The high-level schematic of the SoOPNE is depicted in Figure 1 and comprises the following components:

2.2.1. Initialization Data and Information Block

This block serves to prepare all necessary information for the remainder of the system. A GNSS receiver furnishes prior knowledge regarding the “Real” position of the receiver. The output of the GNSS receiver undergoes analysis via a “GNSS switch”, which verifies the validity of the received information. A configurable “TLE Download Manager” verifies the integrity of TLE files and retrieves them from available sources if necessary. The “Timing Source” module supplies the system with local, NTP, or GPS-based clock timing information. The “AWGN” block generates and normalizes additive white Gaussian noise, representing the overall noise of the channel and measurement system, with adjustable power to be incorporated into the extracted features, such as Doppler curves. As a special case, this block can assume SNR ≡ ∞ to calculate the best possible accuracy for a specific system configuration. The “Initial Seed-point” module furnishes the selected estimation algorithm with initialization conditions. Given our assumption that the receiver possesses prior knowledge of its position or, at least, the last estimated position (P_in), it is presumed that the “Initial Seed-point” block will utilize this information to select a starting point for the estimation algorithm. Therefore, in the absence of recursive mode activation, the SoOPNE employs a specific Pin for all rounds of calculations, yielding

$$P_{sp}^m=k{P}_{in};\begin{array}{ccc}& (k\in R^{+},m\in N& P_{in}\in R^3\end{array},c.t.e)$$

(1)

This module can be bypassed by the “Recursive Mode” module, which utilizes the last calculated navigation information, Pinm, as the initial seed-point for the subsequent round of calculations. Hence, to generalize Equation (1), we have

$$P_{sp}^{m+1}=\left\{\begin{array}{c}\mathrm{Recursive} \mathrm{Mode} \mathrm{off}:k{P}_{in}\begin{array}{ccc}& (k\in R^{+},m\in N& P_{in}\in R^3)\end{array}\\ \mathrm{Recursive} \mathrm{Mode} \mathrm{on}\text{:} \left\{\begin{array}{c}k{P}_{in};\begin{array}{ccc}& (k\in R^{+},m\in N& P_{in}\in R^3);\end{array}\begin{array}{cc} & m=1\end{array}\\ k{P}_{sp}^m;\begin{array}{ccc}& (k\in R^{+},m\in N& P_{sp}^m\in R^3);\end{array}\begin{array}{cc} & m>1\end{array}\end{array}\right.\end{array}\right.$$

(2)

The value of k signifies the distance of the initial seed-point from the actual position of the receiver in each round of calculation. Therefore, it directly influences the final accuracy of the estimation algorithm. While the SoOPNE is not confined to specific values of k, for k = 1, the initial seed-point will precisely match the output of the previous round of estimation. In the case of non-stationary receivers, where the estimated position of the receiver varies between rounds, k represents the estimated displacement of the receiver and takes the form of k_x, k_y, and k_z. The “Prediction Parameters” block governs overall simulation configuration settings, such as simulation duration or the frequency of the received SoOP signals.

2.2.2. Prediction Module

This module utilizes the TLE file, receiver position, and information from the “Prediction Parameters” module to compute the trajectory of the selected satellites. The requisite parameters for the SGP-4, SDP-4, and TBK models include time (t₀), first derivative of mean motion (Δ), second derivative of mean motion (Δ²), the drag term (p_r), inclination (i), right ascension of the ascending node (Ω), eccentricity (e), argument of perigee (ϖ), mean anomaly (θ_epoch), and mean motion (v). Thus, for the SGP-4 model, we have

$$SGP4(t_0,\Delta ,{\Delta }^2,p_r,i,\Omega ,e,\omega ,{\theta }_{epoch},v)=\left\{\begin{array}{c}{\left.p_{S{V}_p}{\left(p_{a_1},p_{a_2},p_{a_3}\right)}_{ECEF}\right|}_{t_0}\\ t_s<t_0<t_s+\Delta t\begin{array}{cccc}\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & \end{array}& & & \end{array}\\ {\left.v_{S{V}_p}\left(v_{S{V}_x},v_{S{V}_y},v_{S{V}_z}\right)\right|}_{t_0}\end{array}\right.$$

(3)

The output of the SGP-4 model is the Earth-Centered, Earth-Fixed position of the space vehicle. The “Orbital Predictor” block extracts the navigation features, such as Doppler shift, and adapts it to the requirements of the “Estimation block”. Assuming that SV_p is visible from the position of the receiver during Δt seconds starting from ts, then its position and velocity at any arbitrary point in time can be expressed as shown in (3). Therefore,

$${\left.l_{S{V}_p}\right|}_{t_0}={v_p}^{-1}{\left({\left({\left.p_{a_1}\right|}_{t_0}-p_1\right)}^2+{\left({\left.p_{a_2}\right|}_{t_0}-p_2\right)}^2+{\left({\left.p_{a_3}\right|}_{t_0}-p_3\right)}^2\right)}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$$

(4)

where l_SV represents the latency of the received signal, P_r(p₁, p₂, p₃) denotes the real position of the receiver. Additionally, the satellite-to-receiver line-of-sight vector can be calculated as

$${A_{LoS}|}_{t_0}={P_{S{V}_p}|}_{t_0}-P_r=({p_{a_1}|}_{t_0}-p_1,{p_{a_2}|}_{t_0}-p_2,{p_{a_3}|}_{t_0}-p_3)$$

(5)

By defining the General Vector Norm (P-Norm) as

$$‖A‖={\left({\displaystyle \sum _{a_i=1}^N{\left|A_{a_i}\right|}^p}\right)}^{p^{-1}};\begin{array}{cc}& N\in N\end{array};A_{a_i},p\in R;p\ne 0$$

(6)

the Doppler shift of the received SoOP signal can be calculated as

$$f_d=\left(v_p\left(v_p+\left({\left.A_{LoS}\right|}_{t_0}÷‖{\left.A_{LoS}\right|}_{t_0}‖\right).{\left.v_{S{V}_p}\right|}_{t_0}\right)f_t\right)-f_t$$

(7)

where f_t is the transmitted frequency of the SoOP. The “÷” sign represent the element-wise division operation. Also, “.” represents the dot product of vectors. Figure 2 represents the orbital trajectory of some SVs on 24 April 2024 for 45 min starting at 09:40:35 AM, Eastern Time Zone.

2.2.3. Estimation Block

The navigation information carriers necessitate an estimation algorithm to compute the navigation results. The overall process of the SoOPNE remains independent of the type of selected estimation algorithm(s). The chosen estimation algorithm for the SoOPNE is an Extended Kalman Filter (EKF)-based estimation algorithm. Theoretically, the SoOP receiver block can capture signals from n satellites simultaneously, ideally from different constellations. Each detected signal will be converted into a set of navigation features such as

$$X_{S{V}_n}\to \left\{l_{S{V}_n},A_{Lo{A}_{S{V}_n}},f_{d_{S{V}_n}},v_{S{V}_n}\right\}$$

(8)

Assuming the receiver has prior knowledge of the transmitters’ clock drift (see Section 2.1.2), the SoOP estimating algorithm can “theoretically” utilize all of the provided information as long as n ≥ 3. So, the initial seed-point of the estimation algorithm can be defined as

$$P_{S{P}_i}=\left\{\begin{array}{c}k{P}_{initial}\begin{array}{cc}& if i=1\end{array}\\ P_{E{S}_{i-1}}\begin{array}{cc}& if i\ne 1\end{array}\end{array}\right.$$

(9)

where P_ES is the estimated position from the last round of calculations. Additionally, the Covariance matrix, P_n×n, can be defined as

$$if diag:R^n\to R^{n\times n},P_{n\times n}=diag\left(\sum \right):\sum \in R_{>0}^n$$

(10)

and

$$R_{n\times n}=k_{Convergence}{I}_{n\times n}$$

(11)

where Σ controls the convergence speed of the estimation algorithm. The measured Doppler shift is independent of the predicted signal and contains distortions from the channel effects, receiver, and transmitter impairments. So, for the j^th set of X_SV,

$$V_{j_{1\times q}}={\left.f_{d_{S{V}_j}}\right|}_{predicted}-{\left.f_{d_{S{V}_j}}\right|}_{measured}$$

(12)

where q is the minimum available samples for the frequency domain for all the available SVs. Also,

$$H_{j_{1\times q}}=v_{S{V}_j}÷‖{\left.A_{Lo{S}_{S{V}_j}}\right|}_{t_0}‖-A_{LoS}\otimes \left({\displaystyle \frac{A_{Lo{S}_{S{V}_j}}.v_{S{V}_j}}{{‖{\left.A_{Lo{S}_{S{V}_j}}\right|}_{t_0}‖}^3}}\right)$$

(13)

So,

$$K=P\times H^{\prime }\times {\left(H\times P\times H^{\prime }+R\right)}^{-1}$$

(14)

And

$$if P_{E{S}_j}\to X_j, then X_{j+1}=X_j+K{V}_j^{\prime }$$

(15)

X_j+1 contains the latest estimated value of the position. To update the required parameters for the next round of estimation, we have

$$P_{i+1}=\left(I-K\times H\right)\times P_i$$

(16)

To highlight the impact of spatial parameters on the accuracy of the estimation method, the algorithm will utilize the minimum required number of available satellites, m = 3. As a Best-Case Condition, we assume that the algorithm will select 3 satellites with maximum access time. To show the basic performance of the SoOPNE, Figure 3 represents the positioning results using IridiumNext constellation signals for different values of SNR while the recursive mode is activated.

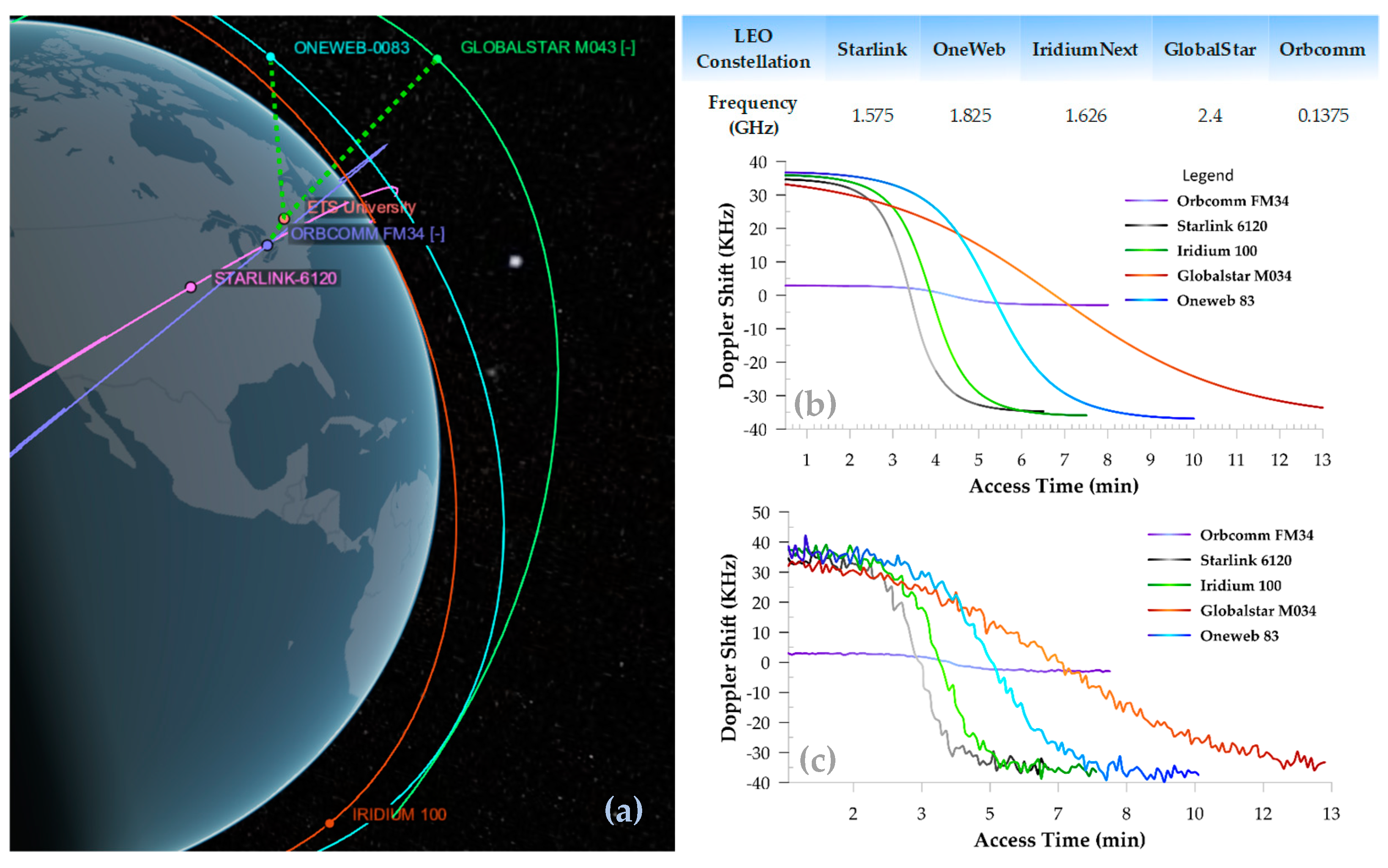
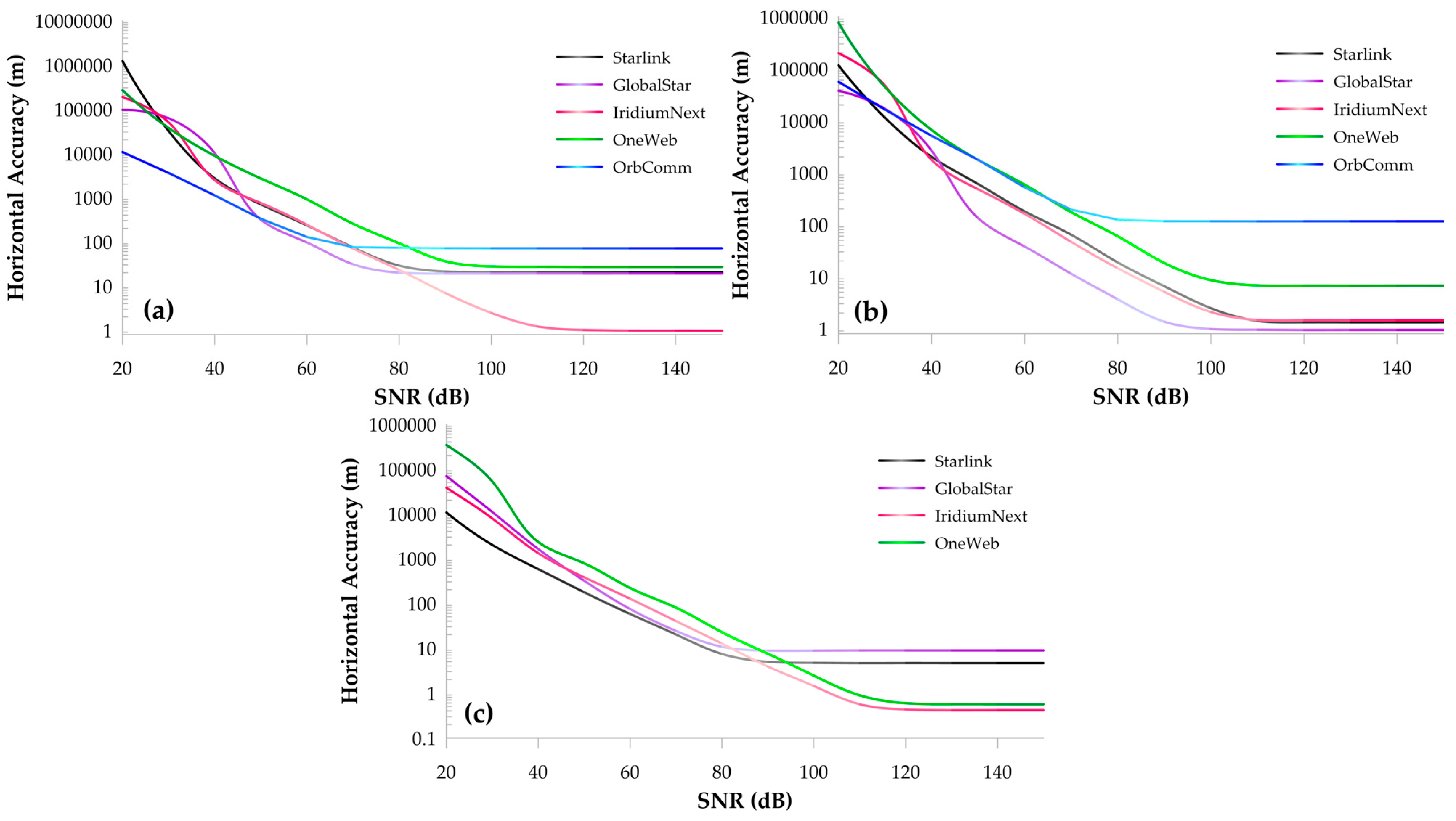
3. Simulation and Results

3.1. Effect of Different Latitudes

Using the latest TLE file for 24 April 2024 at 09:40:00 AM (EST), the simulation has been conducted for m = 3, at three different latitudes and for different SNRs. Figure 3 illustrates the horizontal accuracy of the proposed EKF-based SoOP positioning algorithm for five different LEO constellations. As observed, the Orbcomm constellation does not cover high latitudes, resulting in no satellite from this constellation being available at the selected position. Figure 4 represents the dependency of horizontal accuracy to receiver’s latitude.

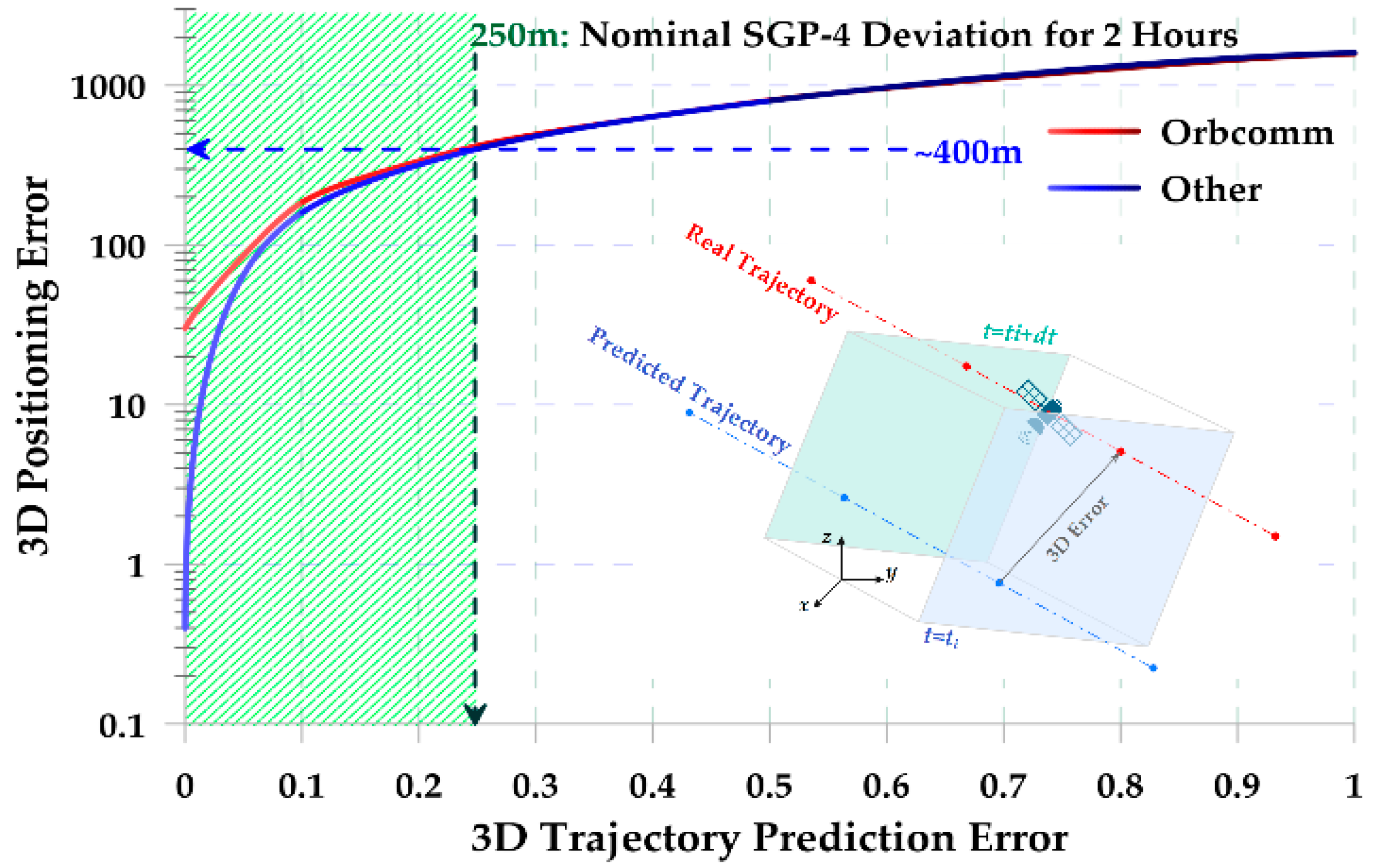
3.2. Inconsistency of the Real and Predicted SV Orbital Trajectory

The predicted position of the selected satellites is one of many input parameters of the estimation algorithm. As a physical system, the overall model should be causal. While the estimation algorithm does not possess explicit information about the real trajectory, as it is hidden in other measured parameters, the predicted trajectory should ideally align with it. The main sources of error in this predicted trajectory are the inherent TLE error at epoch, time-dependent errors of the SGP-4 model, and errors caused by the orbital correction maneuvers of the SVs. In this simulation, it is assumed that the TLE file does not have any error at epoch. Then, different values of error are added to the predicted orbital trajectory of the satellites. Additionally, to observe the effect of the error on positioning accuracy, it has been assumed that SNR ≡ ∞. The results are depicted in Figure 5.

4. Discussion

As SoOPs and their transmitters are not specifically designed for navigation purposes, uncertainties in their key features will inevitably affect the accuracy of navigation algorithms. Among these uncertainties, the effect of spatial parameters has not been thoroughly investigated in previous works. These parameters were categorized into receiver-related and transmitter-related categories, and each was simulated using SoOPNE. As shown in Section 3.1, the EKF-based SoOP algorithm exhibits different performances for different LEO constellations. In ideal conditions (very high SNRs) and at high latitudes, the accuracy is almost 10 times better for Iridium-Next and Oneweb. For reasonable SNRs (e.g., 60 dB), Starlink and GlobalStar yield more accurate results. At middle latitudes, Orbcomm delivers the worst accuracy, while Starlink and Iridium-Next exhibit nearly identical performance. Over the equator, the overall arrangement of expected accuracy differs, with GlobalStar showing the best performance and Oneweb having the lowest accuracy for reasonable SNRs. Comparing these results, it is evident that optimizing the accuracy of the SoOP algorithm requires a satellite selection block. Satellite selection should be based on, but not limited to, the approximate position of the receiver. Additionally, through extra simulations, it has been demonstrated that the algorithm is not sensitive to the receiver’s altitude. As described in Section 3.2, the trajectory of the satellite is another source of uncertainty in SoOP navigation. All three types of errors mentioned in Section 3.2 can be modeled by a drift between the predicted and real SV trajectories. Assuming that during the first 2 h after the publication of TLE, the rate of increase in the drift is linear, the final nominal value of the drift of the predicted trajectory is approximately 250 m. This drift can cause a navigation error of approximately 400 m, regardless of the selected constellation. Furthermore, it has been shown that the direction of the drift does not significantly affect the magnitude of the navigation error. Since the SGP-4 model utilizes TLE files to predict the future trajectory of the satellites, it does not have any information about the orbital correction maneuvers of the satellites after TLE file publication. Thus, the only way to address this problem is to employ multiple sets of satellites for positioning in parallel. This approach allows for the detection and discarding of erroneous satellite sets and facilitates adjustments in the satellite selection block.

5. Conclusions

While SoOP navigation methods have introduced a new trend in navigation technology, some of their properties have remained unexplored. This paper investigates the effect of spatial parameters, receiver-related and transmitter-related spatial properties, on the EKF-based SoOP algorithm using a simulation platform, the SoOPNE, with a typical EKF-based SoOP algorithm. The investigation of receiver-related spatial parameters reveals that the accuracy of the algorithm is not correlated with the receiver’s altitude, but it highly depends on its latitudes. Additionally, simulations for transmitter-related spatial parameters demonstrate that while the SGP-4 (when using a TLE file) is unable to predict the orbital correction maneuvers of the SVs, the difference between SGP-4 trajectory prediction and the SV’s real trajectory can lead to significant navigation errors. To address the first problem, a dynamic satellite selection block has been proposed to adapt the set of selected satellites based on some guidelines, including the receiver’s approximate position. Furthermore, parallel processing of multiple sets of satellites will enhance the robustness of the system against various threats, including the effects of unwanted errors in TLE files of a constellation or orbital correction maneuvers.