Abstract
For the unrelated parallel machine scheduling problem, an improved Spider Monkey Optimization algorithm incorporating a variable neighborhood search (VNS) mechanism (VNS-SMO) is proposed to minimize the makespan, total tardiness, and total energy consumption. The VNS-SMO incorporates six types of neighborhood searches based on the objective characteristics to strengthen the optimization performance of the algorithm. To verify the effectiveness and superiority of VNS-SMO, first, Taguchi experiments were used to determine the algorithm parameters, and then three instances of different scales were solved and compared with the traditional algorithms NSGA-II, PSO, and SMO. The experimental results indicate that VNS-SMO significantly outperforms the comparison algorithms on IGD, NR, and C-matrix metrics, fully demonstrating its comprehensive advantages in convergence, distribution, and diversity.
1. Introduction
The unrelated parallel machine scheduling problem (UPMSP) is one of the most widespread among the parallel machine scheduling problems [1]. UPMSP has a broad industrial background, with involvement in textiles, tobacco, and other manufacturing industries [2]. And UPMSP has been mathematically proved to be an NP-hard problem [3], which is difficult to solve due to its significant computational complexity. Early solution methods were dominated by exact solution methods and heuristic rules [4]. As the problem scale and the quantity of objective values increase, the computational complexity of exact solution methods grows exponentially. While heuristic rules are easy to implement, the solution quality is usually not high enough to generate near-optimal solutions. As a result, research has gradually shifted toward metaheuristic algorithms, such as the Artificial Bee Colony (ABC) algorithm, Particle Swarm Optimization (PSO), and other similar methods.
However, these algorithms often encounter certain limitations, especially when dealing with the complexities of multi-objective optimization and complex constraints. The inherent shortcomings of traditional metaheuristic methods make it difficult to meet the requirements for efficiency and solution quality. For example, PSO tends to perform poorly in terms of convergence, while ABC suffers from low search efficiency [5]. Aiming to address the defects of the basic algorithms, more and more studies are focusing on the innovation and optimization of the algorithms, and the use of neighborhood search, as an effective local optimization strategy, is gradually becoming more widespread. For example, to address the UPMSP considering preventive maintenance, Lei and He [6] proposed an adaptive Artificial Bee Colony (ABC) algorithm and designed a variable neighborhood search mechanism to enhance the exploitation ability of the algorithm. Qin et al. [7] proposed the Hybrid Discrete Gray Wolf Optimization Algorithm (HDMGWO) to address the premature convergence characteristics of the Gray Wolf Algorithm (GWO), which avoids premature convergence through the introduction of neighborhood search operations.
In view of this, this paper adopts a combination of the Spider Monkey Optimization (SMO) algorithm and VNS to solve the unrelated parallel machine scheduling problem. The SMO algorithm has stronger global search capability than other meta-heuristic algorithms due to its group collaboration mechanism characteristic, and the population fission–fusion concept within the SMO algorithm grants it a greater ability to surpass the local optimum [8]. By integrating neighborhood search, the algorithm’s local exploitation capability is enhanced, thereby improving the solution quality and search efficiency for complex problems.
2. Description of the Problem and Scheduling Model
2.1. Description and Optimization Analysis
Suppose that jobs need to be processed on unrelated parallel machines . The decision involves determining the processing sequence of the jobs and their assignment to the machines. The optimization objectives are to minimize the makespan (), total tardiness (), and total energy consumption (). According to the three-field notation [9], the problem is represented as , where denotes non-preemptive operations, is the makespan, is the total tardiness, and is the total energy consumption.
Due to its complex combinatorial optimization structure, multi-objective conflict characteristics and heterogeneous resource constraints, the multi-objective optimization problem of UPMSP results in the exponential growth of its solution space. Therefore, the optimization characteristics of the three objectives of the problem are analyzed to provide a reference basis for algorithm exploration and development and design. The following are the optimization characteristics of the three objective values:
- (1)
- For the objective , jobs should be assigned to the machines with the shortest possible processing times to reduce the makespan.
- (2)
- For the objective , jobs with shorter due dates should be prioritized to reduce total tardiness.
- (3)
- For the objective , jobs should preferably be assigned to machines with lower processing energy consumption.
2.2. Mixed-Integer Programming Model
This study makes the following assumptions: (1) all jobs arrive at time zero; (2) each machine handles one job at a time, and processing is continuous and non-interruptible; (3) the jobs have no weights.
To formulate the model, the relevant symbols and definitions used in the mixed-integer programming are listed in Table 1.

Table 1.
Symbols and variables for constructing the mixed-integer programming model.
The mixed-integer programming model constructed using the parameters and variables shown in Table 2 is as follows.

Table 2.
Mixed-integer programming model.
The objective functions are defined in Models (1)–Models (3). Constraint (4) establishes the definition of the makespan, while Constraint (5) determines the completion time for each job. Constraint (6) specifies the method for calculating total tardiness, and Constraint (7) defines the tardiness for each individual job. Constraint (8) provides the formula for computing total energy consumption. Constraints (9) and (10) specify that each job is assigned to one location on a machine, with no location being shared by multiple jobs. Constraints (11) and (12) describe the start and completion times for the first position. Constraints (13) and (14) define the start and completion times for the f-th position on machine . Finally, constraints (15) define the 0–1 decision variables.
3. Improved SMO Algorithm
To address the multi-objective optimization characteristics of the UPMSP, a Spider Monkey Optimization algorithm integrated with a variable neighborhood search mechanism (VNS-SMO) is proposed. The algorithm utilizes the distributed collaborative mechanism of the spider monkey algorithm (SMO) to achieve global search, and enhances the local exploitation through a variable neighborhood structure to improve the Pareto solution set. The flowchart of the VNS-SMO algorithm is shown in Figure 1.
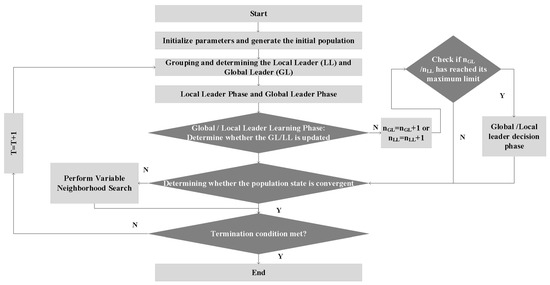
Figure 1.
Flowchart of VNS-SMO algorithm.
3.1. Initial Population Generation
First, a random job sequencing method is adopted, which shuffles the processing order of all jobs. This forms the first layer of the encoding, which is job sequencing encoding. Next, the sorted jobs are randomly assigned to different machines, ensuring that each machine receives at least one job. This constitutes the second layer of the encoding, which is machine assignment encoding. Finally, after the job sequencing and machine assignment are complete, decoding is performed based on the job sequence on each machine to generate a complete solution. The above process is repeated to create the initial population.
3.2. Local Leader and Global Leader Phases
Firstly, the population is split into subgroups. For each subgroup, the best solution based on Pareto dominance is identified, and one solution is chosen as the local leader . Subgroups’ individuals update their positions based on the . Similarly for the global leader , an individual is chosen as the global leader among the Pareto frontiers of the population. Individuals within the population rely on the information to update their individual positions. The flow of the local leader stage and global leader stage update methods is shown in Figure 2, where is the crossover rate and is the mutation rate.
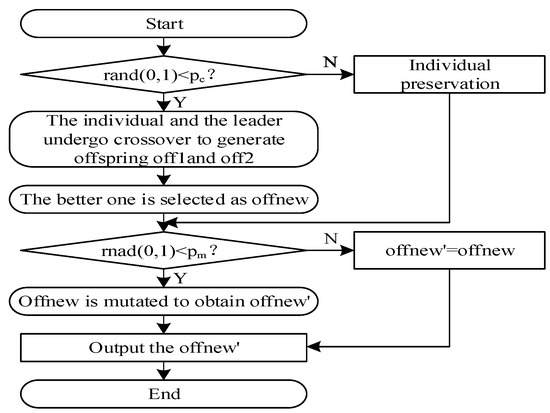
Figure 2.
Local/global leader stage flowchart.
3.3. Global and Local Leader Learning Phases
The learning phase is used to record the number of updates of the global leader and the local leader , and to detect whether the leader has fallen into a local optimum due to a long period of non-updating. For tracking the update count of the global leader , a global counter is used. If the is not updated, then the counter is incremented as ; otherwise, it is reset as .
Since the local leader is defined within the context of subgroups, a local counter is used to track the update status of each subgroup’s . If the fails to update, then the counter is incremented as ; otherwise, it is reset as . The maximum limit of the counter is set to five. If the maximum count is reached, the algorithm proceeds to the corresponding decision-making phase.
3.4. Local and Global Leader Decision Phases
Based on the count in the learning phase, if the local leader () reaches the maximum allowable limit, the algorithm enters the local leader decision phase. In this phase, an individual performs crossover with the global leader to update its position.
If the global leader reaches the maximum allowed number of updates, the algorithm enters the global leader decision phase. In this phase, the characteristics of the SMO algorithm—namely the concepts of fission and fusion—are introduced. After entering this phase, if the number of subgroups has not reached the maximum allowed number , then the number of subgroups is increased as . If has already reached the maximum , all subgroups are merged into a single group.
3.5. Variable Neighborhood Search Mechanism
After several phases of SMO operation, the VNS mechanism is introduced. Before entering the variable neighborhood search operation, the population state needs to be judged. If the population exhibits a convergence state, a larger step size of the cross-variable operation is needed to update the individual , and if the population shows a stagnation state, a smaller step size of the neighborhood operation is needed to better balance the efficiency and effectiveness of the algorithm. The distance CD between the non-dominated solutions and the approximate Pareto front is calculated to evaluate the population state.
Z represents the optimal Pareto front, and denotes the number of non-dominated solutions. is the threshold value. If , the state is considered converged; otherwise, it is regarded as stagnated.
According to the optimization characteristics of the objectives , and , six types of neighborhood structures are designed to optimize the three objectives. The specific operations are shown in the Table 3 below.

Table 3.
Neighborhood structures.
4. Experimental Design and Result Analysis
4.1. Experimental Design
To evaluate the performance of the VNS-SMO algorithm, the NSGA-II algorithm [10], the PSO algorithm [11], and the basic SMO algorithm [12] were used as comparison algorithms. The experimental data consist of the jobs , machines , processing times , processing energy consumption , and job due dates , where , and . The detailed experimental data are shown in Table 4.

Table 4.
Experimental parameters.
4.2. Parameter Tuning
Parameter tuning is performed for the VNS-SMO algorithm, including population size (popsize), maximum number of iterations (MaxT), crossover rate , and mutation rate .
Parameter tuning across different problem scales is conducted using the Taguchi method, with the settings summarized in Table 5.

Table 5.
Taguchi parameter tuning.
4.3. Computational Experiments and Discussion
NSGA-II, PSO, and SMO are selected as comparison algorithms, and each algorithm is independently executed 10 times on each problem instance. The Inverted Generational Distance (IGD), C-matrix, and Non-dominated Rate (NR) of the four algorithms are calculated. The experimental results are presented in Table 6.

Table 6.
Comparison of results from different algorithms.
The results demonstrate that the VNS-SMO algorithm outperforms NSGA-II, PSO, and the basic SMO algorithms in terms of overall performance across different scales.
In terms of IGD metrics, VNS-SMO maintains the lowest value among the scale instances, and in particular, the large-scale instances have an IGD value of 0, which is extremely convergent. The base SMO, on the other hand, is still inferior to VNS-SMO, although its IGD metrics are better than those of NSGA-II and PSO. This is due to the fact that VNS-SMO incorporates a neighborhood search mechanism and possesses a stronger ability to exploit and jump out of local optima. The NSGA-II and PSO algorithms show a significant increase in IGD metrics when the problem scale increases, indicating that they tend to fall into local optimality and converge poorly in large solution spaces.
Regarding the NR metrics, VNS-SMO achieves significant improvement at different scales, with a large-scale NR of 1. In contrast, NSGA-II and PSO have lower NR metrics (close to 0 at the medium scale and 0 at the large scale), indicating the significant advantage of VNS-SMO.
The C(A,*) metric (the average of Algorithm A and the C matrices of the other three algorithms) of VNS-SMO increases with size and basically covers the non-dominated solutions of the other algorithms. The base SMO, while superior to NSGA-II and PSO, is also significantly inferior to VNS-SMO.
In summary, the VNS-SMO algorithm exhibits excellent performance in a wide range of instance sizes, outperforming NSGA-II, PSO, and basic SMO in terms of convergence, diversity, and distribution. This benefit is attributed to the algorithm’s integration of a neighborhood search strategy, which enhances local exploitation and the ability to escape local optima, on top of the SMO’s multi-group collaboration and population fission–fusion mechanisms. In contrast, NSGA-II and PSO are prone to fall into local optimality when the solution space increases. And the base SMO lacks large-scale local fine search, and its overall performance is not as good as that of VNS-SMO.
5. Conclusions
A modified spider monkey algorithm (VNS-SMO) incorporating a variable neighborhood search mechanism is designed for the multi-objective scheduling problem of unrelated parallel machines. The algorithm introduces six types of neighborhood search operations for multi-objective optimization characteristics, based on having multiple group synergy and fission–fusion mechanisms. The experimental results show that the IGD, NR, and C-matrix metrics of the VNS-SMO significantly outperform those of the other comparison algorithms.
The base SMO algorithm is sub-optimal, indicating that the introduction of the neighborhood search mechanism enhances the local exploitation ability and helps the algorithm avoid being stuck in local optima within expansive solution spaces. In summary, the VNS-SMO algorithm shows strong global search ability and local optimization ability, especially in the case of increasing solution space, and exhibits excellent performance.
Future research can further improve the neighborhood search strategy and explore its application to other scheduling problems to further enhance the generality and applicability of the algorithm.
Author Contributions
Conceptualization, Z.J. and Y.C.; methodology, Z.J. and Y.C.; software, Z.J.; validation, Z.J. and Y.C.; formal analysis, L.P. and Y.C.; writing—review and editing, Z.J. and M.R.; visualization, Z.J.; supervision, M.R.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, Y.I.; Kim, H.J. Rescheduling of unrelated parallel machines with job-dependent setup times under forecasted machine breakdown. Int. J. Prod. Res. 2020, 59, 5236–5258. [Google Scholar] [CrossRef]
- Silva, C.; Magalhaes, J.M. Heuristic lot size scheduling on unrelated parallel machines with applications in the textile industry. Comput. Ind. Eng. 2006, 50, 76–89. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among combinatorial problems. In 50 Years of Integer Programming 1958–2008: From the Early Years to the State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2009; pp. 219–241. [Google Scholar]
- Arnaout, J.P.; Musa, R.; Rabadi, G. A two-stage Ant Colony optimization algorithm to minimize the makespan on unrelated parallel machines—Part II: Enhancements and experimentations. J. Intell. Manuf. 2014, 25, 43–53. [Google Scholar] [CrossRef]
- Nasiri, M.M. A modified ABC algorithm for the stage shop scheduling problem. Appl. Soft Comput. 2015, 28, 81–89. [Google Scholar] [CrossRef]
- Lei, D.; He, S. An adaptive artificial bee colony for unrelated parallel machine scheduling with additional resource and maintenance. Expert Syst. Appl. 2022, 205, 117577. [Google Scholar] [CrossRef]
- Qin, H.; Fan, P.; Tang, H.; Huang, P.; Fang, B.; Pan, S. An effective hybrid discrete grey wolf optimizer for the casting production scheduling problem with multi-objective and multi-constraint. Comput. Ind. Eng. 2019, 128, 458–476. [Google Scholar] [CrossRef]
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider monkey optimization algorithm for numerical optimization. Memetic Comput. 2014, 6, 31–47. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and Approximation in Deterministic Sequencing and Scheduling a Survey. Ann. Discrete Math. 1979, 5, 287–326. [Google Scholar]
- Wang, S.; Liu, M. Multi-objective optimization of parallel machine scheduling integrated with multi-resources preventive maintenance planning. J. Manuf. Syst. 2015, 37, 182–192. [Google Scholar] [CrossRef]
- Gao, J.; Tan, Y.; Li, D.; Zhang, J.; Wang, Y. Discrete Particle Swarm Optimization for Solving Unrelated Parallel Machine Scheduling Problem with Age-Based Maintenance; CIMS: Ahmedabad, India, 2023; pp. 1–18. [Google Scholar]
- Chen, Y.; Zhong, J.; Mumtaz, J.; Zhou, S.; Zhu, L. An improved spider monkey optimization algorithm for multi-objective planning and scheduling problems of PCB assembly line. Expert Syst. Appl. 2023, 229, 120600. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).