High-Fidelity Versus Reduced-Order Numerical Models for Sound Transmission Loss Prediction of Acoustic Metamaterials †
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background
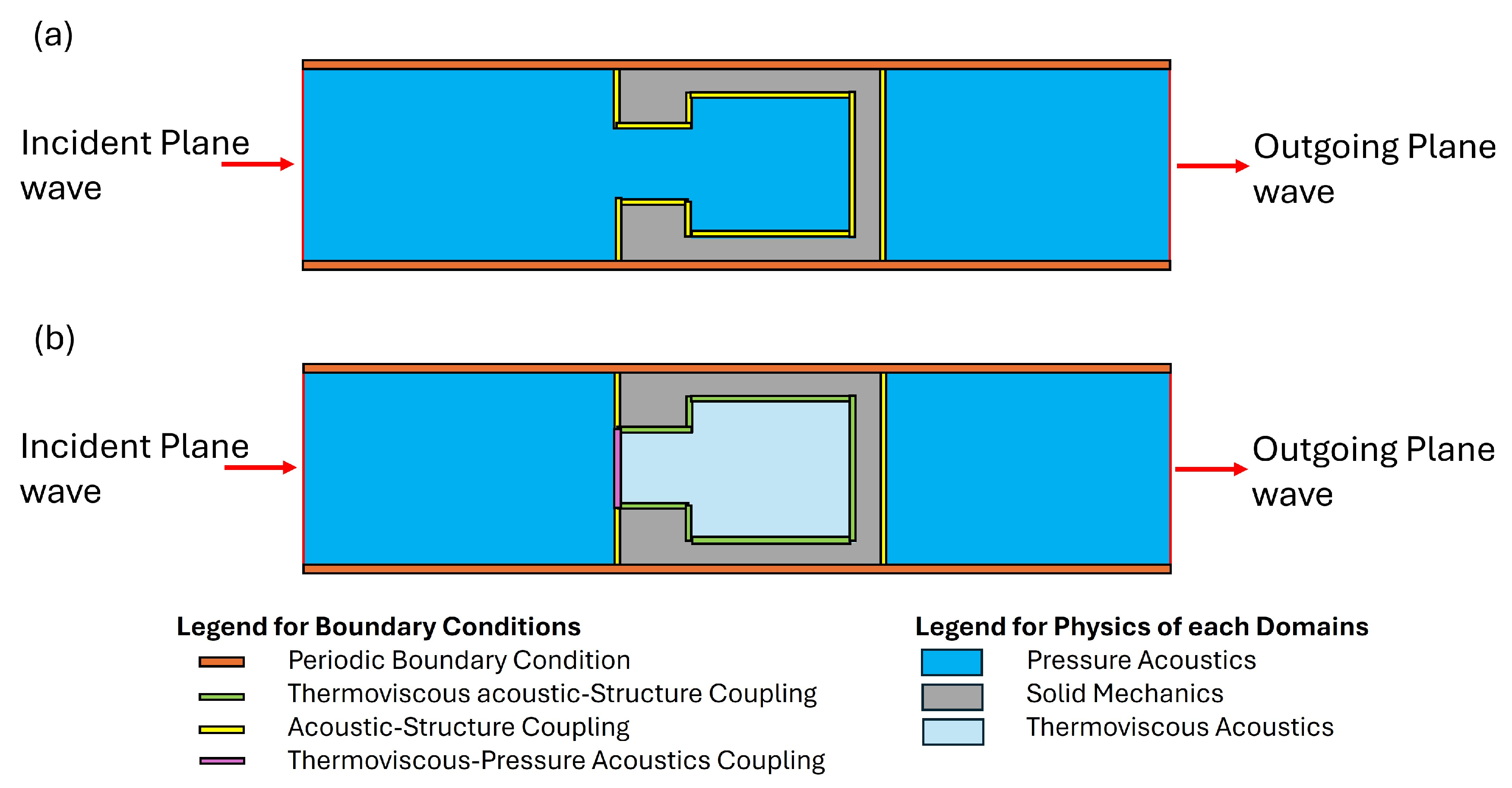
2.1.1. High-Fidelity Numerical Model (HFM)
2.1.2. Reduced-Order Numerical Model (ROM)
2.2. COMSOL Implementation
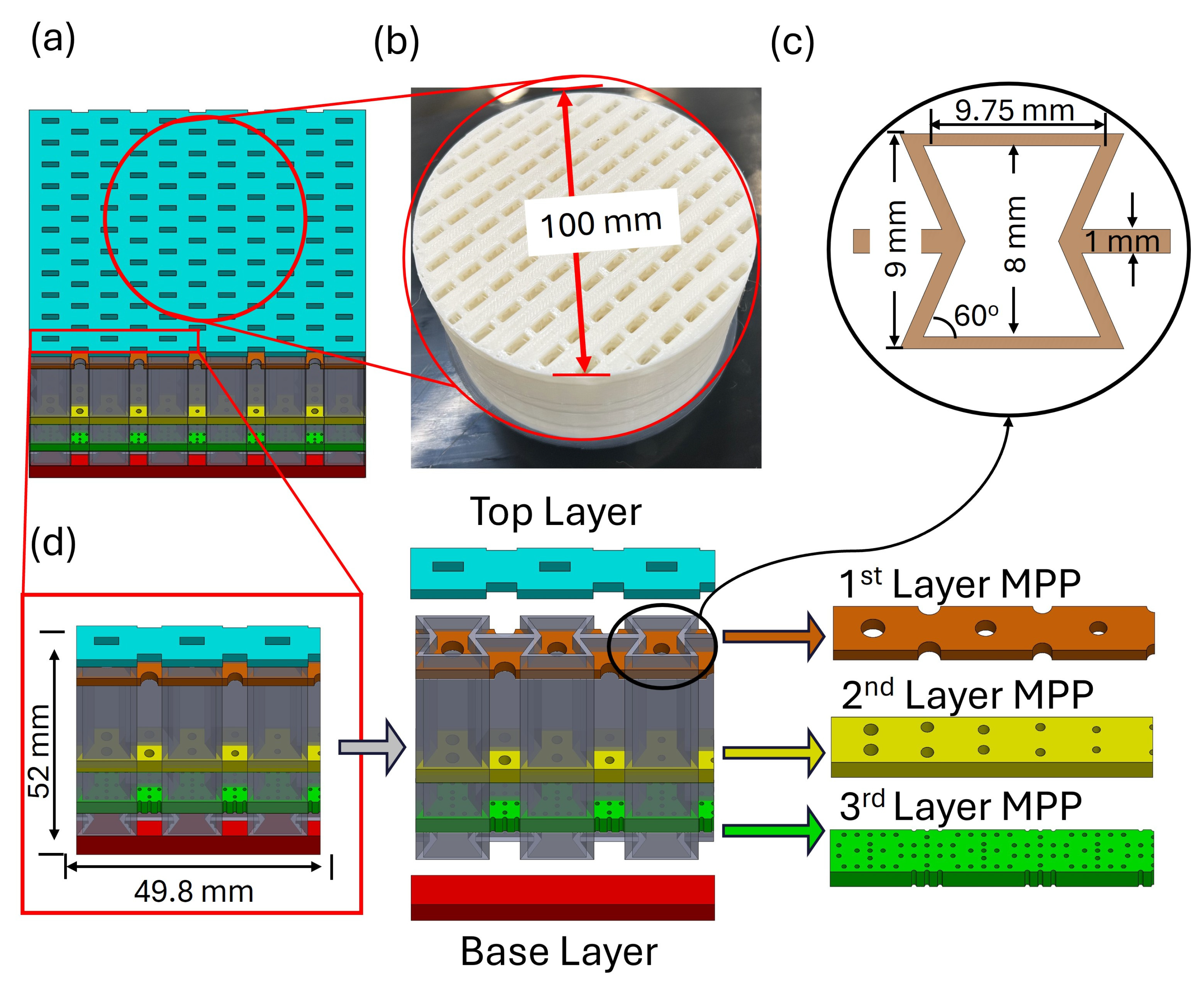
2.3. Modeling Framework
2.4. Experimental Framework
3. Case Studies
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alberti, G.; Portelli, D.; Galletti, C. Healthcare professionals and noise-generating tools: Challenging assumptions about hearing loss risk. Int. J. Environ. Res. Public Health 2023, 20, 6520. [Google Scholar] [CrossRef]
- Bengtsson, J. Low Frequency Noise During Work. Effects on Performance and Annoyance. Doctoral Thesis, Göteborgs universitet/University of Gothenburg, Göteborg, Sweden, 2003. [Google Scholar]
- Bisogno, A.; Scarpa, A.; Di Girolamo, S.; De Luca, P.; Cassandro, C.; Viola, P.; Ricciardiello, F.; Greco, A.; De Vincentiis, M.; Ralli, M. Hearing loss and cognitive impairment: Epidemiology, common pathophysiological findings, and treatment considerations. Life 2021, 11, 1102. [Google Scholar] [CrossRef] [PubMed]
- Fulton, S.E.; Lister, J.J.; Bush, A.L.H.; Edwards, J.D.; Andel, R. Mechanisms of the hearing–cognition relationship. Semin. Hear. 2015, 36, 140–149. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Heating, ventilation, and air conditioning (HVAC) noise detection in open-plan offices using recursive partitioning. Buildings 2018, 8, 169. [Google Scholar] [CrossRef]
- Waye, K.P. Effects of low frequency noise and vibrations: Environmental and occupational perspectives. In Encyclopedia of Environmental Health; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ciochon, A.; Kennedy, J.; Leiba, R.; Flanagan, L.; Culleton, M. The impact of surface roughness on an additively manufactured acoustic material: An experimental and numerical investigation. J. Sound Vib. 2023, 546, 117434. [Google Scholar] [CrossRef]
- Li, F.; Chen, Y.; Zhu, D. Revealing the Sound Transmission Loss Capacities of Sandwich Metamaterials with Re-Entrant Negative Poisson’s Ratio Configuration. Materials 2023, 16, 5928. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Chua, J.W.; Lim, C.H.; Yu, X.; Wang, Z.; Zhai, W. Architected lightweight, sound-absorbing, and mechanically efficient microlattice metamaterials by digital light processing 3D printing. Virtual Phys. Prototyp. 2023, 18, e2166851. [Google Scholar] [CrossRef]
- Lin, C.; Wen, G.; Yin, H.; Wang, Z.-P.; Liu, J.; Xie, Y.M. Revealing the sound insulation capacities of TPMS sandwich panels. J. Sound Vib. 2022, 540, 117303. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Z.; Li, Z.; Zeng, K. Design, manufacture, and characterisation of hierarchical metamaterials for simultaneous ultra-broadband sound-absorbing and superior mechanical performance. Virtual Phys. Prototyp. 2022, 18, e2111585. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Wu, Q.; Chen, H.; Chen, J.J.; Yu, Y.K.; Tracy, S.; Huang, G.L. A Fano-based acoustic metamaterial for ultra-broadband sound barriers. Proc. R. Soc. A 2021, 477, 20210024. [Google Scholar] [CrossRef]
- Costa-Baptista, J.; Fotsing, E.R.; Mardjono, J.; Therriault, D.; Ross, A. Design and fused filament fabrication of multilayered microchannels for subwavelength and broadband sound absorption. Addit. Manuf. 2022, 55, 102777. [Google Scholar] [CrossRef]
- Fan, J.; Song, B.; Zhang, L.; Wang, X.; Zhang, Z.; Wei, S.; Xiang, X.; Zhu, X.; Shi, Y. Structural design and additive manufacturing of multifunctional metamaterials with low-frequency sound absorption and load-bearing performances. Int. J. Mech. Sci. 2023, 238, 107848. [Google Scholar] [CrossRef]
- Fotsing, E.R.; Dubourg, A.; Ross, A.; Mardjono, J. Acoustic properties of periodic micro-structures obtained by additive manufacturing. Appl. Acoust. 2019, 148, 322–331. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, S.; Meng, H.; Xin, F.; Huang, L.; Chen, T.; Zhang, C.; Lu, T.J. Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound. Sci. Rep. 2017, 7, 43340. [Google Scholar]
- Chen, L.; Ji, H.; Tang, Y.; Wang, H.; Qiu, J. Enhancing sound absorption of Helmholtz resonators through microlattice metamaterials lining. Thin-Walled Struct. 2025, 215, 113465. [Google Scholar] [CrossRef]
- Song, Z.; Chen, W.; Jin, S.; Zhang, H.; Shan, F.; Qu, S. Low-frequency sound absorption enhancement in multi-layer honeycomb metamaterials with embedded long-curved-neck Helmholtz resonators. Appl. Acoust. 2025, 240, 110909. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Pang, Y. Effect of the size and pressure on the modified viscosity of water in microchannels. Acta Mech. Sin. 2015, 31, 45–52. [Google Scholar] [CrossRef]
- Kim, J.; Choi, E.; Jeon, W. Lightweight soundproofing meta-panel for separate wide frequency bands. Mech. Syst. Signal Process. 2023, 184, 109647. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Duan, Y.; Zhou, X. Broadband sound reduction in space-coiling ventilation structures with microperforated shells. Appl. Acoust. 2025, 235, 110676. [Google Scholar] [CrossRef]
- Yang, H.; Seong, W. Acoustic Transmission Loss of a Cylindrical Silencer Filled with Multilayer Poroelastic Materials Based on Mode-Matching Method. J. Mar. Sci. Eng. 2024, 12, 2109. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Acoustics Module User Guide, version 6.2. User’s Manual. COMSOL AB: Stockholm, Sweden, 2022.
- Naveed, A.B.; Mubashar, A.; Khan, M.K.A.; Munir, A.; Khan, K.A. Additively manufactured hybrid auxetic structures for enhanced low frequency acoustic performance through experiments and modelling. Sci. Rep. 2025, 15, 23460. [Google Scholar] [CrossRef] [PubMed]




| Feature | Pressure Acoustics | Thermoviscous Acoustics |
|---|---|---|
| Physics Basis | Linearized Euler equations (ideal fluid) | Linearized Navier–Stokes, continuity, energy equations (real fluid) |
| Governing Equation | Scalar Helmholtz equation | Coupled system equations (momentum, continuity, and energy) |
| Dependent Variables | p | p, u, T |
| Loss Mechanisms | No viscous or thermal losses. Approximated effective medium models for porous materials | Explicitly accounts for viscous and thermal dissipation throughout the fluid, particularly within boundary layers |
| Fluid Properties | ρ0, c0 | ρ0, μ, μB, k, Cp, α0, βT |
| Computational Cost | Low | High |
| Typical Use Cases | Cases where losses are dominated by solid material or geometric spreading | Cases where boundary layers are critical for accurate energy dissipation |
| Material Property | Value | Material Property | Value |
|---|---|---|---|
| Speed of Sound in Air | 343 m/s | Density of Polymer | 1250 kg/m3 |
| Density of Air | 1.25 kg/m3 | Poisson’s Ratio | 0.3 |
| Elastic Modulus of Polymer | 1.146 GPa |
| Parameter | Setting | Parameter | Setting | Parameter | Setting |
|---|---|---|---|---|---|
| Nozzle Diameter | 0.4 mm | Chamber Temperature | 50 °C | Nozzle Temperature | 230 °C |
| Layer Height | 0.2 mm | Print Speed | 50 mm/s | Retraction Length | 2 mm |
| Infill Density | 100% | Retraction Speed | 40 mm/s | Bed Temperature | 60 °C |
| Sample | Elements | DoF | Time | |||||
|---|---|---|---|---|---|---|---|---|
| HFM | ROM | HFM | ROM | Reduction | HFM (s) | ROM (s) | Reduction | |
| 1 | 122,817 | 122,201 | 816,699 | 488,550 | 40% | 4774 | 1320 | 72% |
| 2 | 499,395 | 514,373 | 2,996,756 | 1,860,513 | 38% | 21,073 | 3761 | 82% |
| 3 | 541,306 | 551,015 | 3,248,671 | 1,982,152 | 39% | 23,206 | 3402 | 85% |
| 4 | 146,185 | 145,692 | 949,727 | 532,078 | 44% | 4933 | 930 | 81% |
| 5 | 549,646 | 549,638 | 3,265,383 | 2,018,754 | 38% | 25,414 | 3389 | 87% |
| 6 | 546,423 | 546,501 | 3,246,763 | 2,006,352 | 38% | 25,332 | 3330 | 87% |
| 7 | 601,235 | 609,021 | 3,593,199 | 2,207,896 | 39% | 25,531 | 4138 | 84% |
| 8 | 583,236 | 583,749 | 3,481,190 | 2,144,067 | 38% | 24,394 | 3606 | 85% |
| 9 | 519,537 | 519,813 | 3,150,826 | 1,913,664 | 39% | 20,274 | 3304 | 84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naveed, A.B.; Mubashar, A.; Khan, M.K.A.; Tariq, A.; Khan, K.A. High-Fidelity Versus Reduced-Order Numerical Models for Sound Transmission Loss Prediction of Acoustic Metamaterials. Eng. Proc. 2025, 111, 17. https://doi.org/10.3390/engproc2025111017
Naveed AB, Mubashar A, Khan MKA, Tariq A, Khan KA. High-Fidelity Versus Reduced-Order Numerical Models for Sound Transmission Loss Prediction of Acoustic Metamaterials. Engineering Proceedings. 2025; 111(1):17. https://doi.org/10.3390/engproc2025111017
Chicago/Turabian StyleNaveed, Ali Bin, Aamir Mubashar, Muhammad Khizer Ali Khan, Ammar Tariq, and Kamran A. Khan. 2025. "High-Fidelity Versus Reduced-Order Numerical Models for Sound Transmission Loss Prediction of Acoustic Metamaterials" Engineering Proceedings 111, no. 1: 17. https://doi.org/10.3390/engproc2025111017
APA StyleNaveed, A. B., Mubashar, A., Khan, M. K. A., Tariq, A., & Khan, K. A. (2025). High-Fidelity Versus Reduced-Order Numerical Models for Sound Transmission Loss Prediction of Acoustic Metamaterials. Engineering Proceedings, 111(1), 17. https://doi.org/10.3390/engproc2025111017






