Next Article in Journal
Hybrid Optimization of Hardfacing Conditions and the Content of Exothermic Additions in the Core Filler During the Flux-Cored Arc Welding Process
Previous Article in Journal
High-Frequency Induction Drive Analysis for Common Mode and Differential Mode Impedance Characteristics
Previous Article in Special Issue
Engineering Parameter Design for CO2 Geological Storage: Research Progress and Case Analyses
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Eng
Volume 7
Issue 1
10.3390/eng7010024
eng-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Underground Hydrogen Storage in Saline Aquifers: A Simulation Case Study in the Midwest United States

by
Emmanuel Appiah Kubi
1,*,
Hamid Rahnema
1,
Abdul-Muaizz Koray
1 and
Babak Shabani
2
1
Department of Petroleum Engineering, New Mexico Institute of Mining and Technology, Socorro, NM 87801, USA
2
INTERA Incorporated, 101 W Kirkwood Avenue, Suite 316, Bloomington, IN 47404, USA
*
Author to whom correspondence should be addressed.
Eng 2026, 7(1), 24; https://doi.org/10.3390/eng7010024
Submission received: 18 November 2025 / Revised: 14 December 2025 / Accepted: 24 December 2025 / Published: 3 January 2026
(This article belongs to the Special Issue Geological Storage and Engineering Application of Gases)
Browse Figures
Versions Notes

Abstract

Underground hydrogen storage (UHS) in saline aquifers offers a viable alternative to surface-based storage systems, which are limited by capacity constraints, high operational pressures, complex thermal regulation, low energy densities, and potential safety hazards. This study uses a fully compositional reservoir simulation model to evaluate hydrogen behavior in the Mt. Simon Sandstone in the Illinois Basin. The analysis focuses on the effects of hysteresis, solubility, diffusivity, and production well perforation location on recovery efficiency. Cyclic injection and withdrawal scenarios were simulated to assess storage performance and operational strategies. The results show that accounting for hydrogen diffusivity shows essentially unchanged withdrawal efficiency at 79%, the same as the base case. Solubility causes a slight decrease to 78%, while hysteresis leads to a more significant reduction to 63%. The location of injection well perforations also influences recovery: top-perforated wells increase efficiency from 60% after the first cycle to 74% after six cycles, whereas bottom-perforated injection wells increase efficiency from 56% to 79% over the same period. These findings emphasize the importance of accounting for multiphase flow dynamics and strategic well placement in optimizing UHS system performance. The insights contribute to advancing reliable, large-scale hydrogen storage solutions essential for supporting renewable energy integration and long-term energy security.

1. Introduction

The urgent need to decarbonize the energy sector is catalyzing a fundamental transformation of global energy systems. Achieving international climate targets, such as limiting global warming to 1.5–2 °C, necessitates dramatic reductions in CO2 emissions [1,2]. Energy-related activities, which remain dependent on fossil fuels for approximately 80–85% of their supply, are the predominant source of greenhouse gas emissions [3,4]. In response, governments and industries worldwide are intensifying efforts to deploy renewable energy and advance green technologies. Current projections indicate that total energy demand will increase substantially in the coming decades, with over 80% of this demand still met by oil, gas, and coal. Therefore, meeting net-zero carbon objectives fundamentally depends on replacing these fossil fuels with low-carbon alternatives [5,6]. Transitioning from non-renewable to renewable energy sources is essential for achieving net-zero emissions and addressing climate change [7,8,9]. The magnitude of this challenge is immense: even with ambitious efficiency improvements and grid decarbonization, it is necessary to transition not only electricity generation, but also heating, industry, and transportation away from fossil fuels [10,11,12,13,14,15,16,17,18].
The inherent intermittency of wind and solar generation highlights the critical need for large-scale, long-duration energy storage solutions. In power systems with high levels of renewable energy penetration, periodic surpluses of electricity, whether daily or seasonal, are inevitable when supply outpaces demand. Converting excess renewable electricity into hydrogen via electrolysis has emerged as a leading approach to capturing and storing renewable energy for later use [19]. Hydrogen possesses several compelling attributes as a clean energy carrier. When produced through water electrolysis powered by renewable sources, green hydrogen emits no CO2 at the point of use [20,21,22]. Its gravimetric energy content (120 MJ·kg−1) is approximately three times greater than that of gasoline (44 MJ·kg−1) and more than twice that of methane (50 MJ·kg−1), making hydrogen exceptionally energy dense by weight [23,24]. However, its volumetric energy density at ambient conditions is very low, on the order of 0.010–0.011 MJ·L−1, roughly three orders of magnitude lower than liquid fuels, which necessitates compression or liquefaction for practical storage and transport [25,26,27]. Hydrogen is also a highly versatile energy vector. It can power vehicles via fuel cells, serve as a key feedstock for ammonia and other chemicals and fertilizers, and provide heat or electricity in industrial and power-sector applications, while fuel cells emit only water vapor at the point of use [28,29,30].
Despite the promise of hydrogen as an energy carrier, storing it effectively, particularly over seasonal or multi-month periods, remains a significant challenge [31,32]. Above-ground storage solutions, such as compressed gas tanks or liquid hydrogen cryotanks, are difficult to scale to the massive volumes required for balancing seasonal energy fluctuations and are associated with substantial manufacturing complexity, boil-off losses, and safety concerns at large scale [32,33,34]. Similarly, conventional mechanical storage technologies like pumped hydro and compressed air energy storage are constrained by specific geographic requirements and generally offer lower energy densities than chemical carriers such as hydrogen [35]. As a result, UHS in geological formations has emerged as a highly attractive alternative for long-duration, large-scale energy storage. Geological storage systems, including deep saline aquifers, depleted gas reservoirs, and salt caverns, can in principle provide multi-TWh storage capacities, several orders of magnitude larger than typical surface tank farms, making them suitable for seasonal balancing [36,37,38]. Moreover, subsurface storage mitigates safety and land-use issues, since hydrogen is confined at depth away from the surface environment, and techno-economic assessments consistently indicate that underground storage can achieve lower levelized storage costs per kilogram than large above-ground tank systems at comparable scales [39,40].
UHS leverages the extensive experience gained from natural gas or CO2 storage, utilizing porous rock formations sealed by low-permeability caprocks to securely trap gas [19,41]. However, hydrogen storage in geological formations introduces a distinct set of physical and chemical challenges. Hydrogen’s extremely low molecular weight results in high buoyancy and rapid diffusion compared to heavier gases [42]. Laboratory studies indicate that hydrogen diffuses through typical reservoir rocks significantly faster than methane [43]. While this high diffusivity and buoyancy facilitate rapid withdrawal from reservoirs, they also elevate the risks of leakage. Hydrogen molecules are sufficiently small to escape through microscopic pore networks or minor breaks in seals if containment is not robust [19]. Additionally, hydrogen can contribute to material degradation, such as embrittlement of certain steels and cements used in well infrastructure, necessitating careful material selection and engineering controls. Hydrogen’s low density of approximately 0.09 kg/m3 at standard temperature and pressure, compared to 0.7 kg/m3 for natural gas, means that a given mass occupies a much larger volume, thus reducing storage capacity unless high pressures or cryogenic conditions are employed [44,45]. In summary, the reactivity, diffusivity, and unique storage requirements of hydrogen present challenges distinct from those associated with natural gas or CO2. Overall, the reactivity, high mobility, and unique thermophysical properties of hydrogen lead to storage behavior that differs from that of natural gas or CO2, and the successful design of large-scale storage projects requires detailed knowledge of reservoir and caprock properties, multiphase flow and diffusion processes, and their temperature dependence [43].
Refs. [19,41,46,47,48] understanding the behavior of hydrogen within the subsurface formation is crucial for effective underground storage design [49,50]. This involves thoroughly examining the vertical and horizontal migration patterns of the hydrogen plume [51,52]. The plume spread within reservoirs and aquifers significantly influences the design and operational strategies for injection and production scenarios [53]. Other subsurface gases and potential chemical reactions also play a crucial role in the plume’s behavior [54,55]. Due to its small molecular size, hydrogen’s migration rate is notably faster than methane or CO2, highlighting the need for robust monitoring and modeling strategies to accurately predict and manage its migration post-injection [56,57,58,59,60]. Studies have proposed stability analysis criteria and methods specific to underground storage, highlighting the need for tailored approaches to assess the stability of different types of geological storage structures [61,62,63,64].
Given hydrogen’s distinct behavior, comprehensive reservoir modeling is essential. Key factors to include are hydrogen diffusivity, solubility, relative permeability hysteresis, and interactions with brine and minerals. Recent research has incorporated two-phase compositional flow models (hydrogen-brine systems with interphase mass transfer) to simulate injection and withdrawal cycles [48,55,65]. These studies highlight that hydrogen’s low solubility tends to limit losses to dissolution, but its high buoyancy can cause vertical channeling and gravity override if not mitigated by appropriate well placement and pressure management. Moreover, the extremely low molecular weight of hydrogen necessitates careful handling of diffusion: simulations show that while molecular diffusion typically broadens the plume only slightly, on the order of a few percent in areal extent, its influence becomes more important over long storage times or in low-permeability formations [48,65,66]. In summary, the subsurface approach to hydrogen storage offers a technically compelling solution to the challenge of long-duration energy storage, but it requires integrating fluid properties like density, viscosity, diffusion, solubility, and rock parameters into unified modeling and design workflows that ensure containment, recovery, and cost-effectiveness.
Recent UHS simulation work has progressed well beyond “single-gas in a single aquifer” cases by using compositional and equation-of-state based reservoir models to quantify cyclic inject-withdraw performance across multiple storage media and to explicitly evaluate cushion-gas choices (methane, nitrogen, CO2) through their effects on pressure support, well deliverability, and produced-gas quality via mixing-zone evolution and mass transfer [67,68,69,70]. In depleted reservoirs, recent studies have emphasized how cushion-gas selection and reservoir properties control the recovery–purity tradeoff, including systematic sensitivity analyses of hydrogen mixing with cushion in porous media [71,72]. Building on this body of simulation evidence, the present study advances the aquifer-focused state of the art by applying a formation-scale model to evaluate relative-permeability hysteresis, hydrogen solubility, molecular diffusion, and withdrawal perforation-depth influence on cyclic withdrawal efficiency and plume evolution in the Mt. Simon Sandstone (Illinois Basin).
In this paper, we address a critical gap in understanding UHS in saline aquifers by conducting numerical reservoir simulations using a formation-scale model of the Mt. Simon Sandstone in the Illinois Basin. This formation has favorable porosity/permeability for UHS, but its usage is not fully characterized. We construct a fully compositional two-phase (Hydrogen-brine) simulation model that integrates hydrogen solubility, diffusion, and relative-permeability hysteresis. We then simulate injection and withdrawal cycles to evaluate how these mechanisms affect hydrogen withdrawal efficiencies. Also, we compare scenarios where the injection well is perforated at the same depth as the production well versus when located well below the production well, to see how buoyant plume dynamics and pressure support affect withdrawal efficiency. We also performed a hydrogen plume migration and saturation evolution. Our goals are to quantify hydrogen recovery efficiencies in view of these trapping mechanisms, assess the risk of gas escape, and elucidate how hydrogen’s unique properties influence aquifer storage performance.

2. Materials and Methods

2.1. Geological Setting

The Illinois Basin–Decatur Project (IBDP) represents a large-scale demonstration of carbon capture and storage (CCS) technology, with a designed capacity to sequester up to one (1) million metric tons of CO2. This project, led by the Midwest Geological Sequestration Consortium and located in Macon County, Illinois, commenced its CO2 injection operations in November 2011, targeting the Mt. Simon Sandstone, a regionally extensive and geologically significant formation within the Illinois Basin [73,74]. The Illinois Basin itself extends across Illinois, southwestern Indiana, and western Kentucky (shown in Figure 1), and is recognized for its substantial geological relevance. The Mt. Simon Sandstone, which underlies much of the basin, has been identified as a key reservoir for underground gas storage (UGS), with estimated storage capacities reaching up to 172 billion metric tons [75]. The stratigraphic and lithological properties of the Illinois Basin, and particularly those of the Mt. Simon Sandstone, are fundamental to effective carbon sequestration both regionally and across the broader Midwest [76,77]. Furthermore, the demonstrated capacity for significant CO2 storage in the Mt. Simon Sandstone highlights its potential suitability for future underground hydrogen storage (UHS). The combination of favorable reservoir characteristics and the expansive extent of the Illinois Basin highlights its strategic importance for ongoing and future subsurface storage applications.
The Mt. Simon Sandstone constitutes a prominent Cambrian-age geological formation that extends broadly across the Midwestern United States, serving as the principal saline aquifer for gas sequestration in the region. Within the Illinois Basin, the Mt. Simon has its maximum thickness up to approximately 2600 ft in east-central Illinois and west-central Indiana, making it an ideal candidate for large-scale sequestration projects [78]. At the IBDP site, the Mt. Simon Sandstone is subdivided into three major lithostratigraphic intervals: Lower, Middle, and Upper. The Lower Mt. Simon is particularly conducive for UGS, attributable to its high porosity of up to 27% and high permeability, which can exceed 1000 mD in some locations. This interval is further differentiated into three units—B, A-Upper, and A-Lower—as illustrated in Figure 2. Notably, the A-Lower unit exhibits relatively high permeability and porosity, thereby rendering it especially advantageous for UGS. Ref. [79] attributes these petrophysical characteristics as likely the result of extensive dissolution processes and the presence of coarse-grained arkosic facies. The Mt. Simon Sandstone encompasses a variety of depositional environments, including subaqueous and subaerial coastal zones, lagoons, river plains, and eolian plains [74]. The formation is stratigraphically overlaid by the Eau Claire Formation, which comprise Shale, siltstone, sandstone, and dolomite and function as the primary cap rock and are underlain by low-permeability Precambrian igneous rocks [80]. A stratigraphic column of the formation is shown in Table 1.

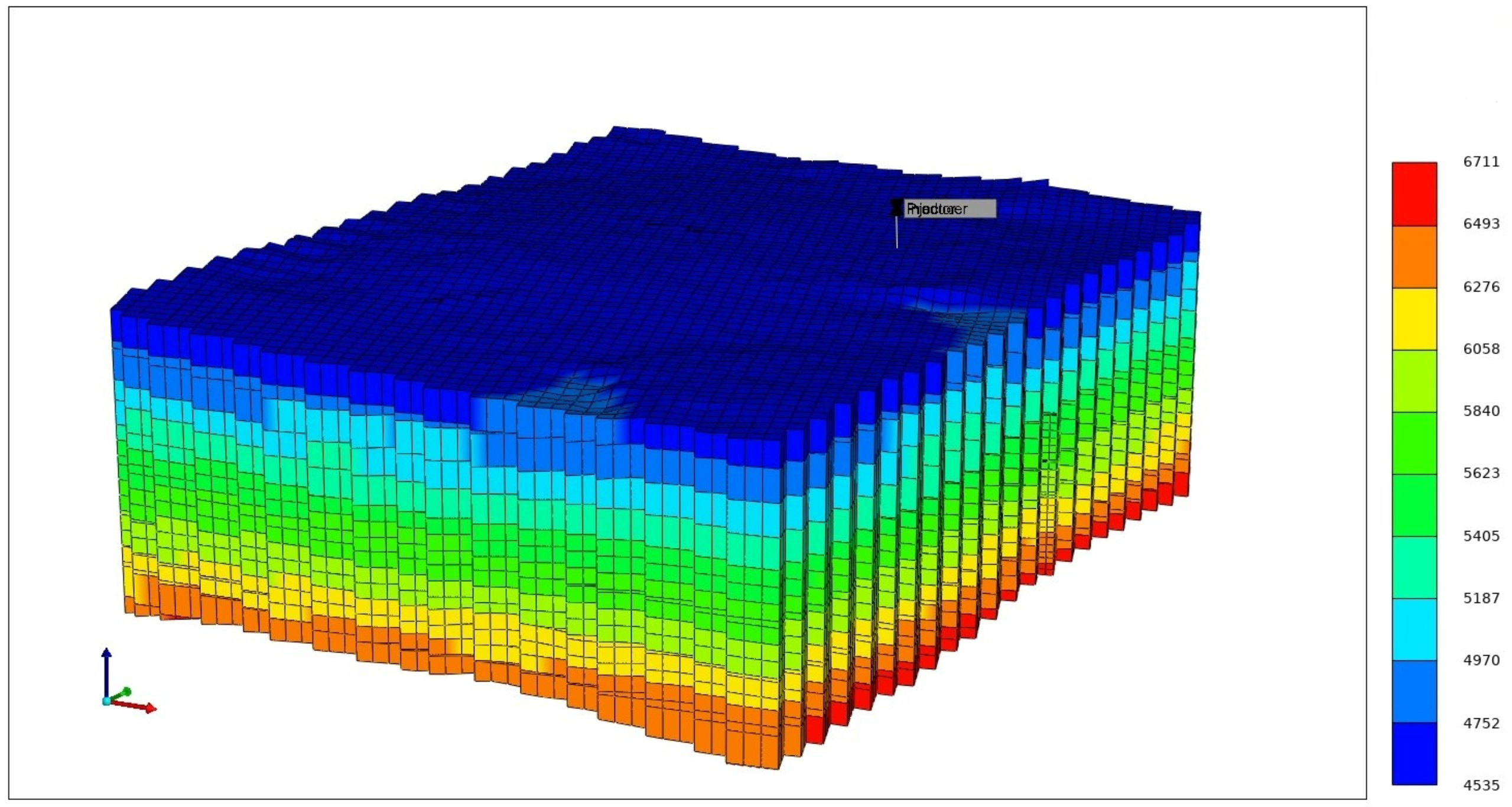
2.2. Geological Model

The study utilizes a 3D geological model of the IBDP developed by Schlumberger. The modeled stratigraphic framework comprises the Mt. Simon Sandstone as the primary reservoir, the Eau Claire Formation as the cap rock, and the Argenta and Precambrian formations as the underlying units. Core data, well logs, and 3D seismic data were used to construct a detailed geological model, covering an area of 9.7 miles by 9.3 miles. A total of twenty (28) faults were interpreted from the seismic data, cutting across the Mt. Simon Sandstone and its underlying formations. The majority of these faults display minor displacements (0–30 ft), while nine (9) faults are characterized by greater offsets (30–50 ft).
The geological model of the entire field was constructed using a structured grid with dimensions of 338 × 324 × 817, resulting in a total of 89,471,304 grid cells. Horizontal grid blocks were set at dimensions of 150 ft × 150 ft, while vertical cell thicknesses ranged from 7 to 200 ft, with the majority measuring 100 ft or 200 ft. To optimize computational efficiency, a polygonal subset measuring 9500 ft × 12,500 ft was extracted from the full-field model and subsequently upscaled to a coarser grid size of 200 ft × 200 ft for the simulation runs. This extracted region delineates the simulation boundary used in the IBDP studies. Figure 3 illustrates the top view of the effective porosity distribution in the full-field model (a) and the simulation model (b). Static properties within the simulation model were systematically upscaled from the full-field dataset to preserve consistency and fidelity to field data. Figure 4 shows the effective porosity (a) and permeability (b) distributions of the Mt. Simon A-Lower and A-Upper zones. Porosity within these zones ranges from 0.12 to 0.28, and permeability values span 10 to 300 mD. Figure 5 shows a comprehensive 3D layout of the simulation model, highlighting its porosity distribution.

2.3. Reservoir Simulation

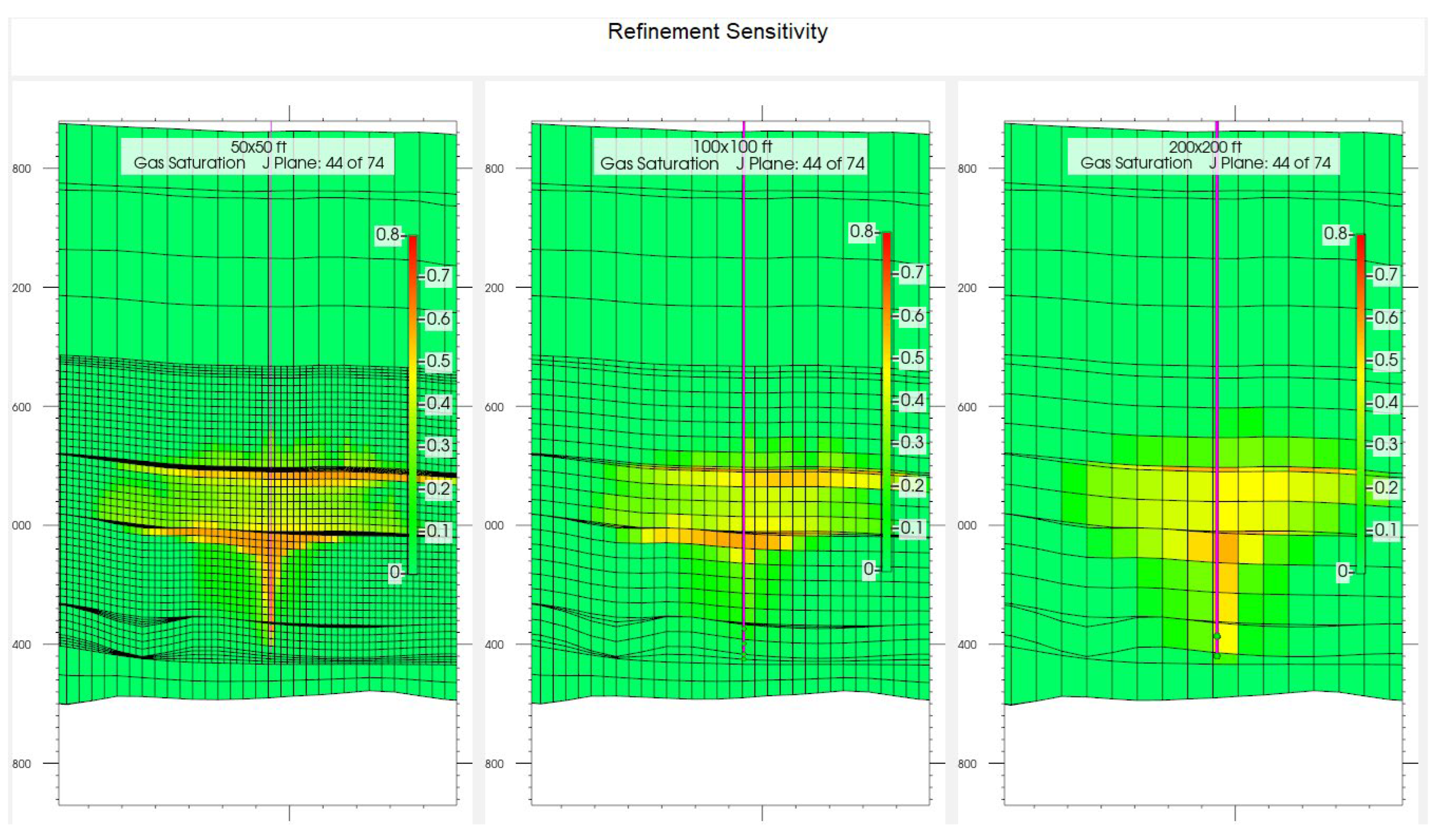
2.3.1. Grid Size Refinement and Selection

Grid refinement was implemented in the vicinity of the injection zone to enhance computational efficiency and improve the spatial resolution of simulation outputs. A targeted area measuring 5000 ft by 4600 ft was refined to a grid size of 100 × 100 ft, with vertical refinement extending from layers 7 to 21, corresponding to depths of approximately 5400 ft (Mt. Simon D–Mt. Simon C) to 6450 ft (Mt. Simon A-Lower–Argenta). The necessity for grid refinement was established through comparative analysis of multiple grid configurations. The initial base case utilized a 200 × 200 ft grid, followed by assessments at 100 × 100 ft and 50 × 50 ft resolutions. During these evaluations, the injection rate was maintained at 27 MM ft3/day, and each scenario was simulated over a one-year period. The simulation time for the 100 × 100 ft grid was less than double that of the 200 × 200 ft grid, whereas the 50 × 50 ft configuration resulted in a simulation time exceeding the base case by over two orders of magnitude. Table 2 summarizes the simulation run times for each grid size considered. The 100 × 100 ft refinement was ultimately selected, as it markedly improved the delineation of gas saturation profiles, particularly in zones of contrasting permeability compared to the coarser model. This enhanced resolution is shown in Figure 6, which displays more precise saturation distributions in the finer grid. Adoption of the 100 × 100 ft grid provided an optimal compromise between computational demand and visualization fidelity for the simulation results.
Boundary conditions were defined under the assumption of a laterally continuous reservoir and impermeable confining units above and below. The top and bottom boundaries were specified as no-flow for both aqueous and hydrogen-rich phases, reflecting the sealing nature of the overlying Eau Claire and underlying Precambrian formations, respectively. Lateral boundaries were prescribed hydrostatic pressure conditions, based on initial reservoir properties derived from the full-field model. Based on field measurements, the model was initialized with a pressure of 2911 psi at a reference depth of 6430 ft, with a corresponding temperature of 122.6 °F at the same depth; at this initial state, the formation was fully saturated with brine [79]. Fluid properties for the simulation were modeled using the CMG GEM simulator, with the Peng-Robinson 1978 Equation of State employed to characterize phase behavior.

2.3.2. Hysteresis, Solubility, and Diffusivity Parameters

Hysteresis in gas phase trapping was modeled using Land’s trapping model [81], which describes the relationship between residual gas saturation and variables such as fluid properties, rock characteristics, and flow dynamics. Land’s model is widely regarded as a foundational empirical approach for representing hysteresis in multiphase flow systems [82]. The residual gas saturation, Sgrh was estimated using Equation (1), while the Land trapping constant was determined using Equation (2)
S g r h = S g h − S g i c 1 + C . ( S g h − S g i c )
C = 1 ( S g r ) m a x − 1
where
‣
Sgrh is the residual gas saturation after hysteresis;
‣
Sgh is the current gas saturation;
‣
Sgic is the gas saturation at the start of the imbibition cycle;
‣
C is a land specific trapping constant;
‣
(Sgr)max is the maximum residual gas saturation.
The solubility of a substance is intricately linked to the fugacity of the component, a parameter that can be precisely quantified using the general form of Henry’s Law. When the Henry’s Law constant for a component is set to zero, it signifies that the substance is effectively insoluble in water under the given conditions. This crucial relationship can be expressed as the product of the component’s concentration in the aqueous phase and the Henry’s Law constant, denoted as H in Equation (3) [83].
Solubility in the simulation was modeled based on the relationship between component fugacity, f and aqueous-phase concentration, as governed by the general form of Henry’s Law [83]. The Henry’s Law constant, H determines the extent of solubility for each component; when H is set to zero, the component is considered insoluble in water under the specified conditions. The quantitative relationship is expressed as the product of the aqueous-phase concentration and the Henry’s Law constant, as shown in Equation (3)
f = x × H
where
f is the component fugacity;
x is the composition of the component in the aqueous phase, mol/L;
H is the Henry’s Law constant, mol/(L·psi).
Additionally, the Li-Nghiem method was applied to correlate Henry’s Law constants within the simulation framework. Diffusive transport was modeled by assigning a diffusion coefficient of 8.5 × 10−5 cm2/s for hydrogen.

2.3.3. Simulation Setup

The injection well was perforated between depths of 6322 ft and 6444 ft, intersecting four discrete vertical layers within the reservoir. Hydrogen was injected at a constant rate of 27 MM ft3/day to investigate system response under elevated pressure conditions. Bottomhole pressure was maintained at 4100 psi, representing 90% of the estimated formation fracture pressure [84]. The injection period spanned six years, commencing on 1 May 2023, and ending on 1 May 2029. During this timeframe, production was set at 38 MM ft3/day, with a minimum bottomhole pressure constraint of 127 psi. The operational schedule consisted of seven (7) months of continuous injection followed by a five (5)-month production phase, cycled annually for the duration of the study. For analysis of plume stability, a separate scenario involved a 24-month injection phase, after which the well was shut in for six months to assess post-injection plume dynamics.

3. Results and Discussion

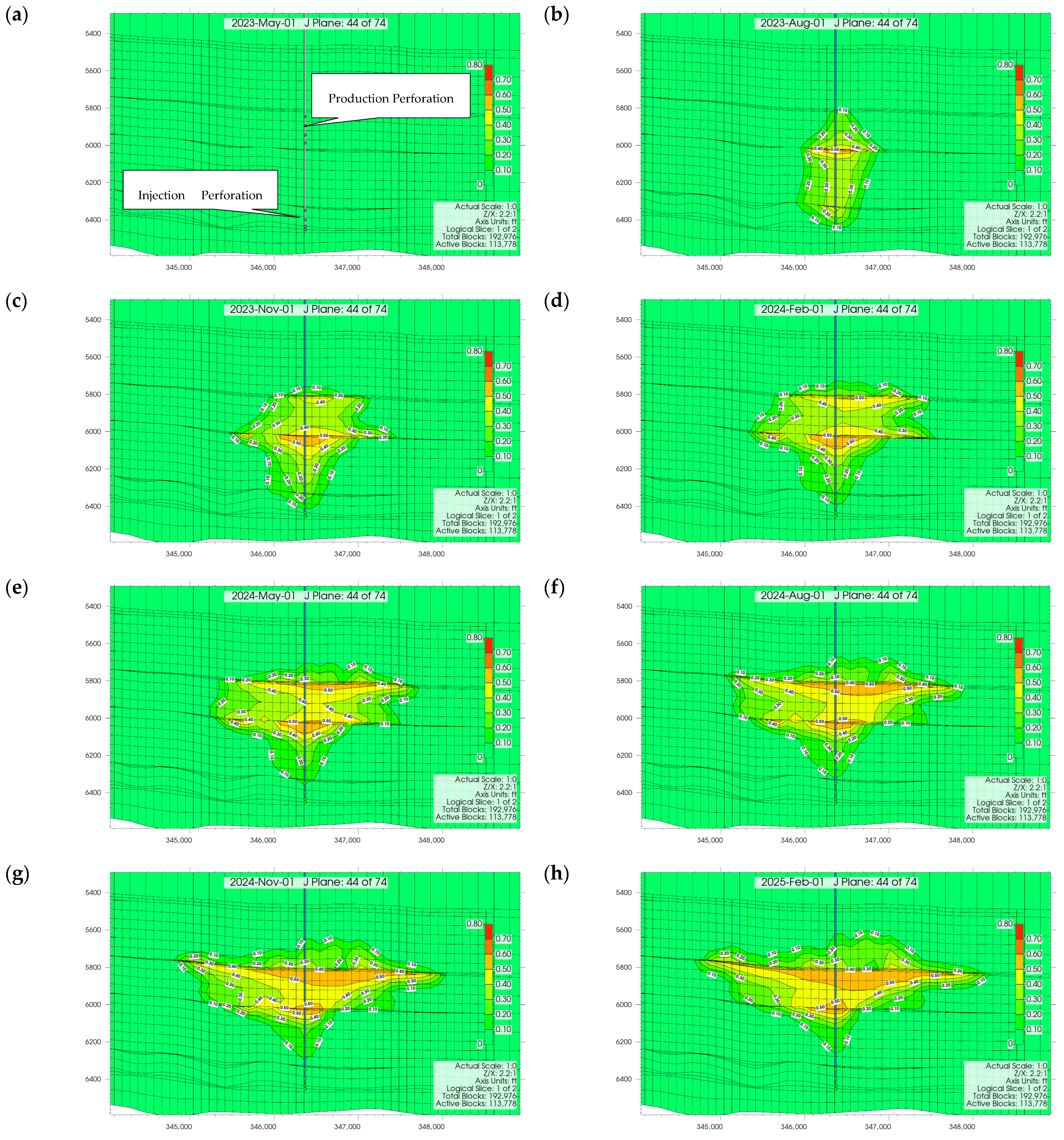
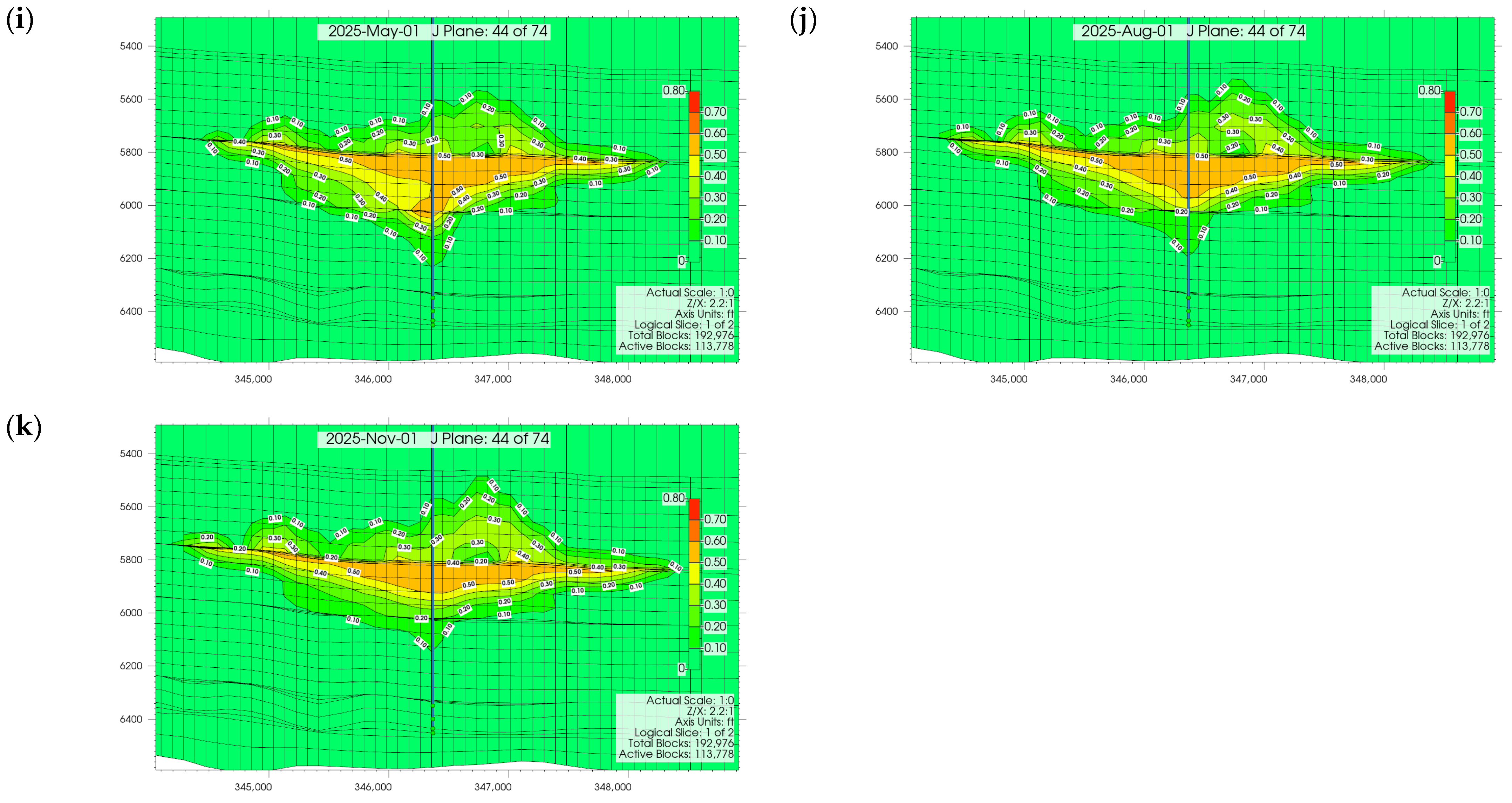
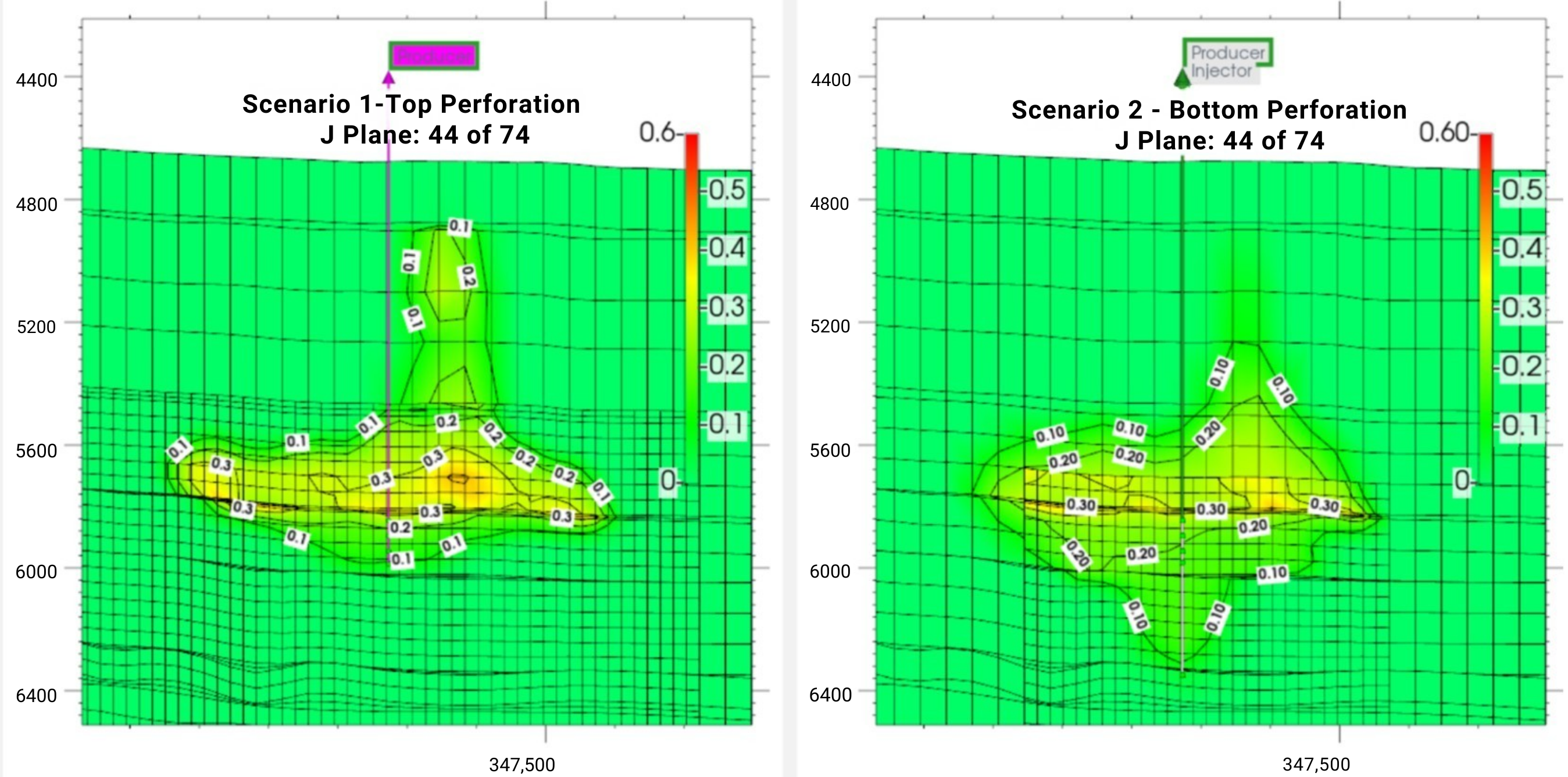
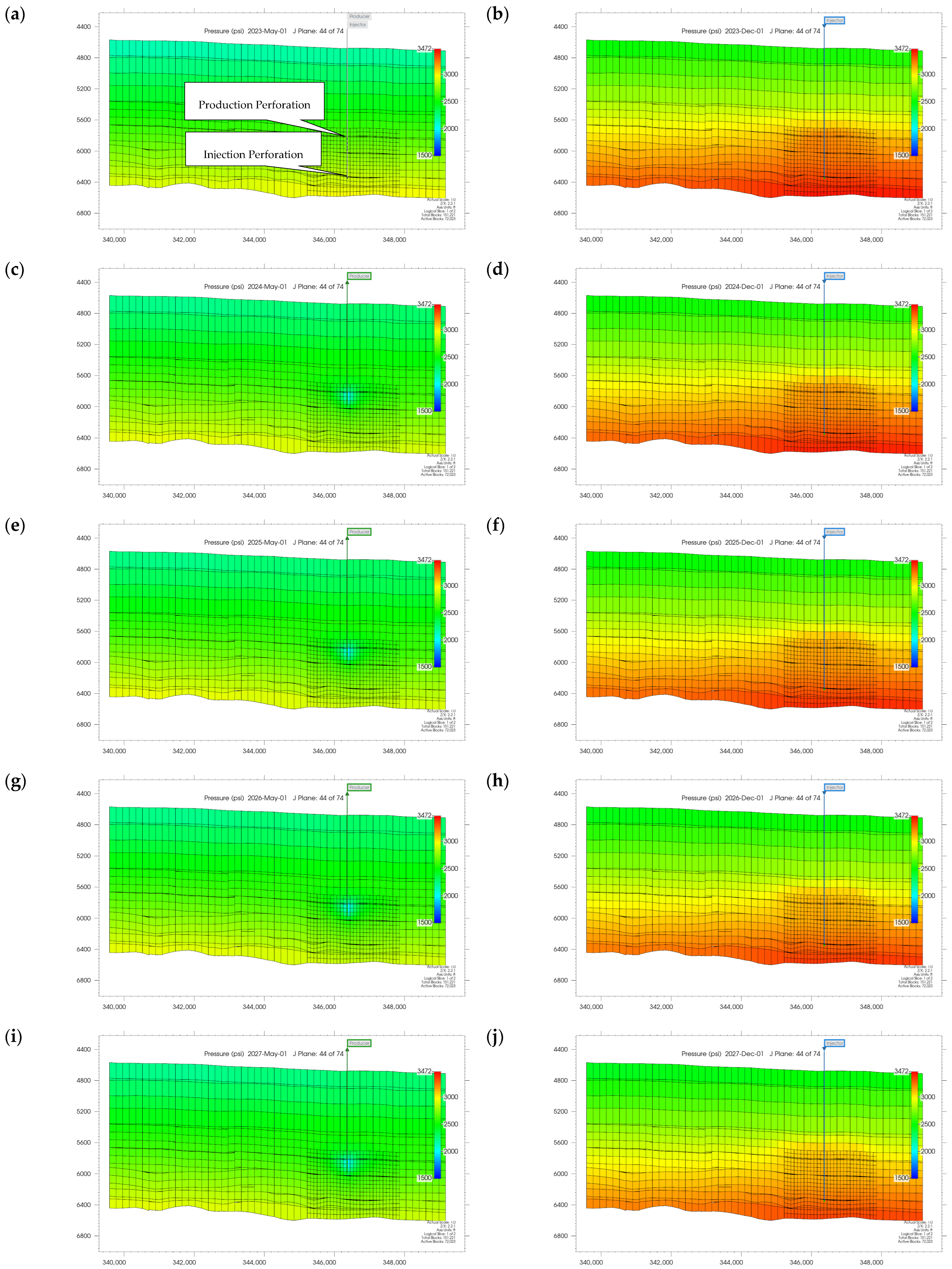
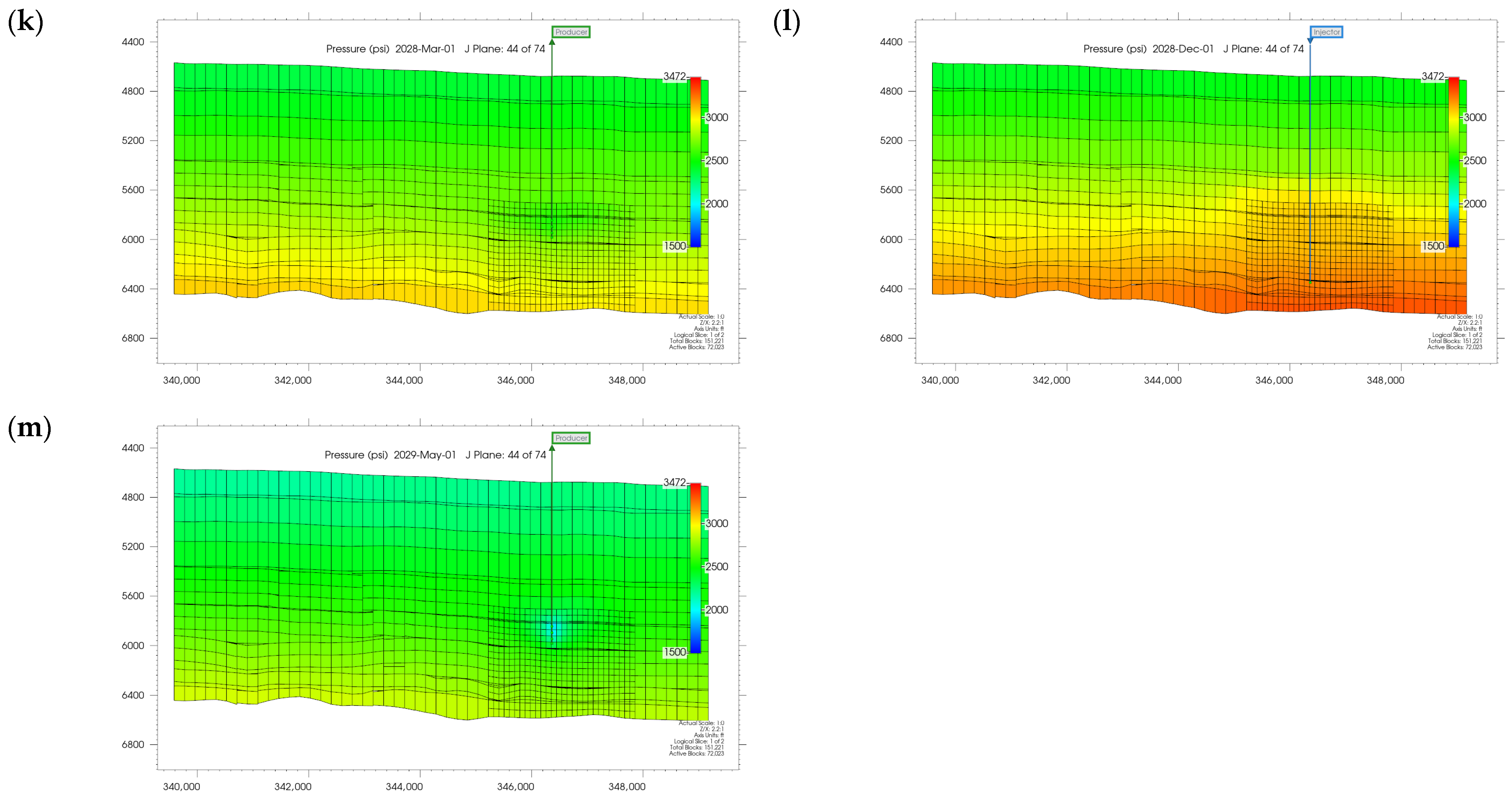
3.1. Plume Stability Analysis

During the 24-month hydrogen injection phase, followed by the 6-month post-injection observation period, the evolution and migration of the hydrogen plume were systematically evaluated. Upon the start of injection, hydrogen exhibited upward migration from the wellbore as a result of buoyancy forces, leading to vertical displacement of resident brine. Hydrogen’s density and viscosity which is much lower than CO2 or methane, create very large buoyancy forces in deep aquifers. Ref. [85] estimate hydrogen buoyancy approximately 3× that of CO2 at 1 km depth, so even moderate hydrogen columns generate high buoyant pressures.
Following this initial upward movement, the plume underwent lateral spreading within the reservoir, highlighting the interplay between buoyant rise and lateral dispersion mechanisms, both of which are crucial to understanding hydrogen migration and distribution within the storage formation. Figure 7a–h depicts the progression of the hydrogen plume, both vertically and laterally. The hydrogen plume initially moves upward until encountering the low-permeability strata, at which point its migration shifted predominantly to a lateral trajectory. A key control on vertical migration is capillary entry pressure of intra-formational seals. Hydrogen accumulates beneath it until the pressure overcomes the capillary threshold. This “accumulation–penetration–breakthrough” cycle is well-documented in CO2 storage studies. Ref. [86] describe how low-permeability layers impose a capillary barrier that retains nonwetting gas, producing a transient secondary seal. Early-stage hydrogen accumulation beneath low-permeability intervals, as shown in Figure 7c, preceded more pronounced lateral migration as local saturation increased.
In our model, once hydrogen pressure at low permeability belt interface exceeds its entry capillary pressure, vertical migration resumes and the plume intrudes into blocks above it, as observed. This is the secondary-seal effect. The plume was laterally extensive under the seal, spreading approximately 3000 ft and only broke through when buoyancy overcame capillarity. Notably, secondary seals channelize flow where nonwetting hydrogen flows preferentially through high-permeability layers while low-permeability layers block it, creating pronounced fingering. Thus, the interplay of buoyancy and capillary forces governs the staged plume migration. The plume rises 600 ft vertically from the bottom of the perforated region, extending into a few blocks of the Mt. Simon D formation.
Preferential upward migration continued, accompanied by a decline in hydrogen saturation below the secondary seal. As shown in Figure 7j,k, the lateral extent of the plume peaked at approximately 3000 ft beneath the Mt. Simon D, narrowing to around 700 ft near the injection well perforation. The maximum lateral radius (3000 ft) implies that radial pressure diffusion was significant; such a footprint means any monitoring or mitigation wells must be placed kilometers apart to intercept the full plume. Importantly, the plume remained entirely within the Mt. Simon sandstone, indicating that the thick Mt. Simon and its within-layer heterogeneities effectively constrained escape.
Although faults are present in portions of the refined simulation domain, the plume did not intersect any major fault structures. In the context of H2 storage, even minor fault activation could create escape routes. Therefore, although our results show no fault intersection, a rigorous site design would characterize fault transmissivity and apply conservative pressure limits. Containment assurance thus hinges not only on avoiding direct fault cuts but also on managing injection to prevent geomechanical failure. Recent coupled flow–geomechanics modeling indicates that storage-induced stress changes can activate caprock fracturing and fault reactivation, creating leakage pathways and potentially leading to substantial cumulative hydrogen losses over multi-year operation if pressure management is not conservative [87]. In our context, such residual trapping greatly aids containment: even as buoyant gas shifts upward, a significant fraction remains immobilized, preventing dissolution or leakage. This trapped hydrogen forms a tail of the plume that will not return to the well, which lowers the recoverable hydrogen but enhances storage security. The observation that the plume remained under the Mt. Simon layers is reinforced by expected residual trapping: the capillary forces at the seal will lock much of the gas in place beneath it. Over time, the plume will further equilibrate under gravity and capillarity, minimizing the risk of rapid upward migration post-shut-in.
Figure 8 shows a three-dimensional visualization of the hydrogen plume at a 5% saturation threshold, further supporting the predominance of vertical migration, as evidenced by the plume’s conical morphology, characteristic of gravity override. The plume shape reflects the high mobility ratio of hydrogen in brine, which drives viscous fingering. Ref. [88] note that hydrogen’s low viscosity leads to unstable, finger-like flow paths and uneven displacement fronts. In our simulation, this is manifested as narrow, upward fingers in high-permeability layers, with brine bypassed in less-permeable zones. Thus, buoyancy-driven segregation quickly establishes a vertically rising plume, while viscous instability promotes lateral spread in high-perm layers. Notably, plume containment was maintained within the Mt. Simon formation throughout the simulation. Despite evidence of both vertical and lateral migration, overall plume expansion was restricted within the sandstone reservoir, likely owing to the large aquifer size. In addition, low-permeability zones within the formation were identified as key controls in constraining lateral and vertical plume migration. After injection ceases, capillary trapping stabilizes the plume. In water-wet sandstones, capillary pressures can immobilize hydrogen ganglia in pore throats. Laboratory studies show that roughly 10–40% of injected H2 remains trapped as disconnected residual saturation once imbibition occurs [38].
Formation heterogeneity critically shapes the plume. The Mt. Simon injection interval in our model is strongly layered. High-permeability sandstone layers, some exceeding 100 mD alternate with tighter zones and the Mt. Simon D shale cap. This contrast creates effective permeability barriers. As [86] emphasize, capillary contrasts and relative-permeability barriers play a key role in shaping the plume. In practice, hydrogen fingers rise rapidly through high-permeability layers, while low-permeability layers temporarily trap hydrogen. We observe exactly this: the plume thickens under low-perm zones, seen in Figure 7c,d, then migrates laterally when vertical flow is impeded. Such lateral dispersion is further enhanced by reservoir-scale pressure gradients and dispersion. Importantly, heterogeneity also aids containment: small pockets of tighter sandstone within the Mt. Simon act as secondary barriers, limiting upward leakage. The simulation shows hydrogen largely confined beneath Mt. Simon D, likely because these intervening low-permeability units create multiple seals. This behavior mirrors CO2 plume studies: for example, a low-permeability layer at the Sleipner site imposed a sharp capillary barrier and required CO2 to build pressure before breaching the zone [86]. Similarly, the Mt. Simon D seal here forces hydrogen to accumulate and expand laterally until breakthrough. Such dynamics highlights that reservoir architecture, such as layer thickness and permeability contrasts, critically influence plume geometry.
These plume dynamics have clear operational implications. To maximize usable storage, the injection well should be placed below major permeability contrasts. Our results (and the efficiency scenarios in Section 3.2) suggest deeper perforations enhance vertical sweep. By injecting beneath the Mt. Simon D unit, buoyant flow is driven fully through the reservoir, exploiting gravity to hold gas under the cap. Conversely, placing perforations too high would fill up and skirt the seal sooner, possibly leading to premature cap pressurization. Hydrogen’s high mobility and diffusivity demand a robust, multi-faceted surveillance program. Ref. [89] emphasize that UHS monitoring must start pre-injection and employ higher-resolution sensors than conventional CO2 storage. For example, high-rate fiber-optic seismic or cross-well acoustic surveys could track the plume front (as in recent field tests [90]. and downhole pressure/temperature sensors can detect unexpected migration. Gas composition and pressure monitoring in nearby offset wells would serve as leakage alarms. Geochemical sampling of formation brine to examine dissolved hydrogen or microbial byproducts is also advised. In short, monitoring must be continuous and sensitive to small changes. The pronounced fingering suggests we should avoid overly high injection rates that exacerbate unstable flow. Consideration of cushion gases (e.g., adding a slug of methane or nitrogen may moderate the mobility ratio and suppress fingering [38]. Pressure management is crucial to prevent fracturing; the simulation’s peak pressures should be kept below rock fracturing thresholds and fault reactivation limits. Well integrity is paramount: cement and casing must be engineered to resist hydrogen’s diffusivity and reactivity.

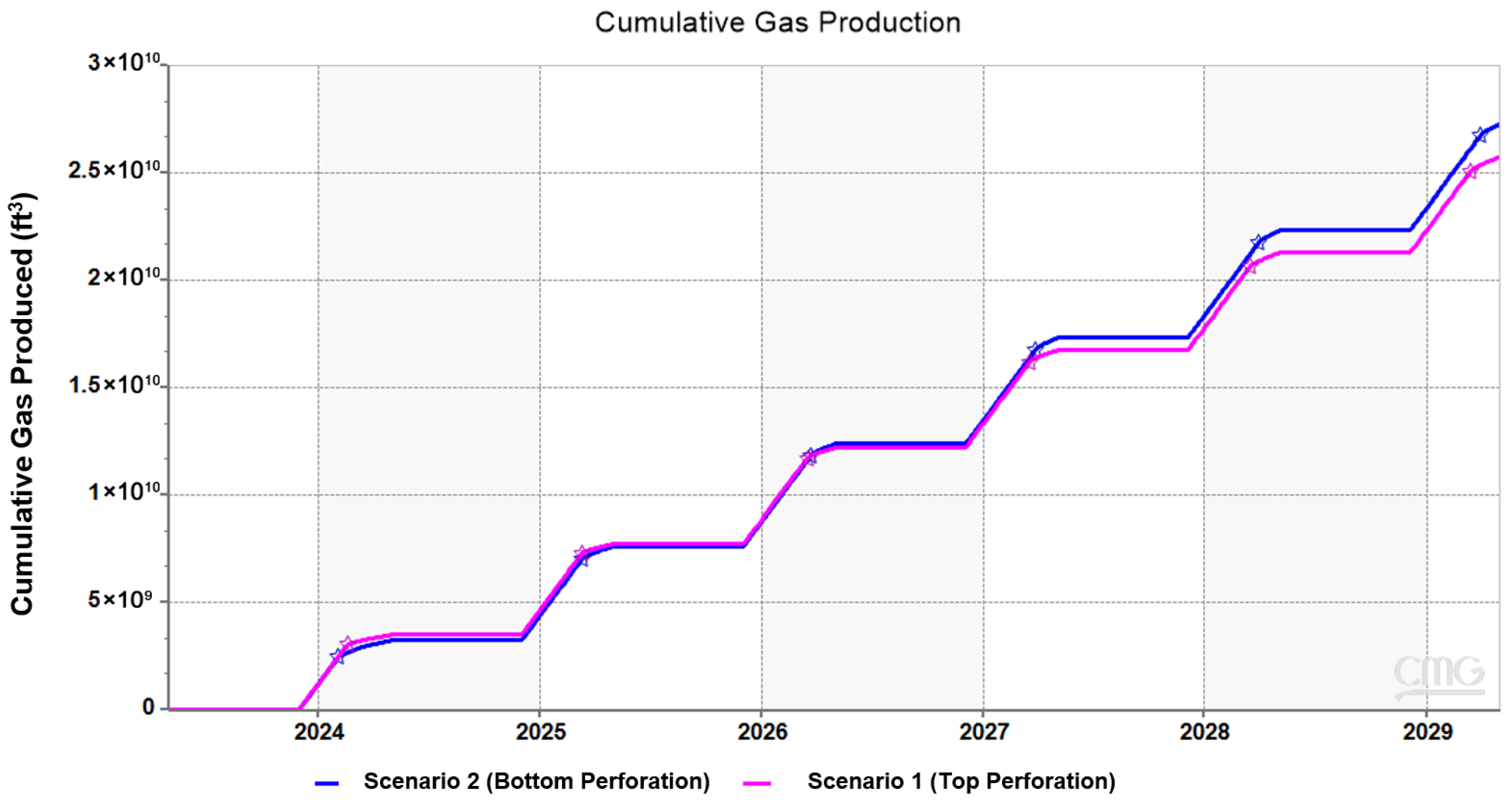
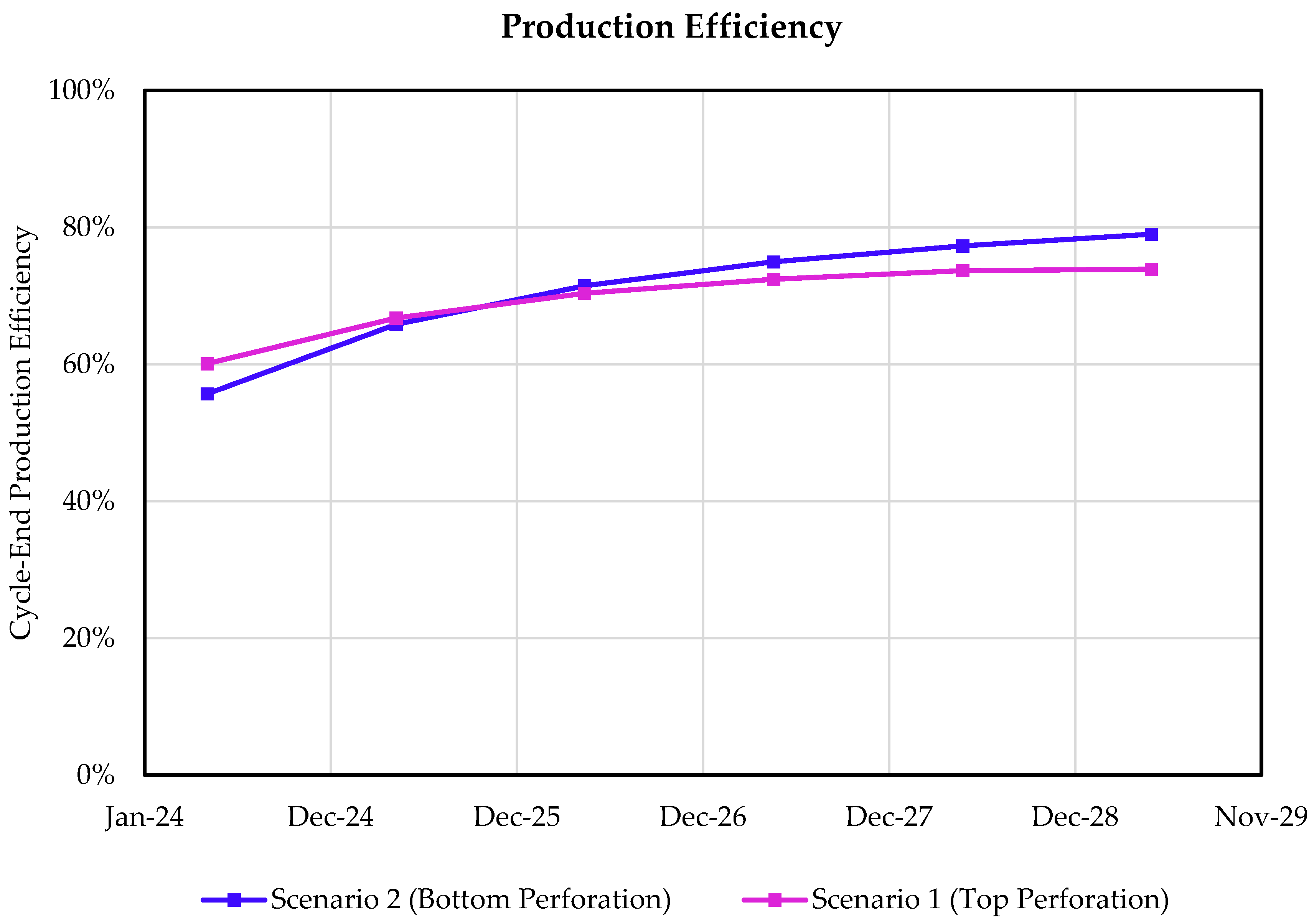
3.2. Effect of Injection Well Perforation Location on Withdrawal Efficiency

Two simulation scenarios were evaluated to assess the influence of injection well perforation depth on production efficiency. In Scenario 1, the injection well was perforated at the same depth as the production well, immediately below the Mt. Simon D formation. In Scenario 2, the injection well perforation interval was positioned approximately 300 ft deeper, from 6322 ft to 6466 ft, well below the production well. Both scenarios were subjected to identical injection scenarios and operational constraints. Comparative analysis focused on the resulting production efficiencies associated with each perforation strategy. Figure 9 and Figure 10 present the respective perforation intervals of the two injection well positions and associated hydrogen injection and production rates for both scenarios.
In the first year, Scenario 2 had a production efficiency of 56%, which was lower than Scenario 1 at 60%. However, as the study progressed, the efficiency of Scenario 2 improved and eventually exceeded that of Scenario 1. By the end of the simulation period, Scenario 2 achieved a cumulative production efficiency of 79%, compared to 74% for Scenario 1. Scenario 2 was selected as the base case for subsequent analyses due to its relatively higher recovery efficiency. Cumulative gas production and year-end production efficiencies for both scenarios are presented in Figure 11 and Figure 12, respectively, and Figure 13 illustrates the remaining gas saturation at the end of the 6-year cycle. Both scenarios initially demonstrated a brief period of stabilized gas production, with the duration of stabilization increasing over time. Scenario 1 showed a rapid rise in production rate followed by steep declines before stabilizing ahead of each subsequent injection phase. Conversely, Scenario 2 displayed a lower initial production rate with a more gradual decline. The pronounced peaks in gas production observed in Scenario 1 were followed by sharp declines, indicative of rapid deliverability depletion or more marked cyclic variations. In contrast, Scenario 2 provided a more sustained production profile, suggesting steadier reservoir depletion and potentially more stable long-term recovery.
The contrasting efficiency trends between Scenario 1 (top perforation) and Scenario 2 (bottom perforation) are primarily governed by buoyancy-driven segregation and how much of the reservoir volume is contacted before the injected gas establishes a connected, high-saturation gas zone. With bottom injection, the injected hydrogen must rise through the formation before accumulating beneath the upper low permeability Mt. Simon D, which increases its residence time and contact with brine during the first cycle. This promotes residual trapping along the upward migration pathway and delays the formation of a thick, laterally continuous gas cap, so the first-cycle withdrawal efficiency is lower. As cycling continues, however, bottom injection progressively builds a larger, more continuous gas cap beneath the caprock and mobilizes hydrogen through a greater vertical interval, improving sweep and connectivity. Once this gas cap is established, the producer can access a thicker, higher-saturation, better-connected hydrogen zone, and incremental losses to trapping and dissolution per unit produced decrease, so cumulative recovery ultimately surpasses the top-perforated case. In contrast, top injection tends to place hydrogen directly near the low permeability Mt. Simon D early, which can yield higher initial recovery but contacts a smaller vertical volume and can promote earlier localized cycling near the completion, limiting long-term sweep and leading to slower growth in cumulative recovery.
The observed lateral migration trends align with findings by [51], who identified analogous dispersion patterns in CO2 plume studies, highlighting the broader applicability of such methodologies to diverse gas storage scenarios. This cross-applicability reinforces the robustness of the approach employed in this study. Additionally, the demonstrated efficiency gains through optimized well perforations correspond with the work of [91], who advocated for similar strategies for gas storage within abandoned coal mines, emphasizing the critical role of well placement in enhancing resource recovery. Ref. [45] further highlights the significance of well integrity and design considerations in UHS, noting that factors such as perforation positioning substantially influence operational efficiency, ref. [36] also reported that moving injection wells lower in the aquifer increases the hydrogen recycle ratio. Together, these insights affirm the importance of strategic well placement and plume stability analysis in optimizing subsurface storage systems. Figure 9 and Figure 10 link the observed efficiency crossover between the two cases to a measurable transition in plume geometry.
Figure 14 and Figure 15 present the pressure profiles for scenario 2 (bottom perforation), which was hereafter used as the base case. Figure 14b–m shows a comprehensive depiction of pressure evolution during the 7-month injection period and subsequent 5-month production period across six operational cycles. Figure 14e illustrates a marked pressure increase during injection, particularly within the high-permeability Mt. Simon A-Lower sandstone. Following each production phase, the pressure distribution closely approximates the initial reservoir conditions, with localized reductions near the injection well. The most substantial increase in average reservoir pressure during injection occurred in the first cycle, rising from 2607 psi to 2990 psi, as depicted in Figure 15. By the end of the first production period, the net pressure change was 19 psi. Cumulatively, across all six cycles, the reservoir experienced an overall pressure reduction of 80 psi. This declining pressure trend is attributable to the combined effects of water production and hydrogen withdrawal.

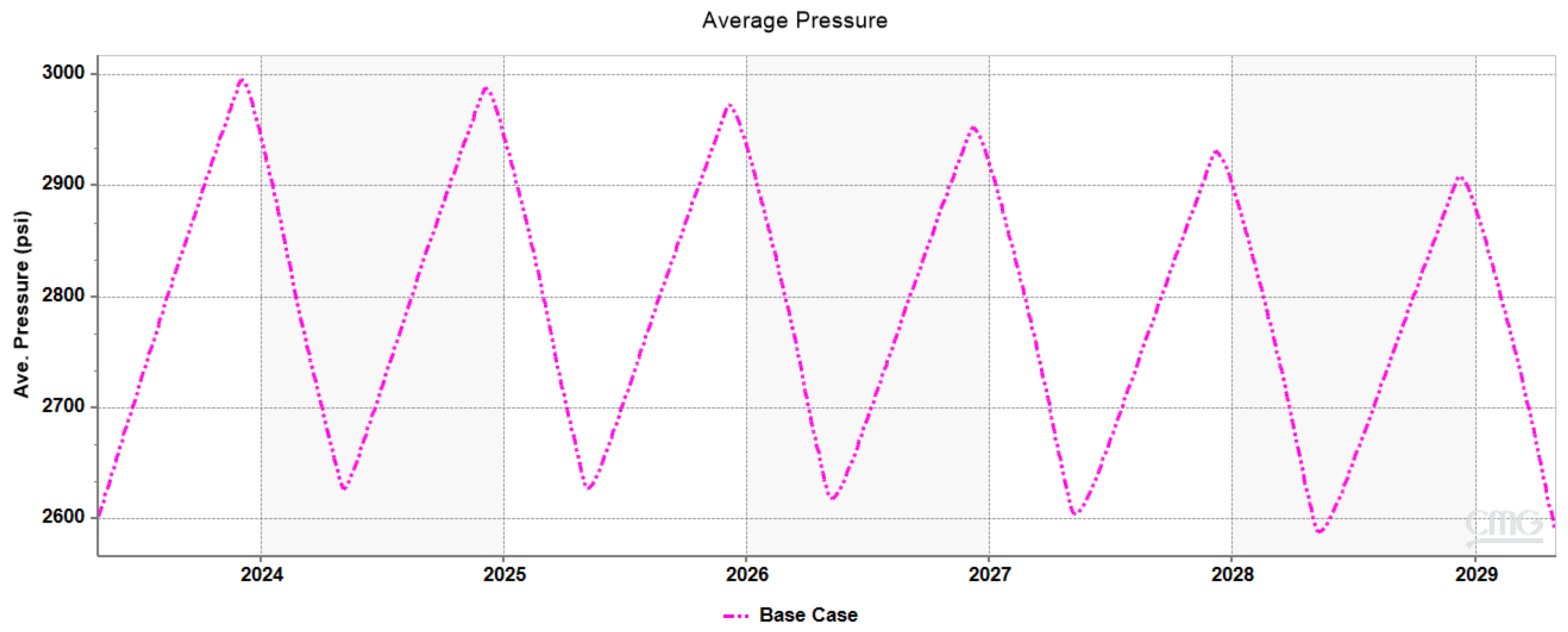
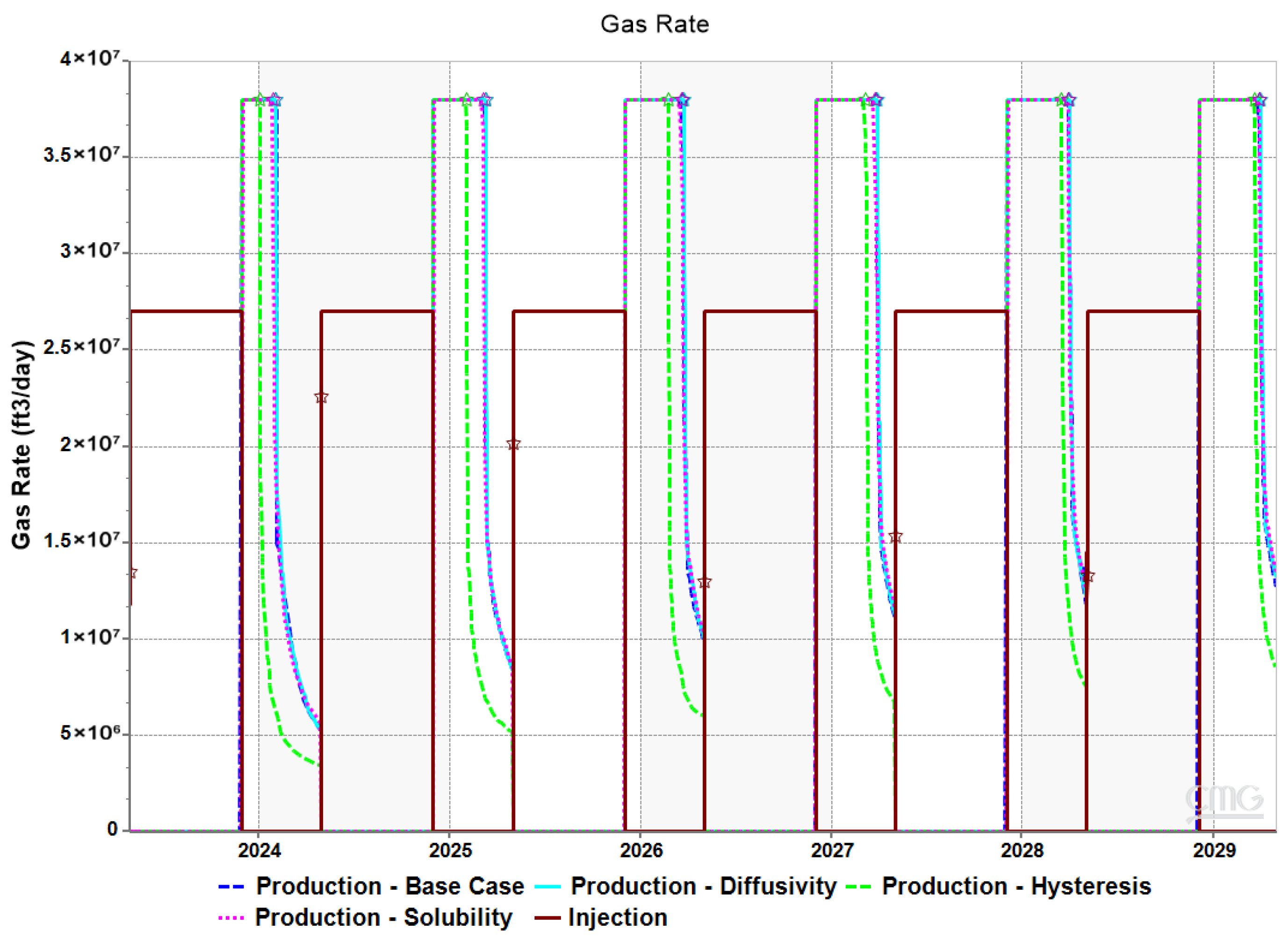
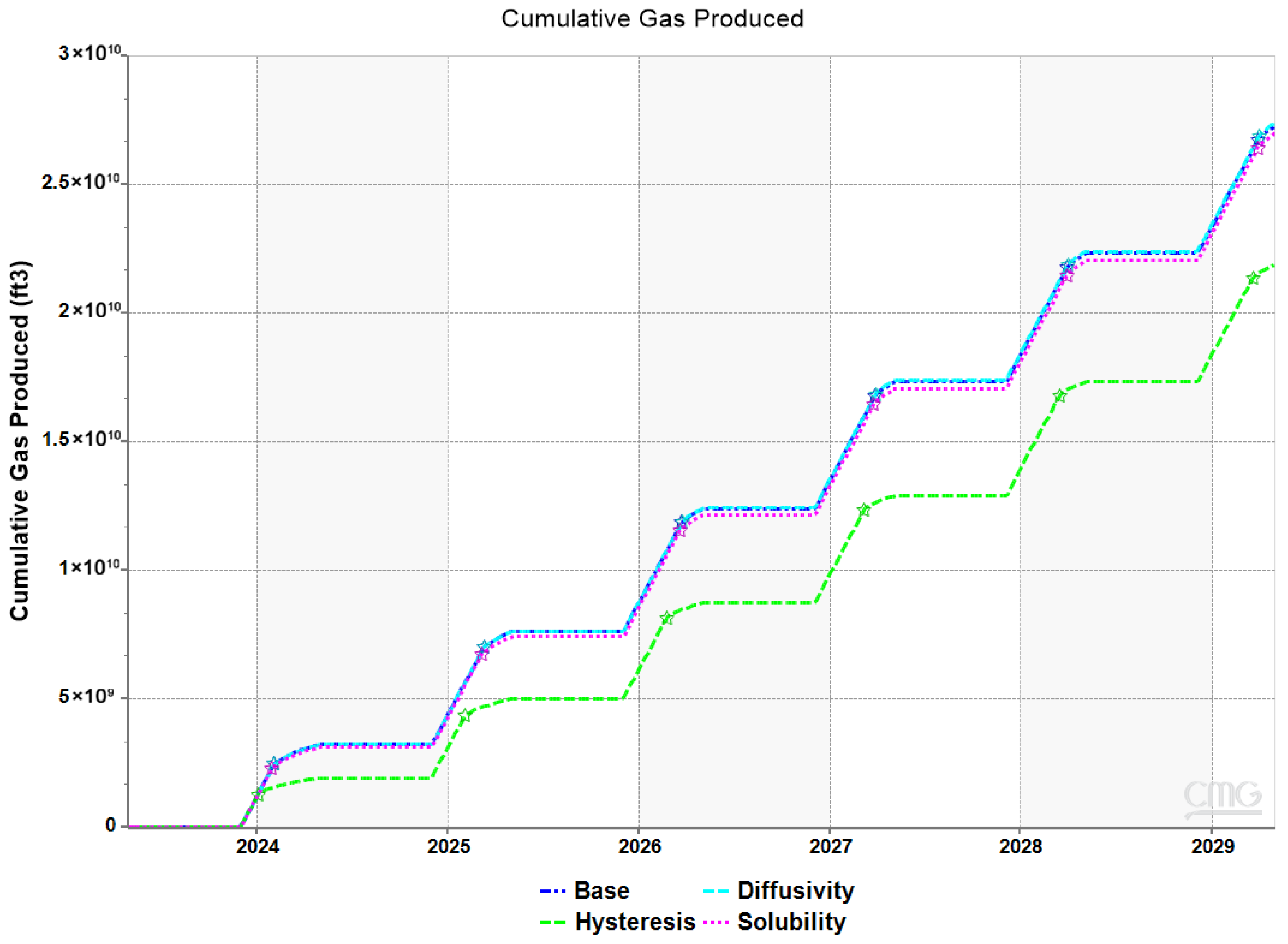
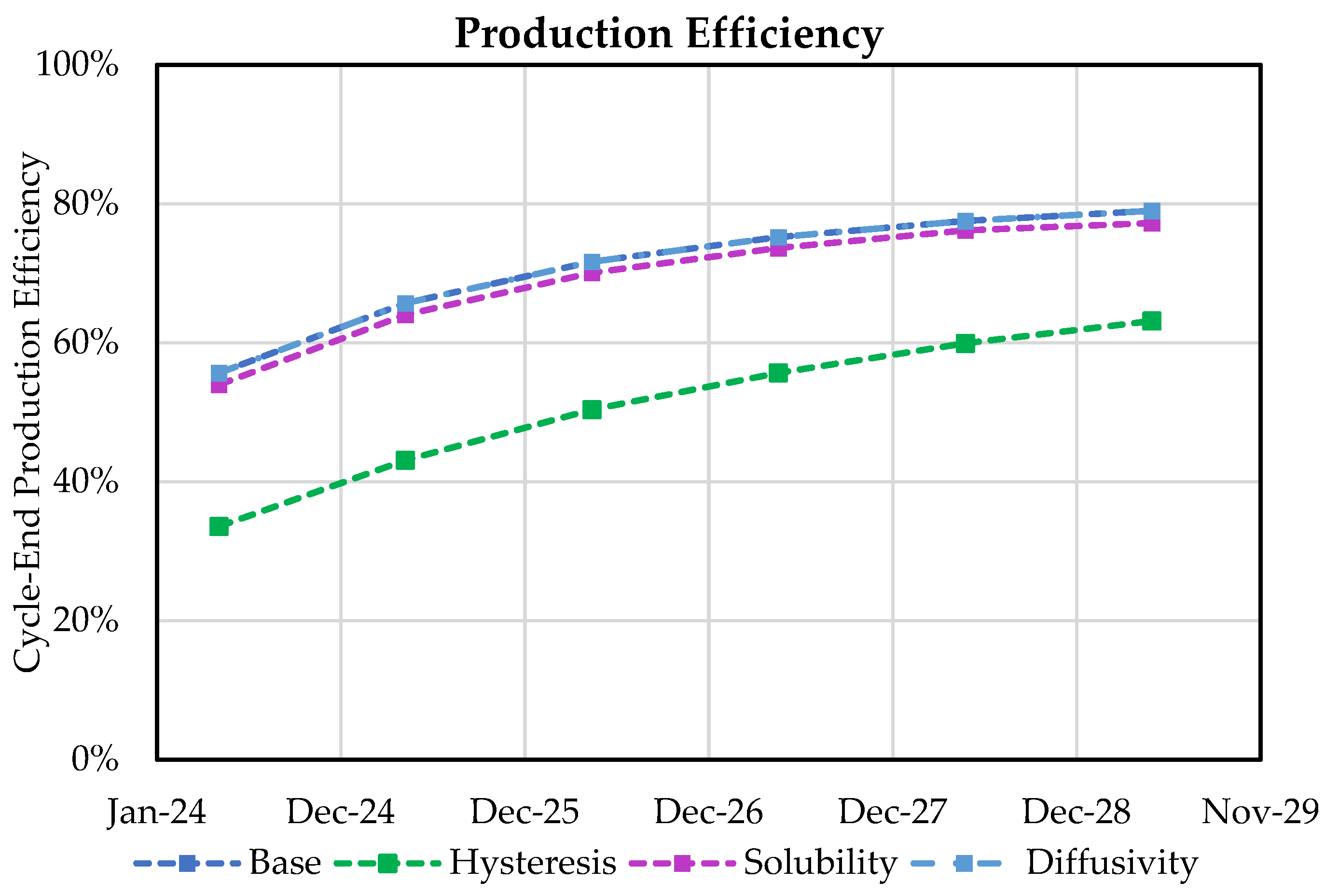
3.3. Impact of Hysteresis, Diffusivity, and Solubility on Withdrawal Efficiency

Figure 16 presents a comparison of hydrogen production rates over time, evaluating the effects of hysteresis, diffusivity, and solubility on withdrawal efficiency. The base case provides the reference benchmark for the system performance. The influence of diffusivity, which is responsible for molecular-scale gas transport through the reservoir matrix, was found to be minimal, as production rates closely mirrored those of the base case. This outcome suggests that molecular diffusion proceeds rapidly within the high-permeability aquifer, rendering its impact on hydrogen production negligible under these conditions. Nevertheless, diffusivity may play a more pronounced role in lower-permeability formations or over longer storage periods, as slower advective flow allows diffusive processes more time to redistribute hydrogen, consistent with findings of [72]. Similarly, the simulation results indicate that hydrogen dissolution into aquifer brine exerts a limited influence on production rates, reflecting the low solubility of hydrogen under reservoir conditions. This observation highlights the dominance of reservoir properties over molecular mechanisms in controlling production behavior for the system studied.
In contrast, the influence of hysteresis on hydrogen production is more substantial, as evidenced by delayed production peaks in the simulation results. Reduced production rates under hysteresis are primarily attributed to the path-dependent nature of reservoir rock permeability. Fluid flow is governed not only by the current reservoir pressure and saturation but also by the historical sequence of these states, which progressively modifies the intrinsic permeability of the formation. As a consequence, hysteresis effects may facilitate more controlled and prolonged hydrogen production, potentially enhancing long-term storage efficiency and offering improved flexibility in meeting variations in peak demand and ensuring supply stability.
The cumulative production profile illustrated in Figure 17 provides critical insights into the influence of diffusivity, solubility, and hysteresis on hydrogen production efficiency. Under the solubility scenario, cumulative production initially mirrors that of the base case; however, a gradual divergence is observed over time, with the solubility scenario ultimately yielding marginally lower cumulative production. Notably, around mid-2027, the solubility curve exhibits a discernible deviation from the base case, signifying a slight reduction in total hydrogen recovered attributable to solubility effects.
The production efficiency plot presented in Figure 18 demonstrates a consistent increase in efficiency over the production years across all evaluated scenarios. Both the base case and the diffusivity scenario begin with an efficiency of 56% at the end of the first year, reaching 79% after the six-year cycle. The solubility scenario exhibits an initial efficiency of 52% at the end of the first year and ends at 78% after the six cycles, indicating a minor decrease in efficiency relative to the base case. Conversely, the hysteresis scenario starts with an efficiency of 33% in the first year and rises to 63% by the end of the study period, reflecting a substantially lower efficiency compared to the base case.
Incorporating relative-permeability hysteresis reduced the cycle-averaged withdrawal efficiency by approximately 20% relative to the base case in this study, indicating that ignoring hysteresis can lead to overestimation in recovery predictions. This qualitative trend is consistent with prior UHS studies. Ref. [92], for example, reported that not accounting for relative-permeability hysteresis can overestimate annual working-gas capacity by 34% and recovered hydrogen volume by 85% in an offshore aquifer. Ref. [93] similarly showed that hysteresis effects interact with wettability and injection/withdrawal schemes to materially alter trapping and recovery in saline aquifers. Differences in the magnitude of the hysteresis impact across studies are expected because reported performance metrics, such as withdrawal efficiency versus annual working gas or recovered volume, hysteresis models and input relative-permeability datasets, reservoir architecture, and cycling strategy vary between studies. Recent work further indicates that hysteresis impacts can impact operational design choices [68,94,95], strengthening the need to evaluate recovery under realistic cycling constraints [92,93,94,95].
Hydrogen’s inherently low solubility in brine, as reported by [96,97], reduces dissolution losses during subsurface storage and adds a distinct advantage over more soluble gases such as CO2. While this property exerts only a minor influence on pressure dynamics and plume migration, it remains a distinguishing factor for UHS. Ref. [98] further observed that even limited hydrogen dissolution can induce localized shifts in pH, facilitating carbonate precipitation and modifying formation permeability within saline aquifers. Ref. [99] measured hydrogen and hydrogen–methane mixture solubility in brines using a PVT cell over 113–131 °F and 14.5–7252 psia, reporting that temperature and brine-composition effects were minor over that range, while gas-mixture composition significantly changed the solubility–pressure trend where lower hydrogen fraction produced a steeper increase. Collectively, these findings corroborate this study’s conclusion that solubility exerts minimal direct influence on storage efficiency, yet subtly modulates reservoir behavior. This highlights its significance in the long-term performance of UHS systems.
The minimal effect of hydrogen diffusivity on storage efficiency observed in this study is consistent with the broader body of literature. Ref. [100] demonstrated that hydrogen diffusivity, particularly in caprock is substantially reduced under water-saturated conditions, in contrast to dry conditions where diffusivity approximately doubles. This speaks to the critical role of caprock water content in mitigating potential hydrogen leakage. Ref. [101] further emphasized that rock microstructure, specifically porosity and tortuosity, exerts a strong control on diffusivity, highlighting the necessity for detailed, site-specific geological characterization in UHS projects. Ref. [102] corroborated these findings, reporting that diffusivity decreases with increasing pressure and salinity. These results reinforce the limited impact of diffusivity on storage efficiency, they also highlight its importance in safety and containment assessments for UHS operations.

3.4. From Reservoir Simulation to Field Deployment: Practical UHS Targets and Usable Energy Measures

To provide quantitative context for the operating constraints modeled here, we compare our cyclic rates and pressure limits with reported UHS demonstrations and with representative hydrogen–brine experimental measurements. First, our injection and withdrawal rates (27 and 38 MMscf/d, respectively) are industrial-scale dispatch values, whereas early demonstrations have typically involved inventories on the order of 1 MMscf at standard conditions. For example, HyPSTER reports injection of 2.6 tons of hydrogen, which corresponds to about 0.98 MMscf at standard conditions into the EZ53 cavern interval at depths of approximately 2760 to 3176 ft [103,104]. In the same project, the salt-cavern operating pressure range is reported as 1160 to 3481 psi, comparable in magnitude to our conservative injection pressure limit selection philosophy [103].
Laboratory observations also provide quantitative bounds for multiphase trapping and recovery processes that influence cyclic performance. In Fontainebleau sandstone, ref. [105] report initial and residual hydrogen saturations of about 4% and 2%, respectively, under the tested conditions, indicating limited trapped hydrogen in that rock type. In contrast, micro-CT studies in sandstone have reported hydrogen occupying up to about 65% of pore volume during drainage with residual hydrogen saturation of about 41% after brine imbibition, highlighting strong rock- and flow-history dependence of trapping [106,107]. Pore-scale visualization at subsurface conditions further shows that measured recovery can differ substantially depending on whether the imbibing brine is pre-equilibrated with hydrogen, for example, 43.1% recovery with non-equilibrated brine versus 31.6% with hydrogen-equilibrated brine, consistent with dissolution effects during cycling [108]. These reported ranges support our conclusion of accounting for hysteresis and dissolution as first-order controls in UHS systems to avoid overestimation in predictive models.
Quantifying the injected hydrogen volume in terms of energy content, British Thermal Units (BTUs) and annual household energy consumption is crucial for evaluating the storage facility’s capacity and supporting strategic energy planning. Calculating the BTU equivalent of stored hydrogen provides a direct measure of its ability to meet anticipated energy demands. Over the six-year simulation period, the cumulative hydrogen production totaled 27.3 billion cubic feet (Bcf), corresponding to an average annual output of 4.55 Bcf. With an average energy content of 312.5 BTUs per cubic foot, this equates to an annual energy yield of approximately 1.42 trillion BTUs (T BTUs), or roughly 0.42 billion kilowatt-hours (G kWh), using a conversion factor of 1 BTU = 0.00029307107 kWh. Given that the average annual household energy consumption in the United States is 11,000 kilowatt-hours [109], the produced hydrogen could supply the energy requirements of approximately 37,882 households per year.

4. Conclusions

This simulation study clarifies the main controls on hydrogen plume migration and recovery in a deep saline aquifer. The injected hydrogen plume rose buoyantly, forming narrow vertical fingers, and transitioned to lateral spreading when encountering lower-permeability strata. Plume growth remained safely contained beneath the Mt. Simon caprock, with internal low-permeability layers acting as effective secondary seals. Hydrogen recovery reached about 79% when we did not incorporate any trapping mechanism. When hydrogen solubility was included, recovery decreased slightly to about 78%, while incorporating relative-permeability hysteresis produced a much larger drop to roughly 63%. Well configuration played a significant role: bottom-hole injection improved recovery from 56% in the first cycle to 79% by the sixth, whereas top-hole injection increased from 60% to only 74% over the same interval. These results confirm that reservoir architecture and flow physics, including buoyancy segregation, viscous fingering, and capillary trapping, strongly influence both plume evolution and recoverable hydrogen volumes.
The findings have direct implications for the design and operation of underground hydrogen storage systems. Maximum sweep is achieved when injection occurs in deeper, higher-permeability intervals below major sealing units, where buoyancy helps confine gas below the caprock. Shallower injection risks prematurely loading the seal and limiting lateral contact with the reservoir. Because hydrogen is highly mobile, injection rates must be managed to reduce unstable fingering, and reservoir pressure must remain below thresholds that could compromise integrity through fracturing or fault activation. Continuous monitoring is critical, ideally combining downhole measurements, distributed sensing, and tracer or geochemical tools to detect deviations from expected plume behavior. Materials selection for wells and cement must also consider hydrogen diffusion and potential chemical interactions. These operational strategies, together with appropriate cycling protocols and cushion-gas management, will help ensure safe injection, effective containment, and strong withdrawal performance.
Future work should couple reservoir-scale flow simulations with geomechanical and fault-reactivation models to evaluate caprock stability and potential leakage pathways under cyclic injection. Additional studies should evaluate how cushion gas influences hydrogen plume movement, withdrawal efficiency, working-gas capacity, and long-term deliverability.

Author Contributions

Conceptualization, E.A.K. and H.R.; Methodology, E.A.K., H.R., A.-M.K. and B.S.; Software, E.A.K. and A.-M.K.; Formal analysis, E.A.K., A.-M.K. and B.S.; Investigation, E.A.K. and B.S.; Writing—original draft, E.A.K.; Writing—review & editing, E.A.K. and A.-M.K.; Visualization, E.A.K. and A.-M.K.; Supervision, H.R. and B.S.; Project administration, H.R. and B.S.; Funding acquisition, H.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

Author Babak Shabani was employed by the company INTERA Incorporated. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
IBDPIllinois Basin–Decatur Project
CCSCarbon Capture and Storage
UHSUnderground Hydrogen Storage
BTUBritish Thermal Units
UGSUnderground Gas Storage

References

  1. Allen, M.; Dube, O.P.; Solecki, W.; Aragón-Durand, F.; Cramer, W.; Humphreys, S.; Kainuma, M. Global Warming of 1.5 °C. Intergov. Panel Clim. Change 2018, 677, 393. Available online: https://www.ipcc.ch/sr15/ (accessed on 4 September 2025).
  2. Jiang, J.; Shi, S.; Raftery, A.E. Mitigation efforts to reduce carbon dioxide emissions and meet the Paris Agreement have been offset by economic growth. Commun. Earth Environ. 2025, 6, 823. [Google Scholar] [CrossRef]
  3. Andrae, A.S.G. Hypotheses for primary energy use, electricity use and CO2 emissions of global computing and its shares of the total between 2020 and 2030. WSEAS Trans. Power Syst. 2020, 15, 50–59. [Google Scholar] [CrossRef]
  4. Executive Summary—World Energy Outlook—Analysis-IEA. Available online: https://www.iea.org/reports/world-energy-outlook-2023/executive-summary (accessed on 6 October 2025).
  5. Borowski, P.F. Renewable Energy Sources Towards a Zero-Emission Economy. Energies 2025, 18, 5473. [Google Scholar] [CrossRef]
  6. Attanayake, K.; Wickramage, I.; Samarasinghe, U.; Ranmini, Y.; Ehalapitiya, S.; Jayathilaka, R.; Yapa, S. Renewable energy as a solution to climate change: Insights from a comprehensive study across nations. PLoS ONE 2024, 19, e0299807. [Google Scholar] [CrossRef] [PubMed]
  7. Nong, D.; Verikios, G.; Whitten, S.; Brinsmead, T.S.; Mason-D’Croz, D.; Rodriguez, S. Early transition to near-zero emissions electricity and carbon dioxide removal is essential to achieve net-zero emissions at a low cost in Australia. Commun. Earth Environ. 2025, 6, 653. [Google Scholar] [CrossRef]
  8. Fankhauser, S.; Smith, S.M.; Allen, M.; Axelsson, K.; Hale, T.; Hepburn, C.; Kendall, J.M.; Khosla, R.; Lezaun, J.; Mitchell-Larson, E.; et al. The meaning of net zero and how to get it right. Nat. Clim. Change 2021, 12, 15–21. [Google Scholar] [CrossRef]
  9. Kubi, E.A. Experimental and Simulation Study of Underground Hydrogen Storage; ProQuest LLC: Ann Arbor, MI, USA, 2023; Available online: https://books.google.com/books?id=Pr4A0QEACAAJ (accessed on 10 June 2025).
  10. Ericson, S.; Engel-Cox, J.; Arent, D. Approaches for Integrating Renewable Energy Technologies in Oil and Gas Operations; The Joint Institute for Strategic Energy Analysis: Golden, CO, USA, 2015. Available online: www.nrel.gov/publications (accessed on 15 October 2025).
  11. Ferro, P.; Wentz, H.; Oyen, S.; Viger, M.; Ngan, C.; Frager, C.; Mulvaney, K.; Lira, S.; Rawson, M. Imagining the hydrogen future of 2050. Interdiscip. Environ. Rev. 2015, 16, 206. [Google Scholar] [CrossRef]
  12. Mishra, P.; Acharya, S.K.; Patnaik, P.P.; Panda, B.S.; Roy, A.; Saha, S.; Singh, K.A. Low-pressure hydrogen storage using different metal hydrides: A review. Int. J. Glob. Warm. 2025, 35, 306–332. [Google Scholar] [CrossRef]
  13. Bahman, N.; Naser, N.; Khan, E.; Mahmood, T. Environmental science, policy, and industry nexus: Integrating Frameworks for better transport sustainability. Glob. Transit. 2025, 7, 29–40. [Google Scholar] [CrossRef]
  14. Dai, J.; Alvarado, R.; Ali, S.; Ahmed, Z.; Meo, M.S. Transport infrastructure, economic growth, and transport CO2 emissions nexus: Does green energy consumption in the transport sector matter? Environ. Sci. Pollut. Res. Int. 2023, 30, 40094–40106. [Google Scholar] [CrossRef]
  15. Dolge, K.; Barisa, A.; Kirsanovs, V.; Blumberga, D. The status quo of the EU transport sector: Cross-country indicator-based comparison and policy evaluation. Appl. Energy 2023, 334, 120700. [Google Scholar] [CrossRef]
  16. Seck, G.S.; Hache, E.; Sabathier, J.; Guedes, F.; Reigstad, G.A.; Straus, J.; Wolfgang, O.; Ouassou, J.A.; Askeland, M.; Hjorth, I.; et al. Hydrogen and the decarbonization of the energy system in europe in 2050: A detailed model-based analysis. Renew. Sustain. Energy Rev. 2022, 167, 112779. [Google Scholar] [CrossRef]
  17. Elegbeleye, I.; Oguntona, O.; Elegbeleye, F. Green Hydrogen: Pathway to Net Zero Green House Gas Emission and Global Climate Change Mitigation. Hydrogen 2025, 6, 29. [Google Scholar] [CrossRef]
  18. Nnabuife, S.G.; Oko, E.; Kuang, B.; Bello, A.; Onwualu, A.P.; Oyagha, S.; Whidborne, J. The prospects of hydrogen in achieving net zero emissions by 2050: A critical review. Sustain. Chem. Clim. Action 2023, 2, 100024. [Google Scholar] [CrossRef]
  19. Fuentes, J.E.Q.; Santos, D.M.F. Technical and Economic Viability of Underground Hydrogen Storage. Hydrogen 2023, 4, 975–1000. [Google Scholar] [CrossRef]
  20. Sharma, S.; Agarwal, S.; Jain, A. Significance of Hydrogen as Economic and Environmentally Friendly Fuel. Energies 2021, 14, 7389. [Google Scholar] [CrossRef]
  21. Pham, T.T.; Mollaamin, F.; Monajjemi, M.; Dang, C.M. A review of 2019 fuel cell technologies: Modelling and controlling. Int. J. Nanotechnol. 2020, 17, 498–513. [Google Scholar] [CrossRef]
  22. Dutta, S.; Dosapati, S.H. Hydrogen storage system integrated with fuel cell. Prog. Ind. Ecol. 2020, 14, 140. [Google Scholar] [CrossRef]
  23. Hamedani, E.A.; Alenabi, S.A.; Talebi, S. Hydrogen as an energy source: A review of production technologies and challenges of fuel cell vehicles. Energy Rep. 2024, 12, 3778–3794. [Google Scholar] [CrossRef]
  24. Nooni, I.K.; Dzogbewu, T.C. Hydrogen Economy and Climate Change: Additive Manufacturing in Perspective. Clean Technol. 2025, 7, 87. [Google Scholar] [CrossRef]
  25. Gunathilake, C.; Soliman, I.; Panthi, D.; Tandler, P.; Fatani, O.; Ghulamullah, N.A.; Marasinghe, D.; Farhath, M.; Madhujith, T.; Conrad, K.; et al. A comprehensive review on hydrogen production, storage, and applications. Chem. Soc. Rev. 2024, 53, 10900–10969. [Google Scholar] [CrossRef]
  26. Navinkumar, T.M.; Bharatiraja, C. Sustainable hydrogen energy fuel cell electric vehicles: A critical review of system components and innovative development recommendations. Renew. Sustain. Energy Rev. 2025, 215, 115601. [Google Scholar] [CrossRef]
  27. Sethia, H.; Priyam, A. Review on hydrogen fuel cells as an alternative fuel. Next Energy 2025, 9, 100460. [Google Scholar] [CrossRef]
  28. Bhuiyan, M.H.; Siddique, Z. Hydrogen as an alternative fuel: A comprehensive review of challenges and opportunities in production, storage, and transportation. Int. J. Hydrogen Energy 2025, 102, 1026–1044. [Google Scholar] [CrossRef]
  29. Barba, J.; Cañas-Carretón, M.; Carrión, M.; Hernández-Labrado, G.R.; Merino, C.; Muñoz, J.I.; Zárate-Miñano, R. Integrating Hydrogen into Power Systems: A Comprehensive Review. Sustainability 2025, 17, 6117. [Google Scholar] [CrossRef]
  30. Rosa, N.; Fereidani, N.A.; Cardoso, B.J.; Martinho, N.; Gaspar, A.; da Silva, M.G. Advances in hydrogen blending and injection in natural gas networks: A review. Int. J. Hydrogen Energy 2025, 105, 367–381. [Google Scholar] [CrossRef]
  31. Moran, C.; Deane, P.; Yousefian, S.; Monaghan, R.F.D. The hydrogen storage challenge: Does storage method and size affect the cost and operational flexibility of hydrogen supply chains? Int. J. Hydrogen Energy 2024, 52, 1090–1100. [Google Scholar] [CrossRef]
  32. Mekonnin, A.S.; Wacławiak, K.; Humayun, M.; Zhang, S.; Ullah, H. Hydrogen Storage Technology, and Its Challenges: A Review. Catalysts 2025, 15, 260. [Google Scholar] [CrossRef]
  33. Anekwe, I.M.S.; Mustapha, S.I.; Akpasi, S.O.; Tetteh, E.K.; Joel, A.S.; Isa, Y.M. The hydrogen challenge: Addressing storage, safety, and environmental concerns in hydrogen economy. Int. J. Hydrogen Energy 2025, 167, 150952. [Google Scholar] [CrossRef]
  34. Morales-Ospino, R.; Celzard, A.; Fierro, V. Strategies to recover and minimize boil-off losses during liquid hydrogen storage. Renew. Sustain. Energy Rev. 2023, 182, 113360. [Google Scholar] [CrossRef]
  35. Salem, A.M.; Khaira, A.M. A mini-review on liquid air energy storage system hybridization, modelling, and economics: Towards carbon neutrality. RSC Adv. 2023, 13, 26380. [Google Scholar] [CrossRef]
  36. Harati, S.; Gomari, S.R.; Gasanzade, F.; Bauer, S.; Pak, T.; Orr, C. Underground hydrogen storage to balance seasonal variations in energy demand: Impact of well configuration on storage performance in deep saline aquifers. Int. J. Hydrogen Energy 2023, 48, 26894–26910. [Google Scholar] [CrossRef]
  37. Girhe, P.; Barai, D.P.; Bhanvase, B.A.; Gharat, S.H. A Review on Functional Materials for Hydrogen Storage. Energy Storage 2025, 7, e70218. [Google Scholar] [CrossRef]
  38. Baru, A.M.; Eyitayo, S.I.; Okere, C.J.; Baru, A.; Watson, M.C. Large-Scale Hydrogen Storage in Deep Saline Aquifers: Multiphase Flow, Geochemical–Microbial Interactions, and Economic Feasibility. Materials 2025, 18, 5097. [Google Scholar] [CrossRef] [PubMed]
  39. Abdin, Z.; Khalilpour, K.; Catchpole, K. Projecting the levelized cost of large scale hydrogen storage for stationary applications. Energy Convers Manag. 2022, 270, 116241. [Google Scholar] [CrossRef]
  40. Chapter 3: LCI Hydrogen—Connecting Infrastructure. In Harnessing Hydrogen: A Key Element of the U.S. Energy Future. National Petroleum Council, 2025. Available online: https://harnessinghydrogen.npc.org/documents/H2-Ch_3-Connecting_Infrastructure-FINAL.pdf (accessed on 11 September 2025).
  41. Małachowska, A.; Łukasik, N.; Mioduska, J.; Gębicki, J. Hydrogen Storage in Geological Formations—The Potential of Salt Caverns. Energies 2022, 15, 5038. [Google Scholar] [CrossRef]
  42. Shahriar, M.F.; Khanal, A.; Khan, M.I.; Pandey, R. Current status of underground hydrogen storage: Perspective from storage loss, infrastructure, economic aspects, and hydrogen economy targets. J. Energy Storage 2024, 97, 112773. [Google Scholar] [CrossRef]
  43. Yang, Y.; Zandanel, A.; Liu, S.; Neil, C.W.; Germann, T.C.; Gross, M.R. Temperature dependence of hydrogen diffusion in reservoir rocks: Implications for hydrogen geologic storage. Energy Adv. 2024, 3, 2051–2065. [Google Scholar] [CrossRef]
  44. Berstad, D.; Gardarsdottir, S.; Roussanaly, S.; Voldsund, M.; Ishimoto, Y.; Nekså, P. Liquid hydrogen as prospective energy carrier: A brief review and discussion of underlying assumptions applied in value chain analysis. Renew. Sustain. Energy Rev. 2022, 154, 111772. [Google Scholar] [CrossRef]
  45. Ugarte, E.R.; Salehi, S. A Review on Well Integrity Issues for Underground Hydrogen Storage. J. Energy Resour. Technol. Trans. ASME 2021, 144, 042001. [Google Scholar] [CrossRef]
  46. Duartey, K.O.; Ampomah, W.; Rahnema, H.; Mehana, M. Underground Hydrogen Storage: Transforming Subsurface Science into Sustainable Energy Solutions. Energies 2025, 18, 748. [Google Scholar] [CrossRef]
  47. Nicoletti, L.; Hidalgo, J.C.; Strąpoć, D.; Moretti, I. H2 Transport in Sedimentary Basin. Geosciences 2025, 15, 298. [Google Scholar] [CrossRef]
  48. Berrezueta, E.; Kovács, T.; Herrera-Franco, G.; Caicedo-Potosí, J.; Jaya-Montalvo, M.; Ordóñez-Casado, B.; Carrión-Mero, P.; Carneiro, J. Laboratory Studies on Underground H2 Storage: Bibliometric Analysis and Review of Current Knowledge. Appl. Sci. 2024, 14, 11286. [Google Scholar] [CrossRef]
  49. Iglauer, S.; Ali, M.; Keshavarz, A. Hydrogen Wettability of Sandstone Reservoirs: Implications for Hydrogen Geo-Storage. Geophys. Res. Lett. 2021, 48, e2020GL090814. [Google Scholar] [CrossRef]
  50. Sekar, L.K.; Kiran, R.; Okoroafor, E.R.; Wood, D.A. Review of reservoir challenges associated with subsurface hydrogen storage and recovery in depleted oil and gas reservoirs. J. Energy Storage 2023, 72, 108605. [Google Scholar] [CrossRef]
  51. Doughty, C. Title Investigation of CO2 Plume Behavior for a Large-Scale Pilot Test of Geologic Carbon Storage in a Saline Formation Investigation of CO2 Plume Behavior for a Large-Scale Pilot Test of Geologic Carbon Storage in a Saline Formation. Transp. Porous Media 2010, 82, 49–76. [Google Scholar] [CrossRef]
  52. Hemme, C.; Berk, W. Hydrogeochemical Modeling to Identify Potential Risks of Underground Hydrogen Storage in Depleted Gas Fields. Appl. Sci. 2018, 8, 2282. [Google Scholar] [CrossRef]
  53. Zhang, Y.; Xue, Z.; Park, H.; Shi, J.; Kiyama, T.; Lei, X.; Sun, Y.; Liang, Y. Tracking CO2 Plumes in Clay-Rich Rock by Distributed Fiber Optic Strain Sensing (DFOSS): A Laboratory Demonstration. Water Resour. Res. 2019, 55, 856–867. [Google Scholar] [CrossRef]
  54. Bagchi, C.; Patwardhan, S.D.; Iglauer, S.; Mahmud, H.B.; Ali, M.F.J. A Critical Review on Parameters Affecting the Feasibility of Underground Hydrogen Storage. ACS Omega 2025, 10, 11658–11696. [Google Scholar] [CrossRef] [PubMed]
  55. Al Homoud, R.; Machado, M.V.B.; Daigle, H.; Sepehrnoori, K.; Ates, H. Enhancing Hydrogen Recovery from Saline Aquifers: Quantifying Wettability and Hysteresis Influence and Minimizing Losses with a Cushion Gas. Hydrogen 2024, 5, 327–351. [Google Scholar] [CrossRef]
  56. Gregory, S.P.; Barnett, M.J.; Field, L.P.; Milodowski, A.E. Subsurface Microbial Hydrogen Cycling: Natural Occurrence and Implications for Industry. Microorganisms 2019, 7, 53. [Google Scholar] [CrossRef] [PubMed]
  57. Doan, Q.T.; Keshavarz, A.; Behrenbruch, P.; Iglauer, S. Hydrogen diffusion into water and cushion gases—Relevance for hydrogen geo-storage. Int. J. Hydrogen Energy 2024, 98, 1099–1106. [Google Scholar] [CrossRef]
  58. Ali, M.; Isah, A.; Yekeen, N.; Hassanpouryouzband, A.; Sarmadivaleh, M.; Okoroafor, E.R.; Al Kobaisi, M.; Mahmoud, M.; Vahrenkamp, V.; Hoteit, H. Recent progress in underground hydrogen storage. Energy Environ. Sci. 2025, 18, 5740–5810. [Google Scholar] [CrossRef]
  59. Penchev, M.; Martinez-Morales, A.A.; Lim, T.; Raju, A.S.K.; Yilmaz, M.; Akinci, T.C. Leakage rates of hydrogen-methane gas blends under varying pressure conditions. Int. J. Hydrogen Energy 2024, 143, 912–920. [Google Scholar] [CrossRef]
  60. Kubi, E.A.; Rahnema, H.; Koray, A.-M.; Shabani, B. Underground Hydrogen Storage: Steady-State Measurement of Hydrogen–Brine Relative Permeability with Gas Slip Correction. Gases 2025, 5, 26. [Google Scholar] [CrossRef]
  61. Zhang, C.; Zhang, Q.; Li, W.; Song, Z.; Wang, J. Stability Analysis on the Long-Term Operation of the Horizontal Salt Rock Underground Storage. Adv. Civ. Eng. 2021, 2021, 6674195. [Google Scholar] [CrossRef]
  62. Zhao, K.; Yu, S.; Wong, L.N.Y. Long-term stability forecasting for energy storage salt caverns using deep learning-based model. Energy 2025, 319, 134854. [Google Scholar] [CrossRef]
  63. Harati, S.; Gomari, S.R. Designing Geometrically Stable Salt Caverns for Underground Hydrogen Storage: A Case Study from Northeast England. Energy Fuels 2025, 39, 17067–17082. [Google Scholar] [CrossRef]
  64. Liu, Z.; Liu, Y. Research on the Stability of Salt Cavern Hydrogen Storage and Natural Gas Storage under Long-Term Storage Conditions. Processes 2024, 12, 2080. [Google Scholar] [CrossRef]
  65. Hashemi, L.; Blunt, M.; Hajibeygi, H. Pore-scale modelling and sensitivity analyses of hydrogen-brine multiphase flow in geological porous media. Sci. Rep. 2021, 11, 8348. [Google Scholar] [CrossRef]
  66. Wang, Y.; Chakrapani, T.H.; Wen, Z.; Hajibeygi, H. Pore-Scale Simulation of H2-Brine System Relevant for Underground Hydrogen Storage: A Lattice Boltzmann Investigation. Adv. Water Resour. 2024, 190, 104756. [Google Scholar] [CrossRef]
  67. Zhao, Q.; Wang, Y.; Chen, C. Numerical simulation of the impact of different cushion gases on underground hydrogen storage in aquifers based on an experimentally-benchmarked equation-of-state. Int. J. Hydrogen Energy 2023, 50, 495–511. [Google Scholar] [CrossRef]
  68. Chai, M.; Chen, Z.; Nourozieh, H.; Yang, M. Numerical simulation of large-scale seasonal hydrogen storage in an anticline aquifer: A case study capturing hydrogen interactions and cushion gas injection. Appl. Energy 2023, 334, 120655. [Google Scholar] [CrossRef]
  69. Heinemann, N.; Scafidi, J.; Pickup, G.; Thaysen, E.; Hassanpouryouzband, A.; Wilkinson, M.; Satterley, A.; Booth, M.; Edlmann, K.; Haszeldine, R. Hydrogen storage in saline aquifers: The role of cushion gas for injection and production. Int. J. Hydrogen Energy 2021, 46, 39284–39296. [Google Scholar] [CrossRef]
  70. Ben Rhouma, S.; Dos Santos, A.; Veloso, F.d.M.L.; Smai, F.; Chiquet, P.; Masson, R.; Broseta, D. H2 storage with CO2 cushion gas in aquifers: Numerical simulations and performance influences in a realistic reservoir model. Int. J. Hydrogen Energy 2024, 110, 101–114. [Google Scholar] [CrossRef]
  71. Huang, T.; Moridis, G.J.; Blasingame, T.A.; Abdulkader, A.M.; Yan, B. Compositional reservoir simulation of underground hydrogen storage in depleted gas reservoirs. Int. J. Hydrogen Energy 2023, 48, 36035–36050. [Google Scholar] [CrossRef]
  72. Lu, J.; Muhammed, N.S.; Okolie, J.A.; Epelle, E.I. A sensitivity study of hydrogen mixing with cushion gases for effective storage in porous media. Sustain. Energy Fuels 2025, 9, 1353–1370. [Google Scholar] [CrossRef]
  73. IBDP. Illinois State Geological Survey (ISGS), Illinois Basin—Decatur Project (IBDP) Well Information, 30 April 2021. Midwest Geological Sequestration Consortium (MGSC) Phase III Data Sets. DOE Cooperative Agreement No. DE-FC26-05NT42588. Submissions—EDX. Available online: https://edx.netl.doe.gov/dataset/illinois-state-geological-survey-isgs-illinois-basin-decatur-project-ibdp-well-information (accessed on 31 October 2025).
  74. Freiburg, J.T.; Morse, D.G.; Leetaru, H.E.; Hoss, R.P.; Yan, Q. A Depositional and Diagenetic Characterization of the Mt. Simon Sandstone at the Illinois Basin-Decatur Project Carbon Capture and Storage Site, Decatur, Illinois, USA. 2014. Available online: http://www.isgs.illinois.edu (accessed on 8 September 2025).
  75. NETL. Illinois Basin-Decatur Project. 2017. Available online: https://www.netl.doe.gov/sites/default/files/2018-11/Illinois-Basin-Decatur-Project.pdf (accessed on 8 September 2025).
  76. Jones, R.A.; McKaskle, R.W. Design and operation of compression system for one million tonne CO2 sequestration test. Greenh. Gases Sci. Technol. 2014, 4, 617–625. [Google Scholar] [CrossRef]
  77. Bacon, D.H.; Ii, R.A.L.; Keating, E.; Carroll, S.; Iranmanesh, A.; Mansoor, K.; Wimmer, B.; Zheng, L.; Shao, H.; Greenberg, S.E. Application of the Aquifer Impact Model to support decisions at a CO2 sequestration site. Greenh. Gases Sci. Technol. 2017, 7, 1020–1034. [Google Scholar] [CrossRef]
  78. Leetaru, H.E.; McBride, J.H. Reservoir uncertainty, Precambrian topography, and carbon sequestration in the Mt. Simon Sandstone, Illinois Basin. Environ. Geosci. 2009, 16, 235–243. [Google Scholar] [CrossRef]
  79. Shabani, B.; Lu, P.; Kammer, R.; Zhu, C. Effects of Hydrogeological Heterogeneity on CO2 Migration and Mineral Trapping: 3D Reactive Transport Modeling of Geological CO2 Storage in the Mt. Simon Sandstone, Indiana, USA. Energies 2022, 15, 2171. [Google Scholar] [CrossRef]
  80. Medina, C.R.; Rupp, J.A. Reservoir characterization and lithostratigraphic division of the Mount Simon Sandstone (Cambrian): Implications for estimations of geologic sequestration storage capacity. Environ. Geosci. 2012, 19, 1–15. [Google Scholar] [CrossRef]
  81. Land, C.S. Calculation of Imbibition Relative Permeability for Two- and Three-Phase Flow From Rock Properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
  82. Spiteri, E.J.; Juanes, R.; Blunt, M.J.; Orr, F.M. A New Model of Trapping and Relative Permeability Hysteresis for All Wettability Characteristics. SPE J. 2008, 13, 277–288. [Google Scholar] [CrossRef]
  83. Henry, W. Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Abstr. Pap. Print. Philos. Trans. R. Soc. Lond. 1832, 1, 103–104. [Google Scholar] [CrossRef]
  84. Yang, F.; Babarinde, O.O.; Okwen, R.; Frailey, S.M.; Whittaker, S.G. Modeling commercial-scale CO2 injection in Mt. Simon Sandstone near Decatur, IL storage sites. In Proceedings of the 14th Greenhouse Gas Control Technologies Conference Melbourne 21–26 October 2018 (GHGT-14), Melbourne, Australia, 21–26 October 2018. [Google Scholar]
  85. Heinemann, N.; Alcalde, J.; Miocic, J.M.; Hangx, S.J.T.; Kallmeyer, J.; Ostertag-Henning, C.; Hassanpouryouzband, A.; Thaysen, E.M.; Strobel, G.J.; Schmidt-Hattenberger, C.; et al. Enabling large-scale hydrogen storage in porous media—The scientific challenges. Energy Environ. Sci. 2021, 14, 853–864. [Google Scholar] [CrossRef]
  86. Zhou, Q.; Birkholzer, J.T.; Mehnert, E.; Lin, Y.F.; Zhang, K. Modeling basin- and plume-scale processes of CO2 storage for full-scale deployment. Ground Water 2010, 48, 494–514. [Google Scholar] [CrossRef]
  87. Talukdar, M.; Zheng, F.; Jha, B. Hydrogen leakage via caprock fracturing and fault reactivation during subsurface porous media storage. Int. J. Hydrogen Energy 2025, 149, 149786. [Google Scholar] [CrossRef]
  88. Ren, B.; Jensen, J.; Duncan, I.; Lake, L. Buoyant Flow of H2 Vs. CO2 in Storage Aquifers: Implications to Geological Screening. SPE Reserv. Eval. Eng. 2023, 26, 1048–1058. [Google Scholar] [CrossRef]
  89. Tarkowski, R.; Uliasz-Misiak, B. Underground Hydrogen Storage: Insights for Future Development. Energies 2025, 18, 5724. [Google Scholar] [CrossRef]
  90. Bakulin, A.; Swaminadhan, S.; Shuster, M. Instrumenting the Devine Site as a Field Laboratory for Hydrogen Injection: Characterization and Monitoring Feasibility Assessment. In Proceedings of the International Meeting for Applied Geoscience & Energy (IMAGE 2025), Houston, TX, USA, 25–28 August 2025; Bureau of Economic Geology, University of Texas at Austin: Austin, TX, USA; Boris Gurevich, Curtin University: Bentley, WA, USA, 2025. [Google Scholar]
  91. Liu, W.; Pei, P. Evaluation of the Influencing Factors of Using Underground Space of Abandoned Coal Mines to Store Hydrogen Based on the Improved ANP Method. Adv. Mater. Sci. Eng. 2021, 2021, 7506055. [Google Scholar] [CrossRef]
  92. Lysyy, M.; Fernø, M.A.; Ersland, G. Effect of relative permeability hysteresis on reservoir simulation of underground hydrogen storage in an offshore aquifer. J. Energy Storage 2023, 64, 107229. [Google Scholar] [CrossRef]
  93. Pan, B.; Liu, K.; Ren, B.; Zhang, M.; Ju, Y.; Gu, J.; Zhang, X.; Clarkson, C.R.; Edlmann, K.; Zhu, W.; et al. Impacts of relative permeability hysteresis, wettability, and injection/withdrawal schemes on underground hydrogen storage in saline aquifers. Fuel 2022, 333, 126516. Available online: https://www.sciencedirect.com/science/article/pii/S0016236122033403?casa_token=YS9NxjJB3pIAAAAA:7wtJ8-YMMmSTp01X5Jy2wlXYI9BS45m253TNqRsguj17O6MSJLkc3tabfKxMTrC6Asy-mXwPIi8 (accessed on 25 October 2025).
  94. Nazari, F.; Nafchi, S.A.; Asbaghi, E.V.; Farajzadeh, R.; Niasar, V.J. Impact of capillary pressure hysteresis and injection-withdrawal schemes on performance of underground hydrogen storage. Int. J. Hydrogen Energy 2023, 50, 1263–1280. [Google Scholar] [CrossRef]
  95. Mahdi, D.S.; Al-Khdheeawi, E.A.; Yuan, Y.; Zhang, Y.; Iglauer, S. Hydrogen underground storage efficiency in a heterogeneous sandstone reservoir. Adv. Geo-Energy Res. 2021, 5, 437. [Google Scholar] [CrossRef]
  96. Raza, A.; Arif, M.; Glatz, G.; Mahmoud, M.; Al Kobaisi, M.; Alafnan, S.; Iglauer, S. A holistic overview of underground hydrogen storage: Influencing factors, current understanding, and outlook. Fuel 2022, 330, 125636. [Google Scholar] [CrossRef]
  97. Amiri, I.I.; Zivar, D.; Ayatollahi, S.; Mahani, H. The effect of gas solubility on the selection of cushion gas for underground hydrogen storage in aquifers. J. Energy Storage 2024, 80, 110264. [Google Scholar] [CrossRef]
  98. Perera, M.S.A. A review of underground hydrogen storage in depleted gas reservoirs: Insights into various rock-fluid interaction mechanisms and their impact on the process integrity. Fuel 2022, 334, 126677. [Google Scholar] [CrossRef]
  99. Tawil, M.; Salina Borello, E.; Bocchini, S.; Pirri, C.F.; Verga, F.; Coti, C.; Scapolo, M.; Barbieri, D.; Viberti, D. Solubility of H2-CH4 mixtures in brine at underground hydrogen storage thermodynamic conditions. Front. Energy Res. 2024, 12, 1356491. [Google Scholar] [CrossRef]
  100. Salina Borello, E.; Bocchini, S.; Chiodoni, A.; Coti, C.; Fontana, M.; Panini, F.; Peter, C.; Pirri, C.F.; Tawil, M.; Mantegazzi, A.; et al. Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks. Energies 2024, 17, 394. [Google Scholar] [CrossRef]
  101. Song, R.; Song, Y.; Liu, J.; Yang, C. Multiscale experimental and numerical study on hydrogen diffusivity in salt rocks and interlayers of salt cavern hydrogen storage. Int. J. Hydrogen Energy 2024, 79, 319–334. [Google Scholar] [CrossRef]
  102. Thiyagarajan, S.R.; Emadi, H.; Hussain, A.; Patange, P.; Watson, M. A comprehensive review of the mechanisms and efficiency of underground hydrogen storage. J. Energy Storage 2022, 51, 104490. [Google Scholar] [CrossRef]
  103. Hydrogen Pilot STorage for Large Ecosystem Replication. Available online: https://www.era.ac.uk/wp-content/uploads/2023/04/02_Leadbetter_Storengy.pdf (accessed on 12 December 2025).
  104. Glöckner, M.; Hevin, G. Model Qualification of Test Caverns on Field Test Data. Available online: https://hypster-project.eu/wp-content/uploads/2025/11/D2.6_Model_qualification.pdf (accessed on 12 December 2025).
  105. Boon, M.; Hajibeygi, H. Experimental characterization of H2/water multiphase flow in heterogeneous sandstone rock at the core scale relevant for underground hydrogen storage (UHS). Sci. Rep. 2022, 12, 14604. [Google Scholar] [CrossRef]
  106. Al-Yaseri, A.; Esteban, L.; Giwelli, A.; Sarout, J.; Lebedev, M.; Sarmadivaleh, M. Initial and residual trapping of hydrogen and nitrogen in Fontainebleau sandstone using nuclear magnetic resonance core flooding. Int. J. Hydrogen Energy 2022, 47, 22482–22494. [Google Scholar] [CrossRef]
  107. Jha, N.K.; Al-Yaseri, A.; Ghasemi, M.; Al-Bayati, D.; Lebedev, M.; Sarmadivaleh, M. Pore scale investigation of hydrogen injection in sandstone via X-ray micro-tomography. Int. J. Hydrogen Energy. 2021, 46, 34822–34829. [Google Scholar] [CrossRef]
  108. Jangda, Z.; Menke, H.; Busch, A.; Geiger, S.; Bultreys, T.; Lewis, H.; Singh, K. Pore-scale visualization of hydrogen storage in a sandstone at subsurface pressure and temperature conditions: Trapping, dissolution and wettability. J. Colloid. Interface Sci. 2022, 629, 316–325. [Google Scholar] [CrossRef]
  109. EIA. Electricity Use in Homes—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/energyexplained/use-of-energy/electricity-use-in-homes.php (accessed on 2 October 2025).
Eng 07 00024 g001
Figure 1. Regional Map of the Illinois Basin. Blue shows the Illinois Basin, and the red square indicates the IBDP site. Modified from [74].
Figure 1. Regional Map of the Illinois Basin. Blue shows the Illinois Basin, and the red square indicates the IBDP site. Modified from [74].
Eng 07 00024 g001
Eng 07 00024 g002
Figure 2. Composite log of the IBDP injection site showing gamma ray, effective porosity, permeability, and zone demarcation from the Eau Claire Shale through Argenta formation.
Figure 2. Composite log of the IBDP injection site showing gamma ray, effective porosity, permeability, and zone demarcation from the Eau Claire Shale through Argenta formation.
Eng 07 00024 g002
Eng 07 00024 g003
Figure 3. Top view of the effective porosity of the full-field model (a) and the simulation model (b) The light-blue rectangle marks the area extracted from the full-field model to define the simulation domain, while the black, hollow circles mark the well locations.
Figure 3. Top view of the effective porosity of the full-field model (a) and the simulation model (b) The light-blue rectangle marks the area extracted from the full-field model to define the simulation domain, while the black, hollow circles mark the well locations.
Eng 07 00024 g003
Eng 07 00024 g004
Figure 4. Effective porosity (a) and permeability (b) in the I direction of the Mt. Simon A Lower and Upper zones.
Figure 4. Effective porosity (a) and permeability (b) in the I direction of the Mt. Simon A Lower and Upper zones.
Eng 07 00024 g004
Eng 07 00024 g005
Figure 5. Porosity distribution of the simulation model.
Figure 5. Porosity distribution of the simulation model.
Eng 07 00024 g005
Eng 07 00024 g006
Figure 6. Grid size sensitivity analyses (The purple line shows the wellbore trajectory, while the green dots mark the perforation intervals).
Figure 6. Grid size sensitivity analyses (The purple line shows the wellbore trajectory, while the green dots mark the perforation intervals).
Eng 07 00024 g006
Eng 07 00024 g007aEng 07 00024 g007b
Figure 7. Hydrogen Plume Evolution, (a) shows the layered permeability for the injection zone for reference, (b–k) shows the plume behavior for the injection period at 3-month intervals for 24 months, (j,k) shows the plume behavior for 6 months post-injection. (Blue line indicates the wellbore trajectory, while the green dots mark the perforation intervals).
Figure 7. Hydrogen Plume Evolution, (a) shows the layered permeability for the injection zone for reference, (b–k) shows the plume behavior for the injection period at 3-month intervals for 24 months, (j,k) shows the plume behavior for 6 months post-injection. (Blue line indicates the wellbore trajectory, while the green dots mark the perforation intervals).
Eng 07 00024 g007aEng 07 00024 g007b
Eng 07 00024 g008aEng 07 00024 g008b
Figure 8. Plume behavior of hydrogen at 5% saturation at 3-month intervals for 24 months of injection and 6 months post-injection . (a) shows the injection zone for reference, (b–k) shows the plume behavior for the injection period at 3-month intervals for 24 months, (j,k) shows the plume behavior for 6 months post-injection (blue line indicates wellbore trajectory).
Figure 8. Plume behavior of hydrogen at 5% saturation at 3-month intervals for 24 months of injection and 6 months post-injection . (a) shows the injection zone for reference, (b–k) shows the plume behavior for the injection period at 3-month intervals for 24 months, (j,k) shows the plume behavior for 6 months post-injection (blue line indicates wellbore trajectory).
Eng 07 00024 g008aEng 07 00024 g008b
Eng 07 00024 g009
Figure 9. Injection well perforation location for scenario 1 (top perforation) and scenario 2 (bottom perforation).
Figure 9. Injection well perforation location for scenario 1 (top perforation) and scenario 2 (bottom perforation).
Eng 07 00024 g009
Eng 07 00024 g010
Figure 10. Gas injection and production rate comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation). (The five pointed stars indicates when injection and withdrawal constraints are met).
Figure 10. Gas injection and production rate comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation). (The five pointed stars indicates when injection and withdrawal constraints are met).
Eng 07 00024 g010
Eng 07 00024 g011
Figure 11. Cumulative gas production comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation). (The five-pointed stars indicates when withdrawal constraints are met).
Figure 11. Cumulative gas production comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation). (The five-pointed stars indicates when withdrawal constraints are met).
Eng 07 00024 g011
Eng 07 00024 g012
Figure 12. Production efficiency comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation).
Figure 12. Production efficiency comparison for scenario 1 (top perforation) and scenario 2 (bottom perforation).
Eng 07 00024 g012
Eng 07 00024 g013
Figure 13. Remaining gas saturation at the end of the 6-year cycle for scenario 1 (top perforation) and scenario 2 (bottom perforation). (Green dots represents perforation intervals).
Figure 13. Remaining gas saturation at the end of the 6-year cycle for scenario 1 (top perforation) and scenario 2 (bottom perforation). (Green dots represents perforation intervals).
Eng 07 00024 g013
Eng 07 00024 g014aEng 07 00024 g014b
Figure 14. Pressure profile of the base case at the beginning and the end of the injection and production cycle for six (6) years. (a–m) shows the pressure evolution during the 7-month injection period and subsequent 5-month production period across six operational cycles (Green dots indicates perforation interval).
Figure 14. Pressure profile of the base case at the beginning and the end of the injection and production cycle for six (6) years. (a–m) shows the pressure evolution during the 7-month injection period and subsequent 5-month production period across six operational cycles (Green dots indicates perforation interval).
Eng 07 00024 g014aEng 07 00024 g014b
Eng 07 00024 g015
Figure 15. Average reservoir pressure profile of the base case for the six-year cycle.
Figure 15. Average reservoir pressure profile of the base case for the six-year cycle.
Eng 07 00024 g015
Eng 07 00024 g016
Figure 16. Gas rate comparison of the different trapping mechanisms with the base case.
Figure 16. Gas rate comparison of the different trapping mechanisms with the base case.
Eng 07 00024 g016
Eng 07 00024 g017
Figure 17. Cumulative produced gas comparison of the different trapping mechanisms with the base case.
Figure 17. Cumulative produced gas comparison of the different trapping mechanisms with the base case.
Eng 07 00024 g017
Eng 07 00024 g018
Figure 18. Yearly cumulative efficiency of the different trapping mechanisms with the base case.
Figure 18. Yearly cumulative efficiency of the different trapping mechanisms with the base case.
Eng 07 00024 g018
Table 1. Stratigraphic column of the Ordovician, Cambrian, and Precambrian sections at the IBDP injection site. Modified from [78].
Table 1. Stratigraphic column of the Ordovician, Cambrian, and Precambrian sections at the IBDP injection site. Modified from [78].
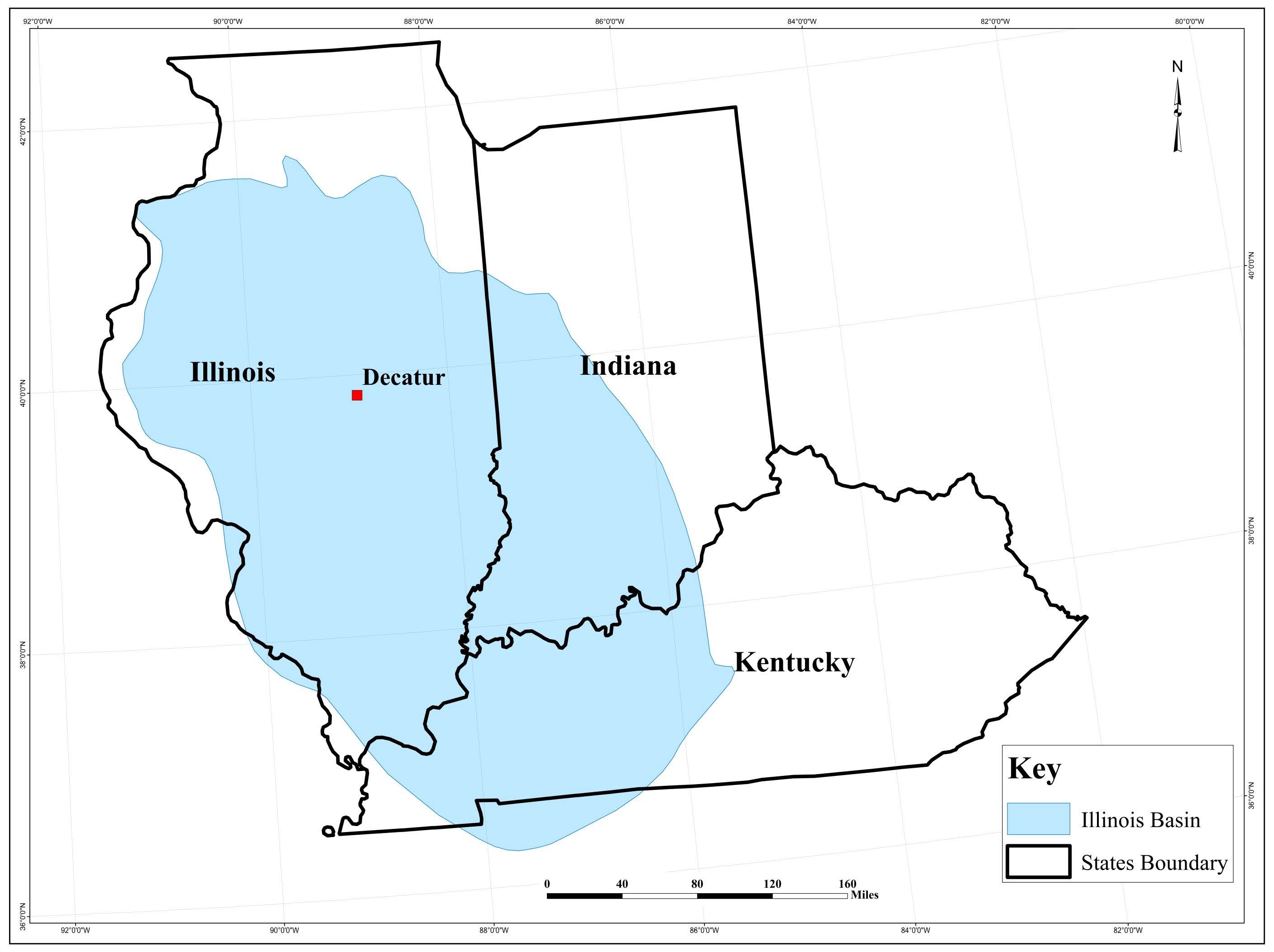
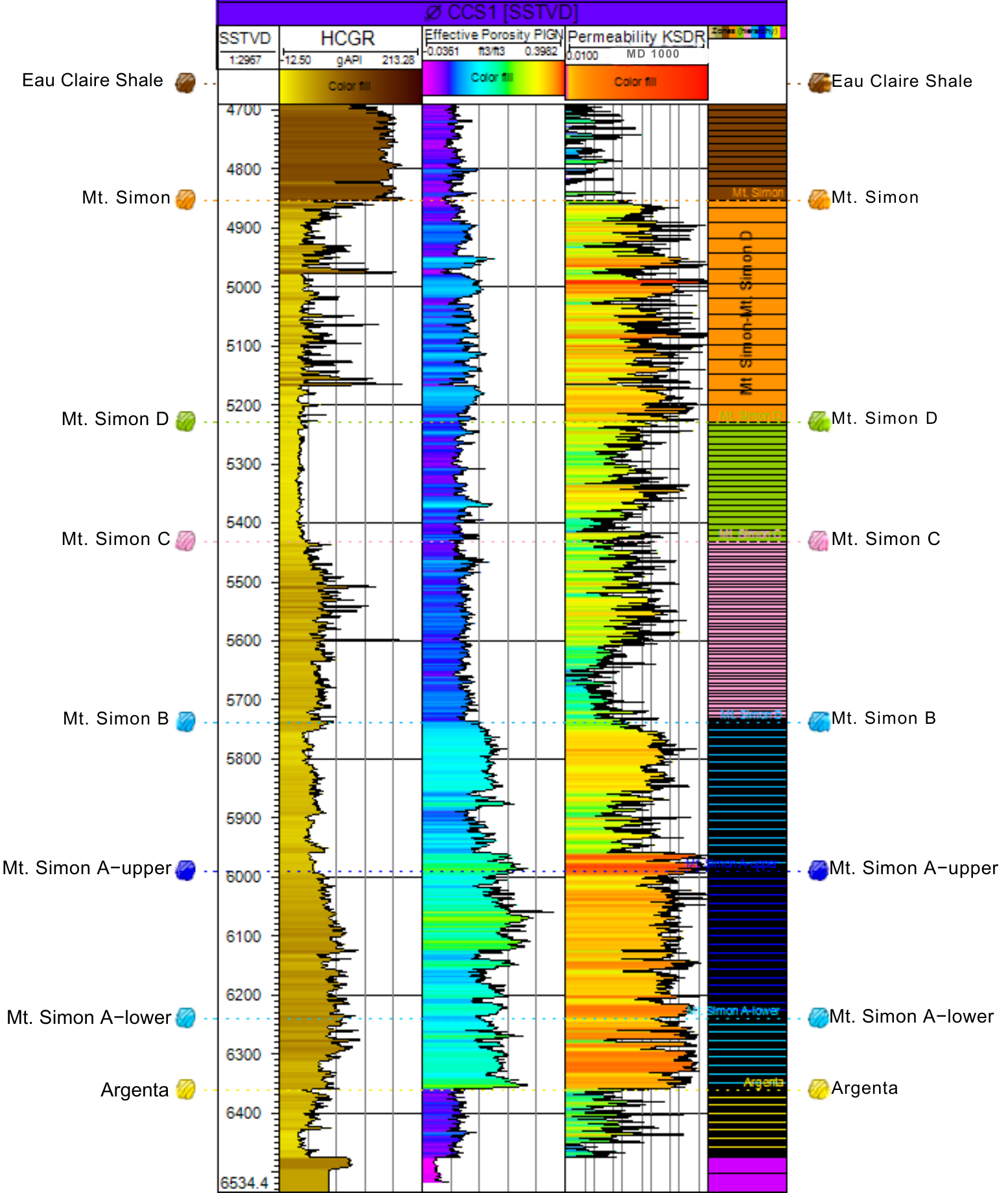
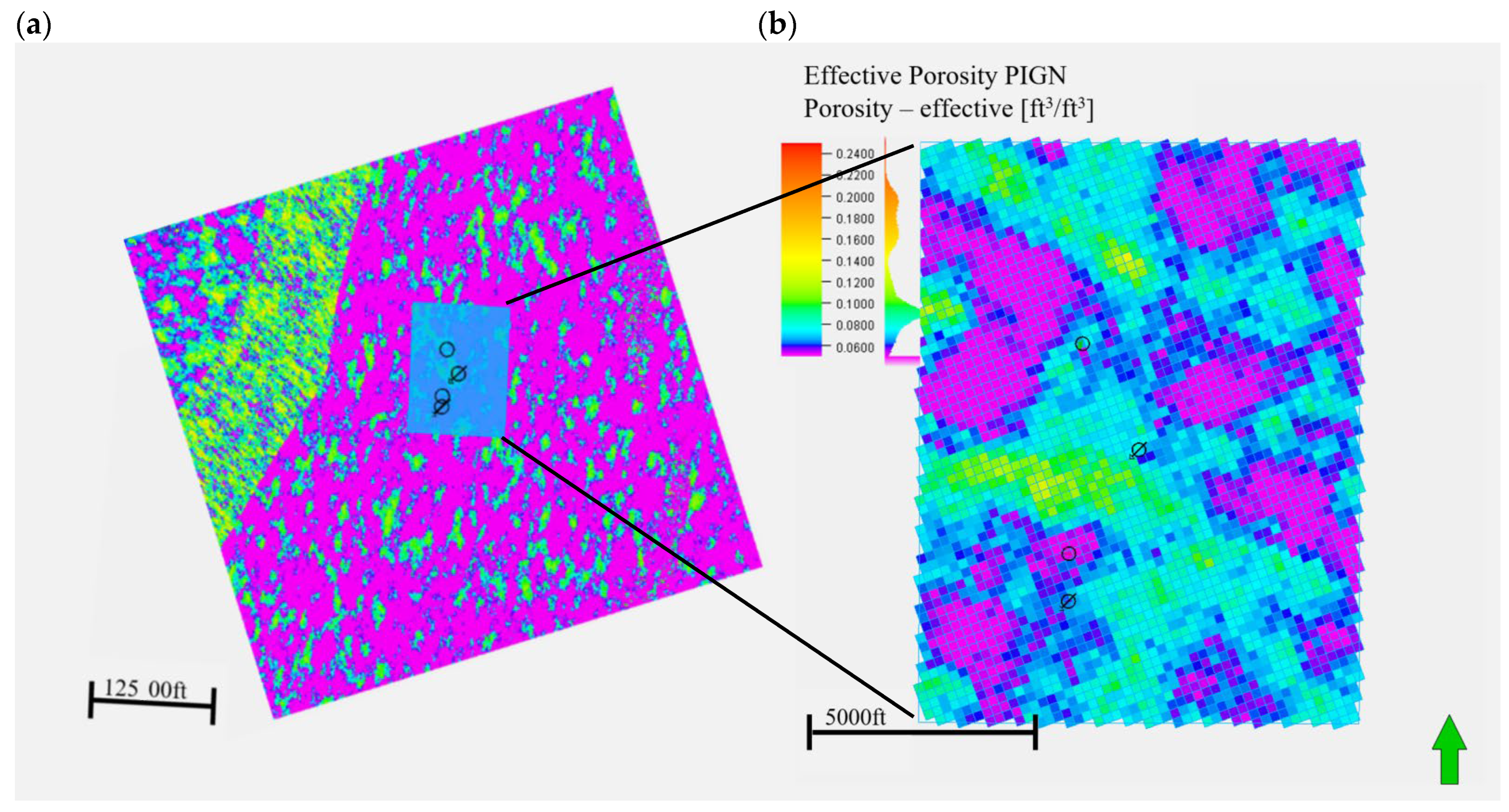
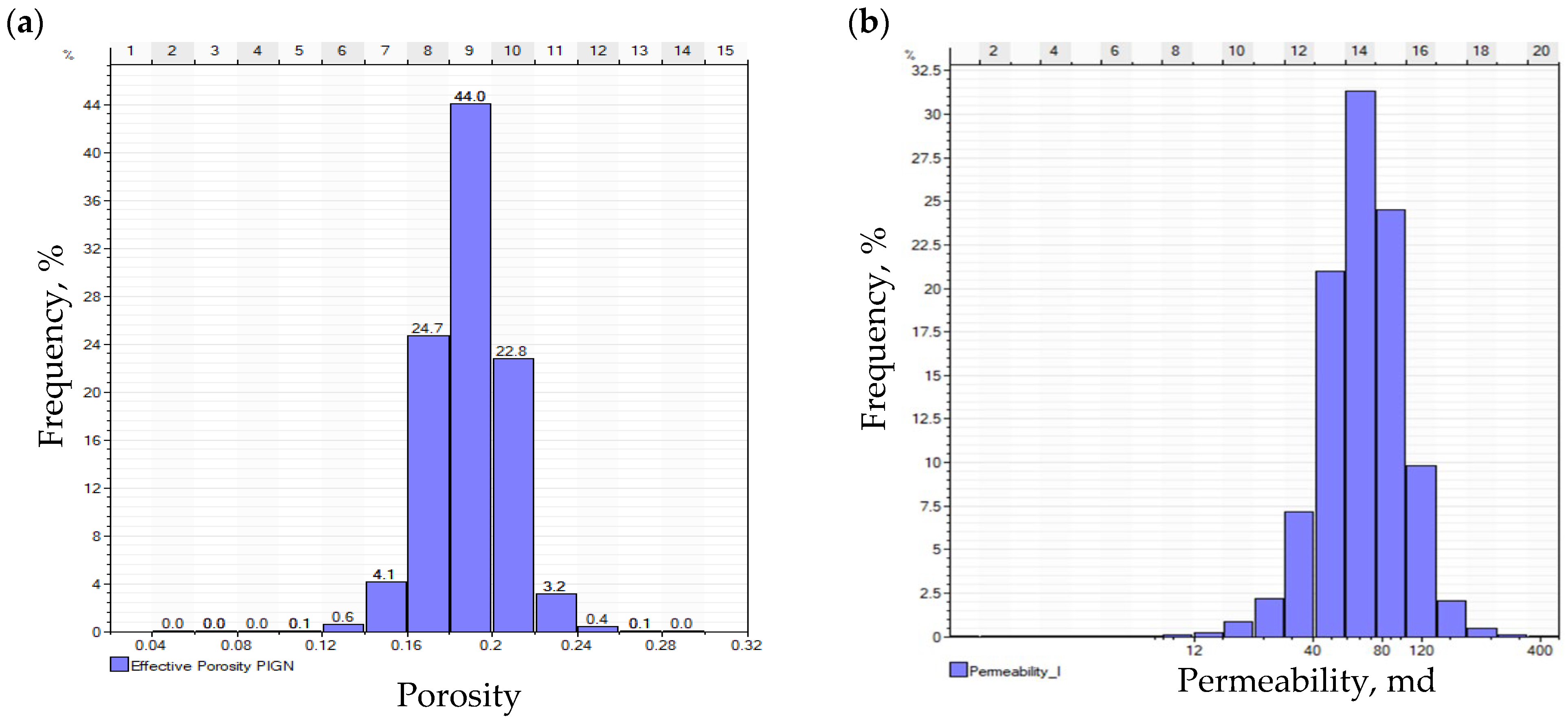
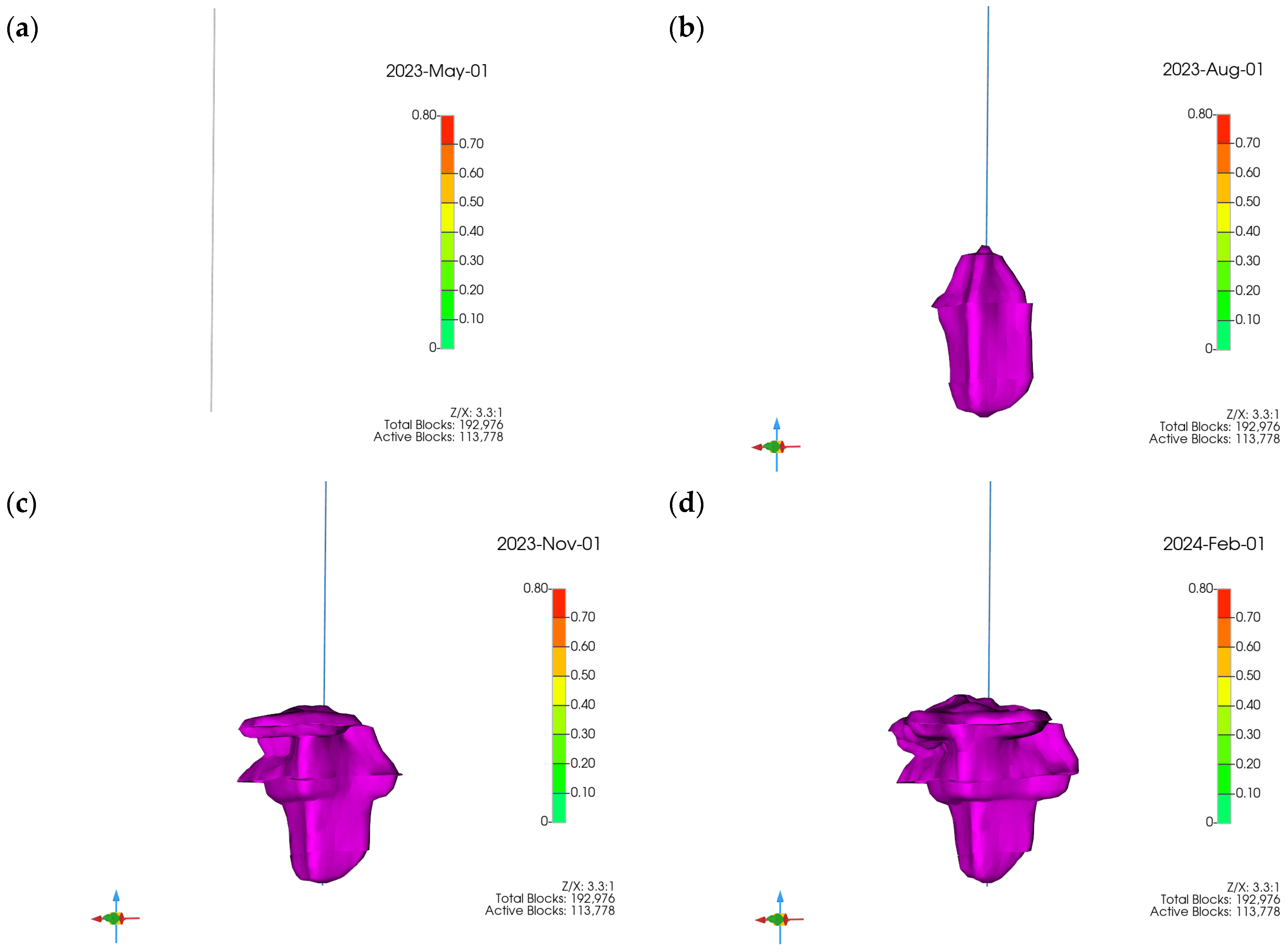
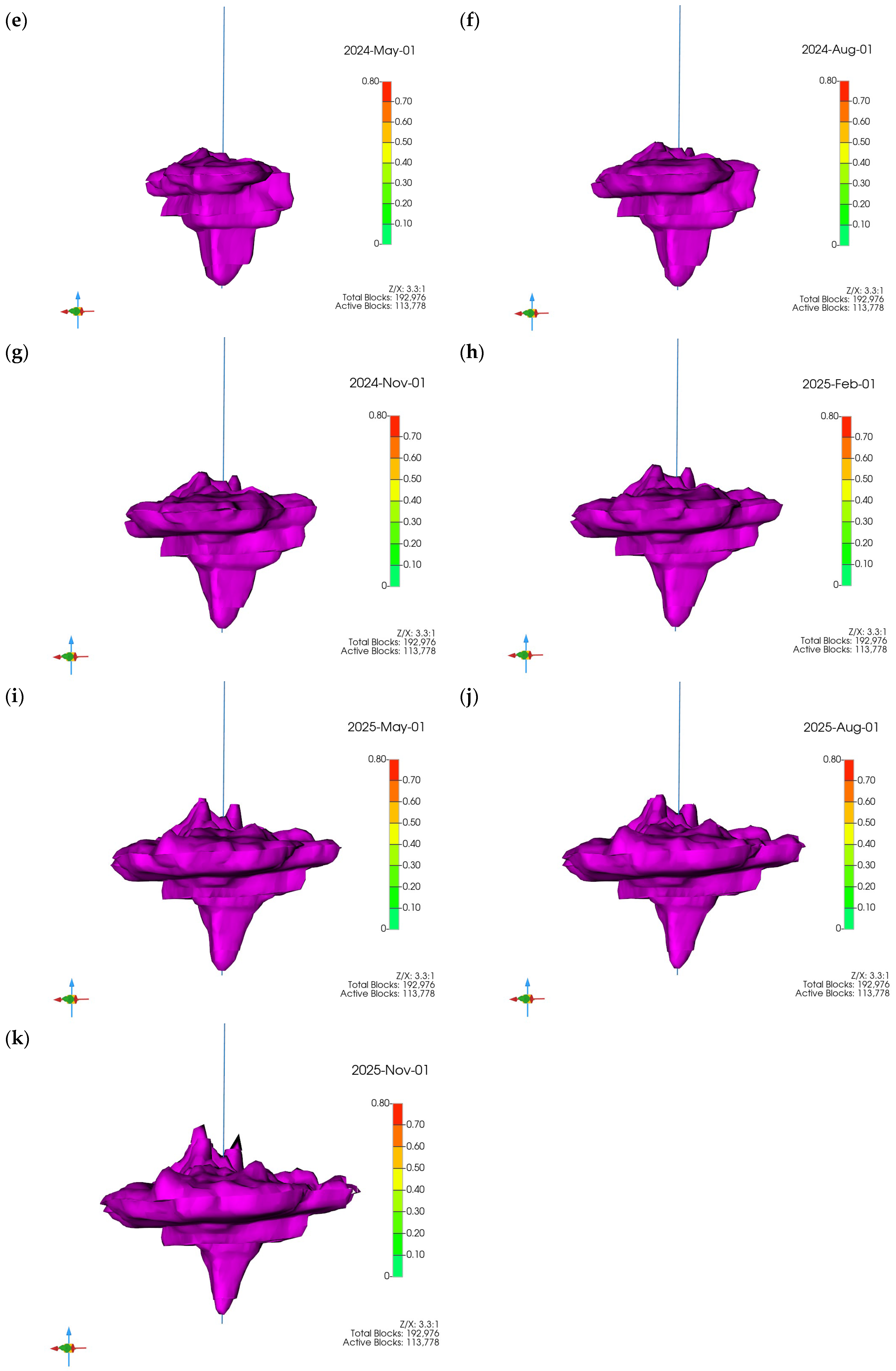
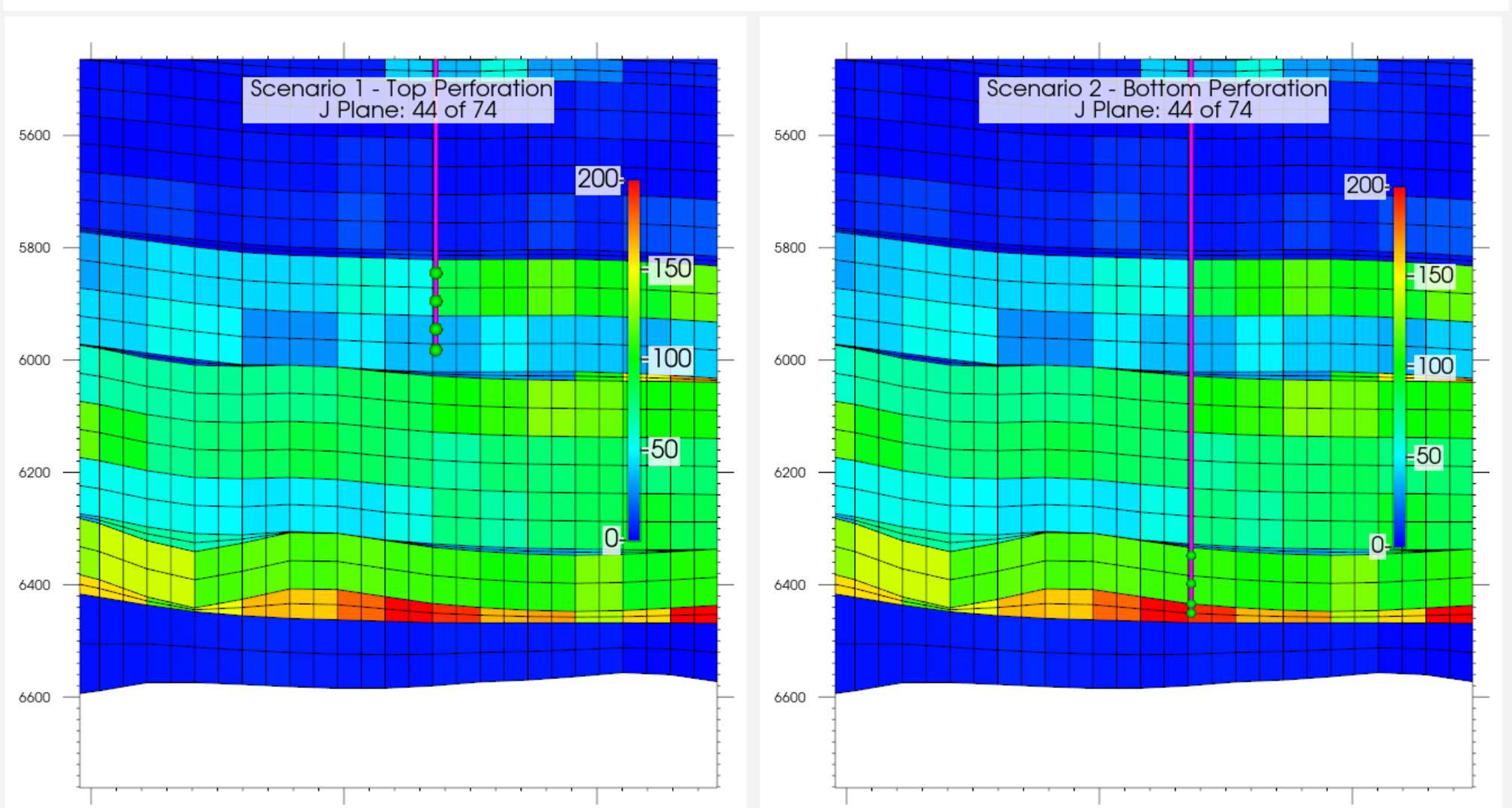
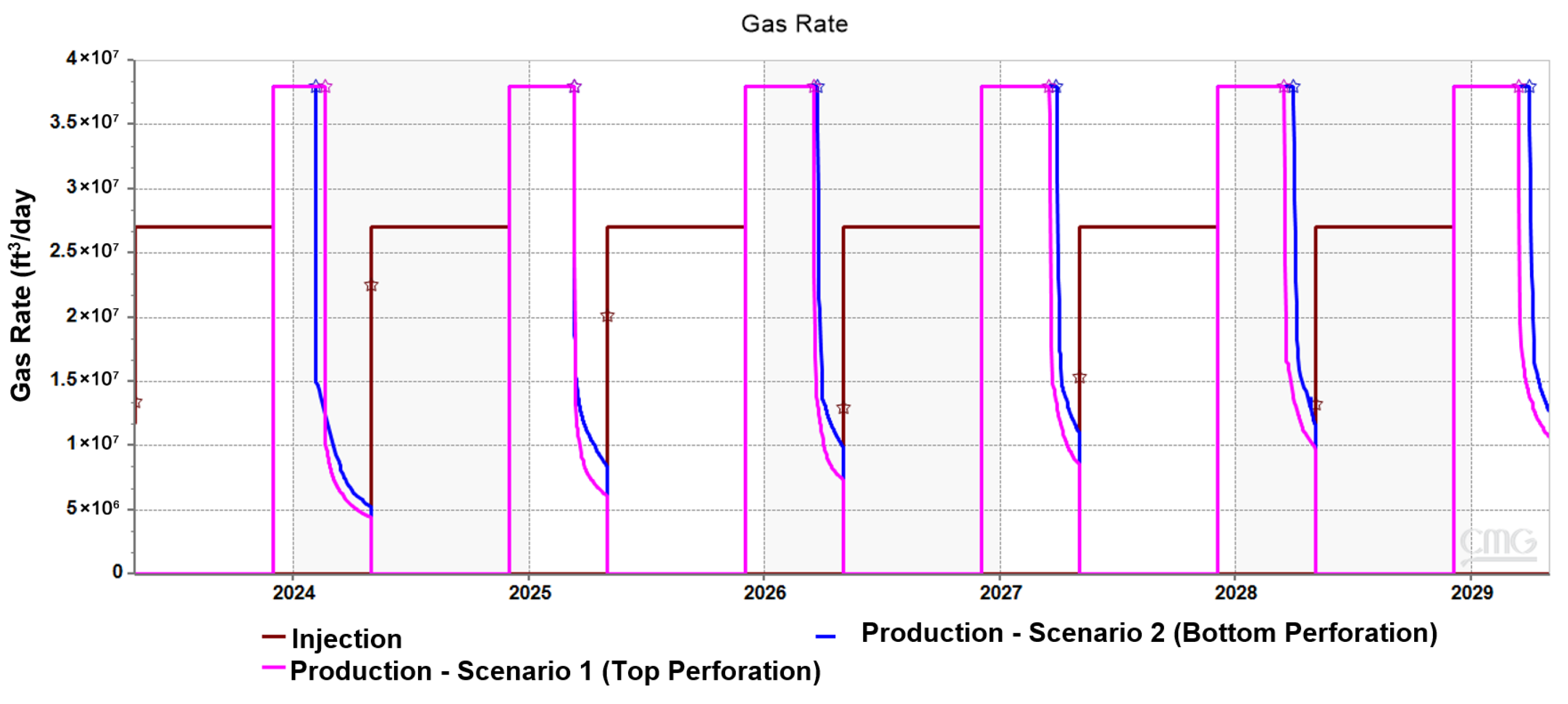
SystemGroupFormation
OrdovicianMaquoketaBrainard
Ft. Atkinson
Scales
GalenaKimmswick
Decorah
Platteville 
AncellJoachim
St. Peter
Praire du ChienShakoppee
New Richmond
Oneota
Gunter
CambrianKnoxEminence
Potosi
Franconia
Ironton-Galesville
Eau Claire
 Mt. Simon
Precambrian  
Table 2. Grid size and simulation time during grid refinement sensitivity.
Table 2. Grid size and simulation time during grid refinement sensitivity.
Grid Size, ftSimulation Time, s
50 × 5097,181
100 × 1001361
200 × 200819
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Appiah Kubi, E.; Rahnema, H.; Koray, A.-M.; Shabani, B. Underground Hydrogen Storage in Saline Aquifers: A Simulation Case Study in the Midwest United States. Eng 2026, 7, 24. https://doi.org/10.3390/eng7010024

AMA Style

Appiah Kubi E, Rahnema H, Koray A-M, Shabani B. Underground Hydrogen Storage in Saline Aquifers: A Simulation Case Study in the Midwest United States. Eng. 2026; 7(1):24. https://doi.org/10.3390/eng7010024

Chicago/Turabian Style

Appiah Kubi, Emmanuel, Hamid Rahnema, Abdul-Muaizz Koray, and Babak Shabani. 2026. "Underground Hydrogen Storage in Saline Aquifers: A Simulation Case Study in the Midwest United States" Eng 7, no. 1: 24. https://doi.org/10.3390/eng7010024

APA Style

Appiah Kubi, E., Rahnema, H., Koray, A.-M., & Shabani, B. (2026). Underground Hydrogen Storage in Saline Aquifers: A Simulation Case Study in the Midwest United States. Eng, 7(1), 24. https://doi.org/10.3390/eng7010024

Article Metrics

Back to TopTop