Field Blast Tests and Finite Element Analysis of A36 Steel Sheets Subjected to High Explosives
Abstract
1. Introduction
2. Materials and Methods
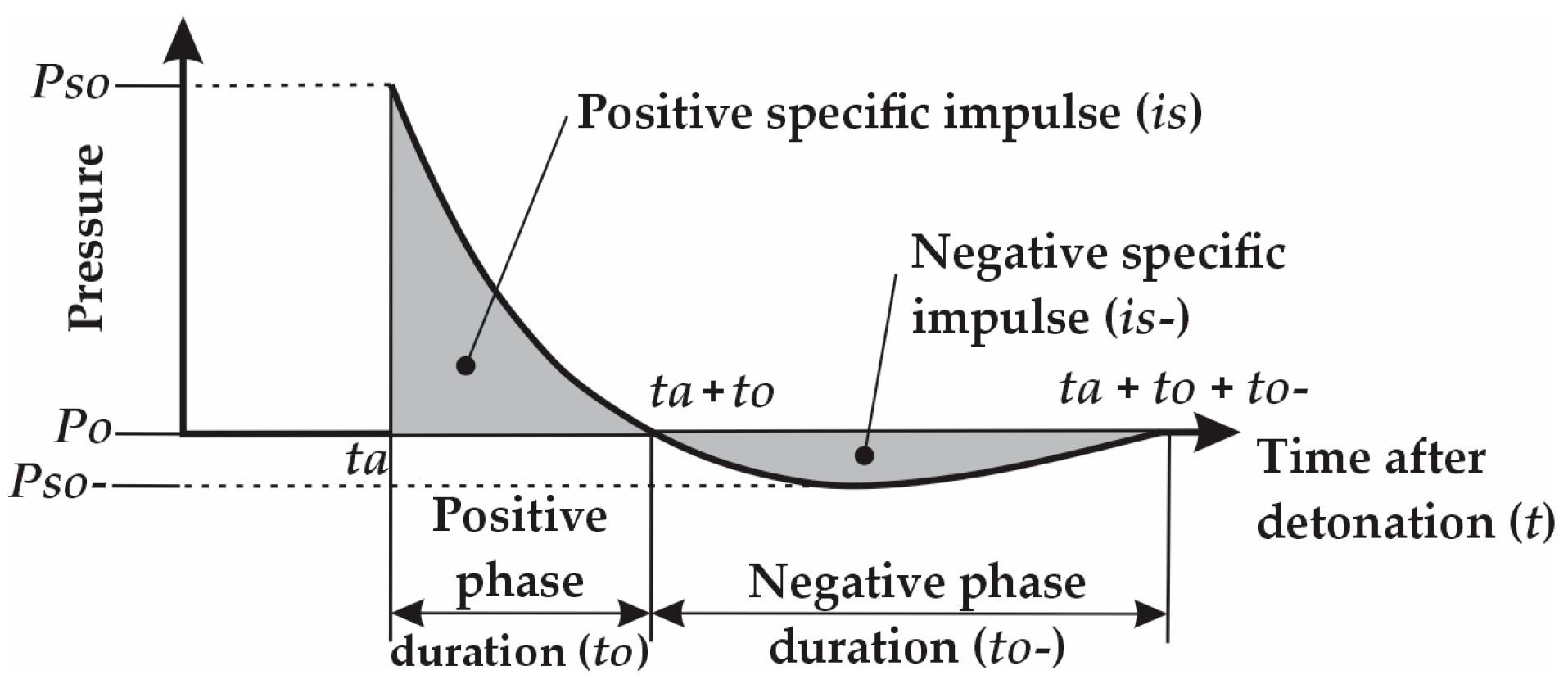
2.1. Blast Load
2.2. Blast Field Tests
2.3. Constitutive Material Models
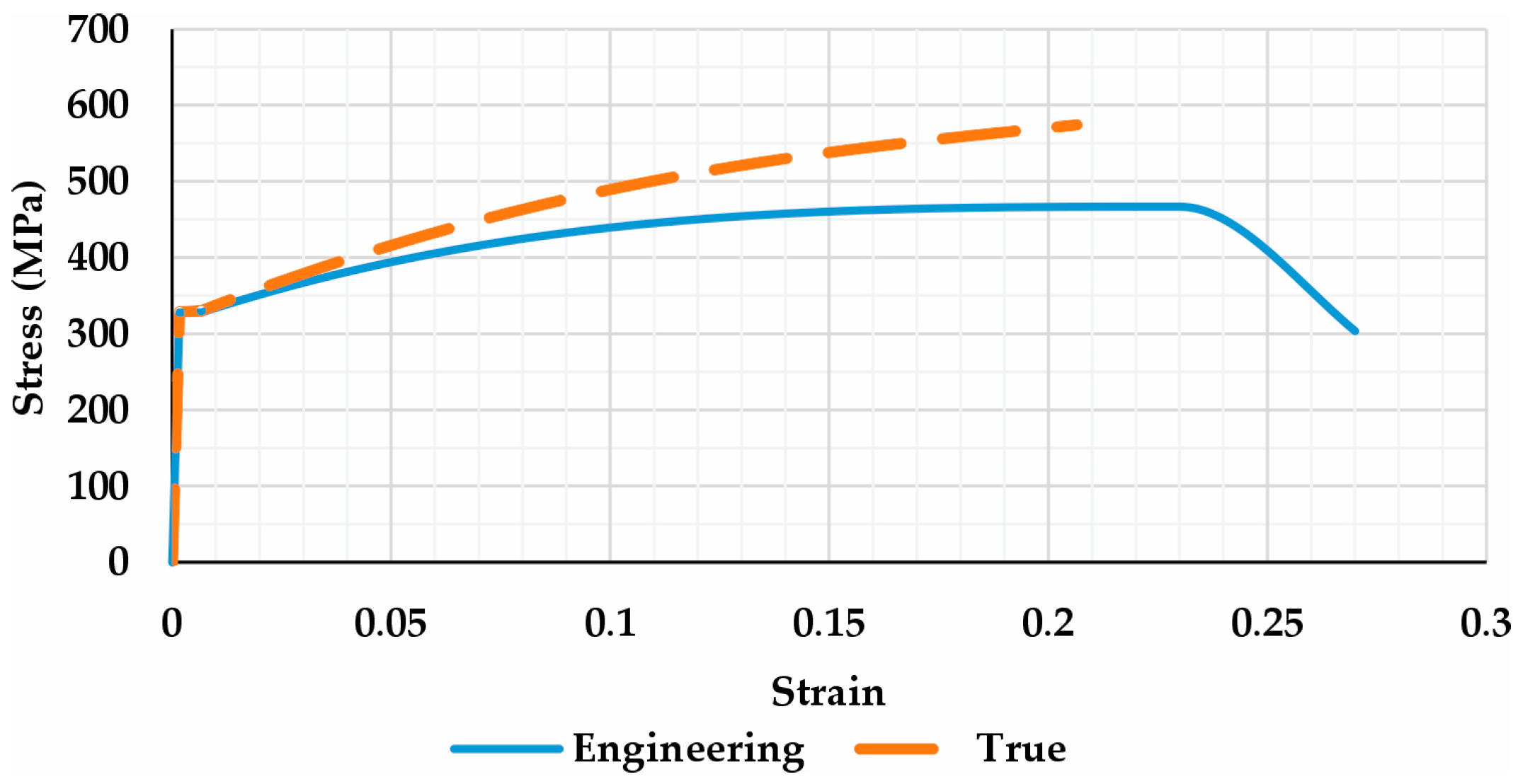
2.3.1. A36 Steel Stress–Strain Curve
2.3.2. Johnson–Cook Constitutive Model
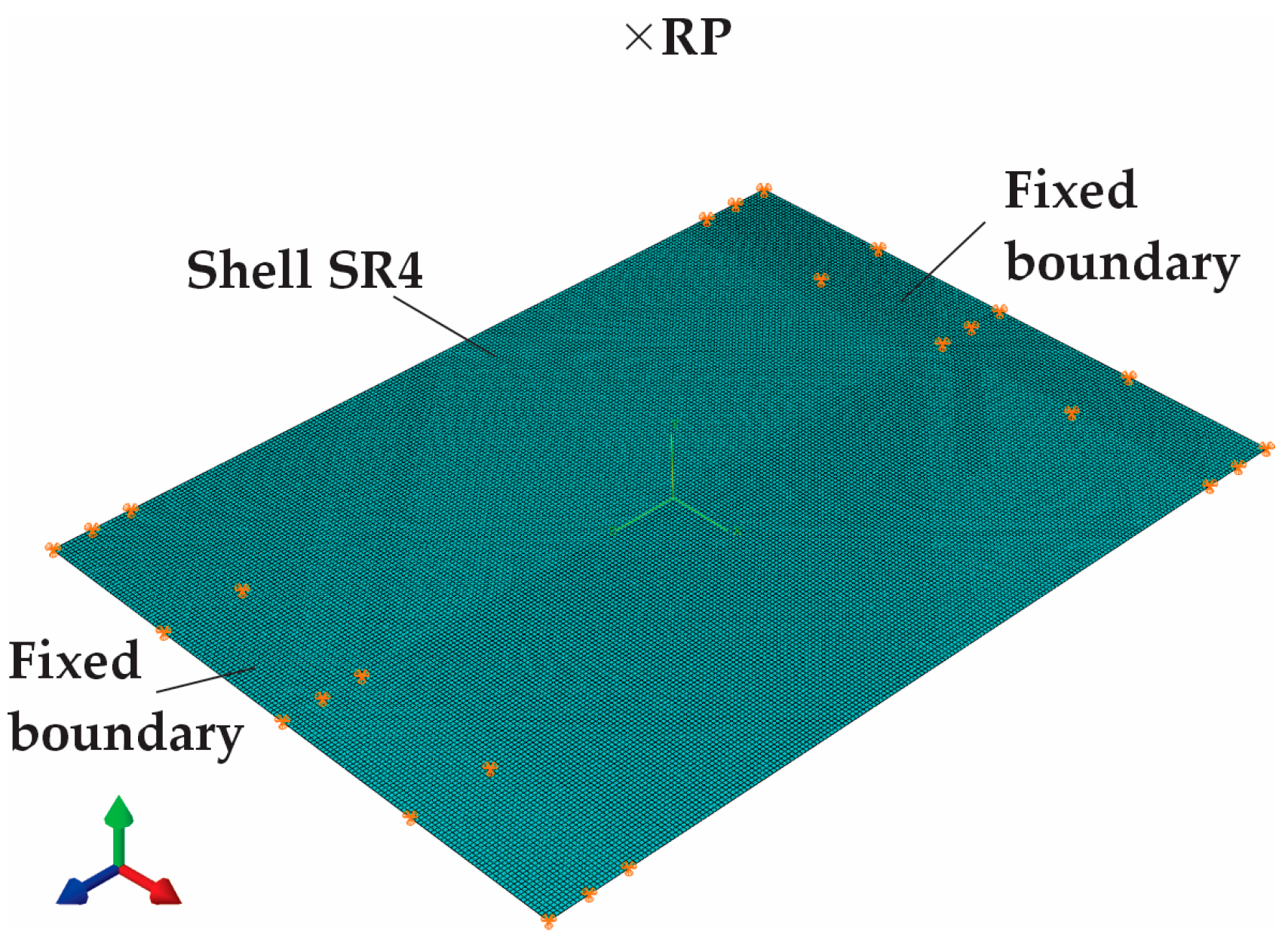
2.4. FEM Simulations
2.4.1. General Aspects
2.4.2. Model Convergence
2.5. Structural Damage Evaluation
3. Results
3.1. Blast Test Results
3.2. Preliminary Setup Simulation Results
3.3. Global Simulation Results
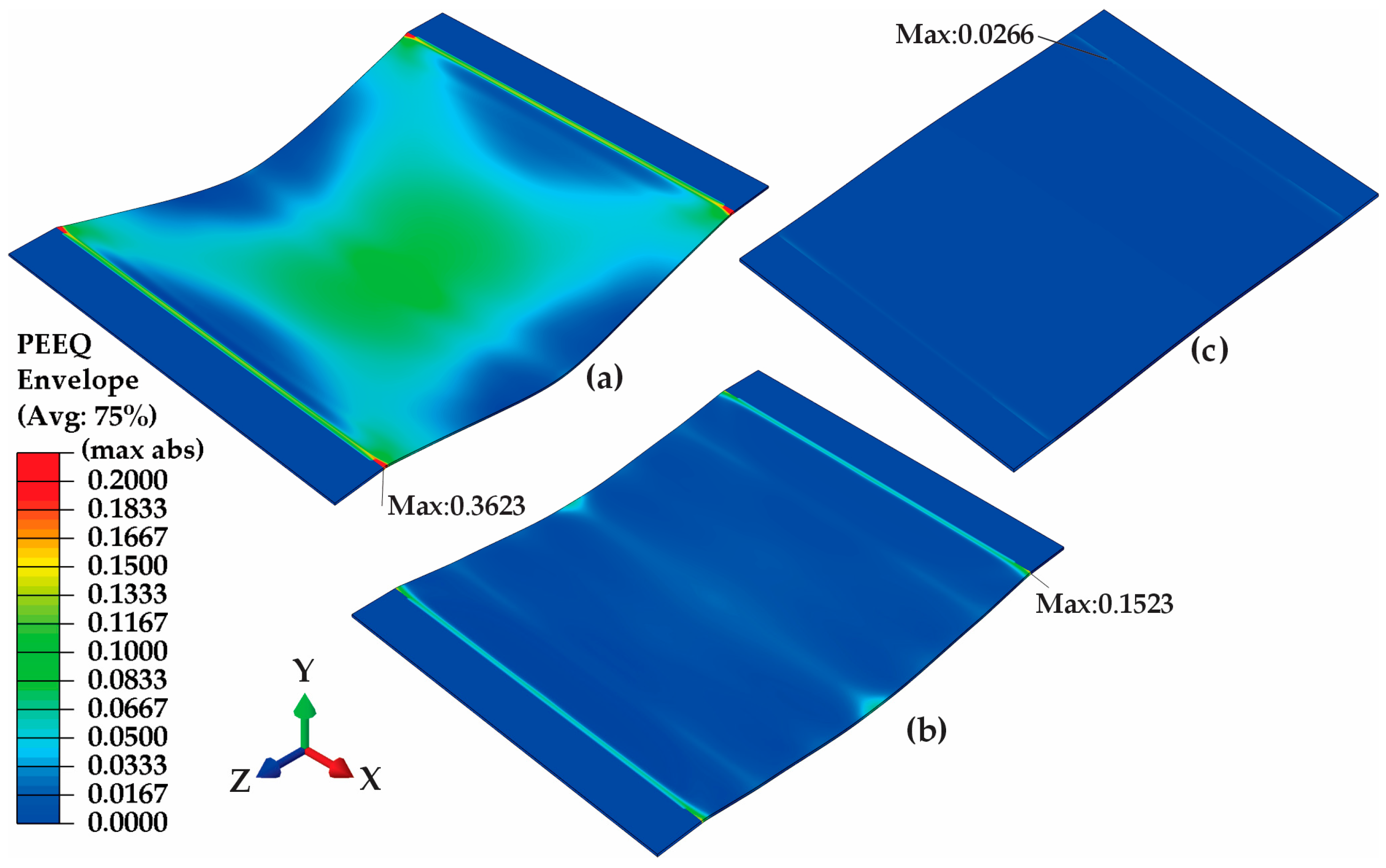
3.4. Detailed Simulation Cases
4. Discussion
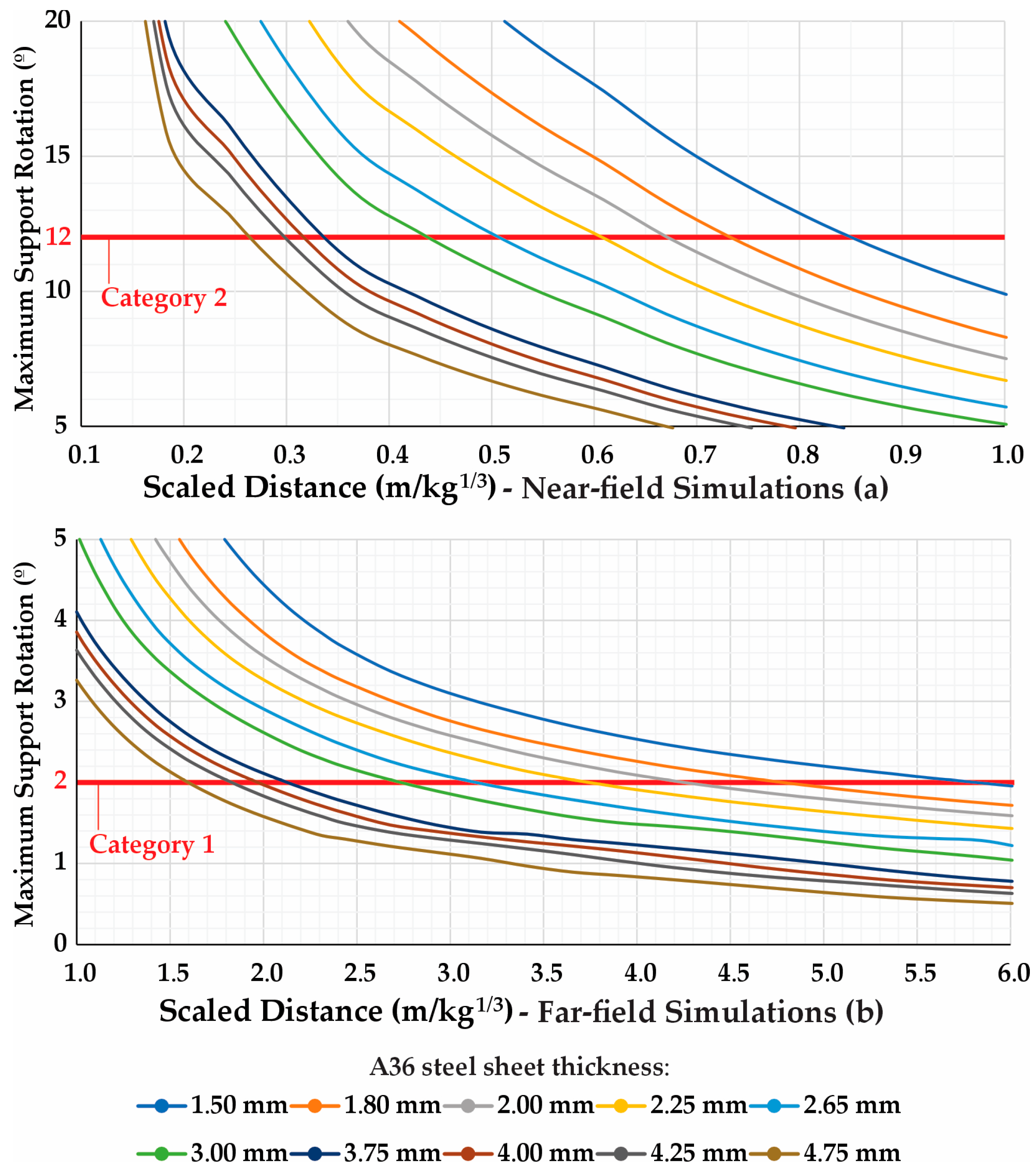
4.1. Preliminary Simulations Analysis
4.2. Global Simulation Analysis
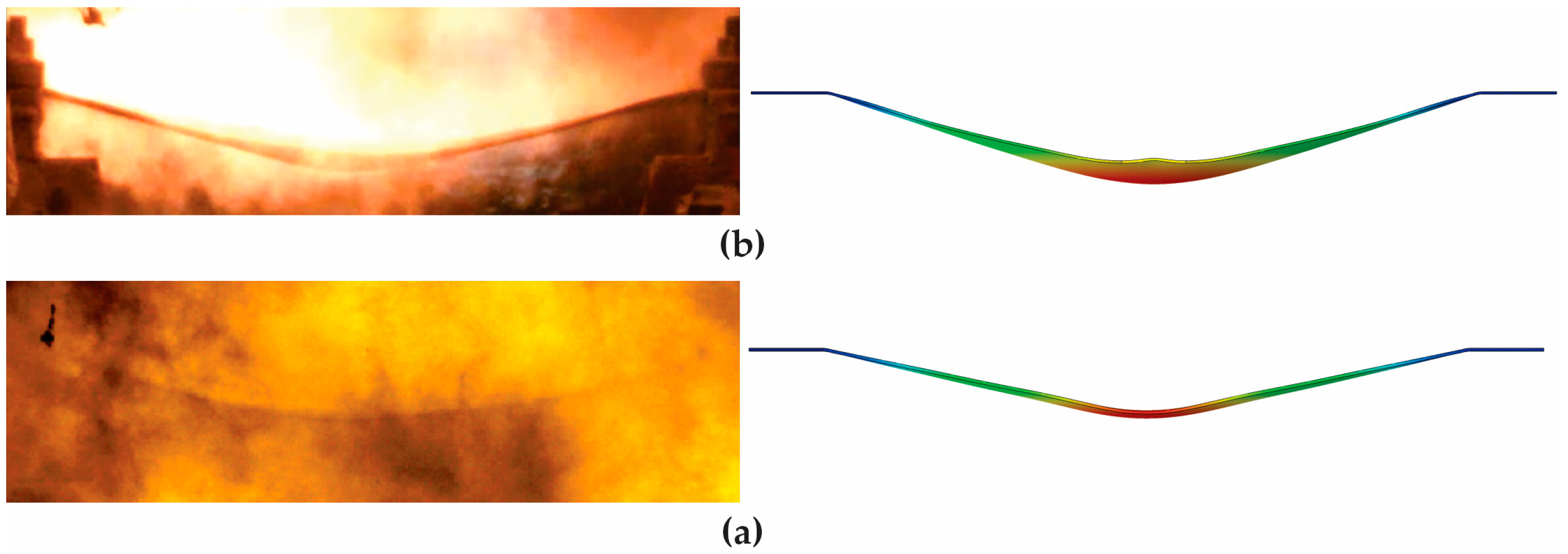
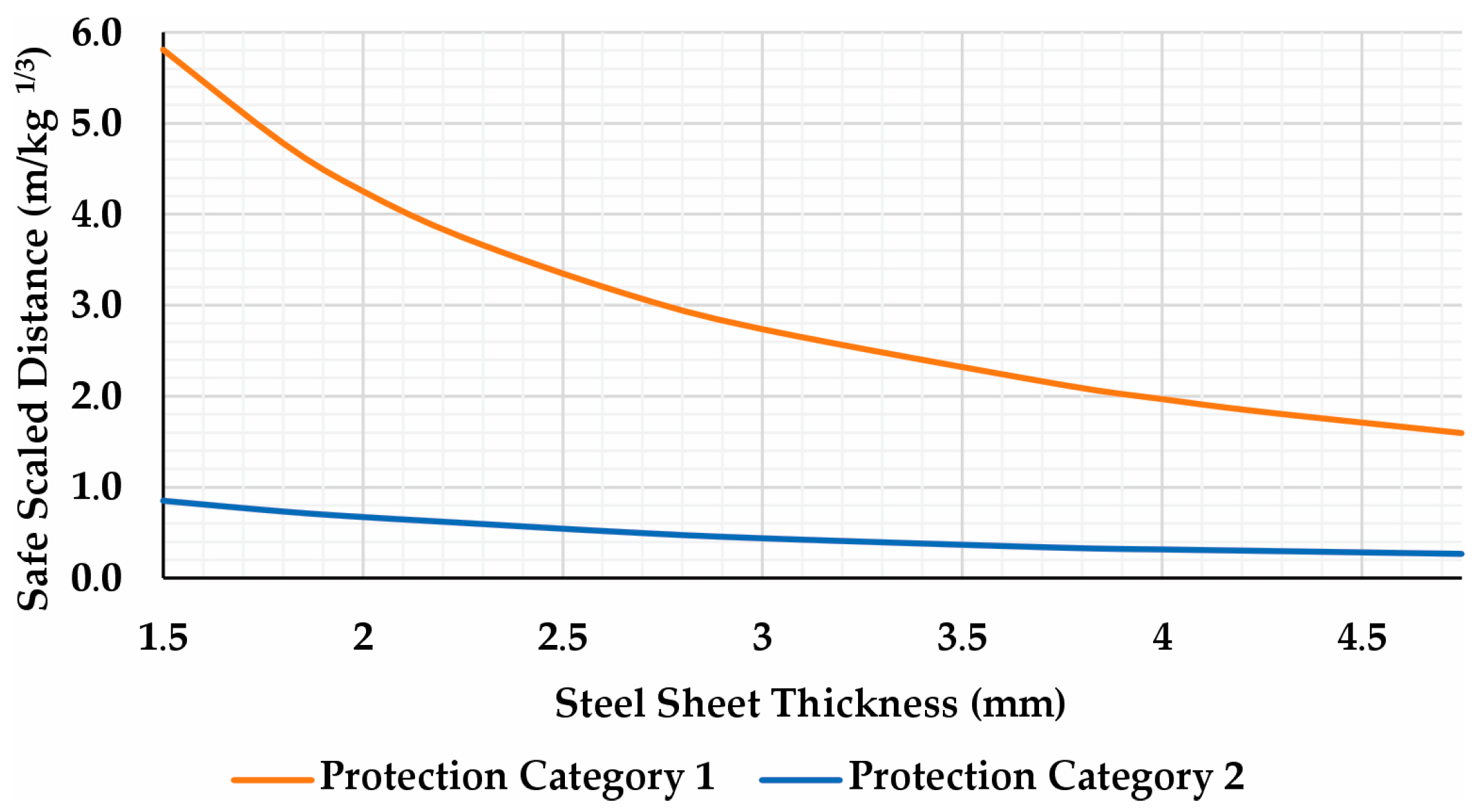
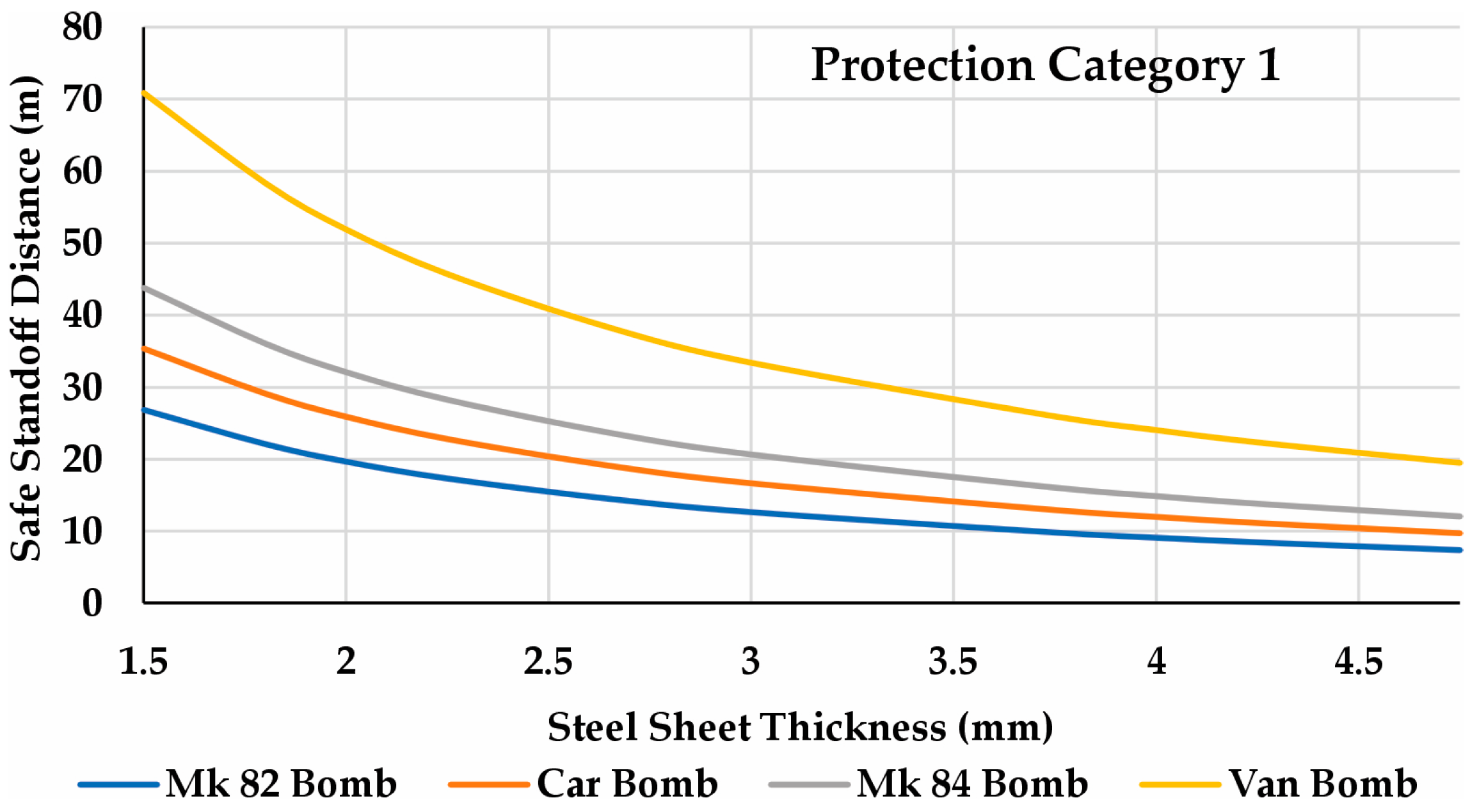
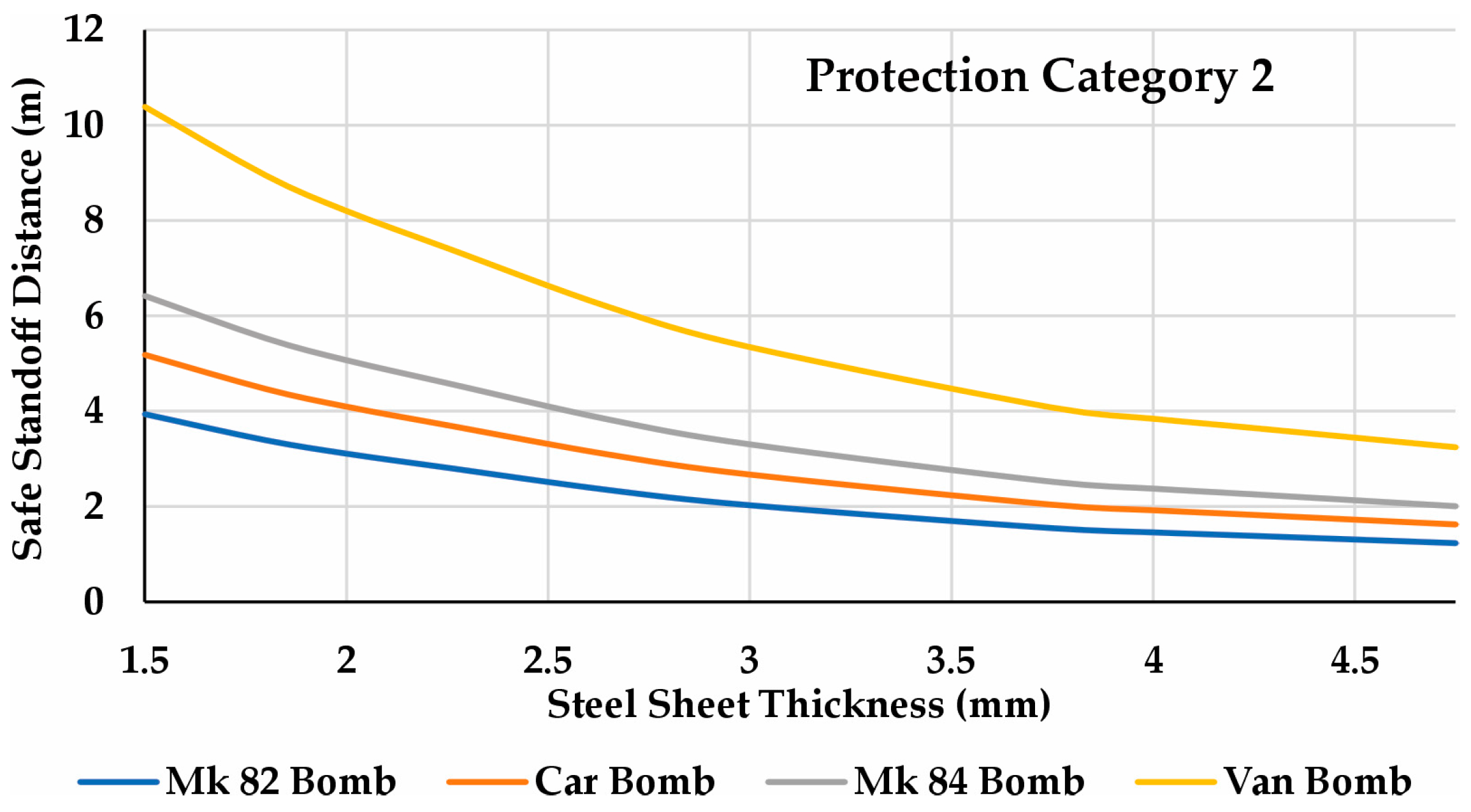
4.3. Comparison of the Simulations with Real Blast Events
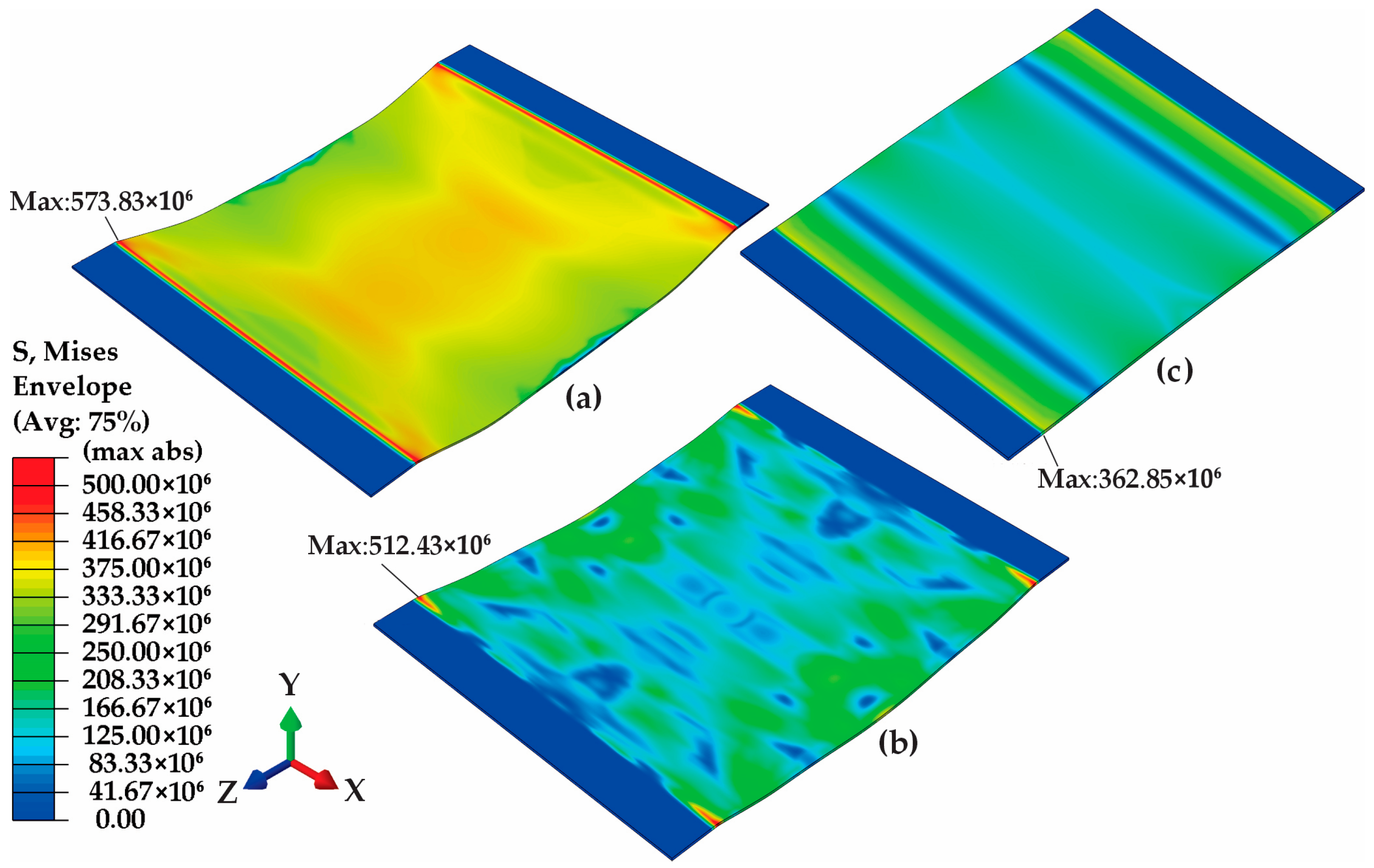
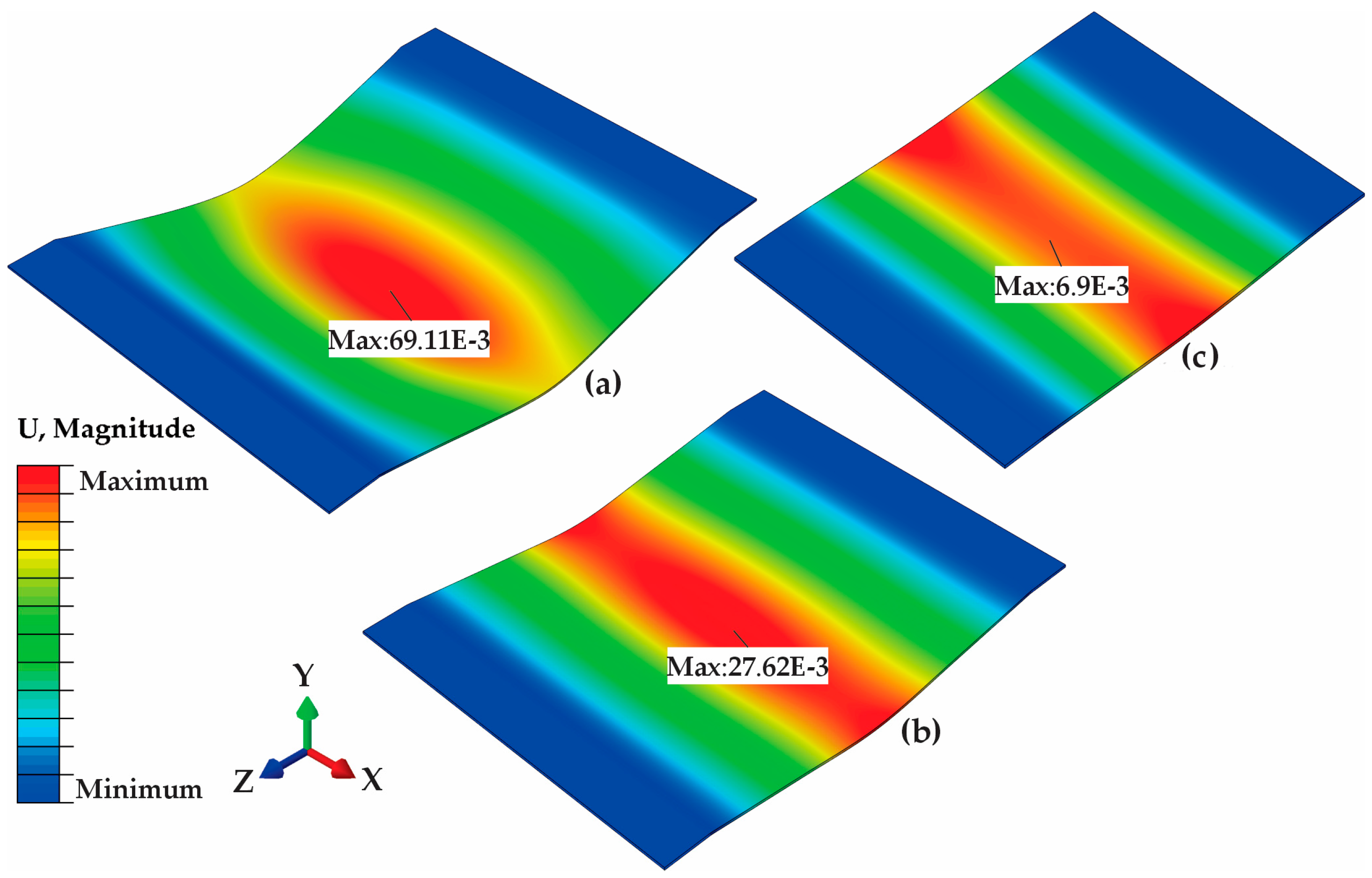
4.4. Detailed Simulation Analysis
5. Conclusions
- This research investigated the behavior of A36 steel thin sheets under the effects of blast loads generated by high-explosive detonations. Results from field blast tests were compared with FEM simulations, and the numerical approach was expanded to include more than 460 simulations. The observed errors were consistent with those reported in the literature, but the significantly larger number of simulations allowed for a more comprehensive analysis of the structural dynamic response across various sheet thicknesses and a broad range of standoff distances. To the authors’ knowledge, no previous studies in the open literature have examined thin steel sheets under blast loading with this level of detail and simulation coverage.
- FEM simulations once again proved to be a reliable method for designing and predicting the structural response to blast loads. This approach is an important tool that reduces the need for field testing, which is expensive, time-consuming, and hazardous, requiring restricted materials and highly specialized personnel.
- Among the different material models evaluated in this study, the stress–strain curve proved to be the most conservative and was therefore adopted in the FEM simulations. It is important to note that the Johnson–Cook model used parameters for A36 steel obtained from publicly available literature, while the stress–strain curve was based on specific laboratory tests conducted on the actual steel batch used in the experiments. For the blast conditions tested in this study, the strain-rate effect did not significantly influence the results.
- This paper presents a comprehensive study on the behavior of steel sheets under different standoff distances and thicknesses. Comparative graphs related real blast events to the required safe distances for different protection categories and steel thicknesses. The results highlight the importance of using more robust structural elements, as thicker steel sheets required significantly shorter safe distances, especially for more restrictive protection categories. Another important conclusion is the relevance of implementing barriers around critical buildings to mitigate potential attacks, since the required safe distance for personnel protection can reach several tens of meters—even when using thicker steel sheets.
- Future work to advance the field should include testing additional cross-sections, spans, boundary conditions, and types of structural steel, using both FEM simulations and blast field tests. This would expand the validation range of the applied methods and provide further insights into the protection of buildings against blast loads. A more in-depth study on the strain-rate effect and the influence and sensitivity of key material parameters of the Johnson–Cook material model applied to blast simulations is also highly recommended.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, X.; Geng, S.; Feng, R. Study on Dynamic Factors of Damped Beam Members Under Exponential Attenuation Loading. Buildings 2024, 14, 3469. [Google Scholar] [CrossRef]
- United Nations. International Ammunition Technical Guidelines—IATG 01.08, 3rd ed.; United Nations: New York, NY, USA, 2021; Available online: https://data.unsaferguard.org/iatg/en/IATG-01.80-Formulae-ammunition-management-IATG-V.3.pdf (accessed on 3 April 2025).
- USDOD. Structures to Resist the Effects of Accidental Explosions—UFC 3-340-02; United States Department of Defense (USDOD): Washington, DC, USA, 2008; p. 1943. Available online: https://www.wbdg.org/FFC/DOD/UFC/ARCHIVES/ufc_3_340_02.pdf (accessed on 3 April 2025).
- Mendonça, F.B.; Urgessa, G.S.; Almeida, L.E.N.; Rocco, J.A.F.F. Damage diagram of blast test results for determining reinforced concrete slab response for varying scaled distance, concrete strength and reinforcement ratio. An. Acad. Bras. Ciênc. 2021, 93, e20200511. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Wang, Y.; Lin, J.; Ma, M.; Hu, J.; Qiu, X.; Wu, C.; Feng, C. Recent advances in polyurea elastomers and their applications in blast protection: A review. J. Mater. Sci. 2024, 59, 14893–14923. [Google Scholar] [CrossRef]
- Anas, S.M.; Alam, M.; Umair, M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures 2021, 31, 428–461. [Google Scholar] [CrossRef]
- Yue, Z.; Zhou, J.; Kong, X.; Xu, Y.; Chen, Y.; Wang, B.; Huang, Y.; Wang, P. Anti-Blast Performance of Polyurea-Coated Concrete Arch Structures. Polymers 2023, 15, 1263. [Google Scholar] [CrossRef]
- Mohotti, D.; Fernando, P.; Weerasinghe, D.; Remennikov, A. Evaluation of effectiveness of polymer coatings in reducing blast-induced deformation of steel plates. Def. Technol. 2021, 17, 1895–1904. [Google Scholar] [CrossRef]
- Cui, Y.; Song, M.; Qu, Z.; Sun, S.; Zhao, J. Research on Damage Assessment of Concrete-Filled Steel Tubular Column Subjected to Near-Field Blast Loading. Shock Vib. 2020, 2020, 8883711. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Li, M.; Li, P.; Zhao, Y.; Liu, Q.; Liu, C.; Ye, P. The Damage to Thick Steel Plates by Local Contact Explosions. Materials 2023, 16, 2966. [Google Scholar] [CrossRef]
- Nawar, M.T.; Eisa, A.S.; Elshazli, M.T.; Ibrahim, Y.E.; El-Zohairy, A. Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings. Infrastructures 2024, 9, 52. [Google Scholar] [CrossRef]
- Nawar, M.T.; El-Zohairy, A.; Arafa, I.T. Finite Element Modeling and Analysis of Perforated Steel Members under Blast Loading. Modelling 2023, 4, 628–649. [Google Scholar] [CrossRef]
- Lim, K.M.; Yoo, D.G.; Lee, B.Y.; Lee, J.H. Prediction of Damage Level of Slab-Column Joints under Blast Load. Appl. Sci. 2020, 10, 5837. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, G.; Zuo, X. Test and Numerical Study on Blast Resistance of Main Girders Coated with Polyurea in Self-Anchored Suspension Bridges. Appl. Sci. 2024, 14, 9280. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, M.; Li, Z.-X.; Hao, H. Damage evaluation of the steel tubular column subjected to explosion and post-explosion fire condition. Eng. Struct. 2013, 55, 44–55. [Google Scholar] [CrossRef]
- Nasry, N.Y.; Aboshok, M.A.; Elsalakawy, T.S.; Hariri, M.O.R.A. Numerical Study for a Reinforced Concrete Structure Under Partially Vented Blast Loads Using LS-DYNA and CONWEP Method. Eng. Res. J. 2025, 54, 111–119. [Google Scholar] [CrossRef]
- Vaghefi, M.; Mobaraki, B. Evaluation of the Effect of Explosion on the Concrete Bridge Deck Using LS-DYNA. Int. Rev. Civ. Eng. 2021, 12, 135. [Google Scholar] [CrossRef]
- Khan, R.; Farooq, S.H.; Usman, M. Blast Loading Response of Reinforced Concrete Panels Externally Reinforced with Steel Strips. Infrastructures 2019, 4, 54. [Google Scholar] [CrossRef]
- Abada, M.; Ibrahim, A.; Jung, S.J. Improving Blast Performance of Reinforced Concrete Panels Using Sacrificial Cladding with Hybrid-Multi Cell Tubes. Modelling 2021, 2, 149–165. [Google Scholar] [CrossRef]
- Anas, S.M.; Al-Dala’ien, R.N.; Shariq, M.; Alam, M. Fortifying Slab Resilience against Touch-Off Explosions: Integration of Innovative Stud Reinforcements and Computational Analysis. Buildings 2024, 14, 1468. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Y.; Wu, Y.; Zhang, J. Dynamic Response of Fiber–Metal Laminates Sandwich Beams under Uniform Blast Loading. Materials 2024, 17, 4482. [Google Scholar] [CrossRef] [PubMed]
- Jamil, A.; Guan, Z.W.; Cantwell, W.J.; Zhang, X.F.; Langdon, G.S.; Wang, Q.Y. Blast response of aluminium/thermoplastic polyurethane sandwich panels–experimental work and numerical analysis. Int. J. Impact Eng. 2019, 127, 31–40. [Google Scholar] [CrossRef]
- Mortar, N.A.M.; Abdullah, M.M.A.B.; Hussin, K.; Razak, R.A.; Hamat, S.; Hilmi, A.H.; Shahedan, N.N.; Li, L.Y.; Aziz, I.H.A. Finite Element Analysis on Structural Behaviour of Geopolymer Reinforced Concrete Beam using Johnson-Cook Damage in ABAQU. Arch. Metall. Mater. 2022, 67, 1349–1354. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Studziński, R.; Gajewski, T.; Malendowski, M.; Sumelka, W.; Sielicki, P.W. A New Blast Absorbing Sandwich Panel with Unconnected Corrugated Layers—Numerical Study. Energies 2021, 14, 214. [Google Scholar] [CrossRef]
- Zhang, B.; Feng, S. A Numerical Study of Blast Resistance of Carbon Fiber Reinforced Aluminum Alloy Laminates. Appl. Sci. 2023, 13, 4906. [Google Scholar] [CrossRef]
- Alias, A.; Amin, A. Blast loaded steel-concrete composite slab. J. Mech. Eng. Sci. 2021, 15, 7874–7884. [Google Scholar] [CrossRef]
- Mubarok, M.A.H.; Prabowo, A.R.; Muttaqie, T.; Muhayat, N. Dynamic Structural Assessment of Blast Wall Designs on Military-Based Vehicle Using Explicit Finite Element Approach. Math. Probl. Eng. 2022, 2022, 5883404. [Google Scholar] [CrossRef]
- Mendonça, F.B.; Urgessa, G.S.; Augusto, A.S.; Rocco, J.A.F.F. Experimental Records from Blast Tests of Ten Reinforced Concrete Slabs. CivilEng 2020, 1, 51–74. [Google Scholar] [CrossRef]
- Kontogeorgos, M.; Fuggini, C. Meta-Material Layout for the Blast Protection of Above-Ground Steel Pipes. Geotechnics 2023, 3, 584–600. [Google Scholar] [CrossRef]
- Ali, E.; Althoey, F. Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material. Buildings 2022, 12, 118. [Google Scholar] [CrossRef]
- Abdallah, M. Numerical study of steel structures responses to external explosions. Int. J. Civ. Environ. Eng. 2020, 14, 117–125. [Google Scholar]
- Derseh, S.A.; Mohammed, T.; Urgessa, G. Numerical study on hybrid metallic sandwich structures subjected to air burst. SN Appl. Sci. 2023, 5, 248. [Google Scholar] [CrossRef]
- Kohzadialvar, S.; Komasi, M.; Beiranvand, B. Analysis of Blast Effect on Nonlinear Behavior of Steel Flexural Frames Using Abaqus Software. J. Civ. Eng. Mater. Appl. 2022, 6, 13–24. [Google Scholar] [CrossRef]
- Abdelrahim, A.; Ali, O.; Mettwaly, I. Inelastic damage of RC slabs subject to blast loads using dynamic analysis: Numerical model validation. Aswan Univ. J. Sci. Technol. 2022, 2, 105–114. [Google Scholar] [CrossRef]
- Simulia. Abaqus, Version 6.10; Dassault Systèmes: Vélizy-Villacoublay, France, 2010. [Google Scholar]
- Augusto, A.S.; Urgessa, G.; Amorim, C.B.; Lopes Júnior, R.E.; Mendonça, F.B.; Rocco, J.A.F.F.; Iha, K. Experimental Characterization of Cast Explosive Charges Used in Studies of Blast Effects on Structures. CivilEng 2025, 6, 20. [Google Scholar] [CrossRef]
- Augusto, A.S.; Urgessa, G.; Rocco, J.A.F.F.; Mendonça, F.B.; Iha, K. Experimental Study on the Use of Polyurethane Elastomers to Enhance Structural Performance of A36 Steel Sheets Under Near-Field Detonation. Appl. Mech. 2025, 6, 28. [Google Scholar] [CrossRef]
- Hyde, D.W. Conventional Weapons Effect (CONWEP)—Application of TM5-855-1; Department of the Army: Vicksburg, MS, USA, 1988. [Google Scholar]
- Kingery, C.N.; Bulmash, G. Technical Report ARBRL TR-02555—Airblast Parameters from TNT Spherical Air Burst and Hemispherical Surface Burst; Aberdeen Proving Ground, Army Armament and Development Center, Ballistic Research Laboratory: Bethseda, MD, USA, 1984. [Google Scholar]
- Phantom. Phantom VEO 640/VEO 440 High-Speed Camera Datasheet; Phantom: Wayne, NJ, USA, 2024; p. 4. Available online: https://www.phantomhighspeed.com/products/cameras/veo/veo640 (accessed on 3 April 2025).
- Companhia Siderúrgica Nacional. Aços Planos Laminados a Quente (Hot-Rolled Flat Steel Sheets). Available online: https://www.csn.com.br/homepage/acos-planos/laminados-a-quente/ (accessed on 3 April 2025).
- Johnson, G.; Cook, W. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Jama, H.H.; Bambach, M.R.; Nurick, G.N.; Grzebieta, R.H.; Zhao, X.-L. Numerical modeling of square tubular steel beams subjected to transverse blast loads. Thin-Walled Struct. 2009, 47, 1523–1534. [Google Scholar] [CrossRef]
- Gomah, M.; Demiral, M. An Experimental and Numerical Investigation of an Improved Shearing Process with Different Punch Characteristics. J. Mech. Eng. 2020, 66, 2020. [Google Scholar] [CrossRef]
- Lee, S.-W.; Chang, S.-H. Experimental investigation of pull-through force of wing-type fastening inserts co-cured in long fiber prepreg sheet (LFPS). Compos. Struct. 2018, 206, 978–986. [Google Scholar] [CrossRef]
- Catálogo de Produtos Laminados (Rolled Products Catalogue). Available online: https://brasil.arcelormittal.com/pdf/produtos-solucoes/catalogos/catalogo-acos-planos.pdf?asCatalogo=pdf (accessed on 1 August 2025).
- Simulia. Abaqus Theory Manual, Version 6.10; Dassault Systèmes: Vélizy-Villacoublay, France, 2010. [Google Scholar]
- Cormie, D.; Geoff, M. Blast Effects on Buildings, 2nd ed.; Thomas Telford: London, UK, 2009. [Google Scholar]
- National Academies; Department of Homeland Security. IED Attack—Improvised Explosive Devices; Department of Homeland Security: Washington, DC, USA. Available online: https://www.dhs.gov/xlibrary/assets/prep_ied_fact_sheet.pdf (accessed on 3 April 2025).





| Parameter | Unit | Value |
|---|---|---|
| Yield strength | MPa | 328 |
| Tensile strength | MPa | 467 |
| Elongation (50 mm gauge) | % | 27 |
| Young’s modulus | GPa | 200 |
| Poisson’s ratio | - | 0.26 |
| Density | g/cm3 | 7.85 |
| Parameter | Unit | Value |
|---|---|---|
| A | MPa | 285.9 |
| B | MPa | 499.8 |
| N | - | 0.228 |
| s−1 | 1.0 | |
| C (considering strain rate) | - | 0.0171 |
| C (disregarding strain rate) | - | 0 |
| Mesh Size | CPU Time 1 | Number of Elements | Max Displacement 500 mm Standoff | Variation 500 mm | Max Displacement 300 mm Standoff | Variation 300 mm |
|---|---|---|---|---|---|---|
| (mm) | (min) | - | (mm) | (%) | (mm) | (%) |
| 40 | 0.4 | 120 | 45.43 | - | 72.12 | - |
| 30 | 0.4 | 252 | 48.99 | 7.84% | 73.20 | 1.50% |
| 20 | 0.5 | 520 | 50.42 | 2.92% | 75.61 | 3.29% |
| 10 | 0.6 | 2060 | 50.99 | 1.13% | 76.79 | 1.56% |
| 5 | 0.7 | 8480 | 51.18 | 0.37% | 77.15 | 0.47% |
| 2.5 | 1.0 | 33,920 | 51.27 | 0.18% | 77.28 | 0.17% |
| 1 | 8.0 | 212,800 | 51.31 | 0.08% | 77.35 | 0.09% |
| Number of Integration Points | CPU Time 1 | Max Displacement 500 mm Standoff | Variation 500 mm | Max Displacement 300 mm Standoff | Variation 300 mm |
|---|---|---|---|---|---|
| - | (min) | (mm) | (%) | (mm) | (%) |
| 3 | 1.0 | 51.15 | - | 77.23 | - |
| 5 | 1.0 | 51.26 | 0.22% | 77.27 | 0.05% |
| 7 | 1.0 | 51.27 | 0.02% | 77.28 | 0.01% |
| 9 | 1.2 | 51.27 | 0.00% | 77.28 | 0.00% |
| Explosive Charge | TNT Equivalence | Reference 1 |
|---|---|---|
| Airdropped Mk-82 bomb | 99 kg | [38] |
| Car bomb | 226 kg | [49] |
| Airdropped Mk-84 bomb | 429 kg | [38] |
| Van bomb | 1815 kg | [49] |
| FEM Simulations | Field Blast Tests | ||||||
|---|---|---|---|---|---|---|---|
| Strain–Stress Curve Model | JC Model Rate Dependent | JC Model NOT Rate Dependent | Test #1 | Test #2 | Test #3 | ||
| Max Displacement (mm) at 500 mm standoff | 51.27 | 44.17 | 45.46 | 51.2 ± 0.5 | 52.5 ± 0.5 | 52.0 ± 0.5 | |
| Max Displacement (mm) at 300 mm standoff | 77.28 | 66.78 | 69.13 | 66.0 ± 0.5 | 65.6 ± 0.5 | 65.9 ± 0.5 | |
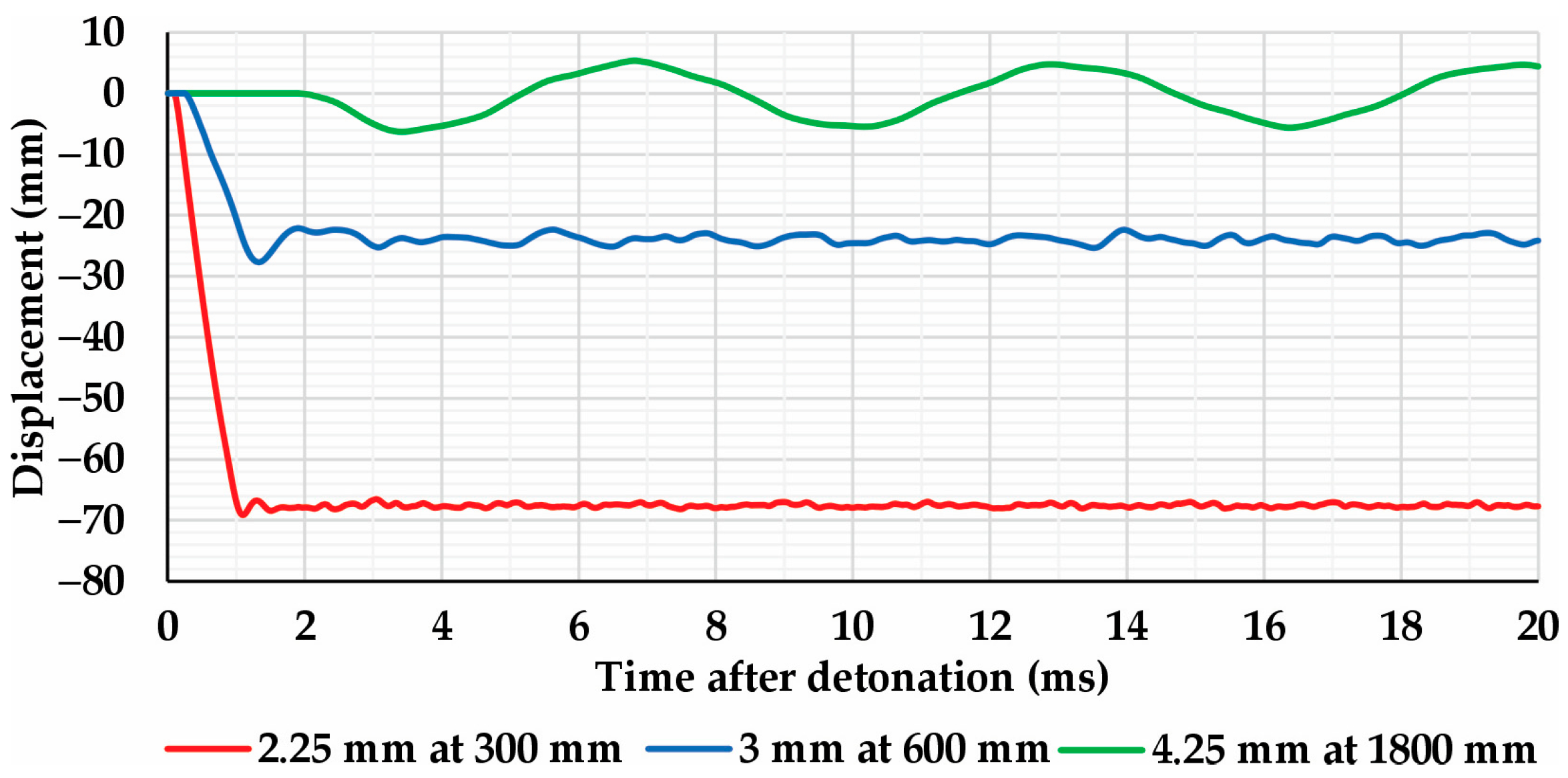
| Scenario | Displacement 1 | θmax 1 | Velocity 1 | Acceleration 2 |
|---|---|---|---|---|
| (mm) | (°) | (mm/ms) | (g) | |
| 2.25 mm at 300mm | 69.11 | 17.78 | 89.89 | 2.47 × 105 |
| 3.00 mm at 600 mm | 27.68 | 7.32 | 35.28 | 5.06 × 104 |
| 4.25 mm at 1800 mm | 6.29 | 1.67 | 7.18 | 2.34 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augusto, A.S.; Urgessa, G.; Rocco, J.A.F.F.; Mendonça, F.B.; Iha, K. Field Blast Tests and Finite Element Analysis of A36 Steel Sheets Subjected to High Explosives. Eng 2025, 6, 187. https://doi.org/10.3390/eng6080187
Augusto AS, Urgessa G, Rocco JAFF, Mendonça FB, Iha K. Field Blast Tests and Finite Element Analysis of A36 Steel Sheets Subjected to High Explosives. Eng. 2025; 6(8):187. https://doi.org/10.3390/eng6080187
Chicago/Turabian StyleAugusto, Anselmo S., Girum Urgessa, José A. F. F. Rocco, Fausto B. Mendonça, and Koshun Iha. 2025. "Field Blast Tests and Finite Element Analysis of A36 Steel Sheets Subjected to High Explosives" Eng 6, no. 8: 187. https://doi.org/10.3390/eng6080187
APA StyleAugusto, A. S., Urgessa, G., Rocco, J. A. F. F., Mendonça, F. B., & Iha, K. (2025). Field Blast Tests and Finite Element Analysis of A36 Steel Sheets Subjected to High Explosives. Eng, 6(8), 187. https://doi.org/10.3390/eng6080187








