Review of Watershed Hydrology and Mathematical Models
Abstract
1. Introduction
1.1. The Development of Hydrology
1.2. Watershed Hydrology
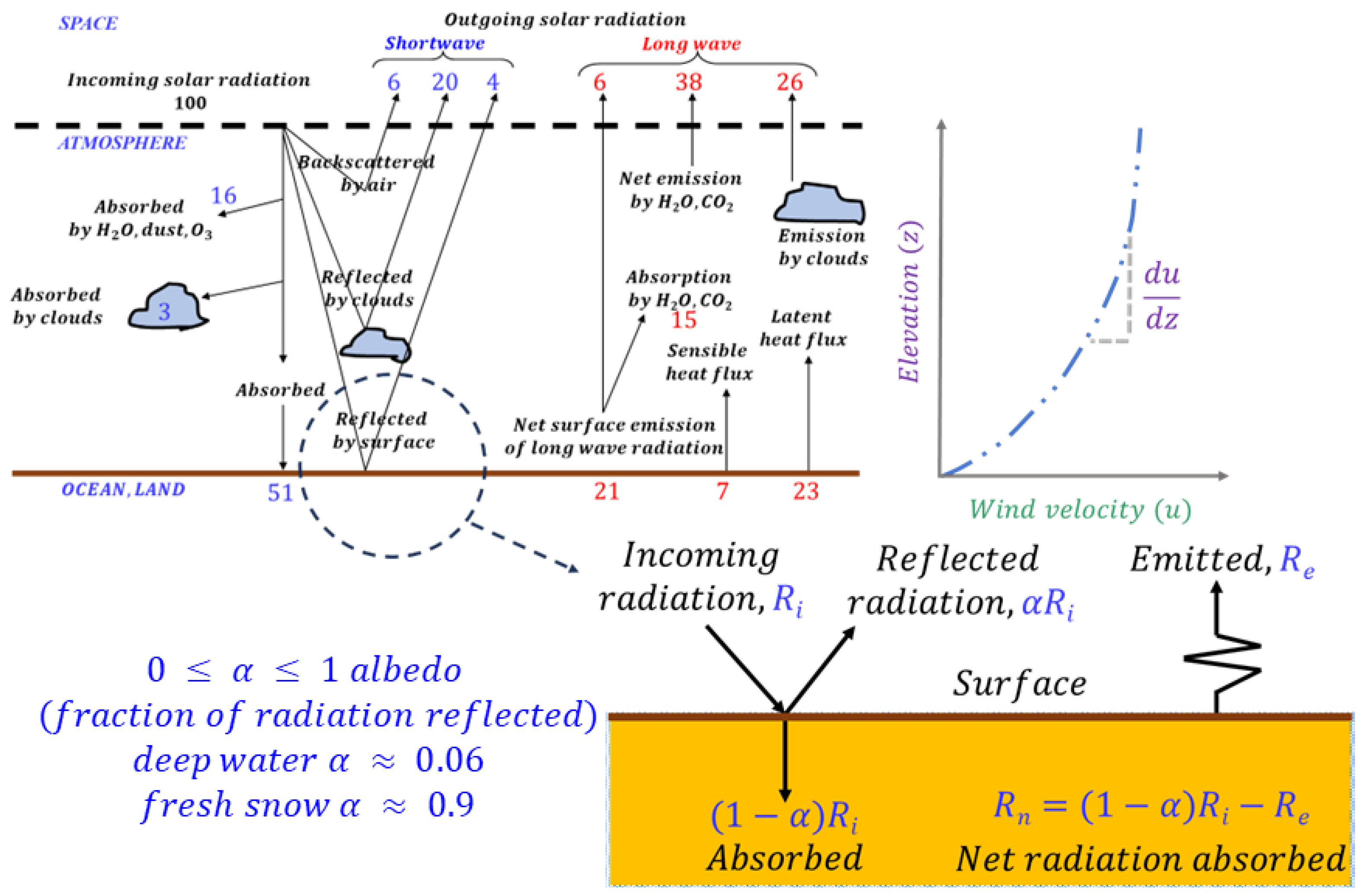
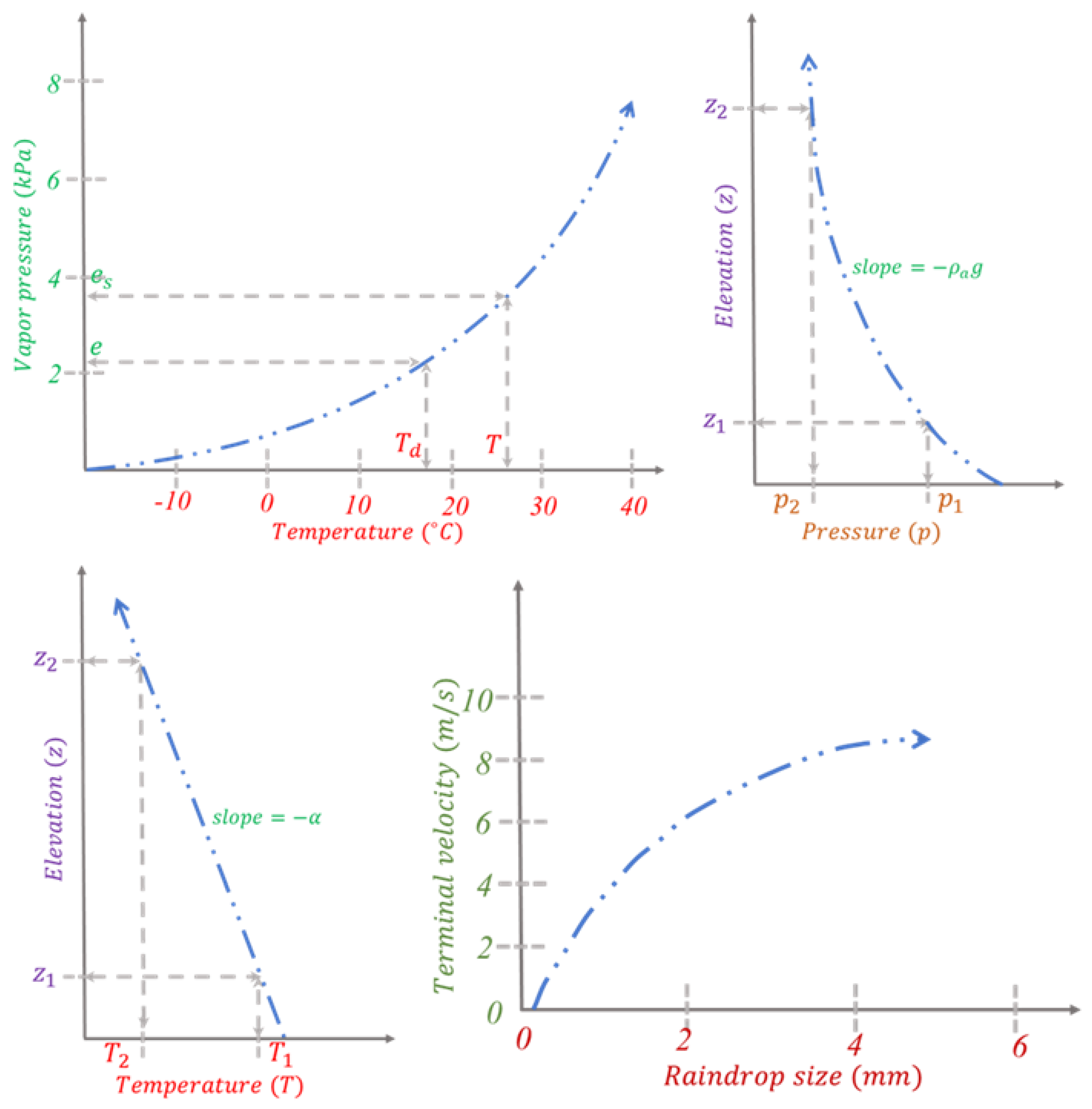
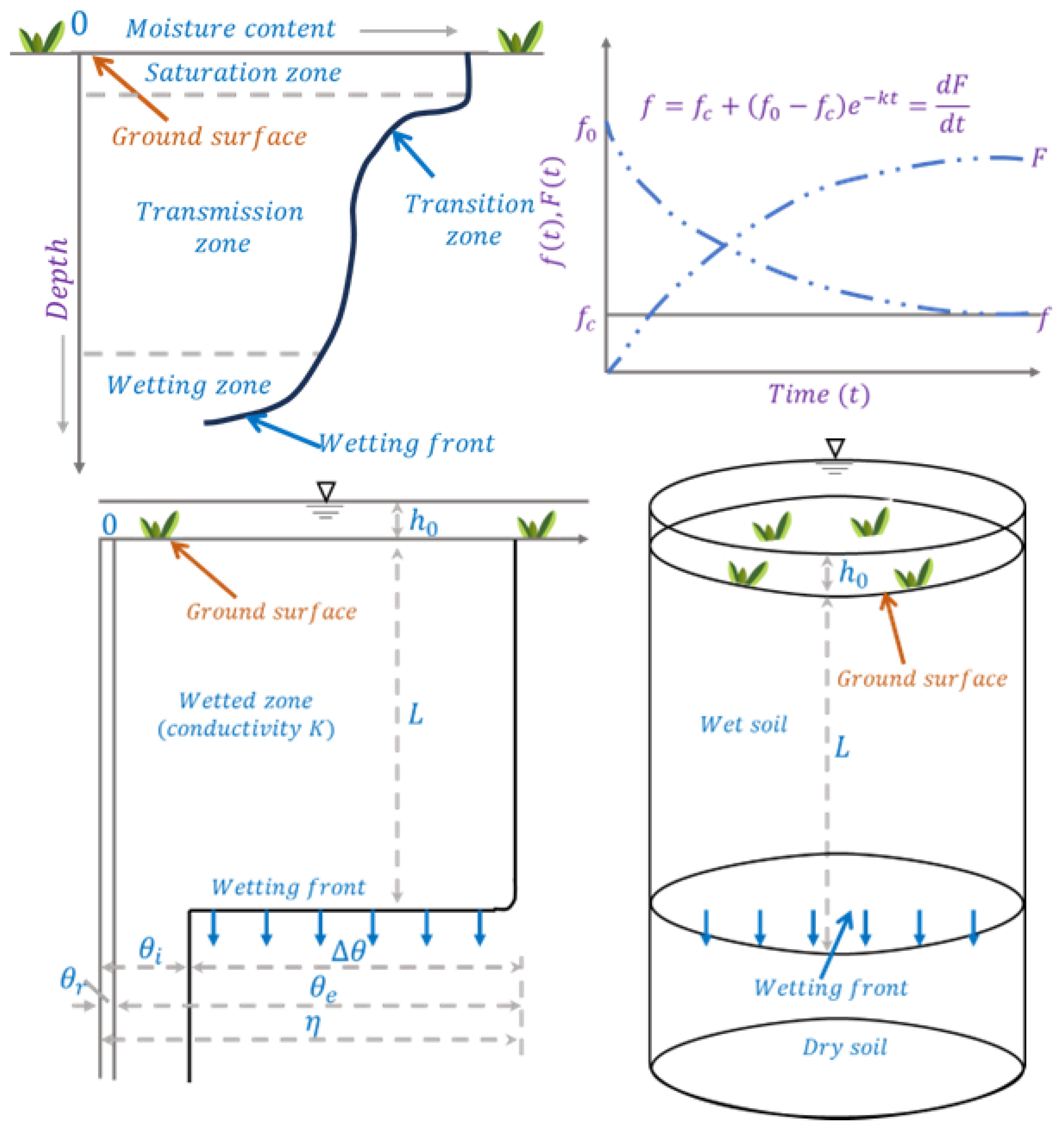
2. Watershed Hydrologic Processes
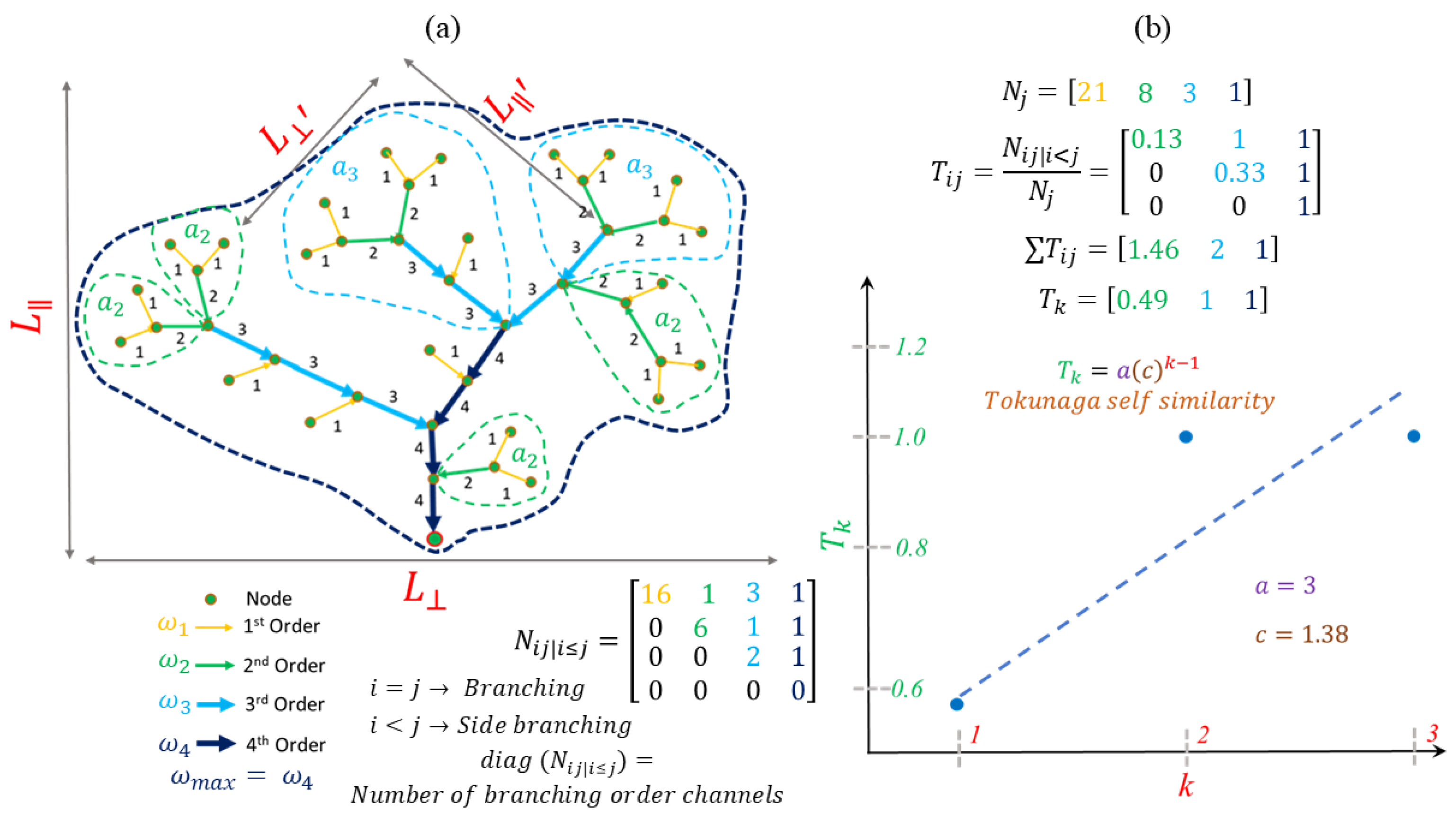
3. River Networks: Primary Transport Features of Watershed
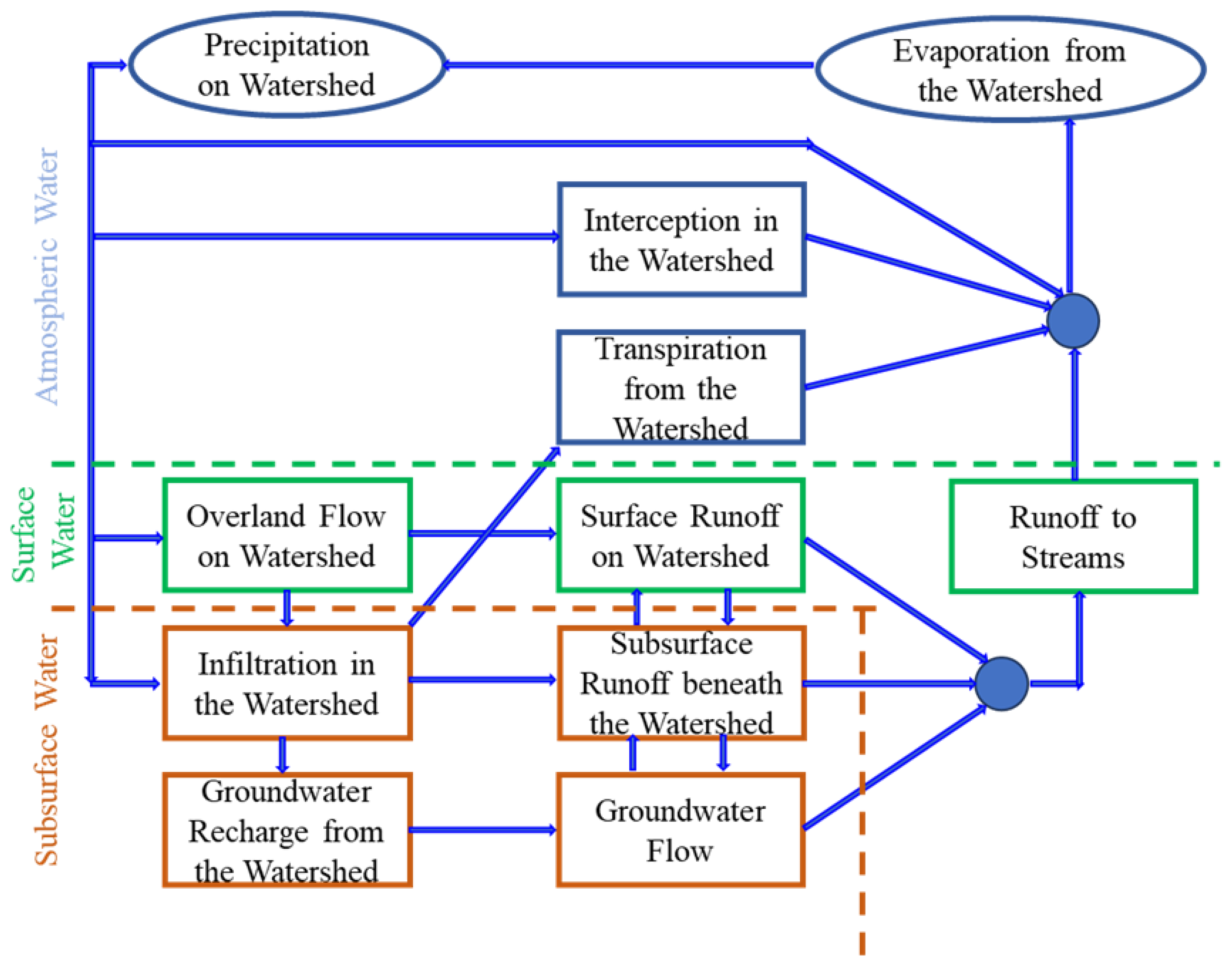
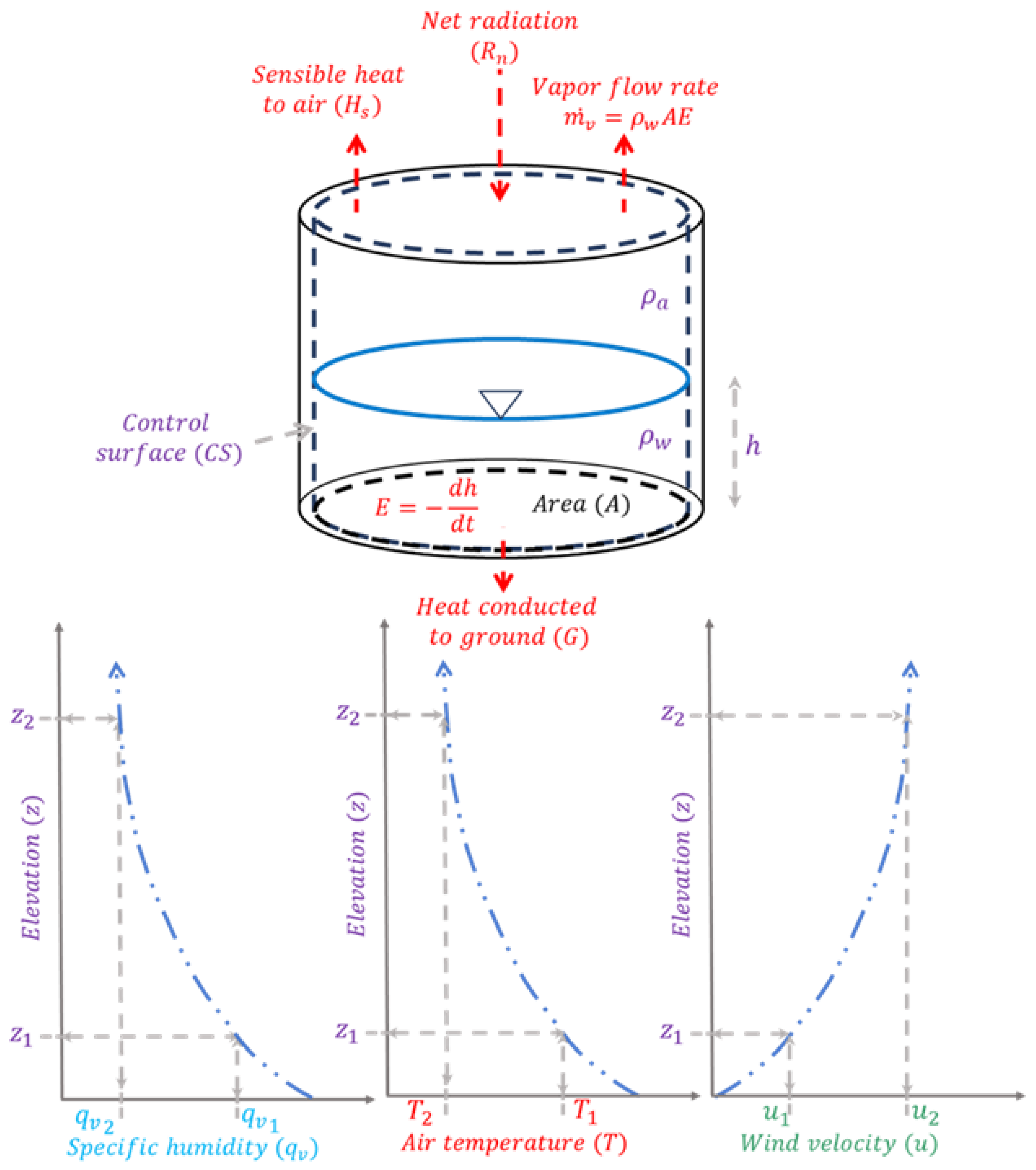
4. Governing Equations for Water Cycle Phases on Watersheds
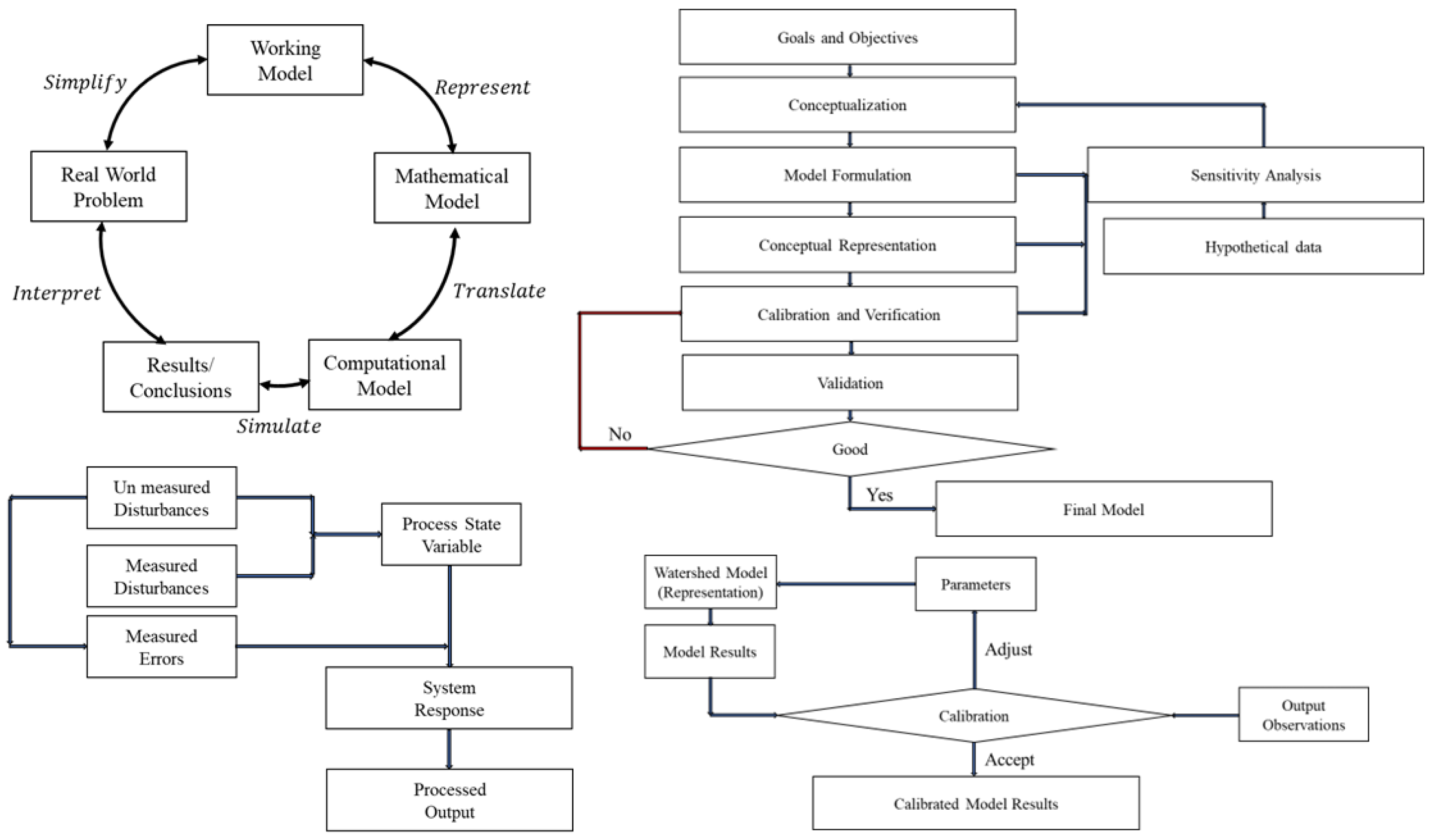
5. Hydrologic Analysis
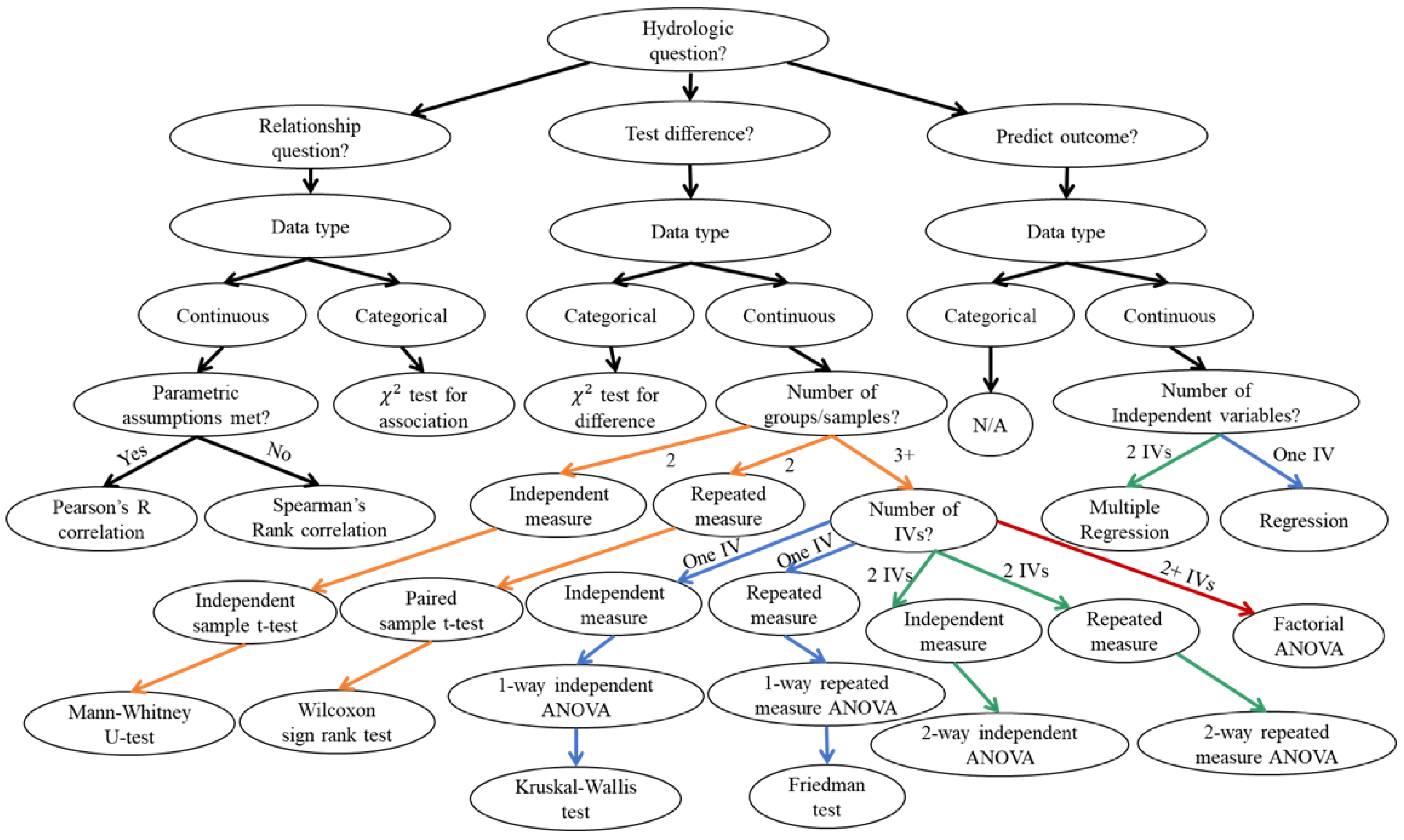
6. Statistics of Watershed Hydrology
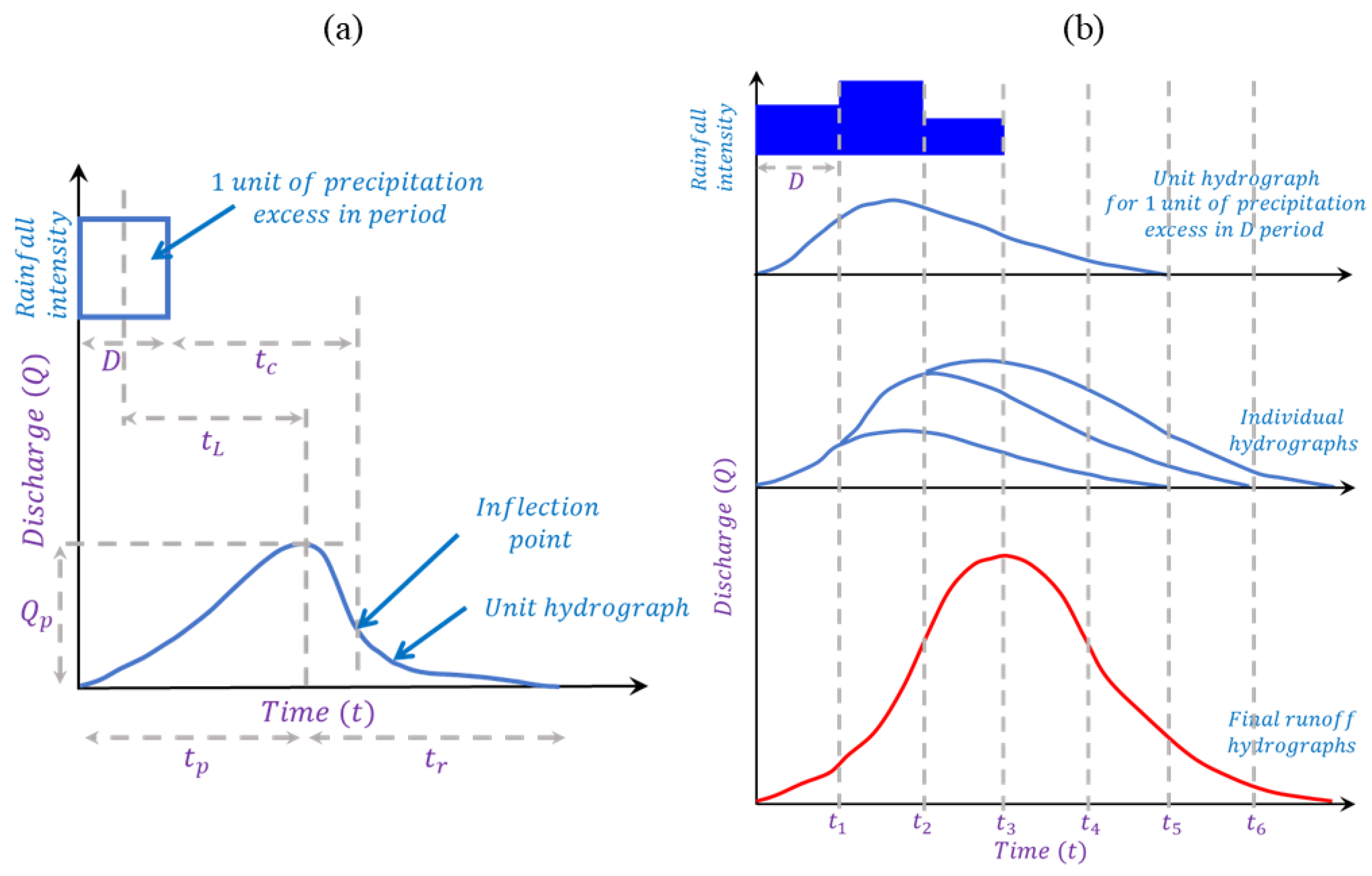
7. Flow Routing on Watershed
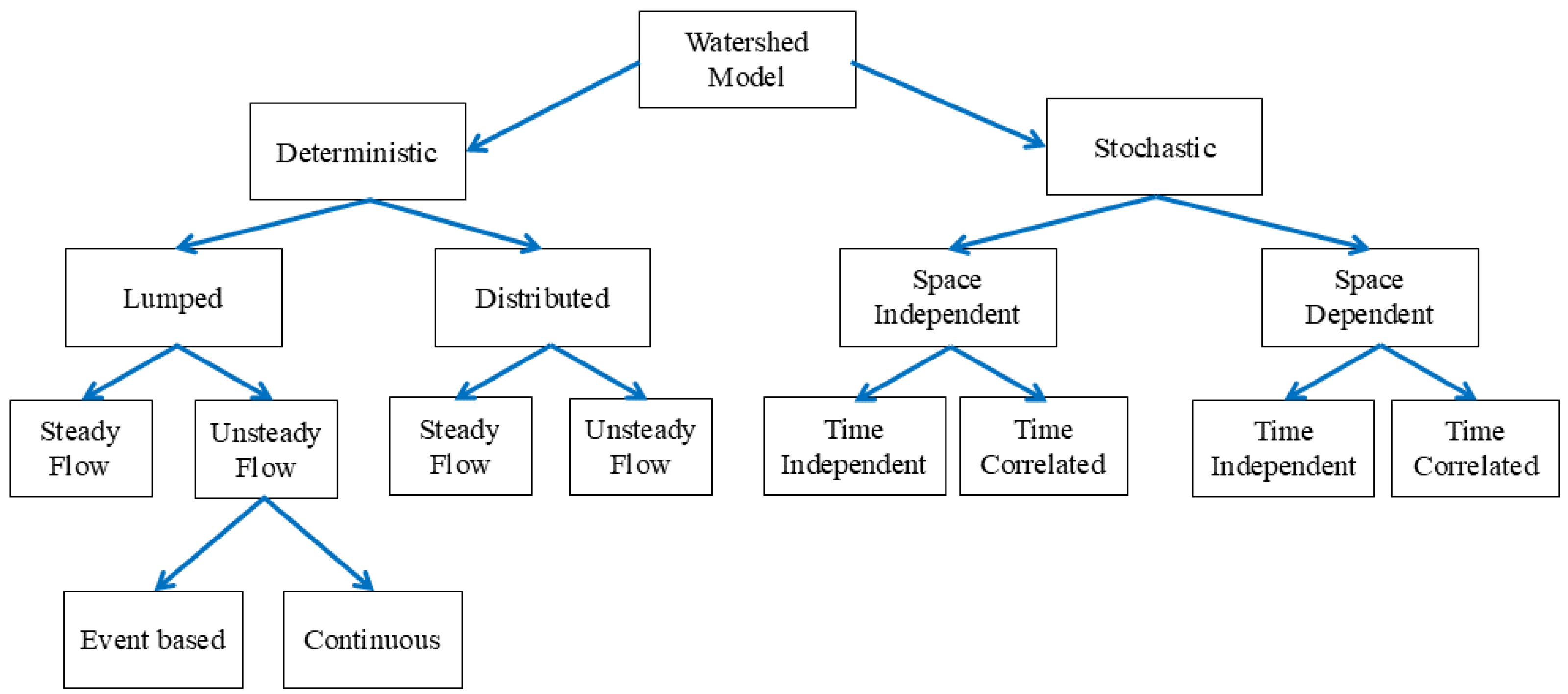
8. Watershed Models
9. Examples of Watershed Models
9.1. Hydrological Simulation Program—FORTRAN (HSPF) Watershed Model
9.2. Hydrologic Engineering Center—Hydrologic Modeling System (-)
9.3. Soil and Water Assessment Tool (SWAT) Model
9.4. MIKE Watershed Models
9.5. Comparative Analysis Across Scale
10. Integration of Climate Change, Artificial Intelligence, and Remote Sensing
11. Limitations of Watershed Models
- The absence of observed discharge data in ungauged basins hinders the calibration of hydrological models, leading to increased uncertainties in predictions. This limitation is particularly pronounced in small basins, where localized hydrological processes may not be well-represented by generalized models [173,174].
- The coarse spatial resolution of many hydrological models makes them less effective in capturing the fine-scale processes characteristic of small basins. This mismatch can result in inaccurate simulations of hydrological responses.
- Theoretical models often involve simplifications and assumptions that may not hold true in specific contexts, leading to structural uncertainties. These uncertainties are exacerbated in small and ungauged basins due to limited knowledge of localized hydrological processes.
- Estimating model parameters in ungauged basins is problematic due to the lack of site-specific data, leading to potential inaccuracies in model outputs.
- Transferring model parameters from gauged to ungauged basins based on physical similarity can improve model performance. This approach leverages existing data to inform predictions in data-scarce regions [175].
- Utilizing satellite observations can enhance hydrological modeling by providing data on variables such as soil moisture and vegetation cover, which are crucial for accurate simulations in ungauged basins [175].
- Employing machine learning models, such as Long Short-Term Memory (LSTM) networks, can improve streamflow predictions in ungauged basins by learning patterns from available data and capturing complex hydrological processes [176].
- Incorporating detailed spatial information about basin heterogeneity into distributed models can significantly improve discharge predictions by accounting for spatial variability in hydrological processes [180].
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Model Name/Acronym | Author(s)/Year | Remarks |
|---|---|---|
| Stanford watershed model (SWM)/Hydrologic Simulation Package—Fortran IV (HSPF) | Crawford and Linsley (1966), Bicknell et al. (1993) | Continuous hydrologic, hydraulic, and water quality simulator |
| Catchment Model (CM) | Dawdy and O’Donnell (1965) | Lumped, event-based runoff model |
| Tennessee Valley Authority (TVA) Model | Tenn. Valley Authority (1972) | Lumped, event-based runoff model |
| U.S. Department of Agriculture Hydrology Laboratory (USDAHL) Model | Holtan and Lopez (1971), Holtan et al. (1975) | Event-based, process-oriented, lumped hydrograph model |
| U.S. Geological Survey (USGS) Model | Dawdy et al. (1970, 1978) | Process-oriented, continuous/event-based runoff model |
| Utah State University (USU) Model | Andrews et al. (1978) | Process-oriented, event/continuous streamflow model |
| Purdue Model | Huggins and Monke (1967) | Process-oriented, physically based, overland flow model |
| Antecedent Precipitation Index (API) Model | Sittner et al. (1969) | Lumped, river flow forecast model |
| Hydrologic Engineering Center—Hydrologic Modeling System (HEC-HMS) | Feldman (1991, HEC (1981, 2000)) | Physically based, event-based, runoff model |
| Streamflow Synthesis and Reservoir Regulation (SSARR) Model | Rockwood (1982), U.S. Army Corps of Engineers (1987), Speers (1995) | Lumped, continuous streamflow simulation model |
| National Weather Service—River Forecast System (NWS-RFS) | Burnash et al. (1973a,b), Burnash (1975) | Lumped, continuous river forecast system |
| University of British Columbia (UBC) Model | Quick and Pipes (1977), Quick (1995) | Process-oriented, lumped or continuous simulation model |
| Tank Model | Sugawara et al. (1974), Sugawara (1995) | Process-oriented, semi-distributed, or lumped continuous model |
| Runoff Routing Model (RORB) | Laurenson (1964), Laurenson and Mein (1993, 1995) | Lumped, event-based runoff simulation model |
| Agricultural Runoff Model (ARM) | Donigian et al. (1977) | Process-oriented, lumped runoff simulation model |
| Storm Water Management Model (SWMM) | Metcalf and Eddy et al. (1971), Huber and Dickinson (1988), Huber (1995) | Continuous hydrologic, hydraulic, and water quality simulator |
| Areal Non-point Source Watershed Environment Response Simulation (ANSWERS) | Beasley et al. (1977), Bouraoui et al. (2002) | Event/continuous, lumped runoff and sediment yield simulator |
| National Hydrology Research Institute (NHRI) Model | Vandenberg (1989) | Physically based, lumped continuous hydrologic model |
| Technical Report-20 (TR-20) Model | Soil Conservation Service (1965) | Event-based, process-oriented, lumped parameter hydrograph model |
| U.S. Geological Survey (USGS) Model | Dawdy et al. (1970, 1978) | Lumped parameter, event-based runoff simulation model |
| Physically Based Runoff Production Model (TOPMODEL) | Beven and Kirby (1979), Beven (1995) | Physically based, distributed continuous hydrologic simulation |
| Generalized River Modeling Package–Système Hydrologique Europeen (MIKE-SHE) | Refsgaard and Storm (1995) | Physically based, distributed, continuous hydrologic and hydraulic model |
| ARNO (Arno River) Model | Todini (1988a,b, 1996) | semi-distributed, continuous rainfall–runoff simulation model |
| Waterloo Flood System (WATFLOOD) | Kouwen et al. (1993), Kouwen (2000) | Process-oriented, semi-distributed continuous flow model |
| Topographic Kinematic Approximation and Integration (TOPKAPI) Model | Todini (1995) | Distributed, physically based continuous rainfall–runoff model |
| Soil-Vegetation-Atmosphere Transfer (SVAT) Model | Ma et al. (1999), Ma and Cheng (1998) | Macroscale, lumped parameter, streamflow simulation model |
| Systeme Hydrologique Europeen Transport (SHETRAN) | Ewen et al. (2000) | Physically based, distributed, water quantity and quality simulator |
| Daily Conceptual Rainfall–Runoff Model (HYDROLOG)-Monash Model | Potter and McMahon (1976), Chiew and McMahon (1994) | Lumped, conceptual rainfall–runoff model |
| Soil Water Assessment Tool (SWAT) | Arnold et al. (1998) | Distributed, conceptual, continuous simulation model |
| Distributed Hydrological Model (HYDROTEL) | Fortin et al. (2001a,b) | Physically based, distributed, continuous hydrologic simulation model |
| Event-based Approach for Small and Ungauged Basins (EBA4SUB) | Petroselli A., Grimaldi S. (2018) | Lumped conceptual event-based rainfall–runoff model [182] |
| Continuous Simulation Model for Small and Ungauged Basins (COSMO4SUB) | Grimaldi S., Nardi F., Piscopia R., Petroselli A. (2021) | Lumped conceptual continuous rainfall-runoff model [178] |
References
- Chow, V.T.; Maidment, D.R.; Larry, W.M. Applied Hydrology; International edition; MacGraw-Hill, Inc.: New York, NY, USA, 1988; Volume 149. [Google Scholar]
- Sarker, S. A Short Review on Computational Hydraulics in the context of Water Resources Engineering. Open J. Model. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
- Dalton, J. Experimental essays on the constitution of mixed gases. Manch. Lit. Philos. Soc. Memo 1802, 5, 535–602. [Google Scholar]
- Hagen, G. Ueber die Bewegung des Wassers in engen cylindrischen Röhren. Ann. Phys. 1839, 122, 423–442. [Google Scholar] [CrossRef]
- Mulvaney, T.J. On the use of self-registering rain and flood gauges in making observations of the relations of rainfall and flood discharges in a given catchment. Proc. Inst. Civ. Eng. Irel. 1851, 4, 18–33. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de Dijon; V. Dalmont: Paris, France, 1856. [Google Scholar]
- Manning, R. Supplement to ‘On the flow of water in open channels and pipes’. Trans. Inst. Civil Eng. Ireland 1895, 24, 179–207. [Google Scholar]
- Rippl, W. The Capacity of Storage-Reservoirs for Water-Slpply. (Including Plate). Minutes Proc. Inst. Civ. Eng. 1883, 71, 270–278. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Hazen, A. Storage to be provided in impounding municipal water supply. Trans. Am. Soc. Civ. Eng. 1914, 77, 1539–1640. [Google Scholar] [CrossRef]
- Sherman, L.K. Streamflow from rainfall by the unit-graph method. Eng. News Record 1932, 108, 501–505. [Google Scholar]
- Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Sarker, S. Fundamentals of Climatology for Engineers: Lecture Note. Eng 2022, 3, 573–595. [Google Scholar] [CrossRef]
- Sarker, S. Investigating Topologic and Geometric Properties of Synthetic and Natural River Networks Under Changing Climate. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2021. [Google Scholar]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical nodes in river networks. Sci. Rep. 2019, 9, 11178. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Sarker, S.; Sarker, T.; Leta, O.T. Analyzing the critical locations in response of constructed and planned dams on the Mekong River Basin for environmental integrity. Environ. Res. Commun. 2022, 4, 101001. [Google Scholar] [CrossRef]
- Singhal, A.; Jaseem, M.; Divya; Sarker, S.; Prajapati, P.; Singh, A.; Jha, S.K. Identifying Potential Locations of Hydrologic Monitoring Stations Based on Topographical and Hydrological Information. Water Resour. Manag. 2023, 38, 369–384. [Google Scholar] [CrossRef]
- Sarker, S.; Sarker, T.; Leta, O.T.; Raihan, S.U.; Khan, I.; Ahmed, N. Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas. Water 2023, 15, 1384. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Adler, R.F.; Nelkin, E. GPCP Version 2.3 Combined Precipitation Data Set; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2015.
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Huxley, J.S.; Teissier, G. Terminology of relative growth. Nature 1936, 137, 780–781. [Google Scholar] [CrossRef]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; US Government Printing Office: Washingtin, DC, USA, 1957; Volume 294.
- Dodds, P.S.; Rothman, D.H. Geometry of river networks. I. Scaling, fluctuations, and deviations. Phys. Rev. E 2000, 63, 016115. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Geometry of river networks. II. Distributions of component size and number. Phys. Rev. E 2000, 63, 016116. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Geometry of river networks. III. Characterization of component connectivity. Phys. Rev. E 2000, 63, 016117. [Google Scholar] [CrossRef] [PubMed]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Melton, M.A. A derivation of Strahler’s Channel-ordering system. J. Geol. 1959, 67, 345–346. [Google Scholar] [CrossRef]
- Shreve, R.L. Statistical law of stream numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- Sarker, S.; Singh, A.; Veremyev, A.; Boginski, V.; Peckham, S. Controllability and heterogeneity of river networks using spectral graph theory approach. Sci. Rep. 2025, 15, 13196. [Google Scholar] [CrossRef]
- Tokunaga, E. The composition of drainage network in Toyohira River Basin and valuation of Horton’s first law. Geophys. Bull. Hokkaido Univ. 1966, 15, 1–19. [Google Scholar]
- Tokunaga, E. Consideration on the composition of drainage networks and their evolution. Geogr. Rep. Tokyo Metrop. Univ. 1978, 13, 1–27. [Google Scholar]
- Tokunaga, E. Ordering of divide segments and law of divide segment numbers. Trans. Jpn. Geomorphol. Union 1984, 5, 71–77. [Google Scholar]
- Abed-Elmdoust, A.; Miri, M.A.; Singh, A. Reorganization of river networks under changing spatiotemporal precipitation patterns: An optimal channel network approach. Water Resour. Res. 2016, 52, 8845–8860. [Google Scholar] [CrossRef]
- Sarker, S.; Sarker, T. Spectral Properties of Water Hammer Wave. Appl. Mech. 2022, 3, 799–814. [Google Scholar] [CrossRef]
- Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: New York, NY, USA, 1960. [Google Scholar]
- French, R.H. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Macmillan: New York, NY, USA, 1966. [Google Scholar]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Sarker, S. Separation of Floodplain Flow and Bankfull Discharge: Application of 1D Momentum Equation Solver and MIKE 21C. CivilEng 2023, 4, 933–948. [Google Scholar] [CrossRef]
- Sarker, S. Hydraulics Lab Manual. engrXiv 2021, 1–66. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Priestley, C.H.B. Turbulent Transfer in the Lower Atmosphere; University of Chicago Press: Chicago, IL, USA, 1959. [Google Scholar]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Iowa, IA, USA, 2013; Volume 1. [Google Scholar]
- Ludlam, F.; Mason, B. The physics of clouds. In Geophysik II/Geophysics II; Springer: Berlin/Heidelberg, Germany, 1957; pp. 479–540. [Google Scholar]
- Monteith, J. The development and extension of Penman’s evaporation formula. Appl. Soil Phys. 1980, 6, 247–253. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J. Microphysics of Clouds and Precipitation Reidel; D. Reidel Publishing Company: Boston, MA, USA, 1978; Volume 19781, p. 714. [Google Scholar]
- Raudkivi, A. Hydrology—An Advanced Introduction to Hydrological Processes and Modelling; Pergamon Press: New York, NY, USA, 1979. [Google Scholar]
- Thornthwaite, C.W.; Holzman, B. The determination of evaporation from land and water surfaces. Mon. Weather. Rev. 1939, 67, 4–11. [Google Scholar] [CrossRef]
- Van Bavel, C. Potential evaporation: The combination concept and its experimental verification. Water Resour. Res. 1966, 2, 455–467. [Google Scholar] [CrossRef]
- Wiesner, C.J. Hydrometereology; Chapman and Hall: London, UK, 1970. [Google Scholar]
- Doorenbos, J.; Pruitt, W. Crop water requirements. FAO irrigation and drainage paper 24. In Land and Water Development Division; FAO: Rome, Italy, 1977; Volume 144. [Google Scholar]
- Jensen, M.E. Consumptive Use of Water and Irrigation Water Requirements; Technical Committee on Irrigation Water Requirements: New York, NY, USA, 1973. [Google Scholar]
- Bouwer, H. Rapid field measurement of air entry value and hydraulic conductivity of soil as significant parameters in flow system analysis. Water Resour. Res. 1966, 2, 729–738. [Google Scholar] [CrossRef]
- Bouwer, H. Surface-Subsurface Water Relations, Chap. 8 in Groundwater Hydrology; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Brakensiek, D.; Engleman, R.; Rawls, W. Variation within texture classes of soil water parameters. Trans. ASAE 1981, 24, 335–0339. [Google Scholar] [CrossRef]
- Brooks, R.H. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1965. [Google Scholar]
- De Marsily, G. Quantitative Hydrogeology; Technical Report; Paris School of Mines: Fontainebleau, France, 1986. [Google Scholar]
- Devaurs, M.; Gifford, G.F. Applicability of the Green and Ampt Infiltration Equation to Rangelands 1. JAWRA J. Am. Water Resour. Assoc. 1986, 22, 19–27. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; Volume 176, pp. 161–177. [Google Scholar]
- Hillel, D. Applications of Soil Physics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Horton, R.E. The role of infiltration in the hydrologic cycle. Eos Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar]
- Horton, R.E. Analysis of runoff-plat experiments with varying infiltration-capacity. Eos Trans. Am. Geophys. Union 1939, 20, 693–711. [Google Scholar]
- Mein, R.G.; Larson, C.L. Modeling infiltration during a steady rain. Water Resour. Res. 1973, 9, 384–394. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J. Application of infiltration theory for the determination of excess rainfall hyetograph 1. JAWRA J. Am. Water Resour. Assoc. 1981, 17, 1012–1022. [Google Scholar] [CrossRef]
- Pearce, A.J.; McKerchar, A. Upstream Generation of Storm Runoff; New Zealand Forest Service: Wellington, New Zealand, 1980. [Google Scholar]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of infiltration. In Advances in Hydroscience; Elsevier: Amsterdam, The Netherlands, 1969; Volume 5, pp. 215–296. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-Ampt infiltration parameters from soils data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Terstriep, M.L.; Stall, J.B. The Illinois Urban Drainage Area Simulator, ILLUDAS; Bulletin (Illinois State Water Survey) No. 58; Illinois State Water Survey: Champaign, IL, USA, 1974. [Google Scholar]
- Wellings, S. Recharge of the Upper Chalk aquifer at a site in Hampshire, England: 1. Water balance and unsaturated flow. J. Hydrol. 1984, 69, 259–273. [Google Scholar] [CrossRef]
- Hooshyar, M.; Wang, D. An analytical solution of Richards’ equation providing the physical basis of SCS curve number method and its proportionality relationship. Water Resour. Res. 2016, 52, 6611–6620. [Google Scholar] [CrossRef]
- Snyder, F.F. Synthetic unit-graphs. Eos Trans. Am. Geophys. Union 1938, 19, 447–454. [Google Scholar]
- Singh, V.P. Hydrologic Systems. Volume I: Rainfall-Runoff Modeling; Prentice Hall: Englewood Cliffs, NJ, USA, 1988; Volume 480. [Google Scholar]
- Sarker, S. Essence of mike 21c (fdm numerical scheme): Application on the river morphology of bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- Tian, L.; Gu, S.; Shao, S.; Wu, Y. Turbulent models of shallow-water equations-based smoothed particle hydrodynamics. Phys. Fluids 2024, 36, 107164. [Google Scholar]
- Song, W.; Yan, H.; Tao, T.; Guan, M.; Li, F.; Xin, K. Modeling transient mixed flows in drainage networks with smoothed particle hydrodynamics. Water Resour. Manag. 2024, 38, 861–879. [Google Scholar] [CrossRef]
- Donigian, A.S.J.; Bicknell, B.; Imhoff, J. Hydrological Simulation Program-Fortran (HSPF); American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 1995. [Google Scholar]
- Donigian, A. Watershed model calibration and validation: The HSPF experience. In TMDLS Conference 2002; Water Environment Federation: Alexandria, VA, USA, 2002; pp. 44–73. [Google Scholar]
- Duda, P.B.; Hummel, P.R.; Donigian, A.S., Jr.; Imhoff, J.C. BASINS/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT 1. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Saleh, A.; Du, B. Evaluation of SWAT and HSPF within BASINS program for the upper North Bosque River watershed in central Texas. Trans. ASAE 2004, 47, 1039–1049. [Google Scholar]
- Kim, S.M.; Benham, B.L.; Brannan, K.M.; Zeckoski, R.W.; Doherty, J. Comparison of hydrologic calibration of HSPF using automatic and manual methods. Water Resour. Res. 2007, 43, W01402. [Google Scholar] [CrossRef]
- Albek, M.; Öğütveren, Ü.B.; Albek, E. Hydrological modeling of Seydi Suyu watershed (Turkey) with HSPF. J. Hydrol. 2004, 285, 260–271. [Google Scholar] [CrossRef]
- Yazdi, M.N.; Ketabchy, M.; Sample, D.J.; Scott, D.; Liao, H. An evaluation of HSPF and SWMM for simulating streamflow regimes in an urban watershed. Environ. Model. Softw. 2019, 118, 211–225. [Google Scholar] [CrossRef]
- Ribarova, I.; Ninov, P.; Cooper, D. Modeling nutrient pollution during a first flood event using HSPF software: Iskar River case study, Bulgaria. Ecol. Model. 2008, 211, 241–246. [Google Scholar] [CrossRef]
- Johanson, R.C.; Imhoff, J.C.; Davis, H.H. Users Manual for Hydrological Simulation Program-Fortran (HSPF); Environmental Research Laboratory, Office of Research and Development, US: Athens, GA, USA, 1980; Volume 80. [Google Scholar]
- Halwatura, D.; Najim, M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Chu, X.; Steinman, A. Event and continuous hydrologic modeling with HEC-HMS. J. Irrig. Drain. Eng. 2009, 135, 119–124. [Google Scholar] [CrossRef]
- Sahu, M.K.; Shwetha, H.R.; Dwarakish, G.S. State-of-the-art hydrological models and application of the HEC-HMS model: A review. Model. Earth Syst. Environ. 2023, 9, 3029–3051. [Google Scholar] [CrossRef]
- Oleyiblo, J.O.; Li, Z.j. Application of HEC-HMS for flood forecasting in Misai and Wan’an catchments in China. Water Sci. Eng. 2010, 3, 14–22. [Google Scholar]
- Sahu, S.; Pyasi, S.; Galkate, R. A review on the HEC-HMS rainfall-runoff simulation model. Int. J. Agric. Sci. Res. 2020, 10, 183–190. [Google Scholar]
- Ramly, S.; Tahir, W. Application of HEC-GeoHMS and HEC-HMS as rainfall–runoff model for flood simulation. In ISFRAM 2015: Proceedings of the International Symposium on Flood Research and Management 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 181–192. [Google Scholar]
- Roy, D.; Begam, S.; Ghosh, S.; Jana, S. Calibration and validation of HEC-HMS model for a river basin in Eastern India. ARPN J. Eng. Appl. Sci. 2013, 8, 40–56. [Google Scholar]
- Gebre, S.L. Application of the HEC-HMS model for runoff simulation of Upper Blue Nile River Basin. Hydrol. Curr. Res. 2015, 6, 1. [Google Scholar] [CrossRef]
- Choudhari, K.; Panigrahi, B.; Paul, J.C. Simulation of rainfall-runoff process using HEC-HMS model for Balijore Nala watershed, Odisha, India. Int. J. Geomat. Geosci. 2014, 5, 253–265. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Bailey, R.T.; Park, S.; Bieger, K.; Arnold, J.G.; Allen, P.M. Enhancing SWAT+ simulation of groundwater flow and groundwater-surface water interactions using MODFLOW routines. Environ. Model. Softw. 2020, 126, 104660. [Google Scholar] [CrossRef]
- Abbas, S.A.; Bailey, R.T.; White, J.T.; Arnold, J.G.; White, M.J.; Čerkasova, N.; Gao, J. A framework for parameter estimation, sensitivity analysis, and uncertainty analysis for holistic hydrologic modeling using SWAT+. Hydrol. Earth Syst. Sci. 2024, 28, 21–48. [Google Scholar] [CrossRef]
- Abbaspour, K.; Vaghefi, S.A.; Yang, H.; Srinivasan, R. Global soil, landuse, evapotranspiration, historical and future weather databases for SWAT Applications. Sci. Data 2019, 6, 263. [Google Scholar] [CrossRef]
- Bailey, R.T.; Bieger, K.; Arnold, J.G.; Bosch, D.D. A new physically-based spatially-distributed groundwater flow module for SWAT+. Hydrology 2020, 7, 75. [Google Scholar] [CrossRef]
- Van Griensven, A.; Ndomba, P.; Yalew, S.; Kilonzo, F. Critical review of SWAT applications in the upper Nile basin countries. Hydrol. Earth Syst. Sci. 2012, 16, 3371–3381. [Google Scholar] [CrossRef]
- Yimer, E.A.; Bailey, R.T.; Van Schaeybroeck, B.; Van De Vyver, H.; Villani, L.; Nossent, J.; van Griensven, A. Regional evaluation of groundwater-surface water interactions using a coupled geohydrological model (SWAT+ gwflow). J. Hydrol. Reg. Stud. 2023, 50, 101532. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.; Bosch, D. Problems and potential of autocalibrating a hydrologic model. Trans. ASAE 2005, 48, 1025–1040. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, a completely restructured version of the soil and water assessment tool. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 115–130. [Google Scholar] [CrossRef]
- Wagner, P.D.; Bieger, K.; Arnold, J.G.; Fohrer, N. Representation of hydrological processes in a rural lowland catchment in Northern Germany using SWAT and SWAT+. Hydrol. Process. 2022, 36, e14589. [Google Scholar] [CrossRef]
- van Tol, J.; Bieger, K.; Arnold, J.G. A hydropedological approach to simulate streamflow and soil water contents with SWAT+. Hydrol. Process. 2021, 35, e14242. [Google Scholar] [CrossRef]
- Bailey, R.T.; Bieger, K.; Flores, L.; Tomer, M. Evaluating the contribution of subsurface drainage to watershed water yield using SWAT+ with groundwater modeling. Sci. Total. Environ. 2022, 802, 149962. [Google Scholar] [CrossRef]
- Sánchez-Gómez, A.; Schürz, C.; Molina-Navarro, E.; Bieger, K. Groundwater modelling in SWAT+: Considerations for a realistic baseflow simulation. Groundw. Sustain. Dev. 2024, 26, 101275. [Google Scholar] [CrossRef]
- Cronshey, R. Urban Hydrology for Small Watersheds; Number 55; US Department of Agriculture, Soil Conservation Service, Engineering Division: Washington, DC, USA, 1986.
- Monteith, J.L. Evaporation and environment. In Symposia of the Society for Experimental Biology; Cambridge University Press (CUP): Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Williams, J.R. Flood routing with variable travel time or variable storage coefficients. Trans. ASAE 1969, 12, 100–0103. [Google Scholar] [CrossRef]
- Singh, R.; Subramanian, K.; Refsgaard, J. Hydrological modelling of a small watershed using MIKE SHE for irrigation planning. Agric. Water Manag. 1999, 41, 149–166. [Google Scholar] [CrossRef]
- Ramteke, G.; Singh, R.; Chatterjee, C. Assessing impacts of conservation measures on watershed hydrology using MIKE SHE model in the face of climate change. Water Resour. Manag. 2020, 34, 4233–4252. [Google Scholar] [CrossRef]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating three hydrological distributed watershed models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef]
- Graham, D.N.; Butts, M.B. Flexible, integrated watershed modelling with MIKE SHE. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2005; pp. 245–272. [Google Scholar]
- Im, S.; Kim, H.; Kim, C.; Jang, C. Assessing the impacts of land use changes on watershed hydrology using MIKE SHE. Environ. Geol. 2009, 57, 231–239. [Google Scholar] [CrossRef]
- Jha, M.K.; Gupta, A.D. Application of Mike Basin for water management strategies in a watershed. Water Int. 2003, 28, 27–35. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Sun, G.; Strauss, P.; Guo, J.; Tang, Y.; Yao, A. Multi-site calibration, validation, and sensitivity analysis of the MIKE SHE Model for a large watershed in northern China. Hydrol. Earth Syst. Sci. 2012, 16, 4621–4632. [Google Scholar] [CrossRef]
- Oogathoo, S. Runoff Simulation in the CANAGAGIGUE CREEK Watershed Using the MIKE SHE Model. Master’s Thesis, McGill University, Montréal, QC, Canada, 2006. [Google Scholar]
- Ghosh, A.; Roy, M.B.; Roy, P.K. Evaluating the performance of MIKE NAM model on rainfall–runoff in lower Gangetic floodplain, West Bengal, India. Model. Earth Syst. Environ. 2022, 8, 4001–4017. [Google Scholar] [CrossRef]
- Agrawal, N.; Desmukh, T. Rainfall runoff modeling using MIKE 11 NAM—A review. Int. J. Innov. Sci. Eng. Technol. 2016, 3, 659–667. [Google Scholar]
- Razad, A.Z.A.; Sidek, L.M.; Jung, K.; Basri, H. Reservoir inflow simulation using MIKE NAM rainfall-runoff model: Case study of cameron highlands. J. Eng. Sci. Technol. 2018, 13, 4206–4225. [Google Scholar]
- Bami, Y.S.; Porhemmat, J.; Sedghi, H.; Jalalkamali, N. Performance evaluation of Mike Nam Rainfall-Runoff (RR) model in daily flow simulation (case study: Gonbad Catchment in Hamedan). J. Appl. Eng. Sci. 2020, 10, 1–6. [Google Scholar]
- Doulgeris, C.; Georgiou, P.; Papadimos, D.; Papamichail, D. Evaluating three different model setups in the MIKE 11 NAM model. In Advances in the Research of Aquatic Environment: Volume 1; Springer: Berlin/Heidelberg, Germany, 2011; pp. 241–249. [Google Scholar]
- Ghebrehiwot, A.A.; Kozlov, D.V. Assessment of applicability of MIKE 11-NAM hydrological module for rainfall runoff modelling in a poorly studied river basin. Afr. J. Food Agric. Nutr. Dev. 2020, 20, 1030–1046. [Google Scholar] [CrossRef]
- Doulgeris, C.; Georgiou, P.; Papadimos, D.; Papamichail, D. Ecosystem approach to water resources management using the MIKE 11 modeling system in the Strymonas River and Lake Kerkini. J. Environ. Manag. 2012, 94, 132–143. [Google Scholar] [CrossRef]
- Thompson, J.; Sørenson, H.R.; Gavin, H.; Refsgaard, A. Application of the coupled MIKE SHE/MIKE 11 modelling system to a lowland wet grassland in southeast England. J. Hydrol. 2004, 293, 151–179. [Google Scholar] [CrossRef]
- Kamel, A. Application of a hydrodynamic MIKE 11 model for the Euphrates River in Iraq. Slovak J. Civ. Eng. 2008, 2, 1–7. [Google Scholar]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Girbaciu, A.; Girbaciu, C.; Petcovici, E.; Dodocioiu, A.M. Water quality modelling using Mike 11. Rev. Chim. 2015, 66, 1206–1211. [Google Scholar]
- Marshall, S.R.; Tran, T.N.D.; Tapas, M.R.; Nguyen, B.Q. Integrating artificial intelligence and machine learning in hydrological modeling for sustainable resource management. Int. J. River Basin Manag. 2025, 1–17. [Google Scholar] [CrossRef]
- Subbarayan, S.; Youssef, Y.M.; Singh, L.; Dąbrowska, D.; Alarifi, N.; Ramsankaran, R.; Visweshwaran, R.; Saqr, A.M. Soil and Water Assessment Tool-Based Prediction of Runoff Under Scenarios of Land Use/Land Cover and Climate Change Across Indian Agro-Climatic Zones: Implications for Sustainable Development Goals. Water 2025, 17, 458. [Google Scholar] [CrossRef]
- Luo, Y.; Ficklin, D.L.; Liu, X.; Zhang, M. Assessment of climate change impacts on hydrology and water quality with a watershed modeling approach. Sci. Total. Environ. 2013, 450, 72–82. [Google Scholar] [CrossRef]
- Marshall, E.; Randhir, T. Effect of climate change on watershed system: A regional analysis. Clim. Chang. 2008, 89, 263–280. [Google Scholar] [CrossRef]
- Keller, A.A.; Garner, K.L.; Rao, N.; Knipping, E.; Thomas, J. Downscaling approaches of climate change projections for watershed modeling: Review of theoretical and practical considerations. PLoS Water 2022, 1, e0000046. [Google Scholar] [CrossRef]
- Bekele, E.G.; Knapp, H.V. Watershed modeling to assessing impacts of potential climate change on water supply availability. Water Resour. Manag. 2010, 24, 3299–3320. [Google Scholar] [CrossRef]
- Dudula, J.; Randhir, T.O. Modeling the influence of climate change on watershed systems: Adaptation through targeted practices. J. Hydrol. 2016, 541, 703–713. [Google Scholar] [CrossRef]
- Johnson, T.E.; Weaver, C.P. A framework for assessing climate change impacts on water and watershed systems. Environ. Manag. 2009, 43, 118–134. [Google Scholar] [CrossRef]
- Cousino, L.K.; Becker, R.H.; Zmijewski, K.A. Modeling the effects of climate change on water, sediment, and nutrient yields from the Maumee River watershed. J. Hydrol. Reg. Stud. 2015, 4, 762–775. [Google Scholar] [CrossRef]
- Leta, O.T.; El-Kadi, A.I.; Dulai, H. Impact of climate change on daily streamflow and its extreme values in pacific island watersheds. Sustainability 2018, 10, 2057. [Google Scholar] [CrossRef]
- Leta, O.T.; El-Kadi, A.I.; Dulai, H.; Ghazal, K.A. Assessment of climate change impacts on water balance components of Heeia watershed in Hawaii. J. Hydrol. Reg. Stud. 2016, 8, 182–197. [Google Scholar] [CrossRef]
- Akhtar, F.; Awan, U.K.; Borgemeister, C.; Tischbein, B. Coupling remote sensing and hydrological model for evaluating the impacts of climate change on streamflow in data-scarce environment. Sustainability 2021, 13, 14025. [Google Scholar] [CrossRef]
- Al Sayah, M.J.; Abdallah, C.; Khouri, M.; Nedjai, R.; Darwich, T. A framework for climate change assessment in Mediterranean data-sparse watersheds using remote sensing and ARIMA modeling. Theor. Appl. Climatol. 2021, 143, 639–658. [Google Scholar] [CrossRef]
- Filatov, N.; Baklagin, V.; Efremova, T.; Nazarova, L.; Palshin, N. Climate change impacts on the watersheds of Lakes Onego and Ladoga from remote sensing and in situ data. Inland Waters 2019, 9, 130–141. [Google Scholar] [CrossRef]
- Ren, C.; Chang, J.; Wang, X.; Niu, C.; Wang, L.; Zhang, J. Coupled SWAT, Stationary Wavelet Transform, and Interpretable Machine Learning to Improve Watershed Streamflow Simulation. Water Resour. Manag. 2025, 39, 3483–3498. [Google Scholar] [CrossRef]
- Karimizadeh, K.; Yi, J. Modeling hydrological responses of watershed under climate change scenarios using machine learning techniques. Water Resour. Manag. 2023, 37, 5235–5254. [Google Scholar] [CrossRef]
- Nguyen, Q.; Shrestha, S.; Ghimire, S.; Sundaram, S.M.; Xue, W.; Virdis, S.G.; Maharjan, M. Application of machine learning models in assessing the hydrological changes under climate change in the transboundary 3S River Basin. J. Water Clim. Chang. 2023, 14, 2902–2918. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ismail, T.; Sa’adi, Z.; Farooque, A.; Yaseen, Z.M. Distributed hydrological model based on machine learning algorithm: Assessment of climate change impact on floods. Sustainability 2022, 14, 6620. [Google Scholar] [CrossRef]
- Kaur, S.; Chavan, S.R. Assessing the impacts of land use and climate change on streamflow generation in the Nowrangpur catchment based on the SWAT–land-use update tool. J. Water Clim. Chang. 2025, 16, 70–91. [Google Scholar] [CrossRef]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Romano, N. Green-Ampt Curve-Number mixed procedure as an empirical tool for rainfall–runoff modelling in small and ungauged basins. Hydrol. Process. 2013, 27, 1253–1264. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Romano, N. Curve-Number/Green–Ampt mixed procedure for streamflow predictions in ungauged basins: Parameter sensitivity analysis. Hydrol. Process. 2013, 27, 1265–1275. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow prediction in ungauged basins: Review of regionalization methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Jimeno-Sáez, P.; Martínez-España, R.; Pérez-Sánchez, J. Novel approaches for regionalising SWAT parameters based on machine learning clustering for estimating streamflow in ungauged basins. Water Resour. Manag. 2024, 38, 423–440. [Google Scholar] [CrossRef]
- Ghaneei, P.; Foroumandi, E.; Moradkhani, H. Enhancing streamflow prediction in ungauged basins using a nonlinear knowledge-based framework and deep learning. Water Resour. Res. 2024, 60, e2024WR037152. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins: Synthesis Across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Cappelli, F.; Volpi, E.; Langousis, A.; Deidda, R.; Perdios, A.; Furcolo, P.; Grimaldi, S. Sub-daily rainfall simulation using multifractal canonical disaggregation: A parsimonious calibration strategy based on intensity-duration-frequency curves. Stoch. Environ. Res. Risk Assess. 2025, 39, 1–19. [Google Scholar] [CrossRef]
- Alipour, M.; Kibler, K.M. Streamflow prediction under extreme data scarcity: A step toward hydrologic process understanding within severely data-limited regions. Hydrol. Sci. J. 2019, 64, 1038–1055. [Google Scholar] [CrossRef]
- Alipour, M. Streamflow prediction in ungauged basins located within data-scarce areas using XGBoost: Role of feature engineering and explainability. Int. J. River Basin Manag. 2023, 23, 71–92. [Google Scholar] [CrossRef]
- Grimaldi, S.; Cappelli, F.; Papalexiou, S.M.; Petroselli, A.; Nardi, F.; Annis, A.; Piscopia, R.; Tauro, F.; Apollonio, C. Optimizing sensor location for the parsimonious design of flood early warning systems. J. Hydrol. X 2024, 24, 100182. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L. GSSHA: Model to simulate diverse stream flow producing processes. J. Hydrol. Eng. 2004, 9, 161–174. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer Science & Business Media: Berlin, Germany, 2013; Volume 42. [Google Scholar]
- Vojtek, M.; Petroselli, A.; Vojteková, J.; Asgharinia, S. Flood inundation mapping in small and ungauged basins: Sensitivity analysis using the EBA4SUB and HEC-RAS modeling approach. Hydrol. Res. 2019, 50, 1002–1019. [Google Scholar] [CrossRef]
- Petroselli, A.; Piscopia, R.; Grimaldi, S. Design discharge estimation in small and ungauged basins: EBA4SUB framework sensitivity analysis. J. Agric. Eng. 2020, 51, 107–118. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, N.; Luo, Y.; Wang, Y.; Ma, Y.; Wang, Y.; Zhang, K. Improving Flood Streamflow Estimation of Ungauged Small Reservoir Basins Using Remote Sensing and Hydrological Modeling. Remote Sens. 2024, 16, 4399. [Google Scholar] [CrossRef]
- Arsenault, R.; Martel, J.L.; Brunet, F.; Brissette, F.; Mai, J. Continuous streamflow prediction in ungauged basins: Long short-term memory neural networks clearly outperform traditional hydrological models. Hydrol. Earth Syst. Sci. 2023, 27, 139–157. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Serinaldi, F. A continuous simulation model for design-hydrograph estimation in small and ungauged watersheds. Hydrol. Sci. J. 2012, 57, 1035–1051. [Google Scholar] [CrossRef]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous hydrologic modelling for design simulation in small and ungauged basins: A step forward and some tests for its practical use. J. Hydrol. 2021, 595, 125664. [Google Scholar] [CrossRef]
- Grimaldi, S.; Volpi, E.; Langousis, A.; Papalexiou, S.M.; De Luca, D.L.; Piscopia, R.; Nerantzaki, S.D.; Papacharalampous, G.; Petroselli, A. Continuous hydrologic modelling for small and ungauged basins: A comparison of eight rainfall models for sub-daily runoff simulations. J. Hydrol. 2022, 610, 127866. [Google Scholar] [CrossRef]
- Muhebwa, A.; Gleason, C.J.; Feng, D.; Taneja, J. Improving discharge predictions in ungauged basins: Harnessing the power of disaggregated data modeling and machine learning. Water Resour. Res. 2024, 60, e2024WR037122. [Google Scholar] [CrossRef]
- Karmakar, S. Advanced Hydrology (Web Course), National Programme on Technology Enhanced Learning, India, 2012. Available online: https://archive.nptel.ac.in/courses/105/101/105101002/ (accessed on 10 April 2021).
- Petroselli, A.; Grimaldi, S. Design hydrograph estimation in small and fully ungauged basins: A preliminary assessment of the EBA4SUB framework. J. Flood Risk Manag. 2018, 11, S197–S210. [Google Scholar] [CrossRef]


| Distribution | Range | Parameter Equations | |
|---|---|---|---|
| Normal | |||
| Log-normal | ; | ||
| Exponential | |||
| Gamma | |||
| Pearson Type III | , , | ||
| Log Pearson Type III | ; | , | |
| Extreme Value Type I |
| Model Type | Hydrologic Models |
|---|---|
| Lumped parameter | Snyder or Clark UH |
| Distributed | Kinematic wave |
| Event | HEC-1, HEC-HMS, SWMM, SCS TR-20 |
| Continuous | Stanford Model, SWMM, HSPF, STORM |
| Physically based | HEC-1, HEC-HMS, SWMM, HSPF |
| Stochastic | Synthetic streamflows |
| Numerical | Kinematic or dynamic wave models |
| Analytical | Rational Method, Nash IUH |
| Models | Application Areas |
|---|---|
| HEC-HMS | Drainage, land use change impact on flooding |
| National Weather Service (NWS) | Flood forecasting |
| Modular Modeling System (MMS) | Water resource planning works |
| University of British Columbia (UBC) and WATFLOOD | Hydrologic simulation |
| Runoff-Routing model (RORB) and WBN | Flood, drainage, land use change impact |
| TOPMODEL and SHE | Hydrologic analysis |
| HBV | Flow forecasting |
| Criteria | - | |||
|---|---|---|---|---|
| Scale suitability | Medium to large | Small to medium | Large | Small to large |
| Temporal scale | Hourly to daily | Sub-hourly to daily | Daily | Sub-hourly to daily |
| Spatial representation | Lumped | Semi-distributed | Semi-distributed | Fully distributed |
| Data requirement | High | Moderate | Moderate to high | Very high |
| User friendliness | Moderate | High | Moderate | Low |
| Enhanced modeling | Water quality | Hydrology only | Sediment/nutrient | Integrated |
| Calibration computation | Complex | Easy | Moderate | Very complex |
| Computational load | Moderate | Low | Moderate | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarker, S.; Leta, O.T. Review of Watershed Hydrology and Mathematical Models. Eng 2025, 6, 129. https://doi.org/10.3390/eng6060129
Sarker S, Leta OT. Review of Watershed Hydrology and Mathematical Models. Eng. 2025; 6(6):129. https://doi.org/10.3390/eng6060129
Chicago/Turabian StyleSarker, Shiblu, and Olkeba Tolessa Leta. 2025. "Review of Watershed Hydrology and Mathematical Models" Eng 6, no. 6: 129. https://doi.org/10.3390/eng6060129
APA StyleSarker, S., & Leta, O. T. (2025). Review of Watershed Hydrology and Mathematical Models. Eng, 6(6), 129. https://doi.org/10.3390/eng6060129







