Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness
Abstract
1. Introduction
2. Materials and Methods
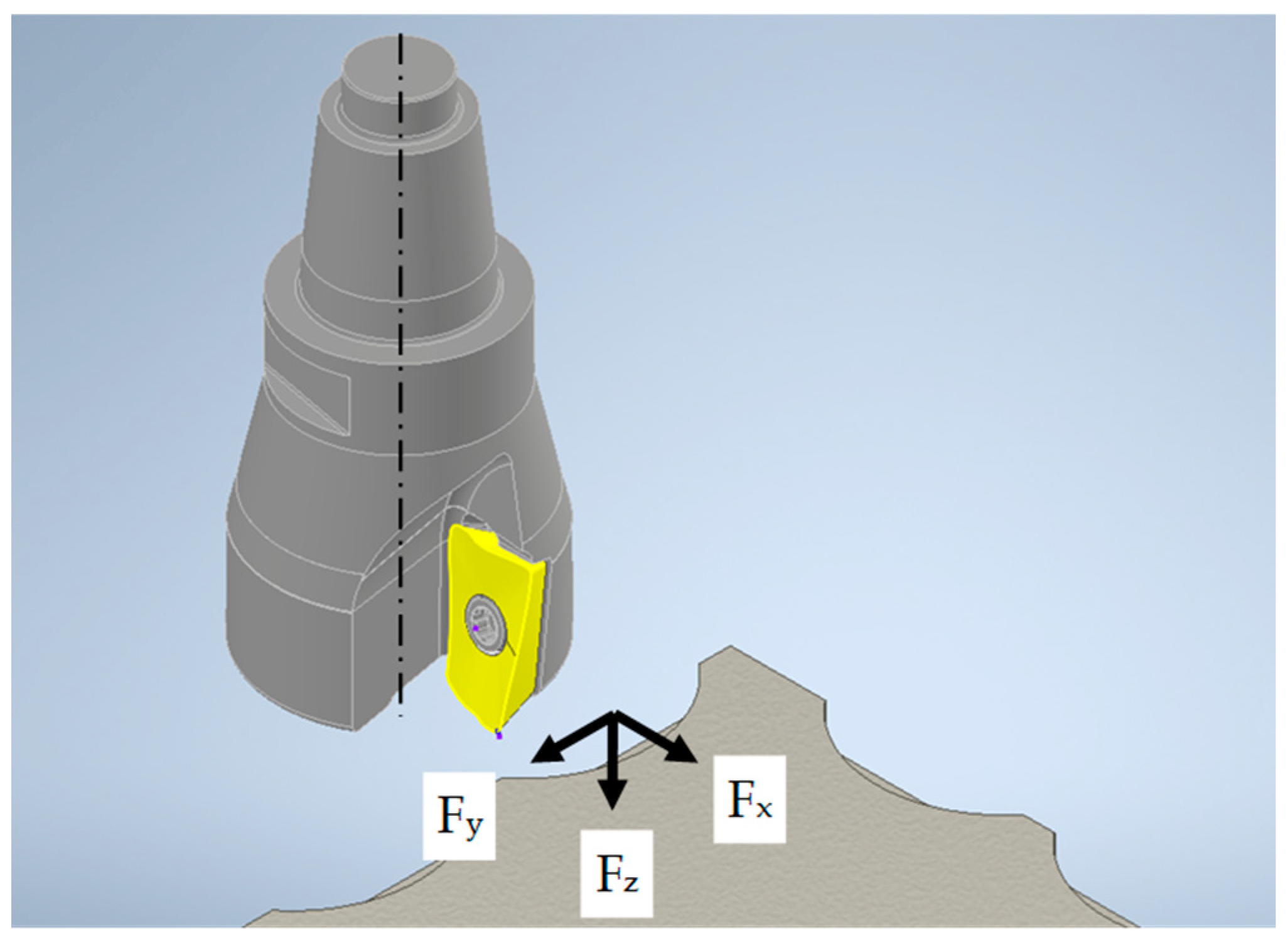
- X-directional force (Fx) is defined as perpendicular to the side surface of the workpiece, oriented from the tool toward the workpiece (radial cutting force).
- The Y-directional force (Fy) is aligned parallel to the machined edge and follows the direction of the cutting speed (tangential cutting force).
- The Z-directional force (Fz) is considered positive when acting downward, in the same direction as the axial feed of the tool (axial cutting force).
3. Results
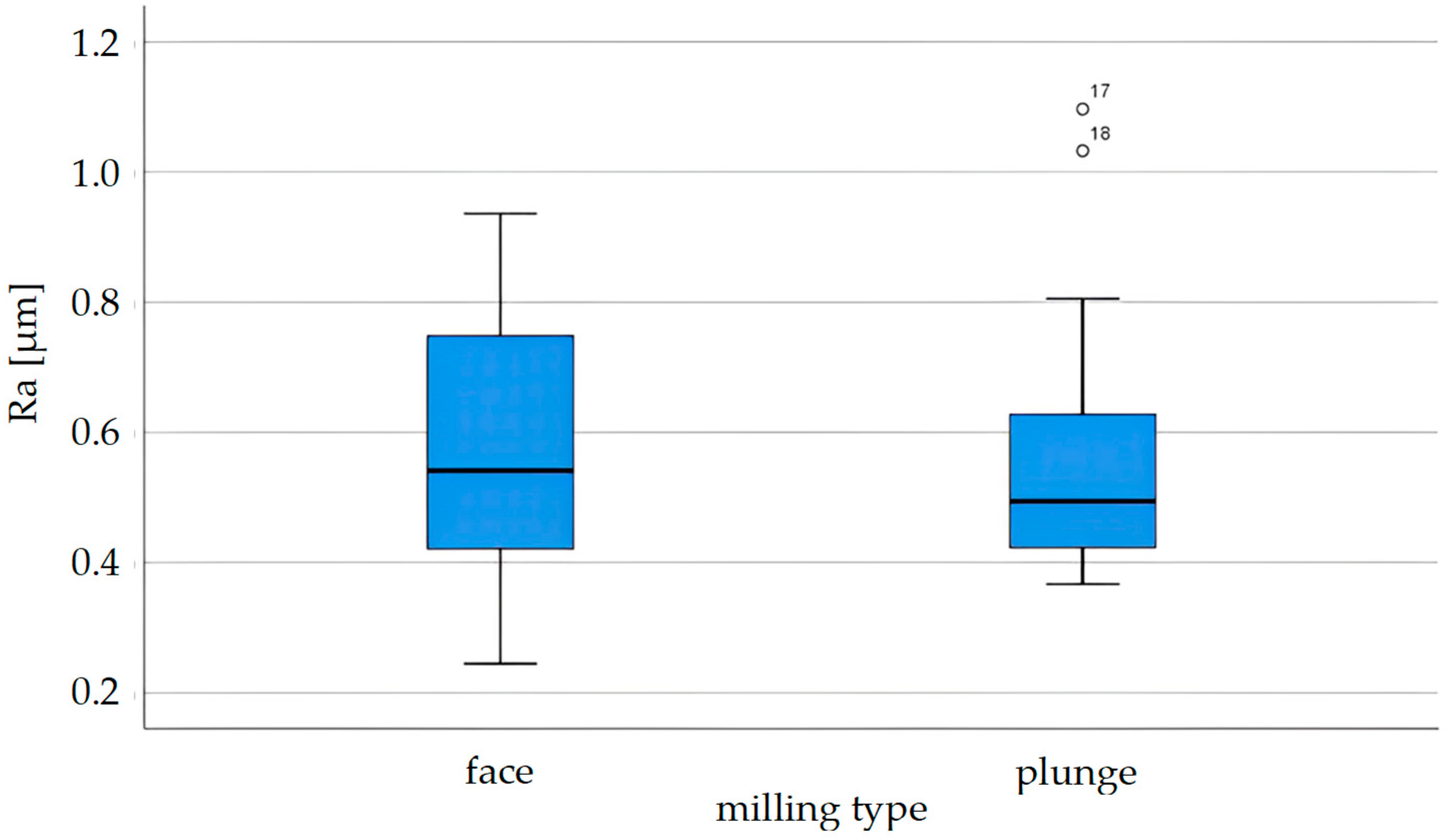
3.1. Surface Roughness
Surface Quality Characterization
3.2. Cutting Forces
4. Discussion
4.1. Evaluation of the Surface Topography
4.1.1. Statistical Analysis of the Surface Roughness
4.1.2. Detailed Analysis of the Side Wall Roughness
4.1.3. Study of the Top Surface Roughness
4.1.4. Comparative Analysis of Plunge and Face Milling
- 1.
- Effect of Depth of Cut (ap):
- 2.
- Effect of Cutting Speed (vc):
- 3.
- Effect of Feed per tooth (fz):
4.2. Evaluation of the Cutting Force
4.2.1. Statistical Analysis of the Cutting Forces
4.2.2. Alterations of the Radial Cutting Force
4.2.3. Study of the Tangential Cutting Force
4.2.4. Analysis of the Axial Cutting Force
5. Conclusions
- Plunge and face milling generate fundamentally distinct surface roughness characteristics, with differences often accentuated by increasing the cutting depth. Key contrasts include the following:
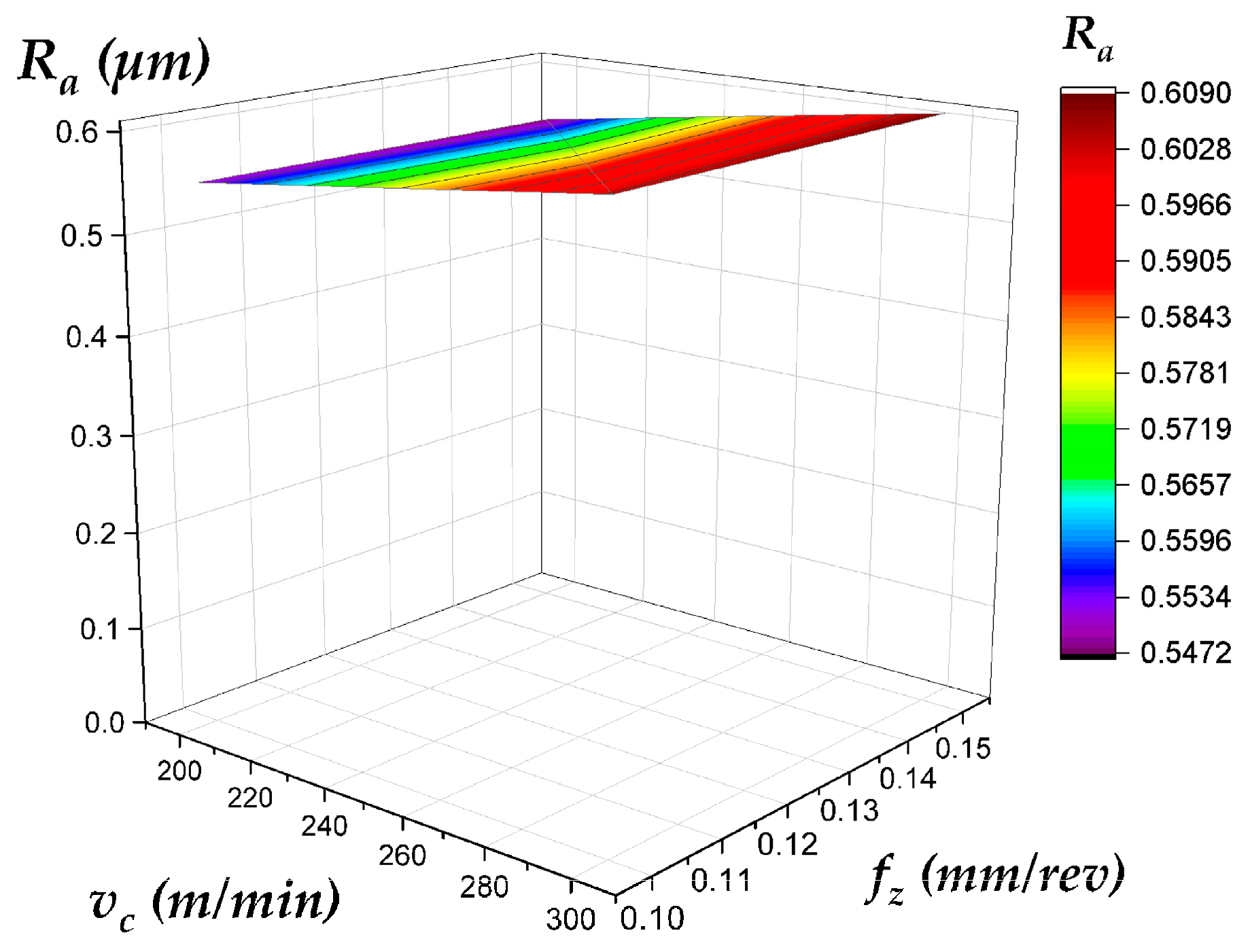
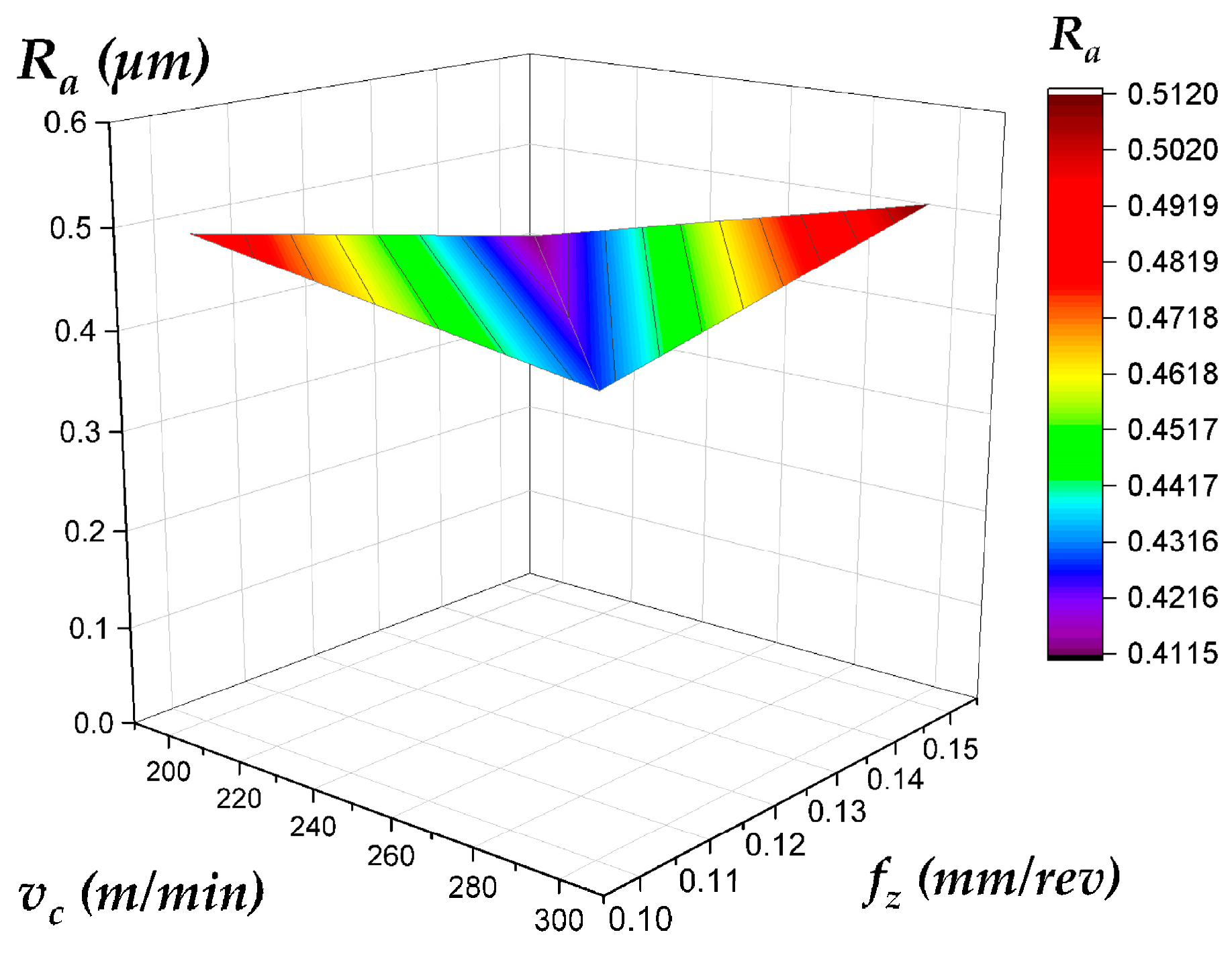
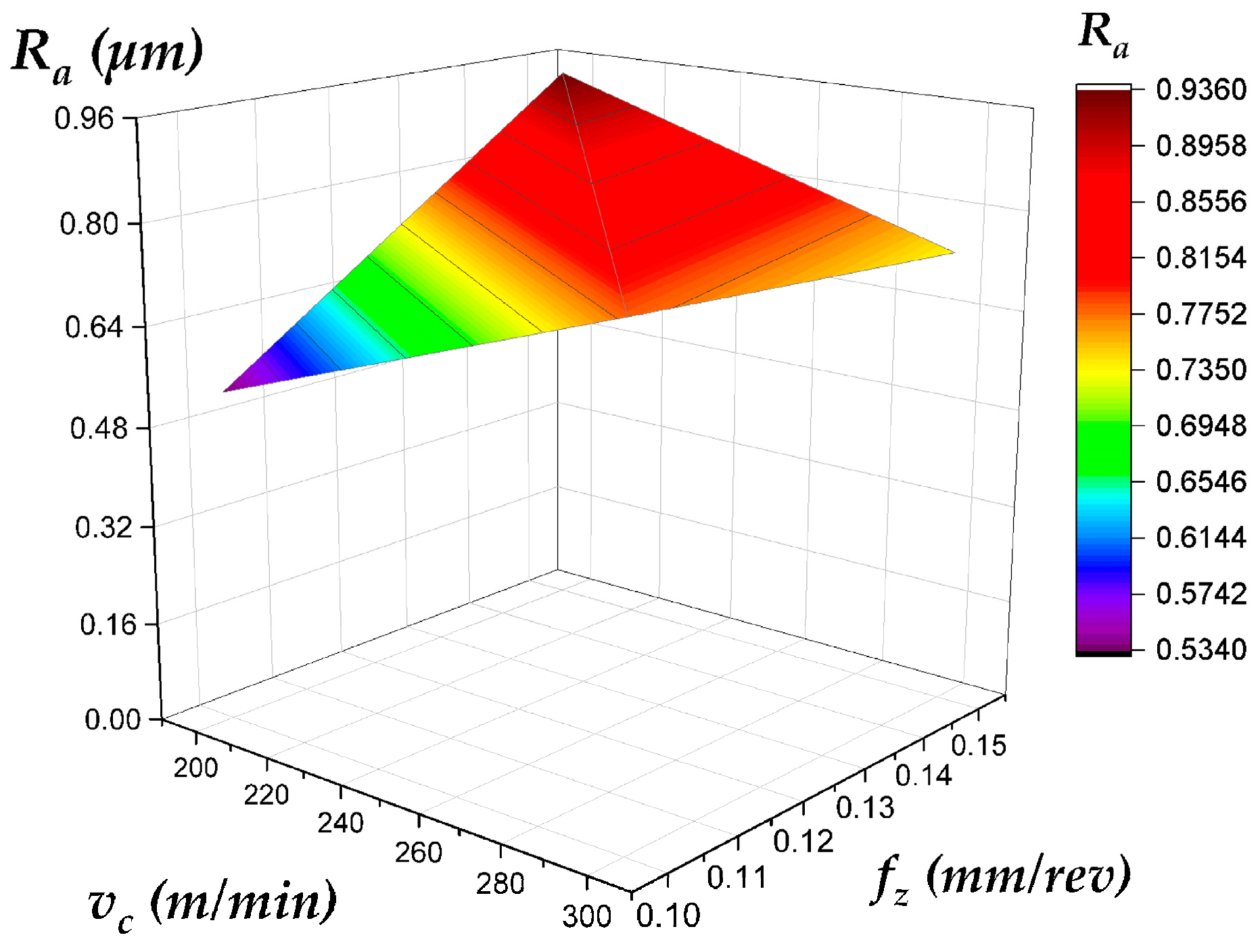
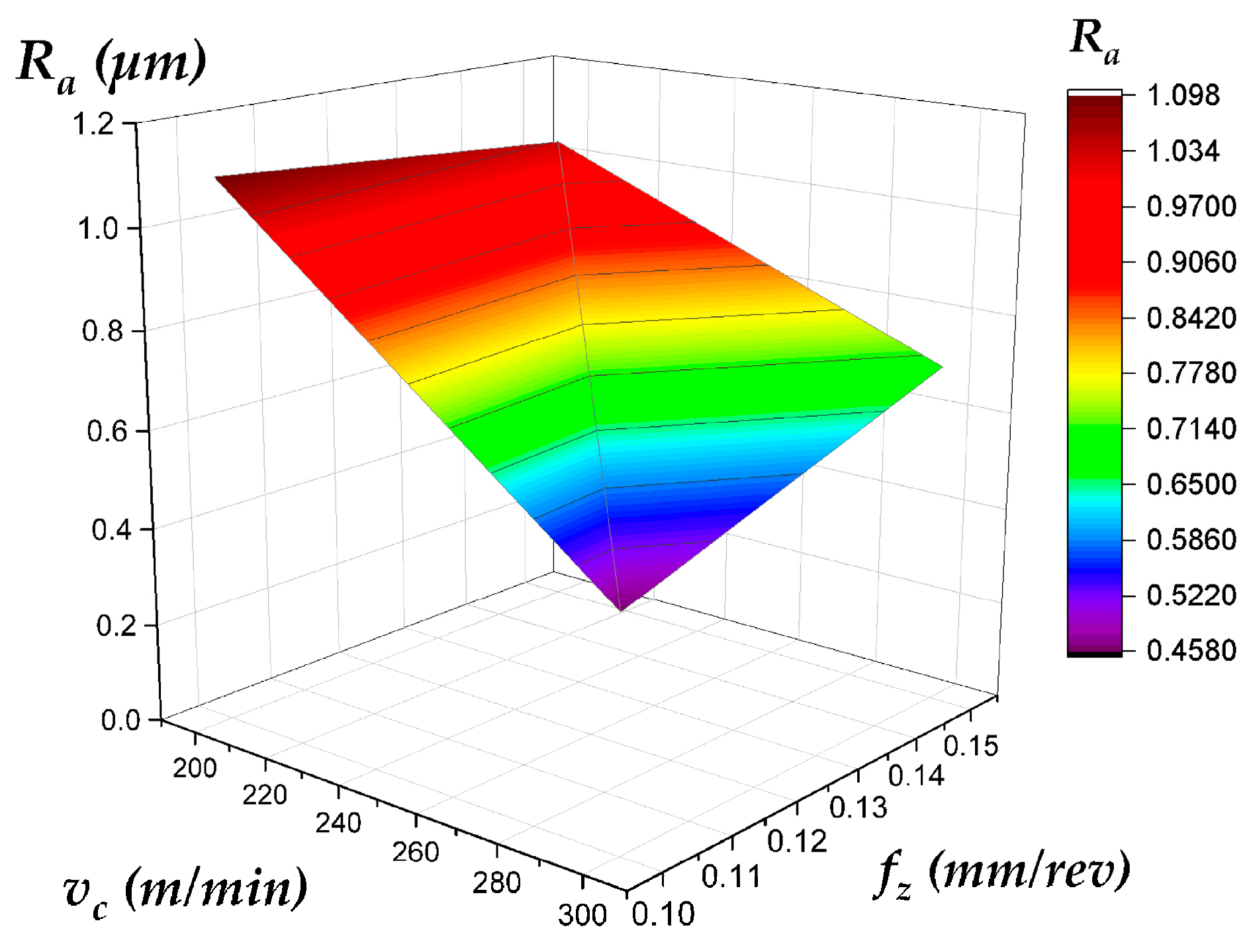
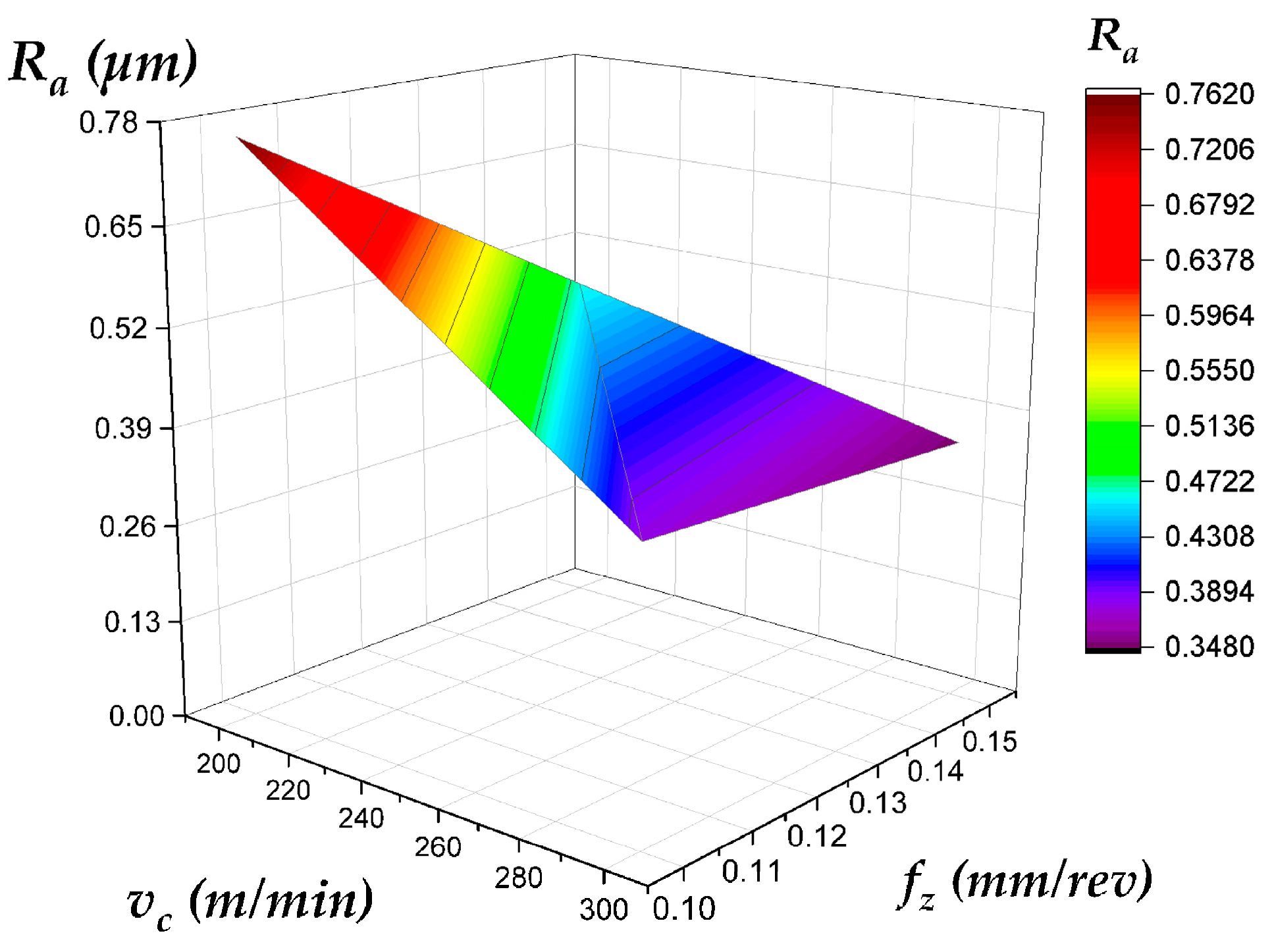
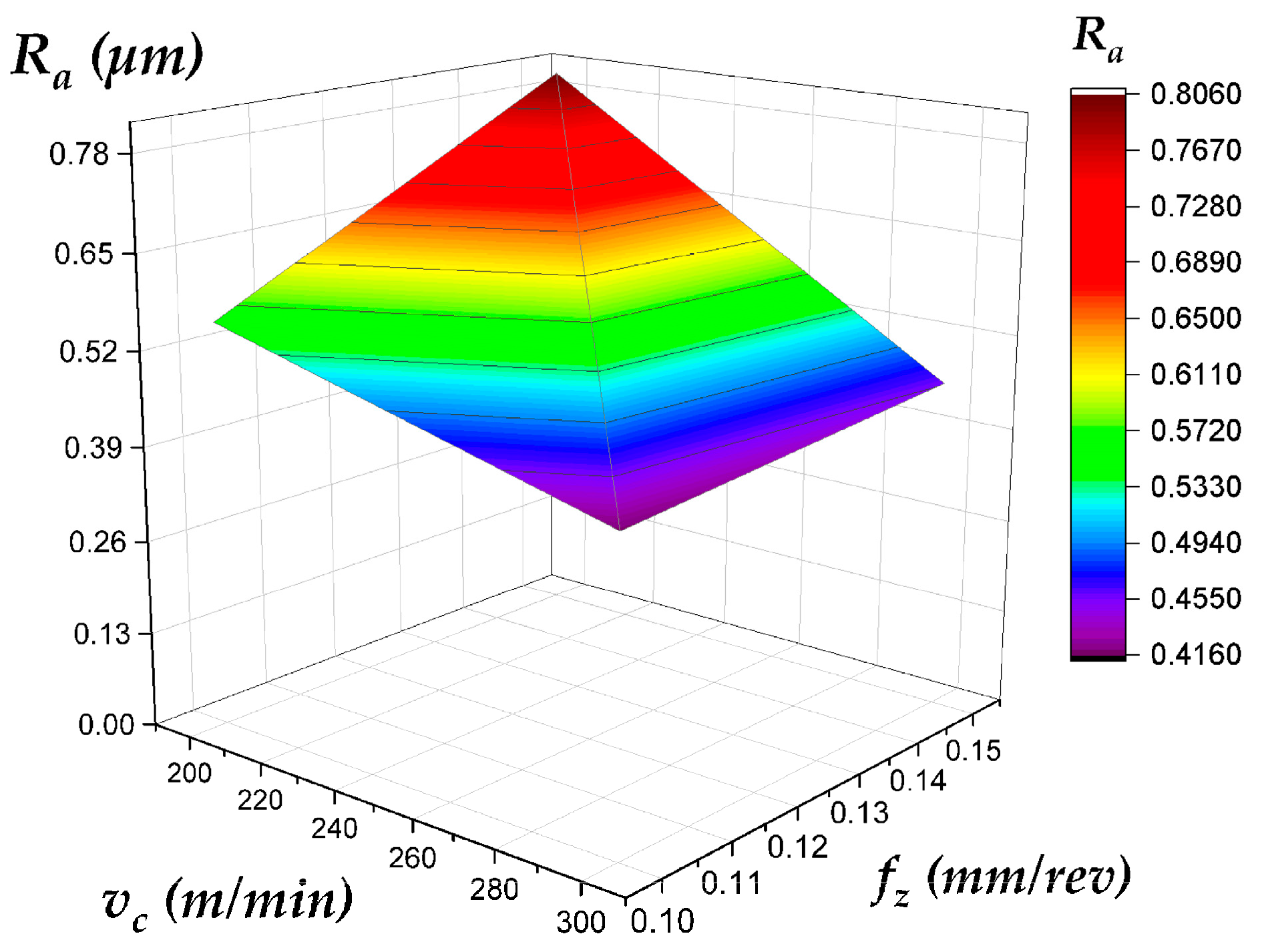
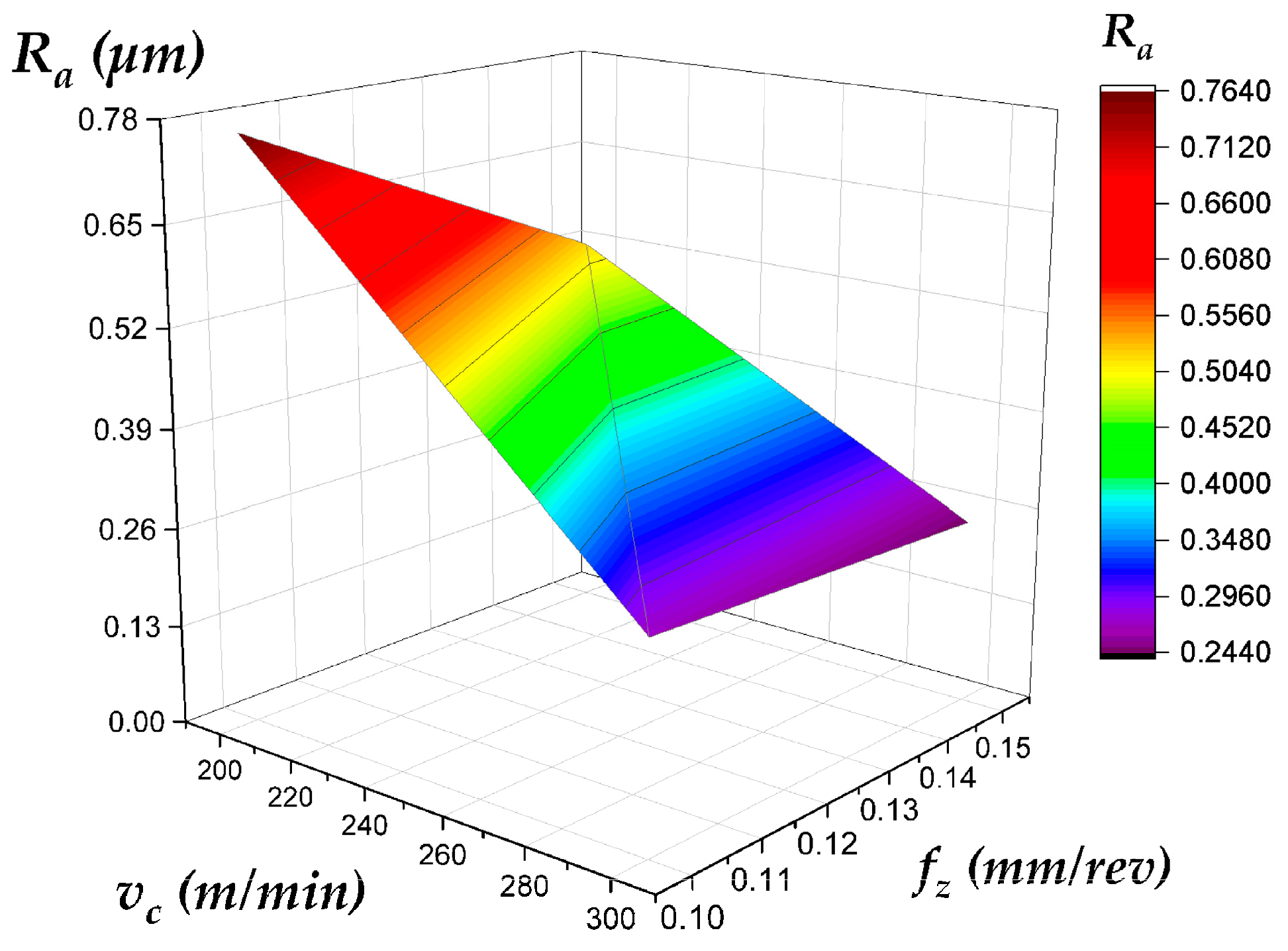
- Topography Variation: Even under identical cutting conditions, plunge and face milling produce different Ra trends (Figure 7) due to variations in tool engagement mechanics, chip evacuation, and dynamic load behavior.
- Depth-Dependent Behavior: Ra values on the side wall and top surface evolve differently with increasing depth of cut (compare Figure 8 and Figure 10 with Figure 9 and Figure 11 for the side wall, and Figure 12 and Figure 14 with Figure 13 and Figure 15 for the top surface), highlighting the complex interaction between process parameters and geometric location.
- Complex changes in chip flow dynamics or interference at greater depths.
- Dominance of specific tool geometry features (e.g., helix angle effects changing nonlinearly with engagement length).
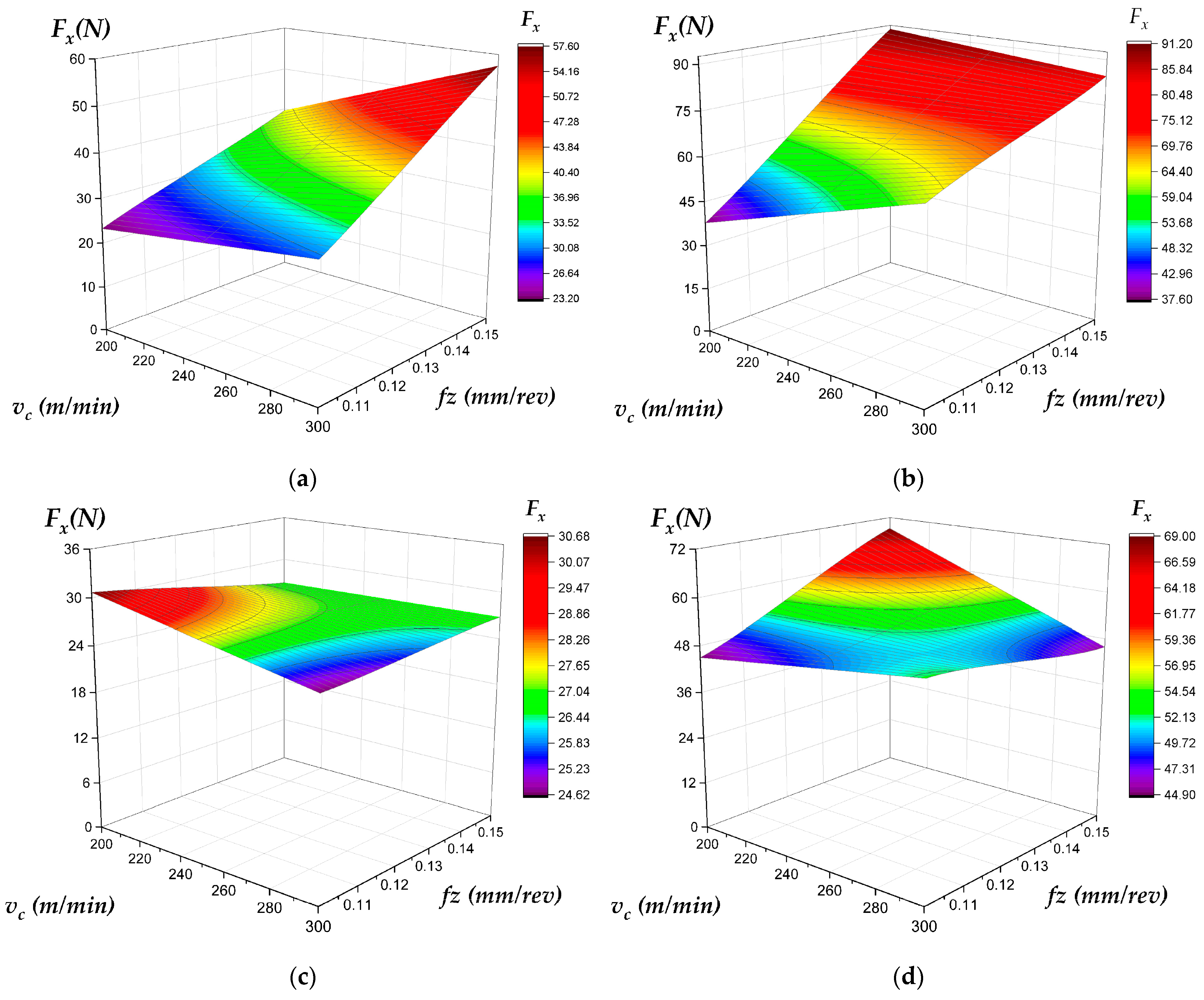
- Feed (fz): Universally, the dominant factor, increasing all the force components for both strategies.
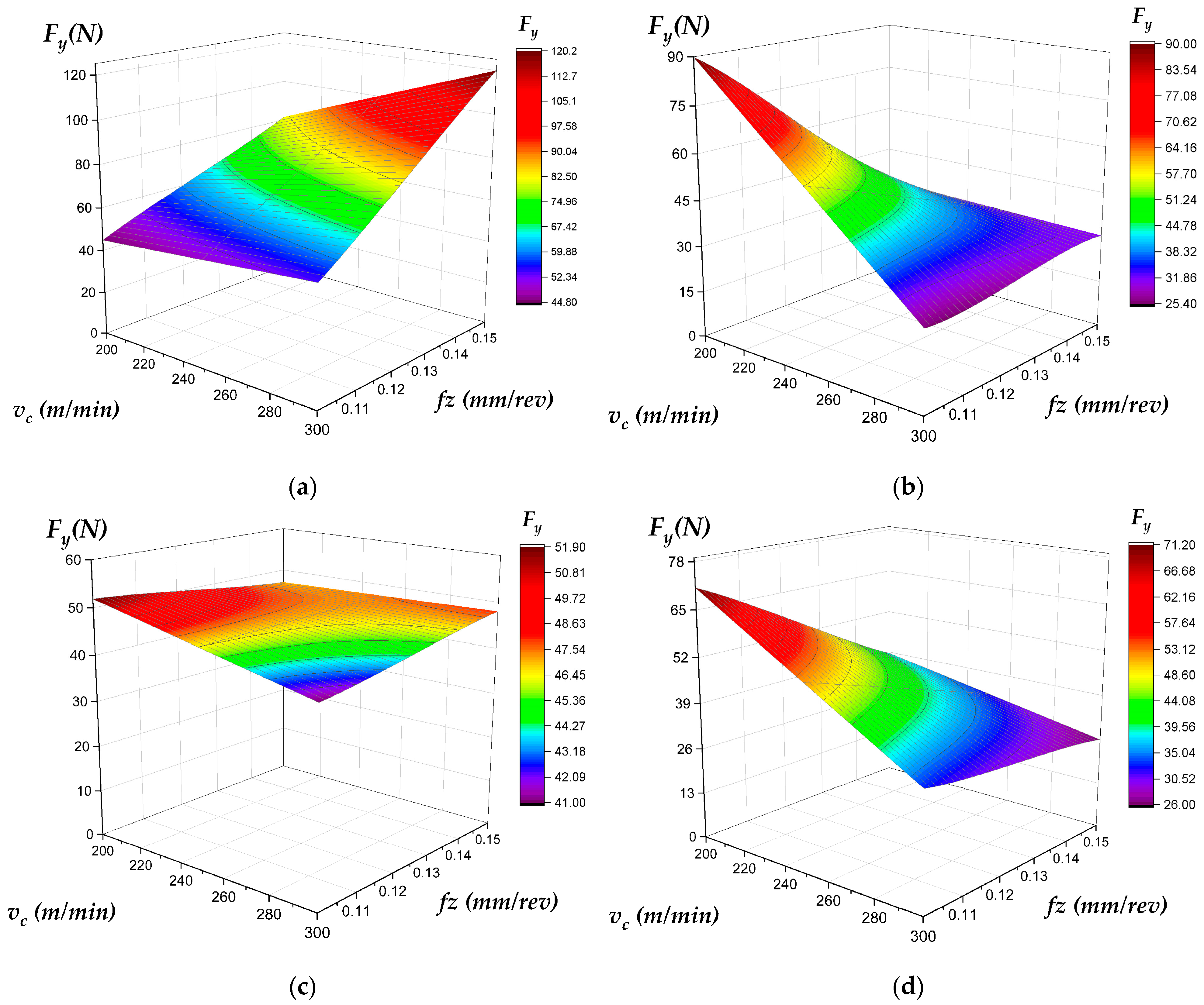
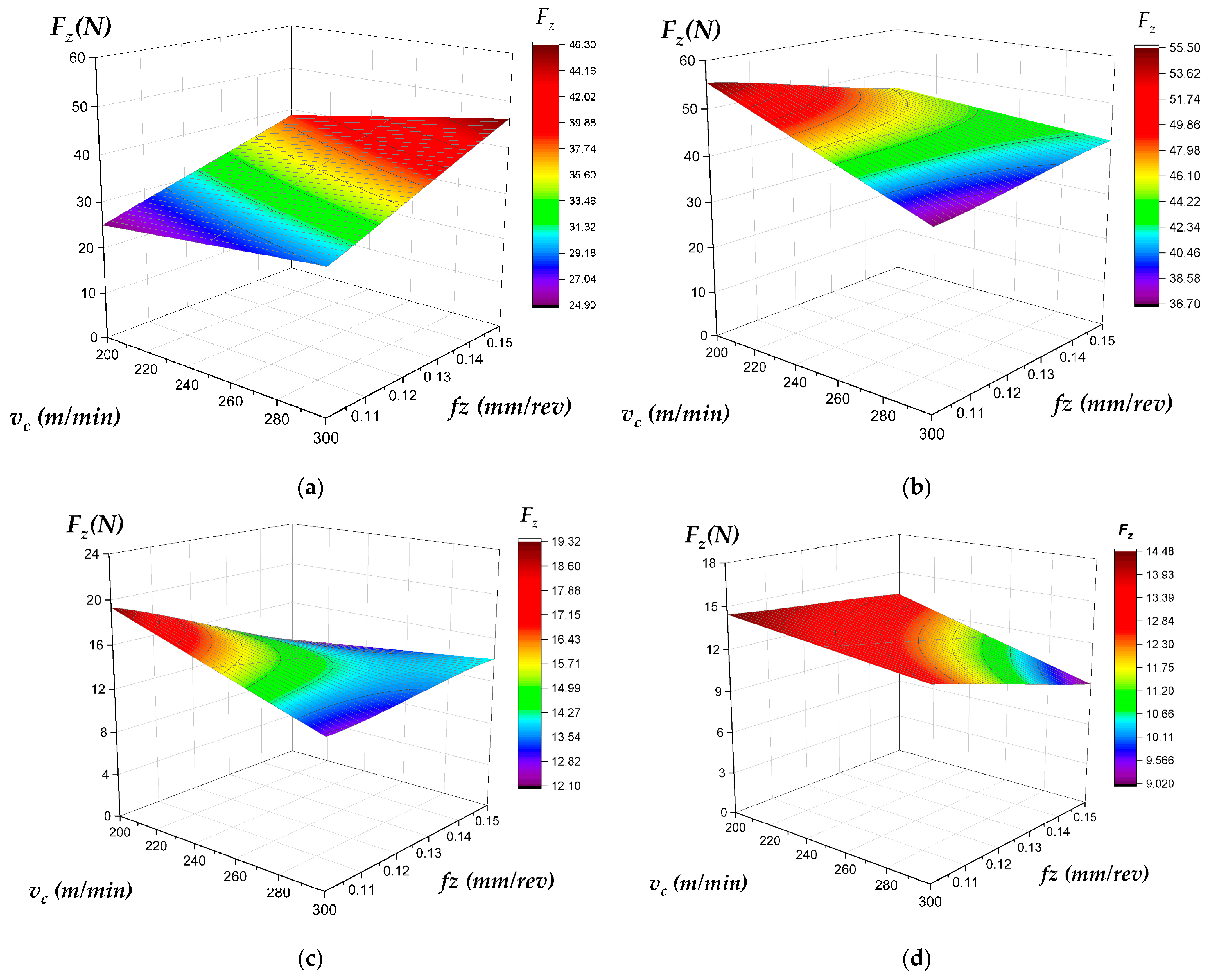
- Depth of Cut (ap): While generally increasing forces as expected (e.g., Fx for both (Figure 16), axial cutting force (Fz) for plunge (Figure 18a vs. Figure 18b), and Fy for face milling (Figure 17c vs. Figure 17d)), the presented data reveals highly anomalous behavior where increasing ‘a’ decreases tangential cutting force (Fy) in plunge milling and axial cutting force (Fz) in face milling (Figure 18c vs. Figure 18d).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, D.C.; Chen, T.W. Surface roughness analysis of high speed milling in grooving. J. Phys. Conf. Ser. 2021, 2020, 012034. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, S.; Xin, H.; Zhang, J.; Yao, C.; Cui, M.; Li, G. Study on tool wear for efficient grooving blisk with disc milling cutter. J. Mech. Sci. Technol. 2023, 37, 5335–5348. [Google Scholar] [CrossRef]
- Gómez, G.; De Lucio, P.F.; Del Olmo, A.; De Pissón, G.M.; Jimeno, A.; González, H.; De Lacalle, L.L. Comparison between milling roughing operations in full slotting manufacturing: Trochoidal, plunge and conventional milling. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 012003. [Google Scholar] [CrossRef]
- Woodrum, R.B.; Barnett, D.H.; Dickens, J.C.; Neuber, A.A. Developing Safe Lathing Parameters for PBX 9501. Propellants Explos. Pyrotech. 2018, 43, 779–788. [Google Scholar] [CrossRef]
- Xin, H.; Shi, Y.; Zhao, T. Compound efficient and powerful milling machine tool of blisk. Int. J. Adv. Manuf. Technol. 2018, 98, 1745–1753. [Google Scholar] [CrossRef]
- Danis, I.; Monies, F.; Lagarrigue, P.; Wojtowicz, N. Cutting forces and their modelling in plunge milling of magnesium-rare earth alloys. Int. J. Adv. Manuf. Technol. 2016, 84, 1801–1820. [Google Scholar] [CrossRef]
- Dong, L.; Chen, M. A comparative experimental study on the rough machining methods of centrifugal three-dimensional impellers. Adv. Mech. Eng. 2024, 16, 16878132241244923. [Google Scholar] [CrossRef]
- Hanzl, P.; Zetková, I. Benefits of a New Approach to Designing Milling Cutter Using Metal Additive Manufacturing. Manuf. Technol. 2019, 19, 385–390. [Google Scholar] [CrossRef]
- Płodzień, M.; Żyłka, Ł.; Sułkowicz, P.; Żak, K.; Wojciechowski, S. High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude. Materials 2021, 14, 2196. [Google Scholar] [CrossRef]
- Pelayo, G.U.; Olvera-Trejo, D.; Luo, M.; Tang, K.; De Lacalle, L.N.L.; Elías-Zuñiga, A. A model-based sustainable productivity concept for the best decision-making in rough milling operations. Measurement 2021, 186, 110120. [Google Scholar] [CrossRef]
- Wakaoka, S.; Yamane, Y.; Sekiya, K.; Narutaki, N. High-speed and high-accuracy plunge cutting for vertical walls. J. Mater. Process. Technol. 2002, 127, 246–250. [Google Scholar] [CrossRef]
- Adesta, E.Y.T.; Avicenna; Hilmy, I.; Daud, M.R.H.C. Toolpath strategy for cutter life improvement in plunge milling of AISI H13 tool steel. IOP Conf. Ser. Mater. Sci. Eng. 2018, 290, 012040. [Google Scholar] [CrossRef]
- Al-Ahmad, M.; d’Acunto, A.; Martin, P. Identification of Plunge Milling Parameters to Compare with Conventional Milling. In Advances in Integrated Design and Manufacturing in Mechanical Engineering II; Tichkiewitch, S., Tollenaere, M., Ray, P., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 461–474. [Google Scholar] [CrossRef]
- Al-Ahmad, M.; D’Acunto, A.; Lescalier, C.; Bomont, O. Modeling of Cutting Forces in Plunge Milling. In AMST’05 Advanced Manufacturing Systems and Technology; CISM International Centre for Mechanical Sciences; Kuljanic, E., Ed.; Springer: Vienna, Austria, 2005; Volume 486, pp. 155–164. [Google Scholar] [CrossRef]
- Ko, J.H.; Altintas, Y. Dynamics and Stability of Plunge Milling Operations. J. Manuf. Sci. Eng. 2007, 129, 32–40. [Google Scholar] [CrossRef]
- Bey, M.; Tchantchane, Z.; Kheidri, L.; Benhenda, N. Toward the automation of the plunge milling strategy for roughing sculptured surfaces from stl models. In Proceedings of the 15th International Research/Expert Conference “Trends in the Development of Machinery and Associated Technology”, TMT, Prague, Czech Republic, 12–18 September 2011. [Google Scholar]
- Bey, M.; Tchantchane, Z. Optimum Combination of Cutting Tools for Roughing Complex Parts Using Plunge Milling Machining Strategy. Available online: https://www.researchgate.net/profile/Mohamed-Bey/publication/321429431_Optimum_Combination_of_Cutting_Tools_for_Roughing_Complex_Parts_Using_Plunge_Milling_Machining_Strategy/links/5a2182feaca2727dd87aa137/Optimum-Combination-of-Cutting-Tools-for-Roughing-Complex-Parts-Using-Plunge-Milling-Machining-Strategy.pdf (accessed on 11 June 2025).
- Varga, J.; Spišák, E.; Gajdoš, I.; Mulidrán, P. Comparison of Milling Strategies in the Production of Shaped Surfaces. Adv. Sci. Technol. Res. J. 2022, 16, 267–274. [Google Scholar] [CrossRef]
- Fnides, M.; Amroune, S.; Slamani, M.; Elhadi, A.; Arslane, M.; Jawaid, M. Optimization of Manufacturing Parameters for Minimizing Vibrations and Surface Roughness in Milling Using Box–Behnken Design. J. Vib. Eng. Technol. 2025, 13, 22. [Google Scholar] [CrossRef]
- Cui, T. Precision Machining of Hard-to-Cut Materials: Current Status and Future Directions. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 861–871. Available online: https://www.webofscience.com/wos/woscc/full-record/WOS:001348288600001 (accessed on 26 November 2024). [CrossRef]
- Zhang, Z.; Liu, Y.; Han, Q.; Zhong, S.; Wang, Y.; Liu, H. The design and cutting performance of variable pitch solid ceramic end milling tools. Int. J. Refract. Met. Hard Mater. 2024, 120, 106579. [Google Scholar] [CrossRef]
- Silva, F.J.; Martinho, R.P.; Magalhães, L.L.; Fernandes, F.; Sales-Contini, R.C.; Durão, L.M.; Casais, R.C.; Sousa, V.F. A Comparative Study of Different Milling Strategies on Productivity, Tool Wear, Surface Roughness, and Vibration. J. Manuf. Mater. Process. 2024, 8, 115. [Google Scholar] [CrossRef]
- Niu, X.H.; Cui, L.Q.; Hao, B.C.; Liu, S.Y.; Zhang, Z.T.; Meng, X.L. Analysis of Plunge Milling Force and Tool Deformation on Cr12. Adv. Mater. Res. 2013, 652–654, 2173–2177. [Google Scholar] [CrossRef]
- Ventura, C.E.; Hassui, A. Analysis of the cutting forces in plunge milling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1808–1818. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Li, L. Wear and Life of K40 Carbide Tool for Plunge Milling GH4169. J. Phys. Conf. Ser. 2023, 2566, 012058. [Google Scholar] [CrossRef]
- Jin, C.; Guo, C.; Gao, Y. Research on cutting vibration characteristics of face-milling involute gear. Def. Technol. 2017, 13, 380–384. [Google Scholar] [CrossRef]
- Tapoglou, N.; Antoniadis, A. 3-Dimensional kinematics simulation of face milling. Measurement 2012, 45, 1396–1405. [Google Scholar] [CrossRef]
- Usubamatov, R.; Bayalieva, C.; Kapayeva, S.; Sartov, T.; Riza, G. Optimization of the face milling operations by the criterion of the maximal productivity rate. Prod. Eng. Res. Dev. 2024, 18, 525–531. [Google Scholar] [CrossRef]
- Jiménez, M.; Romero, L.; Domínguez, I.A.; Espinosa, M.D.M.; Domínguez, M. Additive Manufacturing Technologies: An Overview about 3D Printing Methods and Future Prospects. Complexity 2019, 2019, 9656938. [Google Scholar] [CrossRef]
- Lin, A.Q.; Zheng, M.L.; Fan, C.G.; Yang, L. Surface Morphology Simulation of High Speed Milled of Face Milling Cutters. Adv. Mater. Res. 2011, 305, 225–229. [Google Scholar] [CrossRef]
- Wang, J.; Qi, X.; Ma, W.; Zhang, S. A high efficiency 3D surface topography model for face milling processes. J. Manuf. Process. 2023, 107, 74–87. [Google Scholar] [CrossRef]
- Borysenko, D.; Kundrák, J.; Karpuschewski, B.; Welzel, F.; Maros, Z.; Felhő, C. Surface Residual Stresses in High-Feed Face Milling of Carbon Steel. In Vehicle and Automotive Engineering 4; Jármai, K., Cservenák, Á., Eds.; Lecture Notes in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2023; pp. 648–653. [Google Scholar] [CrossRef]
- Kulenovic, M.; Halilagic, D.; Cekic, A. Model for cutting forces in high speed face milling. In Annals of DAAAM for 2005 & Proceedings of the 16th International DAAAM Symposium: Intelligent Manufacturing & Automation: Focus on Young Researches and Scientists; Katalinic, B., Ed.; DAAAM International Vienna: Wien, Austria, 2005; pp. 213–214. [Google Scholar]
- Kulenovic, M.; Cekic, A.; Halilagic, D. Characteristics of cutting forces in high speed face milling. In Annals of DAAAM for 2004 & Proceedings of the 15th International DAAAM Symposium: Intellignet Manufacturing & Automation: Globalisation—Technology—Men—Nature; Katalinic, B., Ed.; DAAAM International Vienna: Wien, Austria, 2004; pp. 239–240. [Google Scholar]
- Tang, D.; Zhang, G. A Study on Face Milling Force Model Based on Complex Surface Geometry. In Proceedings of the 2009 IEEE 10th International Conference on Computer-Aided Industrial Design & Conceptual Design, Wenzhou, China, 26–29 November 2009; pp. 826–830. [Google Scholar]
- Liu, L.N.; Shi, Z.Y.; Liu, Z.Q. Finite Element Modal Analysis for Face-Milling Cutter. Key Eng. Mater. 2013, 589–590, 19–22. [Google Scholar] [CrossRef]
- Carvalho, H.M.B.D.; Gomes, J.D.O.; Schmidt, M.A.; Brandão, V.L.C. Vibration Analysis and Energy Efficiency in Interrupted Face Milling Processes. Procedia CIRP 2015, 29, 245–250. [Google Scholar] [CrossRef]
- Roshan, M.V.; Sumesh, C.S.; Balaji, S.S.; Manchi, M.V.E.; Reddy, M.U.; Baghad, A. Sustainable Machining: A Case Study on Face Milling of AISI 1045 Steel Using a Multi-Objective Optimization Approach. Int. J. Interact. Des. Manuf. 2024. [Google Scholar] [CrossRef]
- Tibakh, I.; Yallese, M.A.; Belhadi, S.; Kaddeche, M. Multi-response optimisation during face milling of polyoxymethylene copolymer using grey relational analysis and data envelopment analysis based ranking coupled with the Taguchi approach. Adv. Mater. Process. Technol. 2024, 11, 681–706. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, X.-M.; Leopold, J.; Ding, H. Tool Orientation Planning in Milling With Process Dynamic Constraints: A Minimax Optimization Approach. J. Manuf. Sci. Eng. 2018, 140, 111002. [Google Scholar] [CrossRef]
- Ren, J.X.; Yao, C.F.; Zhang, D.H.; Xue, Y.L.; Liang, Y.S. Research on tool path planning method of four-axis high-efficiency slot plunge milling for open blisk. Int. J. Adv. Manuf. Technol. 2009, 45, 101–109. [Google Scholar] [CrossRef]
- El Mehtedi, M.; Buonadonna, P.; Loi, G.; El Mohtadi, R.; Carta, M.; Aymerich, F. Surface Quality Related to Face Milling Parameters in 3D Printed Carbon Fiber-Reinforced PETG. J. Compos. Sci. 2024, 8, 128. [Google Scholar] [CrossRef]
- Raza, M.H.; Hafeez, F.; Zhong, R.Y.; Imran, A. Investigation of surface roughness in face milling processes. Int. J. Adv. Manuf. Technol. 2020, 111, 2589–2599. [Google Scholar] [CrossRef]
- Simunovic, G.; Simunovic, K.; Saric, T. Modelling and Simulation of Surface Roughness in Face Milling. Int. J. Simul. Model. 2013, 12, 141–153. [Google Scholar] [CrossRef]
- Reznicek, M.; Horava, C. The Influence of the Choice of Machining Strategy on Production Technology. Manuf. Technol. 2024, 24, 117–130. [Google Scholar] [CrossRef]
- Abbas, A.T.; Helmy, M.O.; Alqosaibi, K.F.; Parvez, S.; Hasan, A.S.; Elkaseer, A. Improving Maraging Steel 350 Machinability via Wiper Insert-Enhanced Face Milling. Metals 2024, 14, 514. [Google Scholar] [CrossRef]
- Malea, C.I.; Niţu, E.L.; Iordache, D.M.; Tabacu, Ş.L.; Negrea, A.D.; Bădulescu, C. Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions. Materials 2024, 17, 3434. [Google Scholar] [CrossRef]
- Viswanathan, V.; Mongird, K.; Franks, R.; Li, X.; Sprenkle, V. 2022 Grid Energy Storage Technology Cost and Performance Assessment. Energy 2022, 2022, 1–151. [Google Scholar]
- Soori, M.; Jough, F.K.G.; Arezoo, B. Surface quality enhancement by constant scallop-height in three-axis milling operations. Results Surf. Interfaces 2024, 14, 100208. [Google Scholar] [CrossRef]
- Wang, Z. The milling parameters of mechanical parts are optimized by NC machining technology. Front. Mech. Eng. 2024, 10, 1367009. [Google Scholar] [CrossRef]
- Cafieri, S.; Monies, F.; Mongeau, M.; Bes, C. Plunge milling time optimization via mixed-integer nonlinear programming. Comput. Ind. Eng. 2016, 98, 434–445. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, D.; Chen, Z.C.; Ren, J.; Li, X. Tool orientation optimization and location determination for four-axis plunge milling of open blisks. Int. J. Adv. Manuf. Technol. 2014, 70, 2249–2261. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, J.; Zuo, D.; Song, X.; Feng, X. Tool design and cutting parameters optimisation for plunge milling blisk. Int. J. Manuf. Res. 2020, 15, 266–284. [Google Scholar] [CrossRef]
- Pala, M.; Sarma, K.V.; Biswal, S.; Amudhavel, V.; Rao, D.V.G. Investigation of High-Speed Milling and High Efficiency Milling of Ti6Al4V. Int. J. Adv. Eng. Res. Sci. 2021, 8, 22–28. [Google Scholar] [CrossRef]
- Dinh, D.-H.; Do, P.; Iung, B. Maintenance optimisation for multi-component system with structural dependence: Application to machine tool sub-system. CIRP Ann. 2020, 69, 417–420. [Google Scholar] [CrossRef]
- ISO 21920-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile—Part 2: Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 2021.


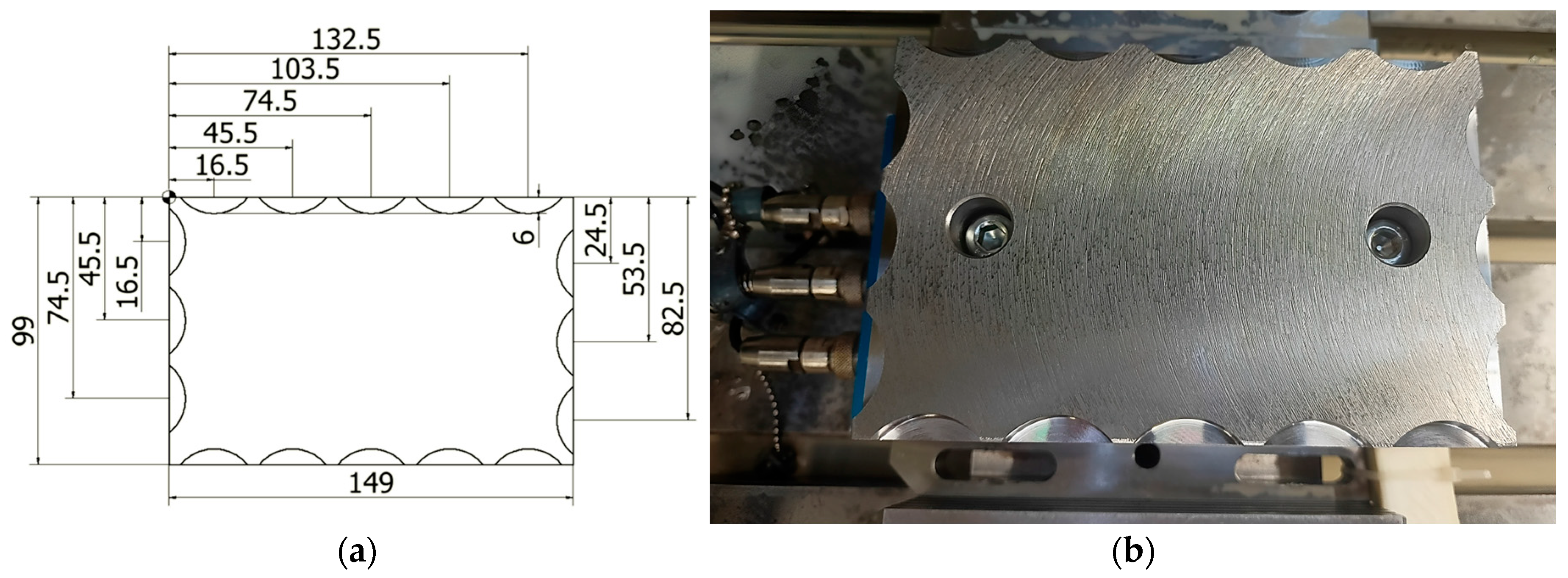


| Parameter | Symbol | Level 1 | Level 2 | Unit | Rationale |
|---|---|---|---|---|---|
| Cutting speed | vc | 200 | 300 | m/min | Covers moderate to high speeds for tool wear and force analysis. |
| Feed per tooth | fz | 0.10 | 0.15 | mm/rev | Represents typical industrial ranges for semi-finish operations. |
| Depth of cut | ap | 1.0 | 1.5 | mm | Tests axial engagement limits for plunge milling stability. |
| Setup | vc (m/min) | fz (mm/tooth) | ap (mm) | n (rpm) | vf (mm/min) |
|---|---|---|---|---|---|
| 1 | 200 | 0.10 | 1.0 | 1989 | 397.9 |
| 2 | 200 | 0.10 | 1.5 | 1989 | 397.9 |
| 3 | 200 | 0.15 | 1.0 | 1989 | 596.6 |
| 4 | 200 | 0.15 | 1.5 | 1989 | 596.6 |
| 5 | 300 | 0.10 | 1.0 | 2984 | 596.8 |
| 6 | 300 | 0.10 | 1.5 | 2984 | 596.8 |
| 7 | 300 | 0.15 | 1.0 | 2984 | 894.8 |
| 8 | 300 | 0.15 | 1.5 | 2984 | 894.8 |
| Plunge Milling | Face Milling | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type | Sample | 1 | 2 | 3 | Mean | 1 | 2 | 3 | Mean |
| Side surface | 1 | 0.334 | 0.38 | 0.389 | 0.367 | 0.523 | 0.506 | 0.622 | 0.550 |
| 2 | 0.488 | 0.511 | 0.486 | 0.495 | 0.554 | 0.531 | 0.557 | 0.547 | |
| 3 | 0.399 | 0.451 | 0.403 | 0.418 | 0.627 | 0.644 | 0.54 | 0.604 | |
| 4 | 0.515 | 0.524 | 0.497 | 0.512 | 0.639 | 0.628 | 0.56 | 0.609 | |
| 5 | 0.455 | 0.522 | 0.503 | 0.493 | 0.469 | 0.547 | 0.588 | 0.535 | |
| 6 | 0.459 | 0.385 | 0.392 | 0.412 | 0.914 | 0.959 | 0.935 | 0.936 | |
| 7 | 0.403 | 0.422 | 0.459 | 0.428 | 0.727 | 0.783 | 0.832 | 0.781 | |
| 8 | 0.49 | 0.585 | 0.46 | 0.512 | 0.586 | 0.826 | 0.796 | 0.736 | |
| Top surface | 1 | 0.938 | 1.145 | 1.207 | 1.097 | 0.792 | 0.735 | 0.755 | 0.761 |
| 2 | 1.001 | 1.073 | 1.024 | 1.033 | 0.507 | 0.455 | 0.429 | 0.464 | |
| 3 | 0.456 | 0.479 | 0.441 | 0.459 | 0.389 | 0.377 | 0.368 | 0.378 | |
| 4 | 0.663 | 0.684 | 0.747 | 0.698 | 0.352 | 0.367 | 0.328 | 0.349 | |
| 5 | 0.533 | 0.564 | 0.574 | 0.557 | 0.889 | 0.803 | 0.596 | 0.763 | |
| 6 | 0.828 | 0.826 | 0.762 | 0.805 | 0.594 | 0.501 | 0.464 | 0.520 | |
| 7 | 0.302 | 0.428 | 0.523 | 0.418 | 0.266 | 0.283 | 0.26 | 0.270 | |
| 8 | 0.4 | 0.499 | 0.469 | 0.456 | 0.265 | 0.235 | 0.233 | 0.244 | |
| Mean | Median | Variance | Std. Deviation | CV | |
|---|---|---|---|---|---|
| Plunge milling | 0.57240 | 0.49417 | 0.049 | 0.222085 | 35.0 |
| Face milling | 0.56069 | 0.54100 | 0.039 | 0.196352 | 38.8 |
| Plunge Milling | Face Milling | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fx | Fy | Fz | Fx | Fy | Fz | |||||||
| M | H | M | H | M | H | M | H | M | H | M | H | |
| ap | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.584 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.584 |
| vc | 0.000 | 0.000 | 0.677 | 0.004 | 0.00 | 0.000 | 0.000 | 0.000 | 0.677 | 0.004 | 0.00 | 0.000 |
| fz | 0.000 | 0.000 | 0.24 | 0.000 | 0.017 | 0.139 | 0.000 | 0.000 | 0.24 | 0.000 | 0.017 | 0.139 |
| Machining Goal | Recommended Strategy | Optimal Parameter Range (from This Study) | Justification and Practical Considerations |
|---|---|---|---|
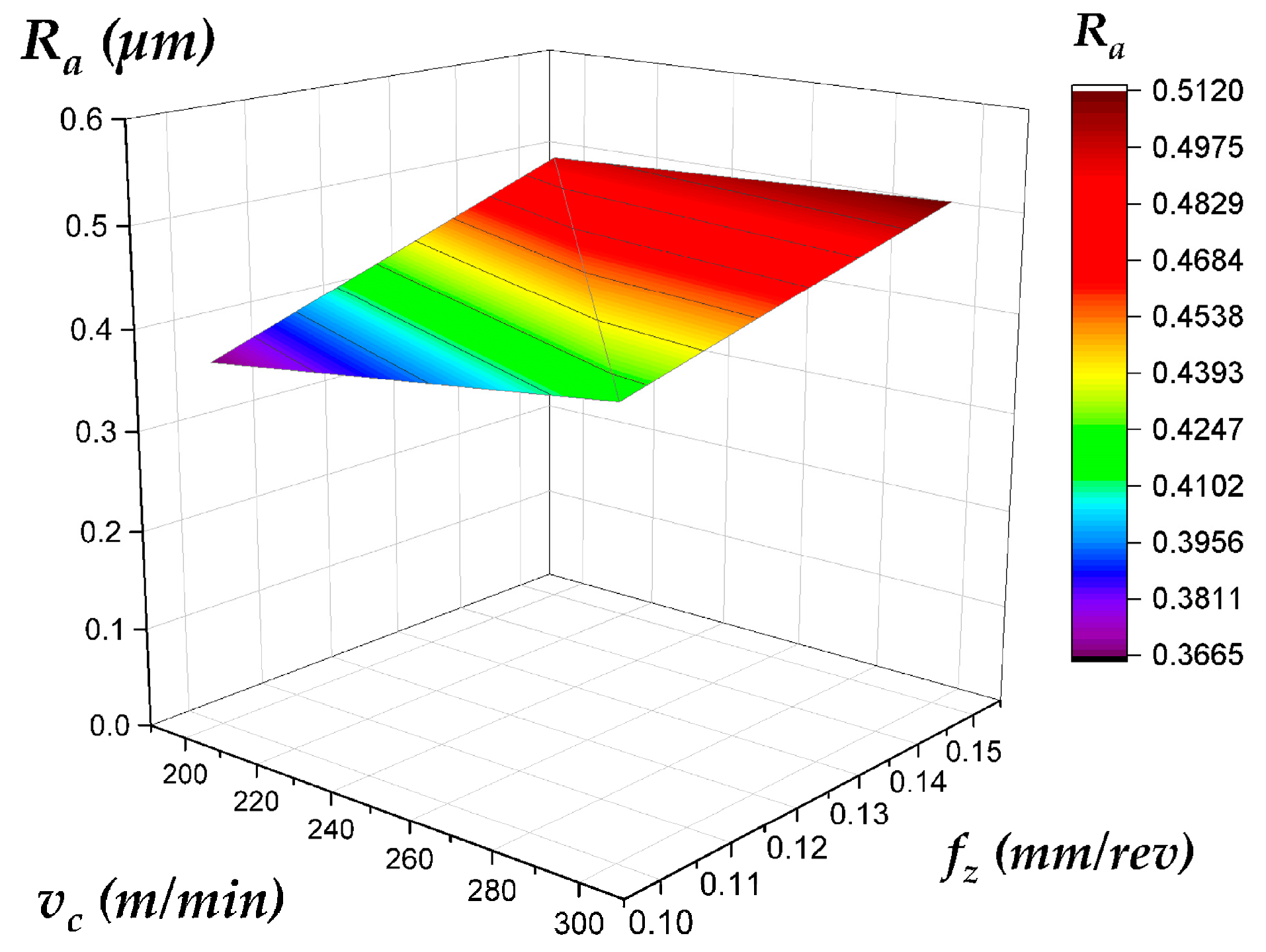
| Best Surface Finish (Top Surface) | Face Milling | Low vc (200 m/min) and High fz (0.15 mm/rev) | Consistently produces a smooth, valley-dominated surface. The counter-intuitive benefit of higher feed (fz) likely relates to a more stable chip formation and wiping effect (Figure 13 and Figure 15). |
| Best Surface Finish (Side Wall) | Face Milling (for predictability) | Low fz (<0.10 mm/rev) | Face milling provides a more predictable and monotonically worsening Ra with increasing fz. Plunge milling can achieve lower Ra but is less stable and prone to high-Ra outliers, making it a higher-risk choice for critical surfaces (Figure 6, Figure 8, Figure 9, Figure 10 and Figure 11). |
| Lowest Cutting Forces | Face Milling | Low fz (0.10 mm/rev) and Low ap (1 mm) | Face milling generates significantly lower forces, especially axial force (fz). This is critical for machining thin-walled components, using less rigid machine setups, or minimizing tool/workpiece deflection to maintain dimensional accuracy (Figure 16, Figure 17 and Figure 18). |
| High Material Removal (Roughing) | Plunge Milling | Moderate vc and High fz (to maximize MRR) | While plunge milling results in much higher axial forces, it is designed for deep cavity roughing. The strategy should be used on a rigid, high-power machine. The high axial force (fz) must be managed to avoid spindle damage or tool failure (Figure 18). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khattab, A.; Sztankovics, I.; Felhő, C. Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness. Eng 2025, 6, 128. https://doi.org/10.3390/eng6060128
Khattab A, Sztankovics I, Felhő C. Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness. Eng. 2025; 6(6):128. https://doi.org/10.3390/eng6060128
Chicago/Turabian StyleKhattab, Afraa, István Sztankovics, and Csaba Felhő. 2025. "Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness" Eng 6, no. 6: 128. https://doi.org/10.3390/eng6060128
APA StyleKhattab, A., Sztankovics, I., & Felhő, C. (2025). Preliminary Experimental Comparison of Plunge Milling and Face Milling: Influences of Cutting Parameters on Cutting Force and Surface Roughness. Eng, 6(6), 128. https://doi.org/10.3390/eng6060128








