Design and Numerical Evaluation of Trailing Edge Deflection Distance-Based Morphing Wing

Abstract

This project’s focus is to create a morphing wing with variable geometry that will improve aerodynamic performance. The NACA 0018 airfoil, known for its stable aerodynamic characteristics and symmetrical shape, is chosen as a base airfoil for modification in this approach. To investigate the effects of flexible trailing edge deformation under aerodynamic loading, various new morphing airfoil designs have been designed and analyzed. Both the performance results of a conventional hinged wing design and morphing airfoil designs were compared. Identifying the most effective airfoil design that could produce higher lift-to-drag ratios, less turbulence, and better overall aerodynamic behavior was the main goal. Because of its elasticity and flexibility, natural rubber latex (Hevea brasiliensis) was utilized as the primary skin material. This allows for a seamless, hinge-free morphing wing. To evaluate aerodynamic efficiency, structural integrity, and material behavior under various situations, computational fluid dynamics simulations were carried out. The most promising airfoil design was determined based on performance. By reducing drag, increasing lift, and reducing mechanical complexity, this new approach offers a sustainable and effective substitute for traditional wing designs, advancing the development of adaptive aeronautical structures.

1. Introduction

Airplanes are among the fastest and most efficient modes of transportation globally. To meet growing demands for performance and fuel efficiency, researchers continually seek innovations, particularly in wing design. Traditional high-lift systems use rigid, mechanically actuated components like trailing edge flaps and leading edge slats. While effective, they increase structural weight and complexity. Moreover, blended wings, flap slots, and fairings contribute significantly to aerodynamic drag and noise [1,2,3]. Hinged connections allow turbulent airflow, which reduces lift, increases drag, and leads to higher fuel consumption and possible negative consequences of excess stress generation, a coupling effect, and loss of functionality as more devices are in wing [4]. Chordwise bending, flexing the wing’s trailing edge along the chord and camber, offers a more efficient alternative. This is enabled through flexible structures and actuators that smoothly deform the wing. Unlike traditional flaps, a morphing wing offers a potential way to improve aerodynamic efficiency and adaptability by allowing it to alter its shape while flying. A morphing wing is achieved by alterations in wingspan, sweep, camber, biomimicry, and twist and then application of the different mechanism [5,6,7,8,9]. Morphing technology allows both chordwise and spanwise shape adaptation, improving maneuverability and aerodynamic performance across a wide range of conditions [10]. Morphing wings outperform hinged configurations by adapting dynamically to various flight conditions, offering improved maneuverability, adaptability, and mission versatility [11]. Fuel efficiency in transport aircraft can be further improved using adaptive morphing trailing edges. Current solutions like cruise flaps (used in aircraft such as the Boeing 787) help reduce drag during cruising, but they offer limited flexibility. Morphing devices like FlexFoil solve this by using a seamless, gap-free surface to adjust camber and flap angles dynamically [12]. Various polymer-based materials like silicone, electroactive polymers (EAPs), and shape memory polymers (SMPs) are used as wind skin as they provide flexibility and durability during morphing [13]. Rubber made from natural rubber latex is a flexible, stretchable, and eco-friendly material with good strength and elasticity [14]. This study proposes a novel morphing wing design using natural rubber latex (Hevea brasiliensis) as a flexible outer skin. The material’s elasticity supports a continuous, single-mold structure, eliminating traditional hinges and gaps. This enhances aerodynamic efficiency by reducing turbulence and drag. A conceptual airfoil design has been structurally analyzed to ensure it withstands aerodynamic forces during deformation. The approach holds promise for improving lift, reducing fuel consumption, and advancing sustainable, high-performance aircraft.

2. Materials and Methods

The design of flexible airfoils necessitates a meticulous selection of materials that can simultaneously offer structural support and the capability to morph under aerodynamic loads. The methodology of research is depicted in Figure 1. Natural rubber latex is selected as the primary material for the outer skin of the morphing wing.

Table 1. Material properties.

Components	Materials	Elastic Modulus [GPa]	Poisson’s Ratio	Yield Strength [MPa]	Tensile Strength [MPa]	Shear Strength [MPa]
Airfoil and Connecting Rod	Aluminum	71.7	0.3	503	572	331
Outer Skin	Natural Rubber	5	0.45	-	23	4

Table 1. Material properties.

Components	Materials	Elastic Modulus [GPa]	Poisson’s Ratio	Yield Strength [MPa]	Tensile Strength [MPa]	Shear Strength [MPa]
Airfoil and Connecting Rod	Aluminum	71.7	0.3	503	572	331
Outer Skin	Natural Rubber	5	0.45	-	23	4

As per Table 1, Natural rubber latex exhibits high elongation, exceptional tensile strength, and remarkable flexibility, making it an ideal candidate for applications requiring repeated flexural deformations. To provide structural support to the morphing wing, aluminum alloy 7075 is to be used for airfoil and internal supports. Aluminum alloy 7075’s lightweight nature, combined with its excellent strength-to-weight ratio, ensures the structural integrity of the wing while minimizing added weight.

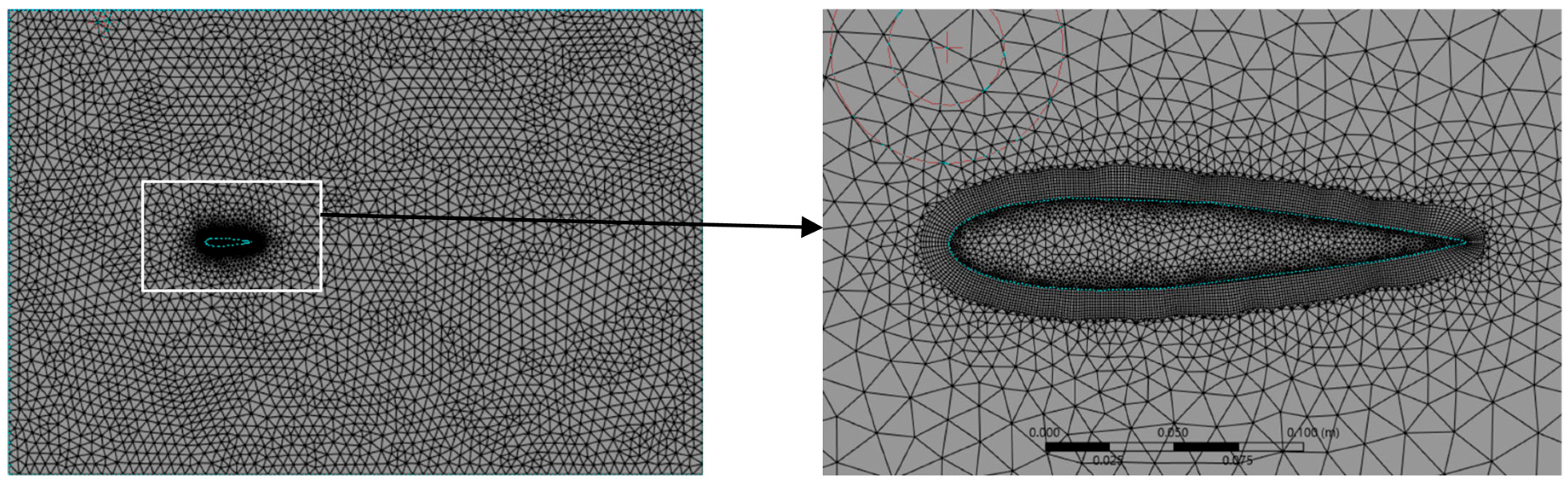
3. Aerodynamic Analysis

A detailed computational fluid dynamics (CFD) study was conducted to investigate the aerodynamic characteristics of a traditional hinged wing configuration and morphing wing. The study aimed to understand the influence of varying tail deflection angles on lift, drag, and overall aerodynamic efficiency under different flow conditions.

To analyze the aerodynamic performance of the morphing wing, a three-dimensional flow domain with size 1 m × 1 m × 1.5 m was carefully created around the airfoil model of 20 cm chord and 15 cm length as shown in Figure 2. The domain was structured as a large rectangular volume, ensuring that airflow around the wing was not influenced by the boundaries. The front face of the domain served as the velocity inlet, where air enters uniformly and begins interacting with the wing geometry. At the rear, the outlet face allowed the airflow to exit smoothly, ensuring that the wake development behind the wing was fully captured. Ample space was provided above, below, and on either side of the wing within the domain to minimize any artificial interference from the walls. In the spanwise direction, the domain extended beyond the physical wing to allow the three-dimensional nature of the flow to be properly represented. Where appropriate, symmetry boundary conditions were used to reduce computational load without compromising accuracy. The wing surface itself was treated as a no-slip wall to capture boundary layer effects realistically. This domain setup was essential for capturing the detailed aerodynamic characteristics of the morphing wing in a 3D environment. To balance computational efficiency and simulation accuracy, in meshing, a global element size of 0.008 m was used. To further enhance mesh resolution near the airfoil and accurately capture critical flow features, the same sizing was applied within the influence region surrounding the wing. A face meshing strategy was employed on the airfoil surface to ensure accurate geometric representation and maintain high mesh quality. A mesh independence study was conducted for elements of 481497, 909186, and 1144601, and the final mesh was selected with drag comparison. For effective boundary layer resolution and accurate turbulence modeling, inflation layers were introduced with a first-layer thickness of approximately 1.0 × 10⁻⁵ m, targeting a y+ value close to 1. This level of refinement enables proper resolution of the viscous sublayer and near-wall flow behavior when using the SST k–ω turbulence model [15].

To ensure the reliability of the simulation results, a mesh independence study was carried out using four grid densities. The results from the medium and fine mesh configurations were found to be closely aligned, despite a significant difference in their total element counts.

The Shear Stress Transport (SST) k–ω turbulence model combines the advantages of the k–ε and k–ω models, providing improved accuracy in predicting flow separation and adverse pressure gradients. The model is based on the Reynolds-Averaged Navier–Stokes (RANS) equations, which describe the conservation of mass and momentum, coupled with two additional transport equations for turbulent kinetic energy (k) and specific dissipation rate (ω).

• Continuity Equation (Mass Conservation)

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho u_j\right)=0$$

(1)

• Momentum Conservation Equation

  $$\frac{\partial }{\partial t}\left(\rho u_i\right)+\frac{\partial }{\partial x_j}\left(\rho u_i{u}_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[{\mu }_{eff}\right(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\left)\right]$$

  (2)

  where ${\mu }_{eff}=\mu +{\mu }_t$ is the effective viscosity and ${\mu }_t$ is the turbulent eddy viscosity.

• Turbulent Kinetic Energy (k) Equation

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho u_{j}k\right)}{\partial x_j}=P_k-{\beta }^{\ast }\rho k\omega +\frac{\partial }{\partial x_j}\left[\right(\mu +{\sigma }_k{\mu }_t\left)\frac{\partial k}{\partial x_j}\right]$$

(3)

• Specific Dissipation Rate ($\omega$) Equation

  $$\frac{\partial \left(\rho \omega \right)}{\partial t}+\frac{\partial \left(\rho u_j\omega \right)}{\partial x_j}=\alpha \frac{\omega }{k}{P}_k-\beta \rho {\omega }^2+\frac{\partial }{\partial x_j}\left[\right(\mu +{\sigma }_{\omega }{\mu }_t\frac{\partial \omega }{\partial x_j}]+2(1-F_1)\rho {\sigma }_{\omega 2}\frac{1}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}$$

  (4)

  where

• ρ—density
• $u_i$, $u_j$—velocity components
• $P$—pressure
• $\mu$—molecular viscosity
• ${\mu }_t$—turbulent eddy viscosity
• $P_k$—production of turbulent kinetic energy
• $\omega$—specific dissipation rate
• $\alpha ,\beta ,{\beta }^{*},{\sigma }_k,{\sigma }_{\omega },{\sigma }_{\omega 2}$—empirical constants
• F₁—blending function for SST

3.1. Hinged Wing

The analysis utilized a symmetric airfoil profile integrated with a discrete hinged flap at the trailing edge as shown in Figure 3, simulating a conventional control surface mechanism commonly used in fixed-wing aircraft. Simulations were performed at five freestream velocities: 20 m/s, 40 m/s, 60 m/s, 80 m/s, and 100 m/s. For each velocity, the tail deflection angle was varied incrementally from 1° to 10°.

The primary aerodynamic performance parameters evaluated included lift force, drag force, lift coefficient (C_l), drag coefficient (C_d), and lift-to-drag ratio (L/D). The results indicated a non-linear aerodynamic response to tail deflection. At a freestream velocity of 100 m/s, the lift-to-drag ratio reached a notable peak of 4.64455 at 8° deflection, where the airflow over the airfoil remained smooth and largely attached, resulting in efficient lift generation with minimal drag penalty. This configuration exhibited stable aerodynamic characteristics, suitable for cruise conditions. However, a maximum L/D ratio of 4.99423 was observed at 9° deflection, representing the highest efficiency recorded among all tested deflections. At this angle, the lift force increased significantly due to a larger deflection-induced camber effect, although drag also rose proportionally. The aerodynamic gains at 10° were largely attributed to favorable pressure redistribution and enhanced suction over the upper surface. Nonetheless, flow behavior around the hinge became considerably more complex.

To better understand the local flow phenomena, a pressure contour of the hinged wing at 10° deflection was examined which is shown in Figure 4. Importantly, the maximum turbulence intensity observed in the hinge region was approximately 196.436 m²/s², indicating a significant rise in turbulent kinetic energy. This intense turbulence was confined to the immediate vicinity of the hinge gap and was primarily the result of strong shear layers and the interaction of high velocity jets with recirculating flow zones. These disturbances, while contributing to higher lift, also reduce overall flow stability and could introduce unsteady aerodynamic loading.

The velocity vector of the hinged wing shows sharp variation from higher magnitude to lower. The vector field revealed that the velocity magnitude was notably high in the region adjacent to the hinged gap, with flow vectors tightly packed and directed through the narrow slot between the wing and flap. This concentrated, accelerated flow led to localized disturbances and turbulent mixing, disrupting the adjacent streamline.

3.2. Morphing Wing

A comprehensive aerodynamic analysis was carried out on a morphing wing design to assess its performance across various trailing edge deflection start points and deflection angles. Wing and tail morphing enhances aerodynamic agility and pitch maneuverability and improves aerodynamic control during high-angle maneuvers [16]. The control of the sliding mode mechanism of the flap of trailing edge was discussed using adaptive reaching law and the importance of circumferentially asymmetric stiffness is pointed out [17]. Trailing edge flapping is not only used in UAVs/aircraft but also used in wind turbines to enhance aerodynamic performance [18]. So, the primary objective of this study was to understand how altering the position at which the morphing begins, measured from the trailing edge toward the leading edge, impacts key aerodynamic characteristics. To achieve this, eight distinct morphing configurations were developed by varying the deflection initiation points at distances of 36 mm, 50 mm, 72 mm, 108 mm, 115 mm, 120 mm, 130 mm, and 150 mm from the trailing edge. These were designated as model-1 through model-8, respectively, as illustrated in Figure 5. Each model effectively represents a different morphing section length from the tailing edge. The closer the deflection starts to the leading edge, the longer the flexible morphing region becomes.

This variation directly influences the way the airflow interacts with the airfoil surface, especially in the rear portion, which plays a crucial role in modifying lift and drag forces. For each of the eight models, trailing edge deflection angles ranging from 1° to 10° were analyzed in 1° increments. Based on the natural rubber latex properties, the corresponding trailing edge deflection was formulated and in total, 80 (8 models × 10 deflection variations) morphing wing models were created. This allowed for a detailed investigation into how small changes in deflection angle affect the aerodynamic performance of the morphing wing. Additionally, to assess behavior under different operational scenarios, simulations were conducted at five distinct freestream velocities like the hinged wing. Figure 5 visually depicts the NACA 0018 airfoil with models-1–8, showcasing how the deflection starting point shifts progressively forward with each configuration. These visual comparisons are essential in understanding the geometric influence of morphing extent on flow behavior. This systematic simulation-based study aimed not only to evaluate the aerodynamic efficiency of each configuration but also to identify optimal combinations of morphing extent and deflection angle that yield the highest L/D ratios. By correlating flow visualization with performance metrics extracted from CFD simulations, the study provides detailed insights into the effectiveness of morphing strategies in enhancing aerodynamic performance.

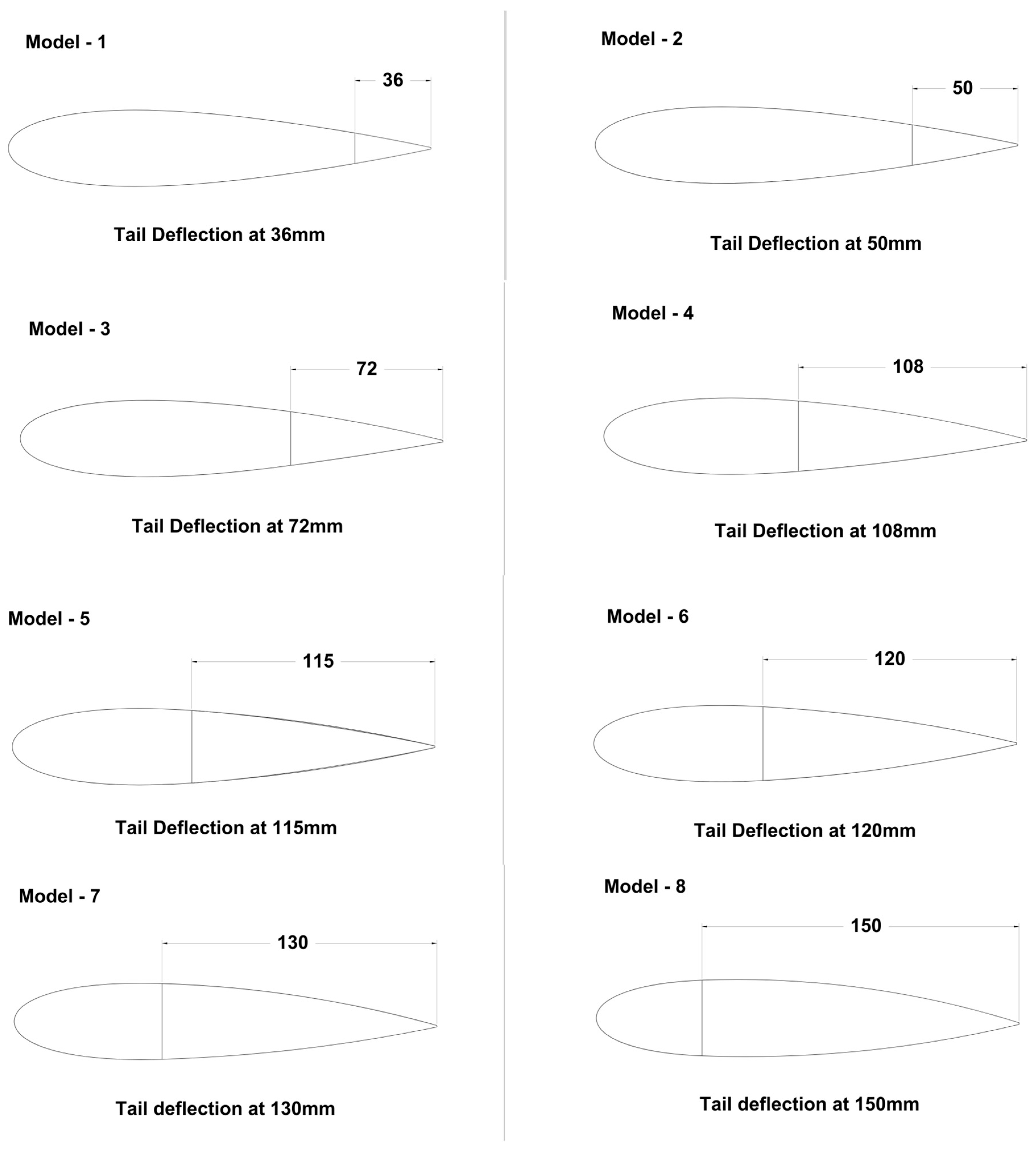
3.2.1. Airfoil Model-1 (36 mm Deflection Point)

Airfoil model-1 features a trailing edge deflection starting 36 mm from the tail of the NACA 0018 airfoil. This configuration was tested across various wind velocities, and it achieved a maximum lift-to-drag (L/D) ratio of 5.82553 at a 9° deflection angle under a freestream velocity of 100 m/s. While this result reflects respectable aerodynamic performance, the shorter morphing length introduced some limitations, particularly in terms of drag reduction. As shown in Figure 6, the pressure contour reveals a well-defined distribution around the airfoil. A maximum pressure of 6.01 × 10³ Pa was recorded at the nose tip, indicating a strong stagnation point where the oncoming airflow slows down and compresses. This high-pressure region extends along the lower surface near the leading edge, while significantly lower pressures were observed on the upper surface, reaching a minimum value. This strong pressure differential that is high on the lower surface and low on the upper surface creates the suction effect that drives lift, in accordance with Bernoulli’s principle.

The pressure gradually decreases along both surfaces toward the trailing edge, becoming more uniform, which suggests stabilized airflow and reduced flow separation. However, due to the shorter morphing length, flow separation occurred slightly earlier compared to longer configurations, contributing to higher drag.

3.2.2. Airfoil Model-2 (50 mm Deflection Point)

The 50 mm trailing edge deflection configuration delivered improved aerodynamic performance compared to the 36 mm model, achieving a maximum lift-to-drag (L/D) ratio of 6.48642 at a 10° deflection under 100 m/s airflow. This improvement is attributed to better pressure distribution and reduced flow separation. As shown in Figure 7, the pressure contour displayed a well-distributed low-pressure region on the upper surface with a minimum pressure. This contributed to effective lift generation while maintaining stable flow.

3.2.3. Airfoil Model-3 (72 mm Deflection Point)

The configuration with a 72 mm trailing edge deflection starting point demonstrated well-balanced aerodynamic performance, achieving a peak lift-to-drag (L/D) ratio of 8.03924 at a 7° deflection angle under a freestream velocity of 100 m/s. This setup produced a moderate yet consistent lift while keeping drag relatively low, indicating that the deflection length and angle were well-optimized for aerodynamic efficiency without inducing excessive flow disturbances. It proved to be both effective and structurally manageable within the tested range, making it a practical choice for morphing wing applications.

As illustrated in Figure 8, the pressure contour revealed a minimum pressure on the upper surface near the nose of the airfoil. This low-pressure region played a key role in generating lift by creating a strong suction effect along the leading edge. The pressure distribution was smooth, and the absence of sharp gradients suggested stable airflow across the surface.

3.2.4. Airfoil Model-4 (108 mm Deflection Point)

This configuration demonstrated significant aerodynamic enhancements, achieving a maximum lift-to-drag (L/D) ratio of 6.69506 at a 7° trailing edge deflection under an inlet velocity of 100 m/s. The aerodynamic performance was notably improved, with the airfoil effectively generating high lift while maintaining relatively low drag, highlighting the efficiency of the morphing trailing edge design at this condition. As illustrated in Figure 9a,b, the combined pressure and velocity contour revealed excellent flow attachment over the upper surface of the airfoil. A pronounced low-pressure region was observed, with a minimum pressure recorded along the upper surface. This strong suction effect contributed significantly to lift generation. The pressure on the lower surface remained higher, producing a favorable pressure differential that supported increased lift force. The streamline visualization showed smooth and clean flow alignment along the airfoil contour, with minimal separation or turbulence, further reducing pressure drag.

3.2.5. Airfoil Model-5 (115 mm Deflection Point)

The aerodynamic performance of airfoil model-5, incorporating a 115 mm morphing deflection at the trailing edge, was thoroughly analyzed under a uniform flow velocity of 100 m/s. Among all the configurations tested, this setup stood out by delivering the highest aerodynamic efficiency, both in terms of lift generation and drag reduction. Notably, the airfoil achieved a peak lift-to-drag (L/D) ratio of 6.69654 at a deflection angle of 7°, which is indicative of optimal aerodynamic performance. Further insights were obtained from the pressure contour plots shown in Figure 10a which provided a clear visualization of the pressure distribution over the airfoil surfaces. The upper surface exhibited a significantly lower pressure zone. The lower surface experienced a relatively higher pressure, and this pressure differential across the airfoil surfaces is what produces the net upward lift force. The pressure contours were smooth and showed no abrupt changes, indicating that the airflow remained attached throughout the surface without signs of separation or turbulence-induced instability.

In addition to pressure data, the turbulence kinetic energy (TKE) provided further confirmation of the design’s aerodynamic efficiency. The peak turbulence kinetic energy observed was 83.55 m²/s², which is considerably lower than the 196.44 m²/s² typically associated with conventional hinged-wing configurations. This reduced level of turbulence implies a more stable and streamlined flow around the morphing airfoil. Interestingly, the region of higher turbulence was found to be located farther downstream, away from the immediate vicinity of the trailing edge. This separation ensures that the turbulent energy has minimal impact on the airfoil’s surface performance, helping to reduce energy losses and enhance flow stability during operation. The velocity field clearly shows that airflow accelerates significantly over the upper surface, with maximum speeds reaching up to 127.4 m/s just past the leading edge. Meanwhile, the lower surface exhibits slower-moving air, as expected in a lifting body. Close to the airfoil surface, lower velocities indicate the formation of a well-behaved boundary layer, again with minimal evidence of flow separation. This smooth behavior suggests that the morphing deflection helps maintain favorable flow characteristics and minimizes pressure drag.

There are no signs of vortex formation or detachment phenomena that typically signal performance degradation. This continuity is essential for maintaining lift and reducing drag, particularly during flight conditions where wing shape changes are involved. The velocity vector plot in Figure 10b provides a more granular look at airflow behavior. It shows the direction and magnitude of airflow around the airfoil and further illustrates the orderly, aligned nature of the flow field. Over the top surface, vectors indicate strong acceleration with only minor disturbances near the trailing edge. This organized flow structure is crucial for ensuring the aerodynamic stability of the airfoil during dynamic morphing operations. The morphing airfoil design—when deflected at the appropriate angle—offers a substantial improvement in aerodynamic performance compared to traditional rigid or hinged configurations.

3.2.6. Airfoil Model-6 (120 mm Deflection Point)

The airfoil configuration incorporating a 120 mm trailing edge morphing deflection showed slightly better aerodynamic performance than the 108 mm setup. At a deflection angle of 7°, this model achieved a maximum lift-to-drag (L/D) ratio of 6.71725, reflecting a small but noticeable gain. While the performance improvement over the shorter deflection was marginal, it still highlights the aerodynamic benefit of increasing deflection length—though with diminishing returns beyond this configuration. The results suggest that extending the deflection further may not yield substantial aerodynamic advantages and could introduce unnecessary structural complexity or increased drag. Detailed CFD simulations revealed favorable flow characteristics throughout the evaluation. As shown in Figure 11a, the pressure contour plot revealed a pronounced low-pressure zone along the upper surface of the airfoil.

The velocity contour plot in Figure 11b indicates that airflow over the upper surface accelerated to a peak velocity of approximately 129.6 m/s, particularly near the leading edge. Meanwhile, the flow beneath the airfoil decelerated, contributing to the pressure difference needed for lift. Lower velocities close to the airfoil surface indicated boundary layer formation, with no signs of premature separation.

The turbulence kinetic energy (TKE) remained low across the airfoil surface with a peak TKE of 78.29 m²/s², which is notably lower than values typically observed in conventional rigid or hinged-wing designs. Most of the turbulence was confined to the downstream region well past the trailing edge, indicating reduced impact on the lifting surfaces.

3.2.7. Airfoil Model-7 (130 mm Deflection Point)

At a trailing edge deflection angle of 7°, the morphing airfoil model-7 configuration exhibited its best overall aerodynamic performance among all tested deflection angles. It achieved a maximum lift-to-drag (L/D) ratio of 6.71905, indicating a highly efficient aerodynamic balance where lift generation was maximized while drag was kept at a manageable level. This configuration appears to represent an optimal performance threshold, beyond which further increases in deflection angle result in diminishing aerodynamic returns due to rising drag and potential flow instabilities. The pressure contour plot, shown in Figure 12a, provides critical insights into the airfoil’s surface pressure distribution under this condition. A moderately sized stagnation region is visible at the leading edge, where incoming airflow decelerates upon impact, causing localized high pressure. Moving along the upper surface, the pressure drops sharply—reaching a minimum pressure indicating a region of accelerated airflow and strong suction that promotes lift generation. In contrast, the lower surface maintains a relatively higher pressure, contributing to a stable and efficient pressure differential essential for generating aerodynamic lift. This pattern confirms the effectiveness of the morphing mechanism in controlling pressure distribution without causing early separation. Complementing the pressure data, the velocity contour in Figure 12b shows a smoothly accelerated airflow over the upper surface, with peak velocities reaching approximately 133.1 m/s near the leading edge. The vectors remain well-aligned and attached across the entire chord length, suggesting minimal boundary layer separation. This attached flow condition is particularly critical for maintaining lift and reducing form drag. Only minor disturbances are observed in the wake region beyond the trailing edge, where some mild flow divergence occurs.

The turbulence kinetic energy (TKE) distribution remained relatively low, with a peak TKE of 76.84 m²/s², concentrated primarily in the downstream wake region rather than near the airfoil surface. This low turbulence level suggests enhanced flow stability and reduced energy losses due to unsteady fluctuations, further contributing to the observed aerodynamic efficiency.

3.2.8. Airfoil Model-8 (150 mm Deflection Point)

The morphing airfoil configuration with an extended trailing edge deflection exceeding the 120 mm mark exhibited the lowest aerodynamic performance among the longer deflection lengths. In model-8 the peak lift-to-drag (L/D) ratio of 6.73947 was observed at a 6° deflection angle. While still aerodynamically functional, this outcome suggests that excessive deflection length can begin to compromise the delicate balance between lift enhancement and drag mitigation. The pressure contour plot shown in Figure 13a reveals a pronounced pressure drop across the upper surface, consistent with accelerated airflow; however, the distribution appears less uniform compared to more optimal configurations. Further evidence of diminished aerodynamic stability is presented in the velocity vector plot, shown in Figure 13b. The airflow over the upper surface remains generally aligned but exhibits increased diffusion and disorganization. The maximum velocity peaks at around 127.6 m/s, primarily concentrated near the leading edge, but the velocity gradient diminishes more abruptly downstream. The vectors in the wake region become increasingly scattered, hinting at incipient flow separation or turbulence accumulation.

The simulation results reinforce these observations, with lower aerodynamic force outputs compared to shorter or moderately deflected configurations. Although the airfoil still maintains smooth transitions across much of the surface, the longer morphing region appears to introduce structural complexity and flow instability beyond the ideal morphing limit. Consequently, while the design remains viable for lift generation, the aerodynamic benefits begin to taper off, signaling that extending the morphing section beyond a certain point, especially without compensatory structural optimization, can negatively impact overall performance. This finding highlights the importance of carefully tuning both deflection angle and deflection length to avoid over-morphing, which may inadvertently degrade rather than enhance the aerodynamic characteristics of flexible airfoils.

4. Results and Discussion

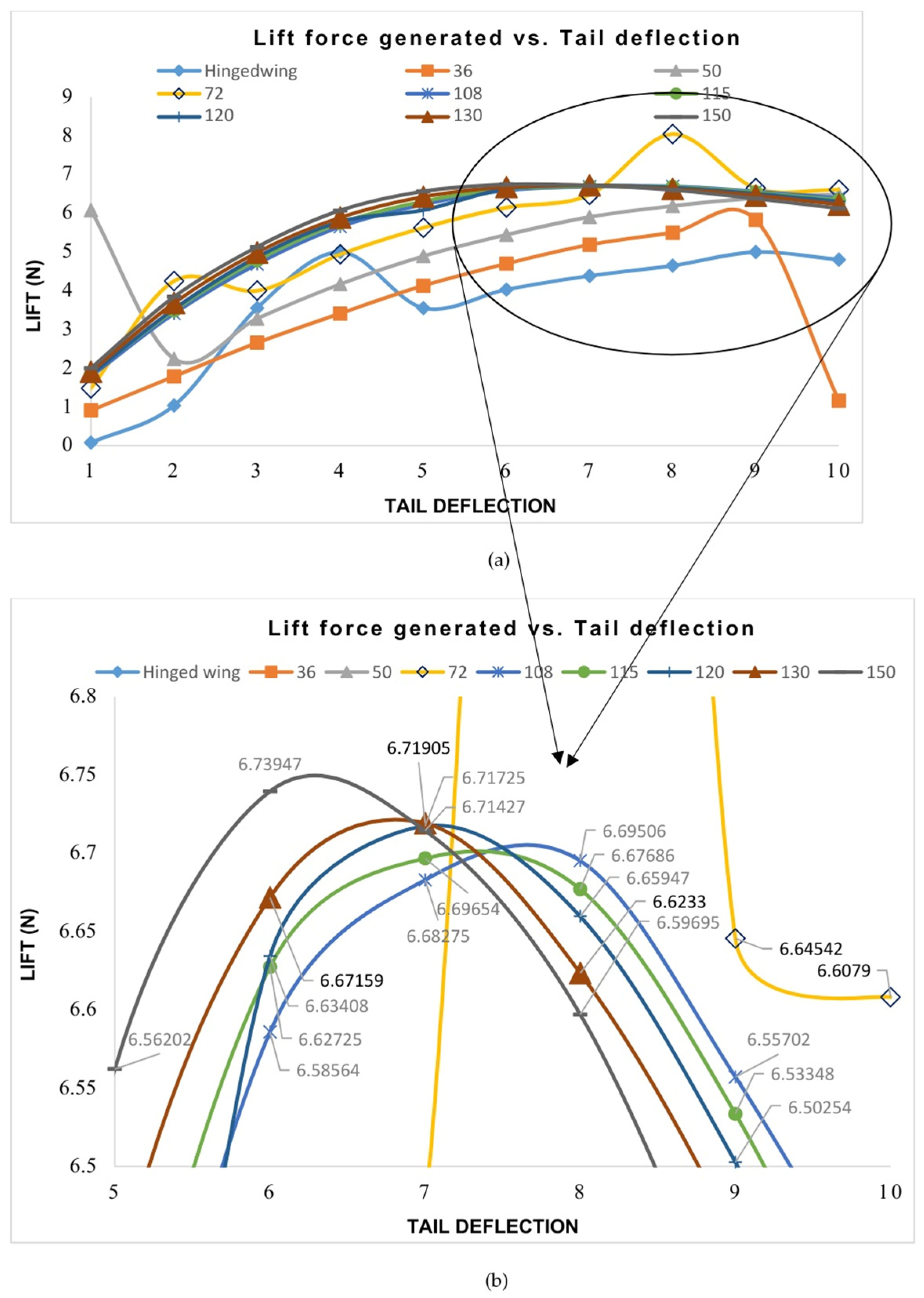
4.1. Lift and Drag Forces

Wing area plays a significant role, with larger wing areas generating more lift;

Table 2. Lift coefficient for both hinged wing and morphing wing.

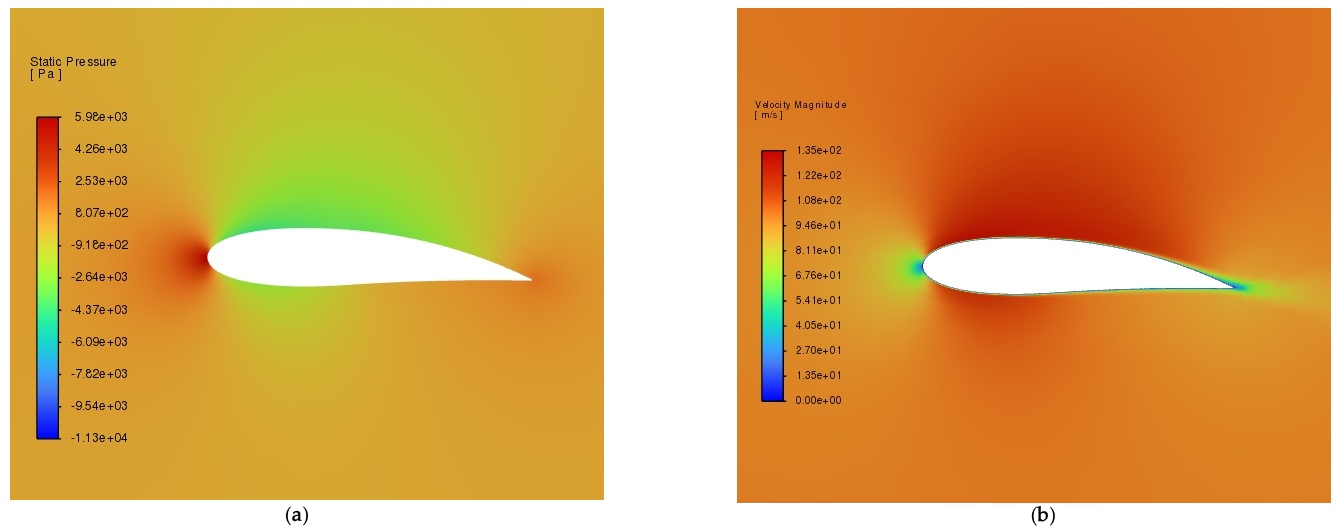
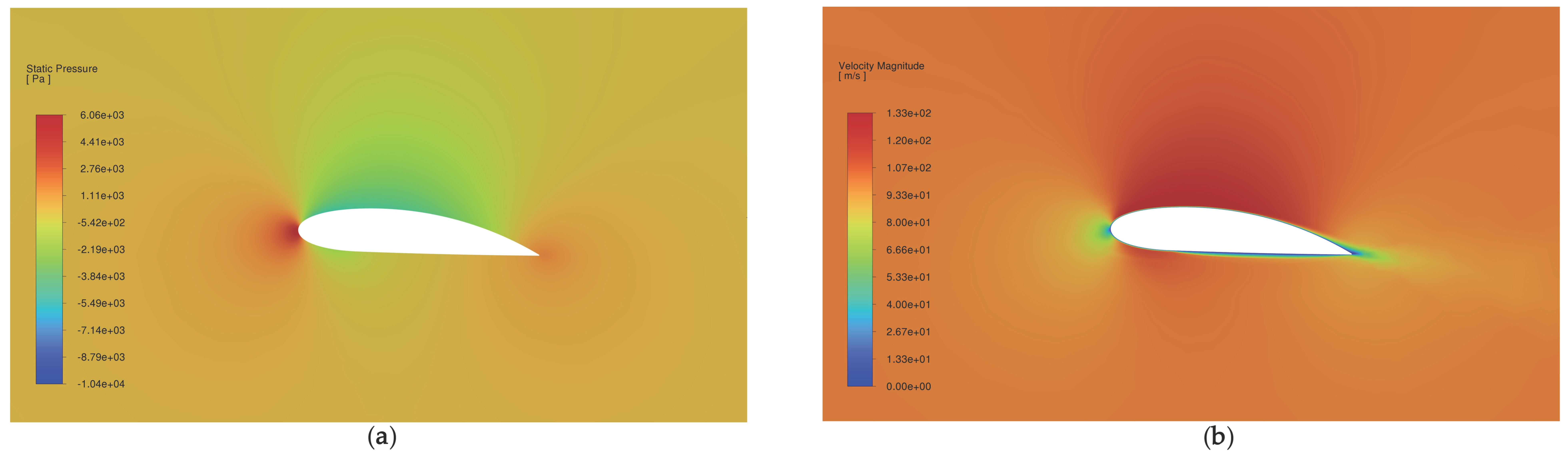
Airfoil	Deflection Angle
	1	2	3	4	5	6	7	8	9	10
Hinged wing	0.00006	0.00117	0.00304	0.00543	0.00304	0.00363	0.00418	0.00477	0.00544	0.01020
Model-1 (36 mm deflection point)	0.00141	0.00278	0.00420	0.00562	0.00705	0.00850	0.00992	0.01142	0.01286	0.01440
Model-2 (50 mm deflection point)	0.00684	0.00174	0.00264	0.00353	0.00443	0.00528	0.00619	0.00706	0.00791	0.00876
Model-3 (72 mm deflection point)	0.00112	0.00235	0.00332	0.00443	0.00552	0.00668	0.00783	0.00952	0.01001	0.01118
Model-4 (108 mm deflection point)	0.00135	0.00270	0.00406	0.00544	0.00685	0.00825	0.00968	0.01109	0.01247	0.01394
Model-5 (115 mm deflection point)	0.00141	0.00278	0.00420	0.00562	0.00705	0.00850	0.00992	0.01142	0.01286	0.01440
Model-6 (120 mm deflection point)	0.00138	0.00281	0.00426	0.00571	0.00639	0.00861	0.01013	0.01161	0.01313	0.01462
Model-7 (130 mm deflection point)	0.00143	0.00294	0.00439	0.00588	0.00739	0.00893	0.01042	0.01198	0.01355	0.01512
Model-8 (150 mm deflection point)	0.00148	0.003028	0.00455	0.006103	0.007702	0.009266	0.011561	0.012485	0.014098	0.015809

shows the lift coefficients obtained for different models at various deflection angles. Airspeed also affects lift, as increased airspeed amplifies the upward force. Air density, which varies with altitude, temperature, and humidity, impacts the amount of lift available in different flight conditions. These factors collectively determine the effectiveness of lift generation and influence the performance and stability of an aircraft in flight. In Equations (5) and (6), L represents the lift force generated, D represents the drag, force $\rho$ represents the air density, V represents the velocity, S represents the surface area of the wing, $C_l$ represents the lift coefficient, and $C_d$ represents the drag coefficient.

$$L={\displaystyle \frac{1}{2}}\rho V^{2}S{C}_l$$

(5)

$$D={\displaystyle \frac{1}{2}}\rho V^{2}S{C}_d$$

(6)

Drag is the resistance that opposes the aircraft’s forward motion and caused by the airplane’s surfaces interacting with the air. As the wing generates lift, it creates turbulence and vortexes at the wingtip, increasing drag and then the drag coefficient, as shown in

Table 3. Drag coefficient for both hinged wing and morphing wing.

Airfoil	Deflection Angle
	1	2	3	4	5	6	7	8	9	10
Hinged wing	0.00076	0.00077	0.00086	0.00109	0.00086	0.00090	0.00095	0.00103	0.19726	0.00212
Model-1 (36 mm deflection point)	0.00075	0.00077	0.00078	0.00082	0.00085	0.00089	0.00094	0.00099	0.00105	0.00075
Model-2 (50 mm deflection point)	0.00113	0.00078	0.00081	0.00085	0.00091	0.00097	0.00105	0.00114	0.00124	0.00135
Model-3 (72 mm deflection point)	0.00076	0.00055	0.00083	0.00090	0.00098	0.00109	0.00121	0.00118	0.00151	0.00169
Model-4 (108 mm deflection point)	0.00076	0.00079	0.00087	0.00096	0.00110	0.00125	0.00145	0.00166	0.00190	0.00218
Model-5 (115 mm deflection point)	0.00076	0.00080	0.00088	0.00098	0.00112	0.00128	0.00148	0.00171	0.00197	0.00227
Model-6 (120 mm deflection point)	0.00075	0.00080	0.00088	0.00099	0.00105	0.00130	0.00151	0.00174	0.00202	0.00232
Model-7 (130 mm deflection point)	0.00075	0.00080	0.00088	0.00100	0.00115	0.00134	0.00155	0.00181	0.00210	0.00243
Model-8 (150 mm deflection point)	0.00074	0.00079	0.00089	0.00101	0.00117	0.00137	0.00172	0.00189	0.00221	0.00258

. Induced drag is higher at lower speeds and decreases with increasing speed, whereas parasite drag increases with speed. The total drag generated can be calculated with the drag equation.

4.2. Lift to Drag Ratio (L/D)

Table 4. Lift–drag ratio for both hinged wing and morphing wing.

Airfoil	Deflection Angle
	1	2	3	4	5	6	7	8	9	10
Hinged wing	0.07400	1.03278	3.54999	4.99456	3.54999	4.02777	4.37964	4.64455	4.99423	4.79921
Model-1 (36 mm deflection point)	0.90456	1.78491	2.65281	3.40974	4.12644	4.69454	5.18253	5.49585	5.82553	1.16153
Model-2 (50 mm deflection point)	6.07433	2.23967	3.27700	4.16702	4.88874	5.43940	5.89825	6.18386	6.38733	6.48642
Model-3 (72 mm deflection point)	1.47872	4.24751	3.99635	4.93519	5.62449	6.14396	6.47149	8.03924	6.64542	6.60790
Model-4 (108 mm deflection point)	1.78520	3.40693	4.68596	5.64781	6.22201	6.58564	6.68275	6.69506	6.55702	6.39135
Model-5 (115 mm deflection point)	1.84773	3.48647	4.78691	5.74364	6.30483	6.62725	6.69654	6.67686	6.53348	6.33644
Model-6 (120 mm deflection point)	1.83496	3.52501	4.85674	5.78015	6.07662	6.63408	6.71725	6.65947	6.50254	6.30256
Model-7 (130 mm deflection point)	1.90578	3.67894	4.98644	5.88672	6.42229	6.67159	6.71905	6.62333	6.45412	6.22174
Model-8 (150 mm deflection point)	1.99526	3.83999	5.12623	6.06879	6.56202	6.73947	6.71427	6.59695	6.37711	6.12176

shows the aerodynamic efficiency, that is, the lift-to-drag ratio (L/D) for various airfoil models. A high L/D ratio indicates that the airplane can generate a large amount of lift with relatively low drag, which is important for fuel efficiency and long-range flight. The L/D ratio is influenced by factors such as the shape of the wings, the angle of attack, and the overall design of the airplane.

Figure 14a illustrates the variation in the lift-to-drag (L/D) ratio for all eight morphing airfoil models and the hinged wing, highlighting the aerodynamic performance differences among the designs. Among these, model-3, featuring a 72 mm trailing edge deflection point, exhibits the highest L/D ratio, reaching a peak value of 8.04 at an 8° deflection angle. This performance indicates that the 72 mm deflection length provides an optimal balance between lift enhancement and drag reduction. Figure 14b further emphasizes this trend, showing the L/D ratio range between 6.5 and 8.0 for better visual clarity, where model-3 consistently outperforms the other configurations. Figure 15 presents a comparison of the lift–drag ratio generated by the hinged wing and the model-3 morphing airfoil across various trailing edge deflection angles. The morphing model-3 displays a nearly linear and progressive increase in lift, demonstrating superior aerodynamic adaptability and stability. In contrast, the hinged wing attains a peak lift of approximately 4.99 units at 9°, after which its performance stabilizes with limited improvement. Conversely, model-3 achieves a maximum lift of about 8.04, reflecting a substantial increase in aerodynamic efficiency. This significant improvement confirms that the seamless morphing mechanism of model-3 ensures smoother airflow control, reduced flow separation, and enhanced lift generation, making it a more efficient and aerodynamically superior alternative to conventional hinged wing designs.

In terms of aerodynamic efficiency, model-3 achieved the highest lift-to-drag (L/D) ratio, reaching a peak value of 8.04 at an 8° deflection angle, while maintaining consistently high values above 6.5 across the entire deflection range. A previously reported benchmark L/D ratio of 9.39 [19] was used to evaluate the aerodynamic performance of the present morphing model. The deviation of approximately 14.4% is within an acceptable range, confirming the model’s reliability. Furthermore, the chosen airfoil configuration was validated with the standard NACA 0018 lift coefficient data [20], ensuring the accuracy of the computational results. When compared to the hinged wing, which reached a maximum L/D ratio of 4.99 at 9°, model-3 demonstrated a significant 61% improvement in aerodynamic performance, highlighting the advantages of its smooth morphing deformation over traditional hinged mechanisms. The turbulence kinetic energy (TKE) analysis further supports this improvement. The model-3 morphing wing recorded a maximum TKE of 84.22 m²/s², which is approximately 57% lower than the 196.44 m²/s² observed in the hinged wing at 10° deflection. This considerable reduction indicates a more stable, attached, and less turbulent flow around the morphing airfoil, contributing directly to enhanced lift and reduced drag. Streamline and velocity vector visualizations of model-3 confirm smooth, attached flow with minimal recirculation and vortex shedding, even at higher angles of attack. In conclusion, model-3 (72 mm deflection point) emerged as the optimal morphing configuration, offering the highest lift force, the most stable and efficient L/D ratio, and significantly reduced turbulence intensity. It clearly outperforms both the traditional hinged wing and other morphing airfoil designs, confirming the aerodynamic superiority of the 72 mm morphing length with moderate deflection angles (6–8°) for efficient, stable, and low-drag flight performance. The design challenges of enabling the internal structure to wrap around natural rubber latex and adapting the internal mechanism to actuate trailing edge are important to consider while manufacturing UAV wings.

5. Conclusions

The computational analysis comparing the traditional hinged wing with various morphing wing configurations based on the NACA 0018 airfoil modified for flexible deflection clearly indicates that model-3 outperformed all other designs. The optimized morphing location for the hinge-less wing is identified at 72 mm from the trailing edge, corresponding to 36% of the total chord length. This configuration provides the most aerodynamically efficient performance, achieving a maximum lift-to-drag (L/D) ratio of 8.04 at an 8° deflection angle. The results confirm that the proposed morphing design delivers excellent aerodynamic stability and efficiency, demonstrating strong potential for further development. Such an approach can enable the future design of hinge-less wings for both manned and unmanned aircraft, minimizing aerodynamic disturbances, eliminating mechanical hinge failures, and reducing the impact of environmental factors commonly associated with conventional hinged-wing mechanisms.