Abstract
Safety is a central concern in aviation, where aircraft operations involve complex processes and interactions exposed to multiple hazards. Addressing these hazards requires systematic risk management and the selection of effective safety measures. This study introduces a novel hybrid multi-criteria decision-making (MCDM) framework that integrates the grey Delphi method, the grey Analytic Hierarchy Process (AHP), and the grey Axial-Distance-Based Aggregated Measurement (ADAM) method. The framework provides a rigorous engineering-based approach for evaluating and ranking safety measures under uncertainty and diverse stakeholder perspectives. Application of the model to aircraft operations demonstrates its ability to identify the most effective measures, including the development of critical infrastructure protection plans, rerouting of flight paths from high-risk areas, and strengthening of regulatory oversight. The proposed methodology advances decision-support tools in aviation safety engineering, offering structured guidance for optimizing resource allocation and improving system resilience.
Keywords:
safety; aircraft operations; hazards; safety measures; MCDM; grey Delphi; grey AHP; grey ADAM method 1. Introduction
The International Civil Aviation Organization (ICAO) defines aviation safety as a state in which the risks of harming people and property are lowered and kept at an acceptable level through ongoing hazard identification and risk control [1,2]. This definition emphasizes the importance of a continuous process of identifying, analyzing, and monitoring hazards as a key element in the management of aviation safety. While aviation disasters are rare events and safety is the top priority in air transport, accidents and serious incidents occur much more frequently. By analyzing events in aviation and their causes, hazards (potential dangers that may lead to accidents) are identified, and measures are developed to prevent, eliminate, and mitigate hazards, thereby reducing the number of undesired events in aviation. To maintain an acceptable level of safety, effective risk management is necessary, which implies timely detection of potential hazards and the application of adequate measures to reduce the likelihood of their occurrence [2]. Recently, significant contributions to improving risk assessment and system reliability methods have been made through advanced approaches based on degradation modeling and artificial intelligence, which enable more accurate failure prediction and risk evaluation under real operational conditions [3,4,5].
In modern aircraft operations, hazard identification and the selection of appropriate risk reduction measures represent key steps in improving safety. Considering the complex interdependence between hazards, the interests of various stakeholders, and potential safety measures, it is necessary to apply a multi-criteria decision-making approach. This study aims to select the most effective safety measures in aircraft operations based on their impact on identified hazards, while taking into account the perspectives of key stakeholders, regulatory authorities, airlines, and service users. This process represents prioritization, i.e., determining which measures have the greatest contribution to reducing the risks of the most critical hazards and should therefore be prioritized in planning and implementation within the safety management system.
To solve this problem, a hybrid multi-criteria decision-making (MCDM) model has been developed, integrating the grey Delphi and grey analytic hierarchy process (AHP) methods for determining the importance of hazards according to stakeholder perspectives, as well as the grey axial-distance-based aggregated measurement (ADAM) method for ranking safety measures. The application of the proposed model to a defined set of hazards and measures enabled the identification of the most effective solutions in terms of reducing the overall safety risk. The obtained results provide decision-making support in the planning and implementation of safety measures, considering the multidimensional nature of the problem and limited resources. The main contributions of the study are reflected in defining specific safety measures associated with the identified 12 general hazards, classified according to ICAO into natural, technical, and economic categories; developing a framework for hazard and safety measure assessment; and creating a new hybrid MCDM method that enables the selection of the most effective safety measures in aircraft operations.
Although there are numerous studies on hazards in aviation, safety measures, and the application of multi-criteria decision-making (MCDM) methods, there is no unified model that integrates these approaches for the selection and ranking of safety measures in aircraft operations. The literature review covers the definition and classification of hazards in aviation, and methods for their identification and analysis (e.g., HAZOP, Job Safety Analysis), as well as approaches to their control (Hierarchy of Hazard Controls) [6,7,8,9]. It also stresses the need for a systematic approach to safety measures through regulatory guidelines (ICAO, FAA) and scientific studies that look at human and organizational factors [1,10,11]. Regarding decision-making methods, the review includes the application of MCDM techniques such as the grey Delphi method for gathering expert opinions and reaching consensus, grey AHP for determining weight coefficients of criteria, and the grey ADAM method for ranking alternatives, highlighting their advantages and limitations as well as the lack of previous integration of these methods into a single unified model [12,13]. This integration contributes significantly to the field of safety management in aviation.
The paper consists of seven sections. Section 2 provides a comprehensive review of relevant literature, structured into three parts: the first addresses the identification and analysis of hazards, the second focuses on risk reduction measures, and the third describes the applied multi-criteria decision-making methods and their key characteristics. Section 3 provides a detailed problem description, clearly establishing the connection between identified hazards and proposed measures. Section 4 is dedicated to methodology, explaining the hybrid MCDM model that combines the grey Delphi and grey AHP methods for determining the importance of hazards from the perspective of key stakeholders, as well as the grey ADAM method for ranking safety measures. Section 5 demonstrates the application of the proposed methodology through the evaluation and ranking of alternatives from a risk perspective, the selection of optimal measures, and a sensitivity analysis of the obtained results. Section 6 encompasses the discussion, highlighting the contributions of the study, its limitations, and practical implications, while Section 7 presents concluding considerations and suggestions for future research.
2. Literature Review
Although the areas of hazard studies in aviation, implementation of safety measures, and application of multi-criteria decision-making methods are widely represented in the literature, to the best of the author’s knowledge, there are no studies that integrate these approaches into a unified framework for the selection and ranking of safety measures in aircraft operations. In this paper, a hybrid multi-criteria decision-making model is developed, which integrates the grey Delphi and grey AHP methods for determining the importance of hazards from the perspective of different stakeholders, as well as the grey ADAM method for ranking safety measures. It is essential to note that, according to the existing literature, these three methods have not yet been combined into a single hybrid model for selecting safety measures in aircraft operations, which represents a significant methodological contribution and fills the existing research gap. For such research to be successful, it is necessary to review each of these areas through relevant literature.
2.1. Hazard
In general, a hazard is any source of potential danger that can cause injury to people, damage to property, degradation of the environment, or disruption of the normal functioning of a system. Many researchers have dealt with the concept of hazards and their definition in the context of occupational safety and risk management. Esterhuyzen and Louw [6] point out that existing theories on safety hazards are often insufficiently structured, and therefore propose a clearer scientific framework for understanding what actually constitutes a hazard. In practice, various methods are employed for hazard identification, including HAZOP (Hazard and Operability Study), which involves a systematic review of critical points in a system and the use of “keywords” to detect operational deviations [7]. In addition, approaches such as Job Safety Analysis classify hazards according to their nature (physical, chemical, ergonomic, biological, or organizational) and describe how they may lead to injuries or other adverse outcomes [8,9,14]. In industrial practice, hazard control is often implemented according to the Hierarchy of Hazard Controls, which prioritizes elimination and substitution of the source of danger, followed by engineering controls, administrative procedures, and, as the last line of defense, the use of personal protective equipment [15].
A hazard in air transport is defined as a situation, condition, or activity that may lead to the occurrence of an undesired event that could cause injury or death to passengers, crew, staff, or third parties, damage to equipment, financial loss, or reduction in the ability to perform the original function. To maintain a certain level of safety in aircraft operations, it is essential to understand how hazards are identified, analyzed, and monitored [2]. A hazard represents a source of potential danger—whether a situation, condition, omission, or malfunction—that can lead to an undesired event. The essence of a hazard lies in pointing to what might go wrong, regardless of whether it will actually occur. The consequence of a hazard relates to the specific outcome that may occur if it remains undetected or if appropriate control measures are not implemented. In other words, the hazard is the cause that creates risk, while the consequence is the outcome resulting from inadequate risk management. Hazards can be divided into three groups: natural hazards, which arise from the environment in which aircraft operations are carried out; technical hazards, which result from different energy sources or safety-critical functions; and economic hazards, which stem from the socio-political environment in which operations take place.
Hazards can be detected even before an undesired event, such as an incident or accident, occurs. They can also be found through proactive and predictive processes that aim to identify them before they cause a safety threat. Hazard analysis involves the assessment of identified sources of danger to determine their probability of occurrence and potential consequences for system safety. Based on this analysis, priorities for preventive and corrective measures are established to reduce the overall level of risk. Hazard documentation includes systematically recording all identified sources of danger, along with descriptions of their characteristics, potential causes, possible consequences, and existing control measures. This process enables the creation of a safety library, which represents an organized database of known hazards and serves as a reference for continuous monitoring, updating, and improvement of the safety management system. Hazards in aviation are approached from different perspectives and methodological frameworks. Čokorilo and Dell’Acqua [16] present in detail the application of safety management systems for hazard identification in aviation, emphasizing a practical and systematic approach to reducing safety risks. Oztekin and Luxhoj [17] apply inductive reasoning to develop risk models based on aviation accident analysis, directly focusing on hazard identification and quantification. Plattner et al. [18] highlight the importance of understanding how people perceive and interpret risk when assessing aviation safety problems. This helps in gaining a more realistic and complete picture of risks and in clarifying the difference between risk and hazard. Risk is defined as the combination of the probability or frequency of occurrence of a hazard and the severity of its consequences [2]. Shyur [19] develops a quantitative model for assessing safety risks, focusing on precise hazard management in aircraft operations. Tang et al. [20] apply game theory and a cloud model for risk assessment in air traffic control systems, aiding in the understanding of factors affecting flight safety. NASA [21] uses Functional Hazard Analysis (FHA) and system-theoretic process analysis for risk assessment in air mobility. Xiong et al. [22] propose the use of machine learning and automated extraction of useful information from large amounts of unstructured textual data to aid hazard identification. Xu [23] applies machine learning to the analysis of narrative safety reports, improving hazard identification. Sun et al. [10] focus on the safety assessment of air traffic control at small and medium-sized airports using machine learning methods. They develop a quantitative model based on the SHEL concept (Software, Hardware, Environment, Liveware) and a cloud model for improved safety assessment.
Although the number of studies on aviation hazards is still limited, it has been growing, especially recently, due to increased reliance on systemic approaches, new technologies, and regulation. All of these studies together provide a comprehensive, multi-dimensional approach to hazard identification and management in aviation, from technical and operational aspects to psychological and systemic factors. However, these studies do not enable the identification and quantification of safety measures for each general hazard in aircraft operations.
2.2. Safety Measures
After hazard identification, hazard analysis, and determination of risk indices, specific safety measures are identified to reduce the overall risk level. These measures involve technical, operational, organizational, and regulatory interventions designed to act both preventively and correctively with respect to recognized potential hazards and causes of potentially critical events and to mitigate safety risks.
The identification of measures is based on the analysis of each hazard, using a combination of sources such as results of past accident investigations [24], regulatory standards and guidelines issued by international and national regulatory bodies (e.g., ICAO, EASA, FAA), as well as applicable safety standards and existing operator procedures, previously conducted safety analyses, and the expertise of available specialists. Measures may include additional personnel training, changes in procedures, installation of technical protection systems, strengthening of oversight mechanisms, or modifications of the regulatory framework. There is a very limited number of scientific studies dealing with the identification and implementation of safety measures in aviation, particularly through safety management systems and risk analysis. Among the key sources is ICAO’s Safety Management Manual (SMM) [1], which provides detailed guidelines for hazard identification, risk reduction, and safety risk management. Reason examines human and organizational factors, emphasizing a systemic approach to accident prevention, while Milovanović analyzes aircraft accidents during takeoff through the application of Reason’s model, providing measures for preventing similar events [2,25]. Furthermore, Milovanović et al. [26] analyze atmospheric electrical discharges and their impact on flight safety, identifying hazards and measures for reducing potential risks. Wiegmann and Shappell [27] focus on human factors in aviation accident analysis and propose specific measures to reduce human error. Lee [28] further examines quantitative risk assessment methods and the selection of measures for their effective reduction in aircraft operations.
Together, these studies provide the foundation for systematic and comprehensive management of safety measures in aviation. However, they do not provide a framework for ranking and prioritizing measures based on their contribution to reducing overall risk.
2.3. Methods Applied in the Model
MCDM helps decision-makers evaluate alternatives based on multiple criteria. In recent decades, a wide range of MCDM methods have been developed, often refined, modified, and combined, to optimize decision-making depending on the problem addressed, maximize advantages, and minimize drawbacks of individual methods [29].
The Delphi method was developed by Dalkey and Helmer [30] and is mainly used for iterative processing of expert opinions until a common consensus is reached [31]. The grey Delphi method combines the Delphi method (anonymous, iterative expert opinion gathering) with the grey system approach, where instead of precise values, grey numbers (intervals) are used to model uncertainty and imprecision of opinions. The Delphi method is applied in situations where subjectivity may pose a risk, when problems are large, complex, and multidisciplinary, when there is uncertainty in the decision-making process, when time constraints exist, when multiple expert opinions are needed; and when anonymity is desirable. Its advantages include anonymity, iterativeness, controlled feedback, and statistically aggregated responses. Some drawbacks include the need for repeated surveys to achieve convergence and high data collection costs, especially in large, complex problems [31]. The Delphi method is widely accepted in the literature and applied either independently or in combination with other MCDM methods to solve various problems, such as the development of blockchain-integrated IoT technologies for food supply chains [32], the definition of road traffic safety indicators [33], the structuring of intermodal terminals [34], the identification and prioritization of key factors affecting labor productivity [35], the ranking of barriers to drone adoption in last-mile logistics [36], the improvement of international activities of university departments [37], or dry port location selection [32]. Nguyen [37] investigates innovation capabilities in the Vietnamese manufacturing sector using the grey Delphi method to reach expert consensus, while Gupta and Jain [38] apply the grey Delphi method to identify and analyze barriers to logistics process improvement in freight transport.
AHP, developed by Thomas Saaty in the 1970s, is a decision-making method for complex situations involving multiple criteria [39]. This method uses a hierarchical problem structure, with the goal at the top, criteria and sub-criteria in the middle, and alternatives at the bottom, enabling systematic pairwise comparison of elements. Based on these comparisons, weight coefficients are calculated, while a consistency check helps identify and correct any inconsistencies in judgment [40]. The flexibility of AHP allows its application across diverse areas, from business decision-making and project management to healthcare, public policy, ecology, and education. However, AHP has limitations. Subjectivity in judgments can affect the reliability of results, particularly if users are inconsistent or biased in comparisons. Additionally, as the number of criteria and alternatives grows, the number of required comparisons increases rapidly, which may complicate the process and demand more time [41]. Despite these challenges, AHP remains valuable due to its clarity and ability to incorporate multiple perspectives, making it effective in both individual and group decision-making contexts.
AHP is one of the most commonly used MCDM methods, especially for determining criteria weights, both independently and in combination with other methods. It has been applied in various problems, such as logistics system scenario ranking [42], medical treatment selection [43], and supplier selection in manufacturing [44]. Cheng and Li [13] combine grey statistical techniques with AHP in the evaluation of park rehabilitation landscapes, reducing subjectivity in indicator selection and weight assignment. Ortega et al. [45] develop a two-stage grey AHP approach for park-and-ride site selection in urban areas, comparing results with FAHP and BWM methodologies. Duleba et al. [46] apply grey AHP to transport mode choice assessment in Budapest, considering public transport, private cars, remote work, and bicycles under uncertain preferences. Tadić et al. [47] apply fuzzy AHP for determining criteria weights, followed by VIKOR for selecting central business district logistics systems. Zhang et al. [48] combine AHP with grey system theory to develop a hierarchical evaluation model of transport safety monitoring systems in Henan Province, China. Tadić et al. [49] combine AHP and MARCOS in a fuzzy environment to rank city logistics initiatives. Li [50] improves the AHP model by combining it with the grey correlation model, applying it in engineering projects.
The ADAM method is an aggregated measurement method based on axial distances [49,51]. The main advantages of the ADAM method compared to other approaches are its simplicity, ease of understanding and use, insensitivity to an increase in the number of criteria, high intuitiveness, and very low risk of rank reversal [51].
The method, either in its original form or in a fuzzy environment, alone or combined with other methods, has been applied to evaluate business models based on circular economy in supply chains [51], biodiversity protection in supply chain management [52], selection of last-mile logistics 4.0 technologies [53], ranking of railway infrastructure managers [54], identification of e-traceability drivers in supply chains [55], selection of initial delivery points for e-commerce [56], selection of the least risky drone for city logistics [57], and evaluation of sustainable intermodal transport routes and drone-based delivery optimization [58,59].
All three methods have significant advantages but also certain limitations depending on the type of problem being solved. This is why they are frequently combined in practice, leveraging their strengths and compensating for their weaknesses. In this way, hybrid MCDM models emerge, which are better suited to complex problem structures and enable more reliable results. Although there are numerous examples of the application of these methods in traditional form, as well as in environments such as rough, fuzzy, or grey numbers, so far, Delphi, AHP, and ADAM have not been combined in a grey environment. This represents a research gap and opens opportunities for new applications and further development of multi-criteria decision-making models.
3. Problem Description
A hazard represents a source of potential danger, i.e., a specific situation, condition, state, failure, or malfunction that may lead to an undesired event. The essence of a hazard lies in its indication of what could go wrong, regardless of whether it actually occurs. Alternatively, the consequence of a hazard refers to the specific outcome that may arise if the hazard remains undetected or if appropriate control measures are not implemented. In other words, a hazard is the cause that creates risk, while the consequence is the ultimate result that may occur due to inadequate risk management. Understanding the distinction between a hazard and its consequence is crucial in safety analyses, as it allows for a clear separation of causes from effects [2].
Analyzing hazards is important because they form the basis of every safety risk in aviation, and understanding them is a prerequisite for effective safety management. By identifying and analyzing hazards, proactive action can be taken before dangerous situations develop into incidents or accidents, enabling prevention rather than reaction. A systematic analysis provides a comprehensive view of potential sources of risk, helps identify which hazards pose the greatest threat, and allows resources to be directed toward mitigating them. In this way, hazard analysis supports evidence-based decision-making both in regulatory bodies and airlines and contributes to the development of a safety culture by fostering awareness and responsibility among all participants in the system. In short, hazard analysis is the foundation of the entire risk assessment process and the selection of safety measures, without which an effective and sustainable safety management system cannot be established. In this study, generic hazards will be analyzed in detail, followed by a proposal for a set of measures aimed at eliminating or mitigating them.
According to the ICAO Safety Management Manual [1], hazards are most commonly divided into three main groups: natural, technical, and economic. Each of these groups includes several specific (generic) hazards. Based on the classification of hazards according to the ICAO Safety Management Manual into these three main groups, 12 general hazards can be defined (Table 1) [2]. Hazards in aviation encompass a wide range of natural, technical, and social factors that may compromise the safety of aircraft operations.

Table 1.
General Hazards [2].
Severe weather and climatic events include hurricanes, snowstorms, droughts, tornadoes, thunderstorms, lightning, and wind shear, while adverse weather conditions encompass frost, freezing rain, heavy rain, snow, wind, and reduced visibility. Geophysical events include earthquakes, volcanic eruptions, tsunamis, floods, and landslides, whereas geographical conditions may pose a threat due to inaccessible terrain or large bodies of water. Natural environmental phenomena include fires, wild animal activity, bird strikes, and damage caused by insects and other pests. Public health-related events cover influenza epidemics and other infectious diseases.
Technical and infrastructure hazards include deficiencies in aircraft and their systems, subsystems, and supporting equipment, as well as deficiencies in infrastructure facilities, tools, and associated equipment, while external technical factors include deficiencies in external structures, systems, and equipment.
Finally, economic hazards are present. When the economy grows and there is increased demand for travel, the number of flights and passengers rises. Higher operational activity can create greater pressure on airline resources, including crew, aircraft, maintenance, and air traffic control systems. It may increase the complexity of operations management and potentially raise the risk of accidents, making economic growth a hazard in itself. Conversely, a recession reduces budgets for maintenance and crew training, while changes in the cost of materials and equipment complicate the timely replacement of parts. These factors indirectly affect safety by limiting the resources necessary to maintain an acceptable level of safety in aircraft operations.
ICAO provides general principles for risk management in aviation. Organizations are encouraged to monitor weather conditions, implement procedures for flying in extreme and adverse conditions, carry out aircraft and infrastructure maintenance programs, develop emergency plans, apply safety measures in accordance with WHO protocols, and ensure regulatory oversight and certification of critical equipment. However, ICAO does not provide a direct, concrete list of safety measures. The measures M1–M35, listed in Table 2, represent a systematization and interpretation of ICAO principles, adapted for practical application and selection of safety measures. Table 2 presents the safety measures (alternatives) for each general hazard. However, some safety measures may contribute to the mitigation of more than one hazard. Accordingly, Table 3 has been created to show the relationship between hazards and safety measures.

Table 2.
Identified Safety Measures for Risk Mitigation.

Table 3.
Relationship between Hazards and Safety Measures.
The relationship between hazards, measures, and stakeholders (Figure 1) can be viewed as a dynamic system in which hazards represent sources of risk, and measures represent the system’s responses to those risks, while stakeholders (regulators, airlines, and passengers) determine the priorities and criteria by which the measures are selected and ranked. In other words, hazards define what can go wrong, measures define what can be done to prevent it, and stakeholders define which aspects of safety are most important in the decision-making process. This tripartite relationship, where technical and operational measures are aligned with regulatory requirements and user expectations, enables a systematic approach to safety management.
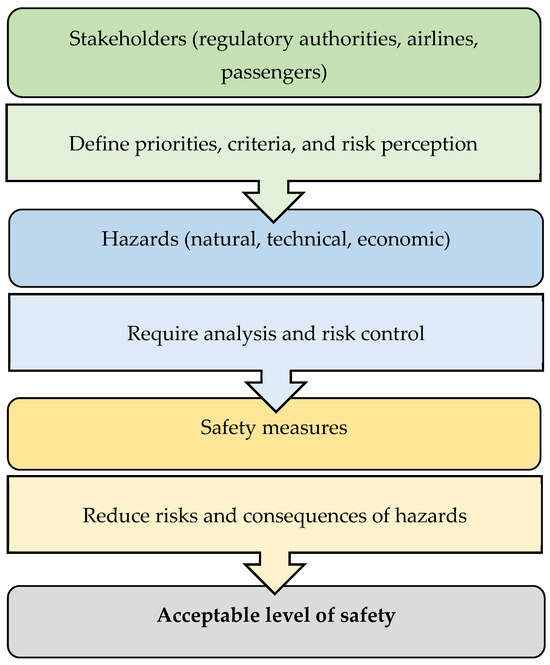
Figure 1.
The relationship between stakeholders, hazards and measures.
Table 3 is created by assessing the impact of each safety measure on every identified hazard. To provide a clearer understanding of how the links in Table 3 were established and, later, how grey ratings were assigned the effect of one specific measure on the identified hazards is explained in detail. The example chosen for this explanation is measure M2.
M2—the measure of implementing flight restrictions and bans in extreme conditions significantly contributes to reducing risks associated with various hazards, which is why different grey ratings were assigned to its impact. Specifically, regarding severe weather and climatic events such as hurricanes, snowstorms, tornadoes, or wind shear, this measure has an extremely high impact because it directly eliminates the exposure of flights to such events, thereby almost completely mitigating the risk. For adverse weather conditions, such as heavy rain, snow, frost, or reduced visibility, flight restrictions and bans prevent aircraft from entering dangerous situations. Geophysical events, such as earthquakes, floods, or landslides, are not always directly related to flight operations, but the restrictions can indirectly help avoid zones affected by extreme weather. Geographic conditions have a moderately low impact, as certain restrictions can be adapted to areas prone to extreme weather events, reducing risk in specific geographic zones. The impact of natural environment phenomena is moderate because flight restrictions reduce the likelihood of aircraft being affected by such events. For public health-related events, measure M2 has no direct impact. The impact of technical deficiencies in aircraft and their systems, and in infrastructure and external facilities, is low to moderately low, because although flight restrictions do not eliminate the cause of technical problems, they can prevent extreme weather conditions from further stressing systems and increasing the probability of failure. Regarding economic factors, such as growth, recession, or material and equipment costs, the measure has no direct impact, as economic conditions are not related to weather or operational restrictions.
Using the same principle, the link between each safety measure and every hazard was established (Table 3).
This study aims to rank the identified safety measures that contribute most significantly to reducing the risks of identified general hazards in aircraft operations, taking into account the priorities of different stakeholders (airlines, regulatory authorities, and passengers).
Defining the context for hazard assessment involves understanding the different perspectives of stakeholders. Regulatory authorities focus on compliance with applicable regulations, monitoring statistical risk indicators, and implementing international standards, such as ICAO and EASA guidelines, to ensure a minimum acceptable level of safety. Airlines view hazards in terms of their impact on operational efficiency, business costs, and potential legal liability in the event of an accident or incident. Service users—passengers, on the other hand—primarily assess hazards through the lens of personal safety and trust in the carrier, with their perception of safety significantly influencing the airline’s reputation and the willingness of passengers to use its services.
4. Methodology
To evaluate hazards and safety measures and obtain final values for assessment and ranking of the measures, a hybrid MCDM model is used. This model combines the grey Delphi and grey AHP methods (Delphi-based grey AHP, or grey D-AHP for short) to determine the weights (importance) of hazards in relation to stakeholder groups and the grey ADAM method for ranking the measures.
The steps of the model are as follows [31,54]:
Phase 1: Defining the structure of the MCDM problem. This includes forming the set of alternatives, determining the relevant criteria and sub-criteria for their evaluation, and identifying the key stakeholders involved in the decision-making process.
Phase 2: Defining the grey scale for evaluating criteria, sub-criteria, and alternatives by the decision-makers (Table 4).

Table 4.
Grey scale for the evaluations [25].
Phase 3: Obtaining weights of criteria and sub-criteria using the grey D-AHP method. Decision-makers, i.e., key stakeholders, compare pairs of criteria using linguistic expressions, which are then transformed into grey values according to the relationships shown in Table 4.
Phase 3.1: Conducting the aggregation of individual evaluations to obtain aggregated values that represent the collective assessment of all decision-makers (key stakeholders). The aggregated evaluations of decision-makers are obtained using the following equations:
where and are the lower and upper bounds of the aggregated grey evaluation , with and represent the lower and upper bounds of the grey evaluation , which indicates the comparison of element (criterion or subcriterion) with respect to element by the decision-maker belonging to stakeholder ; and denotes the number of criteria/subcriteria, while represents the number of stakeholders involved in the process.
Phase 3.2: Formation of the grey decision matrix where each element represents the aggregated comparison value of criteria or sub-criteria :
Phase 3.3: Calculation of the relative weights of criteria and sub-criteria. For each pairwise comparison matrix, it is necessary to determine the priority vector. For this purpose, the LGPP method (Logarithmic Grey Preference Programming—LGPP) is used. The elements of the grey decision matrix are approximated using the logarithms of the grey evaluations ⊗ by applying the following formula:
To obtain the priority values of the elements it is necessary to solve the following nonlinear priority model:
subject to:
represents the objective function to be minimized, while are the values of the priority vector for , and M is a sufficiently large constant (M = . The non-negative deviation variables and are introduced to prevent rom taking negative values. It is desirable that the values of these deviation variables be as small as possible and that they satisfy the following inequalities:
Let be the optimal solution of the model (considering expressions (6) to (11)). The normalized values of the criteria for the grey decision matrix A = are obtained as follows:
where exp() denotes the exponential function. This method provides the normalized weights.
To control the results of the method, a consistency ratio (CR) is calculated for each matrix as follows:
where is the Consistency Index and is calculated using the following formula:
where max is the eigenvalue of the matrix .
denotes the Random Index. For the pairwise comparisons to be acceptable, the consistency ratio should be less than 0.10.
Phase 4: Determining the ranking of alternatives using the extended ADAM method under grey conditions.
Phase 4.1: Defining the elements of the decision matrix , i.e., the vector quantities corresponding to the evaluations of alternatives in relation to the criterion.
where represents grey evaluation of alternative with respect to criterion .
Phase 4.2: Defining the elements of the grey normalized matrix :
where ⊗ are normalized grey evaluations obtained as:
Phase 4.3: Definition of the sorted elements of the grey matrix :
where is the sorted grey value in descending order according to the importance (weight) of the criterion.
Phase 4.4: Determination of the coordinates (x, y, z) of the grey reference point and the grey weighted reference point :
where α is the angle that determines the direction of the vector defining the value of the alternatives, calculated as:
Phase 4.5: Determination of the grey volumes of complex polyhedra as the sum of the volumes of the constituent pyramids, using the following equations:
where , the volume of a pyramid, is obtained using the following equation:
where , the base area of the pyramid, defined by the grey reference point and the grey weighted reference point of two consecutive criteria, is obtained using the following equation:
is the height of the pyramid from the defined base to the apex of the pyramid, which is located at the origin (O), and is obtained using the following equation:
The values used in Equations (17) and (18) are obtained as follows:
where is the Euclidean distance between the reference points of two consecutive criteria.
where and are the vector magnitudes corresponding to the weights of two consecutive criteria.
where is the semiperimeter of the triangle defined by the x and y coordinates of two consecutive criteria and the origin.
where is the Euclidean distance of the reference points of two consecutive criteria from the origin.
Phase 4.6: The final ranking of alternatives is obtained by comparing the corresponding Crisp ( volumes derived from Equation (12) and arranging them in descending order. The best alternative is the one with the smallest volume value.
5. Results
The results obtained by the described methods are presented below. To examine the stability of the solution, a sensitivity analysis was also conducted to assess its response to changes in the weights of the criteria across multiple iterations.
For the application of the grey D-AHP method to determine the weights (importance) of hazards in relation to the stakeholder groups, the input data used were the evaluations of the comparative importance of hazards (natural, technical, and economic) with respect to the key stakeholders (Table 5, Table 6 and Table 7) and the evaluations of the comparison of hazard groups in relation to the key stakeholders (Table 8). To ensure the robustness of expert input in the Delphi process, a purposive selection of 12 experts was conducted to represent the three key stakeholder groups defined in this study: regulatory authorities, airlines, and passengers. The selection criteria included (i) at least 10 years of relevant experience in aviation safety, operations, or passenger rights; (ii) active participation in safety management, regulation, or user representation; and (iii) proven familiarity with risk assessment and decision-making processes. The composition of the expert panel is shown in Table 9.

Table 5.
Comparative ratings of the importance of natural hazards with respect to stakeholder groups (regulatory bodies, airlines, and passengers, respectively).

Table 6.
Importance comparison ratings of technical hazards with respect to stakeholder groups (regulatory bodies, airlines, and passengers, respectively).

Table 7.
Importance comparison ratings of economic hazards with respect to stakeholder (regulatory bodies, airlines, and passengers, respectively).

Table 8.
Importance comparison ratings of hazard groups with respect to stakeholder groups (regulatory bodies, airlines, and passengers, respectively).

Table 9.
Qualifications and professional background of the Delphi panel.
The Delphi procedure consisted of two iterative rounds. In the first round, experts independently assessed the relative importance of the identified hazards using the predefined grey linguistic scale. The aggregated results were then shared with participants anonymously, allowing each expert to review the group responses. During the second round, experts could revise their judgments to achieve convergence. Consensus was considered reached when at least 80% of the responses for each hazard fell within the same or adjacent grey interval. This procedure ensured a balanced integration of expert opinions across stakeholder perspectives and provided a reliable basis for subsequent Grey AHP weighting. The final weights (importance) of the hazards are presented in Table 10.

Table 10.
Final Weights of the Criteria.
By applying Equations (5) to (14), the weights (importances) of the hazards were obtained. The final hazard weights (Table 10), obtained using the grey D–AHP method, reflect the relative importance of each hazard within the structure of the observed problem. Normalization of these values ensures their comparability, allowing the hazards to be ranked according to their impact on the overall safety risk.
For ranking the safety measures, the grey ADAM method is used. The evaluation of safety measures in relation to hazards is presented in Table 10.
By applying Equations (15) to (31), the volumes of the alternatives (Vc) were obtained, which were then normalized to calculate Crisp(Vc). These results, presented in Table 11, were used to determine the final priorities and rank the safety measures.

Table 11.
Evaluation of safety measures (alternatives) in relation to hazards (criteria), final values and ranking.
The final solution to the problem is obtained by ranking the safety measures. The highest-ranked safety measure is A27—Development and Implementation of Critical Infrastructure Protection Plans. This result is largely expected, considering that critical infrastructure (airports, air traffic control, communication and navigation systems, hangars, fuel storage facilities, information systems, etc.) forms the foundation of the aviation system, and its compromise can lead to catastrophic consequences, including disruption of aircraft operations, serious disturbances in business continuity, and endangerment of passengers, crew, and third parties. Critical infrastructure protection plans include risk identification and assessment, definition of preventive and corrective measures, ensuring system resilience through appropriate procedures, technical solutions, and coordination with government authorities and regulatory bodies.
The lowest-ranked measure, i.e., the one with the lowest priority among safety measures, is A6—Use of Aircraft Anti-Icing Systems.
To verify the stability of the obtained solution, a sensitivity analysis was conducted (Table 12). The sensitivity analysis involved creating 18 additional scenarios in which model parameters (simulated data) were varied. In the first four scenarios, the weight of the most significant hazard (C7) was reduced by 25%, 50%, 75%, and 100%. In the next 12 scenarios, the same procedure was applied to the next three most significant hazards (C8, C1, and C2). These hazards were selected because of their prominence relative to the others. In the penultimate scenario, all four of the most significant hazards were completely excluded, while in the final scenario, the importance of all hazards was equalized. Spearman’s Correlation Coefficient (SCC) was also calculated to indicate the correlation between the initial scenario and all other scenarios. The results are presented in the graph (Figure 2).

Table 12.
Alternatives ranking by the scenarios.
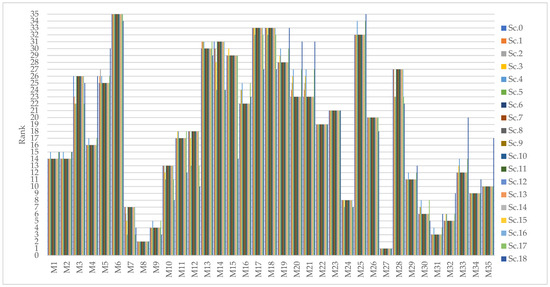
Figure 2.
Sensitivity analysis.
Based on the results of the sensitivity analysis of the ranking of measures across 18 scenarios, it can be concluded that the measures are consistently ranked and that the basic order is largely stable. Measure A27 consistently holds the first position (rank 1) in all scenarios, indicating its highest effectiveness and stability. Similar stability is shown by measures A8 and A31, which occupy very low ranks with minimal deviations, while measure A35 is relatively low-ranked in all scenarios, indicating its lower effectiveness compared to other measures.
Larger changes in ranking were observed for several measures, particularly in scenarios Sc.4, Sc.17, and Sc.18. For example, measure A4 in Sc.4 and Sc.18 moves up from position 16 to 24 and 26, while measure A5 in Sc.18 shifts to rank 30, representing a significant deviation compared to Sc.0. Measure A3 shows smaller variations, with ranks between 22 and 26 in most scenarios, while in Sc.17–Sc.18 it moves to 22 and 25.
To verify the stability of the obtained solution, a sensitivity analysis was conducted (Table 12). The sensitivity analysis involved creating 18 additional scenarios in which model parameters (simulated data) were varied. In the first four scenarios, the weight of the most significant hazard (H7) was reduced by 25%, 50%, 75%, and 100%. In the next 12 scenarios, the same procedure was applied to the next three most significant hazards (H8, H1, and H2). These hazards were selected because of their prominence relative to the others. In the penultimate scenario, all four of the most significant hazards were completely excluded, while in the final scenario, the importance of all hazards was equalized. Spearman’s Correlation Coefficient (SCC) was also calculated to indicate the correlation between the initial scenario and all other scenarios. The results are presented in the graph (Figure 2). Based on the results of the sensitivity analysis of the ranking of measures across 18 scenarios, it can be concluded that the measures are consistently ranked and that the basic order is largely stable. Measure A27 consistently holds the first position (rank 1) in all scenarios, indicating its highest effectiveness and stability. Similar stability is shown by measures A8 and A31, which occupy very low ranks with minimal deviations, while measure A35 is relatively low-ranked in all scenarios, indicating its lower effectiveness compared to other measures. Larger changes in ranking were observed for several measures, particularly in scenarios Sc.4, Sc.17, and Sc.18. For example, measure A4 in Sc.4 and Sc.18 moves up from position 16 to 24 and 26, while measure A5 in Sc.18 shifts to rank 30, representing a significant deviation compared to Sc.0. Measure A3 shows smaller variations, with ranks between 22 and 26 in most scenarios, while in Sc.17–Sc.18 it moves to 22 and 25. SCC values are high, ranging from 0.980 to 0.999, with an average value of approximately 0.994. These values indicate a very high similarity in rankings between scenarios, confirming that the basic order of measures is stable and does not change significantly even with different parameter variations in the analyzed scenarios. In conclusion, the analysis confirms that measure A27 is the most effective and stable across all scenarios, while measures such as A4, A5, and A3 are subject to minor changes in ranking. The stability of rankings across all scenarios demonstrates the reliability of the obtained results and provides a solid basis for adopting these measures as relevant for further implementation.
Among scenarios with more significant deviations in the ranking Sc.4, Sc.17, and Sc.18 show the largest shifts. In Sc.4, where the weight of the most significant hazard (H7) was reduced by 75%, measure A4 shifted notably from rank 16 in the baseline scenario to rank 24. This indicates that the reduced importance of this key hazard directly affected the effectiveness ranking of measures related to it. Similarly, in Sc.18, where the importance of all hazards was equalized, measure A4 further dropped to rank 26, while measure A5 experienced an even more pronounced decline to rank 30. These shifts suggest that measures which were previously more effective due to targeting higher-weighted hazards lose their advantage when hazard weights are balanced. Scenario Sc.17, involving the complete exclusion of all four significant hazards, also showed variations in rankings, particularly with measure A3 moving between ranks 22 and 25, indicating some sensitivity to the absence of these hazards. Outside of these cases, the rankings remained relatively stable, which aligns with the high SCC observed. Overall, the deviations in these scenarios are logically connected to the nature of the parameter changes, reaffirming the robustness of the measure rankings under most tested conditions.
SCC values are high, ranging from 0.980 to 0.999, with an average value of approximately 0.994. These values indicate a high similarity in rankings between scenarios, confirming that the basic order of measures is stable and does not change significantly even with different parameter variations in the analyzed scenarios.
In conclusion, the analysis confirms that measure A27 is the most effective and stable across all scenarios, while measures such as A4, A5, and A3 are subject to minor changes in ranking. The stability of rankings across all scenarios demonstrates the reliability of the obtained results and provides a solid basis for adopting these measures as relevant for further implementation.
6. Discussion
The results of the sensitivity analysis clearly show that the ranking of measures is stable across different scenarios with parameter variations. Measure A27 is consistently ranked as the most effective in all sensitivity analysis scenarios. Immediately following it are measures A8—rerouting air traffic from affected areas, A31—regulatory oversight to maintain safety standards, A9—development of airport emergency plans, and A32—maintaining minimum training and maintenance standards, indicating their key role in enhancing safety. Conversely, measures such as A6—use of aircraft anti-icing systems, A17—passenger health monitoring with thermal cameras, A18—travel restrictions and international coordination, A25—information system protection measures, and A14—vegetation control in the runway zone demonstrated significantly lower contribution and can be considered secondary options in the decision-making process. These results indicate that measures involving strategic planning, regulatory oversight, and training have a dominant impact on reducing safety risk in aircraft operations, whereas those focused on individual technical or operational aspects contribute less and represent secondary options. This distinction between primary and secondary measures confirms conclusions from previous studies emphasizing the importance of an integrated safety approach, where a combination of planning, oversight, and training has a greater effect than isolated technical interventions [1].
Wiegmann and Shappell [27] focus on human factors in aircraft accident analysis and propose specific measures to reduce human errors, while Lee [28] further elaborates quantitative risk assessment methods and the selection of measures for their effective reduction in aviation operations. Together, these studies provide a foundation for systematic and comprehensive management of safety measures in air transport. However, they do not enable the ranking and prioritization of measures based on their contribution to overall risk reduction. This study addresses that gap by applying a hybrid MCDM model that links hazards with corresponding measures and allows their ranking according to contribution to overall risk reduction. The implementation of grey Delphi, grey AHP, and grey ADAM methods enables integrated evaluation and prioritization of measures, directly addressing a previously inadequately treated problem in the literature.
The proposed hybrid multi-criteria decision-making model in this study represents a significant contribution to safety management in aircraft operations. By integrating the grey Delphi and grey AHP methods to determine the weights and significance of identified hazards with the grey ADAM method for ranking safety measures, a systematic and transparent evaluation of measures with the highest impact on risk reduction is achieved. Thus, the model provides clear support to decision-makers in the complex process of prioritizing safety interventions under multiple, and sometimes conflicting, stakeholder interests.
The methodological design of this study builds upon and extends recent developments in hybrid MCDM under uncertainty. While previous studies have effectively combined two grey- or fuzzy-based techniques, such as grey Delphi–AHP [31], fuzzy AHP–VIKOR [47], or fuzzy AHP–TOPSIS [48], these models typically focus on either the consensus-building or weighting phase, without ensuring consistency in aggregation across the entire decision structure. The integration of grey Delphi, grey AHP, and grey ADAM in the present research represents an advancement over these approaches, as it systematically connects three decision levels: (i) expert consensus formation through the iterative grey Delphi process, (ii) hierarchical weighting using grey AHP to capture stakeholder heterogeneity, and (iii) ranking through the grey ADAM method, which introduces a geometric and rank-stable aggregation mechanism. Compared with fuzzy-based hybrid frameworks (e.g., [50,54], the proposed grey model better handles epistemic uncertainty and incomplete information, which are typical in safety-critical aviation contexts where data are imprecise or partially known. Moreover, unlike classical hybrid models such as AHP–TOPSIS or AHP–VIKOR, which may be sensitive to rank reversal and require crisp normalization, the ADAM procedure preserves interval information throughout the evaluation process, enhancing result stability and interpretability. The model therefore provides a more cohesive and uncertainty-resilient decision-support framework, addressing the research gap identified by Krstić et al. [52,53] and aligning with the broader trend in MCDM research toward integrated grey-based architectures that unify expert evaluation, hierarchical analysis, and multidimensional ranking within a single, transparent structure.
The limitations of this research primarily stem from the defined safety measures. The identified measures represent an interpretation and practical adaptation of ICAO principles, rather than an official list prescribed by ICAO. They were developed to enable concrete linking with hazards and evaluation within the methodological framework of the study, ensuring the relevance and applicability of the results. However, the fact that the measures are not officially prescribed but are the result of systematization and expert judgment introduces a certain level of subjectivity.
As with any complex multi-criteria decision-making model, this approach has its limitations. First, although the grey Delphi and grey AHP methods mitigate some shortcomings of classical methods regarding uncertainty and subjectivity, they still rely on expert judgments, which may vary depending on participants’ experience, knowledge, and preferences. This affects the final results and requires a carefully selected and sufficiently representative group of experts. Second, the model assumes that criteria and stakeholder groups are predefined and that their interactions are relatively stable, which can be challenging in dynamic operational conditions. Third, the grey ADAM method requires relatively precise determination of criteria weights, which may be difficult when there is significant uncertainty or conflict in assessments.
The theoretical implications regarding hazards and measures lie in the fact that the hybrid MCDM approach allows systematic evaluation of the significance of hazards (hazard groups) and their linking with corresponding safety measures. This approach contributes to understanding the hazard–measure–risk relationship, demonstrates how complex safety problems can be modeled under uncertainty and multidimensionality, and lays the groundwork for applying and extending the methodology to other sectors with similar complexity. The theoretical implications of this work are reflected in the further development and application of hybrid MCDM methods in aviation safety operations, as well as in understanding how the combination of grey methods can effectively address uncertainty and multidimensionality in safety problems. The proposed approach can be adapted and extended to other sectors with similar characteristics of complexity and multiple stakeholder interests, as well as to future studies incorporating additional dimensions such as environmental and economic aspects. The model does not include an explicit cost dimension or detailed economic analysis, although these aspects are crucial in practice when balancing high safety levels with available resources. Therefore, integrating economic criteria and cost-effectiveness analysis of safety measures represents a direction for further research, which would enable optimal decision-making in the context of limited budgets and competing priorities.
The practical implications for safety management in aircraft operations are manifold. The proposed model allows managers to systematically identify and rank measures with the greatest impact on reducing safety risk, taking into account the interests of various stakeholders. This contributes to optimizing investments in safety measures and more efficient use of available resources. The stability of measure rankings through the sensitivity analysis further confirms the reliability of the model and provides a basis for adopting the most effective measures in practice. Practically, the results of this study can be applied by various stakeholders involved in aviation safety management. Airline safety departments can use the proposed model to prioritize safety initiatives and allocate resources toward measures that yield the highest reduction in operational risk. Aviation regulatory authorities (such as ICAO, EASA, and national civil aviation agencies) may apply the model as a decision-support tool for evaluating compliance strategies and formulating evidence-based safety policies. Furthermore, airport operators and maintenance organizations can utilize the framework to identify weak points within their safety management systems and plan targeted improvements. The model can also serve as a training and analytical tool for safety analysts and auditors, supporting continuous monitoring and enhancement of safety performance across different operational domains. By providing a transparent and structured approach to decision-making, the model facilitates coordination among stakeholders and promotes a data-driven culture of safety within the aviation sector.
7. Conclusions
The topic of this study was the selection of safety measures in aircraft operations. The objective was to rank the identified safety measures according to their contribution to reducing the risk of general hazards in aircraft operations, taking into account the priorities of different stakeholders (regulatory authorities, airlines, and passengers). A hybrid MCDM model integrating the grey Delphi and grey AHP methods for determining the significance of hazards for stakeholder groups, along with the grey ADAM method for ranking safety measures, was developed to address this problem. It is important to note that, according to the available literature, these three methods have not previously been combined within a single hybrid model for selecting safety measures in aviation operations, representing a significant methodological advancement and filling an existing gap in scientific practice. The highest-ranked safety measure is A27—Development and Implementation of Critical Infrastructure Protection Plans, while the lowest-ranked measure is A6—Use of Aircraft Anti-Icing Systems.
Despite the valuable insights provided by the hybrid MCDM model, this study has some limitations that require consideration. Primarily, the model’s reliance on expert judgment introduces a degree of subjectivity, particularly in the determination of grey intervals within the grey Delphi, grey AHP, and grey ADAM methods. This inherent subjectivity may influence the consistency and robustness of the results. Additionally, the static nature of the data used limits the model’s ability to adapt to dynamic operational conditions or evolving safety environments. Future research could enhance the model’s applicability and accuracy by integrating real-time safety data streams, enabling adaptive and timely risk assessments. Moreover, coupling the hybrid MCDM framework with probabilistic risk models could provide a more comprehensive understanding of uncertainties and their impacts on safety decision-making. Expanding the model’s validation across diverse aviation contexts and exploring its potential use in other high-risk industries may also contribute to further methodological refinement and broader practical utility.
The proposed model can serve as a tool for strategic safety management in civil aviation, planning the optimal allocation of investments in safety measures, and supporting decision-making processes that assess the contribution of individual measures to reducing risks to human life. Furthermore, the model can be useful for conducting economic analyses of the justification for safety investments, including the application of statistical value of human life approaches and cost–benefit analysis. Another promising direction for future research is the application of the hybrid MCDM model to solve different problems, both within this field and in other domains.
Author Contributions
Conceptualization, S.T., M.M., M.K. and O.Č.; methodology, S.T. and M.K.; software, M.K.; validation, S.T. and M.K.; formal analysis, S.T., M.M., M.K. and O.Č.; investigation, S.T. and M.M.; data curation, S.T. and M.M.; writing—original draft preparation, S.T., M.M. and M.K.; writing—review and editing, S.T. and M.K.; visualization, M.M.; supervision, S.T., M.K. and O.Č. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are presented within the paper or in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- ICAO. ICAO Doc 9859 Safety Management Manual, 4th ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2018; 170p. [Google Scholar]
- Čokorilo, O. Bezbednost Vazduhoplova, 2nd ed.; Saobraćajni Fakultet–Univerzitet u Beogradu: Beograd, Serbia, 2020. [Google Scholar]
- He, Z.; Wang, S.; Shi, J.; Liu, D.; Duan, X.; Shang, Y. Physics-informed neural network supported wiener process for degradation modeling and reliability prediction. Reliab. Eng. Syst. Saf. 2025, 258, 110906. [Google Scholar] [CrossRef]
- He, Z.; Wang, S.; Liu, D. A nonparametric degradation modeling method based on generalized stochastic process with B-spline function and Kolmogorov hypothesis test considering distribution uncertainty. Comput. Ind. Eng. 2025, 203, 111036. [Google Scholar] [CrossRef]
- He, Z.; Wang, S.; Liu, D. A degradation modeling method based on artificial neural network supported Tweedie exponential dispersion process. Adv. Eng. Inform. 2025, 65, 103376. [Google Scholar] [CrossRef]
- Esterhuyzen, E.; Louw, L.B. Fundamentals of safety hazards: A scientific perspective. Jàmbá J. Disaster Risk Stud. 2019, 11, a675. [Google Scholar] [CrossRef]
- Spanish Association for Standardization and Certification. UNE-EN 61882:2017: Hazard and Operability Studies (HAZOP Studies)—Application Guide; AENOR: Madrid, Spain, 2017. [Google Scholar]
- Thepaksorn, P.; Thongjerm, S.; Incharoen, S.; Siriwong, W.; Harada, K.; Koizumi, A. Job safety analysis and hazard identification for work accident prevention in para rubber wood sawmills in southern Thailand. J. Occup. Health 2017, 59, 542–551. [Google Scholar] [CrossRef]
- Ghasemi, F.; Doosti-Irani, A.; Aghaei, H. Applications, shortcomings, and new advances of job safety analysis (JSA): Findings from a systematic review. Saf. Health Work 2023, 14, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Shen, D.; Yang, D.; Dai, M. Research on safety assessment of air traffic control in small and medium airports based on machine learning. J. Air Transp. Manag. 2025, 126, 102790. [Google Scholar] [CrossRef]
- ASN. Aviation Safety Network. 2025. Available online: https://asn.flightsafety.org/database/databases.php (accessed on 9 September 2025).
- Tadić, S.; Krstić, M.; Zečević, S. Defining the typical structures of the intermodal terminals. In Quantitative Methods in Logistics; Vidović, M., Kilibarda, M., Zečević, S., Radivojević, G., Eds.; University of Belgrade, Faculty of Transport and Traffic Engineering: Belgrade, Serbia, 2020; pp. 67–86. [Google Scholar]
- Cheng, Q.; Li, Q. The application of grey statistical method and analytic hierarchy process in the evaluation of community park rehabilitation landscapes. Hum. Soc. Sci. Commun. 2025, 12, a158. [Google Scholar] [CrossRef]
- Accelerate Platform. Job Safety Analysis (JSA): The Essential Occupational Health and Safety Management Tool 2025. Available online: https://www.ehs.com/2025/06/job-safety-analysis-the-essential-safety-management-tool/ (accessed on 24 October 2025).
- National Institute for Occupational Safety and Health (NIOSH). Hierarchy of Controls; NIOSH: Washington, DC, USA, 2015.
- Čokorilo, O.; Dell’Acqua, G. Aviation Hazards Identification Using Safety Management System (SMS) Techniques. In Proceedings of the 16th International Conference on Transport Science (ICTS 2013), Portorož, Slovenia, 27 May 2013. [Google Scholar]
- Oztekin, A.E.; Luxhoj, J.T. An inductive reasoning approach for building system safety risk models of aviation accidents. J. Risk Res. 2010, 13, 479–499. [Google Scholar] [CrossRef]
- Plattner, T.; Plapp, T.; Hebel, B. Integrating Risk Perception Into Risk Assessment. Nat. Hazards Earth Syst. Sci. 2006, 6, 471–483. [Google Scholar] [CrossRef]
- Shyur, H.J. A Quantitative Model for Aviation Safety Risk Assessment. Comput. Ind. Eng. 2008, 54, 34–44. [Google Scholar] [CrossRef]
- Tang, J.; Wang, D.; Ye, W.; Dong, B.; Yang, H. Safety Risk Assessment of Air Traffic Control System Based on the Game Theory and the Cloud Matter Element Analysis. Sustainability 2022, 14, 6258. [Google Scholar] [CrossRef]
- Graydon, M.S.; Neogi, N.A.; Wasson, K.S. Guidance for Designing Safety into Urban Air Mobility: Hazard Analysis Techniques. In Proceedings of the 2020 AIAA Science and Technology Forum and Exposition, Orlando, FL, USA, 6–10 January 2020; p. 2099. [Google Scholar]
- Xiong, M.; Wang, H.; Wong, Y.D.; Hou, Z. Enhancing aviation safety and mitigating accidents: A study on aviation safety hazard identification. Adv. Eng. Inform. 2024, 62, 102732. [Google Scholar] [CrossRef]
- Xu, Y.; Gan, Z.; Guo, R.; Wang, X.; Shi, K.; Ma, P. Hazard Analysis for Massive Civil Aviation Safety Oversight Reports Using Text Classification and Topic Modeling. Aerospace 2024, 11, 837. [Google Scholar] [CrossRef]
- Reason, J. Managing the Risks of Organizational Accidents; Routledge: London, UK, 1997; 272p. [Google Scholar]
- Milovanović, M. Analiza Udesa Vazduhoplova u Poletanju Primenom Reason Modela, Završni Rad; University of Belgrade, Faculty of Transport and Traffic Engineering: Belgrade, Serbia, 2021. [Google Scholar]
- Milovanović, M.; Čokorilo, O.; Čokorilo, S. Analysis of the Impact of Lightning Strikes on Flight Safety. Int. J. Traffic Transp. Eng. 2022, 12, 352–360. [Google Scholar] [CrossRef] [PubMed]
- Wiegmann, D.A.; Shappell, S.A. A Human Error Approach to Aviation Accident Analysis: The Human Factors Analysis and Classification System; Routledge: London, UK, 2003. [Google Scholar]
- Lee, W.K. Risk Assessment Modelling in Aviation Safety Management. J. Air Transp. Manag. 2006, 12, 267–273. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Veljović, M.; Čokorilo, O.; Milovanović, M. Risk Analysis of the Use of Drones in City Logistics. Mathematics 2024, 12, 1250. [Google Scholar] [CrossRef]
- Dalkey, N.; Helmer, O. An Experimental Application of the DELPHI Method to the Use of Experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Roso, V.; Brnjac, N. Dry port terminal location selection by applying the hybrid grey MCDM model. Sustainability 2020, 12, 6983. [Google Scholar] [CrossRef]
- Singh, R.; Khan, S.; Dsilva, J.; Centobelli, P. Blockchain Integrated IoT for Food Supply Chain: A Grey Based Delphi-DEMATEL Approach. Appl. Sci. 2023, 13, 1079. [Google Scholar] [CrossRef]
- Ma, Z.; Shao, C.; Ma, S.; Ye, Z. Constructing road safety performance indicators using Fuzzy Delphi Method and Grey Delphi Method. Expert Syst. Appl. 2011, 38, 1509–1514. [Google Scholar] [CrossRef]
- Badri, S.A. Identification and Prioritization of Key Factors Affecting Workforce Productivity Using Grey Delphi and Grey DEMATEL: A Case Study. Comput. Sci. Eng. 2024, 4, 13–30. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Radovanović, L. Assessing Strategies to Overcome Barriers for Drone Usage in Last-Mile Logistics: A Novel Hybrid Fuzzy MCDM Model. Mathematics 2024, 12, 367. [Google Scholar] [CrossRef]
- Jan, C.J.; Wang, S.-T. Integrating grey multiple-attribute decision and delphi methods to improve the organization of international activities of university departments (graduate institutes)–with a department (graduate institute) in a national institute of technology as an example (R.O.C.). Expert Syst. Appl. 2013, 40, 877–888. [Google Scholar] [CrossRef]
- Nguyen, P.H. Exploring complexities of innovation capability in Vietnam’s IT firms: Insights from an integrated MCDM model-based grey theory. J. Open. Innov. 2024, 10, 100328. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, N. Enhancing freight logistics: Overcoming barriers and driving sustainable growth with an integrated grey Delphi DEMATEL approach. Benchmarking Int. J. 2025, 32, 2024–2045. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Forman, E.H.; Gass, S.I. The Analytic Hierarchy Process—An Exposition. Oper. Res. 2001, 49, 469–486. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. Ranking of Logistics System Scenarios for Central Business District. Promet—Traffic Transp. 2014, 26, 159–167. [Google Scholar] [CrossRef]
- Schmidt, K.; Aumann, I.; Hollander, I.; Damm, K.; Graf von der Schulenburg, J.M. Applying the Analytic Hierarchy Process in healthcare research: A systematic literature review and evaluation of reporting. BMC Med. Inform. Decis. Mak. 2015, 15, 112. [Google Scholar] [CrossRef]
- Gwarda, K. Using the Analytic Hierarchy Process Method to Select the Best Supplies: A Case Study of a Production Company. Eur. Res. Stud. J. 2022, 25, 430–440. [Google Scholar] [CrossRef]
- Ortega, J.F.; Moslem, S.; Tóth, J.; Ortega, M. A two-phase decision making based on the grey analytic hierarchy process for evaluating the issue of park-and-ride facility location. J. Urban Mob. 2023, 3, 100050. [Google Scholar] [CrossRef]
- Duleba, S.; Çelikbilek, Y.; Moslem, S.; Esztergár-Kiss, D. Application of grey analytic hierarchy process to estimate mode choice alternatives: A case study from Budapest. Transp. Res. Interdiscip. Perspect. 2022, 13, a100560. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. Ranking of logistics system scenarios using combined fuzzy AHP-VIKOR model. Int. J. Traffic Transp. Eng. 2015, 5, 54–63. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Liu, X.; Jian, S.; Li, S.; Yue, J. Research on the establishment and application of a transportation safety supervision evaluation system based on grey analytic hierarchy process. Sustainability 2024, 16, a10600. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Kovač, M. Assessment of city logistics initiative categories sustainability: Case of Belgrade. Environ. Dev. Sustain. 2023, 25, 1383–1419. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Du, X. Improvement of Analytic Hierarchy Process Based on Grey Correlation Model and Its Engineering Application. ASCE-ASME J. Risk Uncertain. Eng. Syst. A 2021, 7, a1001126. [Google Scholar] [CrossRef]
- Veljović, M.; Tadić, S.; Krstić, M. Last Word in Last-Mile Logistics: A Novel Hybrid Multi-Criteria Decision-Making Model for Ranking Industry 4.0 Technologies. Mathematics 2024, 12, 2010. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Tadić, S.; Kovač, M.; Miglietta, P.P. A Novel Axial-Distance-Based Aggregated Measurement (ADAM) Method for the Evaluation of Agri-Food Circular-Economy-Based Business Models. Mathematics 2023, 11, 1334. [Google Scholar] [CrossRef]
- Krstić, M.; Tadić, S.; Miglietta, P.P.; Porrini, D. Biodiversity Protection Practices in Supply Chain Management: A Novel Hybrid Grey Best–Worst Method/Axial Distance-Based Aggregated Measurement Multi-Criteria Decision-Making Model. Appl. Sci. 2025, 15, 1354. [Google Scholar] [CrossRef]
- Kalem, A.; Tadić, S.; Krstić, M.; Čabrić, N.; Branković, N. Performance Evaluation of Railway Infrastructure Managers: A Novel Hybrid Fuzzy MCDM Model. Mathematics 2024, 12, 1590. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Tadić, S.; Miglietta, P.P. Prioritization of e-traceability drivers in the agri-food supply chains. Agric. Food Econ. 2023, 11, 42. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Veljović, M.; Kovač, M. Selection of the starting point of e-order delivery using ADAM method. In Proceedings of the 50th International Symposium on Operational Research, SYM-OP-IS 2023, Tara, Serbia, 18–21 September 2023; pp. 429–434. [Google Scholar]
- Tadić, S.; Mićić, B.; Krstić, M. Evaluating Sustainable Intermodal Transport Routes: A Hybrid Fuzzy Delphi-Factor Relationship (FARE)-Axial Distance Based Aggregated Measurement (ADAM) Model. Sustainability 2025, 17, 6071. [Google Scholar] [CrossRef]
- Roca-Riu, M.; Menendez, M. Logistic Deliveries with Drones: State of the Art of Practice and Research. In Proceedings of the 19th Swiss Transport Research Conference (STRC 2019), Ascona, Switzerland, 15–17 May 2019. [Google Scholar]
- Lu, F.; Jiang, R.; Bi, H.; Gao, Z. Order Distribution and Routing Optimization for Takeout Delivery under Drone–Rider Joint Delivery Mode. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 774–796. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).