Abstract
When loose, saturated sands and non-plastic silts are subjected to undrained cyclic loading, they will generate positive pore pressures. This increase in pore pressures leads to a decrease in effective stress with a corresponding decrease in shear strength and increase in liquefaction susceptibility. For combinations of sand and non-plastic silt, the threshold fines content can be defined as the non-plastic silt fines content at which the soil changes from sand-like behavior to silt-like behavior. Soils below the threshold fines content behave like sands and soils above the threshold fines content behave like silts. During cyclic triaxial and cyclic direct simple shear tests performed on specimens of sand and silt prepared to the same relative density but different fines contents, two rates of pore pressure generation were observed. When compared at five cycles of loading, soils with silt contents above the threshold fines content were found to produce pore pressure ratios as much as 50% higher than those observed for soils with silt contents below the threshold fines content. When evaluated in terms of cycles, cycle ratio, and dissipated energy ratio, the rate of pore pressure generation was found to be more rapid for soils above the threshold fines content than for soils below the threshold fines content.
1. Introduction
Soils consisting of mixtures of sand and non-plastic silt are commonly encountered in engineering practice. Depending on the relative proportions of sand and silt, the soil may behave as a sand or it may behave as a silt. If it behaves as a sand, it will exhibit higher shear strength and lower compressibility relative to the silt. Conversely, if it behaves as a silt, it will exhibit lower shear strength and higher compressibility relative to the sand. Soils that behave as sands have a higher resistance to liquefaction than those that behave as silts. Which of these two behaviors the soil exhibits is dependent upon the non-plastic silt content of the soil relative to its threshold fines content. Insight into the differences between these two soil groups can be gained by examining the rates at which the soils generate pore pressures under cyclic loading.
Data from two previous studies by the authors [1,2] were used to determine whether the rates of pore pressure generation in cyclically loaded non-plastic soils differed between soils with silt contents above the threshold fines content and soils with silt contents below the threshold fines content. The authors studied pore pressure generation data from cyclic triaxial tests and cyclic direct simple shear tests that were performed on specimens prepared to the same relative density but containing different percentages of non-plastic silt. The tests examined had been performed on combinations of three sands and two silts, with silt contents ranging from either 0% to 45% or 0% to 100% by weight.
The rates of pore pressure generation under cyclic loading were found to differ depending upon whether the silt content of the soil was above or below the threshold fines content. Soils with silt contents above the threshold fines content achieved larger pore pressure ratios earlier in the loading process than soils with silt contents below the threshold fines content.
Following a review of threshold fines content and cyclic direct simple shear tests, several terms used in this article will be defined, and a brief review of work previously performed on this topic will be presented. Details of the soils tested and the testing methodologies used will then be presented. Following this, results of the laboratory studies will be described, analyzed, and discussed. Finally, conclusions drawn from the study will be presented.
2. Background
This section first serves as a review of three topics that form an important background for understanding the material covered later in this paper. This section will first present the fundamentals of threshold fines content, then the basics of cyclic triaxial and cyclic direct simple shear tests will be discussed, and the section will conclude with definitions of several important terms used in the paper. These sections will be followed by a brief summary of the work previously performed on this topic.
2.1. Threshold Fines Content
Using a series of cyclic triaxial tests, Polito and Martin [1] showed that the cyclic response of sands containing non-plastic silts is different from that of silts containing sands. This change in behavior occurred at a silt content equal to the threshold fines content. The soils used in the study consisted of mixtures of Yatesville sand and Yatesville silt, as well as mixtures of Monterey #0/30 sand and Yatesville silt. The specimens containing Yatesville sand were prepared to relative densities between 25% and 30%. The specimens containing Monterey #0/30 sand were prepared to relative densities between 48% and 53%. For both cases, the silt contents ranged from 0 to 100%. Cyclic resistance was defined as the cyclic stress ratio required to cause initial liquefaction in 10 cycles of loading.
It was found that cyclic resistance was independent of silt content for mixtures of sand and silt with silt contents below the threshold fines content. Similarly, for mixtures with silt contents above the threshold fines content, the cyclic resistance was again found to be independent of silt content. The cyclic resistance of mixtures above the threshold fines content was found to be lower than cyclic resistance of the mixtures with silt contents below the threshold fines content. This behavior can be seen in Figure 1 for mixtures of Yatesville sand and Yatesville silt.
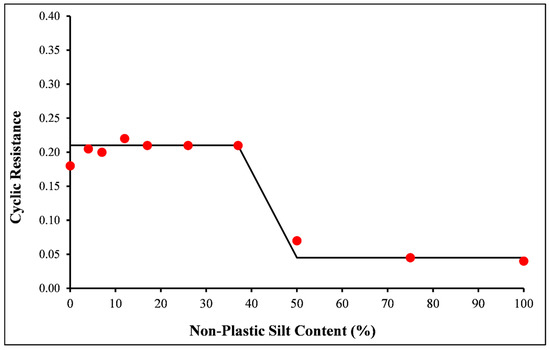
Figure 1.
Variation in cyclic resistance ratio with silt content for specimens of Yatesville sand and Yatesville silt (after Polito and Martin [1]).
The term “threshold fines content” was introduced in the 1990s to describe the fines content at which a soil composed of sand and non-plastic silt transitions from behaving as a sand (i.e., exhibiting high strength and low compressibility) to behaving as a silt (i.e., exhibiting low strength and high compressibility) [3]. This transition point has also been referred to as “the limiting fines content” [4], “the critical fines content” [5], “the limiting silt content” [1], “the limiting fines value” [6], and “the transitional fines content” [7].
Each of these studies found that the static shear strength and/or the resistance to liquefaction of soils composed of sand and non-plastic silt is, in large part, controlled by the amount of silt in the specimen relative to the threshold fines content. In each case, soils with silt contents greater than the threshold value exhibited lower shear strengths and lower cyclic resistances than the soils with silt contents below the threshold value.
For a cohesionless soil with non-plastic fines, the threshold fines content represents the silt content at which the soil transforms from being a sand matrix containing silt particles in its voids to being a silt matrix that contains non-contiguous sand grains. Below the threshold fines content, the soil behaves as a sand. This is because most, if not all, of the silt grains are contained in the voids between the sand grains; as a result, the behavior of the soil is dominated by sand-grain-to-sand-grain contact.
Above the threshold fines content, the soil behaves as a silt. This is because the noncontiguous sand grains are isolated within the silt matrix; as a result, the behavior of the soil is dominated by silt-grain-to-silt-grain contact. The conditions present in a soil when it is below, at, and above its threshold fines content are presented in Figure 2.
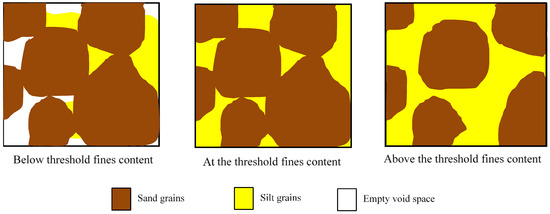
Figure 2.
Schematic of a sand-and-silt mixture below, at, and above the threshold fines content.
There is typically a transition zone between the upper- and lower-bound threshold fines contents. The zone results from the silt beginning to overflow the void spaces and force the sand grains apart. The soil grain interactions at this point consist of a combination of sand-grain-to-sand-grain contacts, silt-grain-to-silt-grain contacts, and sand-grain-to-silt-grain contacts. In the transition zone, the strength and cyclic resistance are intermediate to the strengths and cyclic resistances found above the UBTFC and below the LBTFC. The transition zone may be seen in Figure 1, where it is represented by the slanted portion of the curve located between silt contents of 37% and 50%.
Below the threshold fines content, the silt particles are predominately contained in the pores created by the sand grains. Because the silt particles are housed within the voids created by the sand matrix, a soil’s threshold fines content is a function of both the void ratio of its sand matrix and the void ratio of the silt. The largest void ratio of the sand is its maximum index void ratio, which creates the largest voids between the sand grains and thus the largest volume for housing silt grains. Similarly, the smallest void ratio of the sand is its minimum index void ratio, which creates the smallest voids between the sand grains and thus the smallest volume for silt grains to reside.
If the silt contained in the voids is at its minimum index void ratio, the density of the silt is maximized. Conversely, if the silt contained in the voids is at its maximum index void ratio, the density of the silt is minimized.
The upper-bound threshold fines content (UBTFC) occurs when the sand is at its maximum index void ratio and the silt is at its minimum index void ratio. The lower-bound threshold fines content (LBTFC) occurs when the sand is at its minimum index void ratio and the silt is at its maximum index void ratio. The upper- and lower-bound threshold fines contents can be calculated using Equations (1) and (2), respectively.
where ef,max is the maximum index void ratio of the silt, ef,min is the minimum index void ratio of the silt, es,max is the maximum index void ratio of the sand matrix, es,min is the minimum index void ratio of the sand matrix, Gsf = specific gravity of the silt, and Gss is the specific gravity of the sand.
Using index data reported in the literature for 127 sands and 53 non-plastic silts [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], the upper- and lower-bound threshold fines contents were calculated for the 6731 combinations of sand and non-plastic silt in order to determine a range of typical values for the upper- and lower-bound threshold fines contents. The analysis found that all 6731 combinations had upper-bound threshold fines contents between 15% and 46%, with a mean of 30.5%, a median of 30.8%, and a standard deviation of 4.9%. Similarly, it was found that all of the lower-bound threshold fines contents were between 7% and 38%, with a mean of 16.1%, a median of 16.7%, and a standard deviation of 3.9%. Figure 3 and Figure 4 provide histograms of the distribution of the maximum upper-bound and minimum lower-bound threshold fines contents, respectively.
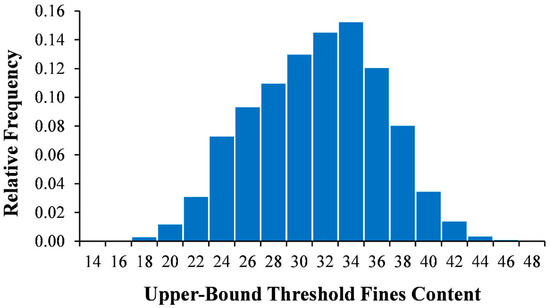
Figure 3.
Distribution of upper-bound threshold fines contents.
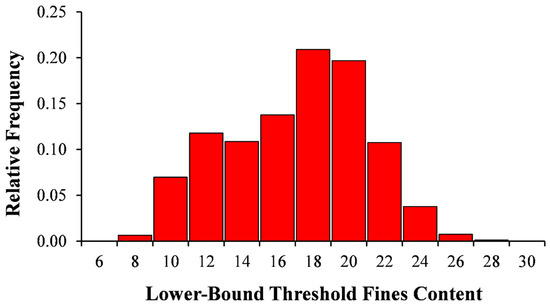
Figure 4.
Distribution of lower-bound threshold fines contents.
In addition to the upper- and lower-bound threshold fines contents, the width of the transition zone was calculated for each combination of sand and silt. These zones represent the range of fines contents over which the soil transitions from sand-like behavior to silt-like behavior. It was found that all of the transition zones had widths between 6% and 30%, with a mean of 14.3%, a median of 13.8%, and a standard deviation of 2.9%. Figure 5 presents a histogram of the widths of the transition zones.
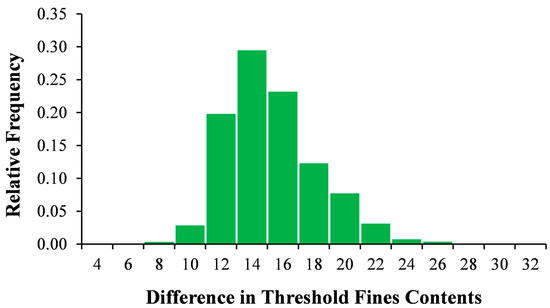
Figure 5.
Distribution of differences between upper- and lower-bound threshold fines contents.
How well the distribution of the threshold fines contents matched a normal distribution was evaluated through quantile testing. The upper-bound threshold fines contents, the lower-bound threshold fines contents, and the widths of the transition zones were all found to be approximately normally distributed. Figure 6 presents the normalcy plots for the three threshold fine contents evaluated. Table 1 presents the results of the quantile testing performed on the threshold fines contents, including the R-value for the distribution and the R-value that needs to be exceeded to declare the distribution a normal distribution at the 5% level.
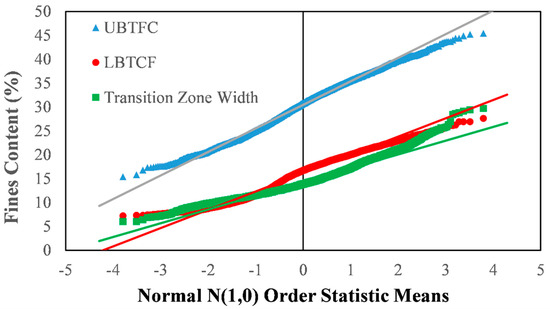
Figure 6.
Normalcy plots for the threshold fines contents.

Table 1.
Results of Quantile tests for normalcy of the threshold fines contents.
2.2. Cyclic Triaxial Tests
Invented in the 1960s, cyclic triaxial tests apply a cyclic axial stress or strain while imposing a condition of constant volume on the specimen [17,18]. The test is performed on a saturated specimen, which is typically isotropically consolidated to some initial effective stress. A constant-volume condition is enforced on the specimen during loading by preventing drainage in the saturated specimen. Because water cannot enter or leave the specimen, its volume cannot change.
When testing a contractive specimen of sand or silt in a cyclic triaxial test, the specimen will generate an increase in pore pressure as the result of the specimen’s tendency for contraction. This increase in pore pressure leads to a decrease in the effective confining stress that is acting on the specimen. Eventually, the effective stress acting on the specimen nears zero, the shear strength of the specimen becomes small, and the specimen begins to undergo large axial deformations. At this point (either zero effective stress or some designated level of axial strain), the soil is deemed to have liquefied.
2.3. Cyclic Direct Simple Shear Tests
Invented in the 1970s, cyclic direct simple shear tests apply a shear stress or shear strain while imposing a condition of constant volume on the specimen [17,18]. The test produces the same changes in effective stress as a corresponding Ko-consolidated, undrained cyclic direct simple shear test performed on a saturated specimen. Because cyclic direct simple shear tests can be performed on dry or partially saturated specimens, they eliminate many of the system compliance and membrane penetration issues that can affect cyclic tests performed using saturated specimens of coarse-grained materials.
The constant-volume conditions are enforced on the specimen by laterally confining it with either a series of metal rings or a wire-wrapped membrane. The rings or membrane prevents lateral expansion during testing, while still allowing shear deformations. The thickness of the specimen is held constant by preventing movement of the top platen during shearing. The fixed specimen thickness combined with the lateral confinement create a situation where the volume of the specimen remains constant.
When testing a contractive specimen of sand or silt in a cyclic direct simple shear test, the specimen will contract in the vertical direction, thereby decreasing the normal stress acting on the stationary top platen. This decrease in normal stress is the equivalent of the decrease in effective stress that would be measured in an undrained test on a saturated specimen. The decrease in the normal stress is also representative of the increase in pore pressure that would be measured in a cyclic direct simple shear test performed on a Ko-consolidated, saturated, undrained specimen. In this paper, when discussing the results of the cyclic direct simple shear tests, the term “pore pressure” will be used in place of “decrease in normal stress” for simplicity.
2.4. Terminology
Four terms that will be used in this paper will now be explained. These terms are “dissipated energy ratio”, “pore pressure ratio”, “cycle ratio”, and “pore pressure generation rate”. When used in this article, these terms are defined as follows:
- (1)
- Dissipated energy ratio, Ws/WsL, is the cumulative amount of normalized dissipated energy per unit volume, Ws, that has been dissipated at a given point during loading divided by the total quantity of normalized dissipated energy per unit volume required to initiate liquefaction in the soil mass, WsL [19].
- (2)
- Pore pressure ratio, ru, is the excess pore pressure that has been generated in the specimen at some point during the test divided by the initial effective stress acting on the specimen [20].
- (3)
- Cycle ratio, N/NL, is the number of the current cycle of loading, N, divided by the number of cycles of loading required to initiate liquefaction, NL [20].
- (4)
- Pore pressure generation rates are calculated based on the rate at which the pore pressure ratio increases with respect to either the dissipated energy ratio or the cycle ratio [19].
2.5. Previous Work Performed in This Area
Several studies have previously investigated the effect of silt content on pore pressure generation rates in cyclic laboratory tests. Ghadr et al. [21] and Karim and Alam [22] used cyclic triaxial tests in their investigations, while Baziar et al. [23] used hollow cylinder torsional tests.
Ghadr et al. [21] performed cyclic triaxial tests on fiber-reinforced mixtures of Firoozkuh 161 sand and non-plastic silt with fines contents ranging from 0 to 50%. The threshold fines content was calculated to be 28% for these soil mixtures. Examination of their published results indicate that the pore pressures generation rates can be separated into two clearly different groups: a slower group consisting of specimens with fines contents of 0 to 20% (i.e., below the threshold fines content) and a more rapid group consisting of specimens with fines contents of 30 to 50% (i.e., above the threshold fines content). This behavior may be seen in Figure 7.
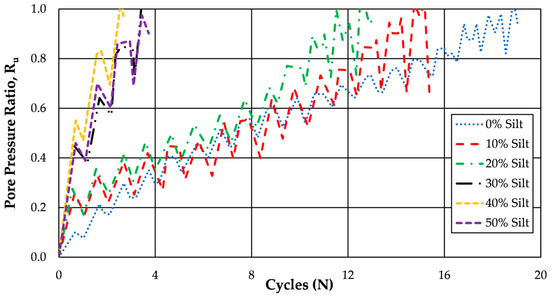
Figure 7.
Pore pressure generation as a function of fines content (after Ghadr et al. [21]).
Karim and Alam [22] performed cyclic triaxial tests on mixtures of fine sand and non-plastic silt at 10 fines contents ranging from 0 to 100%. The threshold fines content was calculated to be 30% for these soil mixtures. Examination of their published results, from tests performed on specimens with relative densities of 60%, indicate that the pore pressure generation rates can be separated into two different groups. One group is the slower group consisting of specimens with fines contents of 0, 10, and 100%. The second group is the more rapid group consisting of specimens with fines contents of 20 to 90% (i.e., above the threshold fines content). The specimens with between 20% and 90% fines generated pore pressures at nearly identical rates, reaching a pore pressure ratio of 0.80 in 7 cycles, while specimens with silt contents of 0%, 10%, and 100% did not reach a pore pressure ratio of 0.8 until 80, 31, and 17 cycles, respectively. This behavior may be seen in Figure 8.
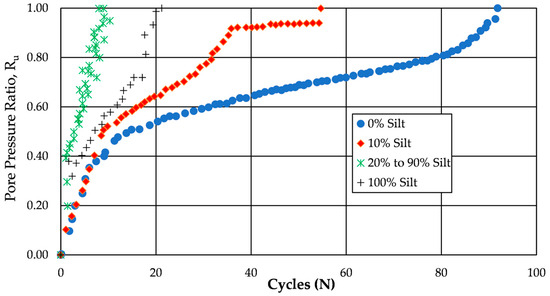
Figure 8.
Pore pressure generation as a function of fines content (after Karim and Alam [22]).
Baziar et al. [23] performed cyclic hollow torsion tests on mixtures of Firouzkooh sand and non-plastic silt at five fines contents ranging from 0 to 100%. The threshold fines content was calculated to be 26% at a relative density of 60% for these soil mixtures. The authors found that soils with fines contents above the threshold fines content required the application of a higher cyclic stress ratio to cause liquefaction in 15 cycles than was required for specimens with silt contents above the threshold fines content. Figure 9 plots the peak pore pressure ratios measured against the cycle ratio.
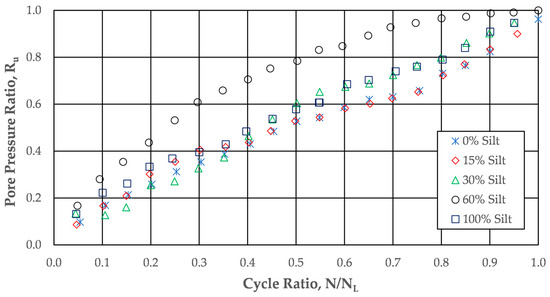
Figure 9.
Peak pore pressure ratio vs. cycle ratio for sands with various non-plastic fines contents (after Baziar et al. [23]).
In addition to studies that have specifically reported data on pore pressure generation rates, it is possible to infer relative pore pressure generation rates from cyclic resistance curves developed using cyclic laboratory tests such as cyclic triaxial or cyclic direct simple shear tests. These curves are plotted using either the applied cyclic stress ratio or the applied strain on the abscissa and the number of cycles of loading required to cause liquefaction on the ordinate. An example of such a series of curves is presented in Figure 10 (after Polito [24]), which shows the cyclic resistance curves for a series of cyclic triaxial tests performed on specimens of Yatesville sand and Yatesville silt at different fines contents prepared to a constant relative density of 25% to 30%. These specimens were all tested at an initial effective confining stress of 100 kPa, and liquefaction was defined as occurring when the pore pressure ratio, Ru, first reached unity.
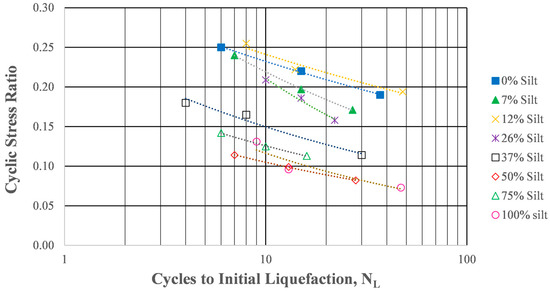
Figure 10.
Cyclic resistances curves for different mixtures of Yatesville sand and Yatesville silt (after Polito [24]).
If one moves along any line of constant cyclic stress ratio in Figure 10, it can be determined how many cycles of loading are required to liquefy a specimen. The rate of pore pressure generation can be quantified as the decrease in effective stress per cycle of loading. Therefore, the fewer cycles of loading that are required to trigger liquefaction, the higher the rate of pore pressure generation.
3. Laboratory Testing Program
In this study, the results of laboratory testing programs reported by Polito and Martin [1] and Polito and Sibley [2] were analyzed to examine how a soil’s non-plastic silt content affects its pore pressure generation rate during cyclic loading, with a focus on the specimen’s fines content relative to the soil’s threshold fines content. The testing performed in the original studies consisted of cyclic triaxial tests [1] and cyclic direct simple shear tests [2]. These tests were performed on specimens of sand with non-plastic silt contents ranging either from 0% to 100% [1] or from 0% to 45% [2] by weight.
The relationships between threshold fines content and pore pressure generation reported in this study are based on 59 cyclic triaxial tests by Polito and Martin [1] and 45 cyclic direct simple shear tests reported by Polito and Sibley [2]. The following sections describe the soils tested and outline the testing methodologies. In these analyses, the use of upper- and lower-bound threshold fines contents were replaced by an average threshold fines content, which is simply the arithmetical average of the upper- and lower-bound threshold fines contents. The average threshold fines content was used when determining whether a specific soil mixture has a silt content above or below the threshold fines content.
3.1. Test Soils
Sand, silt, and combinations thereof form the most common non-plastic soils encountered in engineering practice. As has been previously discussed, the behavior of the soils depends heavily on whether their non-plastic silt content is greater or less than their threshold fines content.
While combinations of gravels and non-plastic silts are also occasionally encountered, insufficient data were available to analyze the effects of non-plastic fines contents on these mixtures. As a result, the scope of this study was limited to the effects of non-plastic fines content on pore pressure generation in mixtures of sand and non-plastic silt.
The test data used in this study were obtained from a study performed by the first author and second author [1] and a second study performed by the first and third authors [2]. The soil mixtures used in those studies were formed by adding non-plastic silt to sand. The three sands used in the studies were Yatesville sand [1], Monterey #0/30 sand [1], and Ottawa C-109 sand [2]. The two silts used in the studies were Yatesville silt [1] and #106 Sil-Co-Sil silt [2]. The non-plastic silt contents selected for the mixtures were chosen because they provided a range of silt contents both above and below the threshold fines content. The properties of these soils and their mixtures are described in in the following sections.
3.1.1. Yatesville Sand
Yatesville sand is a poorly graded, medium to fine sand. It has a specific gravity of 2.72, a maximum grain size (D100) of 0.84 mm, a median grain size (D50) of 0.18 mm, a coefficient of uniformity (Cu) of 2.40, and a coefficient of curvature (Cc) of 0.77. It has a maximum index void ratio (emax) of 0.97 and a minimum index void ratio (emin) of 0.65. Its grain size distribution curve is presented in Figure 11.
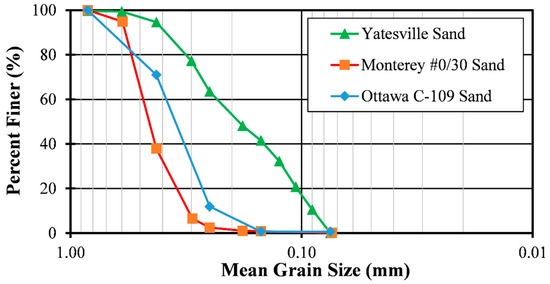
Figure 11.
Grain size distribution curves for the sands used in this study.
3.1.2. Monterey #0/30 Sand
Monterey #0/30 sand is a poorly graded, medium to fine sand. It has a specific gravity of 2.65, a maximum grain size (D100) of 0.84 mm, a median grain size (D50) of 0.43 mm, a coefficient of uniformity (Cu) of 1.48, and a coefficient of curvature (Cc) of 1.04. It has a maximum index void ratio (emax) of 0.82 and a minimum index void ratio (emin) of 0.63. Its grain size distribution curve is presented in Figure 11.
3.1.3. Ottawa C-109 Sand
Ottawa C-109 sand is a poorly graded, medium to fine sand. It has a specific gravity of 2.65, a maximum grain size (D100) of 0.84 mm, a median grain size (D50) of 0.33 mm, a coefficient of uniformity (Cu) of 1.65, and a coefficient of curvature (Cc) of 1.03. It has a maximum index void ratio (emax) of 0.69 and a minimum index void ratio (emin) of 0.50. Its grain size distribution curve is presented in Figure 11.
3.1.4. Yatesville Silt
Yatesville silt is a non-plastic silt. It has a specific gravity of 2.77, a maximum grain size (D100) of 0.074 mm, a median grain size (D50) of 0.031 mm, a coefficient of uniformity (Cu) of 4.38, and a coefficient of curvature (Cc) of 0.93. It has a maximum index void ratio (emax) of 1.723 and a minimum index void ratio (emin) of 0.727. Its grain size distribution curve is presented in Figure 12.
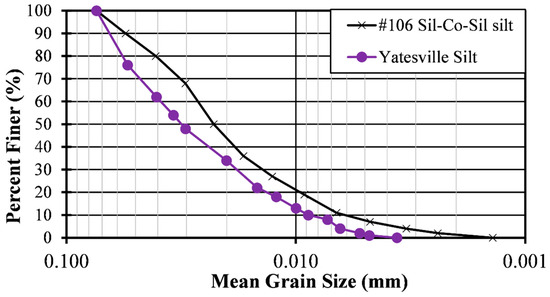
Figure 12.
Grain size distribution curves for the non-plastic silts used in this study.
3.1.5. #106 Sil-Co-Sil Silt
A non-plastic silt, #106 Sil-Co-Sil silt has a specific gravity of 2.61, a maximum grain size (D100) of 0.074 mm, a median grain size (D50) of 0.023 mm, a coefficient of uniformity (Cu) of 4.50, and a coefficient of curvature (Cc) of 1.39. It has a maximum index void ratio (emax) of 1.49 and a minimum index void ratio (emin) of 0.67. Its grain size distribution curve is presented in Figure 12.
3.1.6. Mixtures of Yatesville Sand and Yatesville Silt
In Polito and Martin’s study [1], mixtures of Yatesville sand and Yatesville silt with silt contents ranging from 0% to 100% were created by mixing the sand with an appropriate weight of silt. Ten mixtures of Yatesville sand and Yatesville silt were tested in cyclic triaxial tests. The silt contents tested were 0%, 4%, 7%, 12%, 17%, 26%, 37%, 50%, 75%, and 100%. All specimens were tested at relative densities of between 25% and 30%.
For the combination of Yatesville sand and Yatesville silt, the UBTFC is 36.4%, the LBTFC is 19.6%, and the average of these values is 28.0%.
3.1.7. Mixtures of Monterey #0/30 Sand and Yatesville Silt
In Polito and Martin’s study [1], mixtures of Monterey #0/30 sand and Yatesville silt with silt contents ranging from 0% to 100% were created by mixing the sand with an appropriate weight of silt. Ten mixtures of Monterey #0/30 sand and Yatesville silt were tested in cyclic triaxial tests. The silt contents tested were 0%, 5%, 10%, 15%, 20%, 25%, 35%, 50%, 75%, and 100%. All specimens were tested at relative densities of between 48% and 53%.
For the combination of Monterey #0/30 sand and Yatesville silt, the UBTFC is 33.2%, the LBTFC is 19.5%, and the average of these values is 26.3%.
3.1.8. Mixtures of C-109 Sand and #106 Sil-Co-Sil Silt
In Polito and Sibley’s study [2], mixtures of C-109 sand and #106 Sil-Co-Sil silt ranging from 0% to 45% were created by mixing the sand with an appropriate weight of dry silt. Ten mixtures of Ottawa C-109 sand and silt were tested in cyclic direct simple shear tests. The silt contents tested were 0%, 5%, 10%, 15%, 20%, 25%, 30%, 35%, 40%, and 45%. All specimens were tested at relative densities of 38% to 43%.
For the combination of C-109 sand and #106 Sil-Co-Sil silt, the UBTFC is 28.9%, the LBTFC is 16.5%, and the average of these values is 22.7%.
3.2. Testing Methodologies
Cyclic triaxial tests [1] and cyclic direct simple shear tests [2] were performed to investigate the effect of silt content on pore pressure generation rates in mixtures of sand and non-plastic silt. The specimen characteristics and the test methodologies used in each test are described in the following sections.
3.2.1. Cyclic Triaxial Testing
The pore pressure generation rates of mixtures of Yatesville sand and Yatesville silt and mixtures of Monterey #0/30 sand and Yatesville silt were evaluated using stress-controlled, cyclic triaxial tests [25], following the methodology outlined by Silver [26].
Specimens for the cyclic triaxial tests were 71.0 mm in diameter and 154 mm in height. Specimens were formed by moist tamping, using undercompaction [27] to ensure uniform density throughout the specimen. Following preparation, the specimens were first flushed with CO2 and then backpressure-saturated to a B-value of 0.94 or greater. Next, the specimens were isotropically consolidated to an effective stress of 100 kPa and then subjected to a 1 Hz sinusoidally varying axial stress until liquefaction occurred.
For the cyclic triaxial tests, in this study, liquefaction was defined as occurring when the effective stress first equaled 5 kPa. Each soil mixture was tested at three different cyclic stress ratios.
3.2.2. Cyclic Direct Simple Shear Testing
The pore pressure generation rates of the mixtures of C-109 sand and #106 Sil-Co-Sil silt were evaluated using strain-controlled, cyclic direct simple shear tests [28].
Specimens for the cyclic direct simple shear tests were 71.0 mm in diameter and 12.7 mm in thickness, which yields a diameter-to-height ratio (D/H) of 5.6. Franke et al. [29] recommend a minimum diameter-to-height ratio of four in order to minimize the effects of the lack of complementary shear stresses on the vertical faces of the specimen. Ko-conditions were enforced by surrounding the specimen with a set of stacked brass rings. Each ring had an inside diameter of 71.0 mm, an outside diameter of 95.3 mm, and a thickness of 3.0 mm.
Specimens were formed by dry deposition. Following deposition, a normal stress of 105 kPa was applied to the soil, and then the specimen mold was lightly and symmetrically tapped until the desired density of soil was achieved. During shearing, the location of the upper platen was actively controlled by the testing system to ensure that the specimen thickness remained constant, even as the stress on the platen changed. The specimens were subjected to a 0.1 Hz sinusoidally varying shear strain at the selected shear strain level until liquefaction occurred. For this study, liquefaction was defined as occurring when the normal stress first equaled 5 kPa. Each soil mixture was tested at five different levels of single-amplitude shear strain.
3.2.3. Definition of Liquefaction
As noted, liquefaction was deemed to have occurred in the cyclic direct simple shear tests when the vertical normal stress acting on the specimen first reached 5 kPa. This was chosen as the liquefaction criterion rather than the more common value of 0 kPa because some early specimens (which were not included in this study) reached very low values of normal stress (less than 3 kPa), then plateaued at that level, never quite reaching 0 kPa normal stress.
In the study by Polito and Martin [1], liquefaction was originally defined for the cyclic triaxial tests as occurring when the effective stress on the specimen first reached a value of 0 kPa. However, for consistency with the cyclic direct simple shear tests, the cyclic triaxial test data were reanalyzed for this study assuming that liquefaction occurred when the effective stress acting on the specimen first reached 5 kPa.
4. Results
In this section, the results of the analysis of the laboratory test data are reported. For each series of tests, the results are divided into two groups, the first group containing those specimens with silt contents above the threshold fines content and the second group containing those specimens with silt contents below the threshold fines content. For each group, the mean and the standard deviation of the pore pressure ratios corresponding to dissipated energy ratios of 30%, 60%, and 90% are reported, because they are used in the hypothesis testing discussed in Section 5.
4.1. Results of Cyclic Triaxial Tests
Table 2 presents the results of the cyclic triaxial tests performed both on the mixtures of Yatesville sand and Yatesville silt and the mixtures of Monterey #0/30 sand and Yatesville silt. For each sand type, the results are broken into two groups of specimens: those with silt contents above the threshold fines content and those with silt contents below the threshold fines content. The means and standard deviation of the pore pressure ratios at dissipated energy ratios of 30%, 60%, and 90% are provided for all the specimens with silt contents above the threshold fines contents. Similarly, the means and standard deviation of the pore pressure ratios at dissipated energy ratios of 30%, 60%, and 90% for all the specimens with silt contents below the threshold fines contents are also presented.

Table 2.
Results of cyclic triaxial testing.
4.2. Results of Cyclic Direct Simple Shear Tests
Similar to the cyclic triaxial test data, the results of the cyclic direct simple shear tests performed on mixtures of C-109 sand and #106 Sil-Co-Sil silt are broken into two groups, the first group containing those specimens with silt contents above the threshold fines content and the second group containing those specimens with silt contents below the threshold fines content. The means and standard deviation of the pore pressure ratios at dissipated energy ratios of 30%, 60%, and 90% are provided for each group in Table 3.

Table 3.
Results of cyclic direct simple shear testing.
In order to provide better insight into the data and to aid in comparing them to the results found during previous studies, the pore pressure generation data from the cyclic direct simple shear tests were plotted against the number of cycles of loading. The data presented are for tests that were loaded with an applied shear strain of 0.5%. This plot is presented in Figure 13. It presents the test results in a manner similar to the method used by Ghadr et al. [21] and by Karim and Alam [22]. The plots showing the data from the previous studies were presented in Figure 7 and Figure 8, respectively.
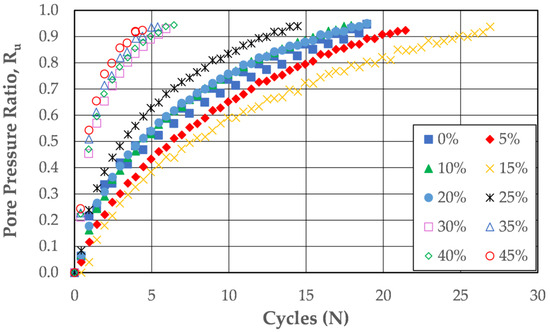
Figure 13.
Pore pressure generation as a function of cycles of loading and silt content from cyclic direct simple shear tests with 0.5% applied shear strain.
In Figure 13, one may observe that there is a gap between the soil mixtures with silt contents below the upper-bound threshold fines content of 28.9% and those with silt contents above the upper-bound threshold fines content. This division between the two groups of soil mixtures is similar to the division seen in the data from the literature presented in Figure 7 (after [21]) and Figure 8 (after [22]). Similar behaviors were observed for the soils tested in the cyclic triaxial tests.
The pore pressure generation data from each of the cyclic direct simple shear tests loaded with an applied strain of 0.5% shear strain were also plotted against the cycle ratio, which is the ratio of the cycle of loading to the number of cycles of loading required to initiate liquefaction. This plot is presented in Figure 14. It presents the test results in a manner similar to the method used by Baziar et al. [23], whose results were presented in Figure 9. Similar behaviors were observed for the soils tested in the cyclic triaxial tests.
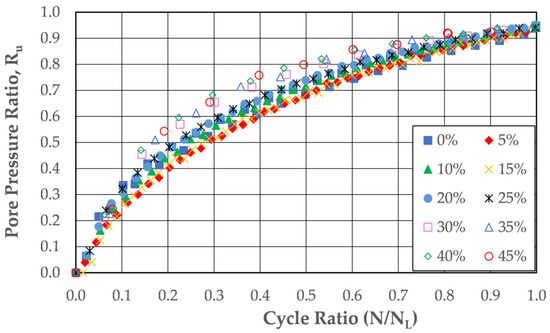
Figure 14.
Pore pressure generation as a function of cycle ratio and silt content from cyclic direct simple shear tests with 0.5% applied shear strain.
In Figure 14, one may see the gap that exists between the soil mixtures with silt contents below the upper-bound threshold fines content of 28.9% and those with silt contents above the upper-bound threshold fines content. This division between the two groups of soil mixtures is similar to the division seen in the data from the literature in Figure 9 (after [23]).
Figure 15 presents a plot of the pore pressure generation data from each of the cyclic direct simple shear tests loaded with an applied strain of 0.5% shear strain against the dissipated energy ratio. The figure shows that, at a given dissipated energy ratio, higher levels of pore pressure ratio are achieved by the soils with silt contents above the threshold fines content. Similar behaviors were observed for the soils tested in the cyclic triaxial tests.
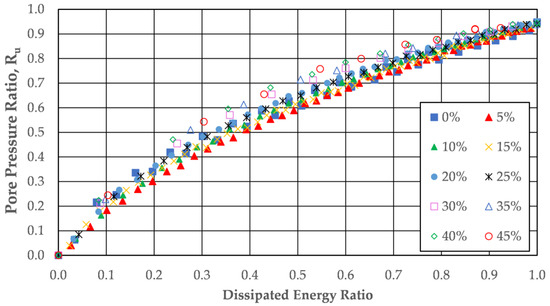
Figure 15.
Pore pressure generation as a function of dissipated energy ratio and silt content from cyclic direct simple shear tests with 0.5% applied shear strain.
5. Analysis and Discussion of Results
Hypothesis testing was used to compare the means of the pore pressure generation rates of specimens with silt contents above the threshold fines content to the means of those with silt contents below the threshold fines content for each of the three soil mixtures at dissipated energy ratios of 30%, 60%, and 90%. The results of the two-sample t-tests are presented in Table 4.

Table 4.
Results of two-sample t-testing.
For the hypothesis testing, two-sample t-testing with unequal variances [30] was used. The null hypothesis selected was that the means of the two groups were the same. The t-tests were conducted at a 5% level of significance. Two-sample t-testing uses the mean and standard deviation from each of two sets of data to determine how likely it is that the two data sets come from the same distribution (i.e., from the same overall data set).
The t-tests indicated that the null hypothesis should be rejected for each of the three combinations of sand and silt at each of the three dissipated energy ratios. This indicates that there is a very high likelihood that the mean pore pressure generation rates are different. This leads to the conclusion that at each of the dissipated energy levels, the pore pressure ratios, and thus the pore pressure generation rates, were statistically different for the soils above the threshold fines content and those below the threshold fines content. In every case, the mean pore pressure generation rates were larger for the soils with non-plastic silt contents above the threshold fines content than they were for soils below the threshold fines content.
It is clear from the data that soils with silt contents greater than the threshold fines content produce larger values of pore pressure ratio during the early cycles of loading than soils with silt contents below the threshold fines content. While more testing is needed to confirm the hypothesis, it is believed that the reason for the larger pore pressure ratios noted in the soils with silt contents above the threshold fines contents is that these soils consist of a silt matrix with embedded sand particles. The silt matrix is more compressible and has a lower stiffness than the soils below the threshold fines content (which consist of a stiffer, less compressible sand matrix with embedded silt particles). The higher compressibility of the soils that have a predominately silt matrix results in their producing higher pore pressures during the initial cycles of loading.
6. Conclusions
This study investigated the effect that a soil’s non-plastic silt content had on the rate of pore pressure generation in cyclically loaded laboratory tests. Special attention was paid to the soil’s silt content relative to its threshold fines content. The investigation was performed on three sets of mixtures of sand and silt with non-plastic silt contents ranging from either 0% to 100% or 0% to 45%. Two of the sets of sand–silt mixtures were tested in cyclic triaxial tests, and one set was tested in cyclic direct simple shear tests.
Hypothesis testing was used to compare the pore pressure generation rates for soils with silt contents above the threshold fines content and for the pore pressure generation rates for soils with silt contents below the threshold fines content. The hypothesis tests were performed at dissipated energy ratios of 30%, 60%, and 90%.
It was concluded that, when evaluated in terms of dissipated energy ratio, soils with non-plastic silt contents above the threshold fines content have more rapid pore pressure generation rates than soils with non-plastic silt contents below the threshold fines content. This behavior was found to occur in both cyclic triaxial and cyclic direct simple shear tests. It was seen at all three dissipated energy ratios examined, for each of the three sets of sand-and-silt mixtures.
The reason for this difference is hypothesized to be the softer, more compressible silt-based soil skeleton that controls the behavior of the soils with silt contents greater than the threshold fines content. Because the specimens tend to be more compressible when sheared under drained conditions, they generate larger pore pressures when sheared either undrained or under constant-volume conditions.
Author Contributions
Analysis, C.P.P.; conceptualization and writing—original draft preparation, C.P.P.; writing—review and editing, C.P.P., J.R.M. and E.L.D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are available by contacting the first author.
Acknowledgments
The first author would like to thank Valparaiso University for the support provided through the Alfred W. Sieving Endowed Chair of Engineering.
Conflicts of Interest
Author Erin L. D. Sibley was employed by the company Mott MacDonald. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Polito, C.; Martin, J.R. The Effects of Non-Plastic Fines on the Liquefaction Resistance of Sands. J. Geotech. Geoenviron. Eng. 2001, 127, 408–415. [Google Scholar] [CrossRef]
- Polito, C.; Sibley, E. Threshold Fines Content and the Behavior of Sands with Non-Plastic Silts. Can. Geotech. J. 2020, 57, 462–465. [Google Scholar] [CrossRef]
- Thevanayagam, S. Effect of Fines and Confining Stress on Undrained Shear Strength of Silty Sands. J. Geotech. Geoenviron. Eng. 1998, 124, 479–491. [Google Scholar] [CrossRef]
- Hazirbaba, K. Pore Pressure Generation Characteristics of Sands and Silty Sands: A Strain Approach. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2005. [Google Scholar]
- Kokusho, T. Liquefaction Strengths of Poorly-Graded and Well-Graded Granular Soils Investigated By Lab Tests. In Earthquake Geotechnical Engineering, Volume 6, 4th International Conference on Earthquake Geotechnical Engineering-Invited Lectures; Thessaloniki, Greece, Kyriazas Pitilakis; Springer: Berlin/Heidelberg, Germany, 2006; pp. 159–184. [Google Scholar]
- Tao, M.; Figueroa, J.L.; Saada, A.S. Influence of Nonplastic Fines Content on the Liquefaction Resistance of Soils in Terms of the Unit Energy. In Proceedings of the Cyclic Behaviour of Soils and Liquefaction Phenomena, Bohum, Germany, 31 March–2 April 2004; A. A. Belkema: Leiden, The Netherlands, 2004; pp. 223–231. [Google Scholar]
- Yang, S.; Lacasse, S.; Sandven, R. Determination of the Transitional Fines Content of Mixtures of Sand and Non-Plastic Fines. Geotech. Test. J. 2006, 29, 102–107. [Google Scholar] [CrossRef]
- Chang, C.; Wang, L.; Ge, L. Maximum and minimum void ratios for sand-silt mixtures. Eng. Geol. 2016, 211, 7–18. [Google Scholar] [CrossRef]
- Belkhatir, M.; Schanz, T.; Arab, A. Effect of fines content and void ratio on the saturated hydraulic conductivity and undrained shear strength of sand–silt mixtures. Environ. Earth Sci. 2013, 70, 2469–2479. [Google Scholar] [CrossRef]
- Bensoula, M.; Missoum, H.; Bendani, K. Critical undrained shear strength of sand-silt mixtures under monotonic loading. Int. J. Civ. Eng. Technol. 2018, 9, 447–455. [Google Scholar] [CrossRef]
- Fourie, A.; Blight, G.E.; Papageorgiou, G. Static liquefaction as a possible explanation for the Merriespruit tailings dam failure. Can. Geotech. J. 2001, 38, 707–719. [Google Scholar] [CrossRef]
- Hazirbaba, K.; Rathje, E.M. Pore pressure generation of silty sands due to induced cyclic shear strains. J. Geotech. Geoenviron. Eng. 2009, 135, 1892–1905. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, M.Z.; Khan, M.B. Experimental approach for assessment of liquefaction in fine sand and silty sand. Int. J. Eng. Sci. Invent. 2016, 5, 68–72. [Google Scholar]
- Lade, P.V.; Liggio, C.D., Jr.; Yamamuro, J.A. Effects of non-plastic fines on minimum and maximum void ratios of sand. Geotech. Test. J. 1998, 21, 336–347. [Google Scholar] [CrossRef]
- Teng, J.; Araki, K.; Yasufuku, N.; Ikeda, H. Experimental study on void ratio characteristics of sand-fines mixture. In Proceedings of the 66th Annual Scientific Lecture Meeting of the Japan Society of Civil Engineers, Matsuyama, Japan, 7 September–9 October 2011; pp. 785–786. [Google Scholar]
- Yilmaz, Y.; Mollamahmutoglu, M. Characterization of liquefaction susceptibility of sands by means of extreme void ratios and/or void ratio range. J. Geotech. Geoenviron. Eng. 2009, 135, 1986–1990. [Google Scholar] [CrossRef]
- Finn, W.D.L. Aspects of constant volume cyclic simple shear. In Proceedings of the Advances in the Art of Testing of Soils Under Cyclic Conditions, Detroit, MI, USA, 24 October 1985; American Society of Civil Engineers: New York, NY, USA, 1985; pp. 74–98. [Google Scholar]
- Finn, W.; Vaid, Y.; Bhatia, S.K. Constant Volume Cyclic Simple Shear Testing. In Proceedings of the Second International Conference on Microzonation for Safer Construction: Research and Applications, San Francisco, CA, USA, 26 November–1 December 1978; pp. 839–851. [Google Scholar]
- Seed, H.B.; Booker, J.R. Stabilization of Potentially Liquefiable Sand Deposits Using Gravel Drains. J. Geotech. Eng. Div. 1977, 103, 757–768. [Google Scholar] [CrossRef]
- Polito, C.; Martin, J.R. Dissipated Energy and Pore-pressure-generation patterns in Sands and Non-Plastic Silts Subjected to Cyclic Loadings. Geotechnics 2024, 4, 264–284. [Google Scholar] [CrossRef]
- Ghadr, S.; Samadzadeh, A.; Bahadori, H.; Assadi-Langroudi, A. Liquefaction resistance of fibre-reinforced silty sands under cyclic loading. Geotext. Geomembr. 2020, 2020, 48. [Google Scholar] [CrossRef]
- Karim, M.; Alam, M. Effect of non-plastic silt content on the liquefaction behavior of sand–silt mixture. Soil Dyn. Earthq. Eng. 2014, 65, 142–150. [Google Scholar] [CrossRef]
- Baziar, M.H.; Shahnazari, H.; Sharafi, H. A laboratory study on the pore pressure generation model for Firouzkooh silty sands using hollow torsional test. Int. J. Civil Eng. 2011, 9, 126–134. [Google Scholar]
- Polito, C.P. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1999. [Google Scholar]
- D5311/D5311M-13; Standard Test Method for Load-Controlled Cyclic Triaxial Strength of Soil. ASTM International: West Conshohocken, PA, USA, 2013. Available online: www.astm.org (accessed on 3 July 2024).
- Silver, M.L. Laboratory Triaxial Testing Procedures to Determine The Cyclic Strength of Soils; National Technical Information Service: Springfield, VA, USA, 1977.
- Ladd, R.S. Preparing Test Specimens Using Undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- ASTM D8296-19; Standard Test Method for Consolidated Undrained Cyclic Direct Simple Shear Test under Constant Volume with Load Control or Displacement Control. ASTM International: West Conshohocken, PA, USA, 2019. Available online: www.astm.org (accessed on 3 July 2024).
- Franke, E.; Kiekbusch, M.; Schuppener, B. A new direct simple shear device. Geotech. Test. J. 1979, 2, 190–199. [Google Scholar] [CrossRef]
- Devore, J. Probability and Statistics for Engineering and the Sciences, 6th ed.; Thompson Learning: Belmont, CA, USA, 2004; pp. 315–324. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).