An Approach to Quantifying the Influence of Particle Size Distribution on Buried Blast Loading

Abstract

Buried charges pose a serious threat to both civilians and military personnel. It is well established that soil properties have a large influence on the magnitude and variability of loading from explosive blasts in buried conditions. In this study, work has been undertaken to improve techniques for processing pressure data from discrete measurement apparatus; this is performed through the testing of truncation methodologies and the area integration of impulses, accounting for the particle size distribution (PSD) of the soils used in testing. Two experimental techniques have been investigated to allow for a comparison between a global impulse capture method and an area-integration procedure from a Hopkinson Pressure Bar array. This paper explores an area-limiting approach, based on particle size distribution, as a possible approach to derive a better representation of the loading on the plate, thus demonstrating that the spatial distribution of loading over a target can be related to the PSD of the confining material.

1. Introduction

Improvised Explosive Devices (IEDs) and landmines form a serious threat to life in military and civilian situations around the world. In 2020, over seven thousand people were killed or injured by landmines or ‘Explosive Remnants of War’ (ERWs) 80% of these were civilians [1]. A better understanding of the behaviour of these explosive charges can lead to better protection against them, thus saving lives and preventing injuries.

Much work has been performed to investigate the effects of explosive loading, especially for military applications, both in free air and with buried charges. The experiments are often conducted at a reduced scale [2] due to the high cost and difficulty of full-scale testing. Hopkinson [3]–Cranz [4] cube-root scaling is regularly used for this purpose. These experiments are supported by numerical modelling efforts [2], although these are often simplified models that do not incorporate soil-specific effects.

Studies have, in the past, failed to take sufficient account of soil conditions in experimentation and for the prediction of loading. Børvik et al. [5] and Kyner et al. [6] used ∼ 200 μm glass microspheres as a synthetic soil to reduce the influence of variable soil conditions. McShane et al. [7] used compressed gas in place of explosives to reduce complexity and increase the ease of experimentation. This was found to be a suitable method of simulating sand-throw interactions with structures, although it only accounts for impulse transfer through said sand throw (ignoring blast-wave transfer).

It has been found that introducing/taking account of these complexities has wide-ranging effects on the loading generated and, thus, it is key that these are accounted for in future work. Hlady [8] used Concrete Fine Aggregate Sand (CFAS), a cohesionless well-graded sand, and compared this against Suffield Prairie Soil (PS), a fine-grained cohesive soil composed mainly of clay. It was found that CFAS led to a greater level of repeatability, alongside a much reduced level of labour required in preparation, compared to the cohesive soil. Fourney et al. [9] conducted small-scale experiments in a range of soil conditions, which showed that soil ejecta contributes the majority of impulsive loading from buried charges. Anderson et al. [10] varied plate and soil parameters in a plate-jump-height experimental setup, finding that increasing the moisture content (and bulk density) resulted in greater momentum transfer. Bergeron et al. [11] carried out a series of small-scale experiments, using high-speed imaging and flash X-ray to capture soil ejecta and air shock detachment at greater distances. This showed that the ejection velocity of the soil decreases with increasing overburden, as does the air shock propagation speed (with this being greatest in a soil surface flush-buried condition). Weckert and Resnyansky [12] also used flash X-ray to capture ejecta expansion in experiments utilising a range of soils of varying PSD for the validation of numerical modelling. Very good agreement was found between the numerical and experimental results for the ejecta-wave expansion rate and shape.

Clarke et al. [13,14] found that the use of well-graded cohesionless soils result in greater variability in total impulse between tests, when compared with uniform cohesionless soils, for all moisture contents and bulk densities. Although geotechnical conditions (such as moisture content and bulk density) could be controlled to a high level, the well-graded nature of ‘Stanag’ (an approximation of the sandy gravel defined by [15]) results in a wider spread of impulse values than in a uniform soil such as Leighton Buzzard Sand (LB). Comparing two LB fractions: ‘Fraction B’ (LB) and ‘25B Grit’ (LBF), with respective $C_u$ (coefficient of uniformity, defined in Equation (1)) values of 1.4 and 3.2, resulting in a higher spread of impulse for LBF by a factor of four, even though similar levels of control of geotechnical conditions were achieved [16], thus demonstrating that increased variability is to be expected with an increasingly well-graded soil. A comparision of the particle size distributions of the soils used in this and other studies is shown in Figure 1.

$$C_u=\frac{D_{60}}{D_{10}}$$

(1)

where $D_{60}$ is the 60th percentile particle size by mass and $D_{10}$ is the 10th percentile particle size.

Computer programs have been used for decades for the prediction of blast loading from buried charges, with much based on earlier work by Westine et al. [19]. Tremblay [20] built on Westine’s work to establish algebraic equations for impulsive loading; however, these do not account for moisture content as a separate influence from soil density. This is necessary as, for a constant bulk density, an increasing moisture content results in increasing impulse delivery [21].

Numerical modelling has begun to capture the specific loading characteristics associated with soil conditions. Børvik et al. [5] and Kyner et al. [6] used discrete-particle-based numerical models to simulate their small-scale soil-analogue experimental work. Grujicic et al. [22,23,24] developed material models for sand that take account of soil parameters including saturation and particle size. It is imperative that experimental results can be gathered and used to validate these models.

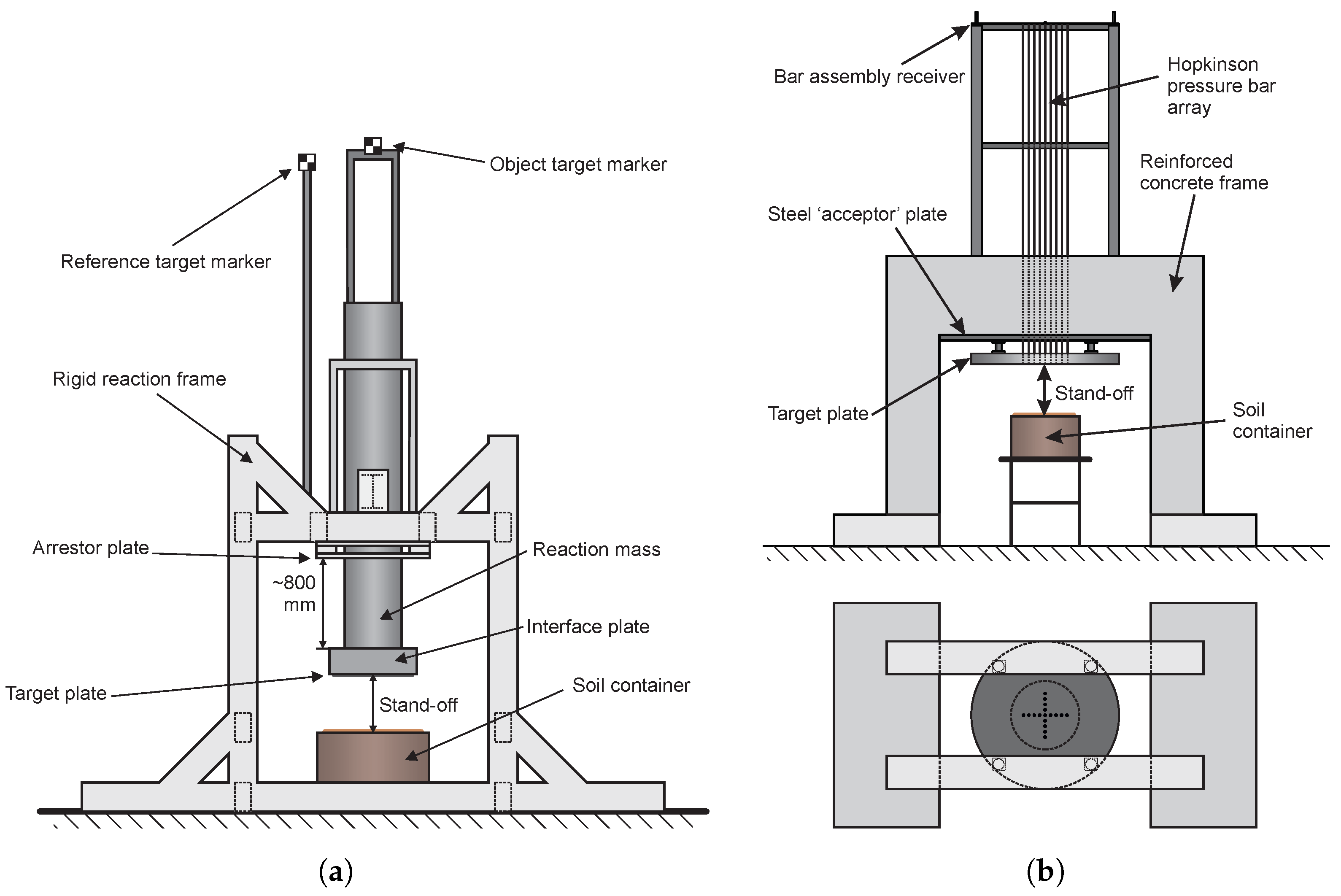
Research at the University of Sheffield has been conducted via two methods: ‘Characterisation of Blast Loading’ (CoBL) and ‘Free-flying mass impulse capture apparatus’ (FFM) [25]. FFM utilised a half-scale (of STANAG Threat Level 2, as defined by [15]) experimental setup wherein a deformable target plate and reaction mass captured the impulse from the buried charge, with the global impulse derived (as in Figure 2a). Hence, this method only captured the overall loading, without the spatial implications.

This spatial relationship has been determined previously using removable tapered plugs in the target plate [26], where their ejection velocity was measured using high-speed video. It was found that, as distance from the centre of the charge increases, the specific impulse decreases exponentially. A more accurate and repeatable experimental method has been developed for the CoBL setup [27] at quarter-scale, using 17 Hopkinson Pressure Bars (HPBs) of 10 mm diameter, arranged radially up to 100 mm from the charge centre in the face of a rigid target plate. Each HPB measures the axial strain, which is converted to stress with a specific impulse integrated for in time [27] and the global impulse interpolated over the instrumented area (as in Figure 2b).

Figure 2. The two experimental setups at the University of Sheffield. (a) FFM (from Figure 3 of Clarke et al. [28]). (b) CoBL (from Figure 2 of Rigby et al. [29]).

Figure 2. The two experimental setups at the University of Sheffield. (a) FFM (from Figure 3 of Clarke et al. [28]). (b) CoBL (from Figure 2 of Rigby et al. [29]).

In well-graded Stanag soil, individual particles can be over twice the size of the HPBs used in the CoBL setup. The total impulse values reported from FFM and CoBL testing are not in agreement for this soil type [17]; the impulse from CoBL is found to be much greater than that expected from scaling FFM, this is not the case for uniform soils. This suggests that the method of determining loading (a simple interpolation between discrete points) could be flawed for this well-graded soil. Hence, work is required to establish the relationship between a soil’s PSD and the distribution and magnitude of impulsive loading.

2. Methodology

In order to address the disparity between the global impulse results for well-graded soil between CoBL and FFM experiments, alterations were required to the method of interpolation between the discrete measurement points (as laid out in Figure 3).

The previous data processing method (as used by Rigby et al. [17] and Clarke et al. [30] for all soil types, outlined in detail in [31]) operated by first importing the voltage signals from the experimental output, converting these to pressure signals then truncating them to a chosen length of time. A breakwire placed within the explosive charge was used to trigger the recording, so the truncation is applied after this time. Next, all of the pressure traces are aligned in time by their maximum pressure, so that, at any time after wave arrival, the value of the pressure can be interpolated between each HPB in the same axial direction (thus eliminating the temporal progression element and reducing the problem to a 1-dimensional interpolation). These four axes (positive xx, positive yy, negative xx, and negative yy) can then be interpolated between to populate the quadrants of a matrix with the expected pressure at every location (to a given mesh size). This occurs for the full test duration, after which the temporal wave-progression is reintroduced to allow the algorithm to represent both the temporal and spatial aspects of the loading. In the previous work, this temporal matrix of pressures over the plate was used to derive a specific impulse and global impulse over the whole plate. This methodology, along with the new interventions proposed herein, is outlined in the flowchart in Figure 4.

2.1. Signal Truncation

Until now, it has been determined that an arbitrary cut-off, sufficiently later than the passing of the pressure wave, can be used to truncate input pressure signals. For the data presented by Clarke et al. [30], these results can be replicated by the use of a cut-off of 1.3 $\mathrm{m}$$\mathrm{s}$ (1.2 $\mathrm{m}$$\mathrm{s}$ after wave arrival), using peak global impulse as the reported values of impulse. Lide et al. [32] state that the speed of a wave in a narrow stainless steel rod is 5000 $\mathrm{m}$/$\mathrm{s}$, which means that over the 6m distance that the wave travels from the strain gauges to the end of the HPB and back, a 1.2 $\mathrm{m}$$\mathrm{s}$ time period will have elapsed before the reflection will interfere with the pressure trace. This length of truncation has been found to have a significant effect on some test results due to the presence of pressure signal ‘drift’ after the loading has occurred. This drift is a phenomenon wherein, on certain tests, the gauge voltage (and, thus, the recorded pressure) does not return to zero after the loading period, even though the true pressure has returned to the ambient level. This can, with enough time to compound, lead to large increases or reductions in the global impulse derived (acceptable if there is a negative drift, as the peak impulse can be measured before the drift causes it to drop, leading to an increased reported impulse value for tests with a positive drift). This drift acts in opposite directions depending on the scope polarity during experimentation, this varied during the testing as it was assumed that it would not affect the results, with the systematic error only identified post-testing. As such, a reduced truncation time of 0.7 $\mathrm{m}$$\mathrm{s}$ was introduced, as this has been found to reduce the influence of pressure drift whilst still capturing the full period of loading. The effects of this can be seen in Figure 5.

2.2. Signal Noise and Filtering

In order to improve the readability of the pressure signals from the experimental apparatus, data smoothing was performed with the purpose of reducing signal noise without affecting the peak pressure and impulse values significantly. A Hampel (median) Filter [33], with various window widths, was trialled with limited success, with some especially noisy signals being improved marginally, though not to an adequate level. Savitzky–Golay filtering [34], as used by Pannell et al. [35] for the removal of noise from specific impulse data, was evaluated also. A first-order fit (moving average) with varying frame lengths was applied, with a frame length of 11 samples (equivalent to approximately 35 μs) selected as appropriate due to negligible reductions in peak pressure and global impulse whilst delivering a significantly ‘cleaner’ pressure signal.

To understand the origin of the noise in the signal, a Fast Fourier Transform (FFT) operation was undertaken to find the Discrete Fourier Transform (DFT) of the raw pressure signals, to determine if there were any dominant frequencies within the signal that could be attributed to physical causes such as electrical noise. Figure 6 shows the frequency spectrums resulting from the FFT process for three tests, showing that the majority of the signal is in the <100 $\mathrm{k}$$\mathrm{Hz}$ range. There is not a secondary peak in the frequency spectrum, suggesting that the noise cannot be attributed to a consistent external source.

Wang and Li [36] used FFTs to filter out high-frequency noise from signals in the Split Hopkinson Pressure Bar experiments, applying a low-pass filter to the FFT output, then performing an inverse FFT to retrieve a low-noise output. The same method was applied in this study. Tyas and Watson [37] state that, “the highest acceptable frequency component in a signal propagating in a steel bar [is limited] to approximately from 250/a to 500/a kHz”, with a being the HPB radius in mm, in this case $a=5$. Thus, the maximum theoretically acceptable frequency would be between 50 and 100 kHz. However, they go on to state that, in blast loading, the situation can be more complicated. They propose a dispersion correction method that results in a bar having “a bandwidth in excess of 1250/a kHz” [37]. Supported by Figure 6, 100 kHz was selected as the maximum frequency cut-off in the current analysis. A comparison between the original pressure signal, with specific impulse take-up for the selected bar, against the Savitzky–Golay filtered and Inverse FFT signals is presented in Figure 7. It can be seen that the Savitzky–Golay filtering is an effective method of reducing signal noise, whilst preserving the pressure peak and specific impulse. However, an inverse FFT method is not suitable as a noise-reduction method as the pressure peak and specific impulse takeup are not preserved. Thus, Savitzky–Golay filtering has been used to process each of the raw pressure signals before further analysis is performed.

2.3. Wave Arrival Time

The subsequent alignment of the pressure signals for interpolation from the maximum value of pressure in each individual signal is relatively good, with signals usually aligned within 50 μs of each other. However, this falls down when the arrival of the wave and the maximum pressure peak do not align (through the presence of a second peak slightly after the first, potentially from initial separation of the shock front and the soil ejecta wave). As such, this alignment was changed to operate by finding the n highest pressure peaks in the signal (n = 5 was selected as the optimum value), then using the time signature of the earliest of these as the arrival time of that pressure wave. This improved the signal alignment substantially and also allowed for the determination of wave expansion speed (across the plate), which can be compared with other experimental blast wave speed data. The transition from raw pressure signals to smoothed, arrival-time-aligned signals is demonstrated for an example LB test in Figure 8. It can be seen that many of these signals exhibit slight negative pressure drift, as outlined previously.

The time of arrival (TOA) of a pressure wave at each HPB for a single test is plotted against the radial distance from the centre of the plate in Figure 9a. A reasonable TOA curve can be seen to occur, growing somewhat exponentially with increasing radial distance, with behaviour exhibited at far-field distances in the air [38]. The corresponding average wave-expansion velocity (calculated from an interpolation of the change in TOA at each HPB over the horizontal distance, from the central HPB) is shown in Figure 9b. This velocity is that of the coupled soil ejecta and blast wave expansion, as the blast wave is found (through HSV) to usually detach from the soil ejecta only at greater distances [11,29]. It can be seen that, after an initial period of instability (indicated by the flat portion of the graph), the velocity reduces with the radial distance. The arrival times are typically variable within the 0–25 mm range, potentially due to experimental error in the centring of the sand bin and charge below the instrumented plate surface, as well as from the influence of sand plumes ejecting ahead of the main wave. The decision was made to limit analysis of the wave speed to radii $\ge 25$ mm due to the unreliability of the data before that point, exacerbated by the presence of only one sensor at the centre rather than the four at every other instrumented distance.

2.4. Comparison of CoBL and FFM

So that the outputs of the modified interpolation algorithm could be reconciled against other data, global impulse values from the FFM tests were used as a comparison [28]. There is a disparity between the CoBL and FFM results for the Stanag tests (as discussed previously and in [17]), with the Stanag global impulse results being consistently higher than those of LB from CoBL testing but the reverse being true in FFM. There are two ways to reconcile the differences in these datasets. The first is that postulated in [17], wherein this higher impulse is caused by a more centralised loading in Stanag (due to a large number of discrete strikes directly above the charge, as well as the higher stiffness of Stanag), captured by the smaller relative instrumented area of CoBL. If this were the case, a greater peak deflection for the same impulse would be expected in plate-deflection experiments, such as that seen for testing performed with charges contained within a steel ‘pot’ (Minepot) in [28]. The peak deflections are marginally higher for Stanag when compared with LB (for the same impulse), but the extent and contribution of this loading centralisation is currently unknown. The second is that the existing area-integration of impulse inaccurately assumes a regular wave of soil expansion (through cubic interpolation) and occurs (disregarding the effects of discrete large particles), resulting in a consistent over-estimation of the global impulse. This study hypothesises that the particle strikes do not occur across the whole plate in this wave-like manner and, instead only occur at a limited number of locations, with the simple interpolation currently acting to skew the results by ‘stretching’ the increased pressure readings over an excessively large ‘zone of influence’. This effect is shown in Figure 10, with strikes at the two HPBs. The interpolation algorithm required alteration so that it could correctly account for discrete particle strikes, on top of a background contiguous wave. This study is intended as a proof of concept to investigate whether it is plausible to correct the interpolation algorithm to account for the effect of discrete particle strikes.

It was determined that this alteration should use an area-limiting scheme, wherein the maximum area surrounding a HPB, over which a recorded pressure would be likely to have been applied, would be determined, as opposed to the existing algorithm that assumed a full 180 degrees of the plate could be influenced by this pressure spike. For example, the existing algorithm would assume that a strike effectively impacts an area of 25 mm by 236 mm at a 75 mm HPB, a total area of 5890 $\mathrm{m}$$\mathrm{m}$${}^2$, when a typical Stanag particle ($D_{50}$) is around 10 mm in diameter (a cross-sectional area of 79 $\mathrm{m}$$\mathrm{m}$${}^2$). As such, it was important to determine a way to limit this area of influence to the true limit that would be expected in the real, uninstrumented regions of the target plate (represented in simplified form for a single axis in Figure 11).

This area limiting, as a consequence of the PSD, has been attempted as a possible method of understanding the behaviour of the soil in blast conditions. A number of approximations have been created, including assuming perfectly plastic collision behaviour and the straight-on impact of particles. Further work is required to establish the validity of these assumptions and to increase accuracy.

2.5. Theoretical Particle Strike Area

In order to establish the area limit for any given particle strike at any HPB, it was first important to consider the known soil parameters that could be used to derive this, the $D_{50}$ value (the median particle diameter) was selected for this purpose. From a particle size distribution graph, the $D_{50}$ can be established, in order to gauge a typical value of the particle size that is representative of the soil as a whole.

This $D_{50}$ value can be used, along with a stone density (assumed as a typical 2700 $\mathrm{k}\mathrm{g}$/$\mathrm{m}$${}^3$, in the calculation of a typical particle mass (assuming a spherical particle). When this is multiplied by the velocity of a strike (determined from average wave-expansion velocity at the relevant radial distance), the momentum of a typical particle strike can be established.

$$I_{\mathrm{strike}}=F_{\mathrm{typ}.}·t_{\mathrm{strike}}=m_{\mathrm{particle}}·v_{\mathrm{avg}.}$$

(2)

This momentum transfer is equivalent to the impulse experienced if a plastic response is assumed (particle obliterated on impact, not usually the case and thus a simplification). The impulse would be greater if the particle were reflected elastically, up to a maximum of twice the incident momentum (for a perfectly elastic collision). This equivalence of recorded impulse to incoming momentum has been shown to be the case for a homogenous sand slug [39], but it is likely a simplification of the behaviour of discrete particle loading. However, the expected increase in impulse due to collision elasticity may be counteracted due to oblique or glancing impacts of particles on HPBs, reducing the incident force; for simplicity, these effects have been ignored in this study.

If divided by the time period of the strike (assumed as 25 μs from initial graphs), the impulse can be converted to a typical force value. This time period is supported by the findings of Liu et al. [40], who found that in a sand slug impact, the soil densification time (and thus strike length) is related to the column height of the soil (the overburden of 28 mm in Stanag testing), H, and the velocity of the soil (see Figure 12):

$$t=\frac{\overline{t}·H}{v_0}$$

(3)

where, for an incompressible (rigid) target, $\overline{t}\approx 1$ when pressure drops to zero ($\overline{t}$ is a non-dimensional time).

Thus, for a 25 μs time period with H = 28 mm, a velocity of 1120 $\mathrm{m}$/$\mathrm{s}$ would be expected, reasonable given the velocities of the soil in Stanag tests (peak average velocities: 864–2637 $\mathrm{m}$/$\mathrm{s}$ and at 100 mm HPB: 636–1050 $\mathrm{m}$/$\mathrm{s}$).

$$\begin{array}{cc}\hfill F_{\mathrm{typ}.}& =\frac{m_{\mathrm{part}.}·v_{\mathrm{avg}.}}{t_{\mathrm{strike}}}\hfill \\ \hfill & =\frac{\frac{4}{3}·\pi ·{\left(\frac{D_{50}}{2}\right)}^3·{\rho }_{\mathrm{stone}}·v_{\mathrm{avg}.}}{t_{\mathrm{strike}}}\hfill \end{array}$$

(4)

If this typical force value is divided by the maximum actual recorded pressure at a given HPB, this will result in the area over which a particle strike should become effective, which can further be reduced to a radius of effect.

$$A_{\mathrm{strike}}=\pi ·{r_{\mathrm{strike}}}^2=\frac{F_{\mathrm{typ}.}}{P_{\mathrm{rec}.}}$$

$$r_{\mathrm{strike}}=\sqrt{\frac{A_{\mathrm{strike}}}{\pi }}=\sqrt{\frac{\left(\frac{F_{\mathrm{typ}.}}{P_{\mathrm{rec}.}}\right)}{\pi }}$$

(5)

$$r_{\mathrm{strike}}=\sqrt{\frac{\frac{4}{3}·{\left(\frac{D_{50}}{2}\right)}^3·{\rho }_{\mathrm{stone}}·v_{\mathrm{avg}.}}{t_{\mathrm{strike}}·P_{\mathrm{rec}.}}}$$

(6)

For example, the testing used Stanag soil with a $D_{50}$ of 10 mm (extracted from Figure 1). For the HPB in test 34 at yy−50, the maximum recorded pressure was 353.7 $\mathrm{M}$$\mathrm{Pa}$ and the average wave speed at 50 mm radius was 1760.65 $\mathrm{m}$/$\mathrm{s}$. Therefore, the effective radius of this particular particle strike can be calculated as below:

$$\begin{array}{cc}\hfill r_{\mathrm{strike}}& =\sqrt{\frac{\frac{4}{3}·{\left(\frac{10\times {10}^{-3}}{2}\right)}^3·2700·1760.65}{25\times {10}^{-6}·353.7\times {10}^{-6}}}\hfill \\ \hfill & =0.0095 \mathrm{m}\hfill \\ \hfill & =9.5 \mathrm{m}\mathrm{m}\hfill \end{array}$$

The particle mass for this theoretical (spherical) $D_{50}$ particle would be:

$$\begin{array}{cc}\hfill m& =\frac{4}{3}·\pi ·{\left(\frac{D_{50}}{2}\right)}^3·{\rho }_{\mathrm{stone}}\hfill \\ \hfill & =\frac{4}{3}·\pi ·{\left(\frac{10\times {10}^{-3}}{2}\right)}^3·2700\hfill \\ \hfill & =1.4 \mathrm{g}\hfill \end{array}$$

The larger particles within the soil have much higher masses but are not representative of the soil as a whole because they are less likely to strike the HPBs due to their lower probability of occurrence. Some of these larger particles are pictured in Figure 13, with masses in the range from 9.70 g to 15.11 g. For reference, a spherical particle of diameter 20 mm has a mass of 11.3 g.

2.6. Application of Area-Limiting: Well-Graded Soil

To apply the area-limiting scheme to the pressure interpolation algorithm and, thus, garner a more accurate picture of the mechanisms occurring, a background-interpolated array was generated, onto which the discrete areas of an array inclusive of particle strikes would be superimposed.

This backgroundarray was generated by finding the time signature of the maximum pressure value at each HPB then removing a 25 μs section of data surrounding this from the signal, effectively removing the period of the particle strike. After performing this action on all 17 HPB signals, these were then interpolated using the original method to create a 3D pressure array.

This interpolation was also carried out on the unaltered data, inclusive of the particle strikes. The circular portions of this array (for the full time of the test), with the appropriate strike radii, were then applied to the background array to create an overall pressure array. This overall pressure array consists of data representing the standard wave of smaller particles expanding from the centre, with limited discrete pressure spikes from larger particle strikes (see Figure 14).

2.7. Application of Area-Limiting: Uniform Soil

This new area-limiting algorithm was experimentally applied to the data from uniform soil (LB) tests in order to gauge its effectiveness. As can be seen from Figure 15, this failed to improve the interpolation of the data as the soil response consists of a contiguous pressure wave of similar-sized particles without discrete particle strikes. This meant that the algorithm removed a large proportion of real data from the array and, therefore, it performed much more poorly than the original method of interpolation.

This mishandling of the data by the algorithm can be explained by calculating the radius of effect of an LB particle strike; thus, it can be seen that this is not an appropriate way to represent a pressure wave of uniform particles. For LB test 15 at the HPB at xx50, the D${}_{50}$ = 0.8 mm (from Figure 1), average wave speed at 50 mm radius was 769.8 $\mathrm{m}$/$\mathrm{s}$, and the maximum recorded pressure was 195.2 $\mathrm{M}$$\mathrm{Pa}$.

$$\begin{array}{cc}\hfill r_{\mathrm{strike}}& =\sqrt{\frac{\frac{4}{3}·{\left(\frac{0.8\times {10}^{-3}}{2}\right)}^3·2700·769.8}{25\times {10}^{-6}·195.2\times {10}^6}}\hfill \\ \hfill & =3.38\times {10}^{-4} \mathrm{m}\hfill \\ \hfill & =0.34 \mathrm{m}\mathrm{m}\hfill \end{array}$$

Constricting the pressure wave peak to only a 0.34 mm radius around each HPB results in the area-limited pressure array represented in Figure 15, which clearly ignores the actual progression of the wave, limiting it to just the background pressure wave from outside of the 25 μs period of ‘strike’.

Therefore, it was determined that this area-limiting process should only be applied to data from soils where the D${}_{50}$ particle size would result in a discrete impulse that forms a sizeable proportion of the global impulse experienced. A 1.4 g D${}_{50}$ Stanag particle, at a typical 1120 $\mathrm{m}$/$\mathrm{s}$ (from the 25 μs strike length established earlier), would (assuming particle plasticity) result in an impulse of 1.57 $\mathrm{N}$$\mathrm{s}$. For a D${}_{50}$ LB particle, with a mass of 0.00072 g, at 1120 $\mathrm{m}$/$\mathrm{s}$, the impulse would be 0.81 $\mathrm{m}$$\mathrm{N}$$\mathrm{s}$, nearly 2000 times less. Given that a global impulse of the magnitude of hundreds of Newton–Seconds is to be expected from this testing, a single typical-particle strike (not accounting for the interpolation causing this error to spread) in Stanag soil could represent a >1% portion of the result, whereas, in LB, this would represent <0.001% (indicating that loading has to occur as part of a contiguous wave in LB soil).

3. Results and Discussion

The results from the CoBL experimental setup, presented herein, correspond to an over-burden (OB) of 28 mm and a stand-off distance (SOD) of 140 mm. A 78g 3:1 cylinder of PE4 explosive was utilised, buried within either LB (a uniform sand with a moisture content of 25% and a bulk density of 1990 $\mathrm{k}\mathrm{g}$/$\mathrm{m}$${}^3$) or Stanag (a well-graded sandy gravel with a moisture content of 14% and a bulk density of 2220 $\mathrm{k}\mathrm{g}$/$\mathrm{m}$${}^3$) both of which were fully saturated. Full saturation was achieved using the method outlined in [13]. The Test IDs used correspond to those in [30] if numerical and are previously unpublished data if alphabetical. The interpolation was carried out with an element size of 5 mm to ensure consistency between tests. It was found that increasing the mesh resolution had a minimal effect on the results.

3.1. Wave-Expansion Velocity

In order to validate the analytical methodology described previously, the wave-expansion velocities found in this study (used to calculate an area-of-effect of a particle strike) were compared against the wave speeds corresponding to arrival time data from work by Ehrgott [41]. In this work, Ehrgott used 2.27 kg C4 charges, buried in different soils with 100 mm OB, and measured the TOA at gauges suspended 500 mm above the soil surface, at varied horizontal distances from the charge centre. This charge size is equivalent to three times the scale of the CoBL tests using Hopkinson–Cranz cube root scaling and, as such, extrapolating the wave speed, on an exponential trendline, to a 300 mm radius of the centre should provide indicative values of expected wave speeds for CoBL data at 100 mm (with CoBL-scaled OB of 33 mm and SO of 167 mm) see Appendix A.

As can be seen in

Table 1. Wave speeds calculated from TOA data from Ehrgott [41], extrapolated to 300 mm for equivalence with CoBL data.

Distance from Blast Centre (mm)	Wave Speed (m/s)
1060	Sandy Soil (Poorly Graded)	625	Silty Sand	606
705		754		793
537		895		1279
300 (Extrapolated)		1028		1672

, for a poorly graded sandy soil, or a silty sand, wave speeds in the range 1028–1672 $\mathrm{m}$/$\mathrm{s}$ are to be expected.

Table 2. Wave speeds calculated from CoBL TOA data.

Soil Type	Test ID	Avg. Wave Speed at 100 mm (m/s)
Stanag, Saturated	Test 34	788.7
	Test 35	657.2
	Test 36	834.5
	Test 37	700.7
	Test A	1050.4
	Test B	636.1
LB, Saturated	Test 15	601.6
	Test 16	523.7
	Test 17	694.2
	Test C	690.7
LB, 2.45% M.C.	Test 7	901.2
	Test 8	1197.3
	Test 9	1610.8
	Test 10	1154.2

displays the wave expansion velocities at 100 mm radius for each CoBL test, where a similar over-burden (at an equivalent scale) in saturated Stanag soil results in speeds in the range 636–1050 $\mathrm{m}$/$\mathrm{s}$ for a stand-off distance of 140 mm (compared with a 167 mm equivalent) and in saturated LB soil 523–694 $\mathrm{m}$/$\mathrm{s}$. These velocities are somewhat lower than those found by Ehrgott [41], likely a factor of a higher level of saturation causing increased soil throw volume due to a higher level of detonation product containment (reducing the expansion velocity). This is corroborated by a similar analysis of CoBL data from low-moisture-content (2.45%) LB resulting in velocities in the range 901–1611 $\mathrm{m}$/$\mathrm{s}$, which agrees much more closely with the range derived from Ehrgott [41].

3.2. CoBL Global Impulse

3.2.1. Full Plate Integration (No Area Limiting)

The global impulse, used as an integration of pressure in time, from a full-plate cubic interpolation between the HPBs, is displayed in

Table 3. Global impulse results without area limiting for 0.7 ms and 1.3 ms truncations of signals from CoBL. * Test 17 data show no difference between truncation times as it was only recorded up to 0.5 ms.

Soil Type	Test ID	Global Impulse (Ns)		Truncation Diff.
		0.7 ms Trunc.	1.3 ms Trunc.
Stanag, Saturated	Test 34	195.81	223.13	14%
	Test 35	182.00	209.84	15%
	Test 36	215.70	245.64	14%
	Test 37	199.33	227.73	14%
	Test A	172.04	188.49	10%
	Test B	222.62	262.40	18%
	Mean	211.48	245.47	16%
LB, Saturated	Test 15	147.09	151.00	3%
	Test 16	155.26	156.25	1%
	Test 17 *	150.46	150.46	0%
	Test C	159.90	180.01	13%
	Mean	153.18	159.43	4%

. The effects of the signal drift can be seen in the difference in the global impulses between the 0.7 ms and 1.3 ms signal truncation times. It can be seen that the Stanag results tend to increase with increased truncation time (due to a large net positive drift). On the other hand, the LB tests have much less of an increase (due to a much reduced net drift). This, if allowed to influence the results, would cause values from the Stanag tests to be inflated when compared to LB tests.

Considering the mean values of the impulse, it can be seen that the ratios of impulses for LB:Stanag is 1.00:1.29 for 0.7 ms truncation and 1.00:1.42 for 1.3 ms truncation (an effect of the higher positive drift), showing the possible effect of discrete particle strikes in skewing the interpolation, as it is expected that the saturated Stanag would have a lower value of impulse than saturated LB [17].

3.2.2. Area-Limiting Well-Graded Stanag

Application of the area-limiting process to the Stanag data results in the values of the global impulse displayed in

Table 4. Global impulse derived from integration of pressure over a 0.7 ms truncation time for an area-limited interpolation between HPBs (from CoBL).

Soil Type	Test ID	Global Impulse (Ns)
Stanag, Saturated	Test 34	125.58
	Test 35	131.59
	Test 36	152.49
	Test 37	132.57
	Test A	114.66
	Test B	152.45
	Mean	134.89

. These results are for a 0.7ms truncation of each of the tests, to reduce the influence of signal drift.

The mean value of global impulse, when this method has been applied, results in a ratio of impulse for LB:Stanag of 1.00:0.88, much closer to the 1.00:0.84 found in FFM testing by Rigby et al. [17].

3.3. Comparison to FFM

The global impulse results can be compared between CoBL and FFM experiments in order to validate the area-limiting method. If it is assumed that the LB total impulse results scale accurately, the ratio of I_CoBL:I_FFM from the mean LB values for each setup (1:40.53) can be used to derive an expected mean value of impulse for Stanag. For reference, geometric scaling alone, through projection of the FFM target plate to the CoBL SOD at the same Hopkinson–Cranz scale, results in a ratio of 1:30.07, however, this does not account for losses in the wave expansion through air. Utilising the LB-equivalency ratio results in an expected mean of 135.29 Ns for Stanag (only 0.3% more than the mean value of 134.89 Ns resulting from the area-limiting process). Given the number of assumptions made throughout this analysis, it is unfair to accept this accuracy as completely true, however, it is indicative that accounting for PSD is viable when analysing the spatial and temporal distributions of loading from buried charges. These assumptions require further investigation in the future. Each of the FFM test results, scaled by the 40.53 scale factor, are displayed in

Table 5. Global impulse data from FFM testing, with impulse values scaled by the LB-equivalency scale factor (40.53). Results marked with * are from [28], with other data previously unpublished.

Soil Type	Total Impulse (Ns)	CoBL-Scaled Impulse (Ns)
Stanag, Saturated	4972.71 *	122.68
	5571.85 *	137.47
	5619.14	138.63
	5370.20	132.49
	5143.27	126.89
	5434.96	134.09
	5858.34	144.53
	5899.26	145.54
Mean	5483.71	135.29
LB, Saturated	6298.68 *	155.40
	6202.10 *	153.02
	6125.52 *	151.13
Mean	6208.77	153.18

.

4. Conclusions

This study has built on existing techniques to understand the spatial and temporal distributions of loading from soils in explosive blasts. Improvements have been made to pressure signal processing, including the use of data smoothing, alongside an improved arrival-time-finding algorithm. Further, a proof-of-concept method of area-limiting pressure spikes from discrete particle strikes was established, validated against another experimental setup to achieve similitude between results. The CoBL data (at one-quarter scale) has been directly compared against FFM (at one-half scale), with the area-limiting approximation allowing for agreement in the total impulsive loading for both well-graded and uniform soils.

From this, it can be understood that the spatial distribution of loading is largely impacted by the effects of a blast in well-graded soil, with high pressure strikes occurring over limited regions on a target. This leads to a lower level of global impulse than previously derived (thus bringing data from the CoBL experiment in line with expectations from FFM). This engenders a new understanding that the particle size distribution of a soil has not only a global effect on loading but also a discrete localised effect when larger particles are present, resulting in major implications for the design of protective structures and materials due to the presence of ‘pockets’ of much higher pressure (and thus specific impulse) loading within the overall wave.