Simulation and Sensitivity Analysis for Various Geometries and Optimization of Solid Oxide Fuel Cells: A Review
Abstract
1. Introduction
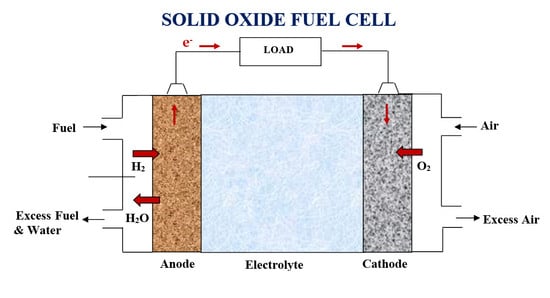
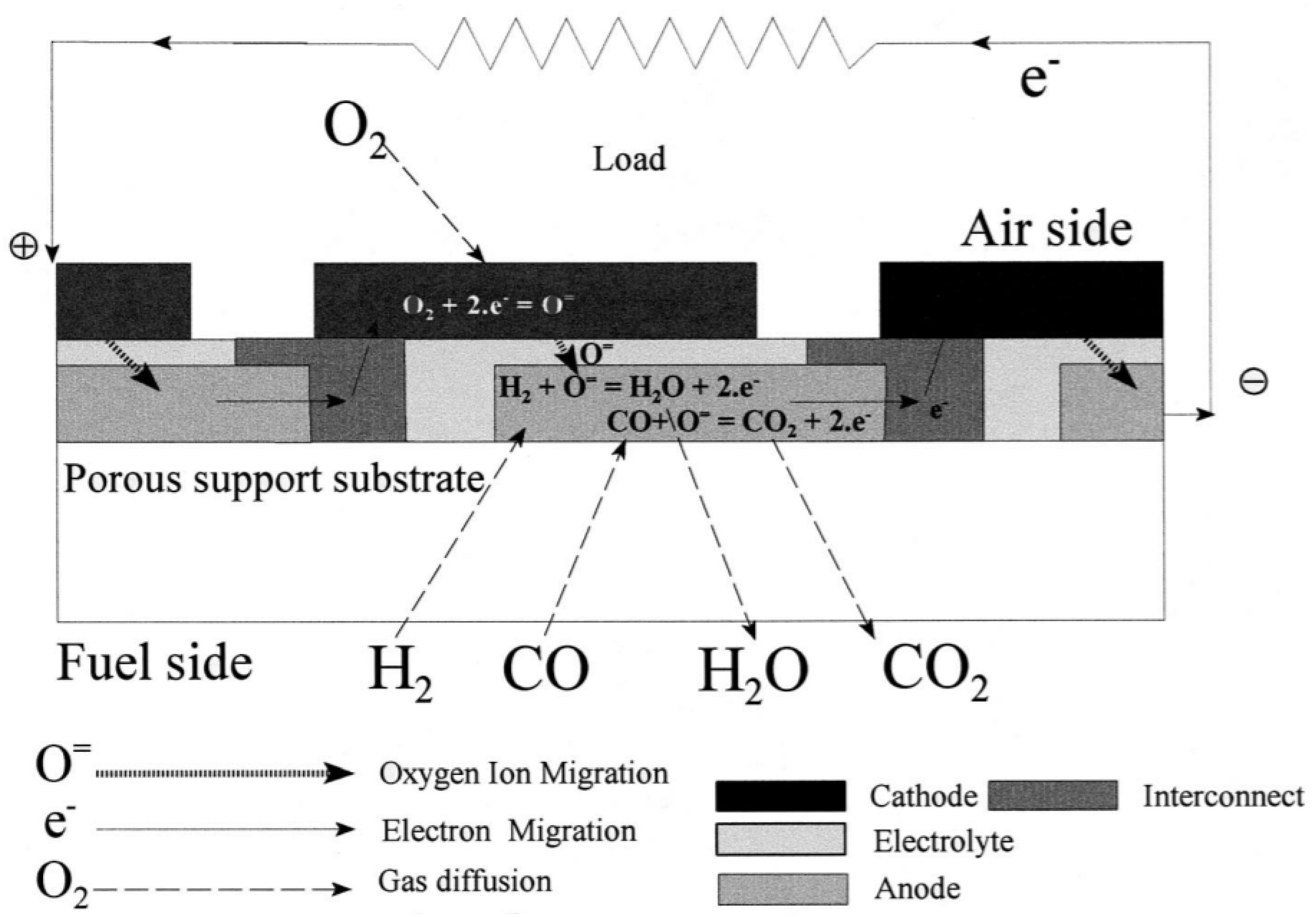
2. SOFC Configuration Design
2.1. SOFC Design
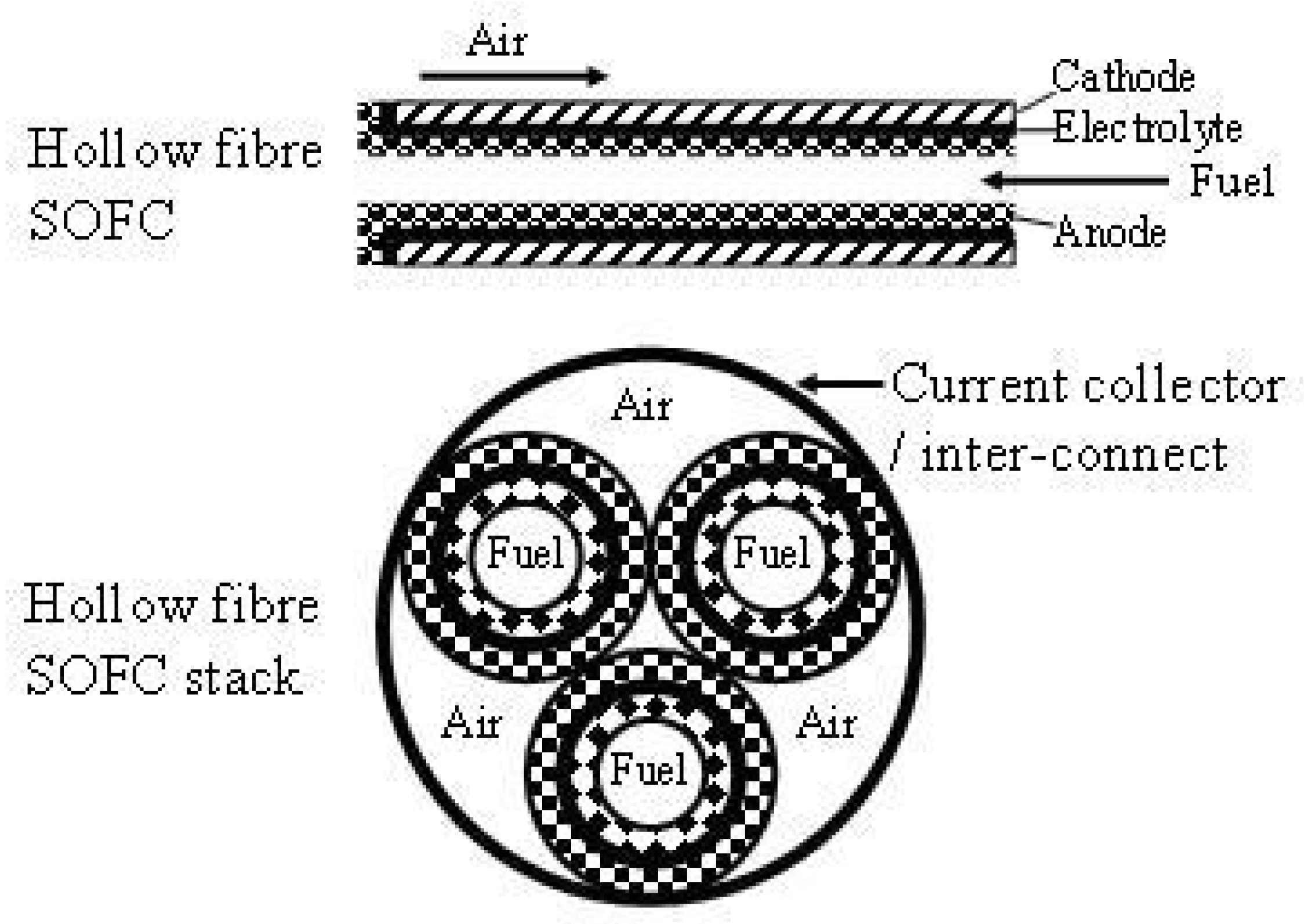
2.2. Micro SOFC
3. Computational Simulations of SOFC
4. Sensitivity Analysis
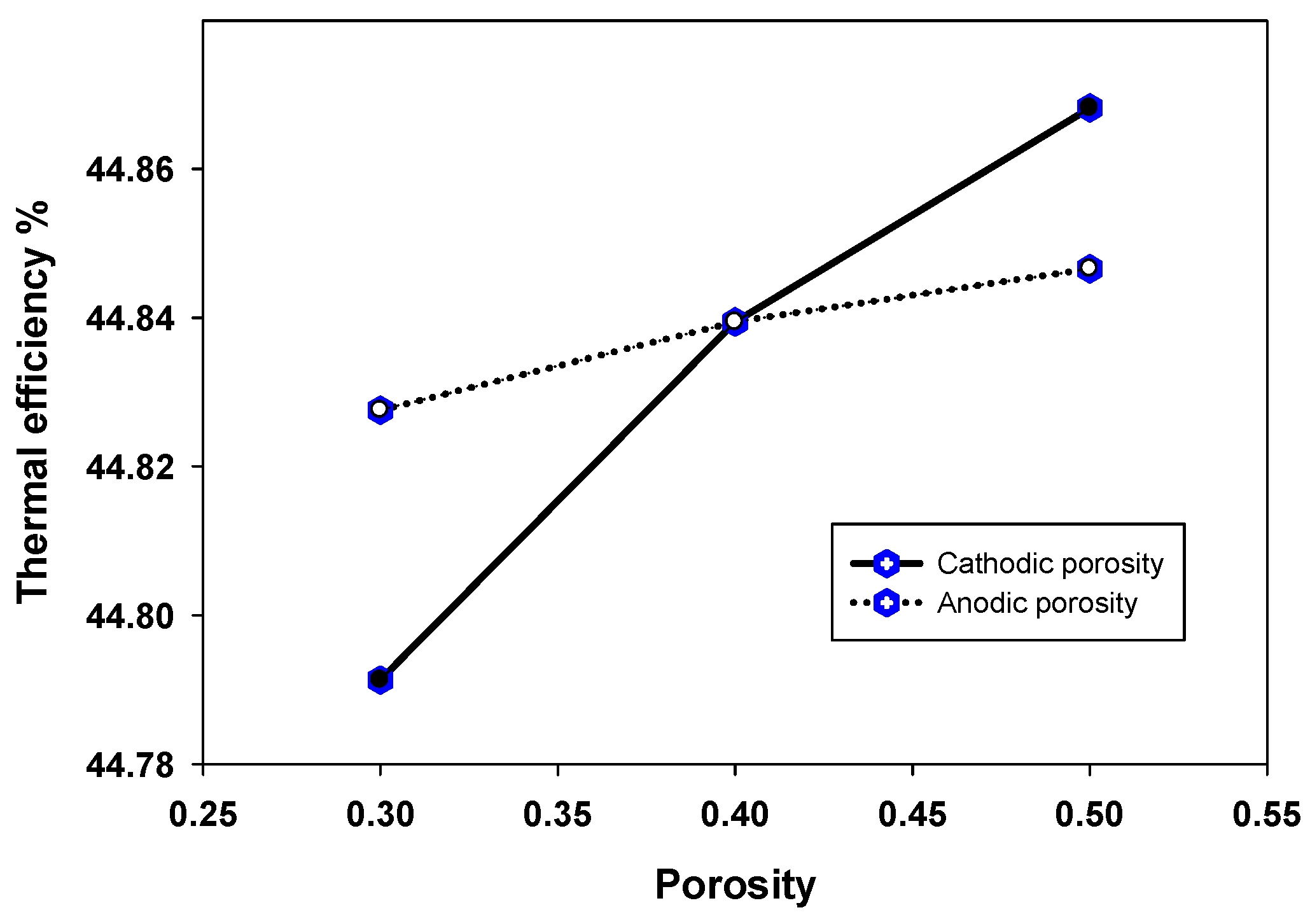
4.1. Sensitivity Analysis of Fuel Cell Design Parameters
4.2. Sensitivity Analysis of Flow Field
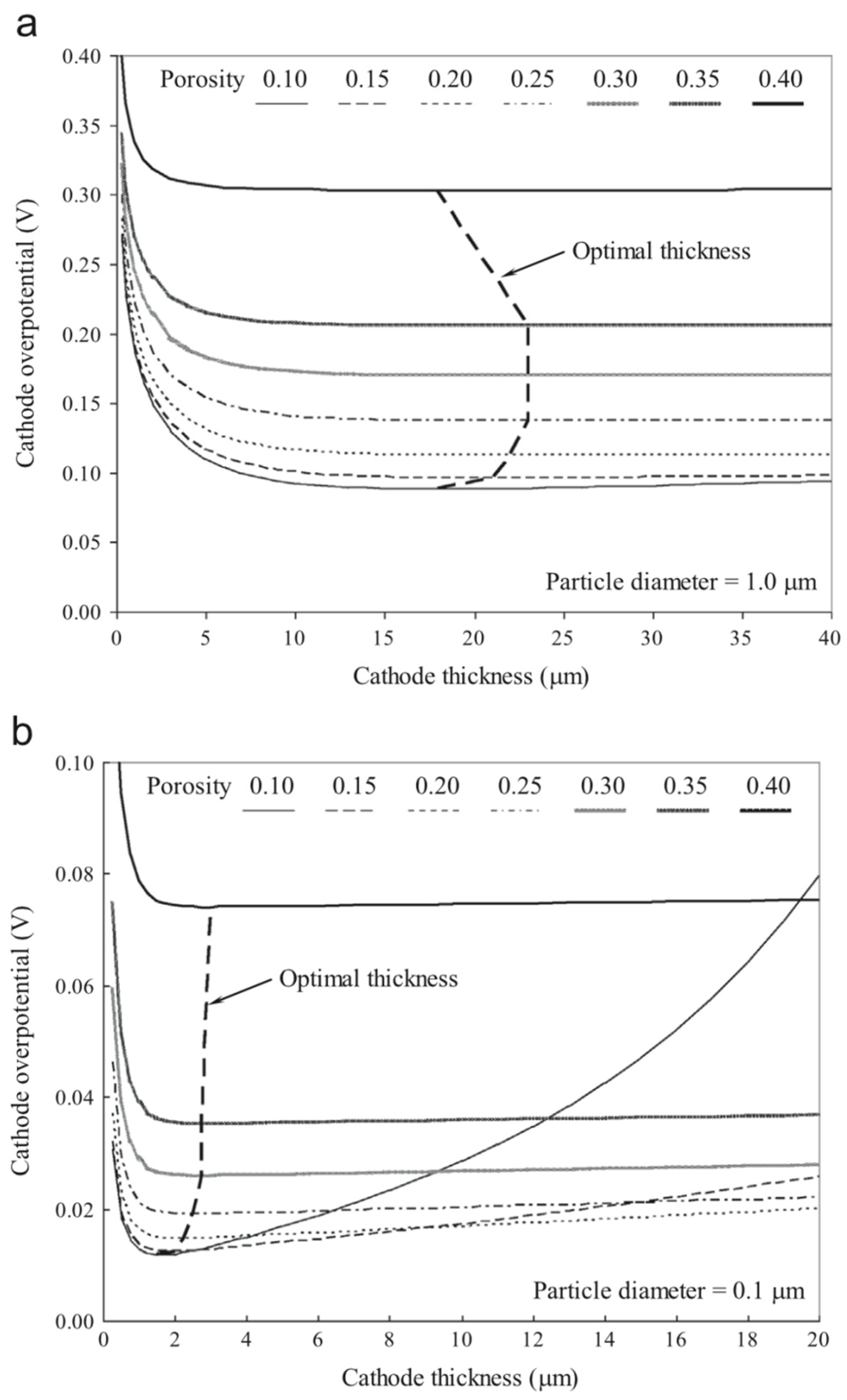
4.3. Sensitivity Analysis of Micro-Structures and Electrodes-Electrolyte Thicknesses for an Efficient Triple Phase Boundary (TPB)
4.4. Effect of Fuel Cell Temperature on the Cell Performance
- Increment in efficiency of thermodynamic conversion can be noted as the temperate for reformed gas (blend of H and CO) is decreased [83].
- The process of sealing gets intricate as the temperature is lowered [15].
- Loss of radiation heat is insignificant for a minute system when temperate is decreased. Therefore, management of heat is eased [20].
5. Optimization of SOFC Operational Parameters
6. Summary and Recommendation
- -
- SOFC materials and micro-structures were reviewed due to their significant impact on the simulation reliability as well as system optimization. A literature review has also been performed on simulation studies focused on the effects of microstructure and materials on fuel cell performance. However, most of the studies use only common SOFC materials in their modelling. More simulation studies are required to compare alternative materials in overall modelling to assess their effect on the efficiency and degradation of the cell. Electrochemical modelling that studies the cell voltage behaviour as a function of the microstructure, geometry and material properties is still under development.
- -
- In the literature, different techniques of SOFC simulations are available. In cell and stack level, 0-D, 1-D, 2-D and 3-D techniques may be chosen according to the purpose of the model. Transient modelling is used if any of the heat-up, start-up, shut-down and load changes or a combination of them requires simulation.
- -
- A critical analysis of available literature proved that detailed research on the simulation of thermal stress and damaging impact upon the SOFC is still in its early stage of development. In most of the presented works, the mechanical and thermal characteristics of the SOFC are represented comprehensively [140,144,146]. There is a lack of simulation reports, however, on the radiative heat transfer between the materials used in SOFCs at the high temperatures. In addition, the literature lacks sufficient information on the energy and exergy analyses of SOFC systems for performance evaluation.
- -
- In order to understand online control and optimization strategies accurately, an effective simulation of the fuel cell system plays a critical role. Therefore, sensitivity analysis of fuel cell parameters using simulation models was reviewed herein. In addition, micro-machined SOFCs are used for portable devices (many electronics and wireless). Hence, optimization and reliability of such devices require further research.
- -
- Combination of an MPS, a deep neural network and a genetic algorithm provides a promising solution for model-based control systems for precisely and quickly analyzing the performances of SOFCs and other non-linear systems. The deep learning algorithm needs to be trained based on experimental data for a wider application under dynamic operating conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Lanzini, A.; Halliop, W.; Cobas, V.; Verkooijen, A.; Aravind, P. Anode recirculation behavior of a solid oxide fuel cell system: A safety analysis and a performance optimization. Int. J. Hydrogen Energy 2013, 38, 2868–2883. [Google Scholar] [CrossRef]
- Aravind, P.; de Jong, W. Evaluation of high temperature gas cleaning options for biomass gasification product gas for solid oxide fuel cells. Prog. Energy Combust. Sci. 2012, 38, 737–764. [Google Scholar] [CrossRef]
- Baldinelli, A.; Barelli, L.; Bidini, G.; Di Michele, A.; Vivani, R. SOFC direct fuelling with high-methane gases: Optimal strategies for fuel dilution and upgrade to avoid quick degradation. Energy Convers. Manag. 2016, 124, 492–503. [Google Scholar] [CrossRef]
- Antonucci, V.; Branchini, L.; Brunaccini, G.; De Pascale, A.; Ferraro, M.; Melino, F.; Orlandini, V.; Sergi, F. Thermal integration of a SOFC power generator and a Na–NiCl2 battery for CHP domestic application. Appl. Energy 2017, 185, 1256–1267. [Google Scholar] [CrossRef]
- Mehr, A.S.; Gandiglio, M.; MosayebNezhad, M.; Lanzini, A.; Mahmoudi, S.M.S.; Yari, M.; Santarelli, M. Solar-assisted integrated biogas solid oxide fuel cell (SOFC) installation in wastewater treatment plant: Energy and economic analysis. Appl. Energy 2017, 191, 620–638. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Hussain, M.A.; Daud, W.M.A.W.; Soroush, M.; Shamiri, A. Mathematical modeling of solid oxide fuel cells: A review. Renew. Sustain. Energy Rev. 2011, 15, 1893–1917. [Google Scholar] [CrossRef]
- Huang, K.; Singhal, S.C. Cathode-supported tubular solid oxide fuel cell technology: A critical review. J. Power Sources 2013, 237, 84–97. [Google Scholar] [CrossRef]
- Bieberle-Hütter, A.; Beckel, D.; Infortuna, A.; Muecke, U.P.; Rupp, J.L.; Gauckler, L.J.; Rey-Mermet, S.; Muralt, P.; Bieri, N.R.; Hotz, N. A micro-solid oxide fuel cell system as battery replacement. J. Power Sources 2008, 177, 123–130. [Google Scholar] [CrossRef]
- Delphi, Fuel Cells Technology. Available online: http://www.delphi.com/manufacturers/auto/fuelcells (accessed on 11 December 2014).
- Topsoe Fuel Cell/Products/Fuel Cell. Available online: http://www.topsoefuelcell.com/sitecore/content/Haldor%20Topsoe/Press/News/2007/20070514%20Topsoe%20Fuel%20Cell%20wins%20Funding%20for%20SOFC%20Fuel%20Cell%20Development.aspx/ (accessed on 11 December 2014).
- Rolls-Royce, Power Systems Company. Available online: http://www.rollsroyce.com/energy/energy_products/fuel_cells/ (accessed on 11 December 2014).
- Acumentrics: Trusted Power Innovations. Available online: http://www.acumentrics.com/fuel-cell-generators.html (accessed on 11 December 2014).
- Shi, J.; Xue, X. CFD analysis of a novel symmetrical planar SOFC design with micro-flow channels. Chem. Eng. J. 2010, 163, 119–125. [Google Scholar] [CrossRef]
- Sammes, N.; Du, Y.; Bove, R. Design and fabrication of a 100 W anode supported micro-tubular SOFC stack. J. Power Sources 2005, 145, 428–434. [Google Scholar] [CrossRef]
- Yu, X.; Long, W.; Jin, F.; He, T. Cobalt-free perovskite cathode materials SrFe1−xTixO3−δ and performance optimization for intermediate-temperature solid oxide fuel cells. Electrochim. Acta 2014, 123, 426–434. [Google Scholar] [CrossRef]
- Wachsman, E.D.; Marlowe, C.A.; Lee, K.T. Role of solid oxide fuel cells in a balanced energy strategy. Energy Environ. Sci. 2012, 5, 5498–5509. [Google Scholar] [CrossRef]
- Pfeifer, T.; Nousch, L.; Lieftink, D.; Modena, S. System design and process layout for a SOFC micro-CHP unit with reduced operating temperatures. Int. J. Hydrogen Energy 2013, 38, 431–439. [Google Scholar] [CrossRef]
- Ding, J.; Liu, J.; Yin, G. Fabrication and characterization of low-temperature SOFC stack based on GDC electrolyte membrane. J. Membr. Sci. 2011, 371, 219–225. [Google Scholar] [CrossRef]
- Torknik, F.S.; Keyanpour-Rad, M.; Maghsoudipour, A.; Choi, G.M. Effect of microstructure refinement on performance of Ni/Ce0.8Gd0.2O1.9 anodes for low temperature solid oxide fuel cell. Ceram. Int. 2014, 40, 1341–1350. [Google Scholar] [CrossRef]
- Brett, D.J.; Atkinson, A.; Brandon, N.P.; Skinner, S.J. Intermediate temperature solid oxide fuel cells. Chem. Soc. Rev. 2008, 37, 1568–1578. [Google Scholar] [CrossRef]
- Grew, K.N.; Chiu, W.K. A review of modeling and simulation techniques across the length scales for the solid oxide fuel cell. J. Power Sources 2012, 199, 1–13. [Google Scholar] [CrossRef]
- Qu, Z.; Aravind, P.; Dekker, N.; Janssen, A.; Woudstra, N.; Verkooijen, A. Three-dimensional thermo-fluid and electrochemical modeling of anode-supported planar solid oxide fuel cell. J. Power Sources 2010, 195, 7787–7795. [Google Scholar] [CrossRef]
- Sanandaji, B.M.; Vincent, T.L.; Colclasure, A.M.; Kee, R.J. Modeling and control of tubular solid-oxide fuel cell systems: II. Nonlinear model reduction and model predictive control. J. Power Sources 2011, 196, 208–217. [Google Scholar] [CrossRef]
- Bavarian, M.; Soroush, M.; Kevrekidis, I.G.; Benziger, J.B. Mathematical modeling, steady-state and dynamic behavior, and control of fuel cells: A review. Ind. Eng. Chem. Res. 2010, 49, 7922–7950. [Google Scholar] [CrossRef]
- Hajimolana, S.; Hussain, M.; Soroush, M.; Wan Daud, W.A.; Chakrabarti, M.H. Multilinear-model predictive control of a tubular solid oxide fuel cell system. Ind. Eng. Chem. Res. 2012, 52, 430–441. [Google Scholar] [CrossRef]
- Ramadhani, F.; Hussain, M.A.; Mokhlis, H.; Hajimolana, S. Optimization strategies for Solid Oxide Fuel Cell (SOFC) application: A literature survey. Renew. Sustain. Energy Rev. 2017, 76, 460–484. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Moradpoor, I. Combined solid oxide fuel cell, micro-gas turbine and organic Rankine cycle for power generation (SOFC–MGT–ORC). Energy Convers. Manag. 2016, 116, 120–133. [Google Scholar] [CrossRef]
- D’Andrea, G.; Gandiglio, M.; Lanzini, A.; Santarelli, M. Dynamic model with experimental validation of a biogas-fed SOFC plant. Energy Convers. Manag. 2017, 135, 21–34. [Google Scholar] [CrossRef]
- Anyenya, G.A.; Sullivan, N.P.; Braun, R.J. Modeling and simulation of a novel 4.5 kWe multi-stack solid-oxide fuel cell prototype assembly for combined heat and power. Energy Convers. Manag. 2017, 140, 247–259. [Google Scholar] [CrossRef]
- Kang, S.; Ahn, K.-Y. Dynamic modeling of solid oxide fuel cell and engine hybrid system for distributed power generation. Appl. Energy 2017, 195, 1086–1099. [Google Scholar] [CrossRef]
- Ho, T.X.; Kosinski, P.; Hoffmann, A.C.; Vik, A. Modeling of transport, chemical and electrochemical phenomena in a cathode-supported SOFC. Chem. Eng. Sci. 2009, 64, 3000–3009. [Google Scholar] [CrossRef]
- Taher, M.A.; Adjiman, C.; Iora, P.; Chiesa, P.; Brandon, N. Model-Based Evaluation of the Production of Pure Oxygen through SOFC/SOEC Integration. ECS Trans. 2011, 35, 2997–3006. [Google Scholar] [CrossRef]
- Luebbe, H.; Hofmann, H.; Bowen, P.; Aschauer, U.; Schuler, A.; Snijkers, F.; Schindler, H.-J.; Vogt, U.; Lalanne, C. Cathode-supported micro-tubular SOFCs based on Nd1.95NiO4+δ: Fabrication and characterisation of dip-coated electrolyte layers. Solid State Ion. 2009, 180, 805–811. [Google Scholar] [CrossRef][Green Version]
- Singhal, S.C. Advances in solid oxide fuel cell technology. Solid State Ion. 2000, 135, 305–313. [Google Scholar] [CrossRef]
- Singhal, S.C. Solid oxide fuel cells for power generation. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 179–194. [Google Scholar] [CrossRef]
- Fuji, H. Status of National Project for SOFC Development in Japan. In Proceedings of the Solid Oxide Fuel Cells Meeting, Palm Springs, CA, USA, 18 November 2002. [Google Scholar]
- Fardadi, M.; McLarty, D.F.; Jabbari, F. Investigation of thermal control for different SOFC flow geometries. Appl. Energy 2016, 178, 43–55. [Google Scholar] [CrossRef]
- Li, A.; Song, C.; Lin, Z. A multiphysics fully coupled modeling tool for the design and operation analysis of planar solid oxide fuel cell stacks. Appl. Energy 2017, 190, 1234–1244. [Google Scholar] [CrossRef]
- Fujii, H.; Ninomiya, T. Status of National Project for SOFC Development in Japan. In Proceedings of the European Solid Oxide Fuel Cell Forum, Lucerne, Switzerland, 1–5 July 2002; Volume 2, pp. 700–707. [Google Scholar]
- Williams, M.C.; Strakey, J.P.; Singhal, S.C. US distributed generation fuel cell program. J. Power Sources 2004, 131, 79–85. [Google Scholar] [CrossRef]
- Godfrey, B.; Föger, K.; Gillespie, R.; Bolden, R.; Badwal, S. Planar solid oxide fuel cells: The Australian experience and outlook. J. Power Sources 2000, 86, 68–73. [Google Scholar] [CrossRef]
- Hwang, J.; Chen, C.O.-K.; Lai, D. Computational analysis of species transport and electrochemical characteristics of a MOLB-type SOFC. J. Power Sources 2005, 140, 235–242. [Google Scholar] [CrossRef]
- Suzuki, M. Residential Energy System Development, 1–3. Available online: http://www.gas.or.jp/en/newsletter/images/22/dl/pdf01.pdf (accessed on 11 December 2014).
- Murthy, S.; Fedorov, A.G. Radiation heat transfer analysis of the monolith type solid oxide fuel cell. J. Power Sources 2003, 124, 453–458. [Google Scholar] [CrossRef]
- Magistri, L.; Bozzolo, M.; Tarnowski, O.; Agnew, G.; Massardo, A.F. Design and Off-Design Analysis of a MW Hybrid System Based on Rolls-Royce Integrated Planar Solid Oxide Fuel Cells. J. Eng. Gas Turbines Power 2007, 129, 792–797. [Google Scholar] [CrossRef]
- Cable, T.L.; Sofie, S.W. A symmetrical, planar SOFC design for NASA’s high specific power density requirements. J. Power Sources 2007, 174, 221–227. [Google Scholar] [CrossRef]
- Gardner, F.J.; Day, M.; Brandon, N.; Pashley, M.; Cassidy, M. SOFC technology development at Rolls-Royce. J. Power Sources 2000, 86, 122–129. [Google Scholar] [CrossRef]
- Ceres Power, Fuel Cell Technology. Available online: http://www3.imperial.ac.uk/engineering/ourresearchhome/impactresearch/cerespower (accessed on 11 December 2014).
- Imperial Collage, Hallow Fibre Solid Oxide Fuel Cell. Available online: http://www3.imperial.ac.uk/electrochemicalengineering/research/currentprojects/tubularsolidoxidefuelcells (accessed on 11 December 2014).
- Nikbin, D. Micro SOFCs: Why small is beautiful. Fuel Cell Rev. 2006, 3, 21–24. [Google Scholar]
- Bieberle-Hutter, A.; Beckel, D.; Muecke, U.; Rupp, J.; Infortuna, A.; Gauckler, L. Micro-solid oxide fuel cells as battery replacement. Mst News 2005, 4, 12. [Google Scholar] [CrossRef]
- Huang, H.; Nakamura, M.; Su, P.; Fasching, R.; Saito, Y.; Prinz, F.B. High-performance ultrathin solid oxide fuel cells for low-temperature operation. J. Electrochem. Soc. 2007, 154, B20–B24. [Google Scholar] [CrossRef]
- Baertsch, C.D.; Jensen, K.F.; Hertz, J.L.; Tuller, H.L.; Vengallatore, S.T.; Spearing, S.M.; Schmidt, M.A. Fabrication and structural characterization of self-supporting electrolyte membranes for a micro solid-oxide fuel cell. J. Mater. Res. 2004, 19, 2604–2615. [Google Scholar] [CrossRef]
- Shao, Z.; Haile, S.M.; Ahn, J.; Ronney, P.D.; Zhan, Z.; Barnett, S.A. A thermally self-sustained micro solid-oxide fuel-cell stack with high power density. Nature 2005, 435, 795–798. [Google Scholar] [CrossRef] [PubMed]
- Hanna, J.; Lee, W.Y.; Shi, Y.; Ghoniem, A. Fundamentals of electro-and thermochemistry in the anode of solid-oxide fuel cells with hydrocarbon and syngas fuels. Prog. Energy Combust. Sci. 2014, 40, 74–111. [Google Scholar] [CrossRef]
- Qi, Y.; Huang, B.; Chuang, K.T. Dynamic modeling of solid oxide fuel cell: The effect of diffusion and inherent impedance. J. Power Sources 2005, 150, 32–47. [Google Scholar] [CrossRef]
- Sarkar, P.; Yamarte, L.; Johanson, L. Tubular micro-solid oxide fuel cell for remote power applications. ECS Trans. 2007, 7, 603–608. [Google Scholar] [CrossRef]
- Lockett, M.; Simmons, M.; Kendall, K. CFD to predict temperature profile for scale up of micro-tubular SOFC stacks. J. Power Sources 2004, 131, 243–246. [Google Scholar] [CrossRef]
- Akhtar, N.; Decent, S.; Kendall, K. Numerical modelling of methane-powered micro-tubular, single-chamber solid oxide fuel cell. J. Power Sources 2010, 195, 7796–7807. [Google Scholar] [CrossRef]
- Alyousef, Y.; Kendall, K. Characterization of the electrochemical performance of micro-tubular solid oxide fuel cell (SOFC). J. Taibah Univ. Sci. 2009, 2, 14–21. [Google Scholar] [CrossRef]
- Cui, D.; Liu, L.; Dong, Y.; Cheng, M. Comparison of different current collecting modes of anode supported micro-tubular SOFC through mathematical modeling. J. Power Sources 2007, 174, 246–254. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Soroush, M. Dynamics and control of a tubular solid-oxide fuel cell. Ind. Eng. Chem. Res. 2009, 48, 6112–6125. [Google Scholar] [CrossRef]
- Akhtar, N. Micro-tubular, single-chamber solid oxide fuel cell (MT–SC-SOFC) stacks: Model development. Chem. Eng. Res. Des. 2012, 90, 814–824. [Google Scholar] [CrossRef]
- Panthi, D.; Tsutsumi, A. Development of a high-performance micro-tubular SOFC based on a hollow fiber support. ECS Trans. 2013, 57, 789–798. [Google Scholar] [CrossRef]
- Serincan, M.F.; Pasaogullari, U.; Sammes, N.M. Effects of operating conditions on the performance of a micro-tubular solid oxide fuel cell (SOFC). J. Power Sources 2009, 192, 414–422. [Google Scholar] [CrossRef]
- Cordiner, S.; Mariani, A.; Mulone, V. An integrated CFD-approch to deisgn micro-tubular Solid Oxide Fuel Cells. In Proceedings of the 2008 Second International Conference on Thermal Issues in Emerging Technologies, Cairo, Egypt, 17–20 December 2008; pp. 85–96. [Google Scholar]
- Cordiner, S.; Mariani, A.; Mulone, V. CFD-based design of microtubular solid oxide fuel cells. J. Heat Transf. 2010, 132, 062801. [Google Scholar] [CrossRef]
- Razbani, O.; Wærnhus, I.; Assadi, M. Experimental investigation of temperature distribution over a planar solid oxide fuel cell. Appl. Energy 2013, 105, 155–160. [Google Scholar] [CrossRef]
- Santangelo, P.E.; Tartarini, P. Fuel cell systems and traditional technologies. Part I: Experimental CHP approach. Appl. Therm. Eng. 2007, 27, 1278–1284. [Google Scholar] [CrossRef]
- Santarelli, M.; Leone, P.; Calì, M.; Orsello, G. Experimental evaluation of the sensitivity to fuel utilization and air management on a 100 kW SOFC system. J. Power Sources 2007, 171, 155–168. [Google Scholar] [CrossRef]
- Andersson, M.; Yuan, J.; Sundén, B. SOFC modeling considering electrochemical reactions at the active three phase boundaries. Int. J. Heat Mass Transf. 2012, 55, 773–788. [Google Scholar] [CrossRef]
- Akbari, V.; Borhani, T.N.G.; Shamiri, A.; Aramesh, R.; Hussain, M.A.; Hamid, M.K.A. 2D CFD-PBM simulation of hydrodynamic and particle growth in an industrial gas phase fluidized bed polymerization reactor. Chem. Eng. Res. Des. 2015, 104, 53–67. [Google Scholar] [CrossRef]
- Abbasi, M.R.; Shamiri, A.; Hussain, M.A. Dynamic modeling and Molecular Weight Distribution of ethylene copolymerization in an industrial gas-phase Fluidized-Bed Reactor. Adv. Powder Technol. 2016, 27, 1526–1538. [Google Scholar] [CrossRef]
- Abbasi, M.R.; Shamiri, A.; Hussain, M.A. A review on modeling and control of olefin polymerization in fluidized-bed reactors. Rev. Chem. Eng. 2019, 35, 311–333. [Google Scholar] [CrossRef]
- Akbari, V.; Borhani, T.N.G.; Shamiri, A.; Hamid, M.K.B. A CFD–PBM coupled model of hydrodynamics and mixing/segregation in an industrial gas-phase polymerization reactor. Chem. Eng. Res. Des. 2015, 96, 103–120. [Google Scholar] [CrossRef]
- Al-Dabbagh, A.W.; Lu, L.; Mazza, A. Modelling, simulation and control of a proton exchange membrane fuel cell (PEMFC) power system. Int. J. Hydrogen Energy 2010, 35, 5061–5069. [Google Scholar] [CrossRef]
- Arpino, F.; Massarotti, N. Numerical simulation of mass and energy transport phenomena in solid oxide fuel cells. Energy 2009, 34, 2033–2041. [Google Scholar] [CrossRef]
- Arteaga-Perez, L.E.; Casas, Y.; Peralta, L.M.; Kafarov, V.; Dewulf, J.; Giunta, P. An auto-sustainable solid oxide fuel cell system fueled by bio-ethanol: Process simulation and heat exchanger network synthesis. Chem. Eng. J. 2009, 150, 242–251. [Google Scholar] [CrossRef]
- Autissier, N.; Larrain, D.; Favrat, D. CFD simulation tool for solid oxide fuel cells. J. Power Sources 2004, 131, 313–319. [Google Scholar] [CrossRef]
- Calise, F.; d’Accadia, M.D.; Palombo, A.; Vanoli, L. Simulation and exergy analysis of a hybrid solid oxide fuel cell (SOFC)–gas turbine system. Energy 2006, 31, 3278–3299. [Google Scholar] [CrossRef]
- Colombo, K.W.E.; Kharton, V.V.; Berto, F.; Paltrinieri, N. Mathematical modeling and simulation of hydrogen-fueled solid oxide fuel cell system for micro-grid applications—Effect of failure and degradation on transient performance. Energy 2020, 202, 117752. [Google Scholar] [CrossRef]
- Xu, H.; Ma, J.; Tan, P.; Chen, B.; Wu, Z.; Zhang, Y.; Wang, H.; Xuan, J.; Ni, M. Towards online optimisation of solid oxide fuel cell performance: Combining deep learning with multi-physics simulation. Energy AI 2020, 1, 100003. [Google Scholar] [CrossRef]
- Qi, Y.; Huang, B.; Luo, J. Dynamic modeling of a finite volume of solid oxide fuel cell: The effect of transport dynamics. Chem. Eng. Sci. 2006, 61, 6057–6076. [Google Scholar] [CrossRef]
- Karcz, M. From 0D to 1D modeling of tubular solid oxide fuel cell. Energy Convers. Manag. 2009, 50, 2307–2315. [Google Scholar] [CrossRef]
- Ota, T.; Koyama, M.; Wen, C.-J.; Yamada, K.; Takahashi, H. Object-based modeling of SOFC system: Dynamic behavior of micro-tube SOFC. J. Power Sources 2003, 118, 430–439. [Google Scholar] [CrossRef]
- Bove, R.; Ubertini, S. Modeling solid oxide fuel cell operation: Approaches, techniques and results. J. Power Sources 2006, 159, 543–559. [Google Scholar] [CrossRef]
- Oh, S.-R.; Sun, J.; Dobbs, H.; King, J. Model-based predictive control strategy for a solid oxide fuel cell system integrated with a turbocharger. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 6596–6601. [Google Scholar]
- Achenbach, E. Three-dimensional and time-dependent simulation of a planar solid oxide fuel cell stack. J. Power Sources 1994, 49, 333–348. [Google Scholar] [CrossRef]
- Recknagle, K.P.; Williford, R.E.; Chick, L.A.; Rector, D.R.; Khaleel, M.A. Three-dimensional thermo-fluid electrochemical modeling of planar SOFC stacks. J. Power Sources 2003, 113, 109–114. [Google Scholar] [CrossRef]
- Kapadia, S.; Anderson, W. Sensitivity analysis for solid oxide fuel cells using a three-dimensional numerical model. J. Power Sources 2009, 189, 1074–1082. [Google Scholar] [CrossRef]
- Horr, S.; Mohcene, H.; Bouguettaia, H.; Moussa, H.B. Performance analysis of AS-SOFC fuel cell combining single and sinusoidal flow field: Numerical study. Renew. Energy Environ. Sustain. 2021, 6, 18. [Google Scholar] [CrossRef]
- Hajimolana, S.; Hussain, M.; Daud, W.W.; Chakrabarti, M. Dynamic modelling and sensitivity analysis of a tubular SOFC fuelled with NH 3 as a possible replacement for H 2. Chem. Eng. Res. Des. 2012, 90, 1871–1882. [Google Scholar] [CrossRef]
- Kakac, S.; Pramuanjaroenkij, A.; Zhou, X.Y. A review of numerical modeling of solid oxide fuel cells. Int. J. Hydrogen Energy 2007, 32, 761–786. [Google Scholar] [CrossRef]
- Jiang, W.; Fang, R.; Khan, J.A.; Dougal, R.A. Parameter setting and analysis of a dynamic tubular SOFC model. J. Power Sources 2006, 162, 316–326. [Google Scholar] [CrossRef]
- Calise, F.; d’Accadia, M.D.; Vanoli, L.; von Spakovsky, M.R. Full load synthesis/design optimization of a hybrid SOFC–GT power plant. Energy 2007, 32, 446–458. [Google Scholar] [CrossRef]
- Yakabe, H.; Hishinuma, M.; Uratani, M.; Matsuzaki, Y.; Yasuda, I. Evaluation and modeling of performance of anode-supported solid oxide fuel cell. J. Power Sources 2000, 86, 423–431. [Google Scholar] [CrossRef]
- Weil, K.S.; Koeppel, B.J. Comparative finite element analysis of the stress–strain states in three different bonded solid oxide fuel cell seal designs. J. Power Sources 2008, 180, 343–353. [Google Scholar] [CrossRef]
- Chiang, L.-K.; Liu, H.-C.; Shiu, Y.-H.; Lee, C.-H.; Lee, R.-Y. Thermo-electrochemical and thermal stress analysis for an anode-supported SOFC cell. Renew. Energy 2008, 33, 2580–2588. [Google Scholar] [CrossRef]
- Dang, Z.; Shen, X.; Ma, J.; Jiang, Z.; Xi, G. Multiphysics Coupling Simulation and Parameter Study of Planar Solid Oxide Fuel Cell. Front. Chem. 2021, 8, 1–11. [Google Scholar] [CrossRef]
- Wei, S.-S.; Wang, T.-H.; Wu, J.-S. Numerical modeling of interconnect flow channel design and thermal stress analysis of a planar anode-supported solid oxide fuel cell stack. Energy 2014, 69, 553–561. [Google Scholar] [CrossRef]
- Lin, Y.; Beale, S. Performance predictions in solid oxide fuel cells. Appl. Math. Model. 2006, 30, 1485–1496. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Rengaswamy, R. Dimensional optimization of a tubular solid oxide fuel cell. Comput. Chem. Eng. 2010, 34, 1789–1802. [Google Scholar] [CrossRef]
- Laurencin, J.; Delette, G.; Lefebvre-Joud, F.; Dupeux, M. A numerical tool to estimate SOFC mechanical degradation: Case of the planar cell configuration. J. Eur. Ceram. Soc. 2008, 28, 1857–1869. [Google Scholar] [CrossRef]
- Ji, Y.; Yuan, K.; Chung, J.; Chen, Y.-C. Effects of transport scale on heat/mass transfer and performance optimization for solid oxide fuel cells. J. Power Sources 2006, 161, 380–391. [Google Scholar] [CrossRef]
- Lu, Y.; Schaefer, L. Numerical study of a flat-tube high power density solid oxide fuel cell: Part II: Cell performance and stack optimization. J. Power Sources 2006, 153, 68–75. [Google Scholar] [CrossRef]
- Recknagle, K.P.; Ryan, E.M.; Koeppel, B.J.; Mahoney, L.A.; Khaleel, M.A. Modeling of electrochemistry and steam–methane reforming performance for simulating pressurized solid oxide fuel cell stacks. J. Power Sources 2010, 195, 6637–6644. [Google Scholar] [CrossRef]
- Huang, C.; Shy, S.; Lee, C. On flow uniformity in various interconnects and its influence to cell performance of planar SOFC. J. Power Sources 2008, 183, 205–213. [Google Scholar] [CrossRef]
- Huang, C.; Shy, S.; Li, H.; Lee, C. The impact of flow distributors on the performance of planar solid oxide fuel cell. J. Power Sources 2010, 195, 6280–6286. [Google Scholar] [CrossRef]
- Yuan, P.; Liu, S.-F. Numerical analysis of temperature and current density distribution of a planar solid oxide fuel cell unit with nonuniform inlet flow. Numer. Heat Transf. Part A Appl. 2007, 51, 941–957. [Google Scholar] [CrossRef]
- Christman, K.L.; Jensen, M.K. Solid Oxide Fuel Cell Performance With Cross-Flow Roughness. J. Fuel Cell Sci. Technol. 2010, 8, 024501–024505. [Google Scholar] [CrossRef]
- Mehrpooya, M.; Akbarpour, S.; Vatani, A.; Rosen, M.A. Modeling and optimum design of hybrid solid oxide fuel cell-gas turbine power plants. Int. J. Hydrogen Energy 2014, 39, 21196–21214. [Google Scholar] [CrossRef]
- Fardadi, M.; McLarty, D.F.; Brouwer, J.; Jabbari, F. Enhanced performance of counter flow SOFC with partial internal reformation. Int. J. Hydrogen Energy 2014, 39, 19753–19766. [Google Scholar] [CrossRef]
- Costamagna, P.; Selimovic, A.; Del Borghi, M.; Agnew, G. Electrochemical model of the integrated planar solid oxide fuel cell (IP-SOFC). Chem. Eng. J. 2004, 102, 61–69. [Google Scholar] [CrossRef]
- Cai, Q.; Adjiman, C.S.; Brandon, N.P. Modelling the 3D microstructure and performance of solid oxide fuel cell electrodes: Computational parameters. Electrochim. Acta 2011, 56, 5804–5814. [Google Scholar] [CrossRef]
- Haanappel, V.; Mertens, J.; Rutenbeck, D.; Tropartz, C.; Herzhof, W.; Sebold, D.; Tietz, F. Optimisation of processing and microstructural parameters of LSM cathodes to improve the electrochemical performance of anode-supported SOFCs. J. Power Sources 2005, 141, 216–226. [Google Scholar] [CrossRef]
- Patcharavorachot, Y.; Arpornwichanop, A.; Chuachuensuk, A. Electrochemical study of a planar solid oxide fuel cell: Role of support structures. J. Power Sources 2008, 177, 254–261. [Google Scholar] [CrossRef]
- Andersson, M.; Yuan, J.; Sundén, B. SOFC modeling considering hydrogen and carbon monoxide as electrochemical reactants. J. Power Sources 2013, 232, 42–54. [Google Scholar] [CrossRef]
- Ferguson, J.; Fiard, J.; Herbin, R. Three-dimensional numerical simulation for various geometries of solid oxide fuel cells. J. Power Sources 1996, 58, 109–122. [Google Scholar] [CrossRef]
- Jia, J.; Abudula, A.; Wei, L.; Jiang, R.; Shen, S. A mathematical model of a tubular solid oxide fuel cell with specified combustion zone. J. Power Sources 2007, 171, 696–705. [Google Scholar] [CrossRef]
- Hussain, M.; Li, X.; Dincer, I. Mathematical modeling of planar solid oxide fuel cells. J. Power Sources 2006, 161, 1012–1022. [Google Scholar] [CrossRef]
- Tanaka, T.; Inui, Y.; Urata, A.; Kanno, T. Three dimensional analysis of planar solid oxide fuel cell stack considering radiation. Energy Convers. Manag. 2007, 48, 1491–1498. [Google Scholar] [CrossRef]
- Chaisantikulwat, A.; Diaz-Goano, C.; Meadows, E. Dynamic modelling and control of planar anode-supported solid oxide fuel cell. Comput. Chem. Eng. 2008, 32, 2365–2381. [Google Scholar] [CrossRef]
- Chen, X.; Wu, N.; Smith, L.; Ignatiev, A. Thin-film heterostructure solid oxide fuel cells. Appl. Phys. Lett. 2004, 84, 2700–2702. [Google Scholar] [CrossRef]
- Gorman, B.P.; Anderson, H.U. Processing of composite thin film solid oxide fuel cell structures. J. Am. Ceram. Soc. 2005, 88, 1747–1753. [Google Scholar] [CrossRef]
- Tang, Y.; Stanley, K.; Wu, J.; Ghosh, D.; Zhang, J. Design consideration of micro thin film solid-oxide fuel cells. J. Micromech. Microeng. 2005, 15, S185. [Google Scholar] [CrossRef]
- Bertei, A.; Nucci, B.; Nicolella, C. Microstructural modeling for prediction of transport properties and electrochemical performance in SOFC composite electrodes. Chem. Eng. Sci. 2013, 101, 175–190. [Google Scholar] [CrossRef]
- Nikooyeh, K.; Jeje, A.A.; Hill, J.M. 3D modeling of anode-supported planar SOFC with internal reforming of methane. J. Power Sources 2007, 171, 601–609. [Google Scholar] [CrossRef]
- Haberman, B.; Young, J. Diffusion and chemical reaction in the porous structures of solid oxide fuel cells. J. Fuel Cell Sci. Technol. 2006, 3, 312–321. [Google Scholar] [CrossRef]
- Iora, P.; Aguiar, P.; Adjiman, C.; Brandon, N. Comparison of two IT DIR-SOFC models: Impact of variable thermodynamic, physical, and flow properties. Steady-state and dynamic analysis. Chem. Eng. Sci. 2005, 60, 2963–2975. [Google Scholar] [CrossRef]
- Damm, D.L.; Fedorov, A.G. Reduced-order transient thermal modeling for SOFC heating and cooling. J. Power Sources 2006, 159, 956–967. [Google Scholar] [CrossRef]
- Li, J.; Kang, Y.-w.; Cao, G.-y.; Zhu, X.-J.; Tu, H.-Y.; Li, J. Numerical simulation of a direct internal reforming solid oxide fuel cell using computational fluid dynamics method. J. Zhejiang Univ. Sci. A 2008, 9, 961–969. [Google Scholar] [CrossRef]
- Yuan, J.; Rokni, M.; Sundén, B. Three-dimensional computational analysis of gas and heat transport phenomena in ducts relevant for anode-supported solid oxide fuel cells. Int. J. Heat Mass Transf. 2003, 46, 809–821. [Google Scholar] [CrossRef]
- Dusastre, V.; Kilner, J. Optimisation of composite cathodes for intermediate temperature SOFC applications. Solid State Ion. 1999, 126, 163–174. [Google Scholar] [CrossRef]
- Bailly, N.; Georges, S.; Djurado, E. Elaboration and electrical characterization of electrosprayed YSZ thin films for intermediate temperature-solid oxide fuel cells (IT-SOFC). Solid State Ion. 2012, 222, 1–7. [Google Scholar] [CrossRef]
- Jing, Y.; Patakangas, J.; Lund, P.D.; Zhu, B. An improved synthesis method of ceria-carbonate based composite electrolytes for low-temperature SOFC fuel cells. Int. J. Hydrogen Energy 2013, 38, 16532–16538. [Google Scholar] [CrossRef]
- Khaerudini, D.S.; Guan, G.; Zhang, P.; Hao, X.; Kasai, Y.; Kusakabe, K.; Abudula, A. Structural and conductivity characteristics of Bi4MgxV2−xO11−δ (0⩽ x⩽ 0.3) as solid electrolyte for intermediate temperature SOFC application. J. Alloys Compd. 2014, 589, 29–36. [Google Scholar] [CrossRef]
- Yang, C.; Ren, C.; Yu, L.; Jin, C. High performance intermediate temperature micro-tubular SOFCs with Ba0.9Co0.7Fe0.2Nb0.1O3−δ as cathode. Int. J. Hydrogen Energy 2013, 38, 15348–15353. [Google Scholar] [CrossRef]
- Xia, C.; Liu, M. Low-temperature SOFCs based on Gd0.1Ce0.9O1.95 fabricated by dry pressing. Solid State Ion. 2001, 144, 249–255. [Google Scholar] [CrossRef]
- Amiri, S.; Hayes, R.; Nandakumar, K.; Sarkar, P. Modelling heat transfer for a tubular micro-solid oxide fuel cell with experimental validation. J. Power Sources 2013, 233, 190–201. [Google Scholar] [CrossRef]
- Cui, D.; Cheng, M. Thermal stress modeling of anode supported micro-tubular solid oxide fuel cell. J. Power Sources 2009, 192, 400–407. [Google Scholar] [CrossRef]
- Fan, P.; Li, G.; Zeng, Y.; Zhang, X. Numerical study on thermal stresses of a planar solid oxide fuel cell. Int. J. Therm. Sci. 2014, 77, 1–10. [Google Scholar] [CrossRef]
- Chiang, L.-K.; Liu, H.-C.; Shiu, Y.-H.; Lee, C.-H.; Lee, R.-Y. Thermal stress and thermo-electrochemical analysis of a planar anode-supported solid oxide fuel cell: Effects of anode porosity. J. Power Sources 2010, 195, 1895–1904. [Google Scholar] [CrossRef]
- Jiang, L.; Wei, T.; Zeng, R.; Zhang, W.-X.; Huang, Y.-H. Thermal and electrochemical properties of PrBa0.5Sr0.5Co2−xFexO5+δ (x = 0.5, 1.0, 1.5) cathode materials for solid-oxide fuel cells. J. Power Sources 2013, 232, 279–285. [Google Scholar] [CrossRef]
- Lin, C.-K.; Chen, T.-T.; Chyou, Y.-P.; Chiang, L.-K. Thermal stress analysis of a planar SOFC stack. J. Power Sources 2007, 164, 238–251. [Google Scholar] [CrossRef]
- Bujalski, W.; Paragreen, J.; Reade, G.; Pyke, S.; Kendall, K. Cycling studies of solid oxide fuel cells. J. Power Sources 2006, 157, 745–749. [Google Scholar] [CrossRef]
- Nakajo, A.; Stiller, C.; Härkegård, G.; Bolland, O. Modeling of thermal stresses and probability of survival of tubular SOFC. J. Power Sources 2006, 158, 287–294. [Google Scholar] [CrossRef]
- Sarmah, P.; Gogoi, T.K. Performance comparison of SOFC integrated combined power systems with three different bottoming steam turbine cycles. Energy Convers. Manag. 2017, 132, 91–101. [Google Scholar] [CrossRef]
- Deseure, J.; Bultel, Y.; Dessemond, L.; Siebert, E. Theoretical optimisation of a SOFC composite cathode. Electrochim. Acta 2005, 50, 2037–2046. [Google Scholar] [CrossRef]
- Costamagna, P.; Costa, P.; Arato, E. Some more considerations on the optimization of cermet solid oxide fuel cell electrodes. Electrochim. Acta 1998, 43, 967–972. [Google Scholar] [CrossRef]
- Calise, F.; d’Accadia, M.D.; Vanoli, L.; Von Spakovsky, M. Single-level optimization of a hybrid SOFC–GT power plant. J. Power Sources 2006, 159, 1169–1185. [Google Scholar] [CrossRef]
- Chachuat, B.; Mitsos, A.; Barton, P.I. Optimal design and steady-state operation of micro power generation employing fuel cells. Chem. Eng. Sci. 2005, 60, 4535–4556. [Google Scholar] [CrossRef]
- Baratto, F.; Diwekar, U.M. Multi-objective trade-offs for fuel cell-based auxiliary power units: Case study of South California Air Basin. J. Power Sources 2005, 139, 197–204. [Google Scholar] [CrossRef]
- Song, X.; Diaz, A.; Benard, A.; Nicholas, J. A 2D model for shape optimization of solid oxide fuel cell cathodes. Struct. Multidiscip. Optim. 2013, 47, 453–464. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Static and dynamic modeling of solid oxide fuel cell using genetic programming. Energy 2009, 34, 740–751. [Google Scholar] [CrossRef]
- Facchinetti, E.; Gassner, M.; D’Amelio, M.; Marechal, F.; Favrat, D. Process integration and optimization of a solid oxide fuel cell–Gas turbine hybrid cycle fueled with hydrothermally gasified waste biomass. Energy 2012, 41, 408–419. [Google Scholar] [CrossRef]
- Yi, Y.; Rao, A.D.; Brouwer, J.; Samuelsen, G.S. Analysis and optimization of a solid oxide fuel cell and intercooled gas turbine (SOFC–ICGT) hybrid cycle. J. Power Sources 2004, 132, 77–85. [Google Scholar] [CrossRef]
- Sadeghi, S.; Ameri, M. Study the Combination of Photovoltaic Panels With Different Auxiliary Systems in Grid-Connected Condition. J. Sol. Energy Eng. 2014, 136, 041008. [Google Scholar] [CrossRef]
- Quddus, M.R.; Zhang, Y.; Ray, A.K. Multi-objective optimization in solid oxide fuel cell for oxidative coupling of methane. Chem. Eng. J. 2010, 165, 639–648. [Google Scholar] [CrossRef]
- Palazzi, F.; Autissier, N.; Marechal, F.M.; Favrat, D. A methodology for thermo-economic modeling and optimization of solid oxide fuel cell systems. Appl. Therm. Eng. 2007, 27, 2703–2712. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Jiang, J.H.; Jian, L.; Zhao, L.; Jiang, J.G.; Wu, X.G.; Xu, L.H. Parameter optimization for tubular solid oxide fuel cell stack based on the dynamic model and an improved genetic algorithm. Int. J. Hydrogen Energy 2011, 36, 6160–6174. [Google Scholar] [CrossRef]
- Wu, X.J.; Zhu, X.J. Optimization of a solid oxide fuel cell and micro gas turbine hybrid system. Int. J. Energy Res. 2013, 37, 242–249. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 2nd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Sciacovelli, A. Thermodynamic optimization of a monolithic-type solid oxide fuel cell. Int. J. Thermodyn. 2010, 13, 95–103. [Google Scholar]
- Vogler, M.; Horiuchi, M.; Bessler, W.G. Modeling, simulation and optimization of a no-chamber solid oxide fuel cell operated with a flat-flame burner. J. Power Sources 2010, 195, 7067–7077. [Google Scholar] [CrossRef]
- Autissier, N.; Palazzi, F.; Maréchal, F.; Van Herle, J.; Favrat, D. Thermo-economic optimization of a solid oxide fuel cell, gas turbine hybrid system. J. Fuel Cell Sci. Technol. 2007, 4, 123–129. [Google Scholar] [CrossRef][Green Version]
- Baharanchi, A.A. Multidisciplinary Modeling, Control, and Optimization of a Solid Oxide Fuel Cell/Gas Turbine Hybrid Power System. Master’s Thesis, University of Miami, Coral Gables, FL, USA, May 2009. [Google Scholar]



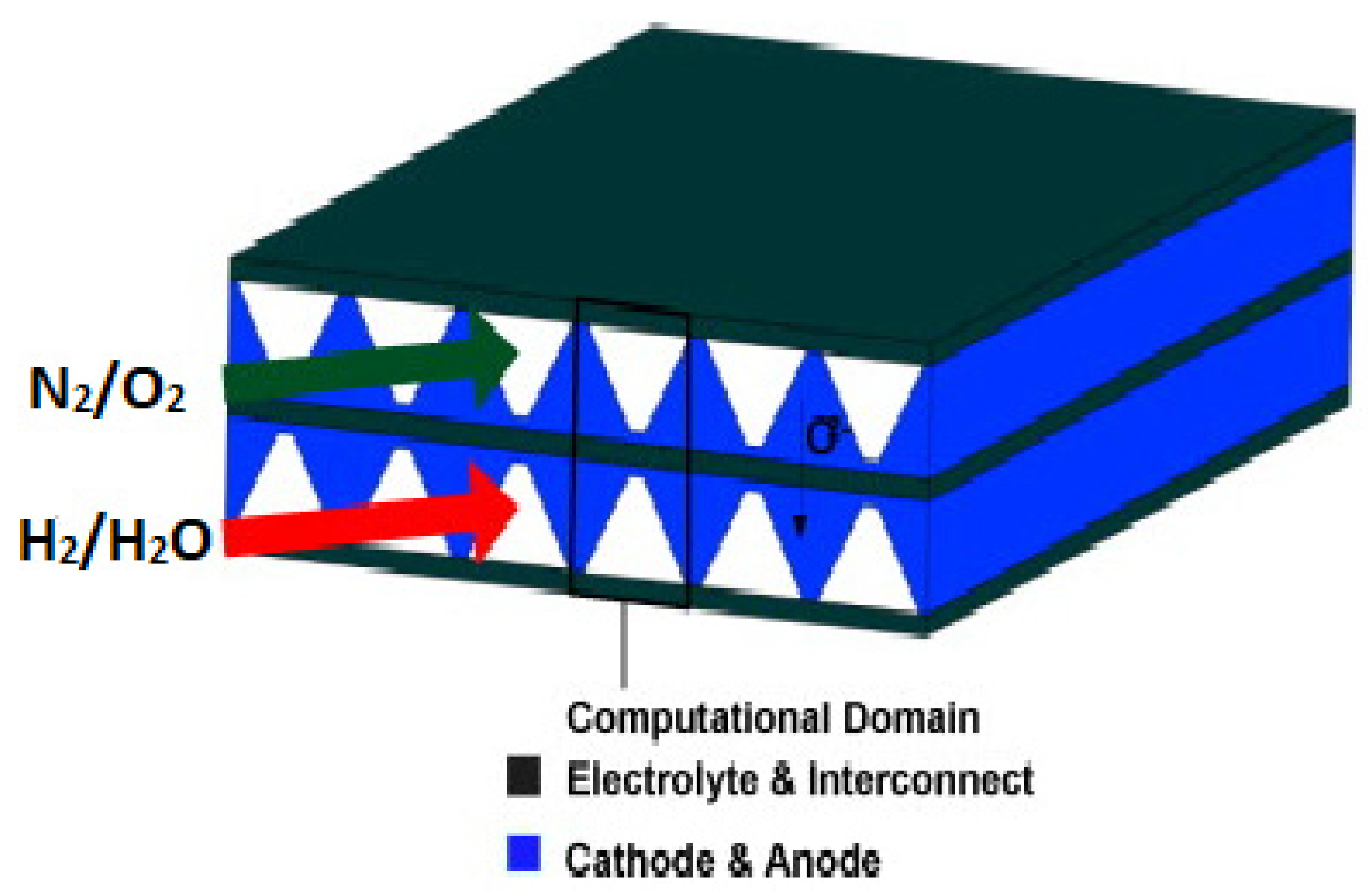



| Cell Configurations | Cell Characteristic | Thermo Mechanical Issues: Thermal Expansion Mismatch Stresses and Propensity to Cracking or Delamination |
|---|---|---|
| Electrolyte-supported | High Ohmic Contribution Low Cathodic Concentration Polarization Low Anodic Concentration Polarization | Minimal Tendency for Delamination due to Thermal Expansion Mismatch |
| Cathode-supported | Low ohmic contribution High cathodic concentration polarization Low anodic concentration polarization | Minimal Tendency for Cracking or Delamination due to Thermal Expansion Mismatch |
| Anode-supported | Low ohmic contribution Moderate anodic concentration polarization Low cathodic concentration polarization | Potential for Electrolyte Film Delamination exists as the YSZ Film is in Biaxial Compression |
| SOFC Design | Characteristics Design | Advantages | Drawbacks | References |
|---|---|---|---|---|
| Planar SOFC | The components are all laminated in a plate-type structure | Low-cost, simplicity in manufacturing and high volume manufacturing with high volumetric power densities. Has higher energy efficiency compared to tubular SOFCs | Difficulties in sealing Internal stresses in cell components due to non-uniform temperature distributions and high manufacturing cost | [33] |
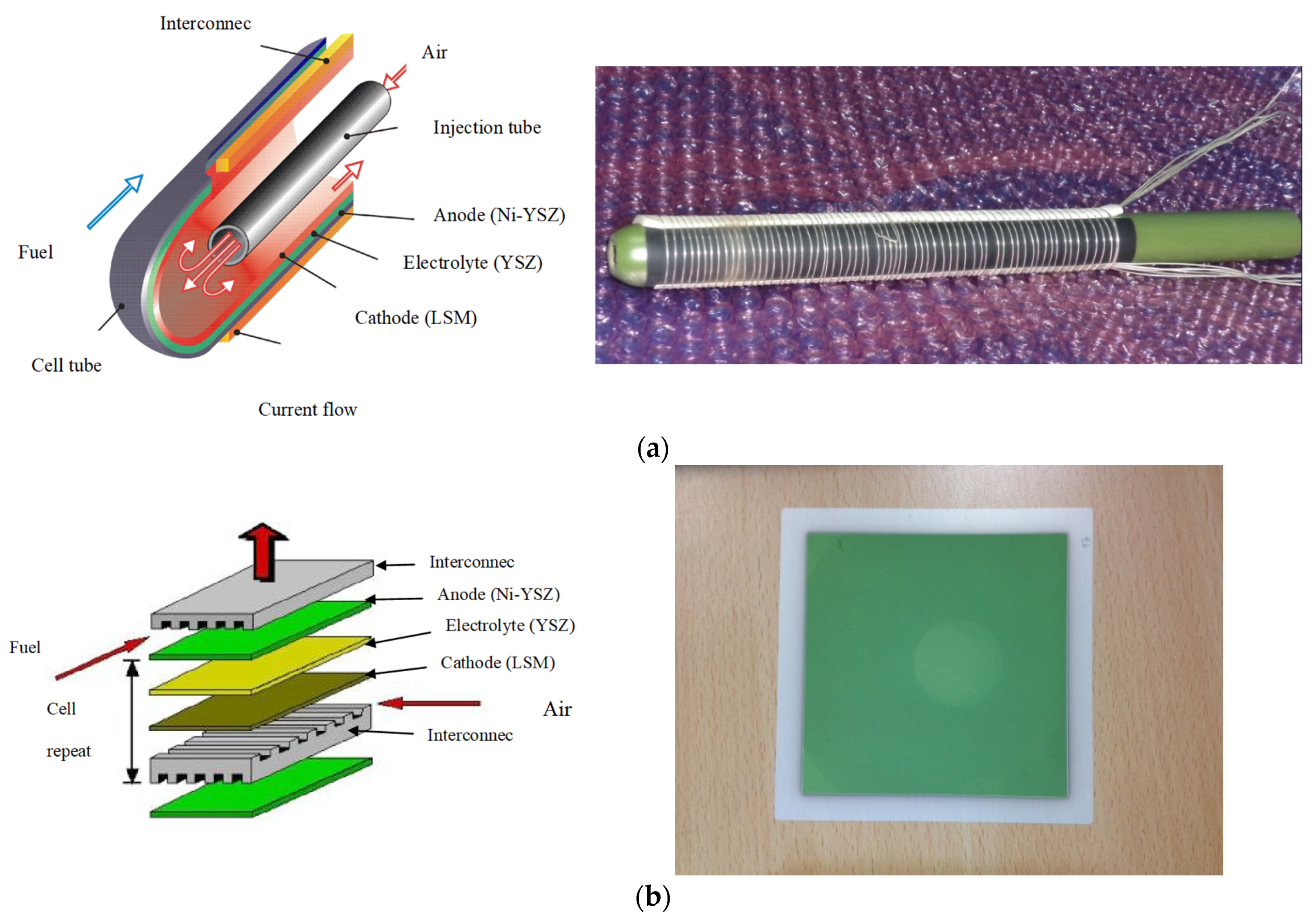
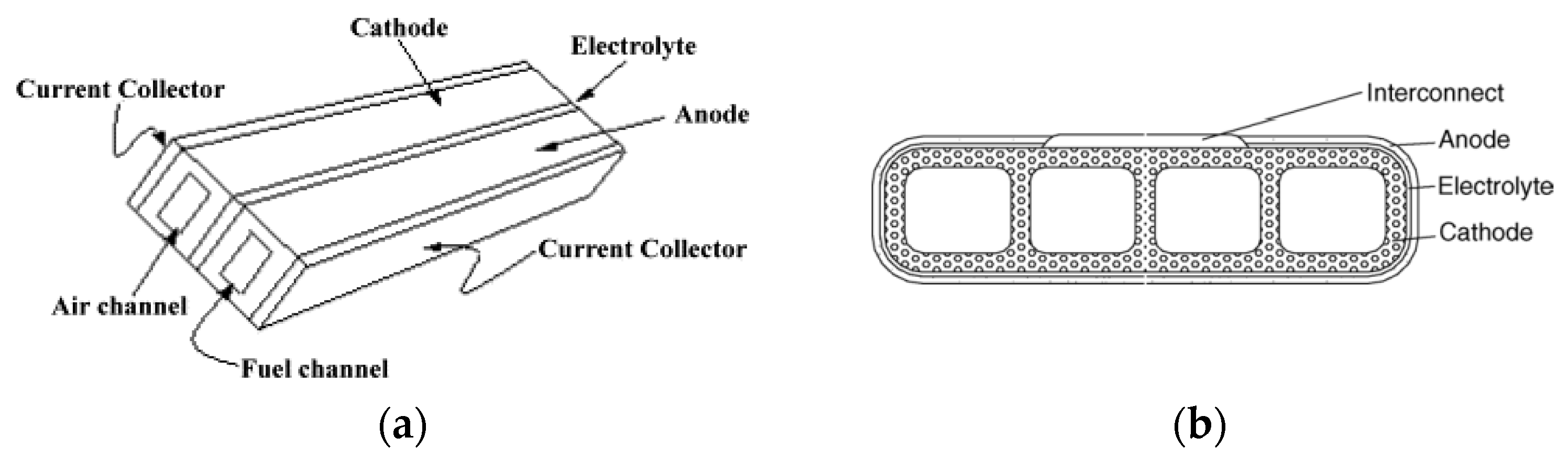
| Tubular SOFC | The components are all laminated in a tube-type structure | Easy to assemble into a cell stack, leading to a lower processing cost | Has a much lower current density than a planar SOFC High ohmic loss | [35] |
| Flat-tube | The tubular geometric design has evolved into a flattened one with ribs in the electrode acting as bridges for current flow | Enhanced power density compared to planar and tubular SOFCs Has a seal-less feature compared to the tubular SOFC Can be configured with a thin cathode layer to decrease the concentration polarization The void space between the cell stacks is reduced | Retains the feature of secure sealing | [34] |
| Bi-electrode supported cell | Uses a freeze tape casting technique | More stable mechanical properties in thermal cycling conditions | This compact design imposes a great challenge on how to effectively feed fuel/gas due to the high diffusion resistance of porous electrodes | [46] |
| μ-SOFCs | Higher energy densities per volume and specific energy per weight are obtained compared to rechargeable batteries A stack of μ-tubular SOFCs is suitable for rapid start-up and shut-down cycles, with only few minutes compared to hours for conventional designs Low cost Low concentration | Lower cell performance | [50,51,52,53] |
| Type | Configurations (mm) | Power Density (mW/cm2) | Electrical Efficiency | |||||
|---|---|---|---|---|---|---|---|---|
| Anode Channel Height | Cathode Channel Height | Anode Width | Cathode Width | Anode Rib Width | Cathode Rib Width | |||
| A | 1 | 1 | 1 | 1 | 1 | 1 | 752.2 | 49.2% |
| B | 0.5 | 1 | 1 | 1 | 1 | 1 | 758.5 (0.83%) | 49.6% |
| C | 1 | 0.5 | 1 | 1 | 1 | 1 | 754.9 (0.36%) | 49.6% |
| D | 1 | 1 | 2 | 1 | 1 | 1 | 755.5 (0.44%) | 49.3% |
| E | 1 | 1 | 1 | 2 | 1 | 1 | 753.1 (0.12%) | 49.7% |
| F | 1 | 1 | 1.4 | 1.4 | 0.6 | 0.6 | 767.4 (2%) | 50.7% |
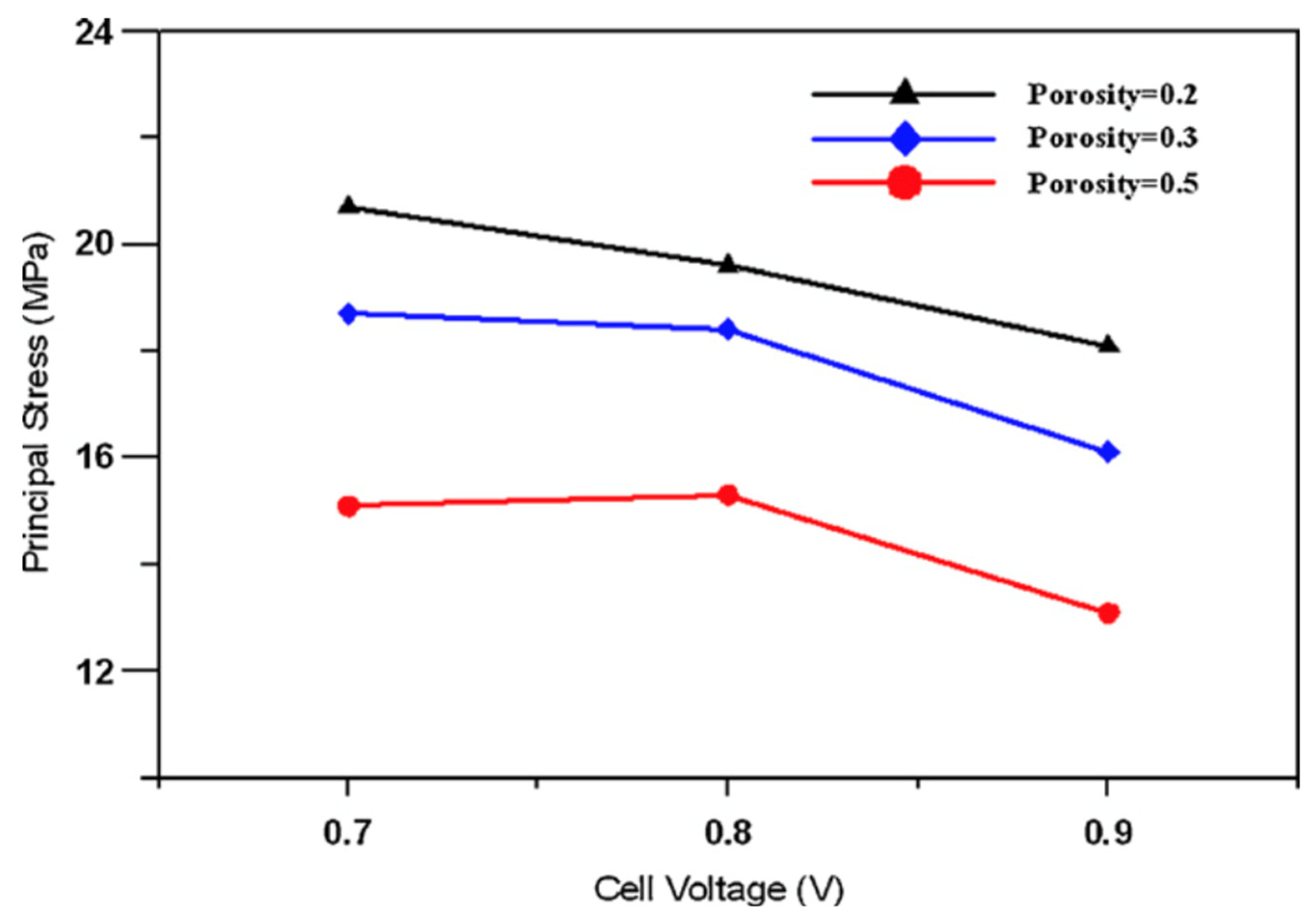
| Prosity | Voltage (V) | PEN (MPa) | Gas Distributors (MPa) | PEN Tmax (°C) | PEN Δ Tmax (°C) |
|---|---|---|---|---|---|
| 0.2 | 0.7 | 20.7 | 42.9 | 821.2 | 12.9 |
| 0.2 | 0.8 | 19.6 | 40.5 | 809.9 | 12.8 |
| 0.2 | 0.9 | 18.1 | 37.3 | 808.3 | 12.5 |
| 0.3 | 0.7 | 18.7 | 42.9 | 823.0 | 12.8 |
| 0.3 | 0.8 | 18.4 | 42.1 | 811.3 | 12.6 |
| 0.3 | 0.9 | 16.1 | 36.8 | 806.8 | 11.9 |
| 0.5 | 0.7 | 15.1 | 42.7 | 824.9 | 12 |
| 0.5 | 0.8 | 15.3 | 43.5 | 812.7 | 13 |
| 0.5 | 0.9 | 13.1 | 36.2 | 805.9 | 11.5 |
| Objective | Constraint | Optimization Method | Refs. |
|---|---|---|---|
| Maximize performance of power production from waste biomass | Temperature | Clustering Pareto evolutionary algorithm | [155] |
| Maximize the system efficiency | Operating pressure | Design of experiments | [156] |
| Maximization of system efficiency and the minimization of specific investment cost | Fuel processing temperature Steam to carbon ratio Fuel utilization Oxygen to carbon ratio Air excess ratio | Based on the use of an evolutionary Algorithm: MOO (Multi-Objective Optimizer) | [159] |
| Parameter optimization: Maximize the output voltage and current density to find cathodic shapes that minimize resistance at the base of the cell | Pressure, temperature | Improved genetic algorithm Finite element modeling for topology optimization | [160] |
| Reducing the annual total cost of power, Reducing the heating and cooling generation and the annual CO2 emissions rate | The amount of fuel provided to the SOFC; The operating temperature of the SOFC; the operating pressure of the SOFC | Evolutionary Multi-objective optimizer | [161] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonekabonimoghaddam, M.; Shamiri, A. Simulation and Sensitivity Analysis for Various Geometries and Optimization of Solid Oxide Fuel Cells: A Review. Eng 2021, 2, 386-415. https://doi.org/10.3390/eng2030025
Tonekabonimoghaddam M, Shamiri A. Simulation and Sensitivity Analysis for Various Geometries and Optimization of Solid Oxide Fuel Cells: A Review. Eng. 2021; 2(3):386-415. https://doi.org/10.3390/eng2030025
Chicago/Turabian StyleTonekabonimoghaddam, Mina, and Ahmad Shamiri. 2021. "Simulation and Sensitivity Analysis for Various Geometries and Optimization of Solid Oxide Fuel Cells: A Review" Eng 2, no. 3: 386-415. https://doi.org/10.3390/eng2030025
APA StyleTonekabonimoghaddam, M., & Shamiri, A. (2021). Simulation and Sensitivity Analysis for Various Geometries and Optimization of Solid Oxide Fuel Cells: A Review. Eng, 2(3), 386-415. https://doi.org/10.3390/eng2030025