Next Article in Journal
Multi-Point Shape Optimization of a Horizontal Axis Tidal Stream Turbine
Previous Article in Journal
Adsorption of Estradiol by Natural Clays and Daphnia magna as Biological Filter in an Aqueous Mixture with Emerging Contaminants
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Eng
Volume 2
Issue 3
10.3390/eng2030021
eng-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Vortex Shedding Suppression: A Review on Modified Bluff Bodies

by
Amir Teimourian
1,* and
Hanifa Teimourian
2
1
Department of Aeronautical Engineering, University of Kyrenia, Kyrenia Harbor, Girne 99320, Turkey
2
Faculty of Engineering, Near East University, Near East Boulevard, Nicosia 99138, Turkey
*
Author to whom correspondence should be addressed.
Eng 2021, 2(3), 325-339; https://doi.org/10.3390/eng2030021
Submission received: 1 April 2021 / Revised: 9 July 2021 / Accepted: 18 July 2021 / Published: 27 July 2021
Browse Figures
Versions Notes

Abstract

:
Vortex shedding phenomenon behind bluff bodies and its destructive unsteady wake can be controlled by employing active and passive flow control methods. In this quest, researchers employed experimental fluid dynamics (EFD), computational fluid dynamics (CFD) and an analytical approach to investigate such phenomena to reach a desired outcome. This study reviews the available literature on the flow control of vortex shedding behind bluff bodies and its destructive wake through the modification of the geometry of the bluff body. Various modifications on the bluff body geometries namely perforated bluff bodies, permeable and porous mesh, corner modification and wavy cylinder have been reviewed. The effectiveness of these methods has been discussed in terms of drag variation, wake structure modifications and Strouhal number alteration.

1. Introduction

Flow properties and wake structures in the premises of bluff bodies fascinates many researchers for years. As bluff bodies have various applications in engineering, there is a growing interest in understanding this phenomenon in industry. A significant feature of the wake region behind bluff bodies is a formation of vortex street and inciting fluctuating forces on the structure, where possible suppression of such a phenomenon is a desired outcome.
The periodic phenomenon incurs destructive unsteady loading on the structure and may lead to catastrophic incidents. Therefore, preventing such destructive fluctuating forces requires a better understanding of this phenomenon during design stages of industrial systems.
Many engineering and industrial applications including the design of skyscrapers, chimneys, offshore structures, bridges and heat exchangers profoundly relies on our understanding of this phenomenon. Wind loading is a key consideration in tall buildings’ design stages and to ensure structural integrity and occupant comfort it is necessary to consider wind-induced stresses and motions. The aerodynamic characteristics and wake flow structure behind bluff bodies, tall buildings for instance, to a great extent depend on the behavior of the separated shear layers from the leading edge. As wind loading can be reduced by controlling the separated flow, a large number of researchers have been investigating the effect of the structural shape modification such as modifying corner shapes on the wind-induced response of structures. Square cross-sectional lighting poles with sharp or round corners, for instance, exhibit large amplitude oscillations with a frequency that is close to the frequency of their first mode.
Therefore, the vortex shedding phenomenon’s importance develops a growing interest in researchers to dedicate their research on this phenomenon to investigate bluff bodies such as a circular cylinder, square cylinder or flat plate resembling structures in engineering [1,2,3,4,5,6,7,8,9]. The application of the research varies from wind turbines and the wind energy sector [10,11,12] to building aerodynamics [13], which provide additional insight to the understanding of the shedding phenomenon for design stages. They investigated different features of vortex shedding, wake flow structure, Strouhal number variation and other aerodynamic parameters. The fluctuating forces are derived from the wake structure and therefore any endeavor for the suppression of the vortex street to reduce such destructive features is valuable. For this purpose, various passive and active flow-control methods have been employed by engineers to protect the structures against the damaging fluid forces acting on the bluff bodies.
The ultimate aim of this review paper is to provide an overview of current and previous works on the suppression of vortex shedding as a reference for aerodynamicist and wind engineers. This paper envisages to review the suppression of vortex shedding through various modifications on the bluff body geometries namely perforated bluff bodies, permeable and porous mesh, corner modification and wavy cylinder in a compact form.

2. Perforated Bluff Bodies

Perforating bluff bodies for flow control and vortex shedding suppression in the wake region attracted several researchers. The concept behind the method is to demonstrate the effect of porosity β (defined as the ratio of open area to the total area), the injection/suction parameter in the case of the active method and the configuration of the perforated surfaces on the vortex shedding phenomenon in the wake region. Therefore, to achieve such a goal researchers have deployed both passive and active flow control methodology.
Çuhadaroğlu and Akansu [14], Çuhadaroğlu and Turan [15], Çuhadaroğlu [16], Turhal and Çuhadaroğlu [17] and Sohankar and Khodadadi [18] employed an active control method with the injection/suction of fluid through the surfaces of the square cylinder to reduce the damaging effect of the vortex shedding phenomenon. Çuhadaroğlu and Akansu [14] conducted an experimental study to investigate the injection effects on the pressure coefficient and drag coefficient of a perforated square cylinder at high Reynolds number between Re = 10,000 and 24,000. Different configurations of injection through the front, top and rear surfaces of the cylinder have been employed. The results revealed that injection through the rear face decreased the drag force. However, injection of fluid through the front face demonstrated opposite results and caused an increase in drag force. Moreover, injection through the other faces have demonstrated negligible effects. Turhal and Çuhadaroğlu [17] experimentally studied the variation of the pressure coefficient, drag coefficient and Strouhal number of a perforated square cylinder (horizontal and diagonal) with fluid injected through various surfaces at a high Reynolds number. The result revealed that in the case of a diagonal square cylinder, surface injection through the top-rear, rear and all surfaces reduced the drag coefficient. However, only injection through all surfaces of a horizontal square cylinder can result in a reduction of drag coefficient. Numerical study on the control of fluid flow by injection through the surfaces of a square cylinder, which have been reported by Sohankar and Khodadadi [18], is one of the latest studies in this context. The simulation demonstrated that in the case of fluid injection through the front surface, Strouhal number decreased by increasing the injection parameter, while aerodynamic force fluctuations were increased.
On the other hand, injection of fluid through the rear face caused a reduction in Strouhal number and drag coefficient. Figure 1 compares the time-averaged streamline contours with injection and without control through the surfaces of a square cylinder. Injection parameter, Γ = Vw/Uin, defined as the ratio of the fluid velocity through the porous wall (Vw) to inlet streamwise velocity (Uin). The injection parameter is positive for blowing (Γ > 0) and negative for the case of suction (Γ < 0). The significant changes of the flow wake structure by employing injection are completely apparent as the vortices disappear for higher injection parameters due to the suppression of vortex shedding.
Çuhadaroğlu and Turan [15] and Çuhadaroğlu [16] numerically studied the effects of uniform injection and suction through a porous square cylinder on the wake flow and its aerodynamic characteristics. It was observed that despite the lower velocity magnitude of injection and suction velocity relative to the main flow, drag and lift coefficients and vortex shedding frequency had been affected significantly. The numerical simulation demonstrated that increasing the suction velocity decreases the drag coefficient for all of the suction configurations (except suction through the rear surface) while the lift coefficient substantially decreases with increasing velocity of suction through the top surface. Moreover, it was demonstrated that injection and suction altered the vortex shedding frequency. While increasing the injection velocity (through most of the surfaces) increases the Strouhal number, increasing the suction velocity exhibits an opposite effect of decreasing the Strouhal number. Therefore, it was observed that the suction application through the top and bottom surfaces of the square cylinder are the most effective configuration to alter the vortex shedding phenomenon.
Saha and Shrivastava [19] numerically investigated the effect of jet blowing into the wake region on the vortex shedding phenomenon. It was reported that the blowing jet lowered the interaction of the separated shear layers and resulted in weak shear layers due to vorticity diffusion and consequently suppressed the vortex shedding. It was demonstrated that vortex shedding suppression can be achieved by a single jet with the uniform exit velocity profile, however a parabolic velocity profile proved to be more effective. An increase in the number of jets reduces the performance of control and as a result a higher value of volume flux is required to achieve complete suppression.
On the other hand, a number of researchers [20,21,22,23,24,25] investigated the passive flow control methodology of perforated surfaces. Castro [21] investigated the wake behind perforated flat plates normal to flow experimentally. The study investigated the effects of porosity β in the rage of 0.0–0.645 on the drag and vortex shedding frequency. The observation demonstrated two distinct flow regimes corresponding to high and low values of plate porosity. It was observed that for a low value of porosity, the vortex street dominates the wake and its strength decreases as the vorticity in the shear layers decreases with the introduction of bleed air. On the other hand, it was suggested for high values of porosity that vortex street is suppressed and the periodic effects are due to far wake instability. Pinar and Ozkan [25] investigated the flow structure around perforated circular cylinders by means of PIV in shallow water flow. The effect of porosities in the range of 0.1 ≤ β ≤ 0.8 with an increment of 0.1 were investigated in terms of velocity, vorticity, turbulent kinetic energy, Reynolds shear stress and streamline topologies. It was observed that the unsteady flow structure and the vortical structures in the wake region downstream of the cylinder affected significantly by the porosity and result in elongated shear layers. The jet-alike flow through the perforated surface of the circular cylinder effectively suppressed the formation of a well-organized Karman vortex street. As the porosity increases, it was observed that the formed vortices on the shear layers are elongated along the direction of the flow. In addition, a significant reduction in fluctuation in the wake region of a perforated circular cylinder has been observed. Based on the observations, a porosity interval of 0.4 ≤ β ≤ 0.8 has been suggested for the most effective suppression of the Karman vortex street. It was observed that as the porosity reaches β = 0.4, the flow structure in the wake region of the perforated circular cylinder dramatically changes and the recirculation region disappears. At this porosity value, the flow emanating through the perforated holes takes the shape of a jet flow and as a result, a significant increase in momentum transfer into the near wake region was observed. In a similar research Durhasan and Pinar [23] investigated the effect of perforation on the flow structure in the downstream wake in deep water for Re = 10,000. The flow emanated from the holes because of increments in porosity prevented the shear layer interaction and consequently elongated the shear layers downstream of the cylinder. Additionally, employing the perforated cylinder results in a significant attenuation of the magnitude of turbulent statistics in comparison with a non-perforated circular cylinder. In agreement with previous work a porosity range 0.4 ≤ β ≤ 0.8 is reported to suppress the Karman vortex street by employing a perforated cylinder. It was also suggested that such a perforated circular cylinder would result in the prevention of vortex induced vibrations. Firat, Ozkan [22] studied the near wakes of perforated hollow cylinders by means of PIV for a Reynolds number of Re = 6900. The circular cylinders with two rows of holes were investigated for various combinations of three-hole diameters and hole-to-hole distances. It was reported that increment in the hole diameter, which is in direct relation to the jet momentum, resulted in increment in the values of time-averaged wake characteristics such as the vortex formation length and length of shear layers. It was observed that the values of the vortex formation length of the perforated circular cylinder was greater than that of the non-perforated cylinder. Hence, by the aid of the jet, the vortex formation phenomena was shifted downstream in the wake region. Teimourian and Hacişevki [20] took a passive flow control approach to investigate perforated surfaces and the effects of fluid entrainment on the vortex shedding phenomenon and possible suppression in the wake region of square cylinder. The research investigated the wake region behind the cylinder in terms of the coherent flow structure, time averaged properties and effectiveness of different perforations.
It was observed that these perforated surfaces have significant effects within the interval of y/D = ±1.0 in the wake behind the square cylinder. The experimental study revealed the effects of various perforated surfaces on velocity profiles and the flow structure while coherent structures have been diminished significantly. The study reported that a square cylinder with all-faces perforated demonstrated the most significant relative reduction in the coherent turbulent kinetic energy compared with other perforations.
The injection or suction modifies the boundary layer development and the vortex formation region. Researchers employing active flow control methodology on perforated bluff bodies demonstrated that high injection of fluid through the rear surface alters the vortex shedding phenomenon. On the other hand, studies on passive flow control suggested that even with a low entrainment flow rate in comparison to the active flow control cases, still the shedding phenomenon has been affected significantly. To sum up, the literature suggested that the pressure coefficient distribution, drag coefficient and the Strouhal number were influenced by the position of the perforated surface and by the injection rate. While the lift and drag fluctuations for the optimum configuration decays, a maximum reduction on the drag force of 72% can be achieved. Yet by increasing porosity, β, the flow fluctuations are substantially reduced in the wake region and results in the suppression of the Karman vortex street due to elongated shear layers and the observation of a reduction in the magnitudes of vortices. The studies on flow control and the suppression of vortex shedding by employing perforated surfaces have been summarized in Table 1.

3. Permeable and Porous Mesh

Employing permeable mesh is classified as the passive wake control method to suppress the vortex shedding in the wake region. Several researchers investigated the effect of porosity on the wake region for various flow conditions.
Gözmen, Akilli [26], Ozkan and Oruc [27] experimentally investigated suppression of vortex shedding in the wake of a circular cylinder by employing a permeable outer cylinder.
Gözmen and Akilli [26] employed various values of porosity to demonstrate its effect on flow control in the wake of the circular cylinder with the outer permeable cylinder. It was observed that vortex shedding has been suppressed significantly downstream the cylinder as porosity increases. In order to control the vortex shedding in the wake, the report suggested the optimum value of porosity as a value of 0.7. While the previous study of Gözmen and Akilli [26] conducted the experiments for a single value of the ratio of the outer cylinder diameter to the inner cylinder diameter (D/d), Ozkan and Oruc [27] investigated the effects of the variation of both the outer cylinder diameter and porosity. It was reported that both parameters have considerable effects on the wake flow behind the circular cylinder. A significant reduction of turbulent kinetic energy and Reynolds stresses was observed as a result of employing the outer cylinder. The results demonstrated that a value of 0.4 ≤ D/d ≤ 0.6 and 1.6 ≤ D/d ≤ 2.0 would achieve a better flow control in the near wake with a remarkable reduction in the turbulent kinetic energy peak value. Cicolin and Freire [28] investigated a circular cylinder with three different types of permeable meshes on the suppression of vortex-induced vibrations by means of PIV. It was observed that the vortex shedding in the wake region has been disrupted and formation length has been increased. Durhasan and Pinar [29] studied the gap between a circular cylinder and a shroud to investigate the effect of shroud porosity and diameter. Therefore, the experiment was conducted for various porosity and diameter ratios at a Reynolds number of Re = 5000. Durhasan and Pinar [29] divided the field of view into four flow regions as demonstrated in Figure 2. These regions are upstream region I (UR I), upstream region II (UR II), downstream region I (DR I) and downstream region II (DR II). Therefore, it was possible to have a closer look at the effects of shroud on these four flow regions.
Figure 3 demonstrates the time-averaged streamline topology for various porosities at different diameter ratios. In comparison to the bare cylinder, the recirculation zone of the cylinder and location of the foci and saddle points are significantly affected for the case of the perforated cylinders. It was observed at porosity values of β ≤ 0.5, the vortex formation of the cylinder occurs only in the gap between the cylinder and the shroud. For β ≥ 0.6 it was observed that in DR I and DR II the formation of the wake flow structures is affected dominantly by the diameter rather than the porosity. It was also revealed that the flow structure in the outer region of the shroud exhibited a similar pattern to the wake region of a single perforated cylinder. In addition, it was reported that employing the shroud will lead to a significant drag reduction between 21% and 87% depending on the values of the porosity and the diameter ratio.
On the other hand, some researchers investigated the wake flow control numerically. Mimeau and Cottet [30] investigated flow control around a semicircular cylinder by employing porous coatings numerically. The simulation is performed by using direct numerical simulations and employing the vortex penalization method. The numerical results demonstrated that the relevant control performances can be achieved by introducing porous layers only at the top and bottom of the solid body permits. Moreover, a significant drag reduction was observed by introducing a thin layer with intermediate permeability in both edges of the back wall. Liu and Wei [31] studied numerically the circular cylinder with a porous materials coating to investigate the effects of surface permeability on the flow control. The three-dimensional simulation demonstrated the underlying physical mechanisms of flow control. It was observed that vorticity in the spanwise direction has been affected more than other directions. In addition, vortex shedding suppression is achieved partly due to a favorable pressure gradient around the porous surface.
The literature suggested that porosity and the permeable cylinder diameter have a substantial effect on the flow characteristics and results in significant reduction in turbulent kinetic energy and Reynolds stresses. In addition, such methodology also is very effective for drag reduction of the cylinder. However, the drag coefficient of the cylinder together with the shroud is higher than the bare cylinder. Table 2 presents the experimental and numerical research on flow control and suppression of vortex shedding by employing a permeable wall on bluff bodies.

4. Corner Modification

Several researchers studied the features of the wake flow for square cylinders with modified corners and suggested a possible aerodynamic forces reduction as a result. In one of the early attempts to understand the effects of coroner modification on the flow structure, Kwok and Wilhelm [32] investigated experimentally the effect of edge configuration on the wind induced response of tall buildings with the rectangular cross section. The experiment demonstrated that slotted corners and chamfered corners reduce both the along-wind and cross-wind responses significantly. Further investigation on the wake energy spectra and wind force spectra characteristics demonstrated that the excitation processes were altered for a chamfered corner. Tamura and Miyagi [33] and Tamura and Miyagi [34] elaborated the effect of corner modification of the square cylinder on the wake flow structures and aerodynamics forces. Tamura and Miyagi [33] observed that a slight corner modification alters the flow structure and result in considerable variation of the aerodynamic characteristics up to approximately 60% of the original value. The report suggested corner modification as a promising passive technique for aerodynamic forces reduction.
In addition, Tamura and Miyagi [34] investigated the effects of corner shape, turbulence intensity and three dimensionality on the aerodynamic forces experimentally. Due to corner rounding, separated shear layers approach the side surface and promote reattachment of flow and reduction in both wake width and drag forces as apparent in Figure 4. Moreover, it was reported that three-dimensional cylinders exhibit a 10% reduction in value of C L R M S in comparison with two-dimensional cylinders. Such observation suggests that the effect of Karman vortices and the resulting lift force are not significant for three-dimensional cylinders. Hu and Zhou [35] conducted several experiments to study the near wake of square cylinders with various corner radii. For the experiments, bluff bodies with a ratio in a range of r/d = 0 (square cylinder) to r/d = 0.5 (circular cylinder) were studied. The experimental result demonstrated that an increase in r/d within the investigated range lead to a decrease in peak value of the strength of shed vortices while the Strouhal number, St, increases by 60%. In addition, vortex wavelength, λ x , and the lateral spacing, λ y , exhibit a reduction as r/d ratio increases. It was suggested that the change in the flow structure from the approximately circular-shaped vortex at r/d = 0 to the laterally stretched vortex at r/d = 0.5 is due to the decrease in wavelength. The leading edge corner dictates significantly the streamlines behavior, angle of the separation and the base pressure. Therefore, it was reported that the leading edge corner modification is more effective on the flow structure in comparison with the trailing edge corner modification. Miran and Sohn [36] performed a numerical study to investigate the effect of rounded corners on the flow structure past a square cylinder for various corner radii ranges from R/D (where R is the corner radius and D is the characteristic dimension of the body) 0 to 0.5. It was observed that the corners affect the flow characteristics significantly. As a result, increasing the corner radius ratio R/D from 0 to 0.2 will lead to a rapid increment in the Strouhal number. Moreover, the square cylinder with corner radius ratio R/D = 0.2 exhibits the minimum values of the mean drag coefficient and the RMS value of the lift coefficient. Dalton and Zheng [37] numerically compared the rounded corner square cylinder and diamond cylinder. It was revealed that rounded corner effects are more significant for the diamond cylinder. It was observed that rounded corners significantly reduced the lift and drag for both square and diamond cylinders. The lift reduction was considerably greater for the diamond orientation. The cut corner modification on the front sharp corners of the square cylinder is another effective method for flow structure alteration and drag reduction [38,39,40,41,42,43]. Kurata and Ueda [41] conducted several experiments to investigate the flow past a rectangular cylinder and effects of small rectangular shaped cut-corners at the front edges on the drag. The results demonstrated the existence of an effective cut-corner dimension where the drag coefficient is less than the value of the circular cylinder drag coefficient for the experiment with the same Reynolds number. This cut dimension was reported to be independent of the breadth to width ratio. Ueda and Kurata [40] performed an extensive numerical and experimental flow visualization studies on flow past a square cylinder with cut-corners at the front-edge to break through the drag reduction mechanism. The results revealed that for cut corner dimensions with significant drag reduction, the separated shear layer from the leading corners of the cylinder reattaches on the side surface. Such reattachment observations result in the narrower Karman vortex street in the wake region. The study observed an optimal cutout dimension on the drag reduction. In addition, optimal drag reduction is achieved when the separated streamline covers the cut-corner and then reattaches along the whole side surfaces. He and Li [39] investigated flow around square cylinders with cut-corners at the front edges experimentally. They observed that the cut corner modification caused fluctuation intensity of the wake to be weakened with a reduction in the wake width. Cut-corners at the leading corners lead to the suppression of the separation over the side surfaces and result in the reduction of wake width. It was observed that while Strouhal number is inversely proportional to the minimum wake width parameter, the drag coefficient is directly proportional to the parameter. Further investigation on the flow structure revealed a reduction in the wake vortex size and strength. The wake vortices formed farther downstream of the cylinders with cut-corners in comparison with unmodified corners. The recirculation flow in the cut-corner facilitates the flow to go around the corner by acting as a virtual shape. On the quest to understand the effects of the corner modification on the flow past square cylinder Ambreen and Kim [38] conducted a more universal study on all proposed modifications namely chamfered, rounded and cut corners. Ambreen and Kim [38] investigated corner modification effects on flow structure and heat transfer in the wake region of the square cylinder. The numerical study focused on the corner roundedness parameter c/D = 0.125 where c and D represent the corner size and cylinder diameter, respectively.
It was observed that corner modifications lead to significant drag reduction up to 19% in comparison with a sharp-cornered cylinder. Such a drag reduction is achieved due to the fact that the upstream modified corners alter the flow with a flow separation from downstream corners and results in a reduction of the wake width and drag coefficient. Low Reynolds numbers (125 < Re < 150) flow around a sharp corner square cylinder, a separated flow from the upstream corners reattaches to the downstream lateral surfaces and as a result deflects the flow towards downstream lateral surfaces. At a higher Reynolds number, the flow reattachment phenomena diminish and therefore for such an entirely detached flow, a wider wake with a lower wake pressure and consequently higher drag coefficient can be observed. In contrast to the sharp corner cylinder, the responsible corners for flow separation are not predetermined for the modified corner cylinder. While the primary upstream corner initiates flow separation for the case of chamfered corners (Figure 5a), for the case of the corner cut (Figure 5b) the recirculating fluid inside the upstream corner deflect the flow towards the secondary upstream. As a result, pressure reduces to a minimum value and therefore flow separation from the upstream corner suppresses. On the other hand, such upstream fluid recirculation leads to an additional pressure increment at the cylinder upstream flow region and as a result exhibits a higher pressure drag than the rounded and chamfered corners. In addition, these modifications lead to an increment of Strouhal number for a chamfered corner square cylinder. It was also observed that modification of the upstream corners is more effective on flow structures and heat transfer characteristics in comparison with downstream corners.
Some researchers combined the effect of corner modification with other parameters on the wake flow. Mola and Bordonaro [44] numerically studied flows over square cylinders with different aspect ratios and cross-sectional shapes to investigate aerodynamic forces variations. As flow over finite length cylinders exhibit 3D characteristics close to the free end region, a low frequency component has been observed. Therefore, mean drag coefficient varies along the cylinder due to loss of vortex shedding synchronization behind the cylinder. It was reported that in the case of the cylinder with rounded corners these variations are less significant in comparison with cylinders with sharp corners. [45], Miran and Sohn [46] and Tong and Sparrow [47] investigated the effect of the angle of attack or incidence angle on the flow structure of square cylinders with modified corners. Carassale and Freda [45] investigated the influence of corner modification on the aerodynamic behavior of square cylinders at the angles of incidence between 0 and 45°, experimentally. It was reported that rounded corners promote the reattachment of the flow on the lateral faces and as a result the critical angle of incidence was reduced. Miran and Sohn [46] observed that the rounded corner cylinder exhibits a lower critical incidence angle in comparison with the sharp corner square cylinder. Therefore, for R/D = 0 (square cylinder) a critical incidence angle of 12° was observed whereas for R/D = 0.1–0.4 a value in the range of 5–10° was reported. On the other hand, Tong and Sparrow [47] conducted a numerical study on the square cylinder at an angle of attack with various degrees of edge chamfer, which make the shapes of the cylinder range from the square to the octagon. The work concentrated on heat transfer characteristics and compared the results of the many investigated configurations. It was reported that the more extensive chamfering results in a lowered dependence of the Nusselt number on the Reynolds number.
The experimental and numerical results demonstrated that modified corners of square cylinder are a promising approach to reduce the drag and lift forces generated behind the cylinder. While in the wake of the square cylinder it was observed that the alternate vortices are deflecting away from the centerline. The wake region of the rounded corner square exhibits a different flow structure and a flow reattachment was promoted. Consequently, as the wake width decreases, a reduction in drag and lift coefficients was observed. Other remarks are that the modification dimension and the location of modified coroners are playing a significant role on the flow structure alternation. As the corner radius ratio, R/D, increases, the Strouhal number also increases. The leading-edge corner significantly affects the streamlines behavior, angle of separation and the base pressure. Therefore, the leading-edge corner modification is more effective on the flow structure in comparison with trailing edge corners. Table 3 lists the conducted research on corner modification for flow control and drag reduction of square cylinders.

5. Wavy Cylinder

Employing a wavy surface for bluff bodies is also suggested in the literature for flow control. The concept is to employ a wavy surface, sinusoidal waviness, for instance to investigate its effect on the wake flow and vortex shedding phenomenon.
In this context, two sets of extensive numerical investigation [48,49,50,51] and combined experimental-numerical studies [52,53,54] have been conducted. Investigations on the wake flow structure of a wavy circular cylinder demonstrated that the wavy cylinder encountered a lower mean drag coefficient than the corresponding drag coefficient for a circular cylinder. Such an observation was due to the formation of a longer wake vortex generated by the wavy cylinder. On the other hand, a significant reduction of the lift coefficient fluctuation of the wavy cylinder was observed. The employed wavy surface led to the formation of 3-D free shear layers, which are more stable than purely 2-D free shear layers. Such free shear layers only roll up into mature vortices at the further downstream position and significantly alters the near wake structures and the pressure distributions around the wavy cylinder. The wake flow structure of a circular cylinder and a wavy circular cylinder illustrated in Figure 6 by means of large eddy simulation (LES) and laser-induced fluorescence (LIF). From the figure alteration of the vortex structure behind a way cylinder is apparent.
On the other hand, investigation on the flow structure in the wake region of the modified square cylinder demonstrated that the three-dimensional free shear layers from the leading edge are widened and lengthened. Therefore, vortices formed further downstream in the wake of modified square cylinder in comparison to the straight square cylinder. Thus, a reduction in the mean drag was observed while the lift fluctuation was suppressed significantly. Organized transverse vortices have been observed along the spanwise direction, which make such a flow control achievable. The free shear layers stabilized by these vortices and therefore forced the roll up process into the vortex at a further downstream position. In comparison with a straight square cylinder a significant force reduction is observed for a wavy square cylinder. The simulation demonstrated more stable three-dimensional free shear layers behind the wavy square cylinder. It was observed that at Re = 100 the free shear layers exhibit a steady flow feature with symmetrical flow patterns behind the modified cylinder with a wavy surface. In agreement with previous studies a reduction in the mean drag coefficient and fluctuating lift coefficient was reported. However, as the aspect ratio and Reynolds number increases such features disappear. The simulation suggested that such a modified cylinder with a wavy surface is not effective in flow separation control.
Recently, Assi and Bearman [55] investigated the vortex-induced vibration of a wavy elliptic cylinder. The experimental study demonstrated that a wavy cylinder exhibits vortex-induced vibrations with similar behavior to a plain cylinder with equivalent diameter. The modification elongated the wake region with significant dimensional features, increased the base pressure and consequently affects the drag coefficient. It was also reported that the elliptical wavy cylinder exhibits more evident 3D features than those of a wavy cylinder with the circular cross section.
Other studies combined other parameters with the wavy cylinder to investigate the flow structure in the wake region. Investigation on the inclined cylinder with a wavy surface [49] demonstrated similar three dimensional characteristics of the wake. It was reported that a significant drag reduction and suppression of lift fluctuation can be achieved by a wavy cylinder at a low angle of inclination while at a large angle of inclination these effects disappear.
New and Shi [56] conducted an experimental study to investigate effects of the aspect ratio of the finite-length on the flow structure of wavy cylinders. The results demonstrated that for high aspect ratio wavy cylinders with a large wavelength, the vortex shedding phenomenon can be altered by modifying the aspect ratio. Such an observation is due to the persistent formation of recirculating regions close to the end-walls under certain wavy cylinder configurations, which affect the distributions of spanwise flows and vortex formation lengths. Wavy cylinder with smaller wavelength demonstrated less sensitivity to variations in the physical configurations.
To sum up, the numerical and experimental studies demonstrated the effectiveness of modified cylinders with a wavy surface on flow control and vortex shedding suppression in the wake of the cylinders. Apparently, the vortex formation region is elongated and the effectiveness of wavy cylinders can be observed in terms of minimization of flow induced vibration and force reduction. Such a force reduction for drag can be substantial with up to a 34% reduction at a higher Reynolds number. Table 4 summarized the conducted research on modified cylinders with a wavy surface.
In conclusion, this paper reviewed different promising methods of vortex shedding suppression through geometry modification on the bluff body. The discussed methods namely permeable and porous mesh, corner modification and wavy cylinder demonstrate promising results in suppressing vortex shedding. The literature suggests the significant effectiveness of vortex shedding suppression in terms of the alteration of turbulent kinetic energy, Reynolds stresses and drag coefficient. These methodologies have potential application in the civil engineering and wind energy sector and their implementation for a more effective vortex shedding suppression is essential for engineers.

Author Contributions

Conceptualization, A.T. and H.T.; writing—original draft preparation, A.T.; writing—review and editing, H.T. Both authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chashechkin, Y.D.; Zagumennyi, I.V. Formation of waves, vortices and ligaments in 2D stratified flows around obstacles. Phys. Scr. 2019, 94, 054003. [Google Scholar] [CrossRef]
  2. Naumov, I.; Litvinov, I.V.; Mikkelsen, R.F.; Okulov, V.L. Experimental investigation of wake evolution behind a couple of flat discs in a hydrochannel. Thermophys. Aeromech. 2016, 23, 657–666. [Google Scholar] [CrossRef] [Green Version]
  3. Shin, B.; Kondo, M. Effect of Gap Ratio on the Wake behind Two Side-by-Side Flat Plates. J. Appl. Fluid Mech. 2019, 12, 1213–1222. [Google Scholar] [CrossRef]
  4. Gao, S.; Tao, L.; Tian, X.; Yang, J. Flow around an inclined circular disk. J. Fluid Mech. 2018, 851, 687–714. [Google Scholar] [CrossRef] [Green Version]
  5. Tian, X.; Hu, Z.; Lu, H.; Yang, J. Direct numerical simulations on the flow past an inclined circular disk. J. Fluids Struct. 2017, 72, 152–168. [Google Scholar] [CrossRef]
  6. Hacışevki, H.; Teimourian, A. Interacting wakes of a narrow and a wide flat plate in tandem arrangement. Fluid Dyn. Res. 2016, 48, 015505. [Google Scholar] [CrossRef]
  7. Teimourian, A.; Hacisevki, H.; Bahrami, A. Experimental study on flow past two inclined flat plates in tandem arrangement. J. Wind Eng. Ind. Aerodyn. 2017, 169, 1–11. [Google Scholar] [CrossRef]
  8. Schmidt, H.-J.; Woszidlo, R.; Nayeri, C.N.; Paschereit, C.O. The effect of flow control on the wake dynamics of a rectangular bluff body in ground proximity. Exp. Fluids 2018, 59, 1–16. [Google Scholar] [CrossRef]
  9. Li, D.; Yang, Q.; Ma, X.; Dai, G. Free surface characteristics of flow around two side-by-side circular cylinders. J. Mar. Sci. Eng. 2018, 6, 75. [Google Scholar] [CrossRef] [Green Version]
  10. Dou, B.; Yang, Z.; Guala, M.; Qu, T.; Lei, L.; Zeng, P. Comparison of Different Driving Modes for the Wind Turbine Wake in Wind Tunnels. Energies 2020, 13, 1915. [Google Scholar] [CrossRef] [Green Version]
  11. Zou, L.; Wang, K.; Jiang, Y.; Wang, A.; Sun, T. Wind tunnel test on the effect of solidity on near wake instability of vertical-axis wind turbine. J. Mar. Sci. Eng. 2020, 8, 365. [Google Scholar] [CrossRef]
  12. Wang, K.; Zou, L.; Wang, A.; Zhao, P.; Jiang, Y. Wind tunnel study on wake instability of twin H-rotor vertical-axis turbines. Energies 2020, 13, 4310. [Google Scholar] [CrossRef]
  13. Chen, Z.; Kim, B.; Lee, D.-E. Aerodynamic Characteristics and Lateral Displacements of a Set of Two Buildings in a Linked Tall Building System. Sensors 2021, 21, 4046. [Google Scholar] [CrossRef] [PubMed]
  14. Çuhadaroğlu, B.; Akansu, Y.E.; Turhal, A.Ö. An experimental study on the effects of uniform injection through one perforated surface of a square cylinder on some aerodynamic parameters. Exp. Therm. Fluid Sci. 2007, 31, 909–915. [Google Scholar] [CrossRef]
  15. Çuhadaroğlu, B.; Turan, O. Numerical simulation of turbulent flow around a square cylinder with uniform injection or suction and heat transfer. Numer. Heat Transf. Part A Appl. 2009, 55, 163–184. [Google Scholar] [CrossRef]
  16. Çuhadaroglu, B. A numerical study on turbulent flow around a square cylinder with uniform injection or suction. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 708–727. [Google Scholar] [CrossRef]
  17. Turhal, A.Ö.; Çuhadaroğlu, B. The effects of surface injection through a perforated square cylinder on some aerodynamic parameters. Exp. Therm. Fluid Sci. 2010, 34, 725–735. [Google Scholar] [CrossRef]
  18. Sohankar, A.; Khodadadi, M.; Rangraz, E. Control of fluid flow and heat transfer around a square cylinder by uniform suction and blowing at low Reynolds numbers. Comput. Fluids 2015, 109, 155–167. [Google Scholar] [CrossRef]
  19. Saha, A.K.; Shrivastava, A. Suppression of vortex shedding around a square cylinder using blowing. Sadhana 2015, 40, 769–785. [Google Scholar] [CrossRef] [Green Version]
  20. Teimourian, A.; Hacişevki, H.; Bahrami, A. Experimental study on suppression of vortex street behind perforated square cylinder. J. Theor. Appl. Mech. 2017, 55, 1397–1408. [Google Scholar] [CrossRef] [Green Version]
  21. Castro, I. Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 1971, 46, 599–609. [Google Scholar] [CrossRef]
  22. Firat, E.; Ozkan, G.M.; Akilli, H. PIV measurements in the near wakes of hollow cylinders with holes. Exp. Fluids 2017, 58, 39. [Google Scholar] [CrossRef]
  23. Durhasan, T.; Pinar, E.; Ozkan, G.M.; Aksoy, M.M.; Akilli, H.; Sahin, B. PIV measurement downstream of perforated cylinder in deep water. Eur. J. Mech. B Fluids 2018, 72, 225–234. [Google Scholar] [CrossRef]
  24. Molin, B. Hydrodynamic modeling of perforated structures. Appl. Ocean Res. 2011, 33, 1–11. [Google Scholar] [CrossRef]
  25. Pinar, E.; Ozkan, G.M.; Durhasan, T.; Aksoy, M.M.; Akilli, H.; Sahin, B. Flow structure around perforated cylinders in shallow water. J. Fluids Struct. 2015, 55, 52–63. [Google Scholar] [CrossRef]
  26. Gözmen, B.; Akilli, H.; Şahin, B. Vortex control of cylinder wake by permeable cylinder. J. Fac. Eng. Archit. 2013, 28, 77–85. [Google Scholar]
  27. Ozkan, G.M.; Oruc, V.; Akilli, H.; Sahin, B. Flow around a cylinder surrounded by a permeable cylinder in shallow water. Exp. Fluids 2012, 53, 1751–1763. [Google Scholar] [CrossRef]
  28. Cicolin, M.M.; Freire, C.M.; Assi, G.R. Suppression of the vortex-induced vibration of a circular cylinder with permeable meshes. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: Chicago, IL, USA, 2014. [Google Scholar]
  29. Durhasan, T.; Pinar, E.; Ozkan, G.M.; Akilli, H.; Sahin, B. The effect of shroud on vortex shedding mechanism of cylinder. Appl. Ocean Res. 2019, 84, 51–61. [Google Scholar] [CrossRef]
  30. Mimeau, C.; Cottet, G.-H.; Mortazavi, I. Passive flow control around a semi-circular cylinder using porous coatings. Int. J. Flow Control 2014, 6, 43–50. [Google Scholar]
  31. Liu, H.; Wei, J. On the role of surface permeability for the control of flow around a circular cylinder. J. Vibroeng. 2016, 18, 5406–5415. [Google Scholar] [CrossRef]
  32. Kwok, K.; Wilhelm, P.; Wilkie, B. Effect of edge configuration on wind-induced response of tall buildings. Eng. Struct. 1988, 10, 135–140. [Google Scholar] [CrossRef]
  33. Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1998, 74, 531–542. [Google Scholar] [CrossRef]
  34. Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
  35. Hu, J.; Zhou, Y.; Dalton, C. Effects of the corner radius on the near wake of a square prism. Exp. Fluids 2006, 40, 106. [Google Scholar] [CrossRef]
  36. Miran, S.; Sohn, C.H. Numerical study of the rounded corners effect on flow past a square cylinder. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 686–702. [Google Scholar] [CrossRef]
  37. Dalton, C.; Zheng, W. Numerical solutions of a viscous uniform approach flow past square and diamond cylinders. J. Fluids Struct. 2003, 18, 455–465. [Google Scholar] [CrossRef]
  38. Ambreen, T.; Kim, M.-H. Flow and heat transfer characteristics over a square cylinder with corner modifications. Int. J. Heat Mass Transf. 2018, 117, 50–57. [Google Scholar] [CrossRef]
  39. He, G.S.; Li, N.; Wang, J.J. Drag reduction of square cylinders with cut-corners at the front edges. Exp. Fluids 2014, 55, 1745. [Google Scholar] [CrossRef]
  40. Ueda, Y.; Kurata, M.; Kida, T.; Iguchi, M. Visualization of flow past a square prism with cut-corners at the front-edge. J. Vis. 2009, 12, 383–391. [Google Scholar] [CrossRef]
  41. Kurata, M.; Ueda, Y.; Kida, T.; Iguchi, M. Drag reduction due to cut-corners at the front-edge of a rectangular cylinder with the length-to-breadth ratio being less than or equal to unity. J. Fluids Eng. 2009, 131, 064501. [Google Scholar] [CrossRef]
  42. Kurata, M.; Hirakawa, K.; Yasutomi, Z.; Kida, T. Effect of cutout at front edges to drag reduction of square prism. Trans. Jpn. Aeronaut. Space Sci. 1999, 47, 174–181. [Google Scholar]
  43. Igarashi, T. Drag reduction of a rectangular cylinder with small rectangular cutout at its edges normal to air-stream. In Proceedings of the Annual Meeting, Japan Society of Fluid Mechanics, Tokyo, Japan, 27–29 September 2005. [Google Scholar]
  44. Mola, A.; Bordonaro, G.; Haji, M.R. Low-frequency variations of force coefficients on square cylinders with sharp and rounded corners. J. Struct. Eng. 2009, 135, 828–835. [Google Scholar] [CrossRef] [Green Version]
  45. Carassale, L.; Freda, A.; Marrè-Brunenghi, M. Experimental investigation on the aerodynamic behavior of square cylinders with rounded corners. J. Fluids Struct. 2014, 44, 195–204. [Google Scholar] [CrossRef]
  46. Miran, S.; Sohn, C.H. Influence of incidence angle on the aerodynamic characteristics of square cylinders with rounded corners. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 269–283. [Google Scholar] [CrossRef]
  47. Tong, J.C.K.; Sparrow, E.M.; Minkowycz, W.J.; Abraham, J.P. A new archive of heat transfer coefficients from square and chamfered cylinders at angles of attack in crossflow. Int. J. Therm. Sci. 2016, 105, 218–223. [Google Scholar] [CrossRef]
  48. Lam, K.; Lin, Y. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Int. J. Heat Fluid Flow 2008, 29, 1071–1088. [Google Scholar] [CrossRef]
  49. Lam, K.; Lin, Y.F.; Zou, L.; Liu, Y. The effect of wavy surface on vortex shedding from an inclined cylinder in turbulent flow. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009. [Google Scholar]
  50. Lam, K.; Lin, Y. Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers. J. Fluid Mech. 2009, 620, 195–220. [Google Scholar] [CrossRef] [Green Version]
  51. Lam, K.; Lin, Y.F.; Zou, L.; Liu, Y. Numerical study of flow patterns and force characteristics for square and rectangular cylinders with wavy surfaces. J. Fluids Struct. 2012, 28, 359–377. [Google Scholar] [CrossRef]
  52. Shen, S.; Miao, W.; Hong, L.U.; Lin, Z. The numerical and experimental investigations of the near wake behind a modified square stay-cable. J. Hydrodyn. Ser. B 2016, 28, 897–904. [Google Scholar] [CrossRef]
  53. Lin, Z.; Lin, Y.-F. Force reduction of flow around a sinusoidal wavy cylinder. J. Hydrodyn. Ser. B 2009, 21, 308–315. [Google Scholar]
  54. Zou, L.; Hu, Y.; Xu, H.B.; Lu, H.; Wang, M. Characteristics of Flow around a Modified Square Prism. Appl. Mech. Mater. 2015, 723, 190–193. [Google Scholar] [CrossRef]
  55. Assi, G.R.; Bearman, P.W. Vortex-induced vibration of a wavy elliptic cylinder. J. Fluids Struct. 2018, 80, 1–21. [Google Scholar] [CrossRef]
  56. New, T.; Shi, S.; Liu, Y. Cylinder-wall interference effects on finite-length wavy cylinders at subcritical Reynolds number flows. Exp. Fluids 2013, 54, 1601. [Google Scholar] [CrossRef]
  57. Darekar, R.; Sherwin, S. Flow past a bluff body with a wavy stagnation face. J. Fluids Struct. 2001, 15, 587–596. [Google Scholar] [CrossRef]
  58. Lee, S.-J.; Nguyen, A.-T. Experimental investigation on wake behind a wavy cylinder having sinusoidal cross-sectional area variation. Fluid Dyn. Res. 2007, 39, 292. [Google Scholar] [CrossRef]
  59. Lam, K.; Wang, F.; So, R. Three-dimensional nature of vortices in the near wake of a wavy cylinder. J. Fluids Struct. 2004, 19, 815–833. [Google Scholar] [CrossRef]
  60. Lam, K.; Wang, F.H.; Li, J.Y.; So, R.M.C. Experimental investigation of the mean and fluctuating forces of wavy (varicose) cylinders in a cross-flow. J. Fluids Struct. 2004, 19, 321–334. [Google Scholar] [CrossRef]
  61. Tammisola, O. Optimal wavy surface to suppress vortex shedding using second-order sensitivity to shape changes. Eur. J. Mech. B Fluids 2017, 62, 139–148. [Google Scholar] [CrossRef] [Green Version]
Eng 02 00021 g001 550
Figure 1. Time-averaged streamlines colored by the pressure coefficient for a different suction/blowing parameter and Reynolds number for the case (a) without a control (|Γ| = 0), (b) with a control (|Γ| = 0.05) and (c) with a control (|Γ| = 0.15) (figure reprinted from Sohankar and Khodadadi [18] Copyright (2015), with permission from Elsevier).
Figure 1. Time-averaged streamlines colored by the pressure coefficient for a different suction/blowing parameter and Reynolds number for the case (a) without a control (|Γ| = 0), (b) with a control (|Γ| = 0.05) and (c) with a control (|Γ| = 0.15) (figure reprinted from Sohankar and Khodadadi [18] Copyright (2015), with permission from Elsevier).
Eng 02 00021 g001
Eng 02 00021 g002 550
Figure 2. Schematic representation of flow regions; figure reprinted from Durhasan and Pinar [29] Copyright (2019), with permission from Elsevier.
Figure 2. Schematic representation of flow regions; figure reprinted from Durhasan and Pinar [29] Copyright (2019), with permission from Elsevier.
Eng 02 00021 g002
Eng 02 00021 g003 550
Figure 3. Time-averaged streamline topology for various porosities at different diameter ratios D/Ds = 0.4, 0.5 and 0.6; figure reprinted from Durhasan and Pinar [29] Copyright (2019), with permission from Elsevier.
Figure 3. Time-averaged streamline topology for various porosities at different diameter ratios D/Ds = 0.4, 0.5 and 0.6; figure reprinted from Durhasan and Pinar [29] Copyright (2019), with permission from Elsevier.
Eng 02 00021 g003
Eng 02 00021 g004 550
Figure 4. Instantaneous vorticity contours around a sharp corner square cylinder (Left), chamfered corners cylinder (Middle) and rounded corners cylinder (Right); figure reprinted from Tamura and Miyagi [33] Copyright (1998), with permission from Elsevier.
Figure 4. Instantaneous vorticity contours around a sharp corner square cylinder (Left), chamfered corners cylinder (Middle) and rounded corners cylinder (Right); figure reprinted from Tamura and Miyagi [33] Copyright (1998), with permission from Elsevier.
Eng 02 00021 g004
Eng 02 00021 g005 550
Figure 5. Streamlines around (a) chamfered and (b) cut corner cylinder at Re = 200; figure reprinted from Ambreen and Kim [38] Copyright (2018), with permission from Elsevier.
Figure 5. Streamlines around (a) chamfered and (b) cut corner cylinder at Re = 200; figure reprinted from Ambreen and Kim [38] Copyright (2018), with permission from Elsevier.
Eng 02 00021 g005
Eng 02 00021 g006 550
Figure 6. Experimental and numerical comparison of vortex structures of a circular cylinder and a wavy cylinder, (a–c) LES simulation; (d–f) LIF flow visualization; figure reprinted from Lam and Lin [48] Copyright (2008), with permission from Elsevier.
Figure 6. Experimental and numerical comparison of vortex structures of a circular cylinder and a wavy cylinder, (a–c) LES simulation; (d–f) LIF flow visualization; figure reprinted from Lam and Lin [48] Copyright (2008), with permission from Elsevier.
Eng 02 00021 g006
Table
Table 1. Selected studies on flow control and suppression of vortex shedding by employing perforated bluff bodies.
Table 1. Selected studies on flow control and suppression of vortex shedding by employing perforated bluff bodies.
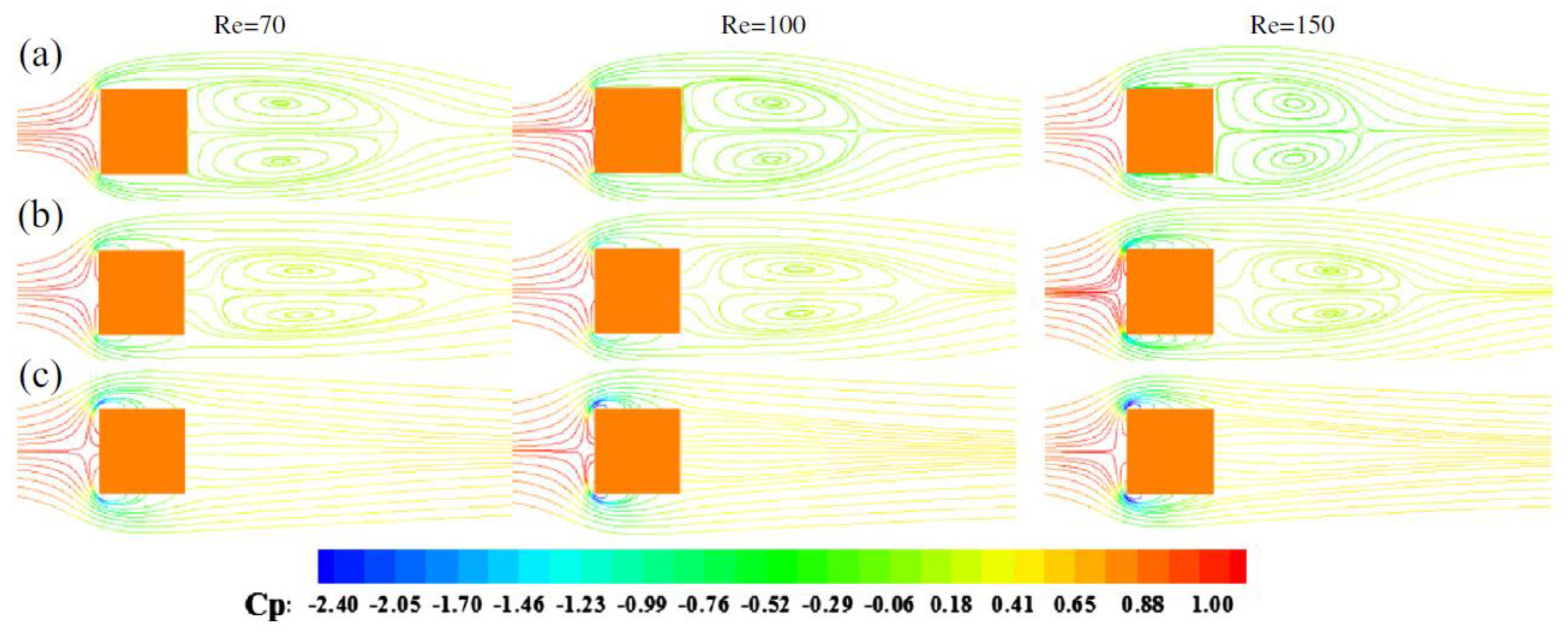
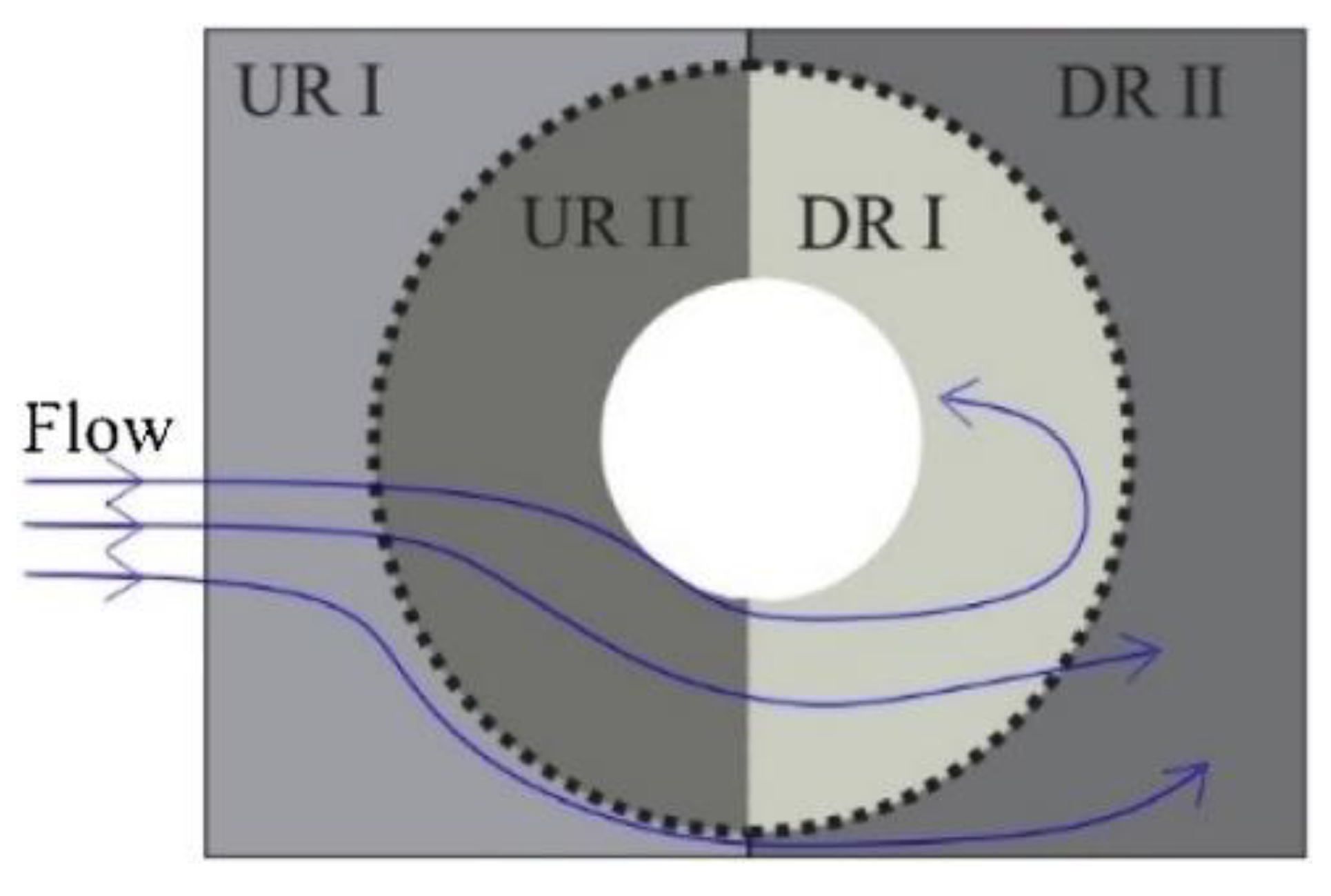
ResearchersFlow ControlReTITechniqueMeasurementsBluff BodyBR
Castro [21]Passive2.5 × 104–9.0 × 104-CTASt, UFP-
Çuhadaroğlu, Akansu [14]Active10,000–24,0001.2–1.5%PTCP, CD, USC-
Çuhadaroğlu and Turan [15]Active21,400-NumSt, CDSC-
Çuhadaroglu [16]Active--NumSt, CD, CLSC-
Turhal and Çuhadaroğlu [17]Active10,000–24,0001.2–1.5%PT, CTASt, CP, CDSC6.5%, 9.2%
Sohankar, Khodadadi [18]Active70–150-NumSt, CP, CD, CLSC5%
Saha and Shrivastava [19]Active100-NumSt, U, CDSC5%
Pinar, Ozkan [25]Passive10,0001%PIVUCC10%
Firat, Ozkan [22]Passive69004.5%PIVSt, UCC7.4%
Teimourian, Hacişevki [20]Passive18,5000.6%CTASt, USC5%
Durhasan, Pinar [23]Passive10,000-PIVUCC-
Re = Reynolds number; TI, turbulence intensity; CTA = constant temperature anemometry; PT = pressure transducer; PIV = particle image velocimetry; St = Strouhal number; CD = drag coefficient; CL = lift coefficient; CP = pressure coefficient; BR, blockage ratio; FP = flat plate; CC = circular cylinder; SC = square cylinder, Num = numerical.
Table
Table 2. Studies on flow control and suppression of vortex shedding by employing a permeable wall on bluff bodies.
Table 2. Studies on flow control and suppression of vortex shedding by employing a permeable wall on bluff bodies.
ResearchersFlow Control Reynolds NumberTechniqueBluff BodyMeasurements
Ozkan and Oruc [27]Passive8.5 × 103PIVCCU
Gözmen and Akilli [26]Passive5.0 × 103PIVCCU, St
Cicolin and Freire [28]Passive103–104PIV, FVCCU, St
Mimeau and Cottet [30]Passive550, 3000DNSSCC-
Liu and Wei [31]Passive4.7 × 104LESCC-
Durhasan and Pinar [29]Passive5.0 × 103PIV, FVCCU, CD
FV = flow visualization; PIV = particle image velocimetry; DNS = direct numerical solution; LES = large eddy simulation; St = Strouhal number; CD = drag coefficient; CC = circular cylinder; SCC= semicircular cylinder.
Table
Table 3. Selected studies on flow control and suppression of vortex shedding by employing corner modification.
Table 3. Selected studies on flow control and suppression of vortex shedding by employing corner modification.
ResearchersFlow Control Reynolds NumberTITechniqueMeasurements
Kwok and Wilhelm [32]CC--CTAU
Tamura and Miyagi [33]RC, CC104–1060.5%PS, Num CD, CL, CP, St
Tamura and Miyagi [34]RC, CC3.0 × 1046.5%, 14%CTA, FBCD, CL, St
Dalton and Zheng [37]RC250, 1000-NumCD, CL, CP, St
Hu and Zhou [35]RC2600, 60000.4%PIV, LDA, FVSt, U
Mola and Bordonaro [44]RC1051%NumCD, CL, St
Carassale, Freda [45]RC1.7 × 104, 2.3 × 1050.2%, 5%PS, FBCD, CL, CP, St
He and Li [39]RC, CC, CU10358%PIVU, St
Miran and Sohn [36]RC500-NumCD, CL, St
Tong and Sparrow [47]CC3.0 × 104 –2.3 × 106-NumNum
Miran and Sohn [46]RC500-NumCD, CL, St
Ueda and Kurata [40]CU200–10,0001%FV, NumU
Kurata and Ueda [41]CU5.0 × 104 –7.0 × 1040.8%, 1.2%CTA, FBCD, St
Ambreen and Kim [38]RC, CC, CU55–200-NumCD, CL, CP, St
TI, turbulence intensity; CTA = constant temperature anemometry; FV = flow visualization; PIV = particle image velocimetry; St = Strouhal number; CD = drag coefficient; CL = lift coefficient; CP = pressure coefficient; PS = pressure sensor; FB = force balance; RC = rounded corner; CC = Chamfered corner; CU = cut-corner, Num = numerical.
Table
Table 4. Selected studies on flow control and suppression of vortex shedding wavy cylinders.
Table 4. Selected studies on flow control and suppression of vortex shedding wavy cylinders.
ResearchersTechniqueReynolds NumberTIBluff Body
Darekar and Sherwin [57]Num10–500-SC
Lee and Nguyen [58]Exp5.0 × 103–2.0 × 1040.08%CC
Lam and Lin [48]Num3000-CC
Lin and Lin [53]Exp, Num3000-CC
Lam and Lin [49]Num3900-CC
Lam and Lin [50]Num100-CC
Lam and Wang [59]Exp200–90000.2%CC
Lam and Wang [60]Exp1.53 × 104–5.05 × 1040.2%CC
Lam and Lin [51]Num100–5000-SC
New and Shi [56]Exp27002%CC
Zou and Hu [54]Exp, Num600, 5900-SC
Shen and Miao [52]Exp, Num100–22,000-SC
Tammisola [61]Num50–100-CC
Assi and Bearman [55]Exp1500–15,0003%EC
CC = circular cylinder; SC = square cylinder; EC = elliptic cylinder; Exp = experimental; Num = numerical.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Teimourian, A.; Teimourian, H. Vortex Shedding Suppression: A Review on Modified Bluff Bodies. Eng 2021, 2, 325-339. https://doi.org/10.3390/eng2030021

AMA Style

Teimourian A, Teimourian H. Vortex Shedding Suppression: A Review on Modified Bluff Bodies. Eng. 2021; 2(3):325-339. https://doi.org/10.3390/eng2030021

Chicago/Turabian Style

Teimourian, Amir, and Hanifa Teimourian. 2021. "Vortex Shedding Suppression: A Review on Modified Bluff Bodies" Eng 2, no. 3: 325-339. https://doi.org/10.3390/eng2030021

APA Style

Teimourian, A., & Teimourian, H. (2021). Vortex Shedding Suppression: A Review on Modified Bluff Bodies. Eng, 2(3), 325-339. https://doi.org/10.3390/eng2030021

Article Metrics

Back to TopTop