Abstract
Modeling risk management systems in construction projects is a complex process because of various internal and external factors and their interrelationships. Fuzzy system dynamics (FSD) have been commonly employed to model and analyze construction risk management systems. To run FSD simulation models, all hard (objective) and soft (subjective) causal relationships between variables must be quantified. However, a research gap exists regarding structured methods for constructing soft causal relationships in FSD models. This paper proposes an adaptive hybrid model consisting of fuzzy analytical hierarchy process, weighted principle of justifiable granularity, and fuzzy aggregation operators to determine crisp values of causality degree for soft (subjective) causal relationships in FSD modeling of construction risk analysis. The proposed model is implemented in analyzing construction risks of a windfarm project to illustrate its applicability. The proposed model generates two results: (1) optimized membership functions for linguistic terms representing the causality degree of soft relationships and (2) the crisp value for the causality degree of soft relationships. The contribution of study is to propose a structured model to improve efficiency and effectiveness of developing FSD quantitative modeling by addressing soft causal relationships between different variables in FSD models and considering multiple risk expertise of heterogeneous experts in construction risk assessment.
1. Introduction
Decision-making procedures in construction projects are complex because a large number of factors and/or variables (e.g., risk events and work packages) are involved that have interrelationships and often-conflicting objectives [1,2]. Large projects with long durations entail a wide range of activities in different areas, as well as opposing stakeholder interests, making them particularly complex. Human actions and subjective reasoning complicate the interacting aspects that must be taken into consideration while making project management decisions [3]. In construction projects, decisions are often made based on analysis of complex systems and imprecise or unstructured data [3]. The influence of uncertainties on project objectives, which can be either positive or negative, may be managed through modeling complicated construction risk and uncertainty management systems comprising risk identification, quantitative and quantitative risk analysis, and planning risk responses [4,5].
In construction, common types of uncertainty include random uncertainty and subjective uncertainty [6]. Random uncertainty has been widely investigated, necessitating enormous amounts of project data to accurately estimate it. However, numerical project data frequently falls short of the amount or quality requirements for successful modeling, or the data may not be fully representative of new project environments. Subjective uncertainty exists in many decision-making processes in construction projects, which stems from the use of approximate reasoning and expert knowledge, which are expressed linguistically [3]. Helton [6] characterized uncertainty’s twofold nature by dividing it into “objective uncertainty” and “subjective uncertainty.” The variability that arises from an environment’s stochastic characteristics is referred to as objective uncertainty, and its concepts are based on probability theory. Subjective uncertainty, on the other hand, results from the use of approximate reasoning and linguistically articulated expert knowledge. Subjective uncertainty is classified by Fayek and Lourenzutti [7] as vagueness, ambiguity, and subjectivity. Vagueness arises from the absence of clear distinctions between important concepts. Ambiguity occurs when an object lacks specific distinctions that define it, from conflicting distinctions, or from both. Subjectivity arises as a consequence of the impact of personal beliefs or emotions rather than objective facts [8].
Fuzzy system dynamics (FSD), a hybridization of system dynamics (SD) and fuzzy logic, is capable of capturing the dynamism and interactivity of real-world system components while addressing the limitations of SD, such as the lack of ability to deal with subjective uncertainties. FSD is concerned with system feedback loops and is capable of modeling systems in which the system variables change continuously through time [3]. FSD can also keep track of the changes in the dynamics of variables (e.g., risk events, work packages) in construction projects. FSD is a suitable simulation approach when the primary areas of interest for the modeler are analyzing the changes in variables in the system over time, detecting the impacts of factors influencing the system’s variables, and capturing vagueness, ambiguity, and subjectivity in linguistic terms [3,9]. Causal loop diagrams (CLDs) are employed in FSD models to map soft (subjective) and hard (objective) causal relationships and causal structures among model variables. When the mathematical form of a causal relationship is known, it is said to be “hard” (e.g., relationship between risk severity and risk impact). Soft causal relationships, on the other hand, are those in which the mathematical form of the causal relationship is unknown (e.g., relationship between the probability of occurrence of a risk event and a secondary risk event) [10,11]. Soft causal relationships are expressed in linguistic terms. Regular or fuzzy arithmetic can be applied for hard relationships depending on the objectivity or subjectivity of variables. However, the literature reveals a lack of structured and systematic methods for constructing and analyzing complex soft relationships among the elements of a system in order to develop CLDs [4].
To develop a quantitative FSD simulation model, the crisp value of all causal relationships (i.e., soft and hard) needs to be calculated. To determine the crisp value of soft causal relationships in practice, it is necessary to determine the membership functions (MBFs) of linguistic terms resulted from a heterogenous expert’s opinions [11]. The opinions of experts about forming MBFs of linguistic terms may differ based on their attitude, knowledge, and experience [12]. Two main categories of MBF estimation are expert-driven approaches, in which MBF elicitation is considered a method of acquiring less or more sophisticated knowledge through interaction with a domain expert, and data-driven approaches, in which the elicitation of MBFs is based on organizing data into a structure [13]. The analytical hierarchy process (AHP) [14] is an expert-driven technique that enables experts to do pairwise assessments of alternatives in order to establish their MBF. There are some limitations to and eventual biases in the aforementioned techniques for eliciting MBFs [15]. The expert-driven method may become broad in nature and may not even be necessarily reflective of the experimental data used to generate these fuzzy sets [16]. This limitation is especially evident when such fuzzy sets are included in the resulting fuzzy model, which may occur as a result of the absence of experimental support for some MBFs [13]. For example, in a construction risk management system, AHP as an expert-driven method is not applicable in forming the MBFs of linguistic terms related to construction risks since employing AHP means all risks and opportunities must be considered as alternatives for pairwise comparison, which can be impossible or very time-consuming [17,18]; for example, for a project with 100 risk events, almost 4900 pairwise comparison among risk events must be performed by each expert to form only probability MBF, and the result is not necessarily linear. On the other hand, because of the difficulty of obtaining qualified numerical data on risk management for construction industry projects, data-driven methods are not applicable in the majority of cases [3,17]. Additionally, using data-driven methods may result in semantically meaningless fuzzy sets [17], which implies that fuzzy clustering could result in some “crowded” fuzzy sets with ambiguous meaning that need to be tuned by an optimization method, such as simulated annealing algorithm, genetic algorithm, or tabu search [15,16]. These limitations make data-driven methods inefficient and time consuming. As a result, their further modifications, when optimizing the fuzzy model that comprises the fuzzy sets, may significantly impair the interpretability of the fuzzy sets and the entire model [15]. Aggregation methods used in previously published FSD approaches do not account for risk management experts’ levels of expertise. In most instances, a moderator or project manager assigns importance weights to experts directly [10]. The principle of justifiable granularity (PJG) is a well-known paradigm and fundamental concept of granular computing, offering robust guidance for structuring information granules based on existing experimental data. PJG can be employed to optimize interval type-2 fuzzy sets and form type-1 MBFs [13].
The current construction literature lacks a structured method for constructing and investigating soft causal relationships in FSD modeling of construction risk analysis. To form the soft causal relationships in an FSD model, MBFs of linguistic terms pertaining to these relationships must be determined. However, both expert-driven and data-driven methods have limitations to forming MBFs of linguistic terms of soft causal relationships by experts, which are necessary to assess them. To address these research gaps, the objective of this paper is to propose an adaptive hybrid model for calculating crisp values of causality degrees of soft causal relationships in FSD modeling of construction risk management. The proposed model consists of fuzzy analytical hierarchy process (FAHP), weighted principle of justifiable granularity (WPJG), and fuzzy aggregation operators. FAHP enables the proposed model to calculate the level of risk expertise (importance weight) of different experts based on several factors and consider these importance weights in both processes of forming MBFs for linguistic terms and integrating experts’ assessments of soft causal relationships. Moreover, WPJG [15] is applied to increase the accuracy of constructing MBFs of soft causal relationships by determining the optimum value of upper and lower bounds before converting them into type-1 MBFs. Furthermore, fuzzy aggregation operators are employed to aggregate the assessments of several heterogeneous experts’ opinions using constructed fuzzy MBFs and the importance weight of each expert. The resulting crisp value of soft causal relationships then can be employed to form CLDs and run the FSD simulation model.
The rest of this paper is organized as follows. First, the advantages and disadvantages of available methods of modeling complex systems in analyzing construction risks are reviewed and compared in Section 2.1. Second, Section 2.2, Section 2.3 and Section 2.4 review and discuss the benefits, literature, and capabilities of techniques used in the proposed model, including FAHP, WPJG, and fuzzy aggregation operators, respectively. In Section 3, the proposed adaptive hybrid model is presented for calculating the causality degree of soft causal relationships in FSD modeling of construction risk management systems. Section 4 reports how the proposed model is implemented in a wind farm project to show how the adaptive hybrid model can be implemented in practice. Finally, Section 5 discusses the contributions, and results of this research are presented, along with potential future extensions.
2. Justification of Applied Techniques in the Proposed Model
This section first discusses the benefits and limitations of several modeling methods for complex systems. The concepts and techniques required for the proposed adaptive hybrid model are then discussed, and it is demonstrated that FSD is more capable than other mentioned techniques to model causal relationships among variables of construction risk analysis systems.
2.1. Reviewing and Comparing Fuzzy System Dynamics and Fuzzy Cognitive Maps Capabilities to Model Construction Risk Management Systems
SD, FSD, cognitive maps, and Fuzzy cognitive maps (FCM) methods allow modeling causal relationships among variables of a complex model. This subsection reviews the merits of mentioned techniques and compares their modeling capabilities.
The first cognitive maps were introduced in 1976 [19] with the goal of representing social scientific knowledge through defined digraphs with arcs representing causal links between nodes. Modeling the knowledge associated with a complicated system is possible using these graph-based structures. There are two major downsides to cognitive mapping [20,21]. The first is a lack of expression power, which causes causal relationships between two variables to be expressed as positive and negative states. Furthermore, cognitive maps lack inference capabilities, which implies we cannot make decisions based on the model’s relationships. FCM, introduced by Kosko [22], is an extension of cognitive maps theory that addresses its limitations. FCM is a modeling approach that relies on knowledge and expertise to describe domains using concepts (i.e., variables, statements, inputs, outputs) and their relationships [23]. Casual signs are substituted by signed and weighted arrows that take values in the [−1,1] interval to address representation capability. Because both ideas and relations have corresponding numerical weights with a coherent meaning for the problem under analysis, simulations can be used to address the reasoning capability problem of cognitive maps. Some limitations when applying FCMs comprise: (1) weights relate the states of concepts rather than changes in state, (2) meaning of iterations and activation function is unclear, (3) a need exists to invert concepts to avoid negative weights, and (4) convergence can be problem and results may not make sense [24,25,26].
On the other hand, SD, developed by Jay Forester in the 1950s [27], is a well-developed continuous simulation technique that can model the dynamic behavior of complex systems and is a viable simulation approach to modeling the complexity of projects [10,11]. One primary goal of SD is to capture how components in a system interact with one another and how changes in one variable influence another over time [28,29]. Xue et al. [30] proposed an SD-based risk model to assess risks of high-speed rail (HSR) projects. However, their proposed model has certain limitations, such as ignoring unavoidable subjectivity in experts’ risk evaluations. Complex construction processes involve subjective variables, which are qualitative in nature and are best expressed using linguistic words. Moreover, since most construction projects lack sufficient historical quantitative data, developing probabilistic distributions for system variables can be difficult [9]. Furthermore, casual relationships of systems cannot be clearly calculated by statistical methods and represented as numerical values because of the lack of sets of similar data [11]. Therefore, to capture the subjective uncertainties of the subjective variables and relationships in the simulation model, SD must be integrated with fuzzy logic, resulting in FSD [9,11]. The FSD technique can capture the dynamism of construction uncertainties and the interactions among project components [9]. FSD also addresses the limitations of FCM since (1) weights are similar to elasticities and their meanings are clear, (2) sensitivity functions modify weights as a function of concept value, (3) if a model contains one or more cycles, calculations are iterated to convergence, and (4) node values are in range of percent of maximum assumed real value [26].
2.2. Fuzzy System Dynamics for Construction Risk Management
FSD was first developed in 1990 [31] by integrating SD with fuzzy logic, which results in improvements of SD technique’s capabilities. System variables with subjective uncertainty and the uncertainty of the relationships among system variables can be represented in FSD models by MBFs rather than probabilistic distributions or deterministic values [9]. Quantitative historical data are not widely available because construction projects are unique, which means there is a lack of data points from which to develop probabilistic distributions to represent the risk factors associated with these projects. Another issue is that the subjective impact of these risk factors is largely based on expert knowledge, and that also includes an uncertainty due to the nature of construction projects [9].
To develop and run an FSD model, both qualitative and quantitative FSD models must be built. The qualitative FSD model (system thinking) allows users to recognize system behavior, whereas the quantitative FSD model allows users to dynamically simulate system behavior and anticipate system state [9,10,11]. As illustrated in Figure 1, SD enables users to understand how components of a system interact with one another and how a change in one variable impacts another variable over time [27]. Thus, utilizing feedback loops and stock and flow structures, a qualitative FSD model may be created. The qualitative model creation process begins with identifying system variables, such as risk events. The qualitative model illustrates the hard and soft relationships and interactions between model variables [27]. Then, to support realistic representation, the initial model boundary and the amount of aggregation are determined. The model border denotes the modeling scope, whereas the aggregation level denotes the subdivision of activities into subsystems [27]. Then, using CLDs and stock and flow maps, the interdependencies, causal structures, feedback structures, stocks, and flows are mapped. Following that, the qualitative model’s layout is constructed [10,27].
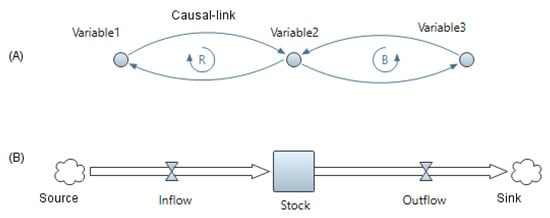
Figure 1.
Components of system dynamics (SD): (A) Causal loop diagrams (CLDs) and (B) stock and flow diagrams (adapted from References [3,9]).
In order to construct the quantitative FSD model, it is necessary to formulate the variables and relationships of the qualitative model to simulate the model. Formulating the objective and subjective system variables and relationships is performed to develop the quantitative FSD model, in which the objective system variables are represented by crisp numbers (e.g., work package cost) and the subjective system variables are represented by MBFs, such as impact and probability of risk events, which are represented using linguistic terms, such as “Very Low” or “High.” Moreover, hard (objective) relationships can be represented by equations, while crisp values of soft (subjective) causal relationships must be calculated initially. Then, an equation comprising the values of impacted and caused variables along with the crisp values of soft causal relationships can be determined, and the FSD simulation can be run [10]. Few research projects have investigated FSD’s applicability to risk modeling and analysis. For example, Loh et al. [32] proposed a framework that combines SD and fuzzy logic to facilitate the development of risk models for autonomous underwater vehicle (AUV) operations in the Antarctic. However, their proposed model does not suggest a systematic method for determining MBFs for linguistic terms representing the causality degree of soft relationships and the crisp value for the causality degree of soft relationships. In addition, Nasirzadeh et al. proposed a fuzzy-based SD approach [33] for integrating risk management procedures for construction projects. In another study, an FSD model with a similar technique was used to establish the best risk allocation percentage between owners and contractors for construction projects [34]. Very few fuzzy variables were considered in the FSD models in either technique. The project objective implications of the risks were evaluated at the project level, and opportunities in the evaluation process were not addressed. In both techniques, a fuzzy Delphi, requiring multiple rounds of modifications to attain an acceptable degree of agreement, was employed for aggregating expert input, but the experts’ expertise levels were not considered. In another study using expert judgement and subjective evaluation, a hybrid FSD model 020 was designed to study the impacts of linked and interacting risk and opportunity events on work package cost in order to estimate work package and project contingencies [10]. However, the model was limited to risk assessment level and ignored risk response planning, which plays a vital role in managing risks.
2.3. Role of Expert’s Level of Risk Expertise in FSD Risk Modeling
Level of experts’ risk expertise must be considered to maximize knowledge elicitation and avoid biased assessments in both forming CLDs and assessing soft causal relationships in FSD risk modeling. Level of risk expertise can be determined based on multiple factors, such as knowledge, credentials, and experience of assessors. Various techniques have been used in construction for this goal. For example, Elbarkouky and Fayek [35] employed a fuzzy expert system (FES) to aggregate expert opinions on roles and responsibilities in project delivery systems and calculated the experts’ weights based on their qualification characteristics. In another study [36], a multi-attribute utility function (MAUF) was utilized to calculate the consensus weight factor for each expert based on their utility values and the relative weight of experience measures for contractor prequalification in surety bonding. Both FES and MAUF, however, have limits when dealing with many criteria. To propose a method for weighting experts according to their level of risk expertise while also handling a large number of criteria, this study employs an extended version of AHP.
AHP is a rational and straightforward measuring theory [14] that has been effectively implemented in the construction industry. AHP is capable of handling a large number of criteria by decreasing the number of necessary comparisons hierarchically. AHP is a structured yet flexible approach that can be easily updated or adjusted. However, the pairwise comparison may cause a dimensionality issue because of the large number of variables compared. Moreover, conventional AHP is incapable of accounting for the imprecise or vague nature of linguistic assessment and uncertainties inherent in expert evaluations. To alleviate this constraint, Laarhoven and Pedrycz [37] proposed a fuzzy analytic hierarchy process (FAHP) was proposed, which is an extended form of AHP that enables professionals to make decisions using linguistic terms represented by fuzzy numbers. Pedrycz and Laarhoven [37] and Buckley [38] modified Saaty’s importance rating scale [14] to allow experts to utilize linguistic terms, expressed as fuzzy number ratios instead of conventional AHP crisp ratios, in pairwise comparison matrices [39]. Thus, fuzzy pairwise comparison matrices were constructed to approximate the imprecise and ambiguous value of human judgment [39]. Given the complexity of construction methods and their inherent uncertainties and subjectivities, it is proposed that, rather than using AHP definite scales, FAHP linguistic scales be used for assigning importance weights to experts in order to more accurately capture their opinions in the proposed model [40]. Additionally, the FAHP model has the benefit of allowing for overlapping linguistic terms that more accurately represent human perspectives, allowing for a smoother transition between diverse viewpoints than the crisp numerical representations of experts’ opinions. In conclusion, the FAHP is a more appropriate model for calculating the level of risk expertise (importance weight) for each expert to be employed in forming MBFs of linguistic terms.
2.4. Weighted Principle of Justifiable Granularity
Conventional approaches for creating fuzzy sets (or information granules) are limited in terms of forming MBFs of linguistic words, which are required for experts to evaluate soft relationships. Both expert- and data-driven approaches rely on expert (user) perception or data (data-driven constructs). PJG can be defined as the approach that maximizes the utility of available experimental data while augmenting the construct with domain knowledge, either in the form of a single component of the general criteria or additional problem-oriented domain knowledge. In this way, the concept can be thought of as representing a middle ground between the two previously mentioned data- and expert-driven approaches [17].
Granular computing, which incorporates fuzzy sets as a formal framework [15,18,41,42], is concerned with obtaining, processing, and transmitting information granules [43]. It becomes critical to identify (construct) information granules, which are utilized as conceptual entities in granular models, predictors, classifiers, and data descriptors as follows. The challenge of creating fuzzy sets has been a cornerstone of the field, serving as a requirement for any future uses of these information granules [15]. A prominent tendency in granular computing that is also evident in fuzzy sets is to study and apply higher-order information granules [43]. Regarding intervals, a more advanced sort of construct presents itself in the form of granular intervals, that is, intervals whose limits are no longer integers but information granules. This trend toward increasing the variety of information granules is readily seen in the form of type-2 (particularly interval-valued) or order-2 fuzzy sets [15,44].
PJG [43,44] is a prominent paradigm and one of the core foundations of granular computing, providing strong guidelines for dealing with constructing information granules in a structured way based on available experimental evidence [15,45]. For further extensions and applications, refer to Pedrycz [17,44]. The PJG objective is to create an information granule that is empirically justifiable (i.e., can be justified by experimental data) and conceptually meaningful (i.e., having a well-defined semantics) [17]. These two intuitive criteria are represented as the coverage criterion and the specificity criterion. The term coverage refers to the amount of data that is positioned behind the formed information granule; coverage indicates the degree to which an information granule is backed up by existing experimental data. Specificity is concerned with the semantics of the information granule, emphasizing the granule’s meaning [15,17]. PJG can be extended to accommodate scenarios in which individual data are linked with weights, which can be used to assess their quality, which may vary from element to element [43,46]. Consequently, PJG and WPJG can be potential solutions in constructing MBFs of linguistic terms.
2.5. Fuzzy Aggregation Operators
The use of aggregation operators is key in every aggregation process. Aggregation operators are divided into two categories: crisp aggregation operators combine expert preferences expressed as crisp numbers, whereas fuzzy aggregation operators combine expert preferences expressed as linguistic phrases (which can be transformed to interval numbers, or fuzzy numbers). When group decision-making contains solution alternatives and options that cannot be accurately evaluated with a precise numerical value, linguistic evaluation and natural language are used in order to offer a more meaningful representation of experts’ judgments. Therefore, in a group decision-making situation, fuzzy aggregation operators are employed to integrate the numerous experts’ linguistically expressed preferences.
Several applications demand fuzzy aggregation in construction group decision-making procedures. A review of the literature confirms that numerous fuzzy aggregation operators have been proposed, comprising fuzzy weighted average (FWA) [47], fuzzy ordered weighted average (FOWA) [48], fuzzy number-induced ordered weighted average (FN-IOWA) [49], fuzzy weighted geometric operator (FWG) [50], and fuzzy similarity aggregation method (FSAM) [51]. Selecting an aggregation operator depends on its characteristics and application.
Several properties for aggregation operators can determine the best option for each context. These properties comprise: (1) commutativity condition, which says the ordering or ranking of arguments is irrelevant and all criteria are equally important, (2) monotonicity, where the criteria and the aggregation output have a non-decreasing relationship in functions, (3) boundary condition, in which the outputs of the aggregation function are constrained to the minimal and maximum bounds of the function, and (4) idempotence, which is the strongest kind of agreement or unanimity, which is said to occur after the same initial value is aggregated n times and the outcome is the same as the initial value [52]. FOWA is commutative, monotonic, bounded, and idempotent.
Smolikova and Wachowiak [53] employed several aggregation operators to evaluate a case study, and they discovered that the FWG and FOWA operators provide more flexibility in fulfilling analysis requirements than FWA. The FOWA aggregation operator is the most often used aggregation operator in construction risk assessment [52]. Moreover, when working with fuzzy numbers, mathematical operations are critical because the fuzzy number format is not always preserved (e.g., multiplication of triangular fuzzy numbers). The FOWA aggregation operator simplifies the process of getting the product of two fuzzy numbers without modifying the fuzzy number format. Additionally, while evaluating reciprocal fuzzy pairwise comparison matrices in FAHP, the FOWA aggregation operator demonstrates exceptional efficiency and effectiveness. Furthermore, several fuzzy aggregation operators have been tested in the construction risk management domain, and the symmetric mean absolute percentage error (SMAPE) has been calculated, indicating that FOWA provides the smallest error [52]. As a result, FOWA is employed in this study as the aggregation operator for various assessments of heterogenous experts.
3. Methodology: Developing Adaptive Hybrid Model to Form CLDs in FSD Modeling
Development of an FSD model, as discussed in Section 2.1, is divided into two general phases: (1) creating a qualitative model and (2) developing a quantitative model. Qualitative modeling allows for identification of system variables and causal relationships, as well as the development of stocks and flows. In the quantitative modeling phase, the values of variables should be established using crisp numbers and probability distributions. Moreover, all causal relationships and interdependencies among the model variables should be formulated in order to run the model and identify the effect of variables [27]. So, while mathematical equations are always used to define hard relationships, soft causal relationships can be determined in three steps, as illustrated in Figure 2.
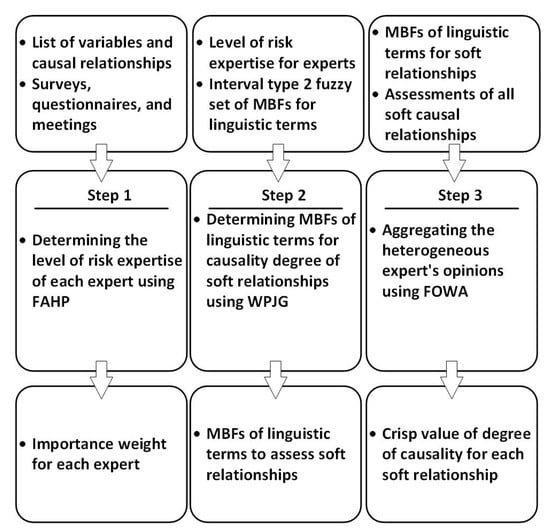
Figure 2.
Inputs and outputs of all steps in adaptive hybrid model to determine soft causal relationships in fuzzy system dynamics (FSD) modeling.
The 3-step process for determining soft causal relationships begins with evaluating experts’ risk expertise to enhance knowledge elicitation and avoid making faulty judgments using FAHP. The output of the first step, which is determining the importance weight for each expert, can be utilized in the second step where MBFs of linguistic terms (e.g., “Low” or “High”) for assessing causal relationships are built, optimized, and aggregated in order to use the knowledge and skills of all project decision makers and experts. In step 2, interval type-2 fuzzy sets are initially formed that contain all possible viewpoints of the experts. Then, constructed interval type-2 fuzzy sets are optimized and integrated using WPJG, resulting in MBFs of linguistic terms for the assessment of soft causal relationships. In the third step, all qualified experts are required to assess degree of causality for soft causal relationships based on optimized and aggregated MBFs in the second step. Then, the FOWA aggregation operator is used to aggregate the assessments of all experts. The output of the first step, importance weight for each expert, is utilized as one of inputs of third step, since FOWA is a weighted aggregation operator. Next, the aggregated fuzzy degree of causality between variables can be established and defuzzified to obtain the crisp degree of causality. The details of each step are described as follows.
3.1. Step 1—Determining the Importance Weight of Each Expert Using FAHP
When aggregating expert judgments of the degrees of soft causal relationships among variables in the model, the importance weights of the experts must be accounted for. For example, Monzer et al. [52] recommended assessing experts’ level of risk expertise based on seven criteria comprising experience, knowledge, professional performance, risk management practice, project specifics, reputation, and personal qualities and skills. These criteria are employed in this paper to calculate level of risk expertise (importance weight) for each expert. Each of the seven criteria has quantitative or qualitative subcriteria, and for each of the qualitative attributes assessed using a preset rating scale (1–5), detailed information can be found in Monzer et al. [52]. The importance weights of the experts, (Wk), are derived using FAHP weight-assigning approach after analyzing the experts’ level of expertise based on the mentioned attributes. Unlike standard AHP, which utilizes crisp numbers, the FAHP approach allows experts to do pairwise comparisons using fuzzy linguistic evaluations [54]. As a result, the FAHP approach is used to calculate the relative weights of qualifying attributes and criteria based on expert pairwise assessments. For further information about FAHP equations and concepts, refer to Monzer et al. [52]. The importance weight of each expert can be employed in both steps 2 and 3 in order to (1) form MBFs of linguistic terms for degree of causality and (2) aggregate several assessments of degree of causality.
3.2. Step 2—Forming MBFs of Soft Causal Relationships Using WPJG
Linguistic terms (e.g., “Very Low” or “Very High”) for illustrating the causality degree of soft causal relationships are defined in order to enable experts to assess them. Defined linguistic terms for causality degree of soft relationships among variables are fuzzy numbers. These fuzzy numbers can be represented by triangular or trapezoidal fuzzy numbers, since the most popular forms for fuzzy numbers with open intervals of real numbers are triangular and trapezoidal [7,12]. Trapezoidal fuzzy numbers are a subset of triangular fuzzy numbers. The degree of causality between variables is denoted in this model by five linguistic terms: ”Very Low,” “Low,” ”Medium,” “High,” and ”Very High.” Various MBFs for causal relationships are established and aggregated in order to benefit from the collective knowledge and expertise of all project decision makers and experts. A type-1 fuzzy set projects a single crisp number for the membership degree of each linguistic term, whereas interval type-2 fuzzy sets project an interval for the membership degree of each linguistic term [55,56,57]. Consequently, interval type-2 fuzzy sets are more appropriate because they give more information than type-1 fuzzy sets and are more accurate. In addition, an interval type-2 fuzzy set encompasses all possible viewpoints. Consequently, the intervals’ lower and upper bounds are initially defined in this step by the lowest and highest heights of the MBFs constructed for linguistic terms (e.g., ”Low,” “Medium,” “High”) to assess degree of causality using the information from various risk experts.
After forming interval type-2 fuzzy sets of linguistic terms, the WPJG is applied in order to optimize these intervals and construct information granules. Coverage and specificity are two essential requirements invoked by the WPJG. The two criteria are at odds, which means that increasing coverage decreases specificity, and vice versa. Therefore, constructing information granules is a result of tradeoff between them, and there is an optimization problem with a multiplicative form of the objective function, shown by Equation (1), where D is an information granule based on the available experimental evidence resulting in a form of a collection of one-dimensional numeric data, and D = {x1, x2, …, xN}, where xk ∈ R. Coverage is expressed as the cardinality (count) of the data X included in the interval [m,b], assuming m is the numeric representative of a data set, such as a median. In addition, specificity can be related directly with the length of the interval and define any decreasing function of the length that is |m − b| or |m − a|, where a and b are the optimized values of the lower and upper bounds of the interval, respectively.
V(b) = coverage × specificity
Equation (1) can be implemented separately for the lower and upper bounds of the interval as follows:
V(b) = f1(card{xkD|med(D) < xk ≤ b}) × f2(|med(D)−b|),
V(a) = f1(card{xk ∈ D|a ≤ xk< med(D)}) × f2(|med(D)−a|).
By maximizing V(b), we achieve an optimal value of b, which is to say,
bopt = arg maxb V(b)
The optimal upper bound bopt can be obtained by maximizing the value of V(b), namely V(bopt) = maxb>med(D)V(b). The lower bound of the information granule is constructed in the same way: aopt, that is, V(aopt) = maxa<med(D)V(a).
The importance weights of each expert calculated in the last step using FAHP can be integrated with PJG, resulting in WPJG. To form WPJG, Equations (2) and (3) can be extended to deal with situations where data are associated with relative weights [17]. In this case, given the data form (xi, wi), where wi represent weights in the range of an [0,1] interval, w = [w1, w2, …, wN], the upper and lower bounds can be determined by maximizing the performance index V as follows:
where med(D,w) is a weighted median as follows:
After implementing WPJG and optimizing the upper and lower bounds of interval fuzzy sets, MBFs are type-reduced to standard MBFs for the purpose of performing crisp output computation. In this research, the procedure described in Reference [12] is used to transform an interval type-2 MBF to a type-1 MBF.
3.3. Step 3—Aggregating the Heterogeneous Expert’s Opinions Using Aggregation Operators
In step 3, MBFs of linguistic terms determined in the previous step are utilized to assess degree of causality for soft causal relationships. Assessments of several experts are aggregated using FOWA. The FOWA aggregation operator is a weighted aggregation operator for combining the linguistic opinions of diverse experts [48,49], as a simple extension of the ordered weighted average (OWA) operator used in uncertain scenarios where the available data input and knowledge source may be evaluated using fuzzy numbers [51,52]. FOWA supports parameterization of a family of aggregation operators, including the fuzzy maximum, fuzzy minimum, and fuzzy average criteria. Additionally, FOWA shares many of the same characteristics as OWA [48]. Letting 𝑓: Θ𝑛 → Θ, where Θ is the set of all fuzzy numbers, the formula for applying FOWA is:
where is the weighting vector, and ∈ Θ, which means are fuzzy number representing experts’ opinions. In addition, , and , and
is the largest jth of the [17]. Here, the weighting vector 𝑤𝑗 is calculated in Step 1 using FAHP. The aggregated fuzzy number of causality degree among variables can then be determined and is defuzzified to calculate crisp degree of causality. Consequently, crisp values of causality degree are employed to form CLDs and run the FSD model to assess construction risks.
4. Case Study: The Proposed Adaptive Hybrid Model
The main purpose of the case study was to illustrate how to implement the proposed model for analyzing risks of a construction project. The proposed model was employed as part of forming an FSD simulation model for analyzing construction risks of a real wind farm power generation construction project, since authors had access to some project information. However, the model can be implemented in any kind of construction project. Implementation of the proposed model is illustrated to (1) form MBFs of causality degree for soft causal relationships and (2) determine the crisp value of causality degree for soft causal relationships. To maintain confidentiality of project information, some actual information and value of used relationships and variables were substituted in the case study for some hypothetical data. Names and values of some variables comprising risks, risk responses, secondary risks, and assessments of causality degree for soft causal relationships are substituted. However, actual data and information were utilized to calculate experts’ level of risk expertise. Moreover, the type of objective and subjective variables and the types of hard and soft relationships between them are real and were extracted from a risk analysis model of a real wind farm project in North America. The real wind farm project had eight construction work packages, which are categorized as civil, structural, and electrical.
FSD modeling begins with qualitative modeling, followed by quantitative modeling, to formulate all identified variables and relationships. The process of developing a qualitative model starts with the identification of system variables (e.g., risk events) and all hard and soft relationships and interactions between variables. Additionally, it incorporates the feedback structure for various variables (e.g., response actions that are available to address identified risks). The initial model boundaries, as well as the degree of aggregation, may then be determined in order to achieve the objective of realistic representation. Although the model boundary indicates the extent of the modeling exercise, the aggregation level indicates the breakdown of activities into subsystems. Using CLDs, stock and flow maps, and other tools, the interdependencies, causal structures, feedback structures, stocks, and flows are all visualized and represented graphically. Next, the layout of the qualitative model is developed, as depicted in Figure 3.
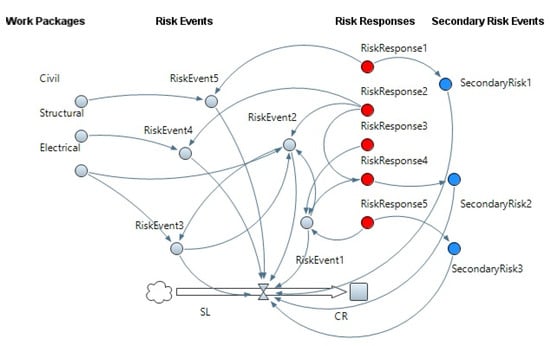
Figure 3.
Graphical representation of FSD model in qualitative step in Anylogic software.
To formulate soft causal relationships in the quantitative modeling phase, the proposed model in this study is implemented in the following three steps.
4.1. Step 1: Determining Risk Expertise
In the first step in formulating soft causal relationships, the experts’ level of risk expertise (importance weights) is calculated. The criteria for choosing experts were their engagement in the project, their overall years of experience, their years of risk management experience, and the number of similar projects in which they had participated. A diverse group was established from four real experts who were actively involved in the project. Each expert was a part of the project team and had worked on more than five comparable-scale projects. They had an average of 23 years of total construction experience and an average of 12 years of risk management experience [10].
In Step 1 of determining soft causal relationships, the risk expertise levels (importance weights) of the experts were determined using a combination of numerical and linguistics attributes, as detailed in Table 1. Next, the evaluation data were normalized to the range [0,1]. Then, the weights assigned to the criterion and subcriteria were used to compute the experts’ level of risk expertise. The FAHP weight assignment technique was then used to compute the importance weights (Wk) of the four experts, W1, W2, W3, and W4. Calculated weights, such as each expert’s importance weight (risk expertise), must be normalized before being used as the expert’s importance weight. The experts’ importance weights are relative weights that, when added, equal 1. This guarantees that the opinions of experts with a higher weight of importance have a greater effect on the experts’ collective evaluation. The four experts’ importance weights were 0.25, 0.27, 0.22, and 0.26.

Table 1.
Expertise level of the experts in risk management (list of criteria names adapted from reference [52]).
4.2. Step 2: Constructing MBFs of Soft Causal Relationships
In the second step, MBFs of linguistic terms for assessing causality degree of soft relationships are formed by expert opinions using WPJG. The following phase establishes linguistic terms, their scales, and associated fuzzy sets in order to analyze the degree of causality for project components with soft causal relationships. So, Step 2 begins with gathering opinions of several experts about the scales of linguistic terms of causality degree (e.g., “Very Low,” “Low,” “Medium,” “High,” and “Very High”). For example, based on the opinion of Expert 1, the linguistic term “Very Low” for causality degree ranges from 0 to 18 percent with the membership value of 1 in 0 percent. Then, interval type-2 fuzzy sets of each linguistic term are constructed for degree of causality in soft causal relationships. Interval type-2 fuzzy sets capture more uncertainty than their type-1 counterparts [55,57,58,59]. Thus, the opinions of all experts are employed to form interval type-2 fuzzy set. Since there were four experts in the project whose opinions were critical to risk modeling, interval type-2 fuzzy sets were employed to account for all MBFs these experts proposed. The interval type-2 fuzzy set was constructed by calculating the lowest and highest bounds of the proposed MBFs.
Then, the tradeoff between specificity and coverage of each interval is conducted using the WPJG and considering it as a multiplicative optimization problem [17,44,46]. The parametric WPJG can mitigate the influence of irrelevant and biased opinions. Equations (5) and (6) are employed to determine the optimized upper and lower bounds of each interval by maximizing the performance index.
For crisp output calculation, type-2 fuzzy sets are subsequently converted to standard MBFs. The process of converting an interval type-2 fuzzy set to a type-1 fuzzy set, proposed by Fateminia et al. [13] and Pedrycz [17], is applied in this study. The objective of the type reducing process is to determine the line that best fits these interval fuzzy values. Initially, mean and domain values are used to represent the interval fuzzy values statistically. The interval sets are represented by their corresponding mean points in the x–y space, which are (0,1), (10,0.75), (15,0.6), and (20,0.05). The mean values of all interval type-2 fuzzy sets may not be linear. Therefore, to get the best-fit linear equation, a linear equation between (0,1) and the mean point of each interval set is required to be solved for an x-axis intercept value. Statistically, the modeled linguistic term should fall inside the range [13,17]. Here, is the mean of the interval type-2 fuzzy set’s left endpoints, and is the mean of the set’s right endpoints. If the endpoint uncertainties are removed, the preceding interval type-2 fuzzy set degrades to a type-1 fuzzy set with a = b = = . The mean of these points is at = 22 with standard deviation s = 3.06. Consequently, the optimized MBFs for various linguistic terms are similarly calculated as illustrated in Table 2. The optimized fuzzy numbers in Table 2 can be employed to assess risks and opportunities in the next step.

Table 2.
Linguistic terms and fuzzy numbers for assessing the degree of causality.
4.3. Step 3: Aggregating Assessments
In the third step of the model, several experts assess the causality degree of soft causal relationships based on linguistic terms constructed in Step 2 (Table 2). Then, FOWA is employed to aggregate the assessments of the four experts, resulting in creation of a single fuzzy number that reflects the group’s opinion. Experts offer their evaluations of causality degree for soft causal relationships using linguistic terms that are represented by fuzzy numbers that are optimized and formed in step 2. The importance weights of the experts, calculated in Step 1 using FAHP, are utilized by FOWA as the weight vector for the experts’ assessments in order to reflect their level of expertise. The aggregated fuzzy number of causality degrees across variables are then calculated. Finally, aggregated fuzzy number of causality degree is defuzzified to obtain the crisp value for degree of causality for the soft causal relationship.
4.4. Results and Discussion
The proposed hybrid model results in calculated the crisp value of causality degree for soft causal relationship among each pair of variables (e.g., variables 1 and 2) while considering the level of risk expertise for each assessor. Crisp values of causality degree for soft causal relationships are employed to formulate the value of the second variable (affected by first variable through a soft causal relationship) in different time steps of the FSD simulation. As a result, the FSD simulation model comprising of soft causal relationships can be quantified and run in simulation software (e.g., Anylogic) to evaluate construction risks.
The crisp value of causality degree for soft causal relationships among project components in this study are: 0.37 between risk event 2 and work package-electrical; 0.56 between risk event 2 and risk event 3; 0.6 between risk response 1 and secondary risk 1; and 0.40 between risk event 1 and risk response 5. The crisp value of causality degree can be utilized to formulate the soft causal relationships between interrelated variables in FSD modeling. The suggested adaptive hybrid model can provide industry professionals with a systematic and structured approach to modeling complex construction risk systems through FSD simulation comprising soft causal relationships. The model can be a potential alternative for traditional techniques (e.g., modified horizontal approach) for determining the MBFs of linguistic terms for degree of causality. Traditionally, modelers used to utilize the modified horizontal approach coupled with curve fitting, which is an expert-driven and direct method, to develop MBFs of linguistic terms. The modified horizontal approach is very straightforward to apply and enables condensing of many questions into a single one. However, it is highly reliant on expert judgments and is, thus, susceptible to mistakes owing to experts’ subjectivity and inconsistency in responding to questions.
The interval type-2 fuzzy sets used in the proposed adaptive hybrid model capture more uncertainties compared to standard fuzzy sets, offer better knowledge representation, and accounts for the opinions of a larger number of experts compared to standard fuzzy sets. Moreover, WPJG optimizes these interval type-2 fuzzy sets by maximizing the performance indexes of two criteria—coverage and specificity—, thereby mitigating the impact of irrelevant and biased expert opinions. The suggested model is an alternative to existing techniques for eliciting MBFs, such as fuzzy clustering and AHP, which are ineffective for eliciting MBFs for risk analysis linguistic terms. Additionally, the proposed model meets the requirements for (1) aggregating expert opinions on the MBFs of identified linguistic terms, (2) aggregating expert evaluations of soft causal relationships, and (3) removing irrelevant and biased opinions.
5. Conclusions and Future Research
Decision-making in construction projects is a complex process involving a large number of risks and uncertainty that requires efficient modeling and computing techniques to mitigate the impacts of risk and uncertainty on project objectives and to manage project contingency reserve. In this paper, an adaptive hybrid model was proposed for improving the efficiency of constructing CLDs in FSD modeling of complex construction risk analysis systems. The model integrates FAHP, WPJG, and FOWA to (1) form and optimize the MBFs of linguistic terms and (2) aggregate assessments of causality degree for each soft causal relationship made based on the constructed MBFs. FAHP is employed to determine the level of risk expertise (importance weight) of various experts based on several criteria. WPJG is applied to determine the optimal value of the upper and lower bounds of interval type-2 MBFs of soft causal relationships, and FOWA is utilized to aggregate the opinions of heterogenous experts.
This study contributes to the modeling and analysis of risks in construction projects by proposing a systematic and organized technique via an adaptive hybrid model for calculating the crisp value of causality degree for soft causal relationships among the elements of construction projects. The proposed model can address the following issues with prior techniques: (1) considering the level of risk expertise (importance weights) of several experts in both developing the MBFs of linguistic terms and assessing the degree of causality based on constructed developed MBFs, (2) mitigating the influence of irrelevant and biased opinions on the development of MBFs for linguistic terms of causality degree, and (3) aggregating several expert’s assessments of causality degree of soft causal relationships.
The results of the proposed adaptive hybrid model for FSD modeling of construction risks are: (1) optimized MBFs of linguistic terms for causality degree of soft causal relationships and (2) the crisp value of causality degree of soft causal relationships. The first result can be employed in assessing degree of causality of soft causal relationships among project variables by experts, and the second can be utilized in formulating the value of impacted variable based on the value of caused variable in each time step of the FSD simulation. The study results will enable risk analysts to: (1) calculate the crisp value of soft causal relationships when quantitative project data falls short of the quantity or quality required for effective modeling and (2) benefit from the opinions of several experts while modeling the dynamic behavior of complex construction projects using FSD. The developed adaptive hybrid model was implemented on a hypothetical case study that was extracted from a real wind farm project.
When determining the degree of causality, the experts’ importance weights were assumed to remain constant for a particular project, independent of the work package being evaluated. However, some experts are more informed than others or have more relevant backgrounds for a certain work package. Therefore, the weights assigned to experts must vary according to the work package being evaluated. Thus, future research should focus on the creation of a weighting technique that accounts for the level of expertise of the experts assigned to the work package under evaluation. Additionally, the proposed model can be implemented in several FSD models of construction risk analysis to compare the results with conventional methods (e.g., modified horizontal approach coupled with curve fitting).
Author Contributions
Conceptualization, S.H.F.; Methodology, S.H.F.; Software, S.H.F.; Writing—original draft preparation, S.H.F.; Writing—review and editing, S.H.F., P.H.D.N. and A.R.F.; Supervision, A.R.F.; Project administration, A.R.F.; Funding acquisition, A.R.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Industrial Research Chair in Strategic Construction Modeling and Delivery (NSERC IRCPJ 428226–15), which is held by Aminah Robinson Fayek. The authors gratefully acknowledge the financial support provided by industry partners and NSERC through the Chair.
Data Availability Statement
All data, models, and code generated or used during the study appear in the submitted article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdelgawad, M.; Fayek, A.R. Risk management in the construction industry using combined fuzzy FMEA and fuzzy AHP. J. Constr. Eng. Manag. 2010, 136, 1028–1036. [Google Scholar] [CrossRef]
- Fateminia, S.H.; Seresht, N.G.; Fayek, A.R. Evaluating risk response strategies on construction projects using a fuzzy rule-based system. In Proceedings of the 36th International Symposium on Automation and Robotics in Construction (ISARC), International Association for Automation and Robotics in Construction (IAARC), Banff, AB, Canada, 21–24 May 2019; pp. 282–288. [Google Scholar]
- Fayek, A.R. Fuzzy Hybrid Computing in Construction Engineering and Management: Theory and Applications; Emerald Group Publishing: Bingley, UK, 2018. [Google Scholar]
- Ahmadi-Javid, A.; Fateminia, S.H.; Gemünden, H.G. A method for risk response planning in project portfolio management. Proj. Manag. J. 2020, 51, 77–95. [Google Scholar] [CrossRef]
- Fateminia, S.H.; Siraj, N.B.; Fayek, A.R.; Johnston, A. Determining project contingency reserve using a fuzzy arithmetic-based risk analysis method. In Proceedings of the 53rd Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2020; p. 10. [Google Scholar]
- Helton, J. Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty. J. Stat. Comput. Simul. 1997, 57, 3–76. [Google Scholar] [CrossRef]
- Fayek, A.R.; Lourenzutti, R. Introduction to fuzzy logic in construction engineering and management. In Fuzzy Hybrid Computing in Construction Engineering and Management; Emerald Publishing Limited: Melbourne, Australia, 2018; pp. 3–35. ISBN 978-1-78743-869-9. [Google Scholar]
- Klir, G.J. Fuzzy Set Theory; Prentice-Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Raoufi, M.; Seresht, N.G.; Fayek, A.R. Overview of fuzzy simulation techniques in construction engineering and management. In Proceedings of the 2016 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS), Institute of Electrical and Electronics Engineers (IEEE), El Paso, TX, USA, 31 October–4 November 2016; pp. 1–6. [Google Scholar]
- Siraj, N.B.; Fayek, A.R. Hybrid fuzzy system dynamics model for analyzing the impacts of interrelated risk and opportunity events on project contingency. Can. J. Civ. Eng. 2021, 48, 979–992. [Google Scholar] [CrossRef]
- Siraj, N.B.; Fayek, A.R. Fuzzy system dynamics for modeling construction risk management. In Proceedings of the Construction Research Congress 2016 American Society of Civil Engineers (ASCE), San Juan, Puerto Rico, 31 May–2 June 2016; pp. 2411–2421. [Google Scholar]
- Pedrycz, W. Why triangular membership functions? Fuzzy Sets Syst. 1994, 64, 21–30. [Google Scholar] [CrossRef]
- Fateminia, S.H.; Sumati, V.; Fayek, A.R. An Interval Type-2 Fuzzy Risk Analysis Model (IT2FRAM) for determining construction project contingency reserve. Algorithms 2020, 13, 163. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Pedrycz, W.; Wang, X. Designing fuzzy sets with the use of the parametric principle of justifiable granularity. IEEE Trans. Fuzzy Syst. 2015, 24, 489–496. [Google Scholar] [CrossRef]
- Pedrycz, W. Knowledge-Based Clustering: From Data to Information Granules; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Pedrycz, W. An Introduction to Computing with Fuzzy Sets: Analysis, Design, and Applications; Intelligent Systems Reference Library; Springer International Publishing: London, UK, 2020; Volume 190. [Google Scholar]
- Pedrycz, W.; Gomide, F. An Introduction To Fuzzy Sets: Analysis and Design; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Miller, A.J. Structure of Decision: The Cognitive Maps of Political Elites; Axelrod, R., Ed.; Princeton University Press: Princeton, NJ, USA, 1976; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Stach, W.; Kurgan, L.; Pedrycz, W. Expert-based and computational methods for developing fuzzy cognitive maps. In Computational Intelligence; Springer Science and Business Media LLC: Berlin, Germany, 2010; Volume 247, pp. 23–41. [Google Scholar]
- León, M.; Rodriguez, C.; García, M.M.; Bello, R.; Vanhoof, K. Fuzzy cognitive maps for modeling complex systems. In Advances in Artificial Intelligence, Proceedings of the Mexican International Conference on Artificial Intelligence (MICAI) 2010, Mexico City, Mexico, 8–13 November 2010; Lecture Notes in Computer Science; Sidorov, G., Hernández Aguirre, A., Reyes García, C.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6437, pp. 166–174. [Google Scholar]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Papageorgiou, E.; Stylios, C.; Groumpos, P.P. Unsupervised learning techniques for fine-tuning fuzzy cognitive map causal links. Int. J. Human-Computer Stud. 2006, 64, 727–743. [Google Scholar] [CrossRef]
- Glykas, M. (Ed.) Fuzzy Cognitive Maps: Advances in Theory, Methodologies, Tools and Applications; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2010; Volume 247. [Google Scholar]
- Papageorgiou, E.I. (Ed.) Fuzzy Cognitive Maps for Applied Sciences and Engineering: From Fundamentals to Extensions and Learning Algorithms; Intelligent Systems Reference Library; Springer: Berlin/Heidelberg, Germany, 2013; Volume 54. [Google Scholar]
- Gregor, B. Using Fuzzy Cognitive Maps to Model Policy Issues in the Face of Uncertainty and Limited Data. Webinar. National Institute for Transportation and Communities. 2017. Available online: https://nitc.trec.pdx.edu/events/professional-development/using-fuzzy-cognitive-maps-model-policy-issues-face-uncertainty-and (accessed on 10 June 2021).
- Sterman, J. Business Dynamics: Systems Thinking and Modeling for a Complex World; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Boateng, P.; Chen, Z.; Ogunlana, S.; Ikediashi, D. A system dynamics approach to risks description in megaprojects development. Organ. Technol. Manag. Constr. Int. J. 2012, 4, 593–603. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Afshar, A.; Khanzadi, M. System Dynamics Approach to Optimum Response Selection in Construction Project Risks, 3rd ed.; International Project Management Conference; Iran University of Science and Technology: Tehran, Iran, 2007. [Google Scholar]
- Xue, Y.; Xiang, P.; Jia, F.; Liu, Z. Risk assessment of high-speed rail projects: A risk coupling model based on system dynamics. Int. J. Environ. Res. Public Heal. 2020, 17, 5307. [Google Scholar] [CrossRef] [PubMed]
- Levary, R.R. Systems dynamics with fuzzy logic. Int. J. Syst. Sci. 1990, 21, 1701–1707. [Google Scholar] [CrossRef]
- Loh, T.Y.; Brito, M.P.; Bose, N.; Xu, J.; Tenekedjiev, K. Fuzzy System Dynamics Risk Analysis (FuSDRA) of autonomous underwater vehicle operations in the antarctic. Risk Anal. 2020, 40, 818–841. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Afshar, A.; Khanzadi, M.; Howick, S. Integrating system dynamics and fuzzy logic modelling for construction risk management. Constr. Manag. Econ. 2008, 26, 1197–1212. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Khanzadi, M.; Rezaie, M. Dynamic modeling of the quantitative risk allocation in construction projects. Int. J. Proj. Manag. 2014, 32, 442–451. [Google Scholar] [CrossRef]
- Elbarkouky, M.M.G.; Fayek, A.R. Fuzzy preference relations consensus approach to reduce conflicts on shared responsibilities in the owner managing contractor delivery system. J. Constr. Eng. Manag. 2011, 137, 609–618. [Google Scholar] [CrossRef]
- Awad, A.; Fayek, A.R. A decision support system for contractor prequalification for surety bonding. Autom. Constr. 2012, 21, 89–98. [Google Scholar] [CrossRef]
- Van Laarhoven, P.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Li, J.; Zou, P.X.W. Fuzzy AHP-based risk assessment methodology for PPP projects. J. Constr. Eng. Manag. 2011, 137, 1205–1209. [Google Scholar] [CrossRef]
- Chen, P.; Wang, J. Application of a fuzzy AHP method to risk assessment of international construction projects. In Proceedings of the 2009 International Conference on Electronic Commerce and Business Intelligence, Beijing, China, 6–7 June 2009; pp. 459–462. [Google Scholar] [CrossRef]
- Zadeh, L. From computing with numbers to computing with words. From manipulation of measurements to manipulation of perceptions. IEEE Trans. Circuits Syst. I Regul. Pap. 1999, 46, 105–119. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Pedrycz, W.; Homenda, W. Building the fundamentals of granular computing: A principle of justifiable granularity. Appl. Soft Comput. 2013, 13, 4209–4218. [Google Scholar] [CrossRef]
- Pedrycz, W. Granular Computing: Analysis and Design of Intelligent Systems; eBook Published 2018; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Pedrycz, W.; Vukovich, G. Abstraction and specialization of information granules. IEEE Trans. Syst. Man. Cybern. Part B (Cybern.) 2001, 31, 106–111. [Google Scholar] [CrossRef]
- Wang, D.; Pedrycz, W.; Li, Z. Granular data aggregation: An adaptive principle of the justifiable granularity approach. IEEE Trans. Cybern. 2019, 49, 417–426. [Google Scholar] [CrossRef]
- Sadiq, R.; Kleiner, Y.; Rajani, B. Aggregative risk analysis for water quality failure in distribution networks. J. Water Supply Res. Technol. 2004, 53, 241–261. [Google Scholar] [CrossRef] [Green Version]
- Yager, R.R. OWA aggregation over a continuous interval argument with applications to decision making. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2004, 34, 1952–1963. [Google Scholar] [CrossRef]
- Merigó, J.M.; Casanovas, M. Induced aggregation operators in decision making with the Dempster-Shafer belief structure. Int. J. Intell. Syst. 2009, 24, 934–954. [Google Scholar] [CrossRef] [Green Version]
- Gohar, A.S. Identifying and evaluating risks of construction projects in fuzzy environment: A case study in iranian construction industry. Indian J. Sci. Technol. 2012, 5, 1–10. [Google Scholar] [CrossRef]
- Hsu, H.-M.; Chen, C.-T. Aggregation of fuzzy opinions under group decision making. Fuzzy Sets Syst. 1996, 79, 279–285. [Google Scholar] [CrossRef]
- Monzer, N.; Fayek, A.R.; Lourenzutti, R.; Siraj, N.B. Aggregation-based framework for construction risk assessment with heterogeneous groups of experts. J. Constr. Eng. Manag. 2019, 145, 04019003. [Google Scholar] [CrossRef]
- Smolíková, R.; Wachowiak, M.P. Aggregation operators for selection problems. Fuzzy Sets Syst. 2002, 131, 23–34. [Google Scholar] [CrossRef]
- Mukherjee, K. A note on limitations of FAHP. In Developments in Advanced Control and Intelligent Automation for Complex Systems; Springer Science and Business Media LLC: Berlin, Germany, 2017; pp. 101–111. [Google Scholar]
- Mendel, J.M.; Wu, H. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: Part 1, forward problems. IEEE Trans. Fuzzy Syst. 2006, 14, 781–792. [Google Scholar] [CrossRef]
- Mendel, J.M.; Wu, H. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: Part 2, inverse problems. IEEE Trans. Fuzzy Syst. 2007, 15, 301–308. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.; Liu, F. Interval type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef] [Green Version]
- Mendel, J.; John, R. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M.; Coupland, S. Enhanced interval approach for encoding words into interval type-2 fuzzy sets and its convergence analysis. IEEE Trans. Fuzzy Syst. 2011, 20, 499–513. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).