Abstract
The fourth industrial revolution has transformed the industry, with information technology playing a crucial role in this shift. The increasing digitization of industrial systems demands efficient sensing and control methods, giving rise to soft sensors that have the potential to replace traditional physical sensors in order to reduce costs and enhance efficiency. This study explores the implementation of an artificial neural network (ANN) based soft sensor model in a water supply system to predict flow rates within the system. The soft sensor is centered on a Long Short-Term Memory (LSTM) artificial neural network model using Monte Carlo dropout to reduce uncertainty and improve estimation performance. Based on the results of this work, it is concluded that the proposed soft sensor (with Monte Carlo dropout) can predict flow rates more precisely, contributing to the reduction in water losses, as well as cost savings. This approach offers a valuable solution for minimizing water losses and ensuring the efficient use of this vital resource. Regarding the use of soft sensors based on LSTM neural networks with a careful choice of Monte Carlo dropout parameters, when compared to the multilayer perceptron model, the LSTM model with Monte Carlo dropout showed better mean absolute error, root mean square error, and coefficient of determination: 0.2450, 0.3121, and 0.996437 versus 0.2556, 0.3522, and 0.9954. Furthermore, this choice of Monte Carlo dropout parameters allowed us to achieve an LSTM network model capable of reducing uncertainty to 1.8290, keeping the error metrics also at low levels.
1. Introduction
The management of water supply systems (WSSs) is increasingly becoming a challenging problem. This is driven by the confluence of growing demand for water resources and the need for energy efficiency, given the considerable energy required for pumping operations. Optimizing these systems plays an important role not only in guaranteeing the quality and quantity of water distributed but also in mitigating environmental impact and reducing operating costs.
According to the National Sanitation Information System, or SNIS, water losses in Brazil’s water distribution systems in 2021 were about 40.25% [1]. Therefore, such losses represent a significant problem that can be mitigated through accurate flow measurement, contributing to the operational efficiency of water supply systems.
During the water supply process, at a given moment, it is stored in reservoirs and then distributed through a dedicated network. In these stages, pressure and flow control are necessary [2]. Applying artificial intelligence technologies is a way to improve the system’s hydroenergetic efficiency through intelligent pressure control in the network, based on past operating data. This can be performed by using fuzzy controllers, which can be designed based on experts’ prior knowledge of the system. In this way, the controller’s decisions are based on nonquantitative variables, whose values are labels and sets of rules. In their work, Flores et al. [3] proposed a fuzzy logic-based pressure control logic, which proved effective in increasing energy efficiency in a distribution network built in a laboratory with series and parallel pump arrangements. Following a similar path, Salvino et al. [4] developed a neural network-based controller to improve the energetic efficiency of water distribution systems, using specific energy consumption (SEC) as a criterion. This kind of pressure control solution developed in the laboratory has proven valid in real water supply systems as was shown by Araújo et al. [5], who applied the pressure provided by a fuzzy control in a model based on MLP artificial neural networks before applying it in a real urban WSS.
Flow and pressure should be measured to exercise the required control. It is interesting to avoid the costs associated with flow meters. This can be achieved through the use of soft sensors, in which software is based on the physical or chemical relationships between properties whose data can be obtained and those that one wants to know to estimate the latter [6].
Conceptually, a soft sensor is a mathematical model implemented in software and used to estimate variables of interest that are difficult to measure through input quantities, called secondary variables, which are easy to measure. This alternative arises from an operational difficulty or high cost in obtaining the desired variable [7]. Sangiorgi et al. [8] classified soft sensors into two types: data-driven and deterministic. The first is fed with time series data to establish mathematical relationships between the measured variables and the sensor output. In the second, the dynamics between the process variables are known and used to estimate the latent variables accurately. In the present work, the soft sensor is of the first type.
The application of soft sensors is possible in several fields. In biology and environmental studies, an example is the work of Lu et al. [9], in which an intelligent algorithm named the improved seagull optimization algorithm (ISOA) and the Gaussian process regression (GPR) were chosen as the central element of a soft sensor able to estimate some key biochemical parameters in marine lysozyme fermentation. ISOA-GPR weighted ensemble learning was shown to perform better (in terms of root mean square and maximum absolute errors) than ISOA-GPR single global predicted value. An advantage of the proposed method is that it needs fewer training data to predict key biochemical parameters.
A possibility of applying soft sensors is measuring quantities to improve industrial processes. For example, Shan et al. [10] developed a predictive control system based on the soft sensor to improve temperature control in Azeotropic distillation. The weight of this controller is optimized with multiobjective genetic algorithms; the soft sensor model is based on TDNN (time-delayed neural network) in order to predict DIPE (diisopropyl ether) and IPA (isopropyl alcohol). This way, some measurement instruments could be avoided, and the proposed control strategy performed better than conventional PID-based. Another possible application of soft sensors in industrial processes is when measuring some key biological parameters during penicillin fermentation as proposed by Hua et al. [11], who developed a hybrid soft sensor based on LSTM and random forest-improved Harris hawks optimization (RF-IHHO), in which the auxiliary variables for penicillin are selected by the RF method.
In particular, soft sensors can measure the flow of substances in industrial processes. The flow of caleado juice, that is, the juice produced after the addition of sulfur and lime in an ethanol manufacturing plant, was proposed by Santos Lima et al. in [12]. Correctly measuring the flow of this juice is important to maintain the decanter’s correct functioning and thermal control’s efficiency. After selecting three input variables (among six available), two soft sensor architectures were tested—a simple one with just inputs and one output, and another with inputs, one output, and a unit delay block in the feedback loop—in order to choose the best one for that specific application. Similarly, soft sensors can be applied to flow measurement in industrial processes in sanitation.
Different artificial intelligence techniques can be used depending on the context of the application and what is intended to be demonstrated. In this work, LSTM neural networks were chosen because they can take advantage of older data, making them ideal for dealing with time series of variable lengths, long-term memories, and the gradient problem. For comparison purposes, models based on convolutional neural networks and multiplayer perceptron were used as reference network topologies. An outlier correction method called TEDA (Typicality and Eccentricity Data Analytics) [13] was chosen because it does not require prior knowledge about the analyzed data and its recursion, which makes it possible to process large volumes of data quickly and online [14].
The two main contributions of this work are the following:
- The LSTM model-based methodology for developing the virtual flow meter, which includes the use of TEDA in water pressure data preprocessing for removing outliers in the water supply dataset;
- Uncertainty reduction in LSTM ANN models using Monte Carlo dropout.
After this introduction, some recent works about the development and application of virtual sensors, which are based on artificial intelligence, to industrial context are mentioned in Section 2, with the aim of showing recent approaches and how the proposal of this work fits into the state of the art. Details related to LSTM and reference ANN (artificial neural network) model topologies are shown in Section 3. The soft sensor development methodology and steps are explained in Section 4. Section 5 is dedicated to exposing how the dataset was obtained and treated. The results obtained using the developed the network model are shown in Section 6, with special emphasis on the influence of ANN model features on the performance of the developed soft sensor and the comparison with other ANN models. Finally, the main conclusions drawn from the work and possibilities for future work are exposed in Section 7.
2. Related Work
In this section, some recent applications of artificial intelligence technologies in the development of soft sensors are explored in order to highlight the artificial intelligence techniques used and position this work as the state of the art.
Shen and Zhiqiang [15] proposed the application of a supervised nonlinear dynamic system (NDS) based on a deep nonlinear generative model named variational autoencoder (VAE) to overcome the difficulty of overcoming the vulnerability of LSTM networks to batch-to-batch variation problems in problems involving industrial processes with a complex, nonlinear dynamic. Their model is based on LSTM neural networks and can deal with nonlinear datasets and complex mathematical models without the need to calculate the joint distribution of the input. An online LSTM network produces a set of separate models. The proposed system determines the most appropriate modeling path through similarity tests. The performance of their approach was tested on two numerical examples and one industrial (debutanizer) example. The coefficient of determination and the RMSE (root mean square error) were used as evaluation metrics. The traditional PLS (partial least squares) model, probabilistic principal component regression (PPCR) model, DPLVM (dynamic probabilistic latent variable model) [16], and supervised LDS (linear dynamic system) were used as reference models. In the first numerical test, it was clear that the best choice of length for the proposed model depends on the number of latent variables, but, in general, it performs better than the reference models. In summary, in order not to dismiss the advantages of using LSTM networks, the authors developed a system in which this network can determine the best modeling of the monitored process.
An indirect measurement of the water flow in a water pumping network was proposed by Flores et al. [17] as a way to avoid the costs associated with physical flow sensors. Artificial neural networks were used to develop this measurement approach due to their generalization capacity and the complexity of the mathematical models describing the systems where the measurements occur. Initially, two topologies of ANN were considered: (1) Multilayer Feedforward Backpropagation with pump rotation speed and pressure measurement as inputs and the flow as outlet, and (2) Nonlinear Autoregressive Exogenous (NARX) with the same outlet and inputs, plus a feedback of past flux outlet. The performance of NARX was superior regarding maximum relative error (MRE), and their proposed approach was tested in a controlled water pumping system by varying the system pressure setpoints using a fuzzy controller. Using NARX to compose this block provided a root mean square error equal to 1.72% in flow estimation. The work in question involves successfully applying soft sensors to estimate water flow in distribution systems. In this case, the tests were performed with laboratory data, without outliers, and no use of Monte Carlo dropout was made.
In Robson et al. [18], a soft sensor was developed to estimate, based on pressure measurements, the flow in water distribution systems, as the relationship between these two physical variables is known. Two types of ANN were tested: MLP and NARX. In that work, only NARX was used to perform real-time flow indirect measurement in real time, considering as a reference the measurements obtained from an electromagnetic flow sensor. The tests were carried out under different conditions, with varying parameters such as valve opening angles, frequency of the pump’s inverter, and pressure setpoint. Average error, maximum error, and standard deviation are the main evaluation metrics used in that work. Given the application of spurious signals in the system, the average relative error and standard deviation were less than 1%. One of the limitations of that work is that the soft sensor was only tested in a laboratory environment and without the presence of outliers. This way, the dataset is less irregular. Furthermore, no use of Monte Carlo dropout was made to improve network performance.
Colmenares et al. [19] used LSTM neural networks to design a soft sensor that measures effluent water’s total chemical oxygen demand quality index. The average values of three performance metrics—mean square error (MSE), coefficient of determination (), and mean absolute percentage error (MAPE)—were used to evaluate the predictive capacity of the model. The authors’ motivations for developing the soft sensor are to reduce associated costs and processing time. A proprietary deep LSTM network was developed for this purpose. The data used to train the network were provided by a reduced model composed of differential equations and named Activated Sludge Model (ASM1). Traditional feedforward neural networks (FFNN) were used as reference networks. LSTM soft sensor output variables were the readily biodegradable soluble substrate and slowly biodegradable particulate substrate, while its input variables were soluble oxygen and active autotrophic and heterotrophic particulate biomass. In estimating both outputs, the LSTM-based soft sensor performed better than FFNN in all metrics, which reveals the advantage of using this estimator. That work shows how the LSTM network can be efficient for designing soft sensors applicable to the water sector. Unlike the present research, Colmenares et al. [19] did not perform outlier treatment or use Monte Carlo dropout.
An LSTM-based soft sensor combined with an autoencoder (AE) was proposed in [20] with the aim of measuring the level of acetic acid on the top of a boiling tower. While the traditional autoencoder has a hidden layer between the encoder and decoder, the proposed model has a complete LSTM network in place of the hidden layer. The encoder selects the essential features of the input data (and, therefore, its dimensionality) in order to reduce the computational effort on the LSTM network. In that research, a backpropagation neural network, a simple LSTM, and a PCA-LSTM (principal component analysis-LSTM) network were used as reference methods. Mean absolute error (MAE), MSE, root mean square error (RMSE), and coefficient of determination were used as evaluation metrics. The proposed network outperformed the reference ones in all metrics. The coefficient of determination achieved by it is 0.806, against 0.722, 0.684, and 0.622 achieved, respectively, by PCA-LSTM, LSTM, and backpropagation. In that article, the author combined the advantages of LSTM networks and autoencoder to improve the quality of predictions compared to reference methods. The contribution highlighted by the authors differs from what was performed in the present research. However, it reveals the current interest in using LSTM in industrial applications.
Xu et al. [21] developed an LSTM network-based soft sensor to monitor and forecast specific performance parameters, such as chemical oxygen demand (COD), ammonium cation, and total nitrogen in a two-staged anoxic–oxic process for wastewater treatment. In that work, the proposed soft sensor received data from lower-cost sensors. To evaluate the prediction capacity of the proposed soft sensor, a soft sensor based on multiple linear regression (MLR) was considered a reference; MAPE, Pearson correlation, and normalized RMSE were used as performance metrics. In the development of a simple LSTM network, look-back periods for influent and effluent parameters were empirically defined, using the median MAPE as criteria. For influent parameters, this metric decreased from 36.5% to 19.8% when the look-back period was increased from 2 to 5 days, and it stagnated from then on. For effluent parameters, the best look-back periods depend on each parameter. It is a period of 3 days for COD, providing 11.8% as MAPE, and two days for total nitrogen, providing 7.9% as MAPE. While the MLR-based soft sensor provides a flat estimate and is unable to follow the nuances in parameter variations, the LSTM-based soft sensor proved capable of predicting several parameters, influent and effluent, with more accuracy. The ability to define the size of the time series of the LSTM networks allowed the optimal look-back period to be determined in order to obtain the best estimate of effluents and influents. Considering the availability of large time series in the present work, this ability to improve network performance by varying the look-back period appears desirable for the intended application (water supply systems).
A recent application of LSTM networks was made by Lei et al. [22], which predicted each modal component of energy produced from wind sources. One of the contributions of that work consists of the application of variational modal decomposition (VMD) to decompose the already processed data into K modal components in order to improve the quality of the soft sensor estimate. In that work, abnormal data (outliers) were detected using the isolated forest algorithm and corrected by multiple imputations and were used as evaluation metrics relative error (RE), MAE, MAPE, and RMSE. The use of VMD in conjunction with LSTM proved to be more advantageous than the use of LSTM alone. In the present work, LSTM was combined with the Monte Carlo dropout method, in which the dropout remains active in the testing phase, obtaining positive results. Therefore, both studies evaluated the impacts of different modifications to the LSTM on the performance of the estimator.
Another example of developing soft sensors based on models which combine bioinspired algorithms with LSTM networks in order to increase their learning rate was performed by Wang et al. [23]. In that work, the hybrid soft sensors ally the whale-optimization algorithm (WOA) to the LSTM network for estimating oxygen content in flue gases. Abnormal data were identified according to criterion 3, and principal component analysis was used to reduce the dimensionality of the dataset. The reference models were other LSTM-based models. As evaluation metrics, RMSE, MAE, MAPE, and the determination coefficient were used. They observed, in the testing phase, that the WOA-LSTM presented a coefficient of determination and MAPE of 0.98664 and 2.2254%, respectively. Among the reference models, the best was the PSO-LSTM, with a coefficient of determination and MAPE of 0.97068 and 2.7191%, respectively. Therefore, the soft sensor based on WOA-LSTM performed better.
The works discussed in this section are summarized in Table 1. Most of these works present soft sensors based on artificial neural networks. In particular, the most recent ones have adopted LSTM-type networks to achieve their objectives. In this work, LSTM was chosen due to the advantages mentioned in the previous section, and the works cited here reinforce the trend towards its adoption. Some of the differences of this work, when compared to those mentioned above, are the incorporation of outlier detection (observed only in [22,23]) and the use of Monte Carlo dropout in addition to the tests carried out in a real water distribution environment.

Table 1.
Comparison of related works: contributions and techniques used.
In this article, we propose an LSTM-based model with Monte Carlo dropout to be used in soft flow sensors with outliers treatment based on TEDA, and the results obtained in field tests are shown in order to demonstrate the validity of the proposed approach in real scenarios.
The methodology for developing the virtual sensor for water supply systems, the use of TEDA in preprocessing, and the demonstration of its successful operation will become clearer in the next sections. The benefits represented by the proposed approach are the reduction in operational costs and installation complexity associated with conventional flow meters.
3. Model Topology
In the present work, ANN of the type LSTM, which is commonly used in time series problems, was chosen for flow prediction due to its ability to retain short-term memories. A very short-term forecast receives as input the delayed values of the five variables in 10 measurements, equivalent to one hour, and returns a prediction at the network output one step ahead of the flow. The model flowchart can be seen in Figure 1.
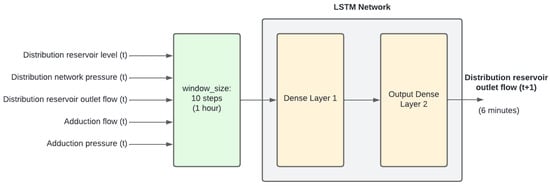
Figure 1.
LSTM model.
The performance of the models based on five predictive variables is analyzed in the present work, and the methodology used to identify the best network configuration for the development of the soft sensor in the context of this project consists of three stages:
- Definition of the number of neurons in the first inner layer: Initially, we proceeded to vary the number of neurons in the input layer. This variation was carried out from N to 5N, with N representing the number of steps past defined in the time window (10 steps).
- Identification of the need for additional layers: After determining the best number of neurons in the first layer, we evaluated whether it would be advantageous to incorporate additional internal layers into the neural network architecture, varying the second layer again from N to 5N.
- Variation of Monte Carlo dropout parameters: We proceeded to the variation of parameters related to the uncertainty technique. This included the variation of the dropout rate, varying from 5% to 15%, and the variation of the parameter value , considering values such as []. These values were chosen based on the model accuracy equation, varying the arbitrary values of the model accuracy in [1, 10, 50, 100, 10,000].
Comparisons among models are made according to conventional metrics evaluation of neural network models, already mentioned above, for each set of selected variables. The uncertainty of the model with some choices of Monte Carlo dropout parameters is calculated.
3.1. LSTM Neural Networks
The LSTM neural networks were introduced by Hochreiter and Schmidhuber [25] and represent a significant advancement in the area of deep learning, particularly in time series processing.
As illustrated in Figure 2, a distinctive feature of LSTM is the existence of three fundamental gates in each node (neuron): the input gate, output gate, and forget gate. In this LSTM cell, and are a hyperbolic tangent and a sigmoid function. The input signal and the previous cell output are concatenated at the forget gate. In brief, the role of the input gate is to insert new information relevant to updating the cell state; the forget gate uses sigmoid function scaling to prevent LSTM networks from processing continuous input streams that are not segmented; finally, the output port determines the hidden state h(t), which makes predictions. The signals and are passed through a sigmoid, producing an output signal . This signal is multiplied by the signal produced after passing the cell state through a hyperbolic tangent function to obtain the next hidden state, [26].
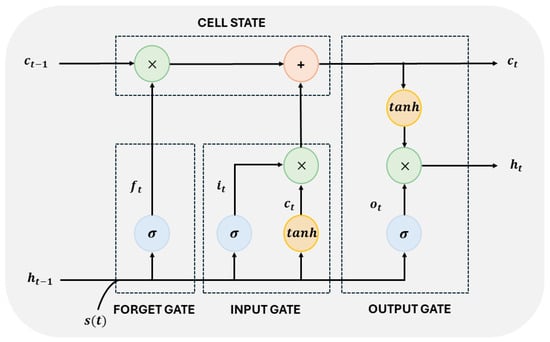
Figure 2.
LSTM node.
The three ports allow LSTM to control the flow of information within the network, which makes it especially suitable for capturing long-term temporal dependencies. Furthermore, LSTMs have been widely adopted for time series due to their remarkable ability to deal with the gradient problem. Unlike traditional neural networks, LSTM mitigates the disappearance of the gradient, allowing relevant information to be maintained for long periods, which is crucial for modeling complex time series in soft sensor design.
In this work, the number of layers of the LSTM network and the number of neurons per layer were varied. Configurations with one or two layers were tested, while the number of neurons per layer was varied from 10 to 50. Among the combinations tested, the network with the best performance was chosen to undergo Monte Carlo dropout analysis. A diagram of the LSTM network model used is illustrated in Figure 3. The figure shows that LSTM networks with up to two hidden layers were considered in the testing phase. The input and output layer nodes are also indicated. In the model design phase, in addition to the Monte Carlo dropout parameters, the main characteristics of the network to be changed were the number of hidden layers and nodes in these layers.
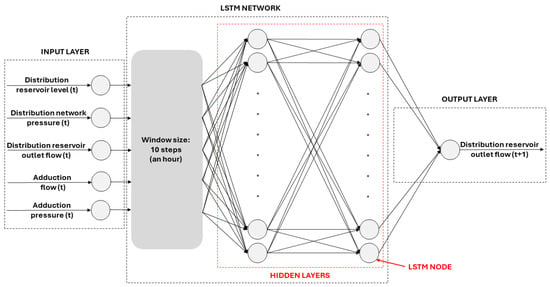
Figure 3.
LSTM network model used in this work.
3.2. Reference Models
The results obtained using the LSTM-based model were compared with those obtained with reference models based on two other neural networks: multilayer perceptron (MLP) and convolutional neural networks (CNNs).
3.2.1. Multilayer Perceptron
Multilayer perceptron is a type of artificial neural network with an architecture composed of three main parts: an input layer, a hidden layer, and an output layer. These layers consist of interconnected artificial neurons in a feedforward structure, meaning the outputs of one layer act as inputs to the next layer.
For the studied case, the input layer comprises the five original features and their respective N temporal delays as illustrated in Figure 4. As N equals 5, and each sample is obtained every 6 min, the model’s input encompasses a delay of 30 min. The MLP neural network has two layers with 30 neurons each. The performance of this configuration was considered better after varying the number of MLP layers between 1 and 2, with the number of neurons varying up to 50. Rectified Linear Unit (ReLu) was used as the activation function.
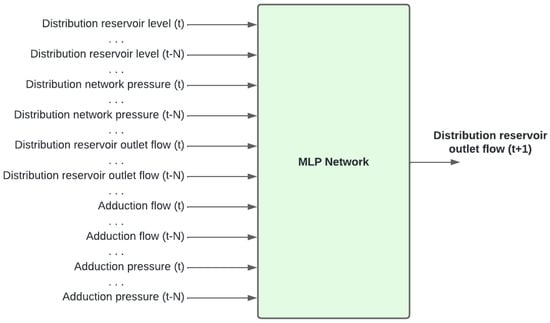
Figure 4.
Multilayer perceptron reference model.
The hidden layers interact through weighted connections, allowing the network to learn the intrinsic relationships within the data. On the other hand, the output layer is the model’s last layer, representing the model’s prediction. At this stage, the predicted values are compared to the actual values, and the backpropagation process ensures that the model’s error is sufficiently minimized. It is also pertinent to highlight that an activation function is employed in each layer to ensure nonlinearity in the neural network.
The MLP applied in this paper incorporates two hidden layers, with 30 neurons activated by the Rectified Linear Unit (ReLu) function.
3.2.2. Convolutional Neural Networks
Convolutional neural networks were initially developed for computer vision tasks but soon gained prominence for their ability to extract useful knowledge and learn the internal representation of high-dimensional data without manual feature engineering. This neural network comprises three types of layers: convolutional, pooling, and fully connected.
These convolutional filters can be considered small windows that traverse the input data through convolution operations between matrices from the feature map. Next, the max-pooling layer extracts maximum values from the convolutional layer using the subsampling technique to reduce the data’s dimensionality while preserving their most important characteristics. Furthermore, the fully connected layer receives the flattened features from the previous layers as input and ensures the appropriate format for prediction.
For the architecture adopted in this work, a convolutional layer and the ReLu activation function were used in the convolutional and fully connected layers. The CNN model’s input data comprise windows of 10 delayed samples that represent different time instants in a time series. This allows the convolutional layer to apply filters and capture temporal information and sequential patterns. The convolutional network used in this work has a single layer composed of eight neurons. To reach this number, the number of neurons in this layer was varied up to 64. The CNN-based soft sensor architecture is shown in Figure 5.
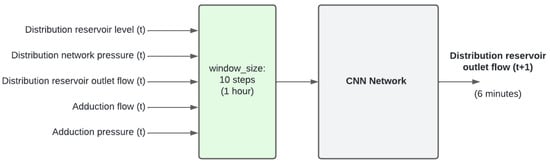
Figure 5.
CNN reference model.
4. Soft Sensor Design
The soft sensor algorithm development methodology is shown in this section. Physical variables obtained from the real water distribution facility were used to estimate the flow. Virtual sensors represent an effective strategy to optimize costs and improve industrial efficiency. While physical sensors require maintenance, calibration, and adjustment plans, replacement with virtual sensors can significantly save manufacturing operations. Furthermore, virtual sensors prevent the unnecessary acquisition of physical sensors, especially as the amount of sensors in a plant increases. Handling large volumes of data coming from these sensors is a challenge. However, virtual sensors are a practical solution, allowing to obtain variables of interest from information already available from other sensors based on mathematical relationships. In this way, virtual instrumentation emerges as a viable alternative for any variable that can be inferred using mathematical methods for real-time monitoring [7].
In the present research, the methodology for creating a virtual sensor has the following five main steps [6]: (1) initial data inspection; (2) identification of steady states; (3) data pre-processing; (4) selection of model; and (5) model validation. This process is illustrated in Figure 6.

Figure 6.
Soft sensor development methodology.
4.1. Dropout-Based Uncertainty Analysis
Every measuring instrument must present a result within a confidence interval delimited (up and down) by the standard deviation of the measured variable. With being the measured value and v being the actual value of the variable of interest, the confidence interval is defined as , for .
In developing virtual sensors based on artificial neural networks, one approach used to reduce its uncertainty is Monte Carlo dropout, which is based on the concept of dropout used for ANN regularization to reduce overfitting and, hence, make a more general model. The method consists of deactivating, in a random way, neurons in the input layers and hidden layers of the ANN as illustrated in Figure 7.
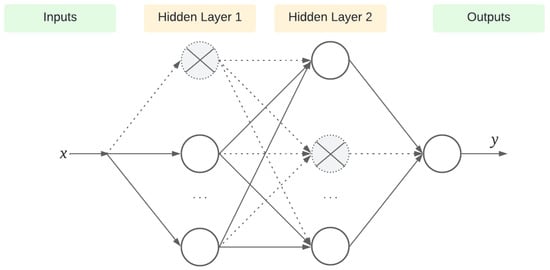
Figure 7.
ANN with node dropout.
In the usual dropout regularization technique, neurons are deactivated only in the training phase of the network, making adjustments to the results, and all neurons are activated in the testing phase. However, in the Monte Carlo dropout technique, dropout remains active during the testing phase, allowing T predictions to be generated differently for the same input, taking into account the randomness of the process dropout. The spread of these forecasts can be used as a measure of uncertainty inherent to the model, known as epistemic uncertainty. In other words, Monte Carlo dropout provides an estimate of the uncertainty associated with virtual sensor predictions, making it possible to calculate a mean and a variance and, based on them, the confidence interval for measurements, which is essential in applications that require high reliability as in real-time monitoring and control systems. Such parameters are calculated according to equations [27]
and
Therefore, the accuracy of the model () is determined through specific hyperparameters such as the L2 regularization weight (), the retention probability (), and length scale (l), which refers to the confidence in the data input. The accuracy is given by [27]
Therefore, the Monte Carlo has the following parameters in Table 2 related to this algorithm, which can be varied in developing the model to obtain better performance.

Table 2.
Monte Carlo dropout parameters.
Predicted flow samples form an uncertainty interval around the actual value to be predicted. Briefly, Monte Carlo dropout reduces this interval, making the predicted samples closer to the real samples. This is how the performance of the LSTM-based model with dropout Monte Carlo outperforms that of the one based on a simple LSTM network.
4.2. Metrics for Model Evaluation
A rigorous evaluation must be carried out to determine the quality and performance of the developed models. This involves quantifying learning achieved during training and comparing model predictions with data-independent test sites reserved for this purpose. With this objective, widely used metrics were employed to analyze the accuracy of models based on time series: the mean square error (MSE), the mean absolute percentage error (MAPE), the mean absolute error (MAE), the root mean square error (RMSE), and the coefficient of determination.
- Mean square error calculates the mean of the squared errors for a number N of samples between the model predictions () and the actual values (). It provides a quantitative measure of the dispersion of errors, highlighting outliers and their magnitude, i.e.,
- MAE represents the average of absolute value errors between forecasts and actual values. It offers a direct view of the size average of errors. It is given by:
- RMSE is the square root of MSE and is widely used to evaluate the model’s overall accuracy, considering both the magnitude and dispersion of errors. It is given by:
- MAPE evaluates the mean absolute error relative to actual values, expressed as a percentage. It allows for understanding relative model performance across different parts of the dataset and is given by:
- The coefficient of determination is the squared correlation coefficient. The coefficient of determination indicates how correlated the predicted variable and those used to feed the predictor are, in other words, how much the change in the predictor variables causes changes in the variables of the estimated variable. It can be calculated using
In addition to these metrics, the kurtosis and skewness of the absolute error distribution (modulus of the difference between the actual flow value and the predicted value) were used.
5. Dataset
Measurements obtained by a local water supply company operating at a small city water distribution station were used to acquire the dataset. These data were obtained from a key point that includes a booster pump station (BPS) and a distribution network that serves approximately 1400 connections, all of which are subject to pressure monitoring.
5.1. Water Supply Network
A diagram of the supply system used in this work is illustrated in Figure 8. In the present work, measurements related to level, pressure, and flow were sent to the SCADA (Supervisory Control And Data Acquisition) system from the water supply company. Such measurements were carried out every 30 s, and the record made every 6 min represents the average number of readings in the time interval.
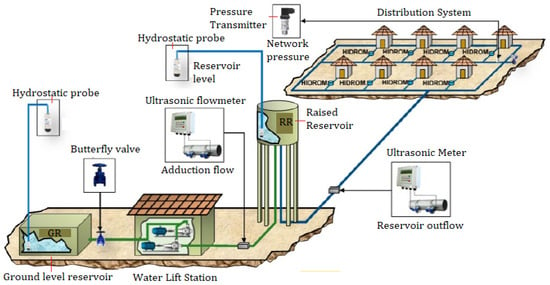
Figure 8.
Small water supply system.
The data frame comprises four secondary variables and the flow, our variable of interest, containing 14,320 samples of each. Based on the opinion of human experts, it was decided to remain with all the variables available for the process. Here, we used the following variables:
- Distribution reservoir level (m);
- Distribution network pressure (mH2O);
- Distribution reservoir outlet flow (L/s);
- Adduction flow (L/s);
- Adduction pressure (mH2O).
In addition to data availability, another criterion when choosing model inputs is correlation analysis among secondary variables and the water flow to be predicted.
It is worth mentioning that the dataset used in training the neural network model was not the same as that used in the testing phase. This ensures that the model’s generalization capacity has been validated.
5.2. Data Acquisition, Treatment and Processing
Data were collected during three months, with a granularity of 6 min. The Figure 9 shows the flow behavior during a single day. The time series corresponding to three months of analysis is represented in Figure 10. From the three-month time series analysis, certain data with unusual behavior can be interpreted as outliers, i.e., an observation that deviates too much from other observations to the point of raising suspicions that it originated through different mechanisms [28], and that needs to be processed. Outliers can originate from failures in industrial processes, for example [29].
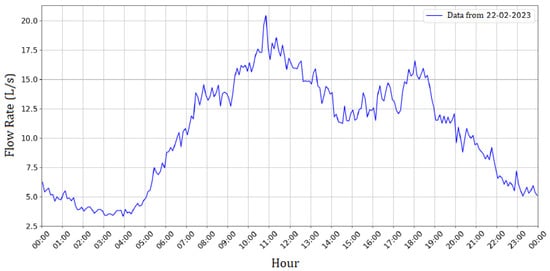
Figure 9.
Flow rate time series in a single day.
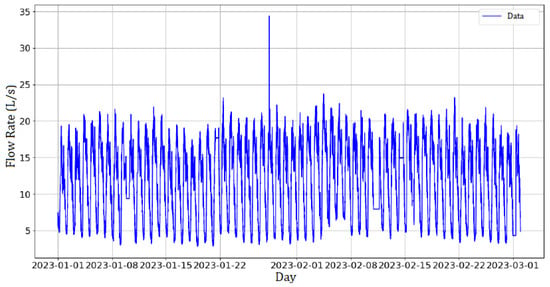
Figure 10.
Flow rate time series in three months.
Before training the models, the data must be treated, aiming to remove noise and outliers. The methodology for data preprocessing is summarized in three main steps: outlier treatment, data normalization, and adduction flow variable adjustment.
The adduction flow variable indicates that the water pump was activated to raise the reservoir level. When the adduction flow is less than or equal to zero, the pump is off, and when it is above zero, the water pump is activated. For this reason, adduction flow was represented by a Boolean variable, zero when it was off, and one when it was on.
5.2.1. Outliers Treatment
Other outlier detection algorithms usually work in one of the following ways [30]: In the first, based on a threshold of statistical information in the data, a binary value is assigned to each sample in order to identify which is, in fact, an outlier. In the second, a parameter is established for the samples’ ranking. The first (or last) samples are classified as outliers in this ranking.
Some of the main ways of identifying outliers are carried out through the threshold [31], i.e., the calculation of abnormal data that are not in the confidence interval , where y is the mean of the dataset and (whose value was set at 3 in the present work) is the deviation standard. Another proposal used in this work is the TEDA framework, which calculates how eccentric a piece of datum is within its set.
The TEDA framework is based on typicality and eccentricity concepts for outlier detection in datasets [13]. In essence, TEDA uses these concepts to identify outliers in datasets. Typicality measures how similar a data sample is to the other samples from the same set. On the other hand, eccentricity evaluates the degree of exceptionality of a piece of datum compared to the others.
TEDA stands out in machine learning due to its advantages over traditional statistical methods, which eliminates the need for the following [32]:
- Making prior assumptions about the distribution of the data, which is a characteristic common in many outlier detection methods;
- Specifying problem-dependent parameters in advance, which can be a challenging task in some situations;
- Assuming independence between individual data samples, which is a restriction in many traditional algorithms;
- Requiring an infinite number of observations; in fact, TEDA demonstrates its effectiveness with just three data samples, which is remarkably efficient.
In addition to typicality () and eccentricity () concepts, another important concept is that of accumulated proximity ().
Considering an n-dimensional data space, represented as , where the distance between points x and y can be defined in several ways, such as the distance Euclidean, data samples are organized as a set of ordered vectors:
Each sample represents the system at a specific time k, allowing this methodology to be adapted to n-dimensional datasets. It allows us to calculate distances for data streams at different instants, the first being and the second ; for any sample equal to or greater than two, it is possible to calculate the distance.
The eccentricity of a sample at a given time k is calculated by the ratio between its accumulated proximity and the sum of accumulated proximity of all other samples as given by [33]:
in which accumulated proximity to a certain point x is defined according to
Typicality is the complement of eccentricity, defined by:
However, it is worth highlighting that typicality and eccentricity are determined based on a minimum set of three distinct samples () since any pair of nonidentical samples presents an equal level of eccentricity.
Storing data samples becomes costly, and most devices have limitations. Therefore, eccentricity and typicality can still be calculated recursively; this way, it is not necessary to maintain a database recording past data, only the last sample received and the values that represent the system at the previous time. The recursive form is represented by [33]:
where the mean and variance are given, respectively, by
and
The Eccentricity Inequality, derived from TEDA, establishes a threshold for the detection of outliers, taking into account the statistical concept of Chebyshev inequality, in order to guarantee that there will be no more than samples that will exceed a distance of relatively to the average [34]. It means that the input parameter m is a parameter that indicates the sensitivity used in the threshold, that is, the higher the value of m, the lower the sensitivity of the method and the lower the number of outliers detected. However, the inequality of eccentricity offers similar results without making hard assumptions about the distribution or independence of data. Thus, such inequality is defined by [35]:
TEDA pseudocode is shown in Algorithm 1.
| Algorithm 1 TEDA pseudocode. |
| while do read a sample if then else update using (14) update using (15) update using (13) update using (16) if then else |
Thus, Figure 11 represents the outliers as data marked in red. After applying the TEDA algorithm, the data presented as outliers are replaced by the general average in that hour.
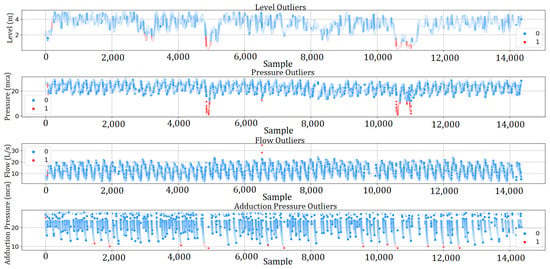
Figure 11.
Outliers identifying.
5.2.2. Data Normalization
Another step in preparing the data is the normalization. The objective is to scale the values of all variables to the range between 0 and 1. This normalization was applied to the entire dataset, ensuring that information was treated consistently, facilitating model training. This approach is essential for effective LSTM performance and convergence, as it reduces disparities in the scales of the variables, making the data more suitable for the learning process.
6. Results
This section presents the results of the main analyses that were proposed. Initially, the various experiments conducted were detailed, and the neural network’s hyperparameters varied. Subsequently, the measurement uncertainty assessment procedure is presented, and the tested configurations are compared. Finally, the results of comparisons with other neural network topologies are shown. This section covers the details of the soft sensor design and presents the evaluation of the results obtained in the experiments.
6.1. Proposed Model
In the model developed with five variables, data were divided into training (70%), validation (10%), and test (20%) sets, totaling 10,035 samples for the training set, 1425 samples for the validation set, and 2860 samples for the test set. All were trained using the same Adam optimization function and with predictions to determine the model uncertainty and the average of the predictions. This quantity was chosen for the number of predictions through experiments throughout the work, realizing that their high variation would not influence better results for the data.
In the present research, the MSE, RMSE, MAE, MAPE, and the coefficient of determination were used as evaluation metrics. The latter was only calculated for the models that presented the best results for each neural network topology. The kurtosis and skewness characteristics of the absolute error distributions were also used to understand the results. These metrics were chosen because they were adopted in the works mentioned above.
Initially, the dropout value, the kernel regularizer, and model accuracy were defined; also, only one internal layer in the network was defined and the variation of neurons was performed, with 50 epochs and a batch size of 32. In Table 3, the results obtained with such variations are shown.

Table 3.
Results of neuron variations in the first layer.
For this first experiment, it was observed that model 2, with 20 neurons, obtained the best performance in terms of MAPE.
6.2. Influence of the Second Layer
One of the fundamental considerations in model improvement is the exploration of different architectures and configurations. By fixing the first layer with 20 neurons, we began to evaluate the influence of adding a second layer to our model. In this way, we observed very similar results to those with just one layer, but the best configuration continues to be that with only 20 neurons. These results are evidenced by metrics such as MAPE and RMSE. The analysis of the results can be viewed in Table 4.

Table 4.
Results of neuron variations in the second layer.
Through comparisons of the results shown in the Table 4 with those obtained with just one-layer models, it was shown that, even without a significant difference, the results with just one internal layer were better for all metrics evaluated.
Therefore, as evidenced previously, it was decided to vary the hyperparameters of the Monte Carlo dropout algorithm using just one layer with 20 neurons.
6.3. Variation of Parameters in Monte Carlo
After defining the number of neurons and internal layers, the Monte Carlo dropout technique was used to analyze the model’s uncertainty.
While certain parameters were subjected to systematic variations, such as the number of predictions (T) and the length scale (l), other parameters were kept constant, such as the probability of dropout (p) and the L2 regularization weight () [36]. The value of l = 0.1 was selected arbitrarily, estimating uncertainty in the acquisition of sensor data. Regarding , the lower its value, the lower the uncertainty of the model. However, not necessarily increasing the value to have a greater range will bring the best result since its variation impacts the weights of the neural network, which may worsen the results of the predictions. These variations aimed to find the ideal values that minimize performance metrics, such as RMSE and the MAPE. The results are shown in Table 5.

Table 5.
Results of Monte Carlo parameter variations.
When adjusting and optimizing the parameters as detailed in Table 5, the test identified sequence number 12, which reached a minimum MAPE value and RMSE. In this context, the model’s measurement uncertainty is around 1.8 times the standard deviation, a highly relevant indicator in predicting water flow for a water supply system. This precision is particularly significant, ensuring that WSS demands are met effectively and reliably.
The results can be viewed in the graphical representation in Figure 12 and Figure 13; the curve in black corresponds to the actual water flow, while the black curve represents the flow predicted by the proposed model. The lilac strip, delimited by the two curves, illustrates measurement uncertainty. Through them, it is possible to observe how the neural network, on average, can follow the actual water flow in the system.
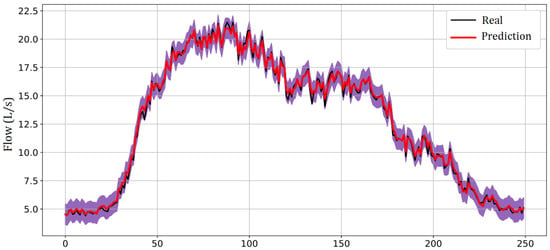
Figure 12.
Flow forecasting for one day using Model 12 of Table 5.
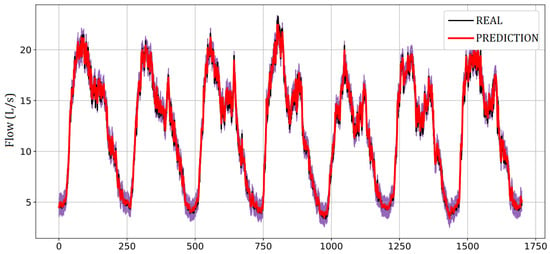
Figure 13.
Flow forecasting for one week using Model 12 of Table 5.
6.4. Comparisons with Other Neural Network Models
When analyzing the absolute value of the difference between the predicted and actual flow values, based on the Shapiro–Wilk and Kolmogorov–Smirnov criteria, it was determined that they do not produce Gaussian profile distributions in any of the types of neural networks used.
The comparison metrics obtained using MLP and CNN are shown in Table 6 and Table 7, respectively. When comparing these values with those obtained using Model 12, which is based on LSTM neural networks and Monte Carlo dropout, it can be seen that Model 12 has better performance in terms of MSE, RMSE, and MAE (0.0974 L2/s2, 0.3121 L/s and 0.2450 L/s), with the MLP being in second place, showing 0.1241 L2/s2, 0.3522 L/s and 0.2556 L/s as MSE, RMSE, and MAE, respectively. The determination coefficient, which measures how well the model makes predictions, was 0.996437 for Model 12. It was a better result than the 0.9954 determination coefficient obtained for MLP.

Table 6.
Best results of MLP implementation.

Table 7.
Best results of CNN implementation.
When comparing the MLP network with Model 2, which maintains Monte Carlo dropout parameters and as and 100, respectively, it is seen that the LSTM loses in the MAE and MAPE criteria. Therefore, choosing better Monte Carlo dropout parameters allowed an LSTM-based configuration to outperform the MLP-based one.
The calculation of skewness and kurtosis of the absolute error for the three network models revealed the following values: 0.56457 and 5.892 for the LSTM, 2.1752 and 33.73308 for the MLP, and 0.8546 and 12.0634 for CNN. The LSTM (Model 12) had the lowest concentration around the MAE (lowest kurtosis). However, it also had the lowest skewness (i.e., smaller tail to the right), which means that the amplitude of the above-average errors was low, and the model provided several errors below average. At the other extreme, the MLP model presented a greater concentration around the MAE (higher kurtosis) but also presented more significant skewness, which means that the absolute errors above the average were more significant than in LSTM Model 12. The CNN network presents intermediate behavior, having, concerning the LSTM errors, a greater concentration of values around the average and a greater amplitude of absolute errors above MAE. Therefore, it was observed that LSTM can provide smoother distortions in terms of absolute errors.
7. Conclusions and Future Works
In this study, data were collected from a water supply system in a small city. An initial analysis of the data was carried out. It was possible to correct outliers through the TEDA algorithm, replacing such values with the general average at that time of day. Subsequently, a soft sensor based on the LSTM neural networks model with Monte Carlo dropout was implemented to forecast flow in water supply systems.
The results obtained from the analyses of the tested models reveal the effectiveness of LSTM recurrent neural networks, even in lower complexity settings with a single inner layer. These networks have demonstrated the remarkable predictive ability of patterns in the flow data samples, evidenced by low MAPE values and RMSE as seen in Model 2 with a MAPE of 3.55% and an RMSE of 0.65, as well as in Model 7 with two inner layers with a MAPE of 3.97% and an RMSE of 0.44. These results indicate that LSTM networks are effective in accurately predicting the flow behavior, even in simpler scenarios.
Taking into account the best result obtained in the network parameter variation neural networks, Model 12 has a MAPE of 2.53% and RMSE of 0.31. Uncertainty analysis, using the Monte Carlo dropout method, validated the accuracy of the proposed model. With a measurement error close to 1.82 l/s, our approach proved to be suitable for the water flow measurement.
When compared to other neural network models, CNN and MLP, LSTM Model 12 proved to be superior in almost all metrics, including the coefficient of determination (0.9954 for MLP versus 0.996437 for LSTM), losing only in MAPE (2.5002 for MLP versus 6.6864 for LSTM). Furthermore, when compared to MLP, LSTM presented a smaller range of absolute errors above the MAE (0.56457 versus 2.1752 kurtosis) despite the lower concentration around this value (5.892 versus 33.73308 skewness).
The soft sensor developed in this work could be used in other water supply systems after adaptation to the available inputs and a new search for the optimal configuration of the neural network, as long as the necessary data are available. The advantage of using Monte Carlo dropout in the LSTM network model has been demonstrated and should be reproducible.
One possibility for future work is integrating the proposed soft sensor into an original IoT system to constitute a complete monitoring and control system. The knowledge acquired from this work could also serve as a basis for the development of soft sensors applicable to water purification systems. This topic has been explored in the recent literature.
Author Contributions
Conceptualization, G.M.R.d.A. and F.M.L.F.; Methodology, G.M.R.d.A., F.M.L.F., A.A.C. and J.M.M.V.; Validation, F.M.L.F. and R.M.D.; Formal analysis, R.M.D., H.P.G. and J.M.M.V.; Investigation, R.M.D., H.P.G. and J.M.M.V.; Resources, P.F.d.M. and A.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the CAGEPA for trusting our work and making a real field situation available to validate the proposed methodology. The authors would like to thank CNPq (Chamada CNPq/AWS N° 64/2022-Faixa A), FAPESQ (EDITAL N° 09/2021 Demanda Universal), the PostGraduate Program in Electrical Engineering of UFPB and the LENHS Laboratory of UFPB for the financial and material support in the development of this work.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from Water and Sewerage Company of Paraíba CAGEPA, and are available from the authors with the permission of Water and Sewerage Company of Paraíba CAGEPA.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- System, N.S.I. Water Indicator Map; Bournemouth University: Poole, UK, 2021. Available online: http://appsnis.mdr.gov.br/indicadores-hmg/web/agua_esgoto/mapa-agua (accessed on 25 May 2024).
- World Health Organization; United Nations Children’s Fund. Global Water Supply and Sanitation Assessment 2000 Report; World Health Organization: Geneva, Switzerland, 2000; pp. 1–80. [Google Scholar]
- Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P. Fuzzy Pressure Control: A Novel Approach to Optimizing Energy Efficiency in Series-Parallel Pumping Systems. Automation 2023, 4, 11–28. [Google Scholar] [CrossRef]
- Salvino, L.R.; Gomes, H.P.; Bezerra, S.d.T.M. Design of a Control System Using an Artificial Neural Network to Optimize the Energy Efficiency of Water Distribution Systems. Water Resour. Manag. 2022, 22, 2779–2793. [Google Scholar] [CrossRef]
- Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P. Fuzzy Control of Pressure in aWater Supply Network Based on Neural Network System Modeling and IoT Measurements. Sensors 2022, 22, 9130. [Google Scholar]
- Fortuna, L.; Salvatore, G.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Morais Júnior, A.A.D.; Brito, R.P.; Sodré, C.H. Design of a Soft Sensor with Technique Neuro-Fuzzy to Infer the Product Composition a Distillation Process. Lect. Notes Eng. Comput. Sci. 2014, 2, 605–608. [Google Scholar]
- Sangiorgi, L.; Sberveglieri, V.; Carnevale, C.; De Nardi, S.; Nunez-Carmona, E.; Raccagni, S. Data-Driven Virtual Sensing for Electrochemical Sensors. Sensors 2024, 24, 1396. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Wang, B.; Zhu, X. Soft Sensor Modeling Method for the Marine Lysozyme Fermentation Process Based on ISOA-GPRWeighted Ensemble Learning. Sensors 2023, 23, 9119. [Google Scholar] [CrossRef]
- Shan, B.; Ma, C.; Niu, C.; Xu, Q.; Zhu, Z.; Wang, Y.; Zhang, F. Soft sensor model predictive control for azeotropic distillation of the separation of DIPE/IPA/water mixture. J. Taiwan Inst. Chem. Eng. 2023, 2023, 105185. [Google Scholar] [CrossRef]
- Hua, L.; Zhang, C.; Sun, W.; Li, Y.; Xiong, J.; Nazir, M.S. An evolutionary deep learning soft sensor model based on random forest feature selection technique for penicillin fermentation process. ISA Trans. 2023, 136, 139–151. [Google Scholar] [CrossRef] [PubMed]
- Lima, J.d.S.; Villanueva, J.M.M.; Catunda, S.Y.C. Modeling a Virtual Flow Sensor in a Sugar-Energy Plant using Artificial Neural Network. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Angelov, P. Anomaly detection based on eccentricity analysis. In Proceedings of the 2014 IEEE Symposium on Evolving and Autonomous Learning Systems (EALS), Orlando, FL, USA, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–8. [Google Scholar]
- Bezerra, C.G.; Costa, B.S.J.; Guedes, L.A.; Angelov, P.P. A new evolving clustering algorithm for online data streams. In Proceedings of the 2016 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Natal, Brazil, 23–25 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Shen, F.; Zheng, J.; Ye, L.; Ma, X. LSTM Soft Sensor Development of Batch Processes With Multivariate Trajectory-Based Ensemble Just-in-Time Learning. IEEE Access 2020, 8, 73855–73864. [Google Scholar] [CrossRef]
- Ge, Z.; Chen, X. Supervised Nonlinear Dynamic System for Soft Sensor Application Aided by Variational Auto-Encoder. IEEE Trans. Control. Syst. Technol. 2019, 27, 323–331. [Google Scholar] [CrossRef]
- Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P.; Catunda, S.Y.C. Indirect Feedback Measurement of Flow in a Water Pumping Network Employing Artificial Intelligence. Sensors 2021, 21, 75. [Google Scholar] [CrossRef] [PubMed]
- Lima, R.P.G.; Villanueva, J.M.M.; Gomes, H.P.; Flores, T.K.S. Development of a Soft Sensor for Flow Estimation in Water Supply Systems Using Artificial Neural Networks. Sensors 2022, 22, 3084. [Google Scholar] [CrossRef] [PubMed]
- Recio-Colmenares, R.; Becerril, E.L.; Tun, K.J.G.; Conchas, R.F. Design of a Soft Sensor Based on Long Short-Term Memory Artificial Neural Network (LSTM) for Wastewater Treatment Plants. Sensors 2023, 23, 9236. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, P.; Zhu, Q. An Improved Industrial Process Soft Sensor Method Based on LSTM. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 12–14 May 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Xu, B.; Pooi, C.K.; Tan, K.M.; Huang, S.; Shi, X.; Ng, H.Y. A novel long short-term memory artificial neural network (LSTM)-based soft-sensor to monitor and forecast wastewater treatment performance. J. Water Process Eng. 2023, 54, 104041. [Google Scholar] [CrossRef]
- Lei, P.; Ma, P.; Changsheng, Z.; Li, T. LSTM Short-Term Wind Power Prediction Method Based on Data Preprocessing and Variational Modal Decomposition for Soft Sensors. Sensors 2024, 24, 2521. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, Z.; Zhang, N. A Hybrid Soft Sensor Model for Measuring the Oxygen Content in Boiler Flue Gas. Sensors 2024, 24, 2340. [Google Scholar] [CrossRef] [PubMed]
- Xiaochu, T.; Yan, J.; Li, Y. Supervised Multi-Layer Conditional Variational Auto-Encoder for Process Modeling and Soft Sensor. Sensors 2023, 23, 9175. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the Interspeech 2014, Singapore, 14–18 September 2014; pp. 338–342. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. IEEE Trans. Instrum. Meas. 1996, 45, 894–899. [Google Scholar]
- Hawkins, D.M. Identification of Outliers; Chapman and Hall: London, UK, 1980. [Google Scholar]
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Chapman and Hall: London, UK, 1980. [Google Scholar]
- Bernieri, A.; Betta, G.F.D.; Liguori, C. On-line fault detection and diagnosis obtained by implementing neural algorithms on a digital signal processor. IEEE Trans. Instrum. Meas. 1996, 45, 894–899. [Google Scholar] [CrossRef]
- Bezerra, C.G.; Costa, B.S.J.; Guedes, L.A.; Angelov, P.P. An evolving approach to data streams clustering based on typicality and eccentricity data analytics. Inf. Sci. 2020, 518, 13–28. [Google Scholar] [CrossRef]
- Angelov, P.P. Outside the box: An alternative data analytics framework. J. Autom. Mob. Robot. Intell. Syst. 2014, 8, 53–59. [Google Scholar] [CrossRef]
- Saw, J.G.; Yang, M.C.K.; Mo, T.C. Chebyshev inequality with estimated mean and variance. Am. Stat. 1984, 38, 130–132. [Google Scholar] [CrossRef]
- Costa, B.S.J.; Bezerra, C.G.B.; Guedes, L.A.; Angelov, P.P. Online fault detection based on Typicality and Eccentricity Data Analytics. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- He, Y.; Wang, P.; Zhu, Q. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML’16), New York, NY, USA, 19–24 June 2016; ACM: New York, NY, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).