Abstract
Chronoamperometric curves for the oxidation of a ferrocenyl derivative via a potential step, calculated using the Cottrell equation, showed less diffusion-controlled currents on a platinum wire electrode. This lower deviation cannot be explained via Butler–Volmer heterogeneous kinetics, but was ascribed to the negatively capacitive current associated with a redox reaction. The deviation in fully oxidized electrical potential corresponds to the non-zero concentration at the electrode surface, which cannot be predicted using the Nernst equation. This equation expresses the relationship between the electrical potential and activity at the electrode surface rather than the concentration. The diffusion equation determines the relationship between the current and surface concentration rather than activity. Negative capacitance or a non-zero concentration may arise from structure formation on the electrode owing to dipole–dipole interactions, which are similar to the generation of double-layer capacitance, including frequency dispersion. Following this concept, we derive expressions for a lowered diffusion-controlled current and time-dependent surface concentration. The negatively capacitive current shows the time dependence of t−0.9, which is similar to the decay of double-layer capacitive currents. The surface concentration decays with t−0.4-dependence.
1. Introduction
Double-layer capacitance (DLC) exhibits frequency dispersion, which can be characterized as a deviation from an ideal level of capacitance. The dispersion belongs to a general phenomenon caused by relaxing the dielectric response of one polarized structure to another [1,2]. It is quantitatively represented via a constant phase element [3,4,5,6,7] and the frequency power laws [8,9,10]. The former has been practically used to measure the deviation from ideal, electrolytic capacitors, whereas the latter has been mathematically explained using the time derivative of a charge, CV [10], where C is the capacitance and V is the time-dependent voltage. Dispersion has been observed in such a wide frequency, range from 0.01 Hz to 10 kHz [7,11], that it cannot be ascribed to the inversion of dipole orientation caused by an external electric field. A single dipole can only be oriented at 1 GHz [12]. The experimental response at much lower frequencies may be caused by complicated interactions between a huge number of dipoles, known as cooperative phenomena [13,14]. An externally applied electric field seems to orient solvent dipoles in a uniform direction to decrease electrostatic energy, as illustrated in Figure 1A. However, the level of interaction energy of hydrogen bonds on electrodes is much larger than field-oriented energy [15], and thus neighboring water dipoles are alternately oriented, as shown in Figure 1B. The parts of dipoles oriented by the field, and thus overcoming thermal fluctuation, can participate in DLC, as shown in Figure 1C, where the time domain is as long as 1 s.
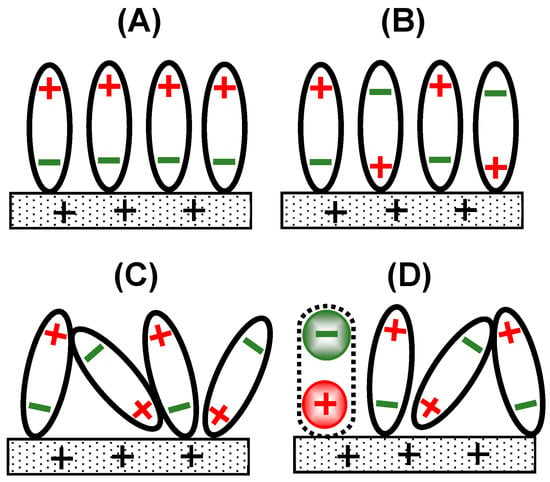
Figure 1.
Illustrations of the orientation of solvent dipoles responding to positive voltage at an electrode when (A) the interaction among the dipoles is neglected, (B) it is stronger than the field-orientation energy, (C) it is balanced with the latter energy and thermally fluctuated, and (D) a redox species is oxidized (+) with a help of a counterion (−).
A charge transfer reaction is associated with electrical neutralization via counterions, which yields a dipole called a redox dipole (−…+ in Figure 1D). The dipole is oriented in the direction opposite to that of the field-oriented solvent dipoles [16]. Therefore, the redox dipole works to suppress DLC, as shown in Figure 1D. When its contribution overcomes the DLC current, the observed capacitance has a negative value [10,17,18,19,20,21,22,23]. Since it takes an unpredictably long time to establish the stable, macroscopic, two-dimensional structure of oriented dipoles, redox reactions may have a relaxation similar to the delay of DLC.
Heterogeneous kinetics, i.e., a delay in attaining the Nernst equilibrium, is expressed using the Tafel equation or Butler–Volmer equation, in which a reaction rate or current exponentially varies with an applied voltage. Exponential dependence refers to the rate-determining step, which involves a transfer of electrons through an electric field, studied via transition state theory [24,25,26], without any influence of alterations of charge neutralization, solvation, chemical complications or adsorption. These influences have been taken into account by introducing reorganization energy to reaction-free energy curves [27,28]. However, evaluated charge transfer rate constants depend on practical conditions, such as measurement techniques [29], curve-fitting methods [30], and sometimes research groups. In fact, reported rate constants of ferrocene in acetonitrile have ranged by over ten thousands [31]. Fast-scan voltammetry can provide heterogeneous rate constants on the order of 0.01 cm s−1 but with much ambiguity, while steady-state voltammetry at ultra-micro electrodes yields rates constants that are too fast [32]. The inconsistency of the observed rates has been explained in terms of solvent reorientation dynamics or solvent friction effects [33]. For example, rates of 1,4-phenylenediamine vary linearly with the inverse of dielectric relaxation time [34], as supported by theories [35,36]. Rates of redox species have been associated with solvent dynamics [29,37], hydrodynamic radius [38], and viscosity [39]. Since other effects such as neutralization are significantly slower than the motion of electrons through electric fields, exponential dependence is not likely to have a true rate, but overall rates may be controlled via a time-dependent pre-exponential factor. It is necessary to suggest a new form of heterogeneous kinetics that includes time variables rather than exponential dependence.
Not only DLC (Figure 1C), but also a charge transfer reaction (Figure 1D), participates in dipole–dipole interactions. The former can be characterized via frequency dispersion, while the latter is characterized via negative capacitance [17,18,19,20,21,22,23]. The two interactions on an electrode surface have a delay that stabilizes surface structure over the whole surface, taking much longer than the time of orientation for one dipole. There is a resemblance between these interactions regarding the delay associated with dipole interactions on the electrode. Here, we describe the detailed concept of resemblance, derive equations for chronoamperometry, devise a potential step experiment for a ferrocenyl derivative, and analyze the experimental data.
2. Theory
The concept of delay or negative capacitance is outlined here. When an oxidation potential is applied to an electrode in solution containing a redox species, the Nernst equation determines the activity of the redox species on the electrode surface. If the activity is equivalent to a concentration on the electrode, the difference between the surface concentration and bulk concentration causes diffusion, the flux of which is observed as current. The current values are specific to applied potentials. This logic is valid for the assumption of the equivalence of activity to the concentration. The activity is a measure of such an effective concentration that the energetical balance is formally satisfied via the Nernst equation. In contrast, concentration is the number density of the redox species without considering any energetical concept. It is concentration rather than activity that can control diffusion equations.
If the dipole–dipole interaction in solvents, for example hydrogen bonding energy, is larger than the standard chemical potential term (the product of the chemical potential times the exchanged charge), the activity value calculated via the Nernst equation is different from concentration. Figure 2 shows an illustrative example of the difference between when a redox species Fc is partially oxidized compared to Fc+ by applying an oxidation potential. The oxidation is associated with charge neutrality via a counterion (Cl−) to form a redox dipole (indicated as two parallel arrows). Water dipoles neighboring Fc+ − Cl− are oriented in the direction opposite to the orientation of Fc+ − Cl− (in imaginary cells (a) and (a′)) in order to decrease the dipole–dipole interaction energy. Those next to (a) should be directed toward the electrode in (b), which can participate in the formation of DLC. The dipolar structure in (a′) is similar to that in (a). If Fc+ in (a′) is not oxidized, the neutral form of Fc has no effect on the orientation of the neighboring water diploes in (b′), which may be thermally fluctuated, reaching the sum of the dipoles and the zero dipole moment in (b′). The interaction energy in [A] is the same as that in [B] for dipole–dipole interactions, resulting in the same chemical potential in [A] as in [B]. Consequently, the concentration on the electrode is different from the activity controlled by the Nernst equation.
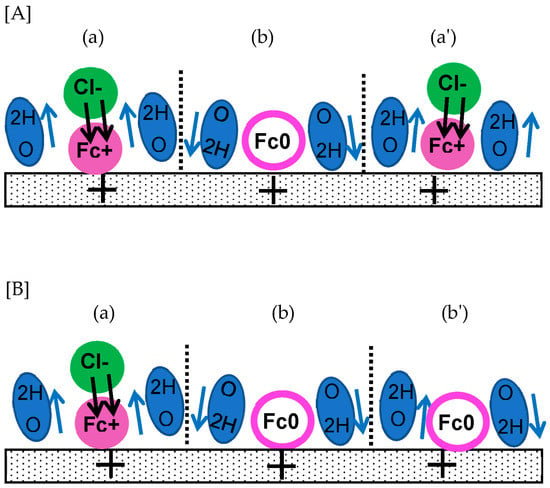
Figure 2.
Arrangements of redox dipoles (black arrows) and solvent dipoles (blue). Since dipole interactions are cancelled (a,a′) with the solvent dipoles, the dipole interaction in (A) is the same as (B). The activity of (A) is the same as (B). Dipoles of (b,b′) work as DLC.
We describe the time dependence of DLC, which is not only reflected in heterogeneous kinetics but also helpful for subtracting the DLC components from the observed components. When voltage V is applied in a step form to DLC, the chronoamperometric current density at t > 0.3 ms can be calculated as follows [40]:
where C1s is the DLC per area at t = 1 s, and λ is the number close to 0.1, according to previous results [40]. It is not in the form of exp(−t/RsC) for a solution resistance, Rs and the DLC, C, because it largely deviates from an ideal capacitance due to frequency dispersion. Since no point of zero charge has been found on a platinum electrode in various aqueous solutions [9,41], V is the step voltage independent of the formal potential of a redox species. Although the decay speed (t−0.9) is larger than the Cottrell’s decay value (t−0.5), the DLC current still survives even at 1 s. This long relaxation caused by the power laws may be involved in the heterogeneous kinetics via dipole interactions.
jdl = λVC1stλ−1
We consider a faradaic current via a one-electron transferring Nernstian redox couple dissolved in a solution. The mass transport of the redox species is assumed to be controlled by time-dependent one-dimensional (x−) diffusion via the diffusion coefficient, D, common to reduced and oxidized species. When a potential is stepped from a fully reduced domain to a given oxidized potential E, a solution of the diffusion equation provides the relationship between the surface concentration, cs, and the observed current density, job [42] as follows:
where c* is the bulk concentration of the redox species, and F is the Faraday constant. The observed current density is the result of subtracting the negatively capacitive density, jN, from Cottrell’s current density, jC:
where:
Here, μ is a positive number close to zero because the behavior of μ seems to be similar to that of λ in the mechanisms, and Crx is the capacitance associated with a redox reaction. The functional form of jN is assumed to be similar to that of DLC (Equation (1)) because of similarity of the current source by the dipole–dipole interaction. Inserting Equation (3) into Equation (2) and carrying out integrations via the Beta function formula cited with Equation (6.2.1) in [43], we have:
where Γ is the gamma function. This equation states that the surface concentration decreases with tμ−1/2 dependence. Although sufficiently oxidized electrical potential is applied to the electrode, the concentration of the reduced species may not instantaneously reduce to zero. The observed currents lower than the Cottrell’s current mean that the concentration values on the electrode are detectable.
cs = c* − F−1(πD)−1/2 ∫0t job(u)(t − u)−1/2 du
job(t) = jC − jN
jC = c*F(D/πt)1/2
jN = μVCrxtμ−1
cs(t) = (μVCrx/FD1/2){Γ(μ)/Γ(μ + 1/2)}tμ−1/2
Observed currents always include the DLC current, i.e., IC − IN + Idl. Each contribution is examined here in order to find which current contributes the most to cs. Chronoamperometric curves were calculated using Equations (1), (4) and (5) for our experimental values of c*, D [21], λ [40] and μ, where the gamma functions were evaluated with use of the approximate Equation (6.1.35) in [43]. They are shown in Figure 3A, and the Cottrell plots (I vs. t−1/2) are shown in Figure 3B. The lower deviation of the current, IC − IN, from the Cottrell equation is noticeable at a time shorter than 0.1 s (t−1/2 > 3 in Figure 3B) and is a kinetic effect. The time-dependent current must include the DLC current (c). The observed current, IC − IN + Idl, is predicted to be curved (d), which is close to the Cottrell equation without the capacitive current. When c* is less than 0.1 mM, values of IC − IN are close to those of Idl. Thus, pulse voltametric currents for low redox concentrations always suffer from capacitive currents [44,45,46].
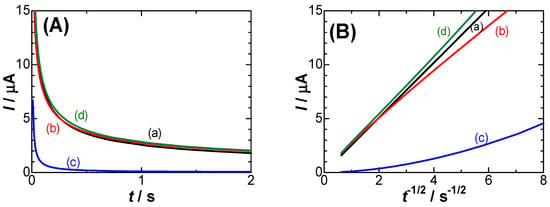
Figure 3.
Chronoamperometric curves (A) and their variations with t−1/2 (B) for (a) IC, (b) IC − IN, (c) Idl, (d) IC − IN + Idl, calculated from Equations (1), (4) and (5) at c* = 1 mM, D = 0.7×10−5 cm2 s−1, μ = 0.1, λ = 0.1, V = 0.2 V, C1s = 30 μF cm−2, Crx = 70 μF cm−2 and the electrode area 1.77 mm2.
It is interesting to compare negative capacitance with Butler–Volmer kinetics, which is expressed in chronoamperometry as [47]:
where:
jBV = c*FD1/2 Λ exp(Λ2t) erfc(Λt1/2)
Λ = k°D−1/2{exp[β(Edc − E°)F/RT] + exp[−α(Edc − E°)F/RT]}
Here, k° is the standard rate constant for the charge transfer reaction, and α and β are the cathodic and anodic transfer coefficients, respectively. Figure 4 shows (A) Cottrell plots and (B) their logarithmic plots calculated using Equation (3) and Butler–Volmer kinetics for three values of Edc − E°. The Cottrell plots for Butler–Volmer kinetics exhibit a nonlinear shape for Edc − E° < 0.10 V, while those for negative capacitance fall on each line with almost zero intercepts. These two kinds of kinetics can be distinguished from the logarithmic plots more clearly than from the Cottrell plots at the two points: (i) the plotted lines for negative capacitance are shown, and (ii) the slopes of the lines are independent of Edc.
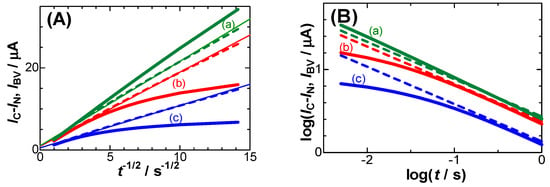
Figure 4.
Variations of (A) IBV (bold solid curves) and IC − IN (dashed curves) with t−1/2 for Edc − E° = (a) 0.15, (b) 0.05 and (c) 0.0 V, and (B) their logarithmic plots when k° = 0.005 cm s−1, α = β = 0.5.
3. Experimental Section
The potentiostat used for the cyclic voltammetry and chronoamperometry was a Compactstat (Ivium, The Netherlands). The working electrode was a platinum wire 0.5 mm in diameter, the 1 mm long tip of which was inserted into the solution. This structure has the advantage of an exposed electrode area that is unaffected by floating capacitance caused by a crevice between the electrode and its insulator during area control [48]. The accurate length was controlled using a Z-stage with the help of an optical microscope. The counter electrode was a platinum wire with an area 100 times larger that of the working electrode, and the reference electrode was Ag|AgCl in saturated KCl solution. The test solutions were deareated for 15 min before each experimental measurement.
All the chemicals were of analytical grade. Aqueous solutions of 1 mM (mM = 10−3 mol dm−3) (ferrocenylmethyl)trimethyl ammonium (FcTMA) and 0.5 M KCl were prepared in distilled and then ion-exchanged water using an ultrapure water system, CPW-100 (Advance, Tokyo, Japan). All the measurements were recorded at a room temperature.
4. Results and Discussion
Figure 5 shows Cottrell plots for the observed chronoamperometric curves in solutions (a) with and (b) without FcTMA when the potential was stepped from the reduced domain (0.26 V) to the limiting domain (Edc = 0.489 V). The linear sweep voltammogram is shown in the inset to specify the potential domain. The difference in the currents of the sweep voltammogram and the chronoamperogram is caused by the large difference in the time scale. The solution resistance was evaluated using Nyquist plots via AC impedance and was found to be 100 Ω. If 4 mV of IR-drop is added to the applied voltage, the effectively maximum current, 40 μA, corresponds to the chronoamperometric time 0.006 s according to the Cottrell equation for D = 0.7 × 10−5 cm2 s−1. On the other hand, the longest and most efficient time deviation from the Cottrell equation is the incidence time for cylindrical diffusion. The current at a cylindrical electrode of radius a is approximately expressed as a(πDt)−1/2 + 0.422 [49]. If 3% errors are allowed to be involved in the current, the longest time, tL, satisfying a(πDtL)−1/2 > 0.422 × 0.03 is tL < 0.2 s. Consequently, the time domain for the analysis is 0.006 s < t < 0.2 s.
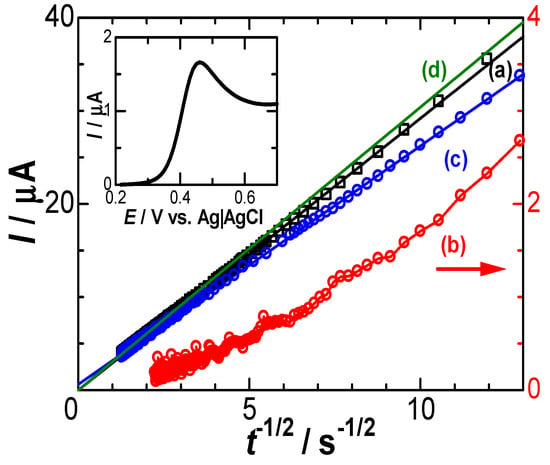
Figure 5.
Cottrell plots of the observed chronoamperograms in the solution of 0.5 M KCl (a) with and (b) without 1 mM FcTMA for the potential stepped from 0.26 V to 0.489 V and for (d) the calculated potential of D = 0.7 × 10−5 cm2 s−1. Plots for the subtracted current against t−1/2 are shown in (c). The inset shows the current–voltage curve in the solution of 1 mM FcTMA and 0.5 M KCl at a scan rate of 0.015 Vs−1. The arrow means that plots (b) follow the right ordinate.
The observed chronoamperometric current in the Cottrell plots exhibited a linear relationship with passing through the origin (a). Since the DLC current (b) was as much as 1/10 of the observed current (a), it was subtracted from the observed current and is shown (c) in Figure 5. The subtracted current shows a still linearity with t−1/2. The Cottrell plot theoretically calculated for c* = 1 mM and D = 0.7 × 10−5 cm s−1 is shown in Figure 5(d). The DLC-included current (a) is ironically close to the Cottrell current (d), indicating that the contribution of kinetics should be numerically similar to the DLC current. The difference between (d) and (c) seems to lie in the contribution of the negative capacitance. This resembles the deviation of the plots of the peak current against the square root of potential scan rates in cyclic voltammetry [21].
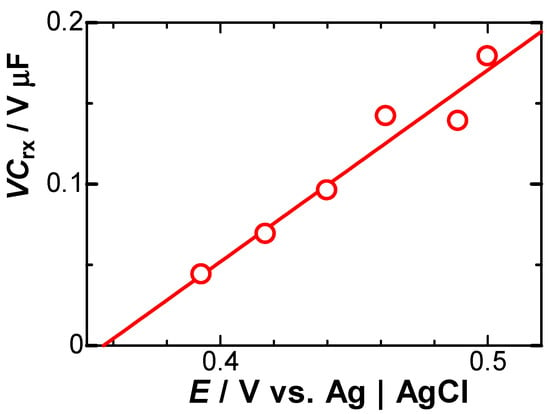
Equation (5) predicts that the negatively capacitive current, which can be evaluated from IN = IC + Idl − Iob, has tμ−1 dependence. In order to examine the power law in IN, we logarithmically plotted IN against t for two values of E, as shown in Figure 6. All the points at each E fell on each line, of which slopes were common and determined to be μ = 0.1. Values of VCrx were obtained from the intercept, as shown in Figure 6, and were plotted against E, as shown in Figure 7. They fell on a line, the slope of which represents Crx, according to Equation (5). The value was Crx = 67 μF cm−2, which is close to 64 μF cm−2 [18] and was obtained via AC impedance and 60 μF cm−2 [21] using fast cyclic voltammetry.
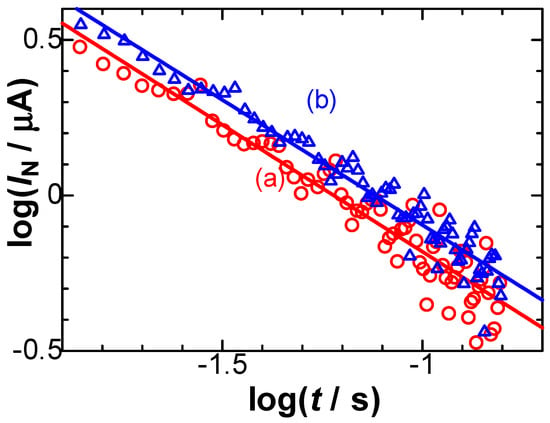
Figure 6.
Logarithmic plots of the negatively capacitive current against time for the current–time curves observed at the stepped potential from 0.26 V to Edc = (a) 0.440 and (b) 0.489 V.
We numerically evaluated cs using Equation (6) for the determined values of μ and Crx at c* = 1 mM. Figure 8 shows the calculated time variation in cs and a dotted line averaged over t < 0.2. The value of cs might be almost zero without any interaction. The average concentration is 0.1 mM, suggesting that it is ineffective in oxidation. Although the potential is in the limiting current domain, the concentration of the reduced species on the electrode is not zero, as illustrated in Figure 1D. Oxidation energy is consumed by decreasing the dipole–dipole interaction on the electrode until the interaction becomes stable. This interaction is also a source of negative capacitance, and hence the non-zero surface concentration is equivalent to negative capacitance. The times at which the concentration at the surface becomes 5% and 2% of the bulk concentration are 0.5 s and 5 s, respectively. This slow relaxation is close to the frequency dispersion of the DLC.
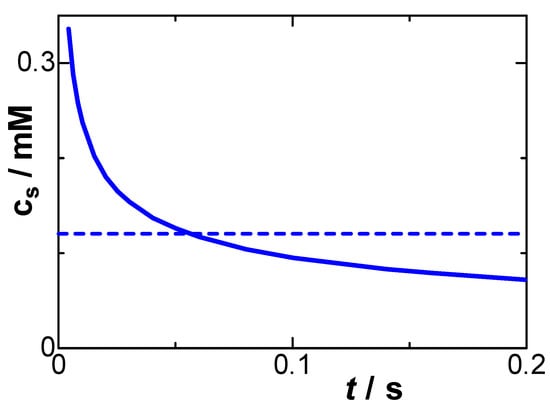
Figure 8.
Time variation of the concentration on the electrode surface, calculated using Equation (6) for μ = 0.1, Crx = 67 μF cm−2, and D = 0.7 × 10−5 cm2 s−1 at Edc = 0.489 V vs. Ag|AgCl. The dashed line is the average concentration for 0 < t < 0.2 s.
Since the linearity of the experimental data presented in Figure 6 is inconsistent with the convex variation of the Butler–Volmer kinetics shown in Figure 4, it is clear that the Butler–Volmer kinetics fails to elucidate our experimental time dependence. It is interesting to determine which kinds of values of k° can be obtained if Butler–Volmer kinetics is applied to the present chronoamperograms in the light of time dependence, especially when the approximate equation for the error function of Equation (7.1.13) in [43] is applied to Equation (7):
The current–time curve can be expressed via a simple calculation as follows:
where:
We evaluated y using experimental data, and plotted (y − 1)2 against 1/t, as shown in Figure 9, at E = 0.393 V. Some data ranging from 10 s−1 < t−1 < 60 s−1 fell on a line, of which the intercept was forced to pass through 1, according to Equation (10). The slope provided Λ and k° = 3 × 10−4 cm s−1 via Equation (8) for α = β = 0.5. However, the plot in Figure 9 does not justify a linear variation in that the slopes decrease over longer periods of time. Values of k° thus decreased with an increase in E and became negative for E < 0.42 V. Since they were not uniquely determined, they are physiochemically insignificant.
exp(x2) erfc(x) = (2/√π)/{x + (x2 + 4/π)1/2}
(y − 1)2 = 1 + 4/πΛ2t
y = 2c*F(D/πt)1/2/jBV
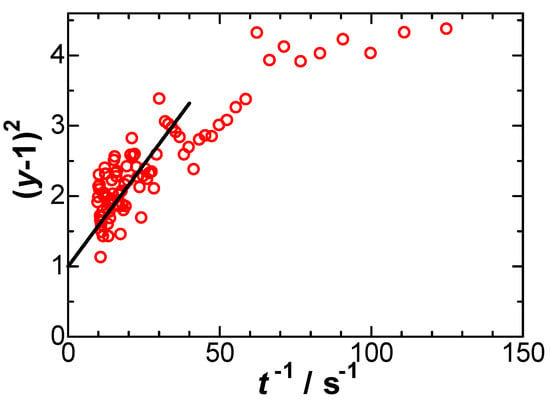
Figure 9.
Plots of y of Equation (9) against 1/t to determine Λ at E = 0.393 V when BV kinetics is applied.
5. Conclusions
A new form of heterogeneous kinetics is presented here, which is revealed by the level of depression in the current caused by the Cottrell current. This amount, being proportional to the power of the time, corresponds to the negative capacitive current brought about by the redox reaction in the physical experiment. The kinetic parameters are the power number and negative capacitance, which has almost the same form as DLC caused by solvent dipole–dipole interaction. This similarity indicates that kinetics should be ascribed to the dipole–dipole interactions activated by the generation of the redox dipole, whereas DLC is activated by the applied electric field. Since dipole interactions on the electrode widely vary and thermally fluctuate, it takes a macroscopic time rather than a microscopic inversion time of one dipole to establish a stable structure both for the kinetics and DLC.
Diffusion current is controlled via the surface concentration, which can be determined by electrode potential on the assumption that the concentration is equivalent to the activity. If electrostatic energy at the electrode is mostly consumed due to the structure formation of solvent dipoles via their orientation, the surface concentration is not sufficiently affected by the electrical potential, and thus the diffusion current does not decrease. The deviation of the concentration from the activity in the Nernst equation is caused by the interaction between the redox dipoles and solvent dipoles, whereas negative capacitance is brought about by redox dipoles sustained by solvent dipoles. This similarity indicates that the model of the negative capacitance may be equivalent to the deviation in concentration from the activity.
The slow relaxation of the solvent interaction triggered by the redox reaction also occurs when an electric field is applied to the electrode. Then, the redox reaction demonstrates a slow relaxation similar to that of DLC. Therefore, both the redox reaction and DLC have a similar power law of the time.
Butler–Volmer kinetics failed to determine the heterogeneous rate constants and was invalid, even in the linearity of time-dependent plots. The determined rate constant was much smaller than values predicted via cyclic voltammetry.
Author Contributions
Conceptualization, K.J.A. and J.C.; methodology, Y.L.; software, Y.L. and K.J.A.; validation, K.J.A. and J.C.; formal analysis, Y.L.; investigation, K.J.A.; resources, J.C.; data curation, J.C.; writing—original draft preparation, K.J.A.; writing—review and editing, Y.L.; visualization, Y.L.; supervision, J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gerhardt, R. Impedance Spectroscopy and Mobility Spectra. In Encyclopedia of Condensed Matter Physics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 350–363. [Google Scholar] [CrossRef]
- Frolov, D.S.; Zubkov, V.I. Frequency dispersion of capacitance–voltage characteristics in wide bandgap semiconductor-electrolyte junctions. Semicond. Sci. Technol. 2016, 31, 125013. [Google Scholar] [CrossRef]
- Lasia, A. Modern Aspects of Electrochemistry, 32; White, R.E., Conway, B.E., Bockris, J.O.’M., Eds.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 1999; p. 143. [Google Scholar]
- Brug, G.J.; Van Den Eeden, A.L.G.; Sluyters-Rehbach, M.; Sluyters, J.H. The analysis of electrode impedances complicated by the presence of a constant phase element. J. Electroanal. Chem. Interfacial. Electrochem. 1984, 176, 275–295. [Google Scholar] [CrossRef]
- Nyikos, L.; Pajkossy, T. Fractal dimension and fractional power frequency-dependent impedance of blocking electrodes. Electrochim. Acta 1985, 30, 1533–1540. [Google Scholar] [CrossRef]
- Zoltowski, P. On the electrical capacitance of interfaces exhibiting constant phase element behaviour. J. Electroanal. Chem. 1998, 443, 149–154. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Robinson, S.A.; Tempel, H.; Kungl, H.; Eichel, R.-A. Physicochemical Mechanisms of the Double-Layer Capacitance Dispersion and Dynamics: An Impedance Analysis. J. Phys. Chem. C 2021, 125, 5870–5879. [Google Scholar] [CrossRef]
- Hou, Y.; Aoki, K.J.; Chen, J.; Nishiumi, T. Solvent Variables Controlling Electric Double Layer Capacitance at the Metal–Solution Interface. J. Phys. Chem. C 2014, 118, 10153–10158. [Google Scholar] [CrossRef]
- Aoki, K.; Hou, Y.; Chen, J.; Nishiumi, T. Resistance associated with measurements of capacitance in electric double layers. J. Electroanal. Chem. 2012, 689, 124–129. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J. Effects of the dipolar double layer on elemental electrode processes at micro- and macro-interfaces. Faraday Discuss. 2018, 210, 219–234. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.-A. Double layer capacitances analysed with impedance spectroscopy and cyclic voltammetry: Validity and limits of the constant phase element parameterization. Phys. Chem. Chem. Phys. 2021, 23, 21097–21105. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Physical Chemistry, 10th ed.; Oxford University Press: Oxford, UK, 2014; pp. 664–665. [Google Scholar]
- Chen, Z.; Wasson, M.C.; Drout, R.J.; Robison, L.; Idrees, K.B.; Knapp, J.G.; Son, F.A.; Zhang, X.; Hierse, W.; Kühn, C.; et al. The state of the field: From inception to commercialization of metal–organic frameworks. Faraday Discuss. 2020, 225, 9–69. [Google Scholar] [CrossRef]
- Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev. 1951, 81, 988–1003. [Google Scholar] [CrossRef]
- Aoki, K.J. Molecular interaction model for frequency-dependence of double layer capacitors. Electrochim. Acta 2016, 188, 545–550. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1989; pp. 158–164. [Google Scholar]
- Aoki, K.J.; Chen, J.; Zeng, X.; Wang, Z. Decrease in the double layer capacitance by faradaic current. RSC Adv. 2017, 7, 22501–22509. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J.; Tang, P. Capacitive Currents Flowing in the Direction Opposite to Redox Currents. J. Phys. Chem. C 2018, 122, 16727–16732. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J.; Wang, R. Stripped Charge of Ag Less than Deposited one Owing to Negative Capacitance Caused by Redox Reactions. Electroanalysis 2019, 31, 2303–2310. [Google Scholar] [CrossRef]
- Tang, P.; Aoki, K.J.; Chen, J. Reduction Charge Smaller than the Deposited One in Cathodic Stripping Voltammograms of AgCl. Am. J. Anal. Chem. 2019, 10, 286–295. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J.; Liu, Y.; Jia, B. Peak potential shift of fast cyclic voltammograms owing to capacitance of redox reactions. J. Electroanal. Chem. 2020, 856, 113609. [Google Scholar] [CrossRef]
- Aoki, K.J.; Taniguchi, S.; Chen, J. Participation in Negative Capacitance of Diffusion-Controlled Voltammograms of Hemin. ACS Omega 2020, 5, 29447–29452. [Google Scholar] [CrossRef]
- Liu, Y.; Aoki, K.J.; Chen, J. A Loss of Charge at Reduction of Hydrogen Ion by Fast Scan Voltammetry. J. Electrochem. Soc. 2022, 169, 036510. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry, 10th ed.; Oxford University Press: Oxford, UK, 2014; pp. 894–901. [Google Scholar]
- Compton, R.G.; Banks, C.E. Understanding Voltammetry, 2nd ed.; Imperial College Press: London, UK, 2010. [Google Scholar]
- Weaver, M.J. Redox reactions at metal–solution interfaces. Weaver, M.J. In Electrode Kinetics: Reactions; Compton, R.G., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1988; Chapter 1. [Google Scholar]
- Marcus, R.; Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 1985, 811, 265–322. [Google Scholar] [CrossRef]
- Hush, N. Electron transfer in retrospect and prospect 1: Adiabatic electrode processes. J. Electroanal. Chem. 1999, 470, 170–195. [Google Scholar] [CrossRef]
- Fawcett, W.R.; Opallo, M. The Kinetics of Heterogeneous Electron Transfer Reaction in Polar Solvents. Chem. Int. Ed. Engl. 1994, 33, 2131–2143. [Google Scholar] [CrossRef]
- Henstridge, M.C.; Laborda, E.; Wang, Y.; Suwatchara, D.; Rees, N.; Molina, A.; Martínez-Ortiz, F.; Compton, R.G. Giving physical insight into the Butler–Volmer model of electrode kinetics: Application of asymmetric Marcus–Hush theory to the study of the electroreductions of 2-methyl-2-nitropropane, cyclooctatetraene and europium(III) on mercury microelectrodes. J. Electroanal. Chem. 2012, 672, 45–52. [Google Scholar] [CrossRef]
- Clegg, A.D.; Rees, N.; Klymenko, O.; Coles, B.A.; Compton, R.G. Marcus theory of outer-sphere heterogeneous electron transfer reactions: High precision steady-state measurements of the standard electrochemical rate constant for ferrocene derivatives in alkyl cyanide solvents. J. Electroanal. Chem. 2005, 580, 78–86. [Google Scholar] [CrossRef]
- Aoki, K.J.; Zhang, C.; Chen, J.; Nishiumi, T. Heterogeneous reaction rate constants by steady-state microelectrode techniques and fast scan voltammetry. J. Electroanal. Chem. 2013, 706, 40–47. [Google Scholar] [CrossRef]
- Henstridge, M.C.; Laborda, E.; Rees, N.V.; Compton, R.G. Marcus–Hush–Chidsey theory of electron transfer applied to voltammetry: A review. Electrochim. Acta 2012, 84, 12–20. [Google Scholar] [CrossRef]
- Opałło, M. The solvent effect on the electro-oxidation of 1,4-phenylenediamine. The influence of the solvent reorientation dynamics on the one-electron transfer rate. Chem. Soc. Faraday Trans. I 1986, 82, 339–347. [Google Scholar] [CrossRef]
- Alexandrov, I. Physical aspects of charge transfer theory. Chem. Phys. 1980, 51, 449–457. [Google Scholar] [CrossRef]
- Calef, D.F.; Wolynes, P.G. Classical solvent dynamics and electron transfer. 1. Continuum theory. J. Phys. Chem. 1983, 87, 3387–3400. [Google Scholar] [CrossRef]
- Weaver, M.J. Dynamical solvent effects on activated electron-transfer reactions: Principles, pitfalls, and progress. Chem. Rev. 1992, 92, 463–480. [Google Scholar] [CrossRef]
- Clegg, A.D.; Rees, N.V.; Klymenko, O.V.; Coles, B.A.; Compton, R.G. Marcus Theory of Outer-Sphere Heterogeneous Electron Transfer Reactions: Dependence of the Standard Electrochemical Rate Constant on the Hydrodynamic Radius from High Precision Measurements of the Oxidation of Anthracene and Its Derivatives in Nonaqueous Solvents Using the High-Speed Channel Electrode. J. Am. Chem. Soc. 2004, 126, 6185–6192. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yang, H.; Bard, A.J. Variation of the heterogeneous electron-transfer rate constant with solution viscosity: Reduction of aqueous solutions of [(EDTA)chromium(III)]- at a mercury electrode. J. Am. Chem. Soc. 1987, 109, 1916–1920. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J.; He, R. Potential Step for Double-Layer Capacitances Obeying the Power Law. ACS Omega 2020, 5, 7497–7502. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Aoki, K.J.; Chen, T.N.J. Invariance of Double Layer Capacitance to Polarized Potential in Halide Solutions. Univers. J. Chem. 2013, 1, 162–169. [Google Scholar] [CrossRef]
- Matsuda, H.; Ayabe, Y.; Elekt, Z. The theory of the cathode-ray polarography of Randles-Sevcik. Phys. Chem. 1955, 59, 494–503. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of mathematical functions, National Bureau of Standards. In Applied Mathematics Series—55; Tenth Printing, Eq. (6.2.1), Eq. (6.1.35), Eq. (7.1.13); National Institute of Informatics: Tokyo, Japan, 1972; pp. 257–289. [Google Scholar]
- Osteryoung, R.A.; Osteryoung, J.; Albery, W.J.; Rogers, G.T. Pulse voltammetric methods of analysis. Phisl. Trans. R. Lond. A 1981, 302, 315–326. [Google Scholar] [CrossRef]
- Lovrić, M.; Osteryoung, J. Theory of differential normal pulse voltammetry. Electrochim. Acta 1982, 27, 963–968. [Google Scholar] [CrossRef]
- Stojek, Z. Pulse Voltammetry. In Electroanalytical Methods; Springer: Berlin/Heidelberg, Germany, 2005; pp. 99–110. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods, 2nd ed.; Kohn Wiley & Sons: New York, NY, USA, 2001; pp. 191–192. [Google Scholar]
- Aoki, K.J.; Chen, J. Tips of Voltammetry. In Voltammetry; IntechOpen: London, UK, 2018; pp. 1–19. [Google Scholar] [CrossRef]
- Aoki, K.; Honda, K.; Tokuda, K.; Matsuda, H. Voltammetry at microcylinder electrodes. Part II. Chronoamperometry. J. Electroanal. Chem. Interfacial Electrochem. 1985, 186, 79–86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).