Parallel Combination of Inner Capacitance and Ionic Capacitance, Apparently Inconsistent with Stern’s Model

Abstract

A double layer capacitance (DLC) has mainly been brought about in the Helmholtz layer rather than in the diffuse layer, as was demonstrated with the invariance of DLC to salt concentration, c, less than 0.5 M (M = mol dm⁻³). The DLC measured here increased with concentrations of KCl and HCl solutions as high as 1 M at a platinum electrode by the ac impedance method. It was represented as a sum of the Helmholtz capacitance and the ionic one which had 0.7 power of the concentrations. The simple addition implies that the Helmholtz contribution and the ionic one should be represented by a parallel combination rather than a series one such as in the Stern model. The disagreement of the experimental values of the DLC with the Gouy–Chapman theory at high concentrations has been conventionally attributed to the effects of packing of ions over their sizes. In this paper, a model of avoiding the packing was introduced, in which ions were distributed in the direction normal to the electrode in the balance of electric motive force and the thermal energy, keeping the uniform distribution on a plane projected to the electrode. The energy balance was taken by using the grand canonical ensemble in statistical mechanics. The ionic contribution had a linear relation with the applied voltage rather than exponential dependence. When a series combination was applied to the Helmholtz capacitance and the ionic one under the condition of difference between the locally anionic DLC and the cationic one, we obtained approximately a parallel combination of the two capacitances because either the anionic or the cationic DLC works predominantly.

1. Introduction

The development of double layer capacitance (DLC) as an electric energy storage has focused [1,2] on the enhancement of the output energy, the power, and cycle stability. Industrial improvements have been conceptually directed [3,4] towards: (a) the geometric feature of electrodes such as the enhancement of specific surface areas, (b) solutions to increase ionic conductance, and (c) an increase in applied voltages. The first item has been realized using porous electrodes or powder electrodes in competition of loss of electric conduction [5]. Secondly, combinations of solvents with salts are significant in order to exhibit highly ionic conduction [6]. Thirdly, inactive electrodes and solutions with widely depolarized voltage domains have been searched tentatively in order to enhance the energetic performance with the square of the applied voltage [7,8]. These improvement techniques have been used on an empirical basis rather than thermodynamic theory.

In contrast, a scientific view of DLC may be directed to variations by measuring variables such as (i) time- and (ii) voltage-dependence as well as roles in (iii) ions, (iv) solvents, and adsorption. A well-known time-dependence (i) is frequency dispersion [9], which has been explained in terms of the concept of the constant phase element (CPE) [10,11,12,13]. The DLC has decreased with an increase in ac-frequency through the power law [14,15,16,17]. As for the voltage-dependence (ii), the DLC does not vary remarkably with dc-voltage in a narrow domain by ac-impedance so that no potential of zero charge (pzc) was observed [14,18,19]. However, measurements in a wide voltage domain have made the dependence specified by current-controlled charge-discharge controls [20]. The effects of ions on the DLC (iii) have not been recognized in the variations of kinds and concentration of salts [14,18] under conventional voltammetric conditions. In contrast, different kinds of solvents (iv) have varied DLC values significantly in the light of effectively oriented dipole moments [18]. Consequently, voltammetrically observed DLC is a phenomenon in the Helmholtz (or inner) layer, which is independent of the diffuse double layer by ionic concentration distributions. These fundamental studies seem to be inconsistent with industrial efforts of enhancing ionic conductance [4,21,22,23,24]. The challenges of examining concentration-dependence [25,26,27,28,29,30,31] have not been supported by thermodynamic bases because of ionic complications.

The ionic effects of the DLC have classically been described by the Gouy–Chapman (GC) theory, which exhibits V-shaped capacitance vs. voltage curves. Since the theory is known to hold only for low concentrations of salts, we attempted to find V-shaped under various ionic conditions to fail [14]. The slight V-shape appeared at concentrations less than 0.05 mM [19]. The direction of finding the V-shape in low concentrations is inconsistent with the industrial improvements to usage of high concentrations. The invalidity of the GC theory has resulted in the extra-condensation of ions beyond the finite size of ions near an electrode by external electric field [32]. Since the observed DLCs occur mostly in the Helmholtz layer, it is not easy to extract an ionic contribution for the GC theory. It is necessary to establish a theory expressing the ionic effect on DLCs even at high concentrations for practical use.

As concentrations in solutions are increased, their thermodynamic properties generally vary from ideal solution to regular solutions, keeping the mixing entropy ideal [33]. A further increase in concentrations deviates the entropy from the ideal mixing owing to the interaction of solutes. The deviation gets more remarkable for electrolytes than non-ionic solutes because of electric interaction over a long distance. As a result, the free energy of ions is influenced both by chemical and electric interaction. This has not been applied to the GC theory, in that the probability of ions in the GC theory is expressed by Boltzmann’s distribution only at electric potential, ϕ, in the form of exp(-zeϕ/k_BT) for the charge valence z and charge e. The probability should include a term of chemical potential, μ, and concentration, c. Since concentrations vary in the double layer domain, local energy is not only varied with zeϕ but also chemical term cμ, i.e., the probability being exp[−(zeϕ + cμ)/k_BT]. In this point, the GC theory belongs to a canonical ensemble. The extension to the inclusion of cμ corresponds to a concept of the grand canonical ensemble.

We would like to interpret the ionic effects in terms of the above concept. The first work is to obtain stable data of DLC in the wide domain of ionic concentrations and voltage without effects of floating capacitance. A technique of avoiding floating capacitance is to use a wire electrode without unstable gaps between an electrode and an insulator [14,16]. Classical data at mercury electrodes are not reliable because mercury metal has not only been dispersed spontaneously to solutions in invisibly micro-droplets but also contained water up to visible volume change [34]. Furthermore, it is important to take into account the frequency dispersion in order to determine DLC values accurately. We show here the concentration- and voltage-dependence of the DLC including frequency-dispersion obtained by ac-impedance at a platinum wire in KCl and HCl solutions. The two kinds of the dependence will demonstrate invalidity of the Stern model but support an equivalent circuit with the parallel combined capacitances. A model based on the grand canonical ensemble is presented to explain not only the two kinds of the experimental dependence but also the equivalent parallel circuit.

2. Materials and Methods

A platinum wire 0.5 mm in diameter was immersed into mixed acid (H₃PO₄ + HNO₃ + CH₃COOH, vol. 2:1:1) to clean the surface [35]. It was used for a working electrode by inserting it into the aqueous KCl solution by a given length, ca. 8 mm, which was determined accurately with an optical microscope. The wire was not sealed with insulating materials in order to avoid floating capacitive current owing to naturally generated gap between the electrode and the insulator. The counter electrode was a platinum wire with an area 100 times larger that of the working electrode, and the reference electrode was Ag|AgCl in saturated KCl solution. The test solution was deaerated for 20 min before the current application. Aqueous solutions of KCl and HCl were prepared with reagents at the analytical grade and distilled and deionized water prepared by CPW-100 (Advantec, Tokyo, Japan). The potentiostat was Compactstat (Ivium, The Netherlands) for ac-impedance measurements and cyclic voltammetry. The conditions of ac impedance were the frequency range from 0.2 Hz to 5000 Hz with the amplitude of 10 mV. All measurements were made at temperature of 25 ± 1 °C. Voltammetric reproducibility was examined at each experimental run. The reproducibility of our voltage-time curves was examined at three runs to be within 5% errors.

3. Results

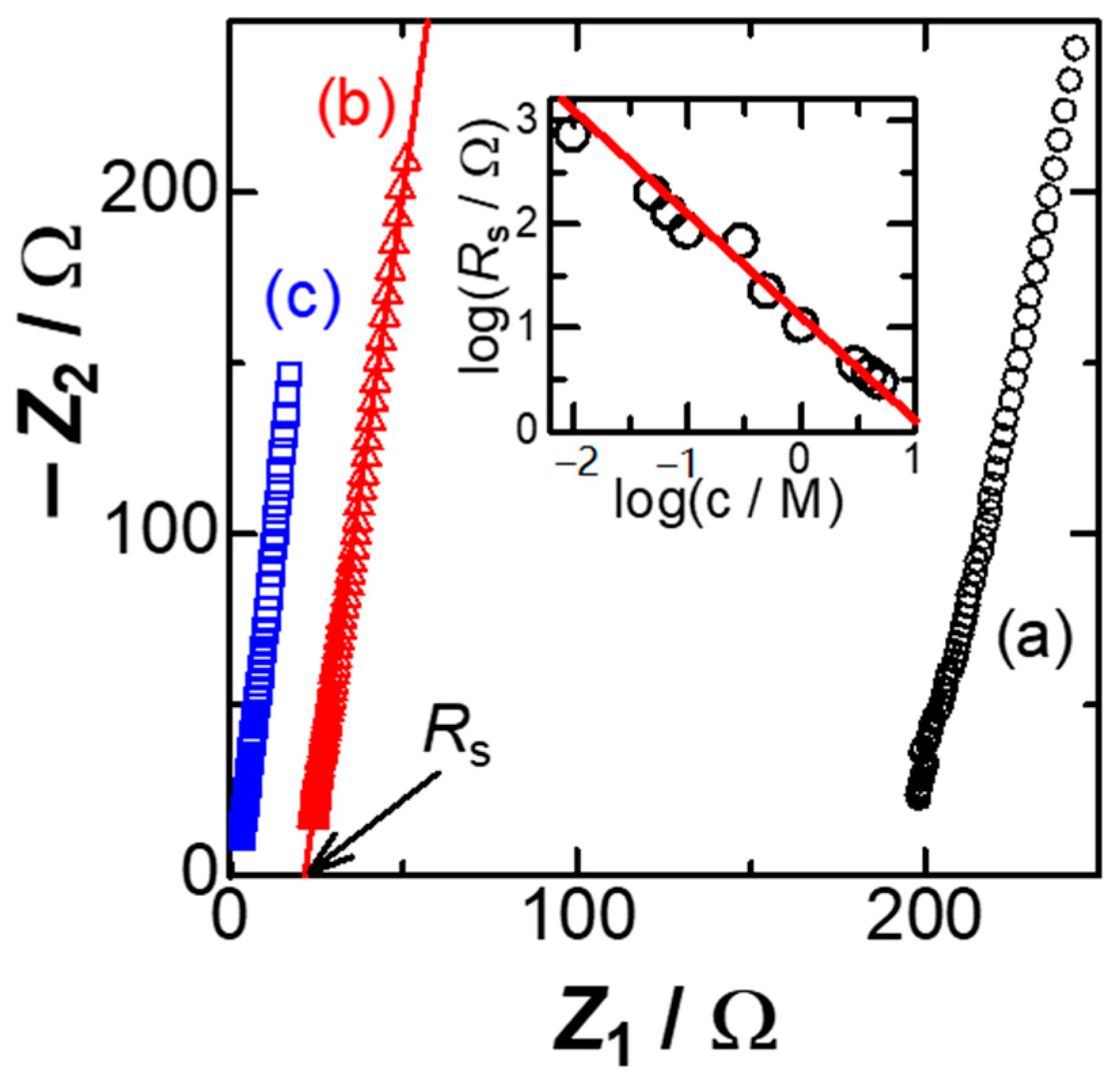
Figure 1 shows Nyquist plots, the real impedance Z₁ vs. the imaginary one, Z₂, at the Pt wire electrode in three concentrations of KCl solutions at the dc-potential, E_dc = 0.0 V vs. Ag|AgCl. All the plots fell on each line, of which a slope of more than 5 represents frequency-dispersion. A value on the Z₁ axis extrapolated to zero of Z₂ is the solution resistance, R_s. Logarithmic plot of R_s against concentration of KCl, c, has a linear relation, as shown in the inset of Figure 1. Although the ideal behavior of the ionic conduction is ∂(log R_s)/∂(log c) = −1, the local slopes at lower concentrations were slightly smaller than −1. This is probably because of leakage of salt from the reference Ag|AgCl electrode to the solution [36].

When the ac voltage of V = V_ace^iωt is applied to the frequency-dispersive capacitance C, the observed ac current density is determined by the time-derivative of the charge, CV, i.e., [16]

J = d(CV)/dt = V{−2πf ² (dC/df) + iωC}

(1)

Since plots of the imaginary admittance against the real one for a flat electrode in simple electrolytes exhibited a line with a constant slope, 1/λ, we have −2πf ²(dC/df)/ωC = λ or −f(dC/df)/C = λ. This is a differential equation for C with respect to f. A solution is

C = C_1Hz f ^−λ

(2)

where C_1Hz is the capacitance value at f = 1 Hz. Inserting Equation (1) into Equation (2) yields for the admittance:

j/V ≡ Y = (λ + i) ωC

(3)

The real and the imaginary admittance subtracting R_s is given by:

Y₁ = (Z₁ − R_s)/{(Z₁ − R_s)² + Z₂²}

(4A)

Y₂ = −Z₂/{(Z₁ − R_s)² + Z₂²}

(4B)

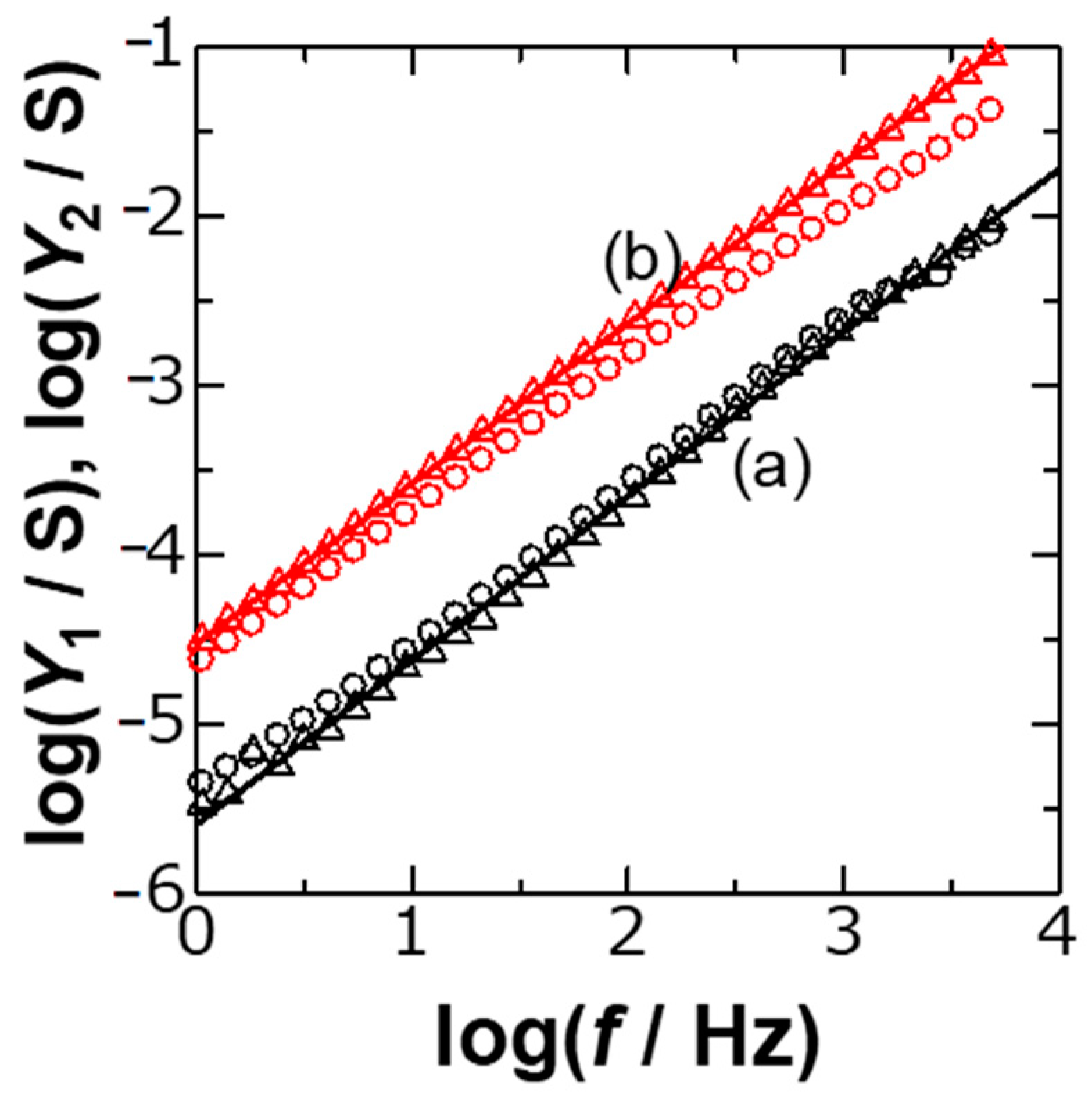
Figure 2 shows logarithmic variations of Y₁ and Y₂ with f, calculated from experimental values of Z₁, Z₂ and R_s, for two concentrations of KCl. The plots fell on each line, as can be predicted from Equations (2) and (3), i.e.,

Y₁ = 2πλ C_1Hz f ^{−λ + 1}

(5A)

Y₂ = 2π C_1Hz f ^{−λ + 1}

(5B)

The slope in the plots in Figure 2 should be 1 − λ, where the approximated values of λ were 0.1. The DLC without frequency dispersion might show λ = 0, or zero resistive component (Y₁ = 0 or Z₁ = R_s). Non-zero values of λ suggest the CPE behavior.

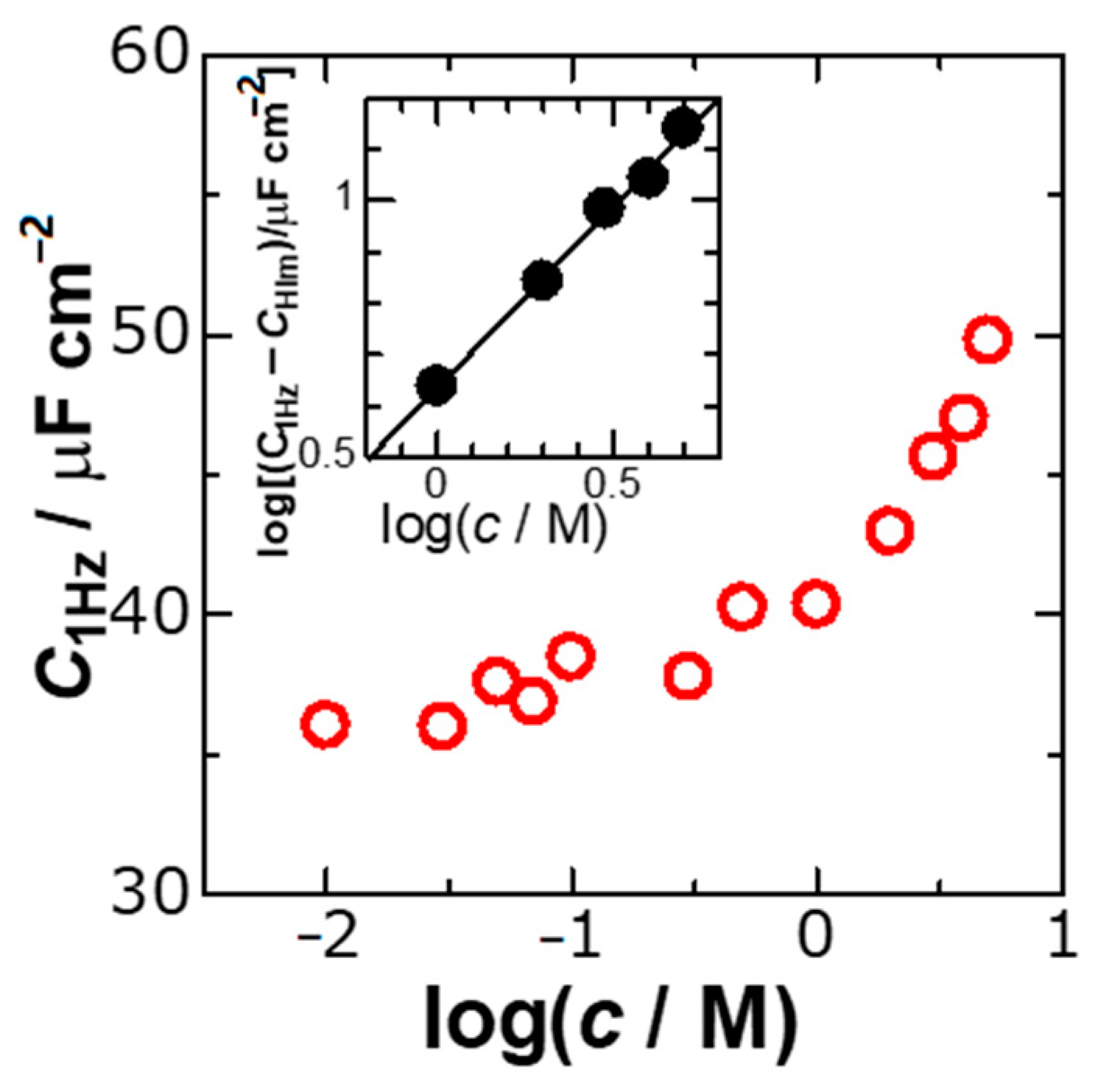
We evaluated C_1Hz from the intercepts of the lines of Y₂ in Figure 2 at each concentration, c, and plotted the values of C_1Hz with c in Figure 3. No variation of C_1Hz for c < 0.3 M can be recognized, whereas an increase in C_1Hz for c > 1 M is remarkable. It is the latter behavior of the ionic effect that we would like to present in this report. The difference of C_1Hz from the capacitance in the Helmholtz layer, C_Hlm (=C_1Hz for c < 0.3 M) represents the ionic contribution to C_1Hz. Logarithmic plots of C_1Hz-C_Hlm against c in the inset of Figure 3 fell on a line with the slope of 0.70, indicating that C_1Hz should be proportional to c^0.7 rather than c itself. This relation implies that the DLC is not formed by ionic distributions due to volume (c-dependence) or the GC theory (c^1/2-dependence) but should be caused by localization of ions involving the two-dimensional factor (c^2/3-dependence). Our new finding is that the extracted ionic capacitance is proportional to the surface concentration (c^2/3).

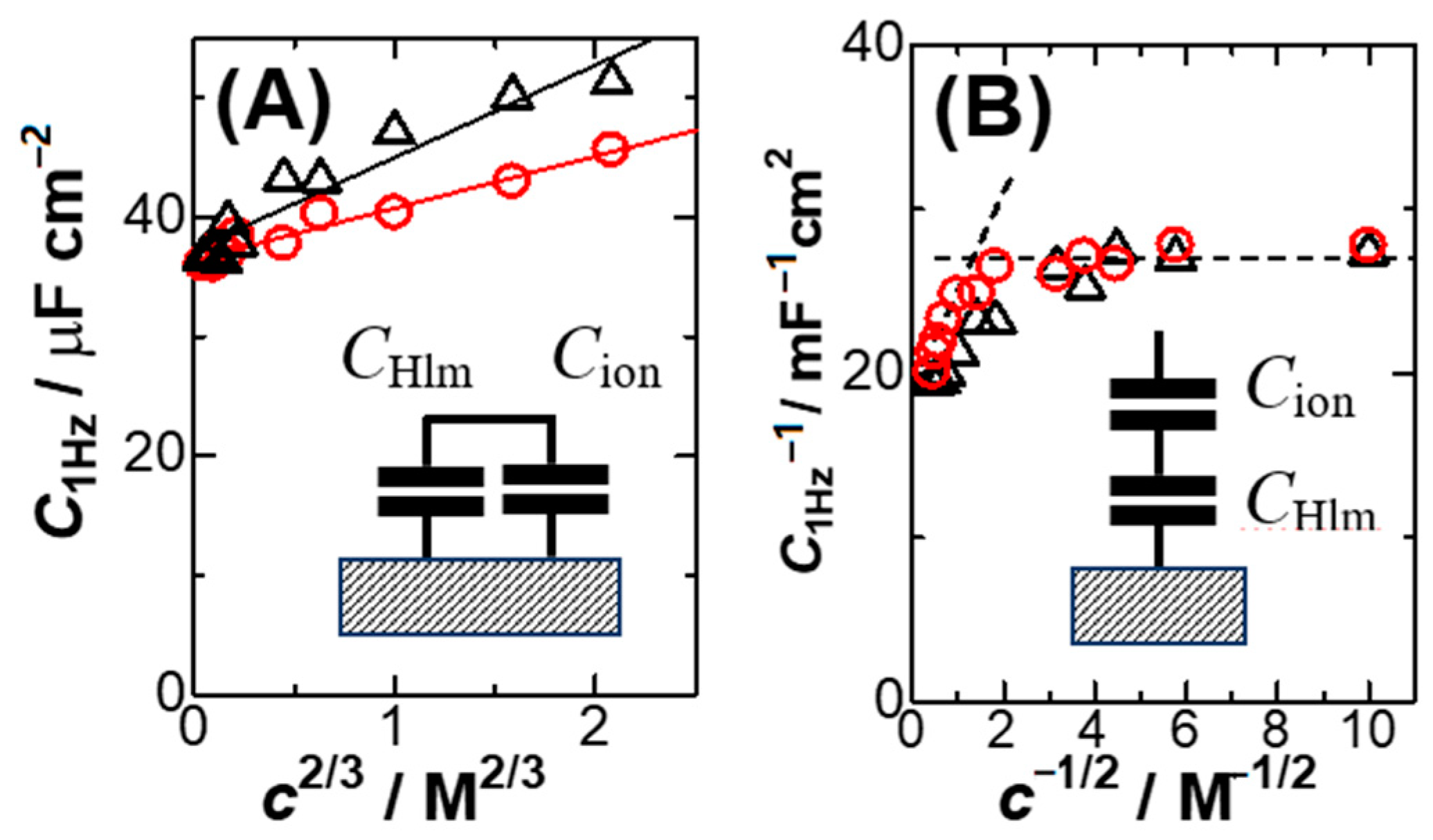
The linearity of the plots in the inset of Figure 3 implies that the capacitance can be expressed by the sum of the c^2/3 term and C_Hlm for a constant k

C_1Hz = k c^2/3 + C_Hlm

(6)

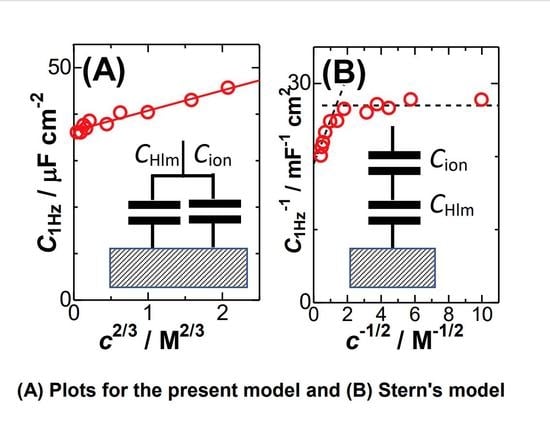
In order to find a quality of the linearity, we plotted C_1Hz against c^2/3 in Figure 4A for KCl and HCl. The quality for KCl (circles) is higher than that for HCl (triangles), probably because high concentrations of HCl are less dissociated electrolytically. Concentrations of HCl determined by pH might enhance the quality. Equation (6) is inconsistent with the Stern model in that the two capacitances are combined in parallel, as shown in the inset of Figure 4A. In order to see a level of the deviation from the Stern model (series connection)

1/C_1Hz = 1/C_Hlm + k’/c^1/2

(7)

We attempted to plot 1/C_Hlm against c^−1/2 in Figure 4B, where k’ is a constant. The non-linear variation suggests the invalidity of the Stern model in the range from 1 mM to 5 M at platinum electrodes. The Stern model should include at least the linear relation of 1/C with c^−1/2. However, there is no report of such plots to our knowledge.

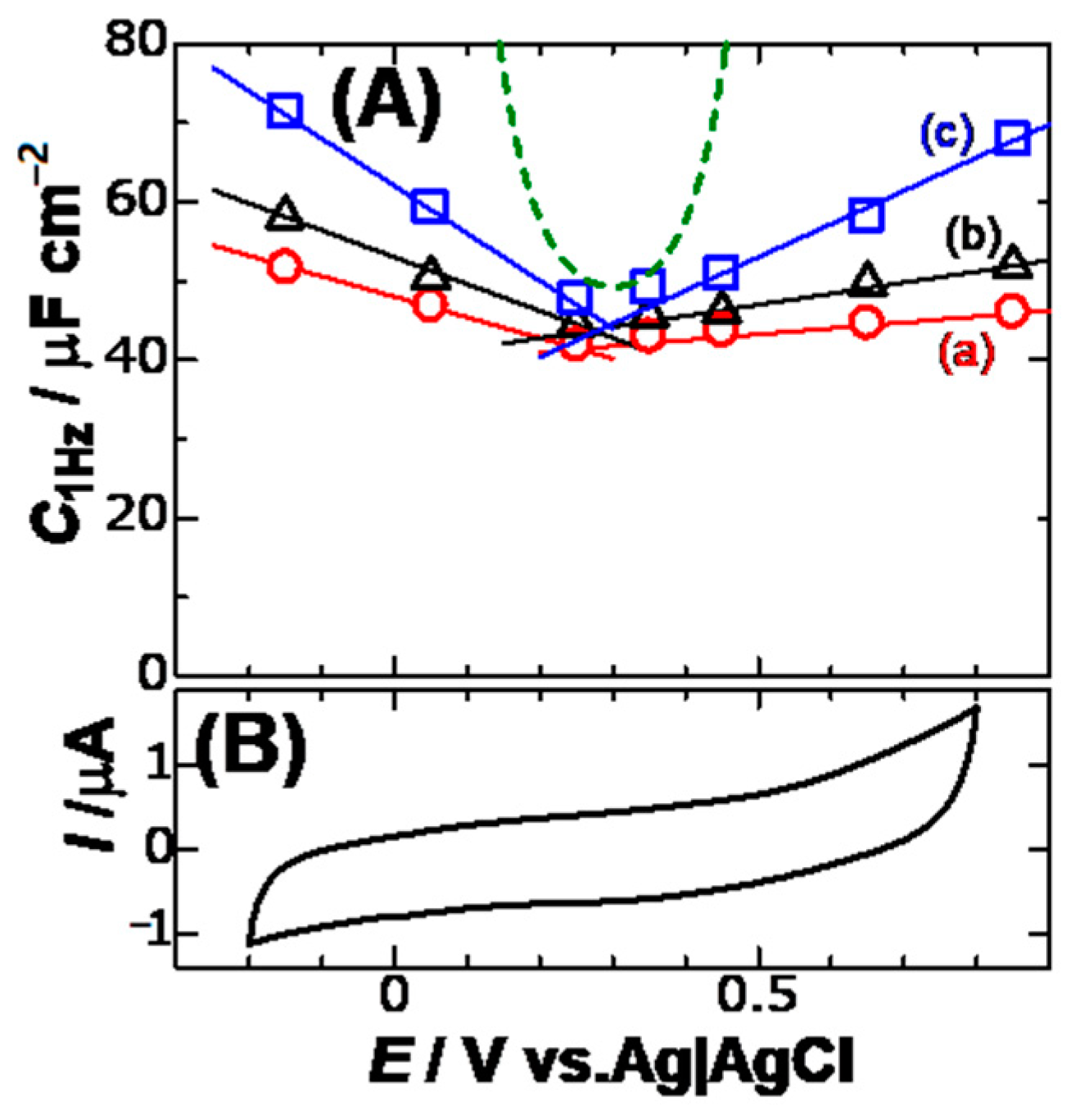
An increase in the electric field is predicted to increase in the DLC because it activates the displacement of ions to relax the applied field. As a result, the variation of the DLC with the dc-potential, E_dc, may exhibit a V-shaped curve, like from the GC theory. Figure 5 shows plots of C_1Hz against E_dc for three concentrations of KCl. Since cyclic voltammograms in this potential domain took a typically capacitive form, the values of C_1Hz in Figure 5 should be capacitance without any faradaic component. A minimum of the variations is found, which is common to the concentrations. This is the pzc, of which value is ca. 0.3 V vs. Ag|AgCl. The minimum indicates that K⁺ has the same interactively electric energy with the electrode as Cl⁻ at this potential. Variations of C_1Hz beyond the pzc were linear rather than an exponential variation. The curves (dashed curve) calculated from the GC theory through:

C = (2cF²ε_rε₀/RT)^1/2 cosh[F(E − E_pzc)/2RT]

(8)

This is shown in Figure 5. The experimental variation is quite different from the GC theory. The magnitude of the slopes of the lines in Figure 5 increased linearly with an increase in the concentration. The increase suggests the attribution of the slopes to ionic effects, being our finding in this report.

The slopes in the plots of logY₂ against log f in Figure 2 were invariant to salt concentrations with the standard deviation less than 0.002 of λ. The invariance indicates that C_Hlm and C_ion reveal a common value of λ. This inspires us to imagine that the frequency-dispersion observed at the time as long as even 1 s or f = 0.16 Hz occurs both in the Helmholtz layer and the ionic diffuse layer in a similar way. Since ions can move almost freely in the diffuse layer, the dispersion can appear naturally. The common dispersion in the Helmholtz layer means that dipoles in the layer should move or have freedom like in ions in solution. Frequency-dispersion is caused by long-term molecular interactions, which can be regarded as belonging to a cooperative phenomenon [16]. The frequency dispersion in the Helmholtz layer occurs through solvent interactions while that in the diffuse layer occurs by ionic diffusion. The common values of λ in spite of the difference in origins mean that two interactions are related each other.

4. Theory and Discussion

Our model of DLCs is composed of C_Hlm and C_ion. The latter has been discussed on the basis of Poisson–Boltzmann’s distribution which leads to GC theory. The GC theory includes a failure in that it predicts condensed ions over finite sizes of ions [36] in the phenomenological viewpoint. The failure in thermodynamic viewpoint results from the expression for concentrations given by the voltage (ϕ)-driven Boltzmann’s distribution, i.e., c_± = k exp[−(±)Fϕ/RT] for a constant k and concentrations for a cation (+) and an anion (−). The energy should not be determined only by the potential but may vary with non-electrically interactive forces. Therefore, it ought to include the chemical potential term, cμ, where μ is the chemical potential of the ion. The introduction of cμ corresponds to the use of a grand canonical ensemble rather than a canonical ensemble. The term of cμ makes the Boltzmann equation non-linear with respect to c_± to fail obtaining explicit forms of c_±. A method of circumventing the complication is to confine ions into cells so that one ion occupies a same volume as in the bulk, and to determine equilibrium distance of the ion from the electrode by the electric force under the thermal fluctuation. As a result, the extra condensation caused by the term, exp[−(±)Fϕ/RT], is prevented by keeping the volume constant. The equilibrium between the electric energy and the thermal energy is obtained by taking the partition function. C_ion can be determined from the average distance of an ion from the electrode. The observed capacitance is a composite of C_Hlm and C_ion.

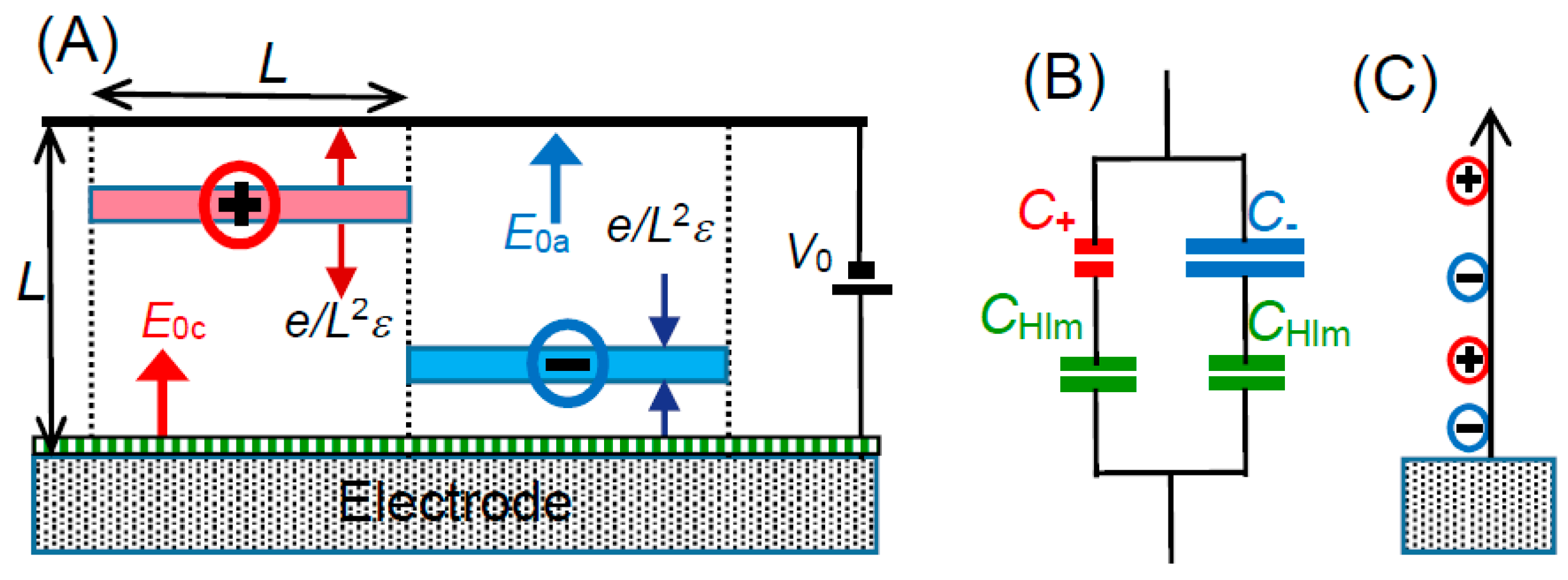
We use here mono-valent ions for the electrolyte with bulk concentration of c. If the cations and the cations are uniformly distributed in the solution, one ion occupies the volume of 1/2cN_A for the Avogadro constant N_A. The volume is assumed to be in a cube of which side length is L = (2cN_A)^−1/3, as illustrated in Figure 6A. A cube includes either a cation or an anion. Cubic cells with cations and anions are arranged alternately. An ion near the electrode generates electric lines starting from the ion and merging the electrode perpendicularly. The electric profiles can be evaluated by means of the technique of the mirror image [37]. Our concern is not the local electric field but the field averaged over the square L² of a cell in contact with the electrode. In order to avoid the complication of profile of electric lines, a spherical ion is assumed to be a uniformly charged plate with the charge density σ = ±e/L², where e is the elemental charge. Then, the plates generate electric fields, ±e/L²ε, according to the Gauss’ law, where ε is the permittivity of the solution. We let an anion be located at a distance x_a from the electrode to which the voltage V₀ is applied externally. We obtain a voltage distribution in the cell from the electric field mixed with the applied field and the anion. By letting the applied electric field be E_0a at x_a, the combined field, E_a, is given by the addition of E_0a by ±e/L², depending on the location of the anion, x_a, so that:

0 < x < x_a: E_a = E_0a + e/L²ε

(9)

x_a < x < L: E_a = E_0a − e/L²ε

(10)

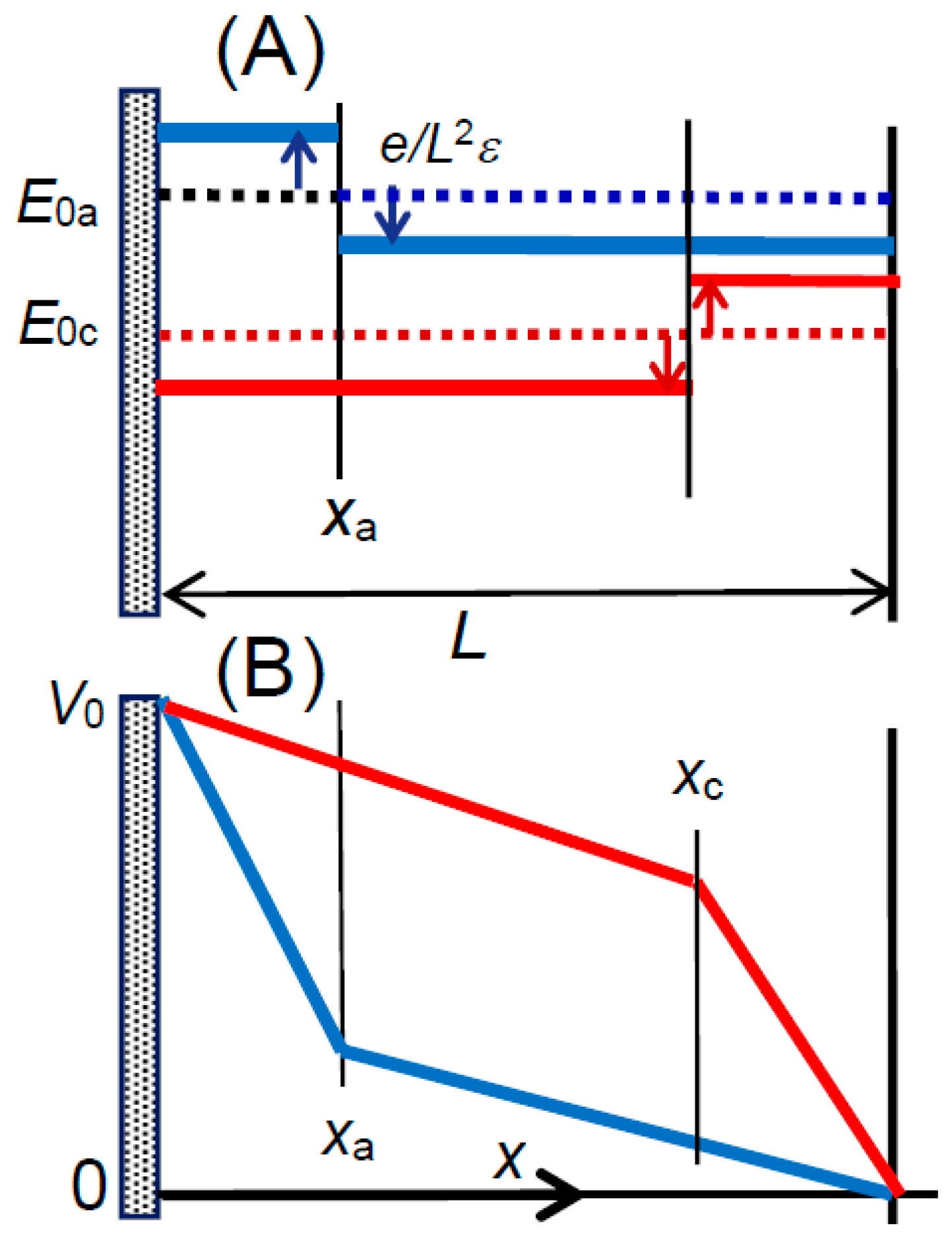
as shown in Figure 6A and Figure 7A. The voltage, V_a, at the anodic cell is given by the integration of −E_a with respect to x. Under the condition of continuity at x_a, eliminating E_0a from the expressions for V_a of the anion yields:

V_a(x) = V₀ − {V₀ + 2(e/Lε)(L − x_a)}x/L  for 0 < x < x_a

(11)

V_a(x) = (1 − x/L)(V₀ − 2x_ae/L²ε)      for x_a < x < L

(12)

of which variations are illustrated in Figure 7B. Our concern lies in V_a(x_a), i.e.,

V_a(x_a) = (1 − x_a/L)(V₀ − 2x_ae/L²ε)

(13)

A typical value of e/Lε is 0.25 V for the relative permittivity ε_r = 78 (dielectric constant of water) and c = 1 mol dm⁻³ or L = 9.4 nm. The voltage distribution in Equation (13) represents a composite energy of eV₀ + cμ/N_A by means of confining ions to a given cell. Therefore, the term of eV_a(x_a) is regarded as the reduced energy for a grand canonical ensemble of eV₀ + cμ/N_A.

We determine x_a by balance of the electric energy eV_a(x_a) with the thermal energy with the help of the canonical ensemble. The probability of the anion at x is expressed by exp[−(−e)V_a(x_a)/k_BT] for the Boltzmann constant, k_B. Since values of x_a can vary from 0 to L, the partition function is given by:

$${\mathrm{Z}}_a={{\int }_0}^L \exp ({eV}_{\mathrm{a}}(x_a)/k_{\mathrm{B}}T)\mathrm{d}{x}_{\mathrm{a}}/L={{\int }_0}^1 \exp [\Phi (1-z)(1-z/\Lambda )]\mathrm{d}z$$

(14)

where Λ = V₀Lε/2e, Φ = eV₀/k_BT and z = x_a/L. The averaged location of the anion is given by

$$\overline{x_a}={{\int }_0}^L x_{\mathrm{a}} \exp ({eV}_{\mathrm{a}}/k_{\mathrm{B}}T)\mathrm{d}{x}_{\mathrm{a}}/Z_{\mathrm{a}}L=L{{\int }_0}^1 z \exp [\Phi (1-z)(1-z/\Lambda )]\mathrm{d}z/Z_{\mathrm{a}}$$

(15)

The definition of a capacitance for the anion, C_a = σ/V_a, to which Gauss’ law is applied to yield C_a = ε/d, where d is the distance between the charged plate and a location supplying the voltage V_a. Since there are two distances, from 0 to x_a and from x_a to L, in series, C_a is given by:

$$C_{\mathrm{a}}=\epsilon \{1{/}_{ }\overline{x_a}+1/(L-\overline{x_a}\left)\right\}$$

(16)

The substitution of e for −e, or change of signs of Λ and Φ, yields Z_c and $\overline{x_c}$. The symmetric profiles of the electric fields at the anionic cell and the cationic one imply $\overline{x_c}$ = L − $\overline{x_a}$, which can derive C_c to the same form as C_a. Since the capacitance caused by ions is the sum of C_a and C_c, i.e.,

$$C_{\mathrm{ion}}=C_{\mathrm{a}}+C_{\mathrm{c}}=2\epsilon L\{1/ \overline{x_a} (L-\overline{x_a}\left)\right\}$$

(17)

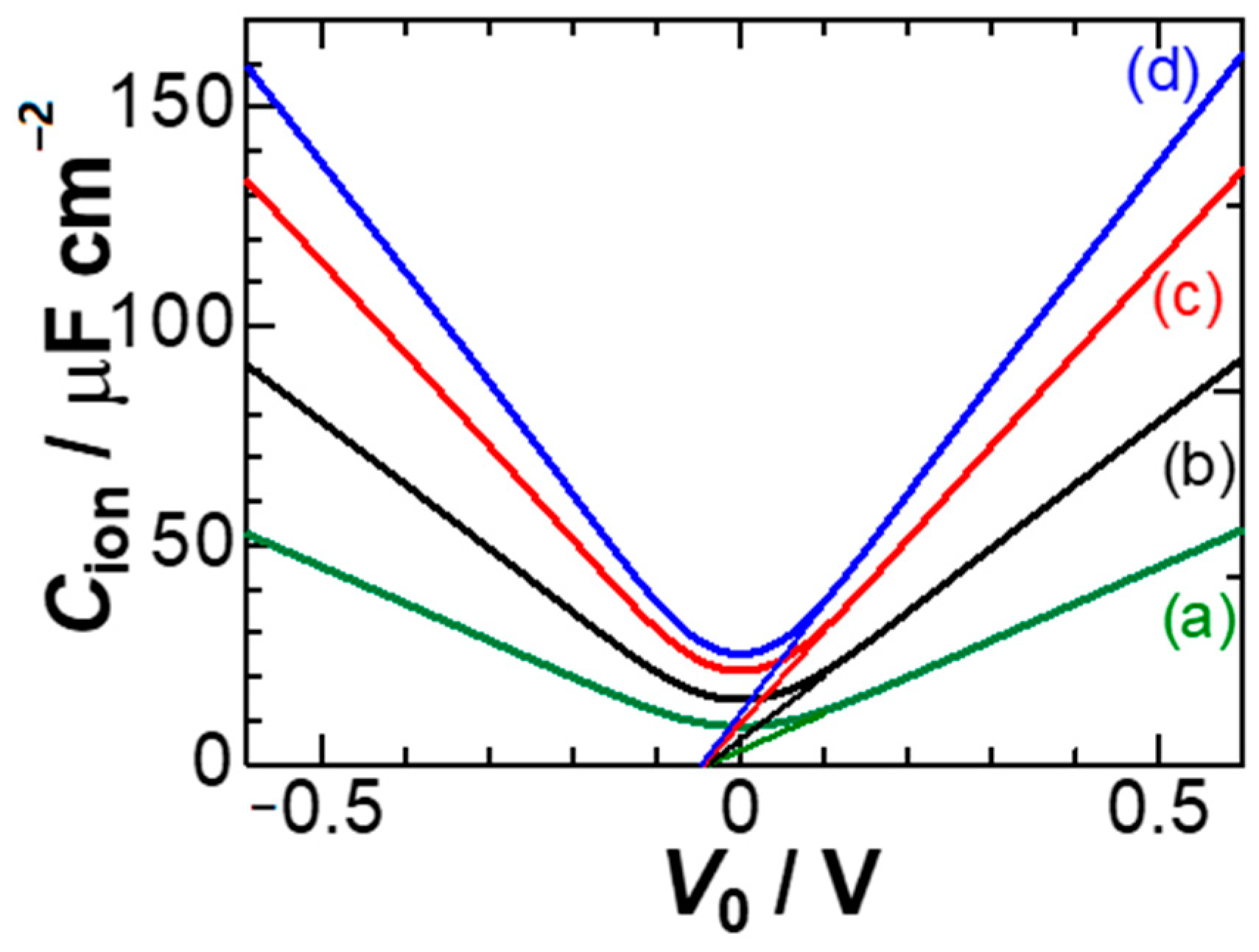
The values of $\overline{x_a}$/L were computed from Equations (14) and (15) for given values of V₀, ε, c at 25 °C by means of numerical computation of the integrals. Although Z_a can be represented by a sum of error functions with complicated forms, the computation of the integral form is easier than that of the error functions. Figure 8 shows dependence of C_ion on V₀ for some ionic concentrations. A feature of the curves is the linear variation in C_ion, which is in contrast to the exponential variation of the GC theory. We try to find an expression for C_ion at large values of V₀. A large value of V₀ makes 1 − z/Λ approximated to 1 in Equations (14) and (15). As a result, Z_a and (x_a)_av are reduced to:

$$Z_a \approx {{\int }_0}^1 \exp [\Phi (1-z)]\mathrm{d}z=({\mathrm{e}}^{\Phi }-1)/\Phi$$

$$\overline{x_a} /L\approx {{\int }_0}^1 z \exp [\Phi (1-z)]\mathrm{d}z/Z_{\mathrm{a}}=\{-1+({\mathrm{e}}^{\Phi }-1)/\Phi \}/\Phi Z_{\mathrm{a}}$$

Combining the two yields $\overline{x_a}$/L ≈ −1/(e^Φ − 1) + 1/Φ ≈ 1/Φ. Consequently, we have for large values of V₀:

$$C_{\mathrm{ion}}=\epsilon /2\overline{x_a} (L-\overline{x_a})\approx (\epsilon /2L){\Phi }^2/(\Phi -1)\approx (\epsilon /2L)(\Phi +1)=(\epsilon /2L)({FV}_0/RT+1)$$

(18)

Therefore, C_ion for large V₀ is linear to V₀. The slope is inversely proportional to L or proportional to c^1/3. Equation (15) means the location of the anion averaged over 0 to L, which provides the anionic capacitance. The observed capacitance is the sum of the anionic capacitance and the cationic one. If the voltage is estimated from the differential capacitance through dV/dσ for the surface charge density σ, it is actually a mean-field voltage in the context of the derivation of the capacitance.

The equivalent circuit in Figure 6B includes basically two types of Stern model, being a series capacitance of C_Hlm and C_a, and a series one of C_Hlm and C_c. The composite capacitances are C_HlmC_a/(C_Hlm + C_a) and C_HlmC_c/(C_Hlm + C_c). Since they take a parallel combination, the further composite capacitance to be observed is given by:

C = C_HlmC_a/(C_Hlm + C_a) + C_HlmC_c/(C_Hlm + C_c)

(19)

When salt concentrations are so high positively that ($\overline{x_a}$)_av < ($\overline{x_c}$)_av like the image in Figure 6A, we can estimate the relation, C_a < C_Hlm < C_c. Applying this relation to Equation (19) under the extreme condition, we can rewrite Equation (19) approximately as:

C ≈ C_Hlm + C_c

(20)

This means that the observed capacitance can be approximated as a sum of the DLC by solvent dipoles and the one of capacitances either by the anion or the cation. As a result, the capacitance behaves as if it might take a parallel combination of C_Hlm and either ionic capacitance (C_c or C_a). This explains the result in Figure 4.

It is interesting to consider the reason why the Stern model deviates from experimental data although it looks reasonable in the concept. The GC equation supporting the Stern model has combined the one-dimensional Poisson’s equation with Boltzmann’s equation so that ions driven both by applied electric field and electric force among inter-ions are dispersed by thermal fluctuation. An anion is attracted for a positive potential toward the electrode, the one-dimensional of the GC theory predicts that the anion attracts a cation until the balance of the repulsion by the applied electric field, as in Figure 6C. As a result, both anions and cations would be concentrated to the electrode over finite size of ions. This unreasonable prediction can be avoided by the one-dimensional electric force to anions and by keeping equilibrium distance in the layers parallel to the electrode, as in Figure 6A. Mathematically, the three-dimensional distribution provides the volume of an anion to be x_aL², while the GC theory gives x_a³.

The calculated values of C_1Hz in Figure 8 are five times larger than the experimental ones in Figure 5A. This may be selection of ε_r (=ε/ε₀) as the bulk value (78) in water. Since water molecules are partially structured with electric field, values of ε_r should be smaller than in the bulk. For example, reasonable values of ε_r are close to 6 in the Helmholtz layers [18,38,39], which has been demonstrated to be the field effect [40].

The slopes of lines in Figure 5A for E_dc < E_pzc are larger than those for E_dc > E_pzc in magnitude. This asymmetry cannot be explained in terms of difference in ionic molar conductivity because of similar values of both K⁺ and Cl⁻ but may be related with difference of ε_r in the K⁺-driven cell and the Cl⁻-driven one.

Our model is to make the field effect on ions only in the direction normal to the electrode and to keep the ionic concentration in planes parallel to the electrode. It corresponds to size effects of ions by occupying ions to give lattice sizes [41], by taking into account the orientational ordering of water dipoles [42], by introducing interaction between the field and hydrostatic pressure [43], and by using molecular dynamics to predict detailed ionic distribution near the point of zero charge [44].

5. Conclusions

The DLC at platinum electrode in KCl and HCl solutions can be represented as a simple sum of the Helmholtz capacitance and the ionic contribution. The sum means a parallel combination of two kinds of capacitances. This combination is inconsistent with the intuitive Stern model. The ionic capacitance is recognized when concentrations are over 1 M. It shows a linear relation with the 2/3 power of the concentrations. This power is equivalent to the two-dimensional concentration, which should be responsible to the ionic DLC, keeping the bulk concentration in the two-dimensional form near the electrode. Therefore, extra accumulation of ions does not occur as in the diffuse layer.

This concept inspires the model of the separation of the anionic cells and cationic ones, in which a capacitance in either cell is predominant to the other. Since a smaller value of the capacitance is a rate-determining step in a series combination of C_Hlm and C_ion, an effective capacitance can be regarded as a parallel combination of (C_Hlm and C_anion) or (C_Hlm and C_cation). The present theory is one of explanations, and hence there may be other possible interpretations.