Investigation of the Applicability of Helium-Based Cooling System for Li-Ion Batteries
Abstract
1. Introduction
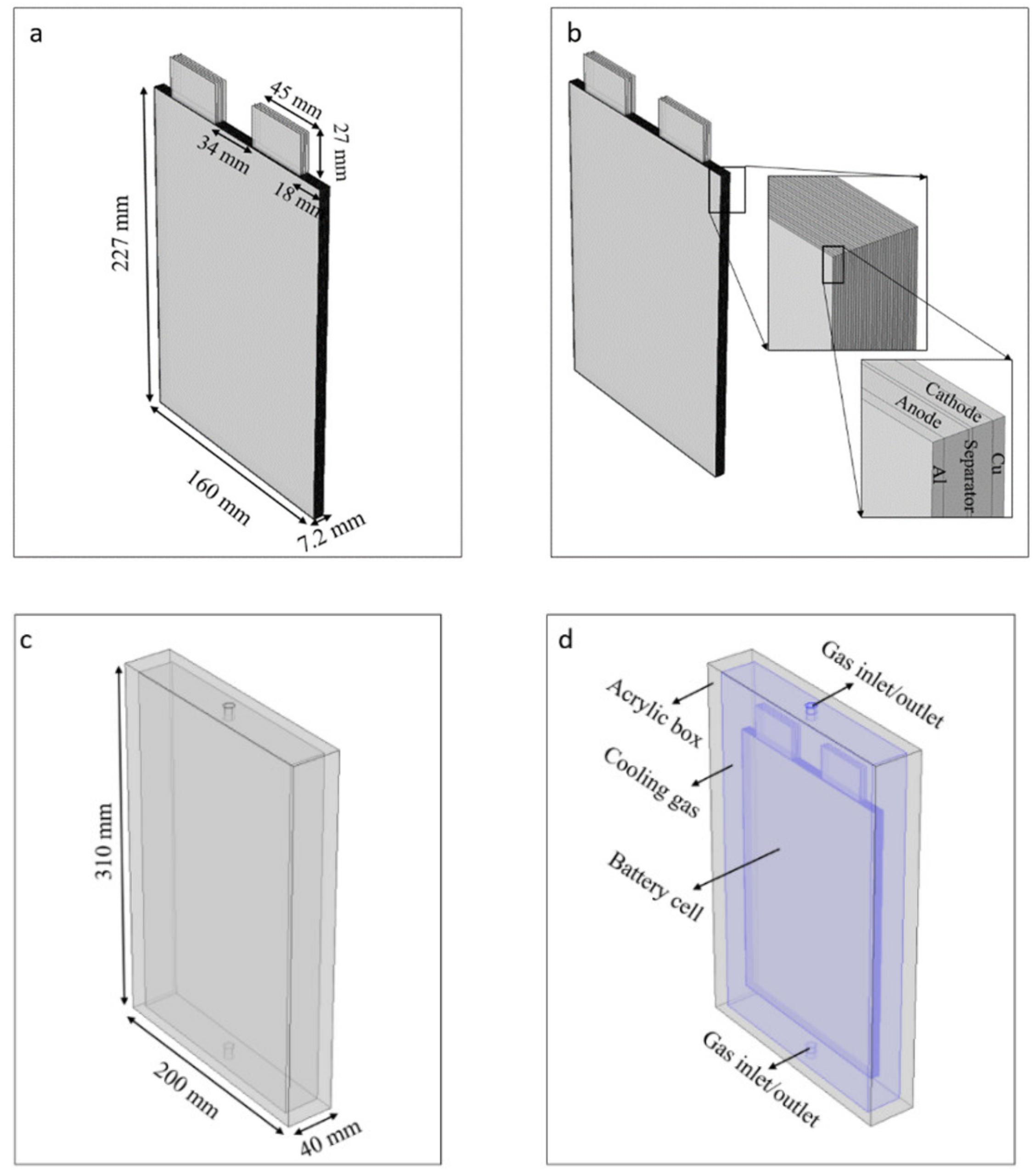
2. Experimental Procedure
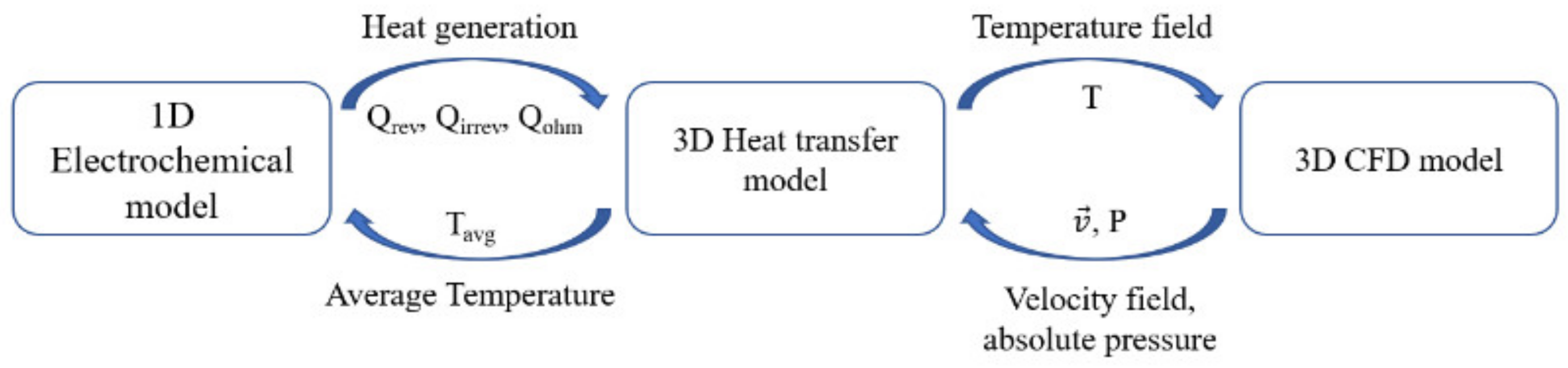
3. Model Development
3.1. Governing Equations
3.2. Numerical 3D Modeling
4. Results and Discussion
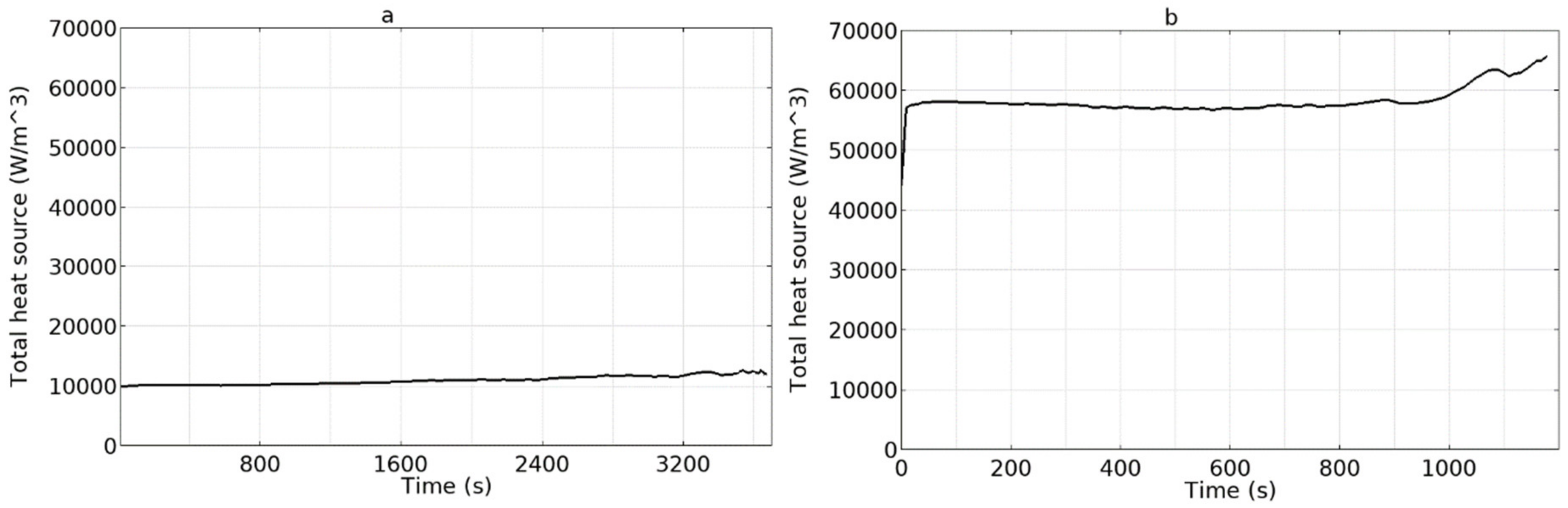
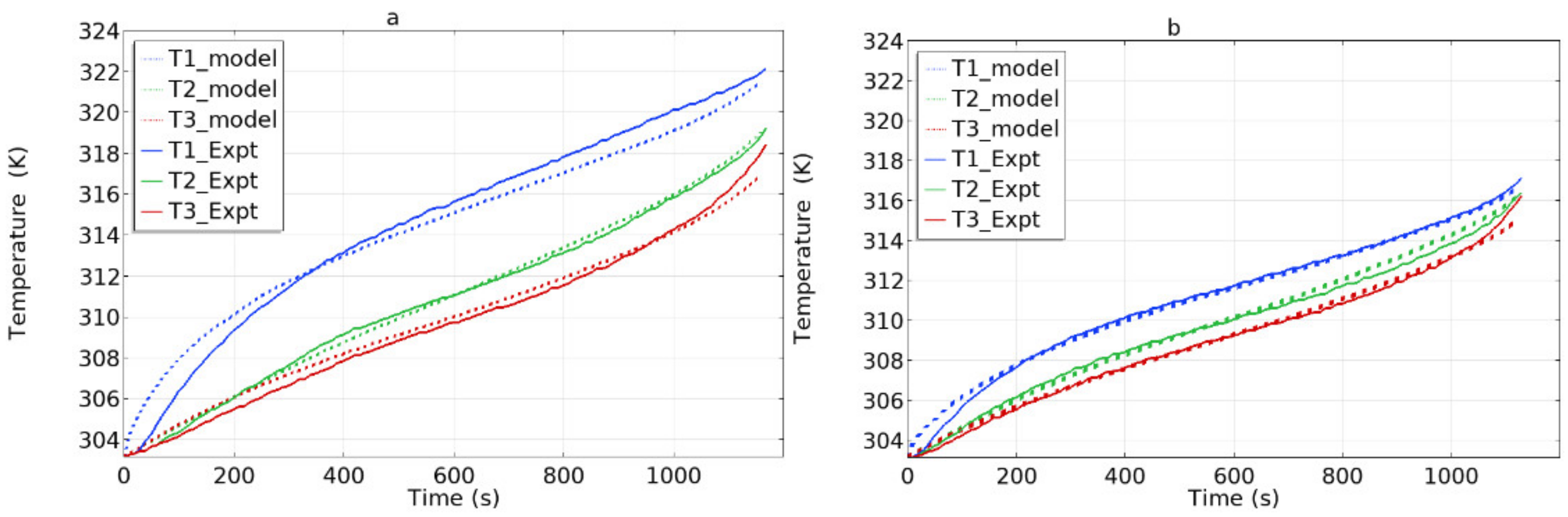
4.1. Model Validation
4.2. Thermal Behavior of the Cell under No-Cooling Condition
4.3. Thermal Behavior of the Cell under Gas-Based Cooling
4.3.1. Comparison of Cooling Performance of the Air and Helium Gas
4.3.2. Effects of Design Parameters
Effects of Inlet/Outlet Diameter
Effects of Flow Direction
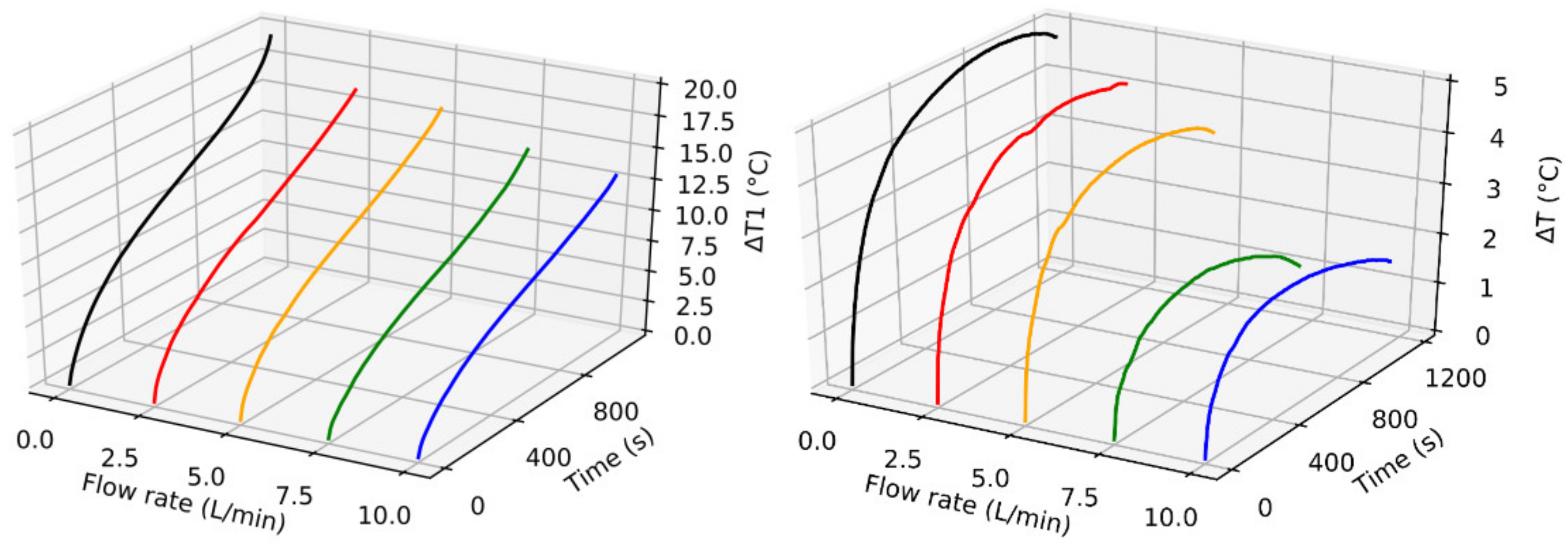
Effects of Inlet Flow Rate
5. Conclusions
- With the perfect thermal and physical properties, the He gas shows promising cooling efficiency compared to air. The He gas at low flow rates offers a close cooling performance with the air at higher flow rates. Therefore, using the He as a cooling medium will decrease the energy consumed for gas circulation.
- The inlet/outlet diameter has a negligible effect on cooling performance.
- The flow direction significantly changes the ΔT1 and ΔT values. The most effective method is to feed the gas from the top inlet where the fresh gas meets the hot regions first.
- The inlet gas flow rate is found to be the most effective parameter in controlling the ΔT1 and ΔT values. However, the higher flow rates result in higher energy consumption for circulating the cooling gas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Electrode specific surface area (m−1) |
| Atab | Cross section of the tab (m2) |
| Cdl | Electrical double layer capacitance (F/m2) |
| ce | Lithium concentration in electrolyte (mol/m3) |
| Cp | Specific heat (J/kg·K) |
| cs | Lithium concentration in solid (mol/m3) |
| cs,0 | Initial lithium concentration in solid (mol/m3) |
| cs,max | Max li ion concentration in solid (mol/m3) |
| cs,sur | Surface concentration of lithium in the active material (mol/m3) |
| De | Diffusion coefficient of Li ion in electrolyte (m2/s) |
| Ds | Diffusion coefficient of Li ion in solid (m2/s) |
| f | Average molar activity coefficient |
| F | Faraday’s constant (96,487 C/mol) |
| Body forces (N) | |
| h | Convective heat transfer coefficient (W/m2·K) |
| I | Identity tensor |
| i0 | Exchange current density (A/m2) |
| iapp | Total applied current density (A/m2) |
| iloc | Local working current density of the cell unit (A/m2) |
| iN | Normal inward current density through the electrode/cc interface (A/m2) |
| k | Reaction rate constant (m2.5/mol0.5·s) |
| L_batt | Battery cell thickness (m) |
| M | Mean molar mass (kg/mol) |
| N | Total number of cell layers |
| P | Absolute pressure (Pa) |
| Qsv | Standard flow rate (m3/s) |
| r | Radios of electrode particle (m) |
| R | Universal gas coefficient (8.314 J/mol·K) |
| S | Inlet cross section area (m2) |
| t | time (s) |
| T | Absolute temperature (K) |
| t+ | Transferring number of Li+ |
| Ueq | Open circuit potential (V) |
| Velocity (m/s) | |
| Vm | Standard molar volume (m3/mol) |
| αa | Anodic transfer coefficient |
| αc | Cathodic transfer coefficient |
| ß | Bulk expansion coefficient |
| εe | Volume fraction of the fillers |
| κeff | Effective ionic conductivity of the electrolyte (S/m) |
| λ | Thermal conductivity (W/m·K) |
| Dynamic viscosity (Pa·s) | |
| ρ | Density (kg/m3) |
| σs | Electronic conductivity of the solid phase (S/m) |
| σe | Ionic conductivity of electrolyte (S/m) |
| Viscos | |
| φs | Solid-phase potential (V) |
| φe | Electrolyte-phase potential (V) |
| Subscripts, superscripts and acronyms | |
| 0 | Initial value |
| b | Box |
| cc | Current collector |
| eff | Efficient |
| f | Fluid |
| i | Indicator (i = pe, ne) |
| e | Electrolyte |
| ext | external |
| ne | Negative electrode |
| max | Maximum |
| pe | Positive electrode |
| s | Solid |
| sep | Separator |
References
- Scrosati, B.; Garche, J. Lithium batteries: Status, prospects and future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
- Hassanpouryouzband, A.; Joonaki, E.; Farahani, M.V.; Takeya, S.; Ruppel, C.; Yang, J.; Tohidi, B. Gas hydrates in sustainable chemistry. Chem. Soc. Rev. 2020, 49, 5225–5309. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources. 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Maleki, H.; Shamsuri, A.K. Thermal analysis and modeling of a notebook computer battery. J. Power Sources. 2003, 115, 131–136. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A critical review of thermal issues in lithium-ion batteries. J. Electrochem. Soc. 2011, 158, R1–R25. [Google Scholar] [CrossRef]
- Tarascon, J.-M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Mater. Sustain. Energy. 2011. [Google Scholar] [CrossRef]
- Wen, J.; Yu, Y.; Chen, C. A review on lithium-ion batteries safety issues: Existing problems and possible solutions. Mater. Express. 2012, 2, 197–212. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Alipour, M.; Ziebert, C.; Conte, F.V.; Kizilel, R. A review on temperature-dependent electrochemical properties, aging, and performance of lithium-ion cells. Batteries 2020, 6, 35. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Ding, Y.; Dang, C.; Li, X. A review on lithium-ion power battery thermal management technologies and thermal safety. J. Therm. Sci. 2017, 26, 391–412. [Google Scholar] [CrossRef]
- Alipour, M.; Esen, E.; Varzeghani, A.R.; Kizilel, R. Performance of high capacity Li-ion pouch cells over wide range of operating temperatures and discharge rates. J. Electroanal. Chem. 2020, 860, 113903. [Google Scholar] [CrossRef]
- Ling, Z.; Zhang, Z.; Shi, G.; Fang, X.; Wang, L.; Gao, X.; Liu, X. Review on thermal management systems using phase change materials for electronic components, Li-ion batteries and photovoltaic modules. Renew. Sustain. Energy Rev. 2014, 31, 427–438. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Huo, Y.; Liu, X.; Li, Y. Thermal management of cylindrical power battery module for extending the life of new energy electric vehicles. Appl. Therm. Eng. 2015, 85, 33–43. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; Zhang, Y. Thermal management optimization of an air-cooled Li-ion battery module using pin-fin heat sinks for hybrid electric vehicles. J. Power Sources 2015, 273, 431–439. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.M.; Rao, Z.H. Thermal performance of lithium-ion battery thermal management system by using mini-channel cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.-H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal management in EV and HEVs: Issues and solutions. Battery Man. 2001, 43, 34–49. [Google Scholar]
- Zhao, R.; Liu, J.; Gu, J. The effects of electrode thickness on the electrochemical and thermal characteristics of lithium ion battery. Appl. Energy 2015, 139, 220–229. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Xue, Q.; Sun, H.; Li, B.; Zou, H.; Yan, Y.Y. Experimental investigation on EV battery cooling and heating by heat pipes. Appl. Therm. Eng. 2015, 88, 54–60. [Google Scholar] [CrossRef]
- Ladrech, F. Battery thermal management for HEV & EV–Technology overview. In Proceedings of the Automotive Summit, Brussels, Belgium, 10 November 2010. [Google Scholar]
- Mousavi, M.; Hoque, S.; Rahnamayan, S.; Dincer, I.; Naterer, G.F. (Eds.) Optimal design of an air-cooling system for a Li-ion battery pack in electric vehicles with a genetic algorithm. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 1848–1855. [Google Scholar]
- Xie, J.; Ge, Z.; Zang, M.; Wang, S. Structural optimization of lithium-ion battery pack with forced air cooling system. Appl. Therm. Eng. 2017, 126, 583–593. [Google Scholar] [CrossRef]
- Alipour, M.; Kizilel, R. Numerical Investigation of Design Parameters Effects on Performance of Cooling System Designed for A Lithium-Ion Cell. J. Therm. Eng. 2020, 6, 257–271. [Google Scholar] [CrossRef]
- Mason, E.; Saxena, S. Approximate formula for the thermal conductivity of gas mixtures. Phys. Fluids. 1958, 1, 361–369. [Google Scholar] [CrossRef]
- Muller, W.H.; Roth, G.; Stautner, W.; Turowski, P.; Lehmann, W.; Graf, F. NMR magnet system with superconducting coil in a helium bath. Google Patents. 1993. Available online: https://patents.google.com/patent/US5220800A/en (accessed on 2 March 2021).
- Arp, V. Forced flow, single-phase helium cooling systems. In Advances in Cryogenic Engineering; Springer: Boston, MA, USA, 1972; pp. 342–351. [Google Scholar]
- Benkowitsch, J.; Krafft, G. Numerical analysis of heat-induced transients in forced flow helium cooling systems. Cryogenics 1980, 20, 209–215. [Google Scholar] [CrossRef]
- Ihli, T.; Ilić, M. Efficient helium cooling methods for nuclear fusion devices: Status and prospects. Fusion Eng. Des. 2009, 84, 964–968. [Google Scholar] [CrossRef]
- Baxi, C.; Wong, C. Review of helium cooling for fusion reactor applications. Fusion Eng. Des. 2000, 51, 319–324. [Google Scholar] [CrossRef]
- Alipour, M.; Esen, E.; Kizilel, R. Investigation of 3-D multilayer approach in predicting the thermal behavior of 20 Ah Li-ion cells. Appl. Therm. Eng. 2019, 153, 620–632. [Google Scholar] [CrossRef]
- Ye, Y.; Saw, L.H.; Shi, Y.; Somasundaram, K.; Tay, A.A. Effect of thermal contact resistances on fast charging of large format lithium ion batteries. Electrochim. Acta 2014, 134, 327–337. [Google Scholar] [CrossRef]
- Samba, A.; Omar, N.; Gualous, H.; Capron, O.; Van den Bossche, P.; Van Mierlo, J. Impact of tab location on large format lithium-ion pouch cell based on fully coupled tree-dimensional electrochemical-thermal modeling. Electrochim. Acta 2014, 147, 319–329. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. A pseudo three-dimensional electrochemical–thermal model of a prismatic LiFePO4 battery during discharge process. Energy 2015, 80, 303–317. [Google Scholar] [CrossRef]
- Chen, K. Heat Generation Measurements of Prismatic Lithium Ion Batteries. Doctor Thesis, University of Waterloo, Waterloo, ON, Canada, 27 September 2013. [Google Scholar]
- Song, W.; Chen, M.; Bai, F.; Lin, S.; Chen, Y.; Feng, Z. Non-uniform effect on the thermal/aging performance of Lithium-ion pouch battery. Appl. Therm. Eng. 2018, 128, 1165–1174. [Google Scholar] [CrossRef]
- Pesaran, A.; Santhanagopalan, S.; Kim, G. Addressing the Impact of Temperature Extremes on Large Format Li-Ion Batteries for Vehicle Applications (Presentation); National Renewable Energy Lab.(NREL): Golden, CO, USA, 2013. [Google Scholar]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries–A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Amine, K.; Liu, J.; Belharouak, I. High-temperature storage and cycling of C-LiFePO4/graphite Li-ion cells. Electrochem. Commun. 2005, 7, 669–673. [Google Scholar] [CrossRef]
- Deshpande, R.; Verbrugge, M.; Cheng, Y.-T.; Wang, J.; Liu, P. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics. J. Electrochem. Soc. 2012, 159, A1730–A1738. [Google Scholar] [CrossRef]
- Karimi, G.; Li, X. Thermal management of lithium-ion batteries for electric vehicles. Int. J. Energy Res. 2013, 37, 13–24. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.-S. Effect of electrode configuration on the thermal behavior of a lithium-polymer battery. J. Power Sources. 2008, 180, 909–916. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Selman, J. A novel thermal management system for electric vehicle batteries using phase-change material. J. Electrochem. Soc. 2000, 147, 3231–3236. [Google Scholar] [CrossRef]

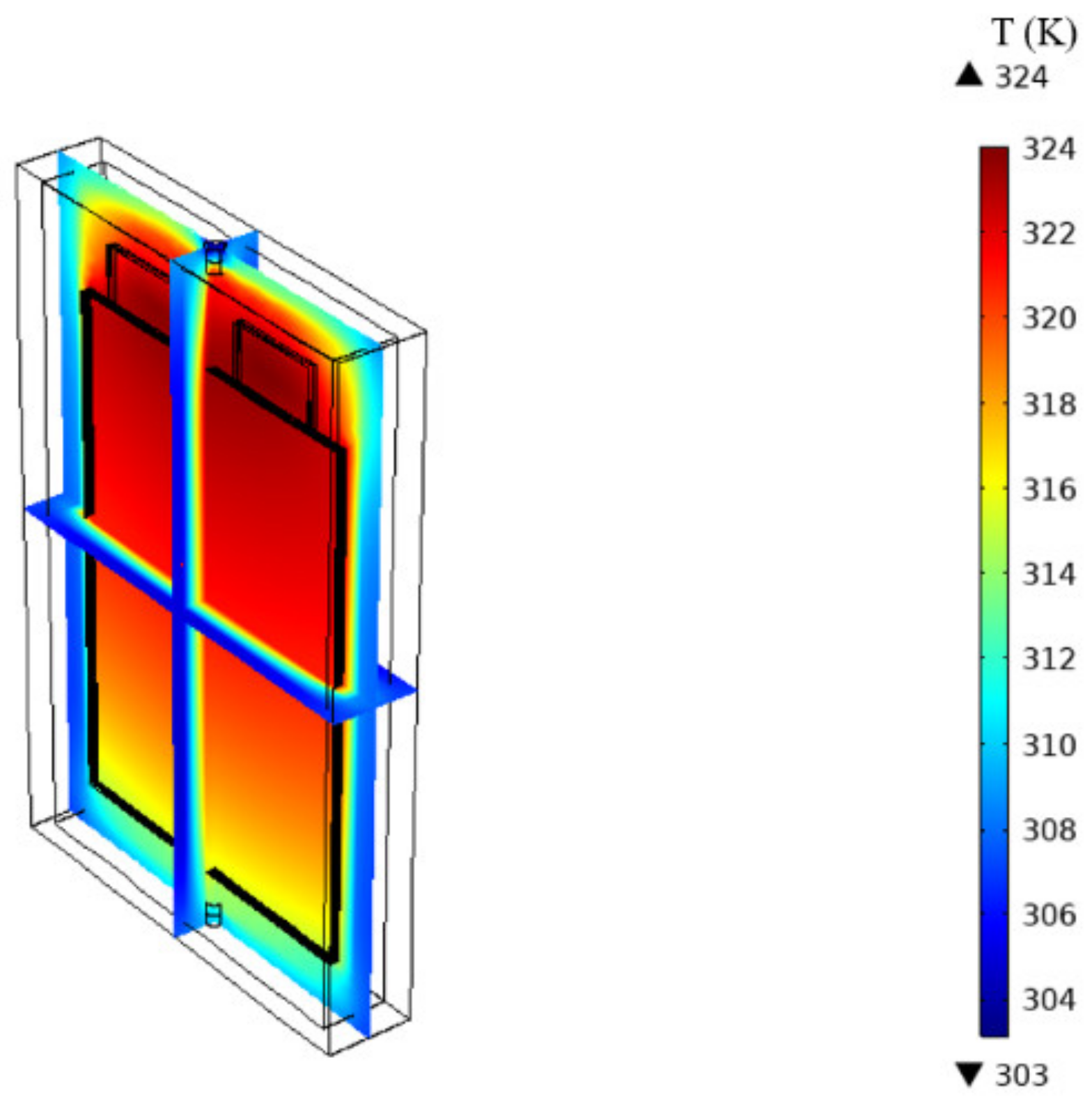
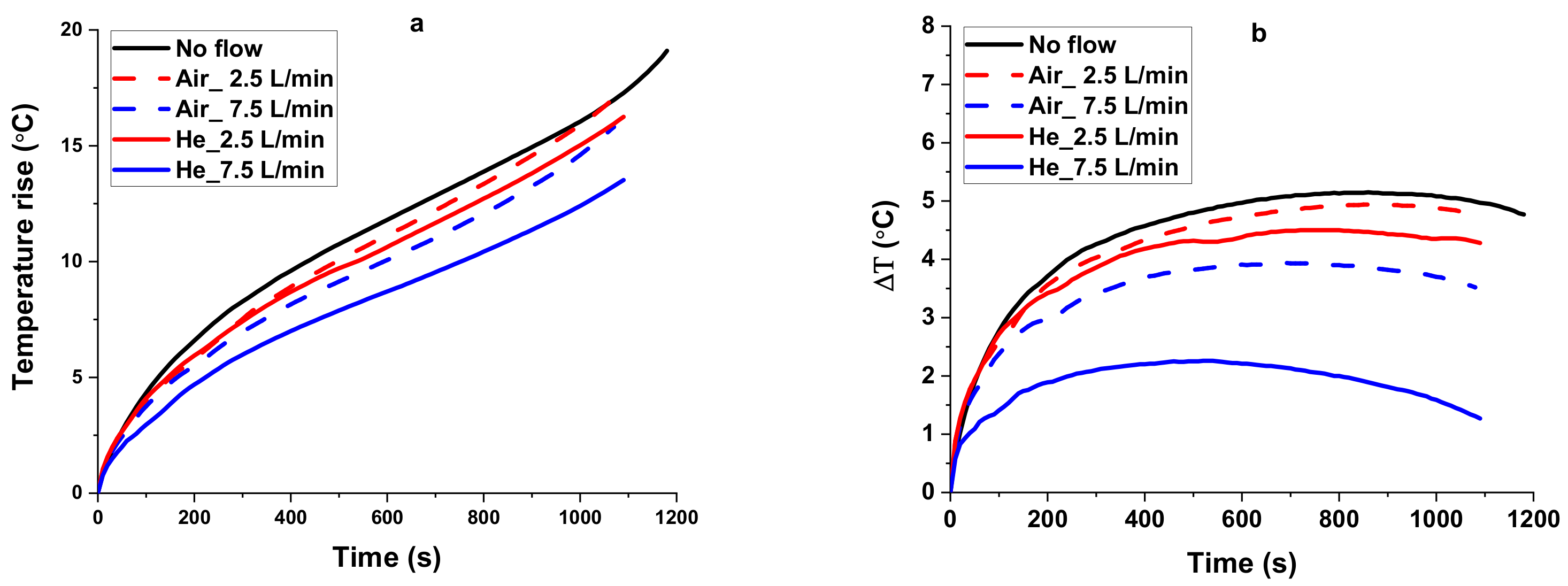
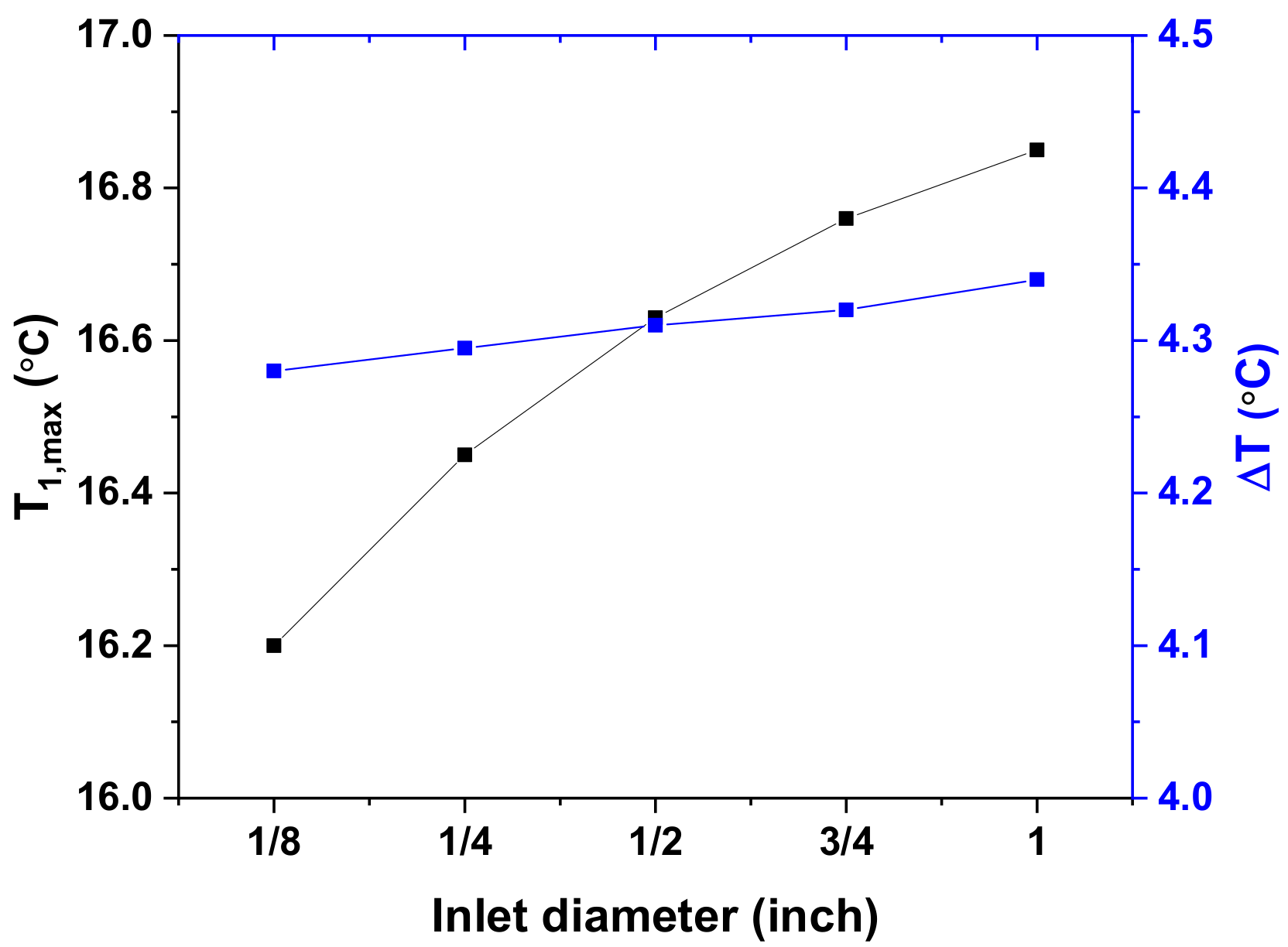
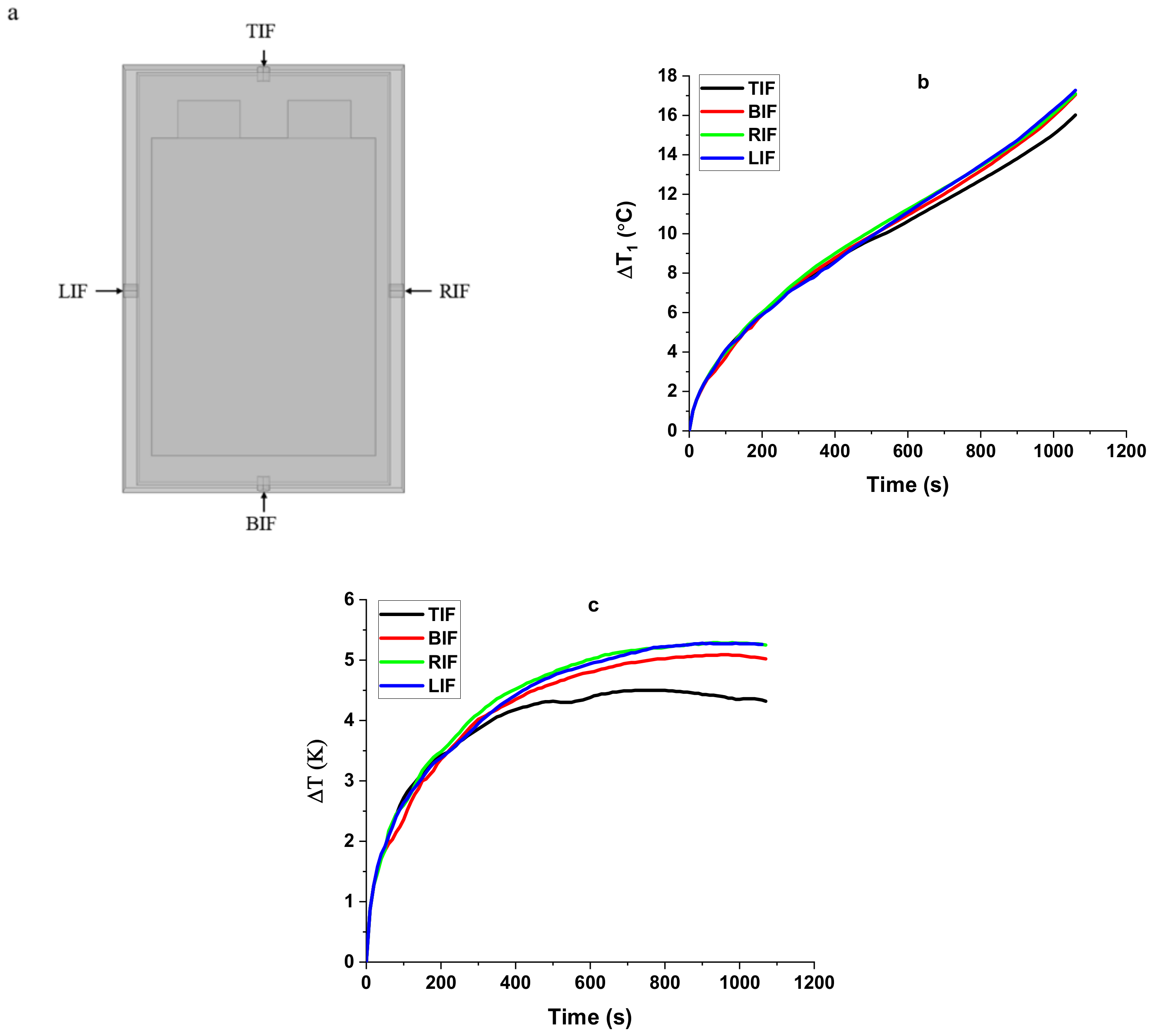
| Item | Air | Helium |
|---|---|---|
| Density (kg/m3) | ||
| Specific heat capacity (kJ/kg·K) | ||
| Thermal conductivity (W/m·K) | ||
| Dynamic viscosity (10−5 Pa·s) |
| SE | No-Flow | |
|---|---|---|
| T1 | 0.73 | 0.27 |
| T2 | 0.22 | 0.29 |
| T3 | 0.41 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alipour, M.; Hassanpouryouzband, A.; Kizilel, R. Investigation of the Applicability of Helium-Based Cooling System for Li-Ion Batteries. Electrochem 2021, 2, 135-148. https://doi.org/10.3390/electrochem2010011
Alipour M, Hassanpouryouzband A, Kizilel R. Investigation of the Applicability of Helium-Based Cooling System for Li-Ion Batteries. Electrochem. 2021; 2(1):135-148. https://doi.org/10.3390/electrochem2010011
Chicago/Turabian StyleAlipour, Mohammad, Aliakbar Hassanpouryouzband, and Riza Kizilel. 2021. "Investigation of the Applicability of Helium-Based Cooling System for Li-Ion Batteries" Electrochem 2, no. 1: 135-148. https://doi.org/10.3390/electrochem2010011
APA StyleAlipour, M., Hassanpouryouzband, A., & Kizilel, R. (2021). Investigation of the Applicability of Helium-Based Cooling System for Li-Ion Batteries. Electrochem, 2(1), 135-148. https://doi.org/10.3390/electrochem2010011






