Analytical Vibration Solutions of Sandwich Lévy Plates with Viscoelastic Layers at Low and High Frequencies
Abstract
1. Introduction
2. Problem Statement
3. Governing Equations
3.1. Single Plate on a Viscoelastic Foundation
3.2. Double-Plate Structure with a Fully Distributed Viscoelastic Layer
3.3. Double-Plate Structure with a Partially Distributed Viscoelastic Layer
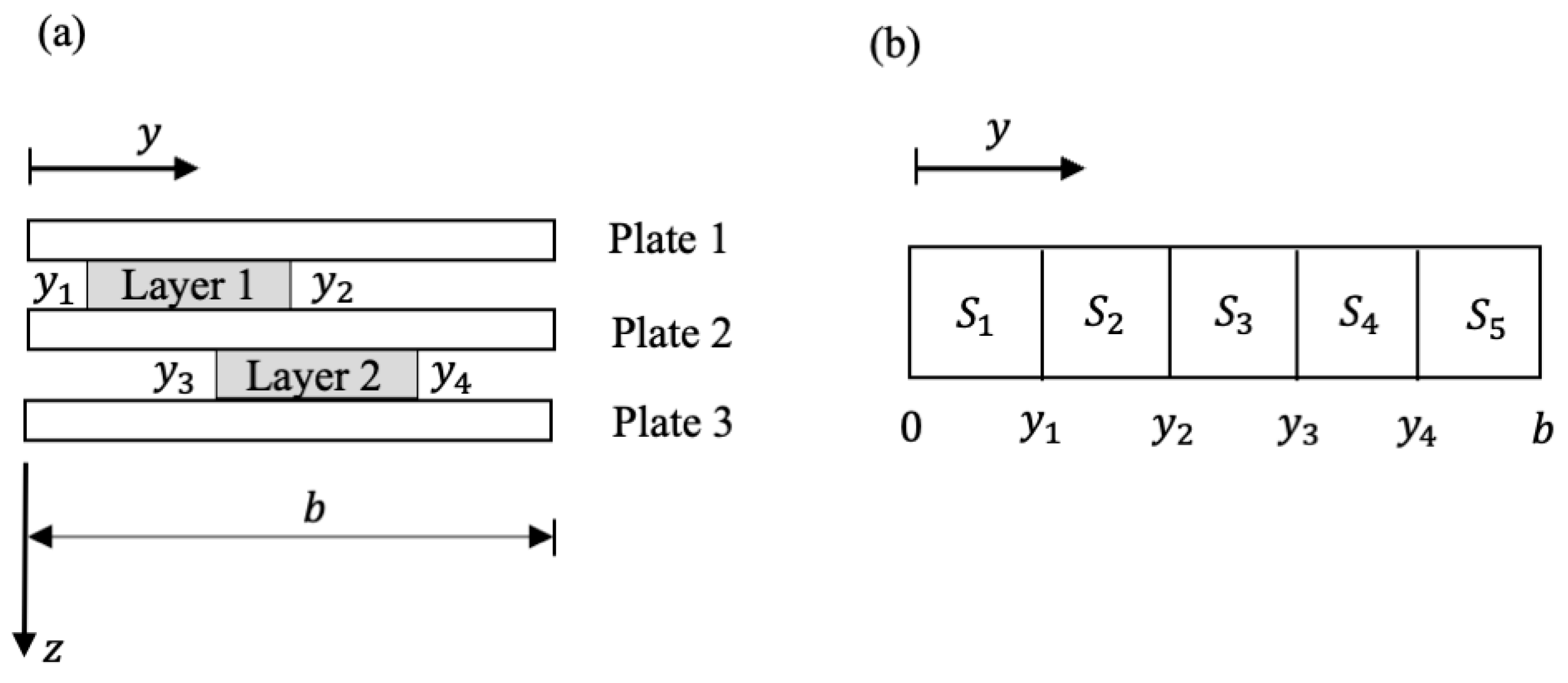
3.4. Three-Plate Structure with Dislocated Viscoelastic Layers
4. State-Space Formulation in the s-Domain
4.1. Formulation for Single Plate on a Viscoelastic Foundation
4.2. Formulation for Double-Plate Structure with a Fully Distributed Viscoelastic Layer
- For plate 1
- For plate 2
4.3. Formulation for Double-Plate Structure with a Partially Distributed Viscoelastic Layer
- State equation
- Boundary condition
4.4. Formulation for Three-Plate Structure with Dislocated Viscoelastic Layers
4.5. Discussion
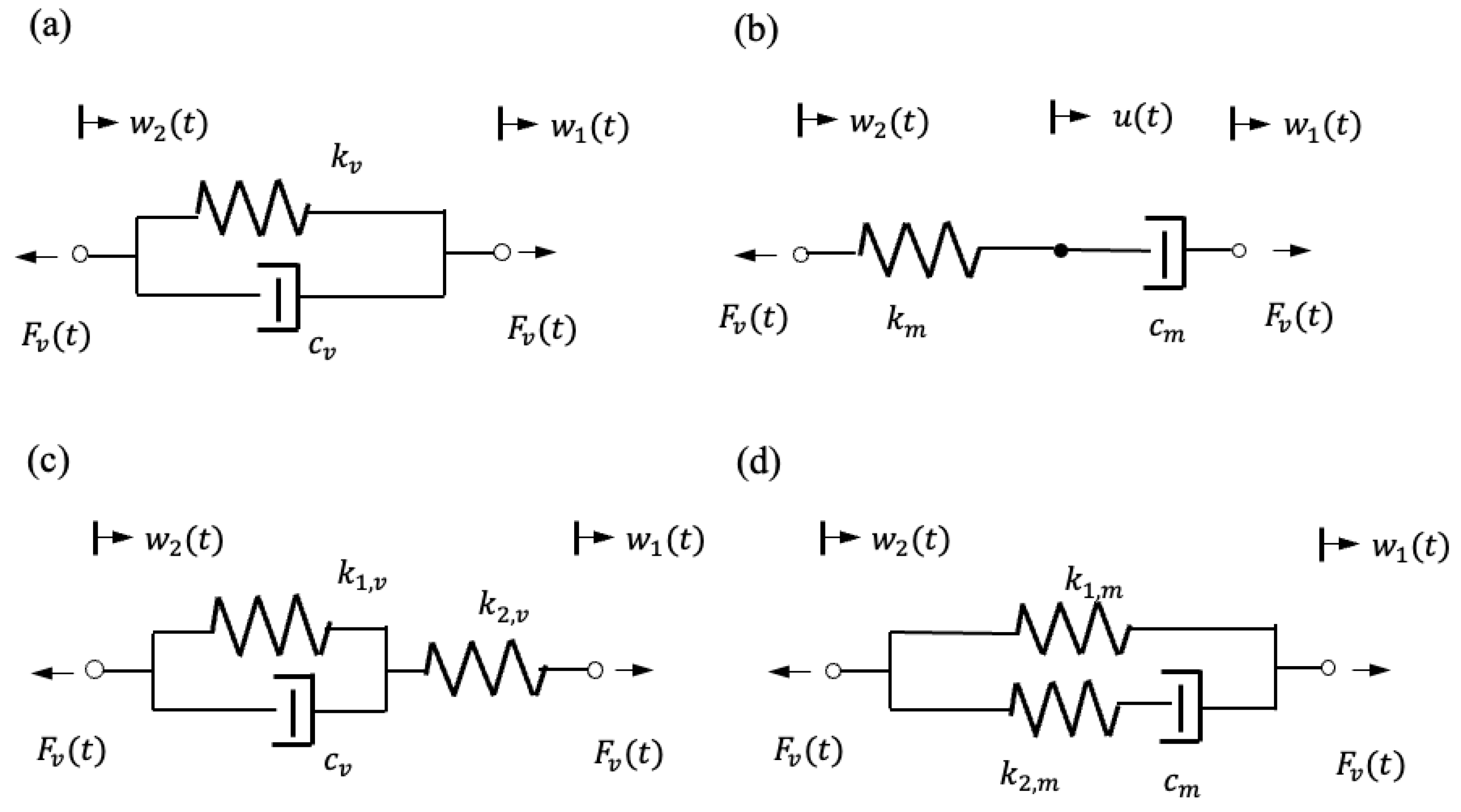
5. Models of Viscoelastic Layers
5.1. Kelvin–Voigt Model
5.2. Maxwell Model
5.3. Standard Linear Solid Models
6. Vibration Analysis by the DTFM
6.1. Plate Structures with Fully Distributed Viscoelastic Layers
- State equation
- Boundary condition
6.2. Plate Structures with Partially Distributed Viscoelastic Layers
6.3. Discussion
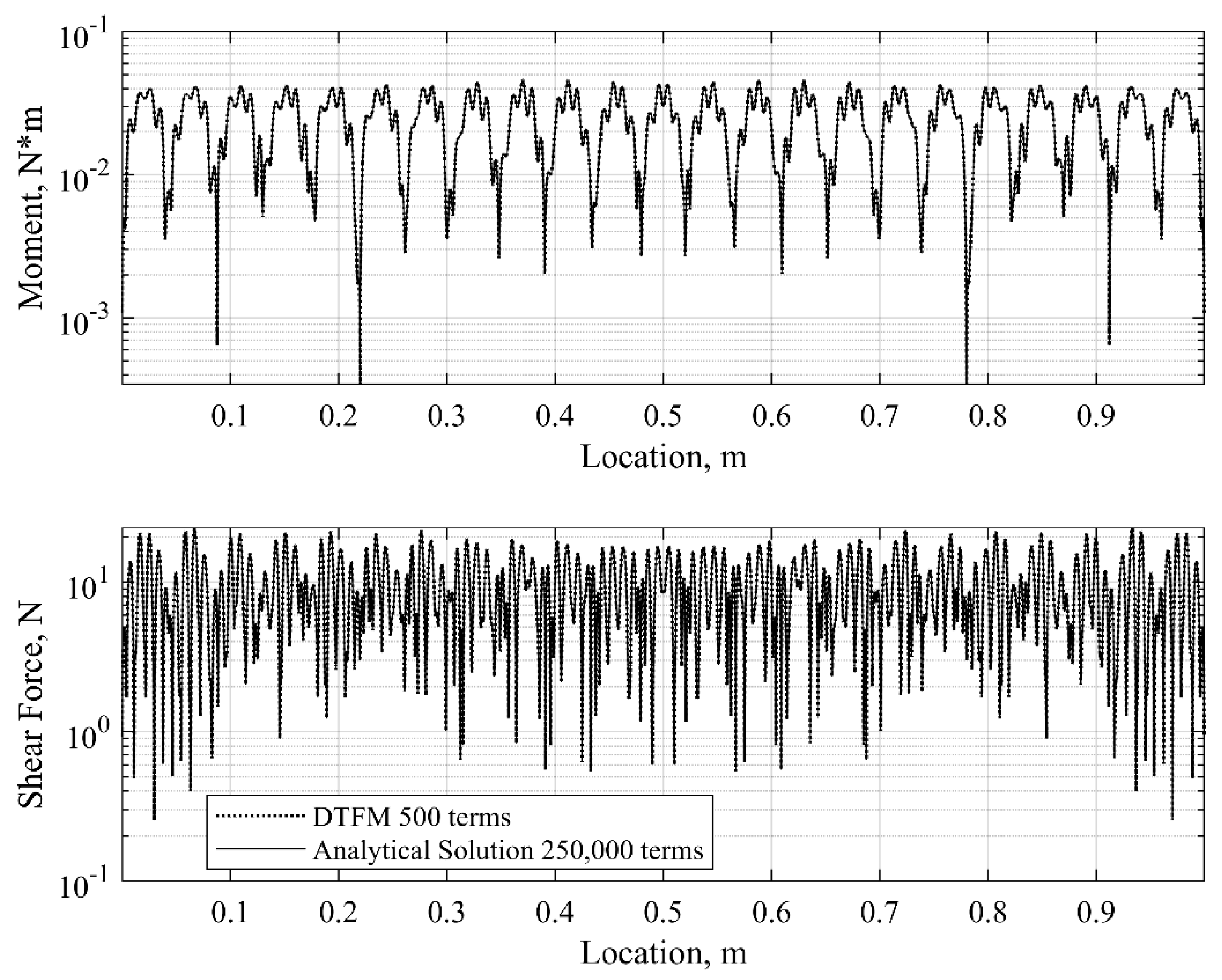
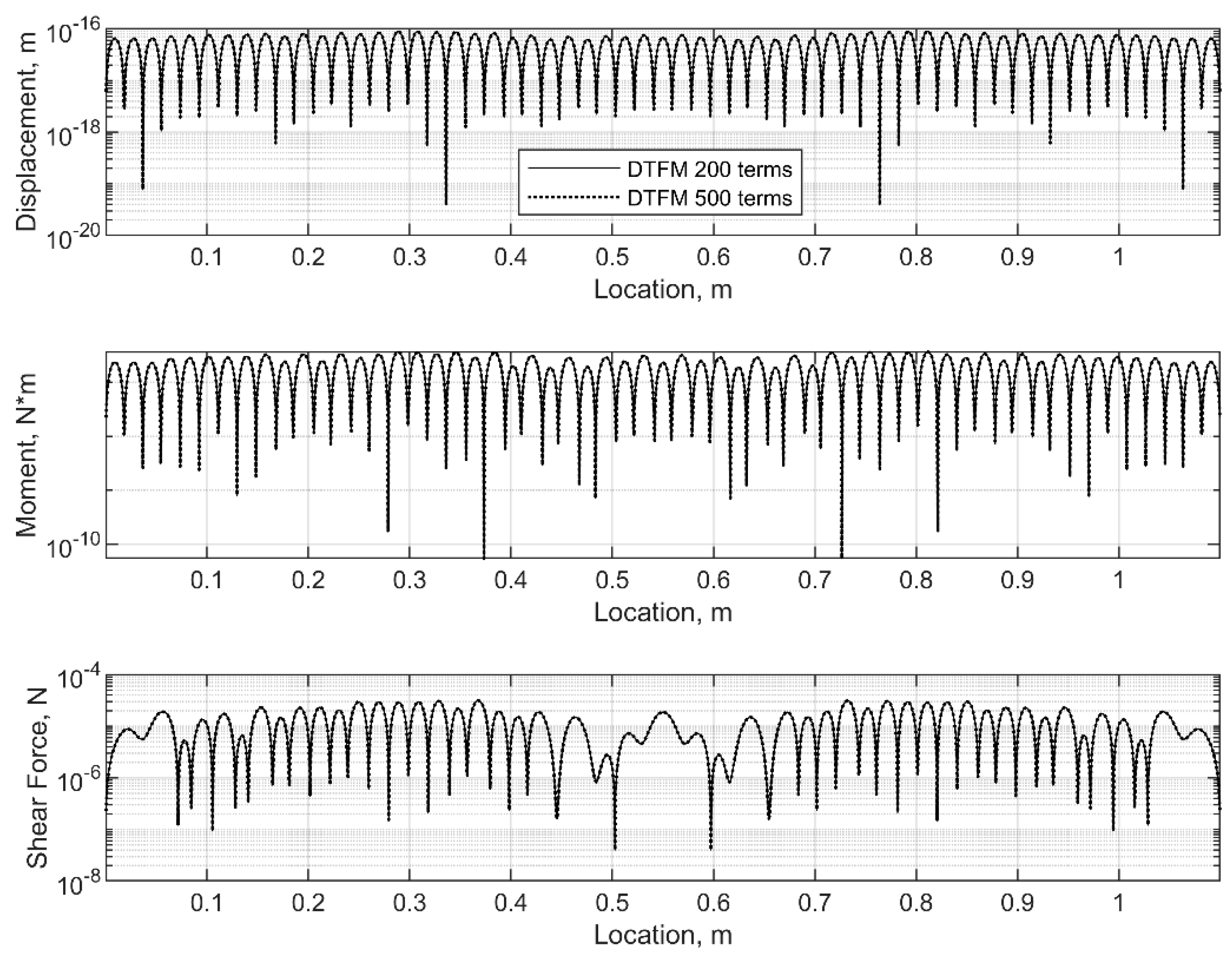
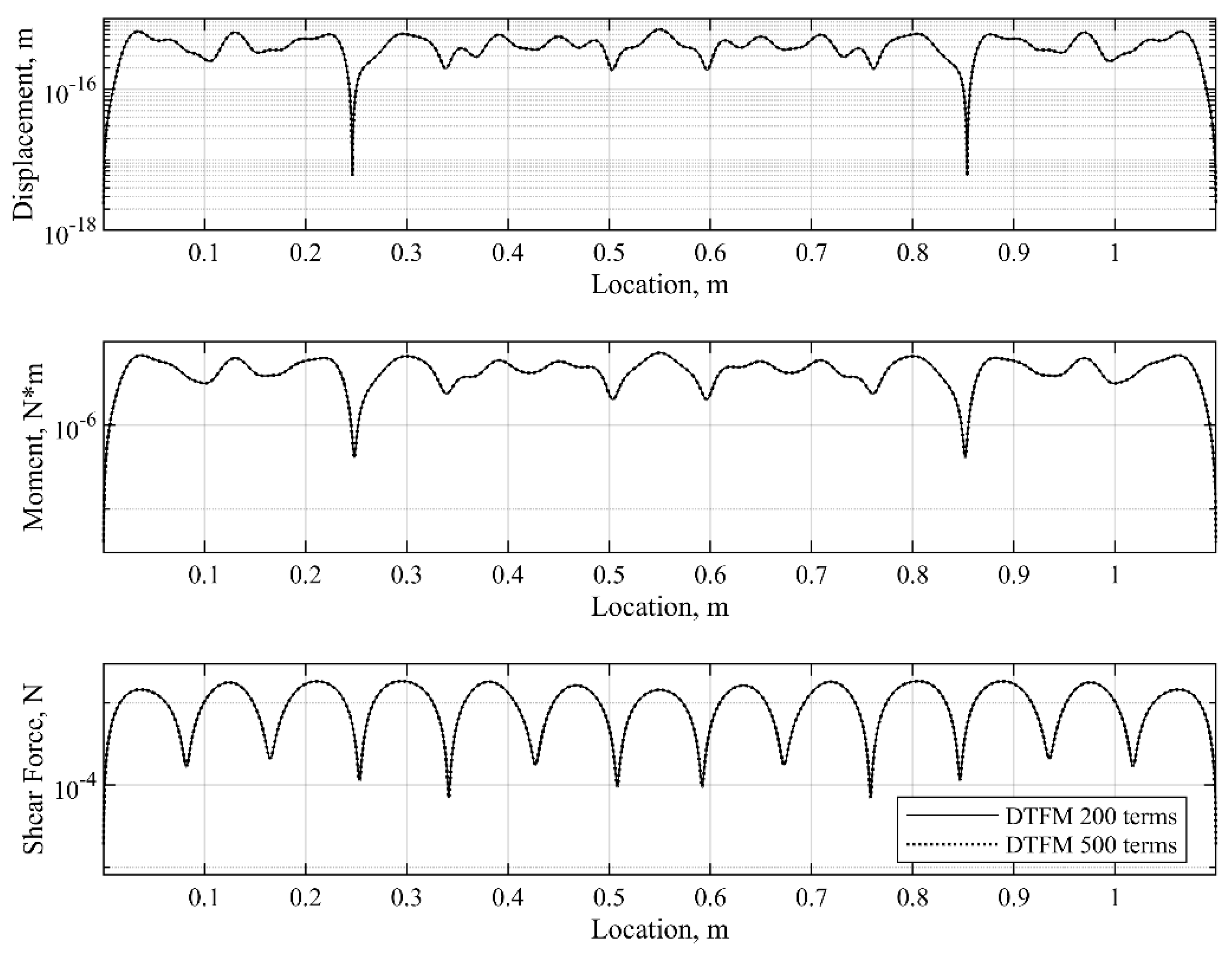
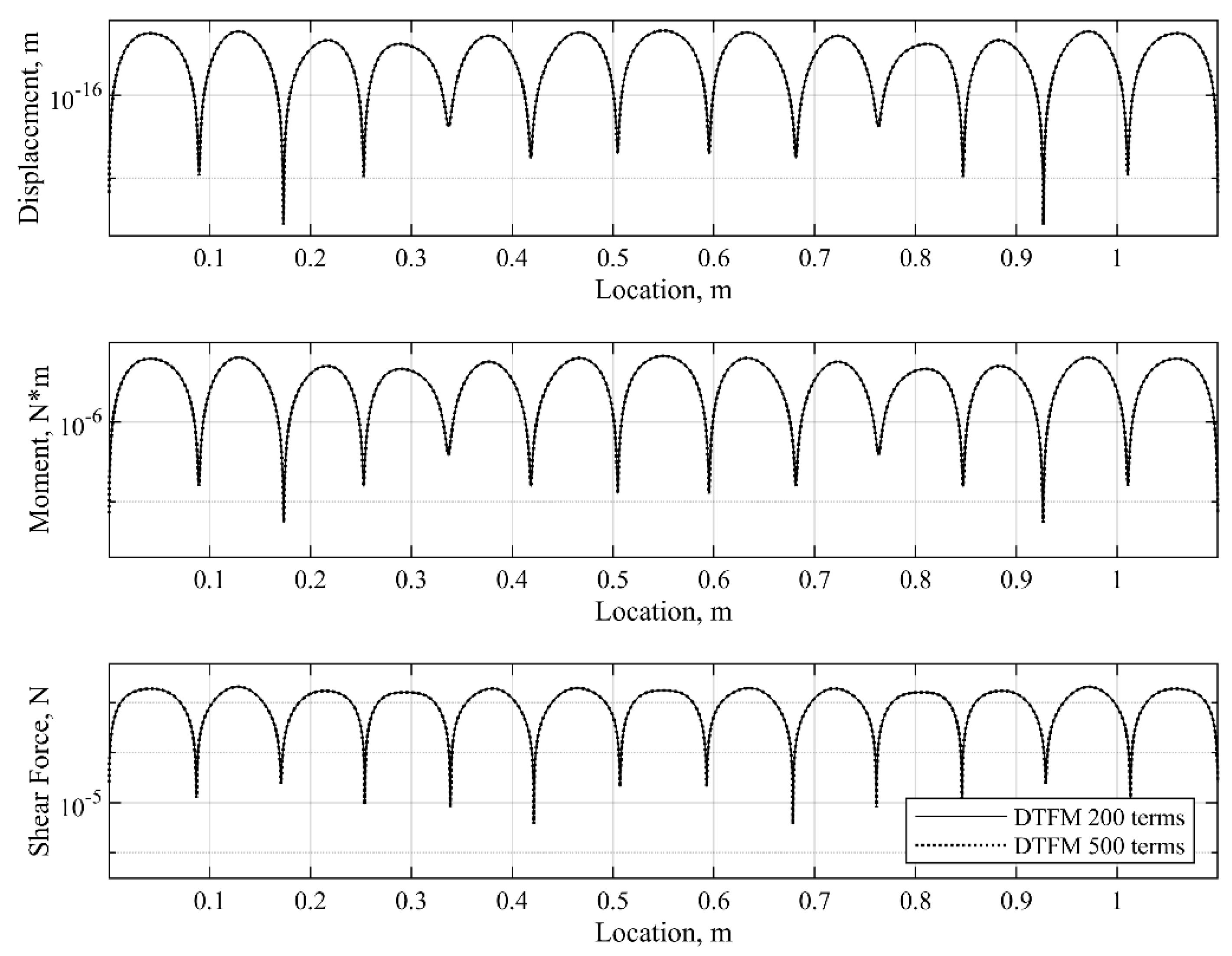
7. Numerical Examples
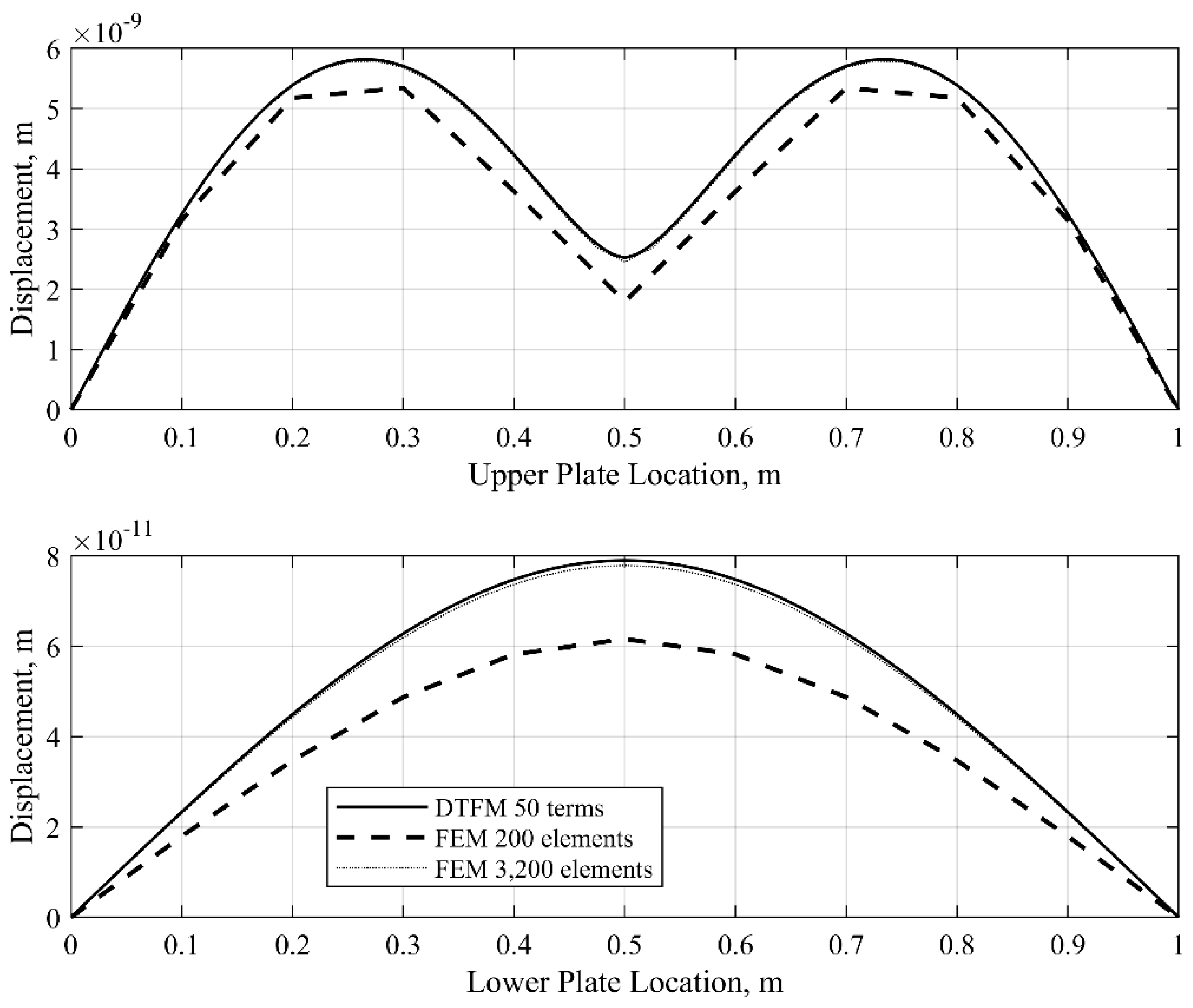
7.1. Example 1: A Double-Plate Structure with a Fully Connected Viscoelastic Layer
7.2. Example 2. A Double-Plate Structure with a Partially Distributed Viscoelastic Layer
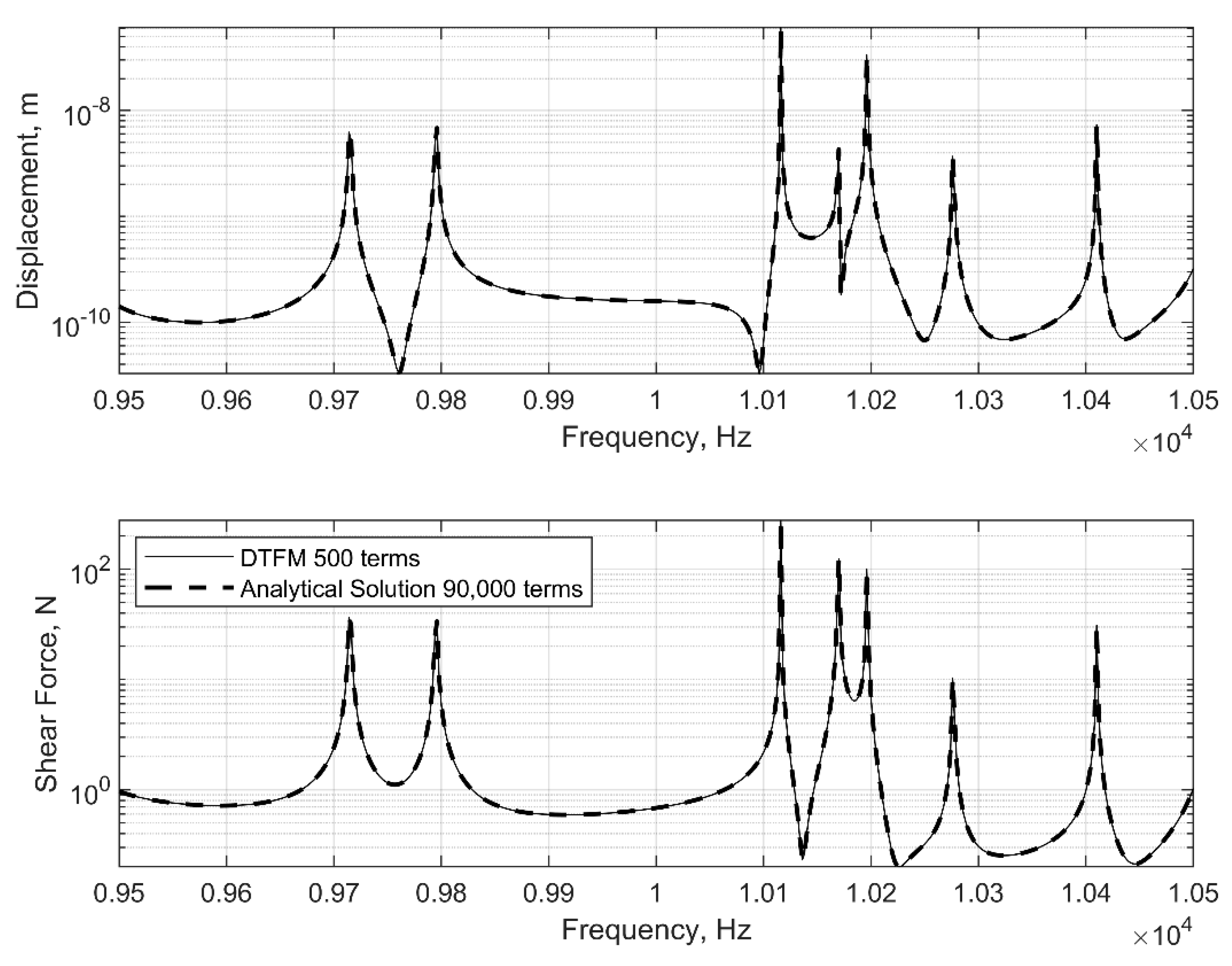
7.3. Example 3. A Three-Plate Structure with Dislocated Viscoelastic Layers
8. Conclusions
- (1)
- The proposed method, which is developed based on the Distributed Transfer Function Method (DTFM), provides an -domain state-space formulation for multi-layer sandwich plates with various configurations (layouts) of viscoelastic layers. This formulation does not rely on any spatial discretization in modeling. As a result, closed-form analytical solutions to the frequency response problem of sandwich Lévy plates with various configurations are obtained for the first time.
- (2)
- One unique feature of the proposed method is that the model development and solution procedure for frequency responses remain unchanged in all frequency regions. This consistency in modeling and analysis differs from FEA-based methods, which need to implement mesh refinement at different frequencies. Accordingly, the DTFM-based approach provides a unified framework for frequency response analysis of sandwich Lévy plates over a wide frequency range.
- (3)
- The proposed method can effectively handle multi-layer sandwich plates with dislocated viscoelastic layers, and it can easily implement different models of viscoelastic materials. These issues would be extremely difficult to manage by conventional analytical methods, if not impossible.
- (4)
- Another special feature of the proposed method is that detailed local information of a sandwich plate in high-frequency vibrations, including the displacements, bending moments, and shear forces of a plate component at any location, can be conveniently obtained from the state vectors. On the other hand, FEA-based methods would require significant effort to determine shear forces, and energy-based methods have difficulty providing detailed local information about the plate response.
- (5)
- The proposed method is illustrated in three numerical examples, where the accuracy, efficiency, and versatility of the DTFM in computing the frequency responses of sandwich Lévy plates is validated through comparison with the FEM and analytical solutions (Navier solutions). It is shown that the DTFM-based analysis works in all frequency regions, from low to high frequencies. Moreover, the simulations reveal that the computational efforts required by the proposed method are much less than those needed by the existing methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mouritz, A.P.; Gellert, E.; Burchill, P.; Challis, K. Review of Advanced Composite Structures for Naval Ships and Submarines. Compos. Struct. 2001, 53, 21–42. [Google Scholar] [CrossRef]
- Ning, H.; Janowski, G.M.; Vaidya, U.K.; Husman, G. Thermoplastic Sandwich Structure Design and Manufacturing for the Body Panel of Mass Transit Vehicle. Compos. Struct. 2007, 80, 82–91. [Google Scholar] [CrossRef]
- Liaw, B.-D.; Little, R.W. Theory of Bending Multi-Layer Sandwich Plates. AIAA J. 1967, 5, 301–304. [Google Scholar] [CrossRef][Green Version]
- Mead, D.J. Passive Vibration Control; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Marynowski, K. Free Vibration Analysis of the Axially Moving Lévy-Type Viscoelastic Plate. Eur. J. Mech. A Solids 2010, 29, 879–886. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. Levy-Type Solution for Free Vibration Analysis of Orthotropic Plates Based on Two Variable Refined Plate Theory. Appl. Math. Model. 2012, 36, 3870–3882. [Google Scholar] [CrossRef]
- Pradhan, K.K.; Chakraverty, S. Free Vibration of FG Levy Plate Resting on Elastic Foundations. Proc. Inst. Civ. Eng. Eng. Comput. Mech. 2016, 169, 3–28. [Google Scholar] [CrossRef]
- Demirhan, P.A.; Taskin, V. Levy Solution for Bending Analysis of Functionally Graded Sandwich Plates Based on Four Variable Plate Theory. Compos. Struct. 2017, 177, 80–95. [Google Scholar] [CrossRef]
- Yekani, S.M.A.; Fallah, F. A Levy Solution for Bending, Buckling, and Vibration of Mindlin Micro Plates with a Modified Couple Stress Theory. SN Appl. Sci. 2020, 2, 2169. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. Levy Solution and State-Space Approach for Hygro-Thermo-Magnetic Bending of a Cross-Ply Laminated Plate on Kerr Foundation under Various Loadings. J. Compos. Mater. 2024, 59, 3–28. [Google Scholar] [CrossRef]
- Du, Y.; Tong, L. Exact Levy-Type Solution for Buckling of Rectangular Composite Plate Reinforced with Graphene Nanoplatelets. Int. J. Struct. Stab. Dyn. 2025, 2650252. [Google Scholar] [CrossRef]
- Oktem, A.S.; Algula, I. Boundary Discontinuous Fourier Solution of Thin Levy-Type Flat and Doubly Curved Shallow Shells. Steel Compos. Struct. 2024, 52, 595–608. [Google Scholar] [CrossRef]
- Rabbiolo, G.; Bernhard, R.J.; Milner, F.A. Definition of a High-Frequency Threshold for Plates and Acoustical Spaces. J. Sound Vib. 2004, 277, 647–667. [Google Scholar] [CrossRef]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis, 4th ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lu, Y.P.; Killian, J.W.; Everstine, G.C. Vibrations of Three Layered Damped Sandwich Plate Composites. J. Sound Vib. 1979, 64, 63–71. [Google Scholar] [CrossRef]
- Akoussan, K.; Boudaoud, H.; Daya, E.-M.; Carrera, E. Vibration Modeling of Multilayer Composite Structures with Viscoelastic Layers. Mech. Adv. Mater. Struct. 2015, 22, 136–149. [Google Scholar] [CrossRef]
- Zarrouk, T.; Nouari, M.; Salhi, J.-E.; Benbouaza, A. Numerical Simulation of Rotary Ultrasonic Machining of the Nomex Honeycomb Composite Structure. Machines 2024, 12, 137. [Google Scholar] [CrossRef]
- Lyon, R.H.; DeJong, R.G. Theory and Application of Statistical Energy Analysis, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1995. [Google Scholar]
- Zhou, R.; Crocker, M.J. Sound Transmission Loss of Foam-Filled Honeycomb Sandwich Panels Using Statistical Energy Analysis and Theoretical and Measured Dynamic Properties. J. Sound Vib. 2010, 329, 673–686. [Google Scholar] [CrossRef]
- Wang, T.; Li, S.; Rajaram, S.; Nutt, S.R. Predicting the Sound Transmission Loss of Sandwich Panels by Statistical Energy Analysis Approach. J. Vib. Acoust. 2010, 132, 011004. [Google Scholar] [CrossRef]
- Hwang, H.D.; Maxit, L.; Ege, K.; Gerges, Y.; Guyader, J.-L. SmEdA Vibro-Acoustic Modelling in the Mid-Frequency Range Including the Effect of Dissipative Treatments. J. Sound Vib. 2017, 393, 187–215. [Google Scholar] [CrossRef]
- Mace, B.R.; Duhamel, D.; Brennan, M.J.; Hinke, L. Finite Element Prediction of Wave Motion in Structural Waveguides. J. Acoust. Soc. Am. 2005, 117, 2835–2843. [Google Scholar] [CrossRef]
- Yang, Y.; Mace, B.; Kingan, M. Prediction of Noise Transmission through Honeycomb Sandwich Panels Using a Wave and Finite Element Method. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Reston, VA, USA, 2018; Volume 257, pp. 122–132. [Google Scholar]
- Alam, N.; Asnani, N.T. Vibration and Damping Analysis of Multilayered Rectangular Plates with Constrained Viscoelastic Layers. J. Sound Vib. 1984, 97, 597–614. [Google Scholar] [CrossRef]
- Rao, M.K.; Desai, Y.M. Analytical Solutions for Vibrations of Laminated and Sandwich Plates Using Mixed Theory. Compos. Struct. 2004, 63, 361–373. [Google Scholar] [CrossRef]
- Foraboschi, P. Three-Layered Sandwich Plate: Exact Mathematical Model. Compos. Part B Eng. 2013, 45, 1601–1612. [Google Scholar] [CrossRef]
- Alaimo, A.; Orlando, C.; Valvano, S. Analytical Frequency Response Solution for Composite Plates Embedding Viscoelastic Layers. Aerosp. Sci. Technol. 2019, 92, 429–445. [Google Scholar] [CrossRef]
- Sabherwal, P.; Belarbi, M.-O.; Raman, R.; Garg, A.; Li, L.; Chalak, H.D.; Houari, M.S.A.; Avcar, M. Free Vibration Analysis of Laminated Sandwich Plates Using Wavelet Finite Element Method. AIAA J. 2024, 62, 824–832. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Y.; Hosen, K.; Pan, J. Free Vibration Properties of Novel Sandwich Plates with a Layered and Rotational Core. Eur. J. Mech. A Solids 2025, 111, 105588. [Google Scholar] [CrossRef]
- Wang, J.; Chang, Z.; Liu, T.; Chen, L. A Review of Linear and Nonlinear Vibration Analysis of Composite Laminated Structures by Computational Approaches: 2015–2024. Nonlinear Dyn. 2025, 113, 10839–10859. [Google Scholar] [CrossRef]
- Yang, B.; Noh, K. Distributed Transfer Function Method: One-Dimensional Problems in Engineering; De Gruyter: Berlin, Germany; ISBN 978-3110758542.
- Noh, K.; Yang, B. An Augmented State Formulation for Modeling and Analysis of Multibody Distributed Dynamic Systems. J. Appl. Mech. 2014, 81, 051011. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, B. Medium-Frequency Vibration Analysis of Timoshenko Beam Structures. Int. J. Struct. Stab. Dyn. 2020, 20, 2041009. [Google Scholar] [CrossRef]
- Liu, S.; Yang, B. A Closed-Form Analytical Solution Method for Vibration Analysis of Elastically Connected Double-Beam Systems. Compos. Struct. 2019, 212, 598–608. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity: An Introduction, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Yang, B. Advanced Mechanical Vibration: Modeling, Analysis, and Simulation; McGraw Hill: New York, NY, USA, 2025; ASIN: B0D5K553DB. [Google Scholar]





| FEM (Elements) | DTFM | |||
|---|---|---|---|---|
| 50 | 200 | 3200 | ||
| 1 | 85.0390 | 86.4263 | 86.8882 | 86.9195 |
| 2 | 88.7757 | 90.1055 | 90.5486 | 90.5786 |
| 3 | 161.1637 | 165.4778 | 167.0437 | 167.1528 |
| 4 | 163.1664 | 167.4287 | 168.9766 | 169.0845 |
| 5 | 260.1657 | 265.3827 | 267.3096 | 267.4445 |
| 10 | 323.0613 | 341.1225 | 348.1126 | 348.6107 |
| 20 | 599.0271 | 645.5216 | 667.3677 | 669.0969 |
| 30 | 897.0924 | 983.4272 | 989.3284 | 989.8729 |
| 40 | 1067.6546 | 1164.9535 | 1204.1859 | 1210.4549 |
| 50 | 1361.6047 | 1510.5935 | 1546.7057 | 1551.3877 |
| FEM (Elements) | DTFM | |||
|---|---|---|---|---|
| 50 | 200 | 3200 | ||
| 1 | 102.8850 | 105.0855 | 105.8691 | 105.9233 |
| 2 | 105.9944 | 108.1316 | 108.8933 | 108.9460 |
| 3 | 207.8806 | 213.1652 | 215.3394 | 215.4956 |
| 4 | 209.4369 | 214.6833 | 216.8422 | 216.9973 |
| 5 | 267.9959 | 274.1810 | 276.7941 | 276.9834 |
| 10 | 369.5161 | 375.1433 | 380.1241 | 380.7771 |
| 20 | 708.8662 | 731.5818 | 756.1503 | 758.2217 |
| 30 | 980.7883 | 993.7429 | 1037.4766 | 1042.3999 |
| 40 | 1270.8757 | 1312.7018 | 1347.0952 | 1351.1562 |
| 50 | 1600.1592 | 1570.7294 | 1624.9480 | 1634.6596 |
| FEM (Elements) | DTFM | |||
|---|---|---|---|---|
| 50 | 200 | 3200 | ||
| 1 | 103.6084 | 105.8236 | 106.6055 | 106.6595 |
| 2 | 105.6672 | 107.8404 | 108.6079 | 108.6609 |
| 3 | 219.8495 | 225.0578 | 227.2117 | 227.3665 |
| 4 | 220.5723 | 225.7630 | 227.9101 | 228.0644 |
| 5 | 250.9591 | 257.1126 | 259.6909 | 259.8766 |
| 10 | 397.4359 | 402.7193 | 406.4568 | 406.7532 |
| 20 | 713.0100 | 765.3261 | 789.3563 | 791.3876 |
| 30 | 981.4164 | 988.2476 | 1042.9694 | 1047.7172 |
| 40 | 1308.6136 | 1313.9311 | 1400.5220 | 1401.4399 |
| 50 | 1523.5747 | 1575.7178 | 1690.4022 | 1699.8813 |
| FEM (Elements) | DTFM | |||
|---|---|---|---|---|
| 300 | 1200 | 4800 | ||
| 1 | 53.7829 | 53.7028 | 53.6821 | 53.6752 |
| 2 | 54.9444 | 54.8623 | 54.8412 | 54.8341 |
| 3 | 57.4559 | 57.3714 | 57.3497 | 57.3425 |
| 4 | 75.1837 | 75.1723 | 75.1687 | 75.1674 |
| 5 | 75.5086 | 75.4956 | 75.4916 | 75.4902 |
| 10 | 217.4733 | 216.8162 | 216.6319 | 216.5686 |
| 20 | 313.8678 | 316.1529 | 316.7388 | 316.9354 |
| 30 | 492.1189 | 490.0905 | 489.4404 | 492.6234 |
| 40 | 657.7398 | 661.2479 | 662.5154 | 662.9800 |
| 50 | 874.2904 | 872.5249 | 870.9846 | 870.5649 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, B. Analytical Vibration Solutions of Sandwich Lévy Plates with Viscoelastic Layers at Low and High Frequencies. Appl. Mech. 2025, 6, 49. https://doi.org/10.3390/applmech6030049
Zhang Y, Yang B. Analytical Vibration Solutions of Sandwich Lévy Plates with Viscoelastic Layers at Low and High Frequencies. Applied Mechanics. 2025; 6(3):49. https://doi.org/10.3390/applmech6030049
Chicago/Turabian StyleZhang, Yichi, and Bingen Yang. 2025. "Analytical Vibration Solutions of Sandwich Lévy Plates with Viscoelastic Layers at Low and High Frequencies" Applied Mechanics 6, no. 3: 49. https://doi.org/10.3390/applmech6030049
APA StyleZhang, Y., & Yang, B. (2025). Analytical Vibration Solutions of Sandwich Lévy Plates with Viscoelastic Layers at Low and High Frequencies. Applied Mechanics, 6(3), 49. https://doi.org/10.3390/applmech6030049




