Theoretical and Experimental Comparisons of Total Solar Transmittance for Polycarbonate Sheet with Twin Wall Rectangular Structure

Abstract

Multiwall polycarbonate sheets are applied as construction elements. Modelling and analysis of thermal processes that occur in this material demand the knowledge of solar transmittance. Values of this parameter determined in laboratory conditions are given in the technical specification of the product. However, the parameter is in practice a complex function depending on the number of factors. This paper presents theoretical and experimental research results for total solar transmittance (TST) for a polycarbonate sheet with twin wall rectangular structure. Theoretical TST is calculated as a product of transmissivity after accounting for light absorption in polycarbonate and of transmissivity after accounting for multiple reflections of solar rays from walls of a channel. The first kind of transmissivity is insignificant and can be neglected. The second one depends on the number of reflection layers, season, and time of day. Experimental TST is determined as the ratio of irradiance under and above the polycarbonate sheet measured by pyranometers. Experimental TST is also a function of time of day and season. Both kinds of TST have an approximately constant value in the time about noon. The theoretical values of TST (0.74) are approximately equal to experimental values of TST (0.75) for the selected summer day. The value of TST in catalogue is equal to 0.82.

1. Introduction

Efficient energy consumption is one of the concepts for the sustainable growth of world economies [1,2]. Building industries [3,4] are some of the biggest energy consumers. In order to optimise energy consumption, numerous new materials are being introduced in construction. Unfortunately, the technical parameters of these materials are not always given in the product’s technical specification or their values are not sufficient for detailed energy analysis.

Multiwall polycarbonate sheets are applied in the construction industry for transparent wall and roof partitions, both inside and outdoors [5,6,7,8,9,10,11,12,13,14]. The following multiwall polycarbonate sheets are accessible on the market: rectangular [10,11,14], truss structure of type X or V [10], and with an internal sine wave (Figure 1).

The proposed construction of a polycarbonate sheet might be more sophisticated, for example, honeycomb [9]. The number of channels in the sheet, determined in terms of its thickness, may be from 1 to 7. The sheet’s construction is decisive for its strength and endurance and, in turn, for its possible applications. Flat or arch-shaped partitions can be made of polycarbonate sheets. However, in order to arch the sheet, a minimal cold bending radius must be preserved.

Authors are focused on fixed or retractable swimming pool enclosures made of polycarbonate [16,17,18,19]. In order to model processes of energy exchange in pools with polycarbonate enclosures, it is essential to have knowledge of, among others, optic properties of enclosure such as reflectance, transmittance, and absorptance for visible and for solar radiations [17].

The present paper considers an enclosure made of a polycarbonate sheet with twin wall rectangular structure. In directories for products, information concerning sheets with a width limited to ca 2.5 m and with thicknesses of 6, 8, and 10 mm can be found. Producers offer sheets with lengths up to several meters [5,6]. In catalogues, values of some of the abovementioned parameters determined in laboratory conditions (according to current standards [20]) are given. The most frequently given parameters are light transmittance (LT) [9,10,11,14], direct solar transmittance (DT) [14], and total solar transmittance (TST) [14]. Some of the producers include also information concerning solar absorptance (A) [14] and solar reflectance (R) [14] in their products [14]. TST is defined as the proportion of incoming solar energy transmitted to the room behind the glazing [21]. It consists of the direct solar transmittance (DT) and secondary internal heat transfer factor, which includes thermal radiation and convective heat transfer.

Definitions of two notions—solar transmittance and solar transmissivity—demand a further explanation, though they are treated as equivalent in many publications. Solar radiation is reflected, absorbed, and transmitted while it transfers through a transparent object. If spectral characteristics of the energy do not change, the parameter that relates to the loss of this solar radiation is transmissivity. However, a polycarbonate enclosure is not a perfectly transparent object and solar energy is partially absorbed while being transferred through the enclosure. The absorption depends on wavelengths and causes changes in spectrum characteristics. In this case, the parameter is defined as transmittance. As a result of absorption, part of solar radiation is changed into heat and emitted to both sides of the transparent object. This paper investigates TST for a pool enclosure.

In practice, siting of the enclosure and its shape can affect the values of parameters that characterise its optical properties. The present paper considers a flat enclosure positioned horizontally. Figure 2 shows possible variants of positioning the flat horizontal enclosure made of polycarbonate sheet with twin wall rectangular structure in a north–south direction. If the axis of one of the channels of this enclosure is drawn, the angle between this axis and the N-S direction is the enclosure’s azimuth. The azimuth of the enclosure can change from value −90° (Figure 2a), through negative values (Figure 2b), to value 0° (Figure 2c); next, it assumes positive values 0° (Figure 2c), and then assumes the value of +90°.

In turn, Figure 3 shows the effect of solar azimuth on direct transmittance through the enclosure under research. If solar refraction on the border between media is neglected, it can be stated that solar radiation must transfer at least through two walls (bottom and top) of polycarbonate (Figure 3b). In the morning and the afternoon, solar radiation transfer through the ribs of channels (Figure 3a) is also possible.

The next parameter decisive for the length of transfer of solar radiation through the material of enclosure is the angle of incidence, or angle of zenith. It is the function of the enclosure’s siting (location) in time. Thus, location in the site defined by latitude ($\Phi$) and longitude (L) must be known. In turn, time is decisive for values of solar declination (time of season) and hour angle (time of day). In the case of the horizontal position of the enclosure, its angle of incidence to the horizontal surface equals zero—that is, $\beta =0°$.

Prior to the present research, Čekon et al. [22,23,24,25] carried out experimental research in conditions of real optical properties for multiwall polycarbonate sheets. Analysis of knowledge of the topic made by these authors shows that there is little information concerning the optical properties of multiwall polycarbonate sheets. Available papers concern polycarbonate sheets produced with dated technologies. Relatedly, Čekon et al. [25] carried out long-lasting experimental research on several currently produced multiwall polycarbonate sheets.

On this basis, they determined changes of the total enclosure’s transmittance in relation to solar radiation and to incidence angle of solar radiation. The research was carried out according to ASTM standards [26].

The relation between TST and clearness index K was investigated in [15]. Zapalowicz and Wojnicki stated that sky cloudiness has no relevant effect on the TST. The experimental values of TST were in the range of 0.6–0.7 and depended on the time of day. Reasons for daily changeability are changes in solar radiation and changes of shares of direct and diffusive radiation in total radiation.

As mentioned earlier, the strategic aim of the research realised by the authors is to elaborate the methodology of thermal calculation for swimming pools with cover. The proper method of TST calculation is one of the elements that is needed to solve this problem. Authors proposed, in paper [19], a simplified method to calculate solar transmittance for any polycarbonate enclosure. Initial analysis research results showed that the above parameter was not a constant value, and it changed depending on time of day and season time. The aim of the present paper is to compare theoretical and experimental values of TST for a flat polycarbonate enclosure under research positioned horizontally for several chosen days of the year. Obtained results allow to further verify the proposed calculation method.

2. Materials and Methods

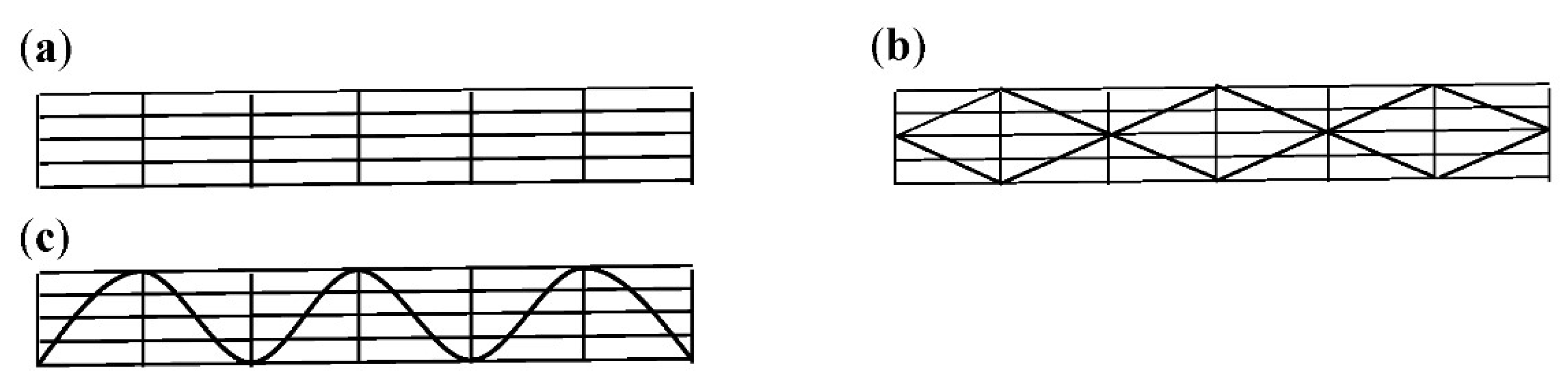
2.1. Object of Research

The object of research of the present paper is a colourless polycarbonate sheet Lexan Thermoclear LT2UV102RS17 with twin wall rectangular structure produced by Sabic Innovative Plastics [5,6]. The producer offers sheets with width up to 2.1 m and with any length up to 13 m. According to technical approval [5], characteristic dimensions of the sheet are as follows: thickness 0.010 m, thickness of the top and bottom walls $\left(0.45\pm 0.1\right)·{10}^{-3}$ m, thickness of the rib $\left(0.36\pm 0.1\right)·{10}^{-3}$ m, area weight $1700·{10}^{-3}$ kg/m². In the case of arch construction, the recommended minimal cold bending radius is 1.5 m. The sheet is finished with an LT2UV protective film that reduces UV radiation—that is, solar radiation with wavelength below 385 nm. Characteristics of solar transmittance for the sheet under research are given in papers [5,6]. Data given by the producer show that, for colourless sheets, light transmittance is LT = 81%, solar reflectance and solar absorptance are equal and the amount R = A = 9%, and total solar transmittance is TST = 82%.

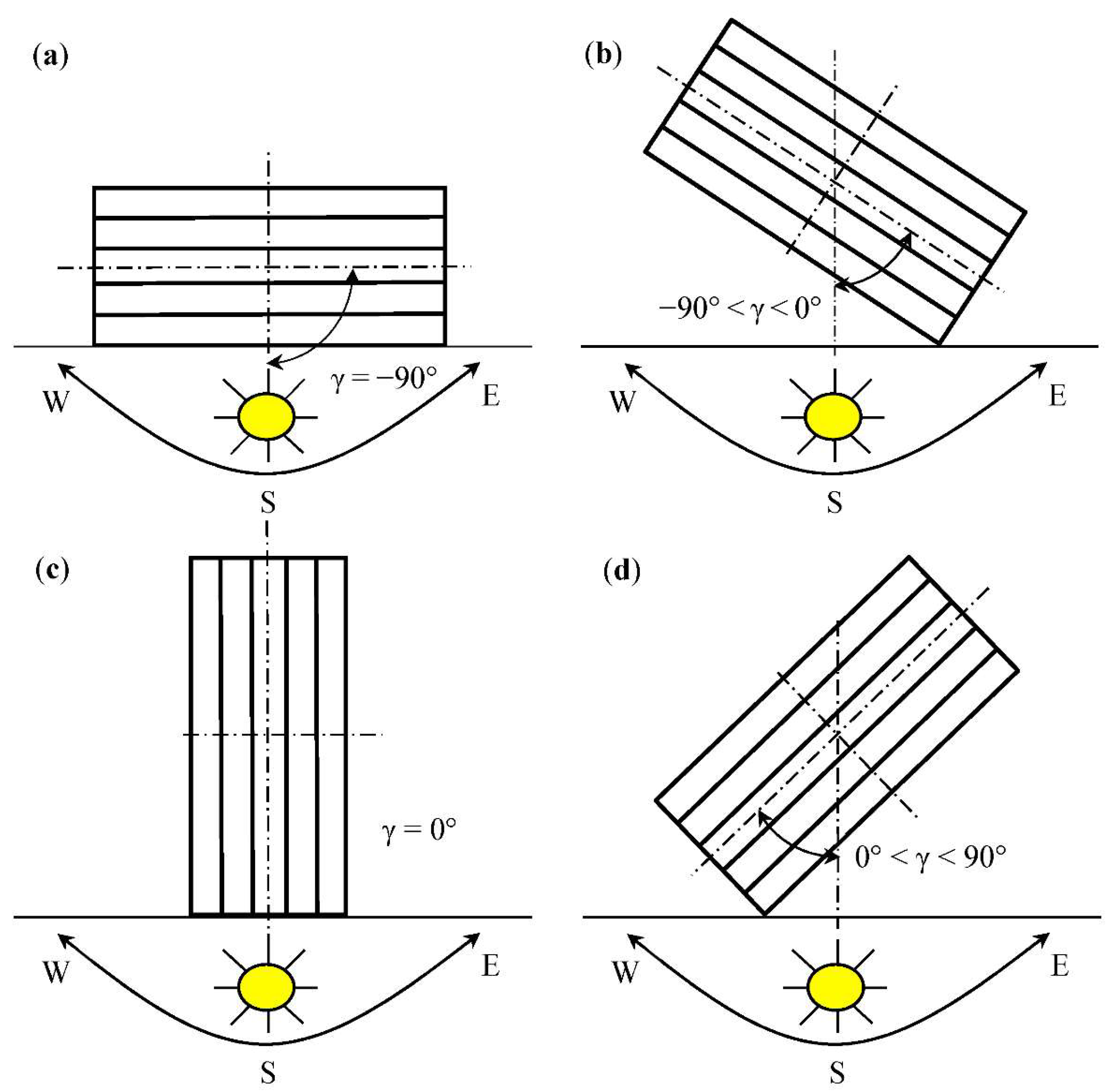
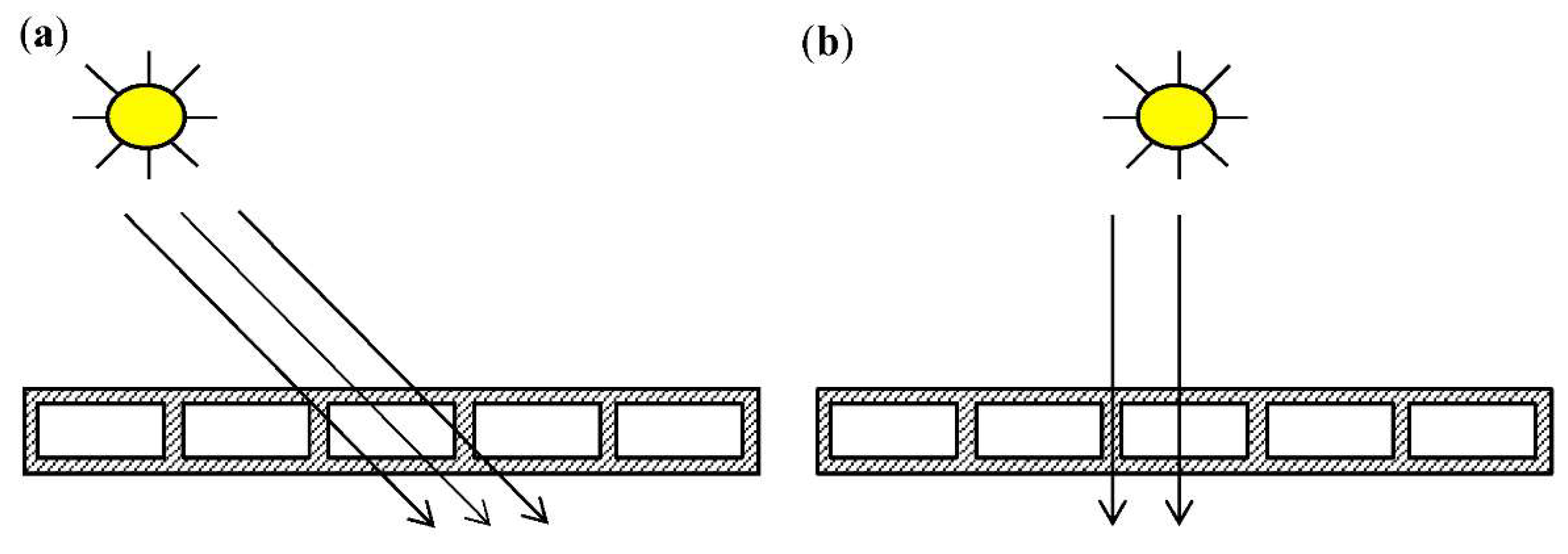
2.2. Methodology of Theoretical Calculation of TST

In order to calculate TST for a flat enclosure made of polycarbonate sheet with twin wall rectangular structure, the calculation methodology given in the paper [27] was used. This methodology was also applied in the paper [19] in order to calculate TST for pool enclosure.

According to this methodology, TST for a multilayer sheet equals the product of transmissivity after accounting for light absorption in polycarbonate and of transmissivity after accounting for multiple reflections of solar rays from walls of the channel:

$${\tau }_c={\tau }_a{\tau }_r$$

(1)

Transmissivity after accounting for light absorption by the polycarbonate can be determined from the relation

$${\tau }_a=exp\frac{-K{\delta }_c}{cos{\Theta }_2}$$

(2)

where $K$ is extinction coefficient, ${\delta }_c$ is total enclosure thickness, and ${\Theta }_2$ is solar refraction angle in polycarbonate.

Solar refraction angle ${\Theta }_2$ can be calculated from the right refraction of light on the borderline of two media with different optical densities by means of the pattern

$$n_{1}sin{\Theta }_1=n_{2}sin{\Theta }_2$$

(3)

In Equation (3), $n_1,n_2$ are solar refraction coefficients for air and polycarbonate; angle ${\Theta }_1$ is the current angle of incidence of solar radiation, measured in the zenith direction.

In turn, transmissivity after accounting for multiple reflections of solar rays from surfaces of layers that created the enclosure can be calculated from the relation

$${\tau }_r=0.5\left[\frac{1-{\rho }_{\perp }}{1+\left(2Z-1\right){\rho }_{\perp }}+\frac{1-{\rho }_{\parallel }}{1+\left(2Z-1\right){\rho }_{\parallel }}\right]$$

(4)

where $Z$ is the number of layers of the enclosure.

Equation (4) is valid for polarised light with two components—parallel and perpendicular. These components depend on reflection coefficients that can be calculated from patterns

$${\rho }_{\perp }=\frac{si{n}^2\left({\Theta }_2-{\Theta }_1\right)}{si{n}^2\left({\Theta }_2+{\Theta }_1\right)}$$

(5)

$${\rho }_{\parallel }=\frac{t{g}^2\left({\Theta }_2-{\Theta }_1\right)}{t{g}^2\left({\Theta }_2+{\Theta }_1\right)}$$

(6)

It results from information given in the Introduction that solar rays incidence angle (${\Theta }_1$) on the enclosure is a complex function dependent on many parameters such as latitude ($\Phi$) and longitude ($L$), solar declination (δ) and azimuth of enclosure (γ), as well as time (ω).

Hour angle of the Sun depends on real solar time and can be determined from the relation

$$\omega =15·\left(t-12.00\right)$$

(7)

Real solar time can be calculated from the equation

$$t=t_{ST}+4·\left(L_{ST}-L\right)+E$$

(8)

In Equation (8), $t_{ST}$ is zone time related to standard meridian, $L_{ST}$ and L are longitudes of the standard meridian and of the site of the enclosure, and E is equation of time.

Value of time equation can be calculated from the equation

$$\begin{gathered} E=229.2·[0.000075+0.001868cosB-0.032077sinB \\ -0.014615\cos \left(2B\right)-0.04089\sin \left(2B\right)] \end{gathered}$$

(9)

where $B=\left(n-1\right)360/365$ and $n$ is a successive day of the year.

Solar incidence angle can be determined from the equation

$${\Theta }_1={90}^{°}-{\alpha }_1$$

(10)

where the altitude angle (${\alpha }_1$) is calculated from the relation

$$\begin{gathered} cos{\alpha }_1=sin\delta sin\Phi cos\beta -sin\delta cos\Phi sin\beta cos\gamma +cos\delta cos\Phi cos\beta cos\omega \\ +cos\delta sin\Phi sin\beta cos\gamma cos\omega +cos\delta sin\beta sin\gamma sin\omega \end{gathered}$$

(11)

Solar declination $\delta$, present in Equation (11), is calculated from the relation

$$\delta =23.45·sin\left[360·\left(284+n\right)/365\right]$$

(12)

If the polycarbonate enclosure is positioned horizontally, Equation (11) can be simplified and the solar incidence angle can be determined from the relation

$$cos{\Theta }_1=cos\Phi cos\delta cos\omega +sin\Phi sin\delta$$

(13)

It is necessary to underline that the presented model includes only the direct radiation and the diffusive radiation is neglected. This model omitted the transport of heat by convection too.

2.3. Methodology of Experimental Determination of TST

In order to experimentally determine temporary values of TST for the enclosure under research, an experimental stand was built. View of the stand is presented in Figure 4.

A section of a polycarbonate sheet with twin wall rectangular structure with dimensions 1x1 m was mounted in a steel frame. The frame was then mounted on a stand placed on the roof of the building of Department of Energy Technologies, ZUT, Szczecin. Channels in the polycarbonate sheet were placed parallel to the E-W direction. A sensor of Kipp&Zonen, type CMP3 pyranometer was placed under the sheet in order to measure the weakened irradiance. A sensor of the same type was applied also to measure irradiance directed on the top wall of the sheet under research. Data from both sensors were registered and stored in a system of data acquisition.

Temporary values of TST were determined on the basis of weakening of irradiance transferred through the polycarbonate enclosure from the equation

$${\tau }_c^{exp}=I_{out}/I_{in}$$

(14)

where $I_{out}$ and $I_{in}$ are irradiance measured under and above the sheet, respectively.

3. Results and Discussion

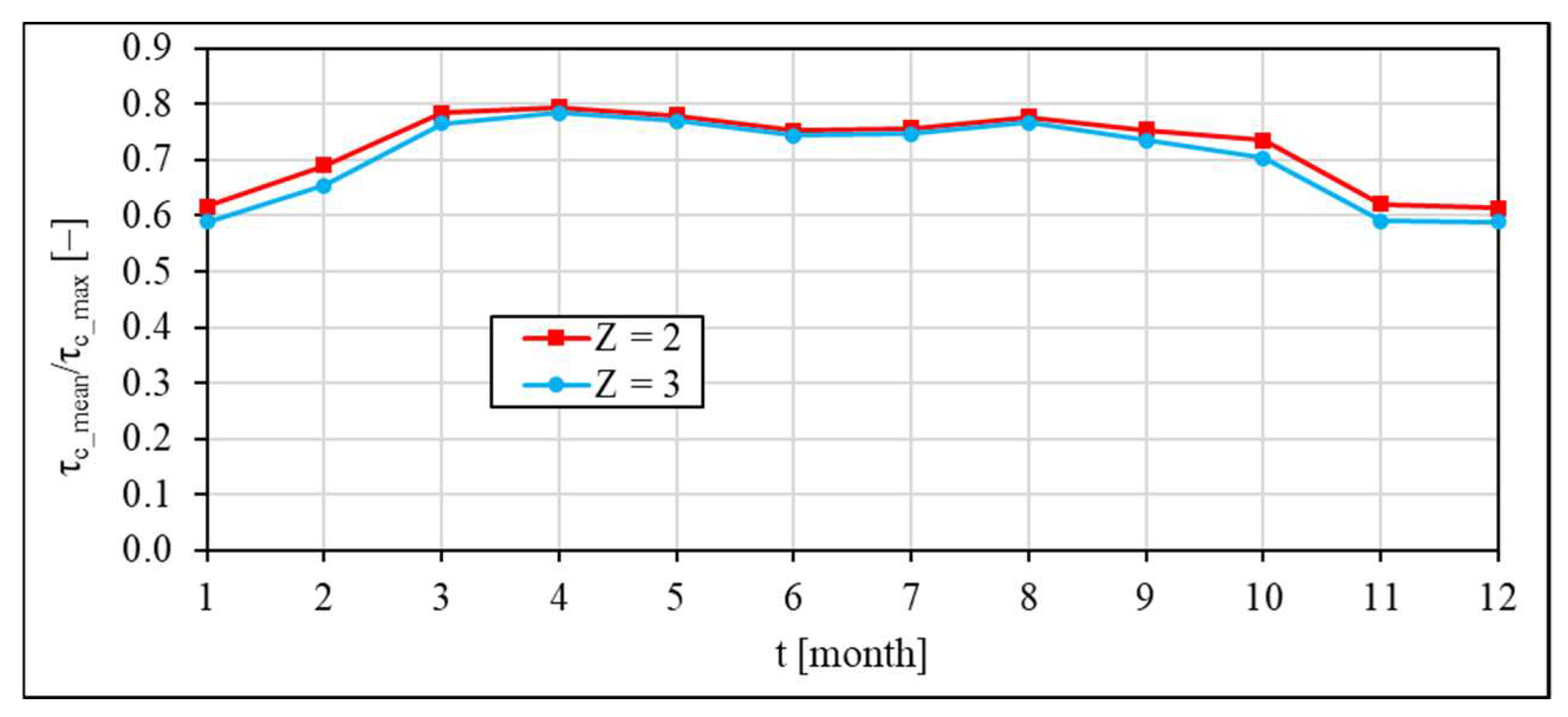
3.1. Results of Theoretical Calculations for TST

Exemplary calculations of theoretical TST were made for a flat, horizontal enclosure of an object in Szczecin (Poland). Geographical coordinates of the site are as follows: latitude $\Phi =53.403° \mathrm{N}$ and longitude $L=14.529° \mathrm{E}$. Calculations were made for characteristic days of each month. These days were chosen assuming that solar declination δ, calculated from Equation (12) and related to these days, was the mean value of solar declinations for the given month. The following days were chosen: 17th of January, 15th of February, 16th of March, 15th of April, 15th of May, 11th of June, 17th of July, 16th of August, 19th of September, 16th of October, 15th of November, 11th of December. Next, values of solar incidence angle ${\Theta }_1$ changing between sunrise and sunset depending on the hour angle were calculated from Equation (13). Calculations were carried on for real solar time changing in hourly intervals. Then, the solar refraction angle ${\Theta }_2$ was calculated, assuming that light refraction coefficients equal $n_1=1$ and $n_2=1.586$, respectively for air and polycarbonate [12]. Further, perpendicular and parallel components of the reflection coefficient were determined from Equations (5) and (6). Transmissivity after accounting for multiple reflections of solar rays from the surfaces of layers that created the enclosure was calculated from relation (4), and it was alternatively assumed that the process of solar ray reflection occurs in two or three layers of polycarbonate. Assuming two polycarbonate layers $Z=2$ for calculations means that solar rays can be reflected only from the bottom wall and from the top wall of the channel (Figure 3b). Meanwhile, assumption of three layers of polycarbonate $Z=3$ also includes the process of reflection of solar rays from the rib between the bottom and top walls of the channel (Figure 3a).

Calculation results for transmissivity after accounting for multiple reflections of solar rays from two or three surfaces of polycarbonate walls as a function of time are presented in Figure 5 and Figure 6. It results from theoretical calculations that, on characteristic days in the winter and the spring–summer season, transmissivity change after accounting for multiple reflections of solar rays from walls of the channel depends strongly on time of day. The parameter achieves its maximal value at noon. Meanwhile, in the summer months, transmissivity change after accounting for multiple reflections of solar rays from walls of the channel in times between 8.00–16.00 h remains in nearly constant value ranges. Maximal values of this parameter obtained at reflections of solar rays from bottom and top layers of polycarbonate equal 0.42—December and 0.82—June. In turn, maximal values of this parameter obtained at reflections of solar rays from bottom and from top and rib layers of polycarbonate equal 0.34 and 0.74 for December and June, respectively.

Values of transmissivity after accounting for absorption of solar radiation by polycarbonate walls as a function of extinction coefficient for characteristic days of January and June are presented in Figure 7 and Figure 8. Calculations were carried out alternatively because the exact value of extinction coefficient for polycarbonate was unknown. Calculations were made for three thicknesses of polycarbonate.

Let L denote the number of walls in which solar radiation is absorbed and converted into heat. Parameter L = 2 is related to the situation when absorption of solar radiation occurs only in the bottom and top walls of the channel. It was assumed that this thickness corresponds to an approximately double thickness of polycarbonate walls (only in front and rear walls). In this case, the total thickness of the polycarbonate equals ${\delta }_c=0.0009$ m. In real conditions, this thickness is higher and corresponds to the way of solar beams in both walls. If it is additionally taken into account that solar radiation is absorbed by the rib, the shortest way of solar rays in the rib is in the perpendicular direction; then, the total thickness of polycarbonate equals ${\delta }_c=0.00126$ m (L = 3). Certainly, the above situation does not occur in real conditions, because the way of solar rays through the rib is longer. Hence, another variant of calculations was assumed, where polycarbonate thickness equalled ${\delta }_c=0.00162$ m (L = 4—doubled thickness of the rib was taken into account). Analysis of calculations results (Figure 7 and Figure 8) shows that transmissivity after accounting for absorption of solar rays by polycarbonate changes its value first by the fourth significant figure. So, transmissivity after accounting for absorption of solar rays by polycarbonate is insignificant for determination of TST of the polycarbonate enclosure under research. This statement is confirmed by the conclusion written in the paper [18]. This kind of transmissivity will be neglected in further calculations.

Then, the value of TST of 0.82, as given in technical data for the polycarbonate sheet under research, is approximately related to the theoretically calculated maximal value of TST when solar ray reflections occur only from the bottom and the top surface walls of the channel (calculations made for summer months).

Figure 9 shows the mean twenty-four-hour values of TST after accounting for multiple reflections of solar rays from two surface and three surface polycarbonate channels, respectively, for characteristic days in particular months. Mean twenty-four-hour values are calculated on the basis of hourly values; hence, obtained runs are only of approximate character. If the mean twenty-four-hour value of this parameter is compared with its maximal value, it can be stated that the ratio of these values for summer months is about 0.75 to 0.80, and for winter months is about 0.60 (Figure 10).

Research results show also that the mean twenty-four-hour value of TST for the characteristic day of June is about three times higher than the value of this parameter calculated for the characteristic day of December, for both variants of calculations (that is, Z = 2 and Z = 3).

It should be noted that the presented model is simplified because only direct radiation is included in TST calculation. In the real condition, it is necessary to introduce to TST calculation the diffusive radiation too. Diffusive radiation is characterised by different incident angles of solar beams. The equivalent incident angle for diffusive solar or correction of incident angle of direct radiation must be introduced to a more complicated model. Furthermore, the new model should include the transfer of energy by convection.

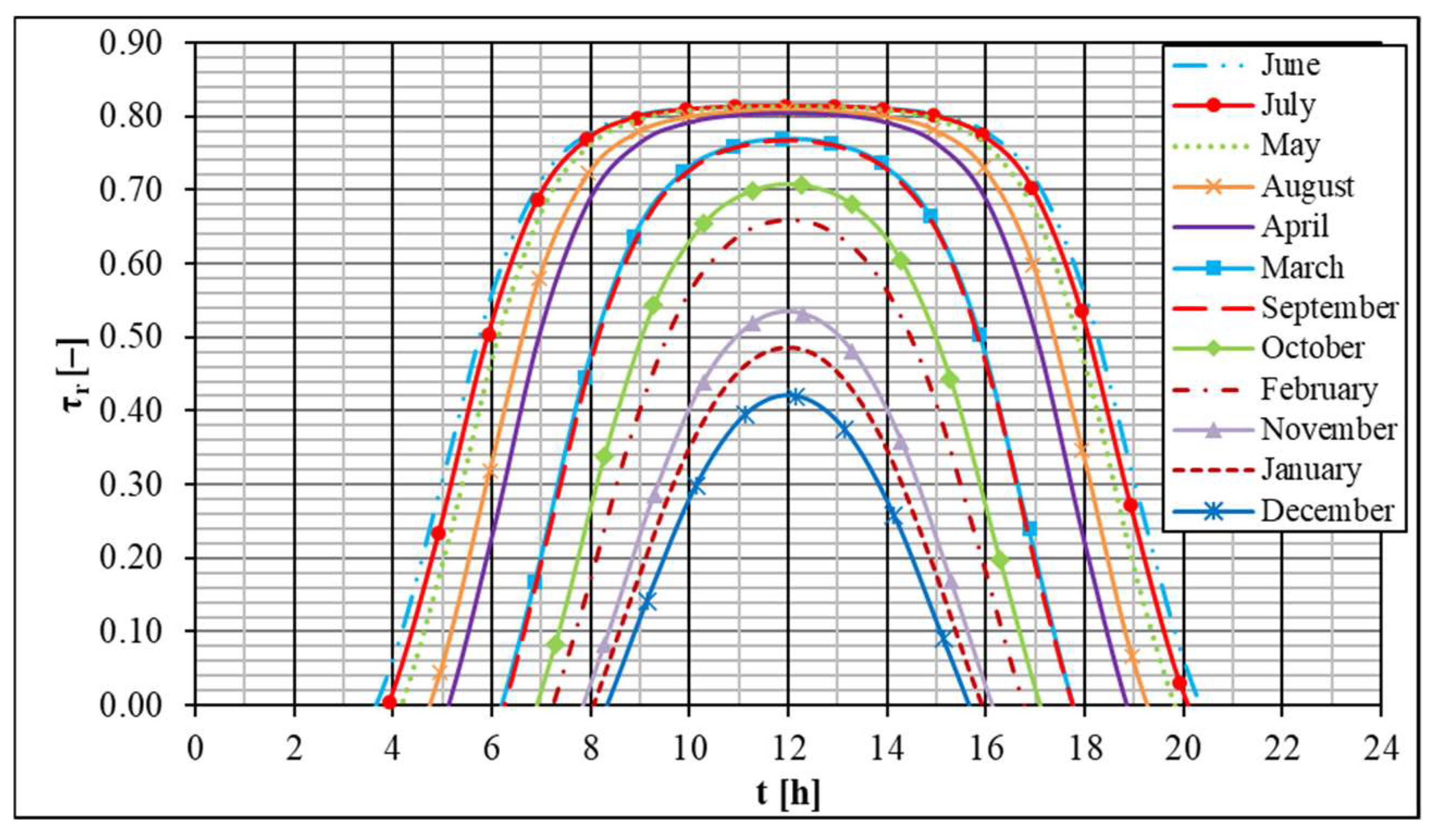
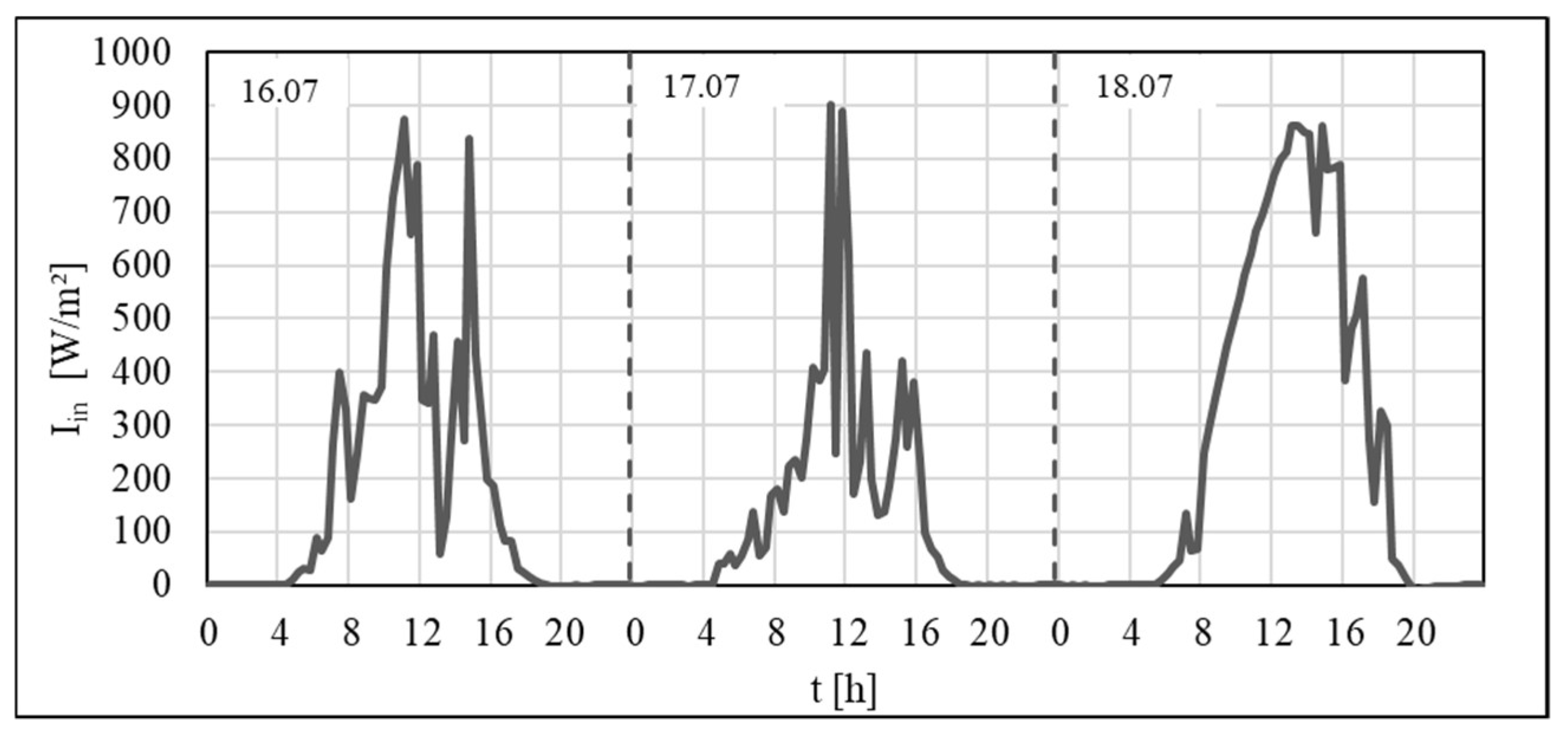
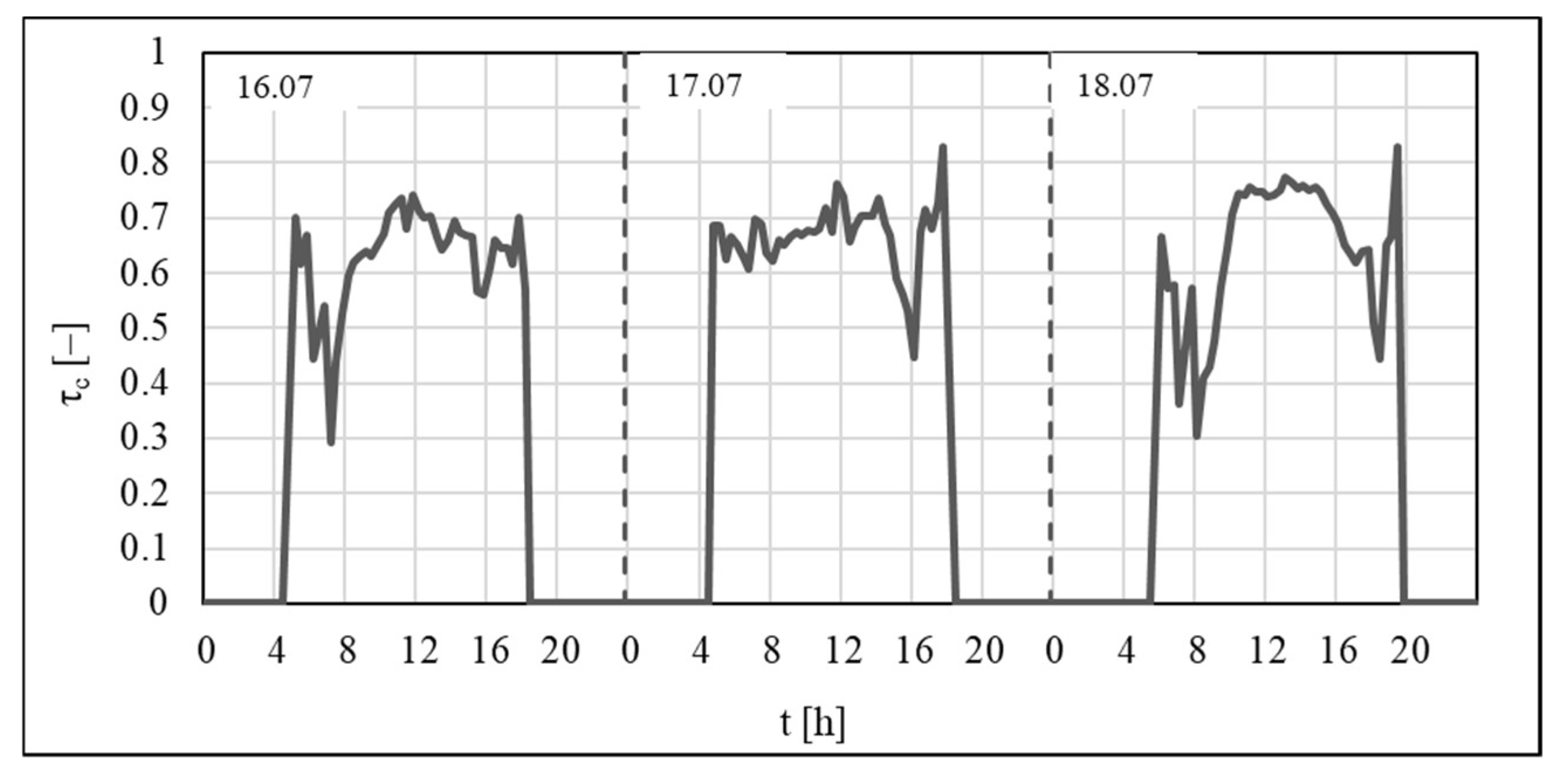
3.2. Calculations Results of Experimentally Determined TST

Experimental research was carried out in the time from the 10th until the 22nd of July 2020. Changes in irradiance were registered every 20 min. Figure 11 shows a change in time of irradiance (subsequent measuring points are shown in the Figure). Measurements were made on the 16th, 17th, and 18th of July 2020. Calculations results for temporary values of TST are presented in Figure 12. Though irradiance changed meaningfully on particular days of research, runs of twenty-four-hour TST changes for the enclosure were of similar character. They were at maximal values at noon and equalled about 0.75. In the morning and in the afternoon, the runs rose respectively fast to their max points and then dropped to the value of zero. Figure 12 shows also the effect of cloudiness, which can significantly diminish the value of TST.

Similar conclusions can be drawn from the long-term research carried out by Čekon et al. [22,23,24,25]. For a polycarbonate sheet, positioned vertically and with a thickness of 10 mm, the measured value of TST equals 0.74, and it is lower than the value of 0.84 declared by producers. The research was carried out according to ASTM G 173 standards, in wavelength ranges from 200 nm to 2500 nm.

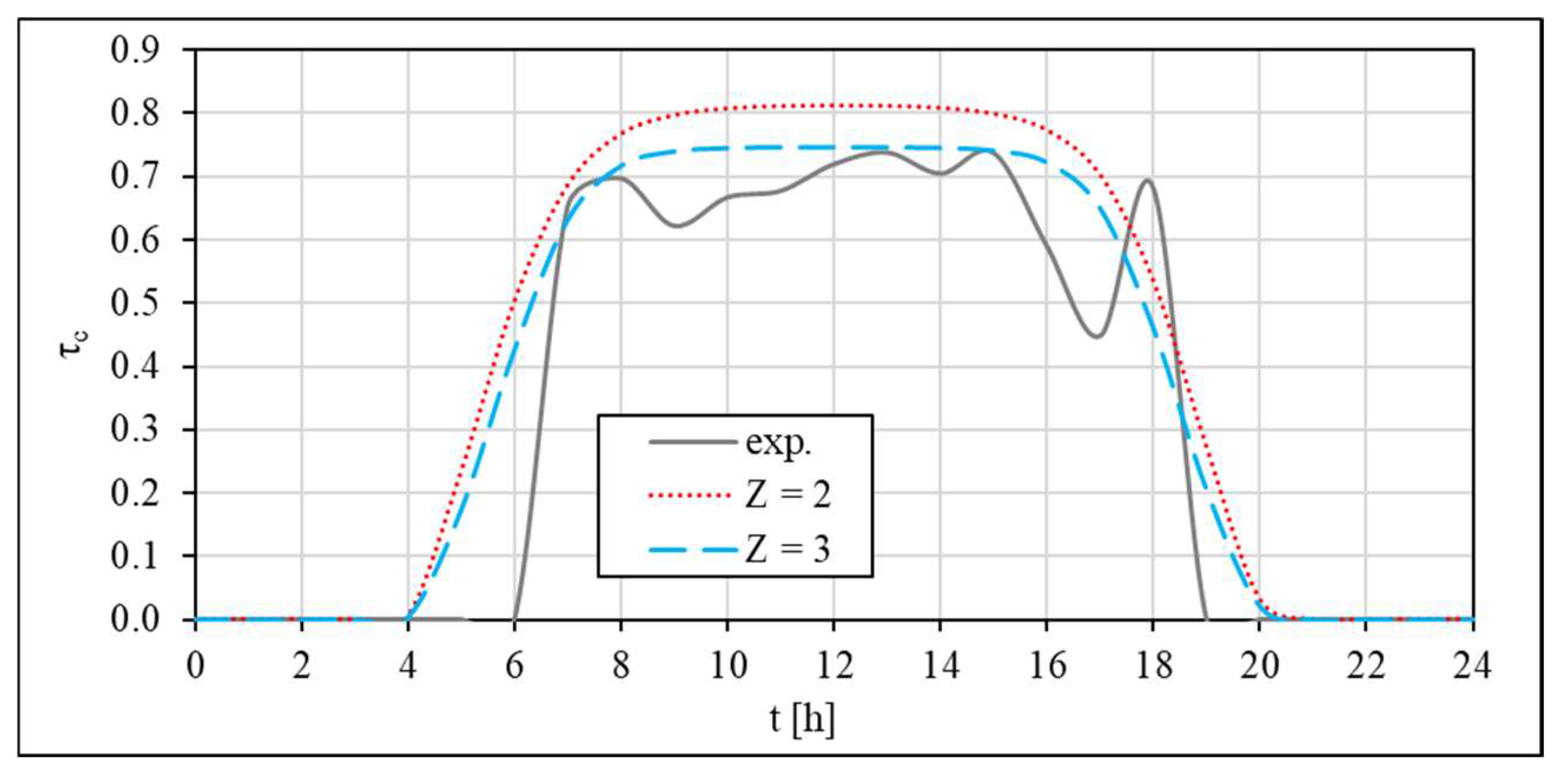
3.3. Comparison of Calculations Results for TST Obtained Theoretically and Experimentally

Figure 13 shows how TST values for the polycarbonate sheet under research change when results from the theoretical model are compared with experimental measurements.

Both the model and experimental research show that the investigated polycarbonate sheet is characterised with an approximately constant value of TST only in the afternoon time and on cloudless days. The method of theoretical calculation, proposed for this parameter, allows us to obtain valid results when it is assumed that the solar rays reflect from three surfaces of polycarbonate. However, it must be noticed that TST calculated in this way has a lower value than the one given in catalogue data.

4. Conclusions

On the basis of theoretical calculations and the conducted experimental research, the following can be stated for the analysed polycarbonate sheet:

(a)

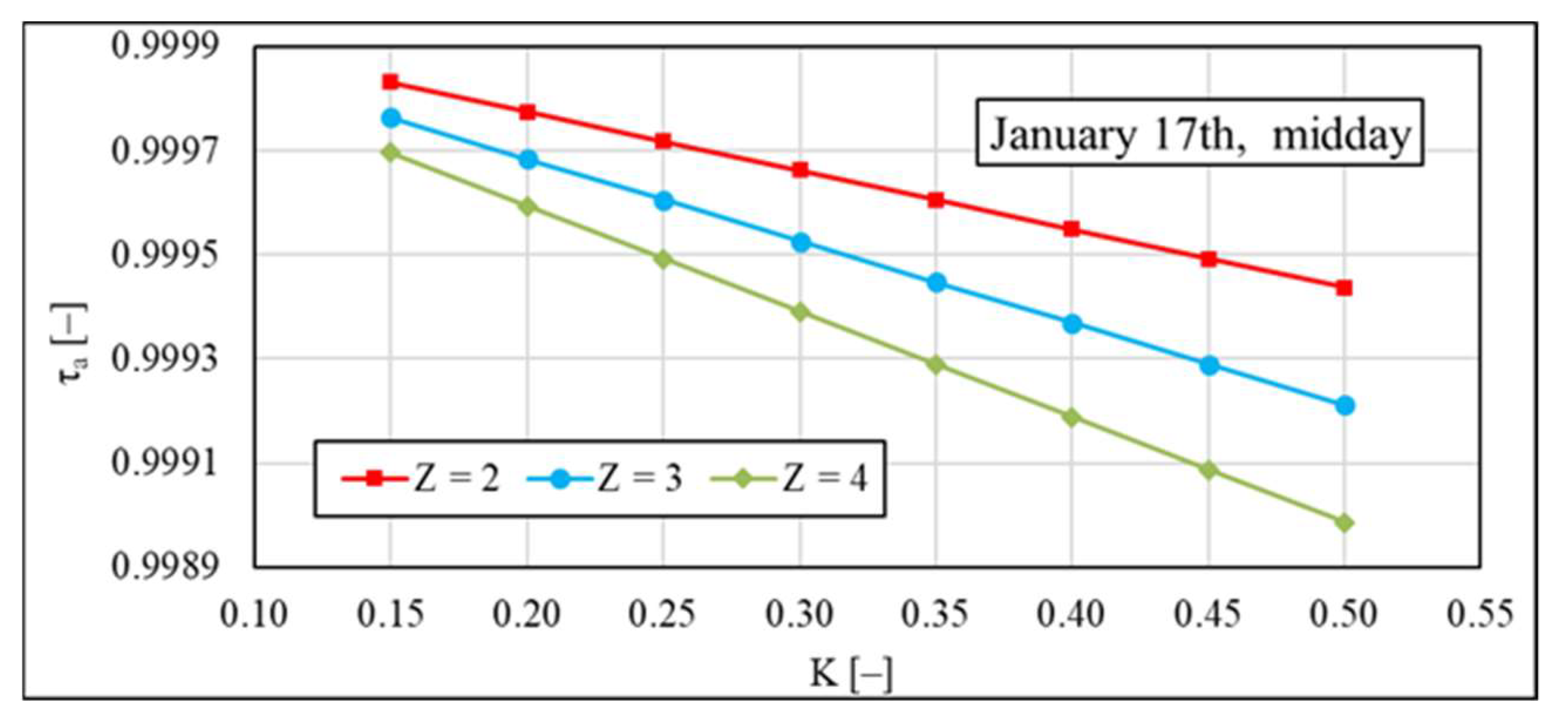
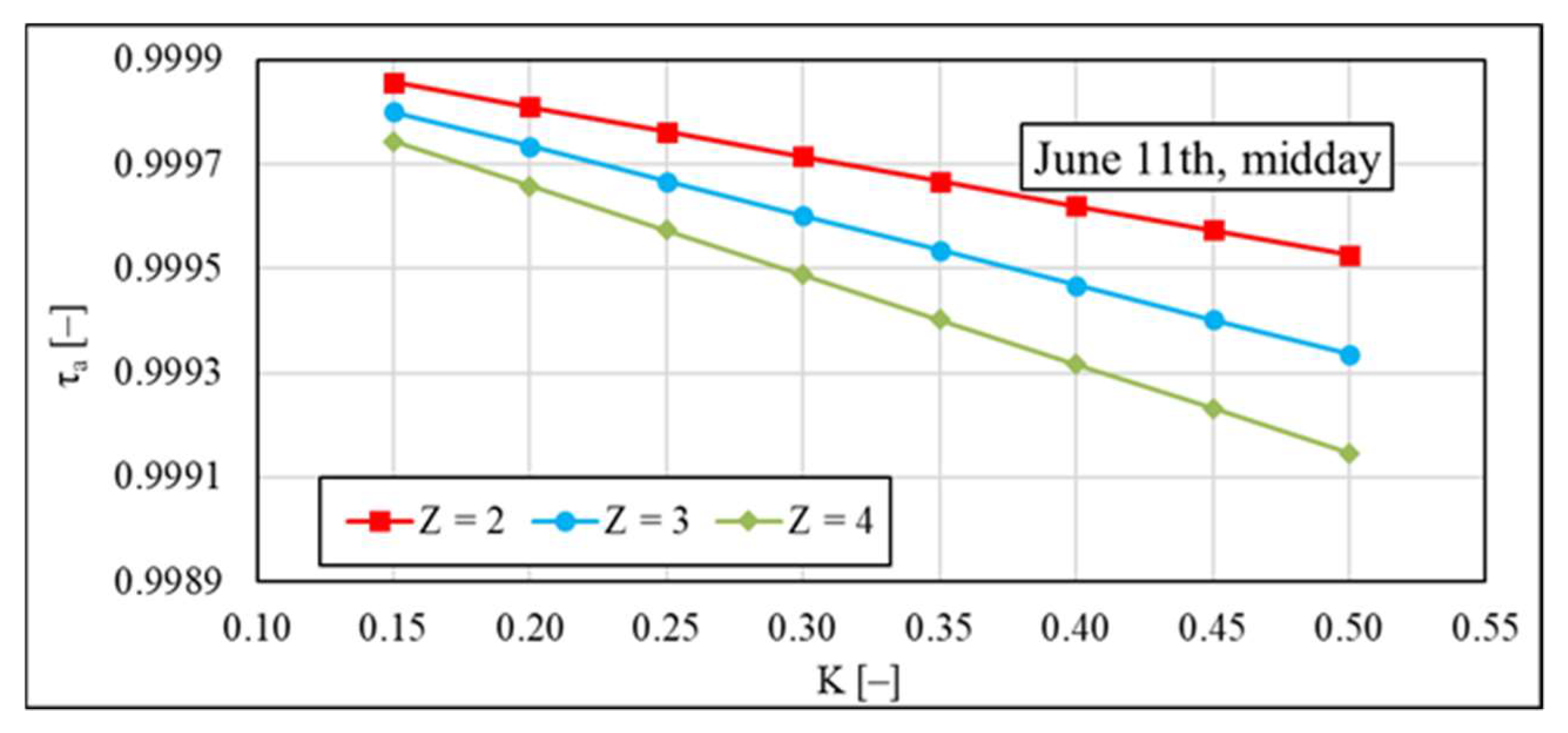
The theoretical value of TST is most of all determined by the value of transmissivity after accounting for multiple reflections of solar rays from the walls of channel; in the case of calculations, it is advisable to assume that solar rays reflect from three surfaces of walls that create the channel; the value of transmissivity after accounting for absorption of solar radiation by polycarbonate is negligible (the approximate value of this last parameter is 0.999).

(b)

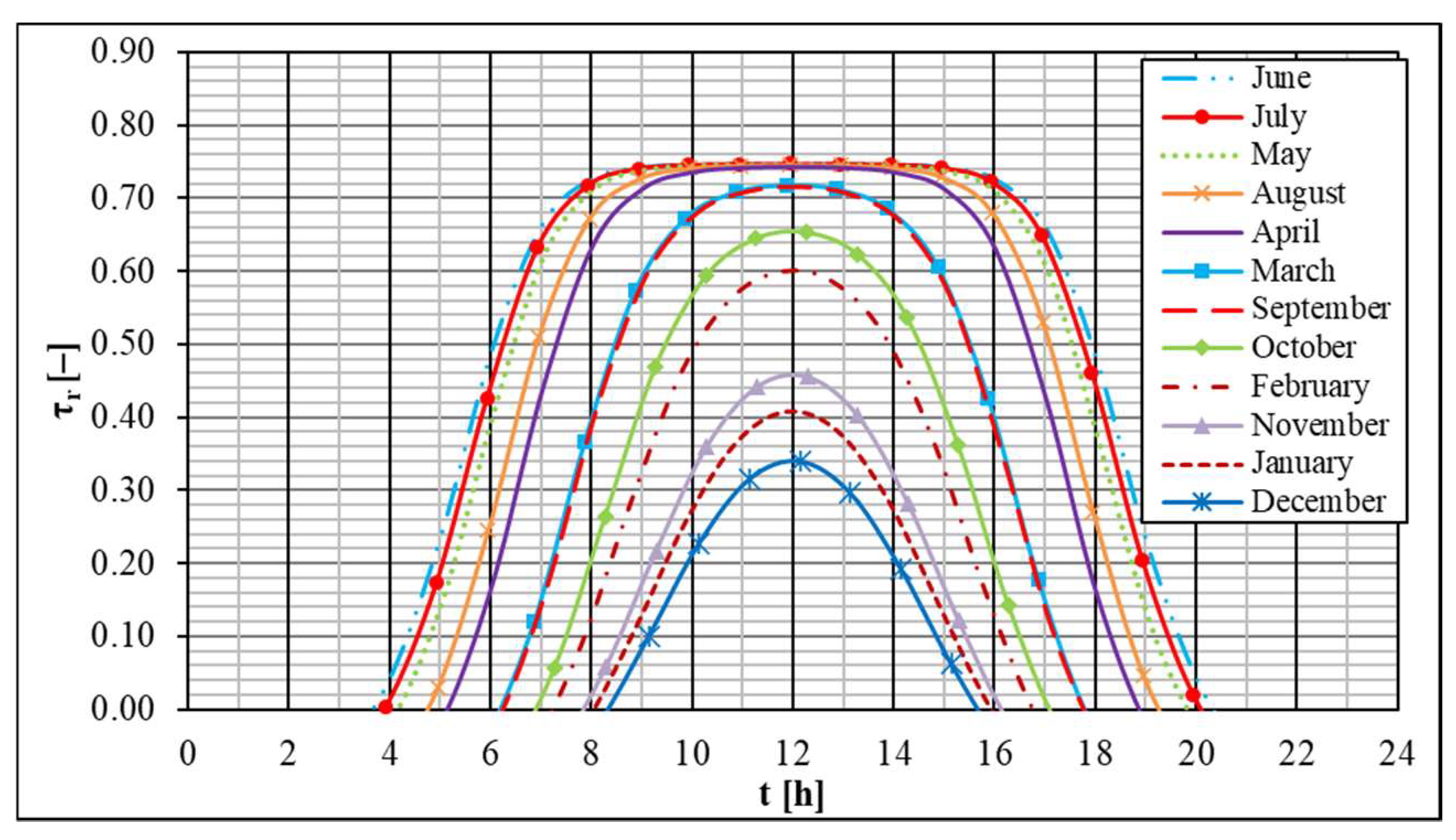
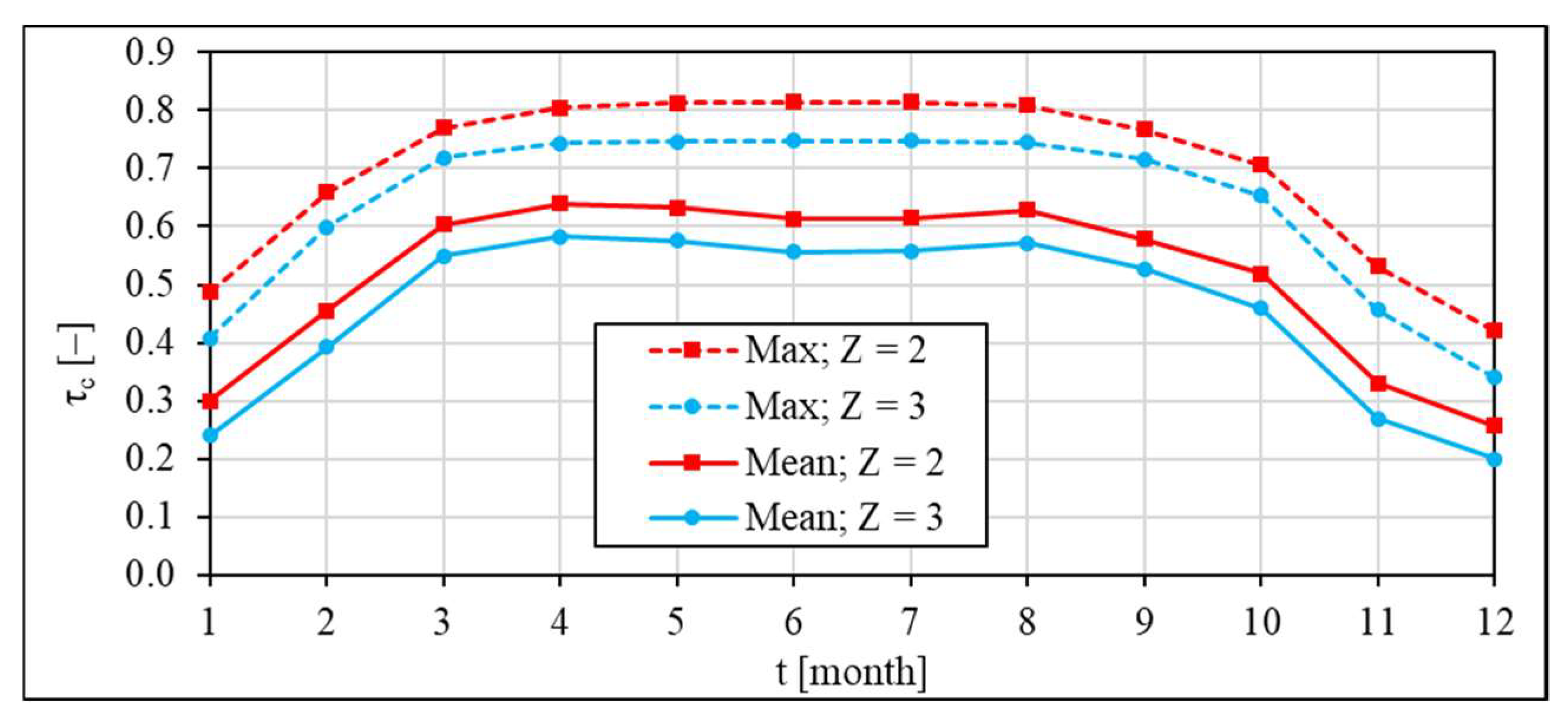
TST changes with both the season of the year and time of day; TST has an approximately constant value in the time about noon; in the morning and in the evening, respectively, fast rise and drop of TST occurs; maximal values of theoretical TST are 0.34 in December and 0.74 in June if the solar rays reflect from three surfaces of walls of the channel; the maximal value of experimental TST is about 0.75 in June; value of TST presented in technical data is constant and equal to 0.82.

(c)

The mean twenty-four-hour theoretical value of TST is about 25% lower than the maximal value obtained for the characteristic day of June; the mean twenty-four-hour theoretical value of TST is about 40% lower than the maximal value obtained for the characteristic day of December; the mean twenty-four-hour theoretical value of TST for the characteristic day of June is about three times higher than the value of this parameter calculated for the characteristic day of December.

(d)

Experimentally determined twenty-four-hour values of TST show similar characteristics of changes independently from irradiance changes on particular days of measurements; the value of TST depends on cloudiness; experimentally calculated and determined values of TST are approximately equal in case of cloudless sky—they are, however, lower than the ones given in product data.

(e)

The theoretical method of TST calculation should be modified. The correction of incident angle resulting from diffusive radiation could be one of the ways to solve this problem. The new model should involve heat transfer by convection too.