Towards Ab-Initio Simulations of Crystalline Defects at the Exascale Using Spectral Quadrature Density Functional Theory
Abstract
:1. Introduction
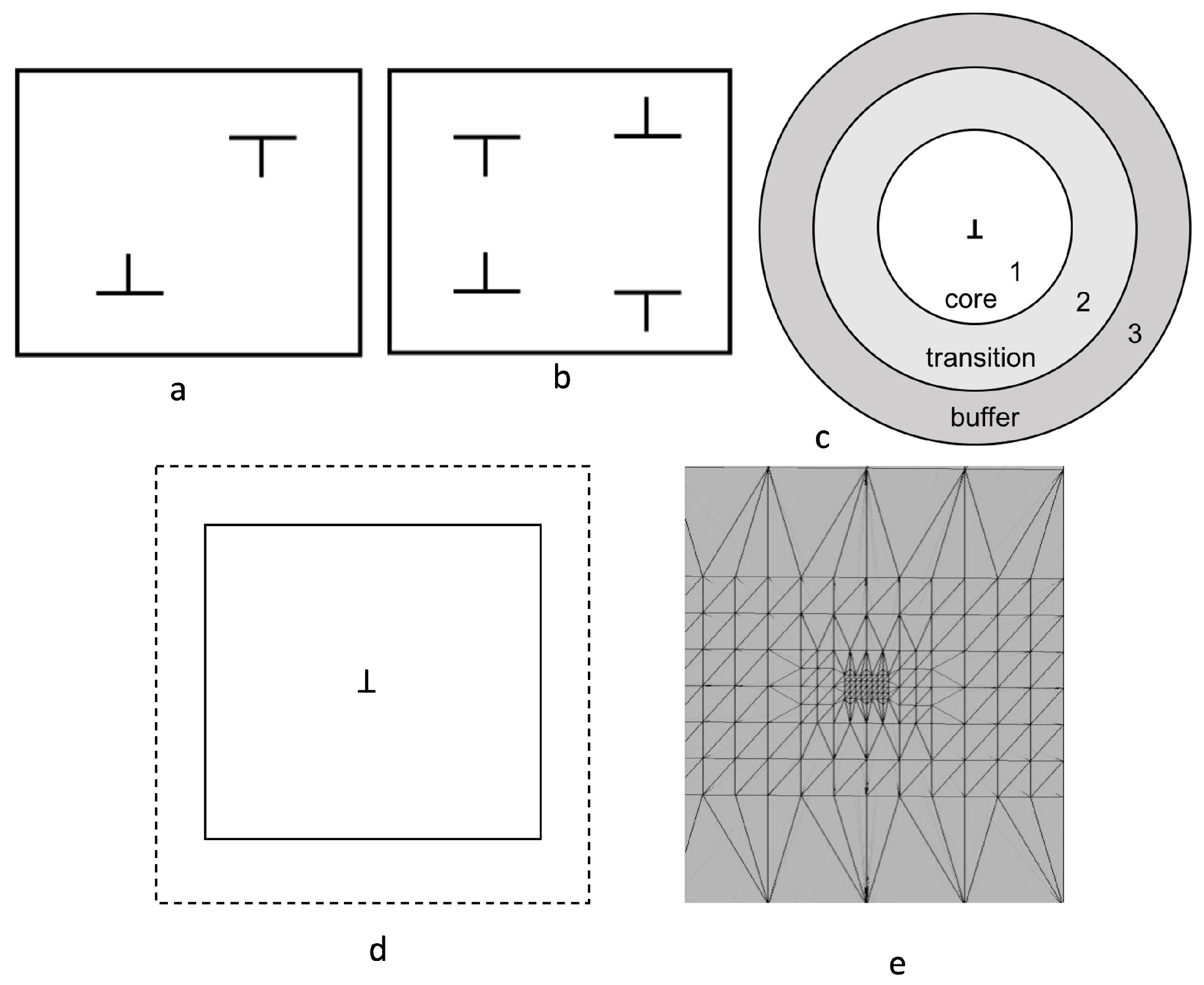
2. Spectral Quadrature
Spatial Coarse Graining
3. Discussion
3.1. Bulk Properties of Elements
3.2. Defects in Magnesium
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Saad, Y.; Tiago, M.L.; Chelikowsky, J.R. Parallel self-consistent-field calculations via Chebyshev-filtered subspace acceleration. Phys. Rev. E 2006, 74, 066704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghosh, S.; Suryanarayana, P. SPARC: Accurate and efficient finite-difference formulation and parallel implementation of Density Functional Theory: Isolated clusters. Comput. Phys. Commun. 2017, 212, 189–204. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Suryanarayana, P. SPARC: Accurate and efficient finite-difference formulation and parallel implementation of Density Functional Theory: Extended systems. Comput. Phys. Commun. 2017, 216, 109–125. [Google Scholar] [CrossRef] [Green Version]
- Motamarri, P.; Das, S.; Rudraraju, S.; Ghosh, K.; Davydov, D.; Gavini, V. DFT-FE—A massively parallel adaptive finite-element code for large-scale density functional theory calculations. Comput. Phys. Commun. 2020, 246, 106853. [Google Scholar] [CrossRef]
- Motamarri, P.; Gavini, V. Subquadratic-scaling subspace projection method for large-scale Kohn–Sham density functional theory calculations using spectral finite-element discretization. Phys. Rev. B 2014, 90, 115127. [Google Scholar] [CrossRef] [Green Version]
- Suryanarayana, P. On spectral quadrature for linear-scaling Density Functional Theory. Chem. Phys. Lett. 2013, 584, 182–187. [Google Scholar] [CrossRef]
- Bowler, D.; Miyazaki, T. O(N) methods in electronic structure calculations. Rep. Prog. Phys. 2012, 75, 036503. [Google Scholar] [CrossRef]
- Ponga, M.; Bhattacharya, K.; Ortiz, M. A sublinear-scaling approach to density-functional-theory analysis of crystal defects. J. Mech. Phys. Solids 2016, 95, 530–556. [Google Scholar] [CrossRef] [Green Version]
- Suryanarayana, P.; Bhattacharya, K.; Ortiz, M. Coarse-graining Kohn–Sham Density Functional Theory. J. Mech. Phys. Solids 2013, 61, 38–60. [Google Scholar] [CrossRef] [Green Version]
- Pratapa, P.P.; Suryanarayana, P.; Pask, J.E. Spectral Quadrature method for accurate O (N) electronic structure calculations of metals and insulators. Comput. Phys. Commun. 2016, 200, 96–107. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Hamel, S.; Bethkenhagen, M.; Pask, J.E.; Suryanarayana, P. Real-space formulation of the stress tensor for O (N) density functional theory: Application to high temperature calculations. J. Chem. Phys. 2020, 153, 034112. [Google Scholar] [CrossRef] [PubMed]
- Ponga, M.; Bhattacharya, K.; Ortiz, M. Large scale ab-initio simulations of dislocations. J. Comput. Phys. 2020, 407, 109249. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Bhattacharya, K. Spectral quadrature for the first principles study of crystal defects: Application to magnesium. J. Comput. Phys. 2022, 456, 111035. [Google Scholar] [CrossRef]
- Rao, S.; Hernandez, C.; Simmons, J.; Parthasarathy, T.; Woodward, C. Green’s function boundary conditions in two-dimensional and three-dimensional atomistic simulations of dislocations. Philos. Mag. A 1998, 77, 231–256. [Google Scholar] [CrossRef]
- Trinkle, D.R. Lattice Green function for extended defect calculations: Computation and error estimation with long-range forces. Phys. Rev. B 2008, 78, 014110. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, J.; Gehlen, P.; Hoagland, R.; Hirth, J. Flexible boundary conditions and nonlinear geometric effects in atomic dislocation modeling. J. Appl. Phys. 1978, 49, 3890–3897. [Google Scholar] [CrossRef]
- Suryanarayana, P.; Pratapa, P.P.; Sharma, A.; Pask, J.E. SQDFT: Spectral Quadrature method for large-scale parallel O (N) Kohn–Sham calculations at high temperature. Comput. Phys. Commun. 2018, 224, 288–298. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Lazicki, A.; Militzer, B.; Yang, L.H.; Caspersen, K.; Gaffney, J.A.; Däne, M.W.; Pask, J.E.; Johnson, W.R.; Sharma, A.; et al. Equation of state of boron nitride combining computation, modeling, and experiment. Phys. Rev. B 2019, 99, 165103. [Google Scholar] [CrossRef] [Green Version]
- Gavini, V.; Bhattacharya, K.; Ortiz, M. Vacancy clustering and prismatic dislocation loop formation in aluminum. Phys. Rev. B 2007, 76, 180101. [Google Scholar] [CrossRef] [Green Version]
- Knap, J.; Ortiz, M. An analysis of the quasicontinuum method. J. Mech. Phys. Solids 2001, 49, 1899–1923. [Google Scholar] [CrossRef] [Green Version]
- Teh, Y.S.; Ghosh, S.; Bhattacharya, K. Machine-learned prediction of the electronic fields in a crystal. Mech. Mater. 2021, 163, 104070. [Google Scholar] [CrossRef]
- Fiolhais, C.; Perdew, J.P.; Armster, S.Q.; MacLaren, J.M.; Brajczewska, M. Dominant density parameters and local pseudopotentials for simple metals. Phys. Rev. B 1995, 51, 14001–14011. [Google Scholar] [CrossRef]
- Huang, C.; Carter, E.A. Transferable local pseudopotentials for magnesium, aluminum and silicon. Phys. Chem. Chem. Phys. 2008, 10, 7109–7120. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976; Volume 8. [Google Scholar]
- Koster, W.; Franz, H. Poisson’s ratio for metals and alloys. Metall. Rev. 1961, 6, 1–56. [Google Scholar] [CrossRef]
- Tamadon, A.; Pons, D.J.; Clucas, D. Flow-Based Anatomy of Bobbin Friction-Stirred Weld; AA6082-T6 Aluminium Plate and Analogue Plasticine Model. Appl. Mech. 2020, 1, 3–19. [Google Scholar] [CrossRef] [Green Version]
- Du Plessis, A.; Yadroitsava, I.; Yadroitsev, I. Effects of defects on mechanical properties in metal additive manufacturing: A review focusing on X-ray tomography insights. Mater. Des. 2020, 187, 108385. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhattacharya, K. Influence of thermomechanical loads on the energetics of precipitation in magnesium aluminum alloys. Acta Mater. 2020, 193, 28–39. [Google Scholar] [CrossRef] [Green Version]




| Element | Crystal Structure | Method | Lattice Constant (a.u.) | Bulk Modulus (GPa) |
|---|---|---|---|---|
| Li | BCC | SQ [11] | 6.87 | 10.0 |
| DFT [24] | 6.77 | 14.0 | ||
| Expt. [24] | 6.77 | 13.3 | ||
| Na | BCC | SQ [11] | 8.01 | 5.0 |
| DFT [24] | 8.21 | 7.1 | ||
| Expt. [24] | 8.21 | 7.3 | ||
| Mg | HCP | SQ [10] | 5.866, 1.626 | 38.75 |
| SQ [15] | 6.043, 1.629 | 38.50 | ||
| DFT [25] | 5.877, 1.624 | 38.40 | ||
| Expt. [26,27] | 6.066, 1.623 | 35.40 |
| Isolated Defects | |||
|---|---|---|---|
| Formation Energy (eV) | |||
| Vacancy | 0.846 | ||
| Al solute | 25.756 | ||
| Defect Pairs | |||
| Nearest Neighbor | Formation Energy (eV) This Work | Binding Energy (eV) Ref. [15] | |
| Divacancy | 1 | 1.565 | 0.127 |
| 2 | 1.596 | 0.195 | |
| 3 | 1.627 | 0.064 | |
| 4 | 1.659 | 0.033 | |
| 5 | 1.659 | 0.033 | |
| 6 | 1.659 | 0.033 | |
| solute-vacancy | 1 | 25.956 | 0.254 |
| 2 | 26.583 | 0.195 | |
| 3 | 26.583 | 0.206 | |
| 4 | 26.722 | 0.125 | |
| 5 | 26.722 | 0.125 | |
| 6 | 26.722 | 0.125 | |
| solute-solute | 1 | 1.066 | 0.238 |
| 2 | 1.081 | 0.223 | |
| 3 | 1.084 | 0.219 | |
| 4 | 1.112 | 0.191 | |
| 5 | 1.134 | 0.169 | |
| 6 | 1.166 | 0.138 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, S. Towards Ab-Initio Simulations of Crystalline Defects at the Exascale Using Spectral Quadrature Density Functional Theory. Appl. Mech. 2022, 3, 1080-1090. https://doi.org/10.3390/applmech3030061
Ghosh S. Towards Ab-Initio Simulations of Crystalline Defects at the Exascale Using Spectral Quadrature Density Functional Theory. Applied Mechanics. 2022; 3(3):1080-1090. https://doi.org/10.3390/applmech3030061
Chicago/Turabian StyleGhosh, Swarnava. 2022. "Towards Ab-Initio Simulations of Crystalline Defects at the Exascale Using Spectral Quadrature Density Functional Theory" Applied Mechanics 3, no. 3: 1080-1090. https://doi.org/10.3390/applmech3030061





