Quantum-Based Maximum Likelihood Detection in MIMO-NOMA Systems for 6G Networks

Abstract

As wireless networks advance toward the Sixth Generation (6G), which will support highly heterogeneous scenarios and massive data traffic, conventional computing methods may struggle to meet the immense processing demands in a resource-efficient manner. This paper explores the potential of quantum computing (QC) to address these challenges, specifically by enhancing the efficiency of Maximum-Likelihood detection in Multiple-Input Multiple-Output (MIMO) Non-Orthogonal Multiple Access (NOMA) communication systems, an essential technology anticipated for 6G. The study proposes the use of the Quantum Approximate Optimization Algorithm (QAOA), a variational quantum algorithm known for providing quantum advantages in certain combinatorial optimization problems. While current quantum systems are not yet capable of managing millions of physical qubits or performing high-fidelity, long gate sequences, the results indicate that QAOA is a promising QC approach for radio signal processing tasks. This research provides valuable insights into the potential transformative impact of QC on future wireless networks. This sets the stage for discussions on practical implementation challenges, such as constrained problem sizes and sensitivity to noise, and opens pathways for future research aimed at fully harnessing the potential of QC for 6G and beyond.

1. Introduction

Wireless communication networks in the upcoming Sixth Generation (6G) era will have to meet increasingly challenging requirements, such as full geographical coverage, high-precision geolocation, and rapid update rates. While Fifth Generation (5G), with millimeter Wave (mmW) technology, can achieve Gigabits-per-second (Gbps) transmission data rates, 6G aims for Terabit-per-second (Tbps) transmission data rates to support applications in the vein of high-quality three-dimensional (3D) video, Virtual Reality (VR), and a combination of VR and Augmented Reality (AR). To address these requirements, advanced techniques like Multiple-Input Multiple-Output (MIMO) and Non-Orthogonal Multiple Access (NOMA) will be necessary [1]. Additionally, the intersection of Quantum Computing (QC) and 6G could lead to synergies and innovative applications: variable radio resource allocation, the optimization of communication systems, advanced signal processing, and others [2].

The fundamental idea of employing multi-antenna base stations to cater to multiple users dates back to the late 1980s. MIMO is a highly promising technology for achieving enhanced data rates by exploiting spatial diversity. This significantly enhances the signal quality, capacity, and reliability of wireless links when compared to conventional Single Input Single Output (SISO) [3], all while ensuring a reasonable Bit Error Rate (BER) and entering the most significant standards in the past decades, including IEEE 802.11n (WiFi) and Long Term Evolution (LTE) [4]. Moreover, MIMO techniques are one of the critical technologies in 5G and beyond (e.g., 6G), and they increase the number of antennas at the Base Station (BS) end [5].

On the other hand, the previous generations of networks have employed orthogonal multiple access (OMA) schemes such as Frequency Division Multiple Access (FDMA) in First Generation (1G) of wireless mobile telecommunications technology, Time Division Multiple Access (TDMA) in Second Generation (2G), Code Division Multiple Access (CDMA) in Third Generation (3G), and Orthogonal Frequency Division Multiple Access (OFDMA) in Fourth Generation (4G). In OMA, users can exploit orthogonal communication resources within a specific time slot, frequency band, or code to avoid multiple access interference [6]. In contrast, NOMA has been recognized as a promising technology to improve the spectral efficiency of mobile communication networks significantly, allowing the simultaneous transmission of multiple user data in the same frequency carrier and time domain [7].

The joint operation of MIMO-NOMA techniques can offer significant improvements in Quality of Service (QoS), Energy Efficiency (EE), and Spectral Efficiency (SE) for future 6G users. Furthermore, it improves fairness among users, boosts throughput, and enhances robustness to channel variations. Many detection techniques have been developed for MIMO-NOMA [8,9], all of them at their core based on refinements of well-known techniques like Zero Forcing (ZF) [10], Minimum Mean-Square Error (MMSE) [11], and Successive Interference Cancellation (SIC) [12], achieving near-optimal performance at low computational complexity. On the contrary, the Maximum-Likelihood Detector (MLD) problem, assuming an uncoded system, is optimal from the BER performance viewpoint because it explores all possible solutions (exhaustive search) in a constellation of symbols to find the transmitted symbol. However, MLD is typically considered a Non-Deterministic Polynomial-Time (NP-hard) problem [13] for conventional (classic) computers because of the discrete nature of the signal constellation [14]. While exhaustive search can be employed for small-scale problems, it becomes impractical for systems using high-order spatial diversity utilization schemes like massive MIMO. In practice, various suboptimal detectors have been developed as approximations to the MLD, which can be broadly categorized as either speed-up versions, such as Sphere Decoding (SD) [15] that are still exponentially complex, or detectors that trade off remarkable BER degradations for polynomial complexity, like Linear Minimum Mean Square Error (LMMSE) [16], Matched Filter (MF) [17], etc.

In 6G scenarios, wireless systems might rely on extensive massive MIMO configurations featuring a larger number of antennas for transmission and reception. However, due to the large amount of data to be processed, the computational complexity of signal processing in such systems [18], specifically detection, will remain a significant challenge [19]. Motivated by this, this work focuses on an uplink MIMO-NOMA scenario, where each mobile User Equipment (UE) transmits its signal to the BS applying Superposition Coding (SC) [20]. Then, the receiver, at BS, needs to distinguish the symbols of each user from the superposed symbol.

An MLD that leverages QC to harness the unique properties of quantum mechanics, such as superposition and entanglement, is proposed. These characteristics would enable the acceleration of specific calculations that would pose significant computational challenges for classical computers. The Quantum Approximate Optimization Algorithm (QAOA) and IBM Quantum computers have been used to implement the detector MIMO-NOMA to solve the combinatorial optimization problem derived from the MLD. Moreover, under the assumption that QC resides in the Noisy Intermediate-Scale Quantum (NISQ) era, we scrutinize and deliberate on the potential “quantum advantage” and the intricacies of QAOA for this particular use case, considering that it can be extended to massive MIMO systems.

The rest of the paper is organized as follows: Section 2 presents the state of the art in QC approaches to NOMA and MIMO. Section 3 gives a brief overview of QC and its main characteristics. Section 4 explains the QAOA approach to implement the quantum MLD for the MIMO-NOMA uplink. Section 5 provides results for the BER, derived from the classical approach of the QAOA running in a quantum simulator and in a real quantum computer. Finally, Section 6 draws the main conclusions of this work.

2. Related Works

2.1. Non-Orthogonal Multiple Access

Lately, there has been growing interest in utilizing quantum techniques to overcome some of the complexity-derived limitations of future 6G communication systems [21], among them being the operation of multi-user versions of digital modulation schemes, both orthogonal and non-orthogonal [22]. Applying quantum methods aims to perform the strategic calculations needed for these schemes but at a much faster pace than classical computation.

Some approaches in the literature are inspired by quantum mechanics principles but do not directly involve QC. For example, in [23], a Quantum Evolutionary Algorithm (QEA) is proposed to solve user pairing in NOMA systems. This method simulates quantum-related concepts like superposition within population-based meta-heuristic optimization algorithms. It uses evolutionary computation methods with a genetic approach to find the optimal user pairing for the highest sum rate. While this approach shows improvement over random pairing, the simulations rely on classical computational resources, such as the Monte Carlo method.

In contrast, recent methodologies directly address the challenge of testing algorithms for NOMA schemes in practical QC environments. For example, ref. [22] details the implementation of NOMA signal detection using Quantum Annealing (QA) on D-WAVE’s development platform. QA aids in discovering the global minimum of a specified cost function, facilitating the maximum-likelihood estimation of each signal at the NOMA receiver. While this process is computationally intensive on classical computers, restructuring the computation and using QA to infer the better-transmitted symbol candidate can enhance the performance of traditional NOMA receivers, mitigating issues associated with SIC in such scenarios. Similarly, ref. [24] employs QA to optimize the MLD for NOMA networks as an alternative to SIC. Notably, despite the QA-assisted MLD demonstrating the same BER performance as a brute-force constellation search, the results indicate a longer execution time. Additionally, parallelization is recommended to expedite the QA execution process. Upon closer examination, this suggests the importance of utilizing all available qubits, as the QA execution time remains independent of the number of qubits being occupied.

2.2. Multiple-Input Multiple-Output

The integration of MIMO technology into the quantum domain began with the implementation of a free-space MIMO system in a Quantum Key Distribution (QKD) scheme as demonstrated in [25], sparking significant research interest and leading to numerous publications on novel free-space QKD schemes [26]. A quantum MIMO communication scheme using quantum teleportation with triplet states was later proposed in [27], enabling the transmission of n-qubit signals through MIMO channels using quantum diversity techniques. More recently, a quantum MIMO architecture for wireless communications was introduced in [28], establishing a theoretical foundation for conveying classical information through quantum states. In addition, research has addressed the complexity of MIMO systems, such as in [29], which presents a quantum algorithm for optimizing power allocation in MIMO by leveraging quantum concepts like entanglement and superposition. Furthermore, ref. [30] proposes a quantum strategy, the Constrained Quantum Optimization Algorithm (CQOA), to minimize transmit power in MIMO systems while meeting users’ bit-rate constraints.

On the other hand, QA and the QAOA are considered exceptional cases, where the problem of minimizing the energy of a quantum state by applying a combination of two Hamiltonians is common to both approaches. Searching the combination of two Hamiltonians prepares the ground state of one of the Hamiltonians as quickly and accurately as possible. While QA smoothly interpolates between the two Hamiltonians, QAOA applies one or the other in sequence.

While implementing the gradient descent method of QA on the identical experimental setups to QAOA, such as IBM Quantum Experience, poses challenges, the hardware and setups offered by D-Wave (which are not considered universal quantum computers but “quantum annealers”) have demonstrated the feasibility of using a similar gradient-based method for optimization. There are recent works that deal with a quantum MLD using QA, such as [31,32]. In [31], the authors discuss the problem of meeting the growing demand for wireless capacity from users using MIMO wireless physical layer techniques, highlighting that algorithms for higher performance systems are computationally demanding and become a limiting factor for wireless capability. To solve this, the authors propose QuAMax, a new MIMO centralized radio access network design implemented on a 2031-qubit D-Wave 2000Q quantum annealer, and perform experiments on real and synthetic MIMO channel traces. Their results show that 10 $\mu s$ of compute time on the 2000Q is enough for 48 users, 48 AP antenna Binary Phase-Shift Keying (BPSK) communication at 20 dB Signal to Noise Ratio (SNR) with a BER of ${10}^{-6}$, and a 1500-byte frame error rate of ${10}^{-4}$. In [32], a comparative performance study is presented, focusing on the D-Wave annealer to handle large-scale optimization problems such as the Quadratic Unconstrained Binary Optimization (QUBO) formulation derived from Maximum Likelihood Channel Decoder problems for MIMO scenarios in Centralized-Radio Access Network (RAN) architectures, which are challenging due to the exponential increase in the solution space with problem sizes. The authors compare the performance of the novel D-Wave Advantage QA device to the D-Wave 2000Q. The researchers extended previous work to large MIMO problems with more complex modulations and larger MIMO antenna array sizes and reported on the improvements and limiting factors they uncover.

Likewise, QAOA empowers gate-model universal quantum computers to address combinatorial optimization problems similar to those tackled by the D-Wave-style QA. Furthermore, opting for QAOA on a gate-model quantum computer offers a distinct advantage over utilizing QA. With QAOA, precision can be increased arbitrarily, whereas QA will only converge to a solution with a probability of 1 as time t approaches infinity, rendering it impractical. In addition, if t is too long, QA is likely not to find the solution, as the probability is not monotonic. In this sense, [33], a paper on fair sampling, has already demonstrated that running QA on a 5-qubit system can only find two of the three possible states. Other researchers argue that it is still uncertain which approach (QA or QAOA) is more effective. The authors of [34] state that classical computers require a vast amount of computation time and memory to simulate the time evolution of an N-spin system using specific algorithms. On the contrary, QAOA offers an advantage since the necessary time evolution can be carried out on a quantum computer and experimentally implemented on a real system as is presented in this work.

3. Quantum Computing

Quantum computing is a field of computer science that explores the principles of quantum mechanics to develop new methods of processing information. Unlike traditional classical computers that use bits to represent and manipulate data as 0 or 1, quantum computers use quantum bits or qubits. Qubits can exist in a superposition of both 0 and 1 states simultaneously, forming a linear combination of those basis states [35]:

$$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle ,$$

(1)

where $\alpha$ and $\beta$ are complex numbers. Measuring a qubit in a superposition state involves collapsing to one of its basis states ($|0\rangle$ or $|1\rangle$). The probability of having $|0\rangle$ or $|1\rangle$ as a result of the measure is known by ${\left|\alpha \right|}^2$ and ${\left|\beta \right|}^2$, respectively.

This ability of qubits to be in multiple states, known as superposition, allows quantum computers to explore many possible solutions to a problem in parallel. Quantum parallelism is a crucial aspect of QC, enabling the exploration of large solution spaces simultaneously and offering the potential for solving complex problems more efficiently than classical computers. The entanglement phenomenon links the states of multiple qubits, enabling them to be correlated so that changes in one qubit instantaneously affect the others no matter the distance between them. This property is used in quantum algorithms to perform complex calculations efficiently.

QC has the potential to revolutionize various fields and has boosted interest worldwide in different areas, including cryptography, optimization, drug discovery, material science, and machine learning. Wireless communications, especially in the upcoming technologies, 6G and beyond, are not far from this interest. Nevertheless, the development of quantum computers requires challenging efforts that involve overcoming various technical, theoretical, and practical obstacles. Qubits are highly sensitive to external factors and tend to lose their quantum properties, a phenomenon known as decoherence. The development of error correction codes to mitigate the impact of noise in quantum devices is defiant, and implementing them in quantum hardware is even more challenging. Building and maintaining the physical infrastructure for QC, including cooling systems that operate at extremely low temperatures, is a substantial technical challenge and has a high environmental impact due to the energy consumption needed to support the required temperature. These and many other examples influence the scalability of quantum computers in terms of the qubits available to accomplish significant results, but despite these challenges, there has been significant progress in the field of QC, and researchers are actively working to address these issues.

4. Quantum Maximum-Likelihood Detector for MIMO-NOMA

In general, NOMA schemes can be classified into power-domain multiplexing and code-domain multiplexing. In power–domain multiplexing, users are assigned different power coefficients according to channel conditions to achieve high system performance. In code-domain multiplexing, different users are allocated different codes and multplexed over the same time–frequency resources, such as Multiuser Shared Access (MUSA), Sparse Code Multiple Access (SCMA), and Low-Density Spreading (LDS). In addition, there are other NOMA schemes such as Pattern Division Multiple Access (PDMA) [36] and Bit Division Multiplexing (BDM) [37].

NOMA can be applied in downlink and uplink scenarios. Figure 1 provides an example of both schemes for two users, showing the main differences, where each mobile user transmits its signal at the same time and in the same frequency band to the BS applying SC, and at the BS, SIC iterations are carried out to detect the signal of mobile users in the case of uplink and vice versa in the downlink. The BS transmits the data, and the receivers (users) decode its data.

In the NOMA uplink, the signal received at BS can be written as

$$\mathbf{y}=\sum _{k=1}^K{h}_k\sqrt{a_{k}P}{s}_k+n,$$

(2)

where $s_k$ is the transmitted symbol of the user k, $h_k$ is the channel gain of the link between the user k and the BS, $0<a_k<1$ is the power allocation, P is the maximum transmission power, n is the Additive White Gaussian Noise (AWGN) with zero mean, and ${\sigma }_n^2$ is the power density.

One of the primary prerequisites for power domain NOMA is the allowance for distinct power levels assigned to each information signal. This becomes particularly relevant in the uplink scenario, where users are positioned at varying distances from the BS. In such cases, the BS receiver must be capable of distinguishing individual user symbols within the amalgamated symbol $\mathbf{y}$. The most commonly employed technique for achieving this is SIC, which entails decoding the signal of the strongest user first, treating the other users as interference. Following this, the decoded user is removed from the received signal to facilitate the decoding of the next user. This iterative process continues until the last user’s information is successfully decoded. It is important to note that an error floor phenomenon can arise during this signal recovery process, where the remaining lower-power signals are managed as interference.

Even though SIC is the leading candidate to be used in NOMA systems for the next generations, it has drawbacks that make exploring other solutions to decode NOMA interesting. The main disadvantages are as follows [22]:

• If an error is made while decoding one iteration, it propagates through other successive ones.
• All the channel information should be known at the receiver to equalize.
• Since the decoding is iterative, complexity increases with the number of users, causing latency problems in some cases.
• Differences in the power levels of each signal should be large enough for successful detection.

All of these limitations become more severe as the number of users increases. Therefore, the MLD is presented in the literature as an alternative to overcome some of its disadvantages.

On the flip side, Figure 2 shows an excerpt of a MIMO system. As depicted, the transmitter and receiver are equipped with several antennas. The signal received in a MIMO system can be formulated as

$$\mathbf{Y}=\mathbf{H}\mathbf{s}+\mathbf{N},$$

(3)

where y∈${\mathbb{C}}^{Nx1}$ is the received signal, $\mathbf{H}$∈${\mathbb{C}}^{NxM}$ is the channel matrix, s∈${\mathbb{C}}^{Mx1}$ is a transmitted symbol vector, and N∈${\mathbb{C}}^{Nx1}$ is the AWGN.

As all variables are complex-valued, throughout the present document, to avoid handling complex-valued variables, (3) is converted to its equivalent real-valued representation by using the following convention:

$$\overline{\mathbf{Y}}=\overline{\mathbf{H}}\overline{\mathbf{s}}+\overline{\mathbf{N}},$$

(4)

where

$$\overline{\mathbf{Y}}=\left[\begin{array}{c}\Re \left(\mathbf{y}\right)\\ \Im \left(\mathbf{y}\right)\end{array}\right],\overline{\mathbf{s}}=\left[\begin{array}{c}\Re \left(\mathbf{s}\right)\\ \Im \left(\mathbf{s}\right)\end{array}\right],\overline{\mathbf{n}}=\left[\begin{array}{c}\Re \left(\mathbf{n}\right)\\ \Im \left(\mathbf{n}\right)\end{array}\right],$$

(5)

$$\overline{\mathbf{H}}=\left[\begin{array}{cc}\Re \left(\mathbf{H}\right)& -\Im \left(\mathbf{H}\right)\\ \Im \left(\mathbf{H}\right)& \Re \left(\mathbf{H}\right)\end{array}\right]$$

(6)

and $\Re (.)$ and $\Im (.)$ are defined as the real and imaginary parts of a complex matrix or vector, respectively.

MIMO systems can turn multi-path propagation and multi-path delay spreads into a benefit for the receiver. The key advantage of MIMO systems is the many orders of magnitude of the SNR at no extra bandwidth. However, non-negligible software and hardware processing complexity is added on both sides (transmitter and receiver).

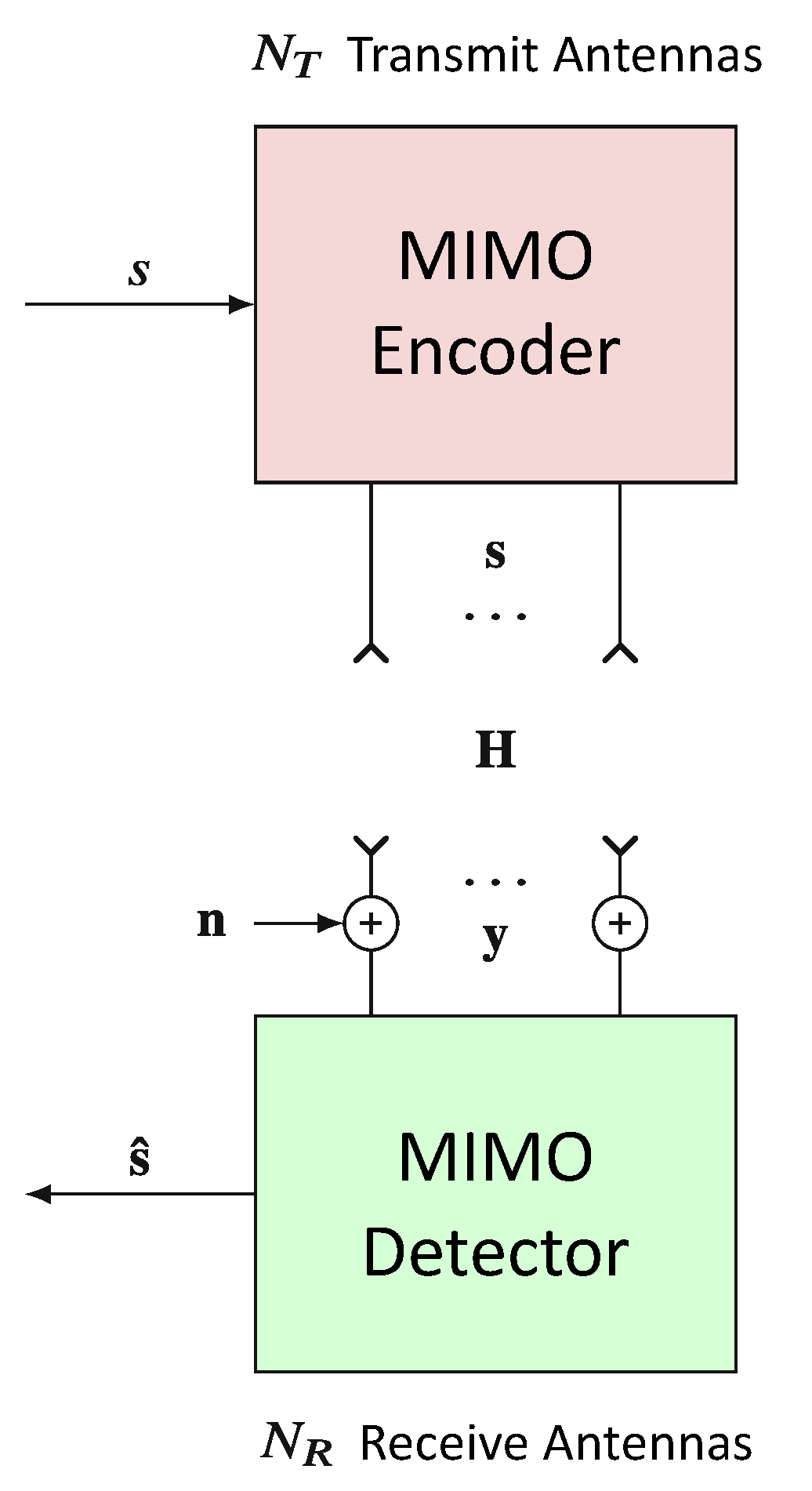
4.1. MIMO-NOMA Detector

Without loss of generality, Figure 2 may also be considered to be representing a single-cell MIMO-NOMA uplink communication system, in which the receiver BS is equipped with receiving $N_R$ antennas, and the cell has K users, each equipped with $N_T$ transmitting antennas, given the condition $N_R=N_{T}K$ and factoring the specific distances and transmitted power levels of each UE into the Equation (7).

We assume that in a previous stage (not shown in Figure 2), a sequence of ${log}_2\left(M\right)$ bits is mapped to a symbol vector $\mathbf{s}$, where M is the number of symbols in the given constellation. For example, in BPSK, one bit is mapped onto a symbol. The symbols are then de-multi-plexed by a MIMO encoder, which transmits an independent symbol over one of the $N_T$ transmit antennas. The receiver, equipped with $N_R$ antennas, receives the transmitted symbols. Each symbol has a channel gain, $h_{i,j}$, which is the gain experienced by the symbol from the i-th transmit antenna to the j-th receive antenna. The elements of the received signal is calculated as follows [38]:

$${\mathbf{y}}_{\mathbf{k}}=\mathbf{H}\sqrt{a_{k}P}{s}_k+\mathbf{N},$$

(7)

where the variables are complex-valued, where $\mathbf{y}$ is the received signal vector $N_R\times 1$, $\mathbf{H}$ is the $N_R\times N_T$ channel matrix composed by each channel gain, $0<a_k<1$ is the power allocation, P is the maximum transmission power, ${\mathbf{s}}_{\mathbf{k}}$ is the $N_T\times 1$ transmitted symbol vector, and $\mathbf{N}$ is a $N_R\times 1$ vector of AWGN superimposed on the received signal. Thus, its elements are

$$n_i=\sqrt{{\displaystyle \frac{w}{2}}}(u+jv),$$

(8)

where u and v are random variables distributed according to the standard normal, and w is the noise power in linear scale, considering that typically $w=-174+10{log}_{10}\left(B\right)$ in dBm, where B is the system bandwidth.

The entries of $\mathbf{H}$ are assumed to be independent and identically distributed, which can be achieved if the antennas are at a distance of at least half a wavelength apart such that no correlation exists between the channel gains. After the signal has been received, the MIMO-NOMA detector obtains an estimate of the transmitted symbols as $\widehat{\mathbf{s}}$, and then each symbol is ready to be processed to obtain its corresponding bit representation such that the BER is minimized. The detector estimates the transmitted symbols by enumerating all possible values for $\mathbf{s}$ and then finds the candidate that minimizes the Euclidean distance between the received signal $\mathbf{y}$ and $\mathbf{H}\sqrt{{\mathbf{a}}_{\mathbf{k}}\mathbf{P}}{\mathbf{s}}_{\mathbf{k}}$ as follows:

$$\widehat{s}=\underset{\mathbf{s}\in {\mathcal{S}}^{N_T}}{arg\; min}\left|\right|\mathbf{Y}-\mathbf{H}\sqrt{a_{k}P}{s}_k{\left|\right|}^2,$$

(9)

where ${\mathcal{S}}^{N_T}$ is the $N_T$-dimension complex constellation set for the modulation scheme selected. In an uncoded system, this brute-force approach yields the optimal BER performance; however, it requires an exponential exploration of $|{\mathcal{S}}^{N_T}|$, (i.e., all constellation points), which is impractical if $N_T$ or modulation orders are large.

The elements of the channel matrix of $\mathbf{H}$ are assumed to have a Rayleigh distribution, which helps model real-world phenomena in wireless communications. It is frequently used to model multi-path fading with no direct Line of Sight (LoS) path, and thus

$$h_{i,j}=(a+jb)\sqrt{{\displaystyle \frac{d_{i,j}^{\eta }}{2}}},$$

(10)

where a and b are random variables distributed according to the standard normal, $d_{i,j}$ is the distance from the i-th transmit antenna to the j-th receive antenna, and typically $\eta =4$, the path loss exponent. According to the previous equation, the channel is generated depending on the order of the MIMO system.

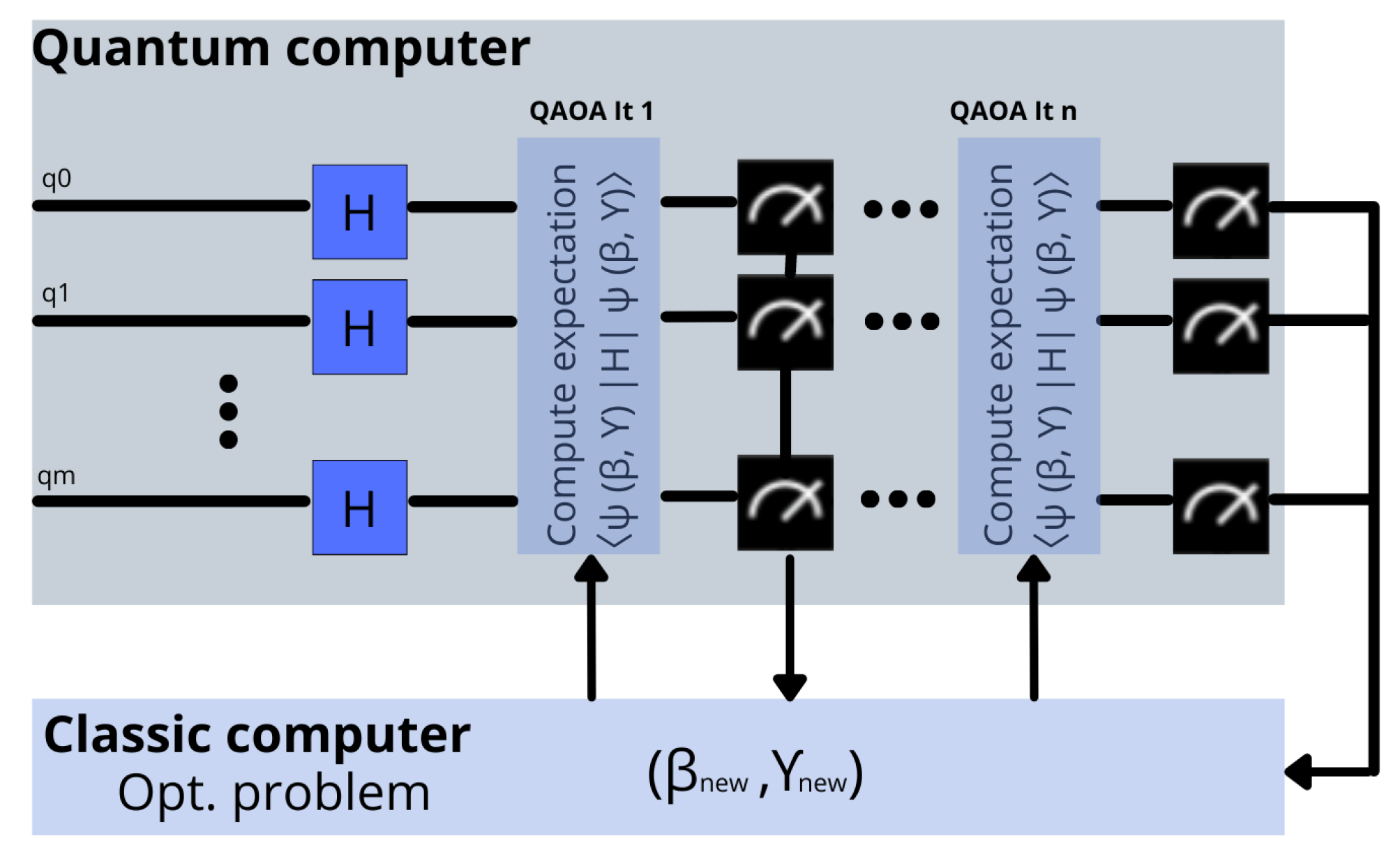
4.2. Quantum Approximate Optimization Algorithm

As quantum technologies continue to advance, the demand for robust algorithms capable of operating on emerging and inherently noisy quantum hardware has similarly intensified. Consequently, Variational Quantum Algorithms (VQAs) have garnered significant attention due to their distinctive approach, which leverages a classical optimizer to train parameterized quantum circuits. VQAs have now been proposed for virtually all potential applications envisioned for QC, and they represent the most promising avenue for achieving quantum advantage. However, several challenges persist, including issues related to these algorithms’ trainability, accuracy, and efficiency.

QAOA is a prominent example of VQAs and a promising approach for making early advancements toward quantum advantages in solving combinatorial optimization problems [39]. The core idea behind QAOA is to represent the objective function $C\left(X\right)$ as a cost Hamiltonian $H_C$ (11) and then search for an optimal bitstring X that achieves a high approximation ratio with significant probability [40]:

$$H_C|x\rangle =C\left(X\right)|x\rangle ,$$

(11)

where $|x\rangle$ is the quantum state that encodes the bitstring X. Finding the minimum eigenvector of the Hamiltonian corresponds to locating the ground state energy of the system, which represents the optimal quantum state. In quantum mechanics, the Hamiltonian denotes the total energy of a system. Thus, solving an optimization problem using quantum techniques begins by converting it into a quantum Hamiltonian, or Hermitian operator, problem. The objective is to find the system’s lowest energy state, which equates to the optimal solution.

QAOA is a variational quantum hybrid (quantum–classical) algorithm due to its implementation through variational quantum circuits. These quantum circuits depend on a set of parameters ($\beta$, $\gamma$), whose optimal values must be found so that the quantum state $\left|\psi \right({\beta }_{opt},{\gamma }_{opt})\rangle$ encodes the optimal solution to the problem [41]. Then, a classical optimizer tunes the circuit parameters and minimizes the measured value. Figure 3 represents the QAOA operation principle [41].

This paper addresses the challenges of maximum likelihood-based detection in future wireless communication networks that utilize massive MIMO systems by proposing an initial phase involving a QAOA-based maximum likelihood detection (MLD) method tailored for MIMO-NOMA systems. The proposed approach is designed with potential scalability to massive MIMO, with a view toward implementation on emerging quantum devices. The choice of QAOA is motivated by several key advantages over other quantum computing methods as outlined in Section 2. Firstly, QAOA has demonstrated effectiveness in comparable research domains [41]. Secondly, as a hybrid quantum–classical algorithm, QAOA leverages the strengths of both quantum and classical computing, making it particularly well suited for current NISQ-era quantum systems. This is especially significant given that NISQ devices are susceptible to errors and noise, which can undermine the precision and reliability of purely quantum algorithms.

Despite the advantages of QAOA, it has the same limitations inherent to current QC technologies such as the one used in the present work (IBM Quantum Experience). These systems are noisy and require multiple runs in the quantum domain (known as “shots”) to account for errors. Also, the limited number of available qubits poses a challenge in scalability validation in practical systems. However, the field is continuously developing new approaches and hardware that could overcome these limitations and take advantage of the unique capabilities of QC. As such, the proposed use of QAOA in MIMO and NOMA detection could represent an important step towards realizing the full potential of QC and hold promise for a wide range of applications in the field of telecommunications.

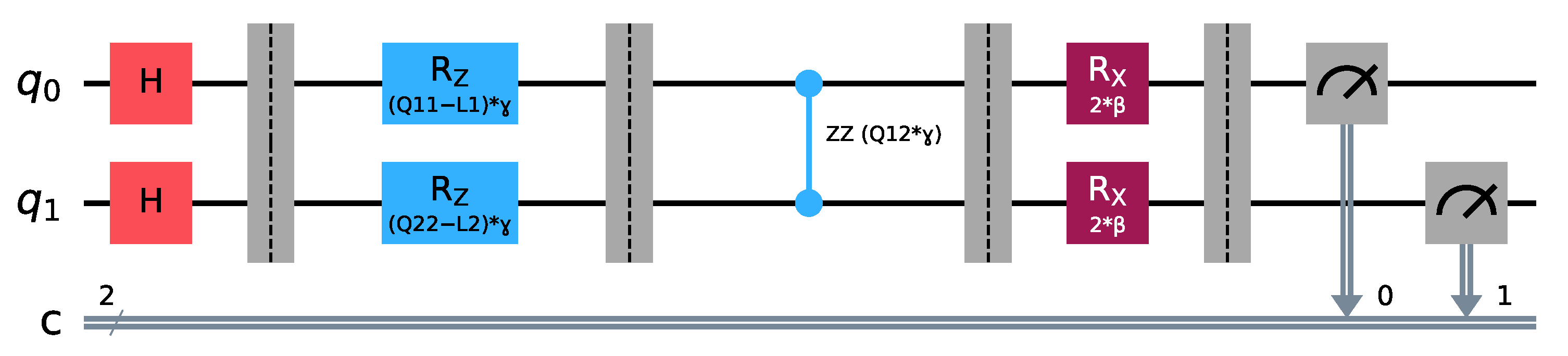
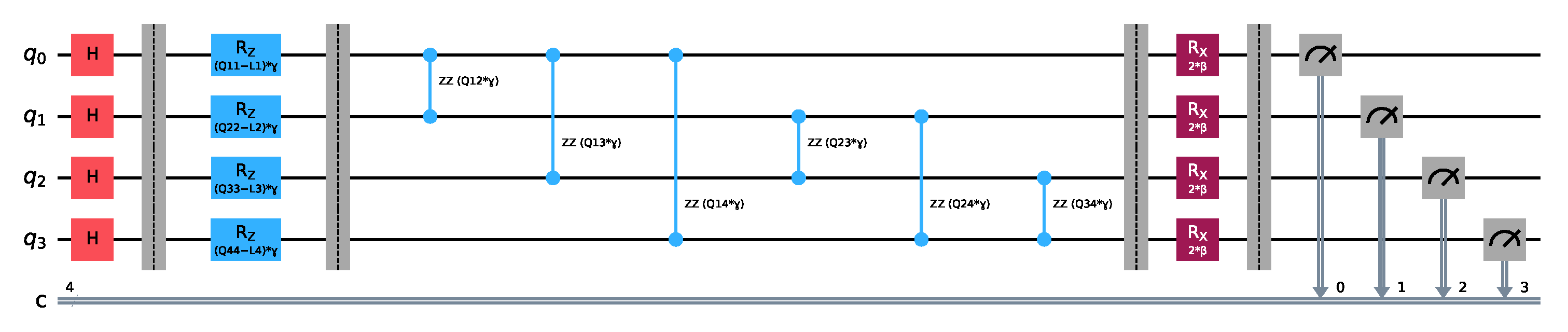
4.3. Quantum MIMO-NOMA Detection

A compelling strategy for addressing combinatorial optimization problems with QC involves reformulating them into the QUBO model, followed by applying QAOA to identify a solution. Thus, the MLD minimization problem proposed in (9) is transformed into a QUBO model to be solved with QAOA. The QUBO model’s significance in addressing numerous combinatorial optimization problems lies in its equivalence to the Ising Model, which plays a crucial role in physics [42]. It provides a simplified representation of the interactions between spins in a physical system, typically in the context of magnetism and phase transitions. Additionally, the primary rationale for the emphasis on QUBO instances in QAOA is tied to hardware limitations. Nevertheless, if the quantum device can implement gates on more than two qubits, there could be a potential advantage in reducing the number of interactions by elevating their order.

A formal definition of the QUBO model is given by

$$min/max({\mathbf{X}}^{T}Q\mathbf{X}+{\mathbf{L}}^T\mathbf{X}),$$

(12)

where $\mathbf{X}$ is a vector of binary decision variables, $\mathbf{Q}$ is a square matrix of quadratic coefficients, $\mathbf{L}$ is a vector of linear coefficients, and $\mathbf{T}$ denotes the transpose of a matrix.

Moreover, assuming BPSK modulation (for simplicity) means that the symbols (i.e., bits) of each transmit antenna $s_k,k\in [1,\dots ,N_T]$ may take up values in the set $\{-1,+1\}$. Accordingly, (9) requires the following simple substitution $s_k=2q_k-1$ due to the QUBO model being valid for binary variables. Higher-order modulation schemes like Quadrature Phase-Shift Keying (QPSK), 16-Quadrature Amplitude Modulation (QAM), and 64-QAM can be utilized. However, this increases both the complexity of the problem and the number of qubits required, which can impact the results due to the limitations of current quantum computers.

An example of a MIMO-NOMA $2\times 2$ BPSK system shows the completed procedure. Two aspects must be considered: First, as it is a MIMO system, the channel is characterized by a matrix, according to (6) in this work. Second, NOMA must have different power $a_1$ and $a_2$ levels, depending on the users’ distances, assuming user 1 to be the weakest (farthest from BS) and user 2 to be the strongest (closer to BS). In accordance with (2) and (9), the MLD in MIMO and NOMA for M = 2 is

$$\widehat{s}=min\left|\right|\mathbf{Y}-\mathbf{H}\left(\sqrt{a_{k}P}(2q_k-1)\right){\left|\right|}^2,$$

(13)

After solving the equation above, with some reordering and grouping similar terms together, the quadratic and linear terms are separated for better compression to form the QUBO model and solve the optimization problem through QAOA. Equations (14) through (24) illustrate the entire process. In the case of quadratic terms, the following are obtained, separating them by $Q_{i,i},Q_{j,j}$ and $Q_{i,j}$, to form the matrix $\mathbf{Q}$:

$$Q_{1,1}=4\sqrt{a_{1}P}(\Re {\left(h_{1,1}\right)}^2+\Im {\left(h_{1,1}\right)}^2+\Re {\left(h_{1,2}\right)}^2+\Im {\left(h_{1,2}\right)}^2)$$

(14)

$$\begin{array}{cc}\hfill Q_{1,2}=& 8\sqrt{a_1{a}_{2}P}(\Re \left(h_{1,1}\right)\Re \left(h_{1,2}\right)+\Im \left(h_{1,1}\right)\Im \left(h_{1,2}\right)\hfill \\ \hfill & +\Re \left(h_{2,1}\right)\Re \left(h_{2,2}\right)+\Im \left(h_{2,1}\right)\Im \left(h_{2,2}\right))\hfill \end{array}$$

(15)

$$Q_{2,2}=4\sqrt{a_{2}P}(\Re {\left(h_{2,1}\right)}^2+\Im {\left(h_{2,1}\right)}^2+\Re {\left(h_{2,2}\right)}^2+\Im {\left(h_{2,2}\right)}^2)$$

(16)

$$\mathbf{Q}=\left[\begin{array}{cc}{Q}_{1,1}& Q_{1,2}\\ 0& Q_{2,2}\end{array}\right]$$

(17)

For linear terms, on the other hand, three distinct contributions are derived and isolated for each user (M = 2) after solving, reordering, and grouping (13):

$$L_{1,1}=-4\sqrt{a_{1}P}(\Re {\left(h_{1,1}\right)}^2+\Im {\left(h_{1,1}\right)}^2+\Re {\left(h_{1,2}\right)}^2+\Im {\left(h_{1,2}\right)}^2)$$

(18)

$$\begin{array}{cc}\hfill L_{2,1}=& -4\sqrt{a_{1}P}(\Re \left(h_{1,1}\right)\Re \left(y_1\right)+\Im \left(h_{1,1}\right)\Im \left(y_1\right)\hfill \\ \hfill & +\Re \left(h_{1,2}\right)\Re \left(y_2\right)+\Im \left(h_{1,2}\right)\Im \left(y_2\right))\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill L_{3,1}=& -4\sqrt{a_1{a}_{2}P}(\Re \left(h_{1,1}\right)\Re \left(h_{1,2}\right)+\Im \left(h_{1,1}\right)\Im \left(h_{1,2}\right)\hfill \\ \hfill & +\Re \left(h_{2,1}\right)\Re \left(h_{2,2}\right)+\Im \left(h_{2,1}\right)\Im \left(h_{2,2}\right))\hfill \end{array}$$

(20)

$$L_{1,2}=-4\sqrt{a_{2}P}(\Re {\left(h_{2,2}\right)}^2+\Im {\left(h_{2,2}\right)}^2+\Re {\left(h_{2,1}\right)}^2+\Im {\left(h_{2,1}\right)}^2)$$

(21)

$$\begin{array}{cc}\hfill L_{2,2}=& -4\sqrt{a_{2}P}(\Re \left(h_{2,2}\right)\Re \left(y_2\right)+\Im \left(h_{2,2}\right)\Im \left(y_2\right)\hfill \\ \hfill & +\Re \left(h_{2,1}\right)\Re \left(y_1\right)+\Im \left(h_{2,1}\right)\Im \left(y_1\right))\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill L_{3,2}=& -4\sqrt{a_1{a}_{2}P}(\Re \left(h_{2,2}\right)\Re \left(h_{2,1}\right)+\Im \left(h_{2,2}\right)\Im \left(h_{2,1}\right)\hfill \\ \hfill & +\Re \left(h_{2,1}\right)\Re \left(h_{1,1}\right)+\Im \left(h_{2,1}\right)\Im \left(h_{1,1}\right))\hfill \end{array}$$

(23)

$$\mathbf{L}=\left[\begin{array}{cc}{L}_{1,1}+L_{2,1}+L_{3,1},& L_{1,2}+L_{2,2}+L_{3,2}\end{array}\right]$$

(24)

Also, note that the number of qubits required equals the number of bits transmitted in total by all antennas (e.g., for MIMO $2\times 2$ with BPSK, only two qubits are needed).

Once the QUBO model has been prepared and its corresponding terms have been established, our attention can be directed toward (11). The cost Hamiltonian of QAOA is defined by the problem Hamiltonian ($H_P$) (26), which contains the cost function, and the mixing Hamiltonian ($H_M$) (27), defined as the sum of single Pauli X-operators on all qubits [43]:

$$H_C|x\rangle =H_P|x\rangle +H_M,$$

(25)

$$H_P|x\rangle =\left(\sum _{i,j=1}^n{x}_i{Q}_{ij}{x}_j+\sum _{i=1}^n{L}_i{x}_i\right)|x\rangle$$

(26)

$$H_M=\sum _{i=1}^n{X}_i$$

(27)

Since our variables are binary, $x_j=x_j^2$ is satisfied. Concerning this assumption, the linear and quadratics contributions can be written in the same matrix notation [42]. Denoting $L_{1,1}+L_{2,1}+L_{3,1}=L_1$ and $L_{1,2}+L_{2,2}+L_{3,2}=L_2$ for simplicity, the new matrix $\mathbf{Q}$ is presented below:

$${\mathbf{Q}}_{\mathbf{2}\times \mathbf{2}}=\left[\begin{array}{cc}{Q}_{1,1}-L_1& Q_{1,2}\\ 0& Q_{2,2}-L_2\end{array}\right]$$

(28)

Following these essential transformations, we can define the problem Hamiltonian using Pauli-Z gates and construct the QAOA circuit for this particular example:

$$\begin{array}{c}\hfill H_P=(Q_{1,1}-L_1)I{Z}_0+(Q_{2,2}-L_2)Z_{1}I+\left(Q_{1,2}\right)Z_1{Z}_0\end{array}$$

(29)

According to (25), the QAOA circuit implemented in Qiskit is shown in Figure 4. Initially, a layer of Hadamard (H) gates is applied to establish superposition across all qubits. Next, $Rz$ gates, representing the linear terms, apply a transformation or rotation to the corresponding qubit, based on the parameter $\gamma$. Similarly, $ZZ$ gates, associated with the quadratic terms, also depend on $\gamma$. Finally, before measurement, the mixing Hamiltonian is implemented using $Rx$ gates, which are parameterized by $\beta$. After measuring the qubits, the optimal parameters for $\gamma$ and $\beta$ could be found by a classical optimizer, such as Cobyla [44], ADAM [45], etc. The purpose of this example is solely to provide a general overview of the procedure, which is why specific numerical values are omitted.

Furthermore, it is crucial to bear in mind that MLD involves an exhaustive search, resulting in four potential solutions for two users in the case of BPSK, for instance. When we introduce variables like varying the transmission power to observe differences in the BER results or changing the number of bits to transmit, there would be numerous iterations necessitating different QAOA circuits. Moreover, adjusting the power allocation coefficient would also impact the results by changing the relative strength of each user in the system. Specifically, the BER would vary with the transmitted power based on the allocated power and the user’s distance from the base station.

Although the presented 2 × 2 MIMO-NOMA example is relatively straightforward and does not require a substantial number of qubits or extensive calculations, the complexity increases dramatically as we scale up the MIMO system order and modulation schemes. Considering a massive MIMO system, and trying to perform the entire optimization process with QAOA from scratch becomes virtually impossible. Thus, QAOA is implemented in libraries such as Qiskit on IBM Quantum, Pennylane by Xanadu, etc.

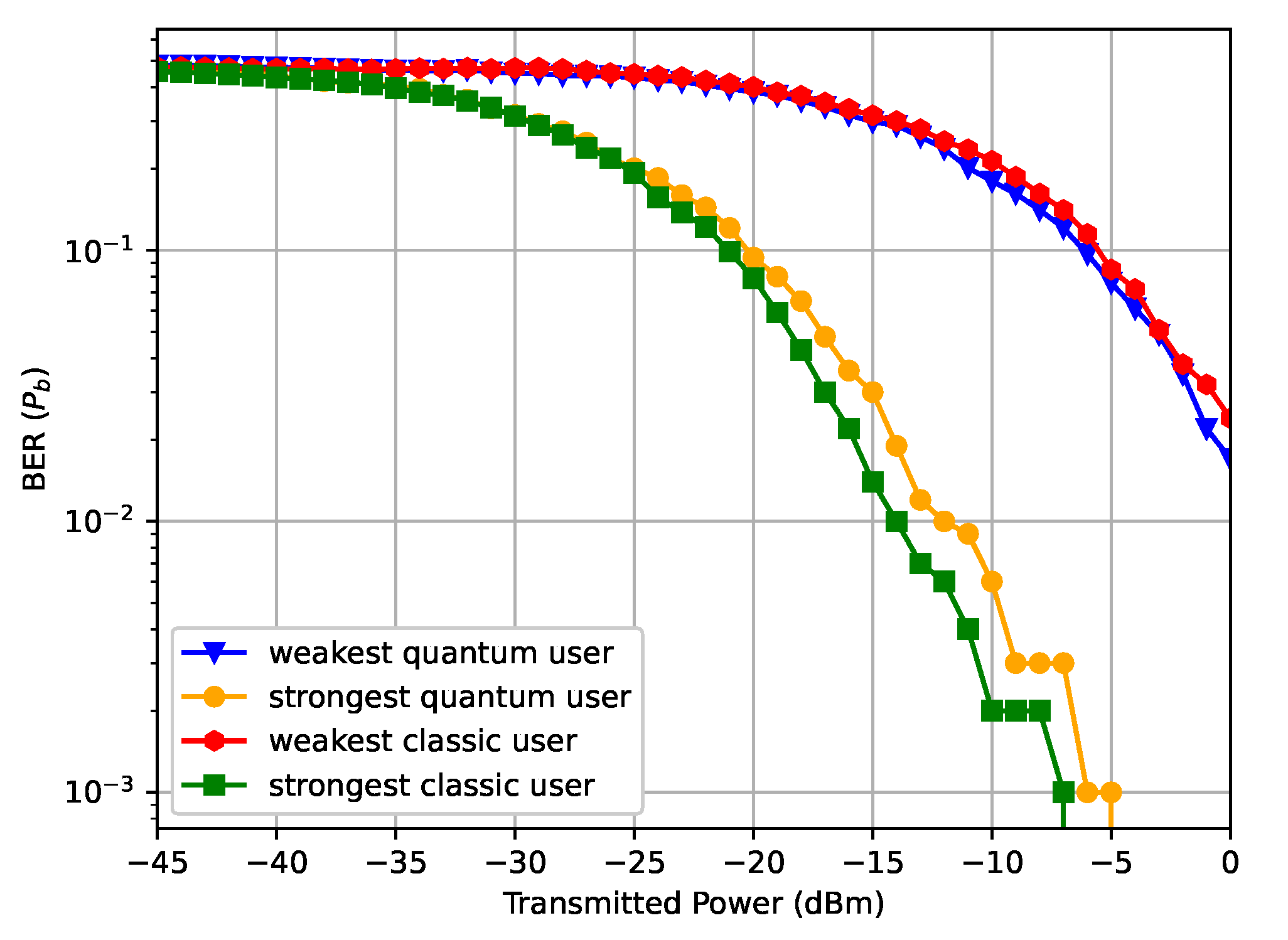
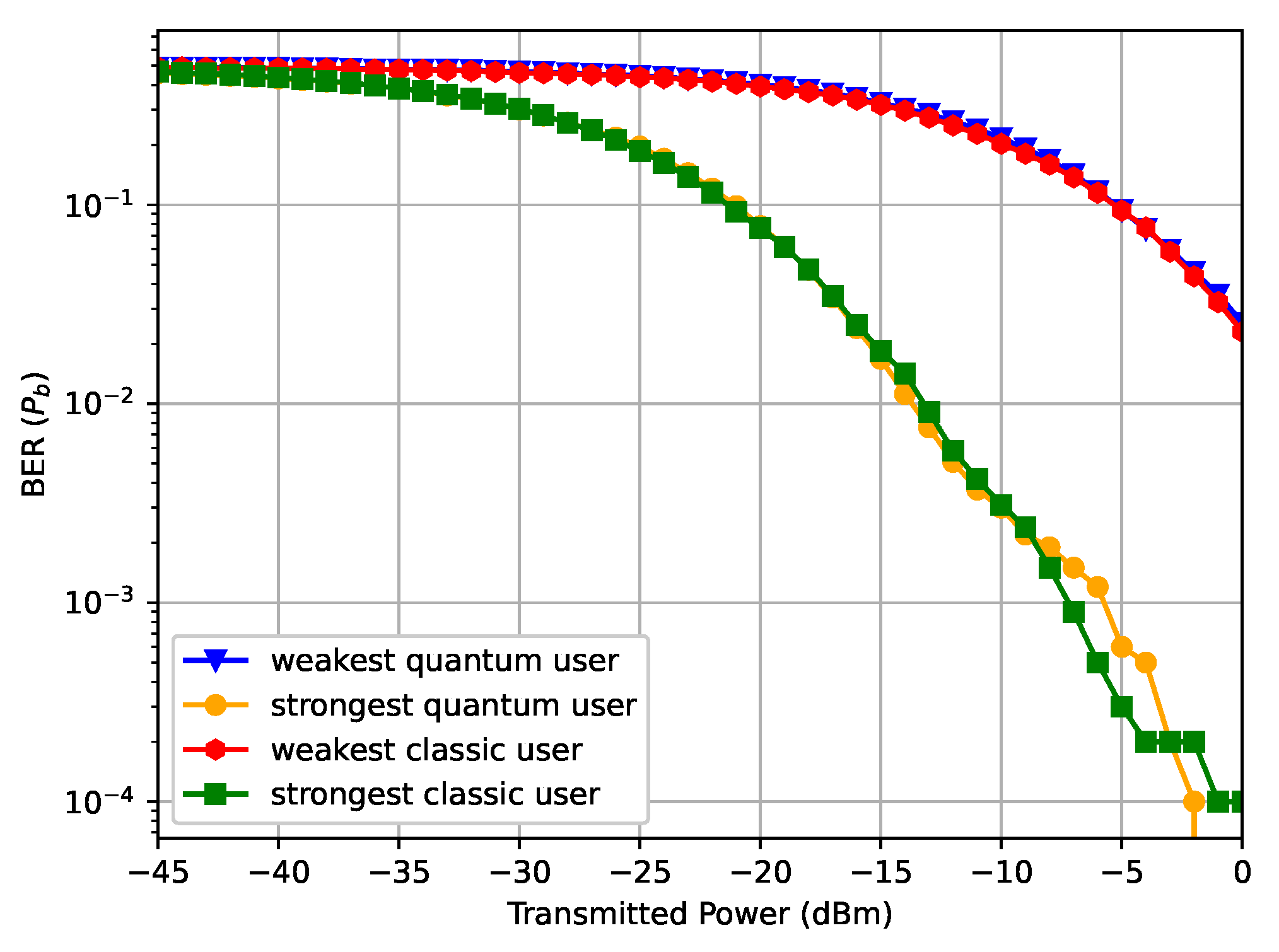
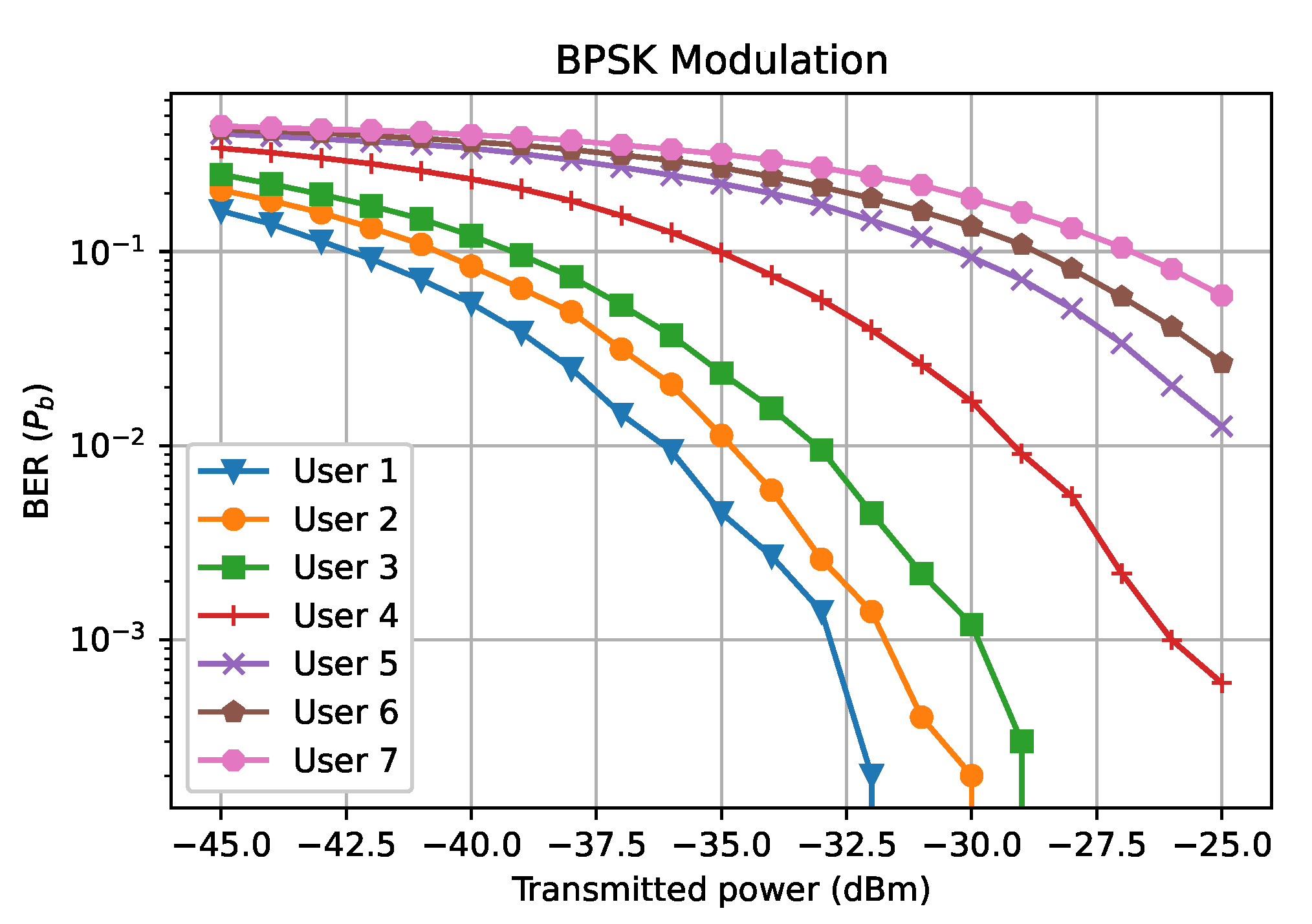
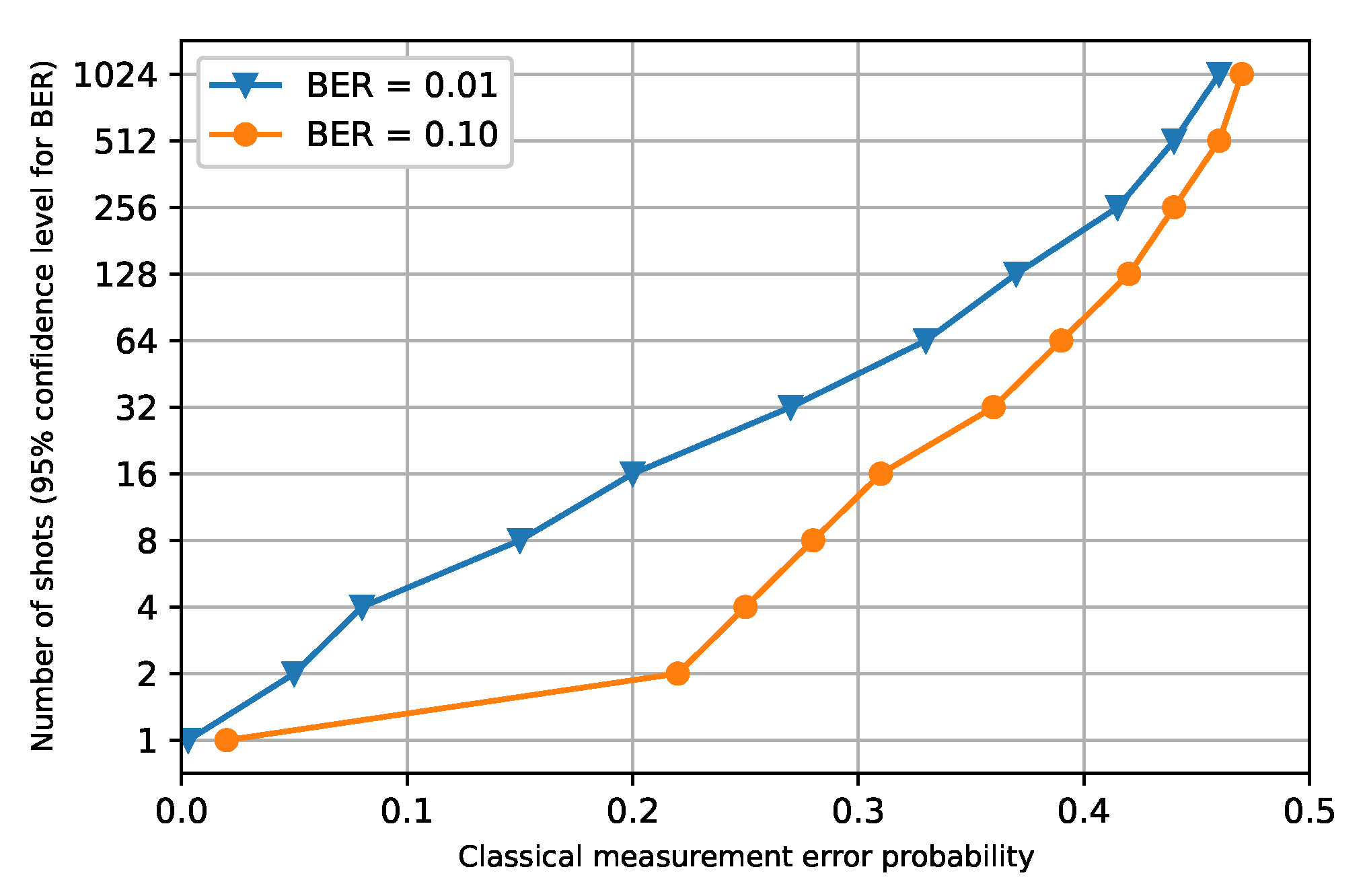
5. Results

This section discusses the results obtained from the quantum MLD for MIMO-NOMA. Concerning the 2 × 2 example, the users be A ($a_A=0.8$, the weakest) and B ($a_B=0.2$, the strongest) are 500 and 200 m away from the receivers. Assuming BPSK modulation, a first experiment, where 1000 bits are sent, is shown in Figure 5. The graph displays the BER values vs. the power transmitted for the two users in the classical version and the quantum version of MLD. The power levels are quantified concerning a reference power of 1 mW, denoted as dBm. Negative values indicate signals with reduced strength (below 1 mW), whereas positive values indicate signals with increased strength.

Classical values are computed using MATLAB to benchmark against the quantum results achieved through the QAOA implemented with (Qiskit-IBM). The quantum version is executed 1024 times (shots) in IBM Quantum systems, which means a long time to obtain the outcomes (12 h). This timeline contains from when the job is created (sent to the system) to when it is executed, going through some phases such as transpiling, validating, queue time, and running time. Transpiling refers to rewriting the given input circuit to match the topology of the quantum device. In other words, the circuit is translated into a circuit that can be run on the backend. This process includes converting the circuit gates into standard basis quantum gates. Validating is the time taken to verify that the circuit can be run, and it depends on the device. The queue time varies depending on how busy the system is and how many other jobs use it. The running time is the time it takes the backend to run the circuit itself, 4.3 s in this case. If the circuit is more complex and/or the number of shots increases, this time increases. IBM Quantum is a cloud-based quantum computing platform that provides access to a wide range of quantum hardware devices and high-performance simulators for prototyping quantum circuits and algorithms [46]. These simulators are designed to allow researchers and developers to explore the behavior of quantum systems under various conditions, including realistic device noise models.

As depicted in the image, it is evident that both the classical and quantum approaches yield similar results for each transmitted power level: the BER decreases as the power increases. In particular, it should be observed that the BER for users A and B diverges as the power varies, aligning with the anticipated outcome based on the varying distances of their respective locations relative to the receiver.

Next, the same system is tested, increasing the number of bits sent. With 10,000 bits, the graph lines in Figure 6 are smoother, and both approaches appear almost equal. The quantum method yields increasingly enhanced results, approaching the performance of conventional MIMO-NOMA detection. As expected, BER decreases when the power increases for all cases.

Despite being a straightforward example, it has been shown that potential use cases such as detection in MIMO-NOMA will be developed based on QC since its implementation in classical systems will be extremely challenging in the 6G era. When the number and quality of qubits increase enough, a quantum MLD will provide an optimal service to users in future wireless communication technologies. Additionally, as QAOA applies superposition and quantum parallelism, the time taken for a 2 × 2 system could be similar to a higher-order system, being the main advantage of quantum mechanics and quantum computation applied to this use case.

Another example is given in Figure 7, which illustrates a 4 × 4 system where users are positioned at distances of $d=[100,120,150,200]$, with corresponding $a_k$ values of [0.1, 0.15, 0.25, 0.5] for each user. Remarkably, in the preceding graph, the resemblance between classical and quantum outcomes is less pronounced compared to the 2 × 2 scenario. This divergence is primarily attributed to the fact that, as the system’s size grows, the QAOA circuit influence becomes more substantial, and the inherent noise and instability of qubits directly impact the results. Conversely, when the complexity of the optimization problem intensifies, the results become exceedingly precise, aiming for a substantially superior solution. It is worth highlighting that varying factors such as user-to-BS distances, adjustments in power allocation coefficients, and increasing the number of bits for transmission could lead to substantial variations in these results.

The quantum circuit for the 4 × 4 MIMO-NOMA system is illustrated in Figure 8. As noted earlier, the number of qubits reflects the total number of bits transmitted across all antennas; for instance, a MIMO 4 × 4 system using BPSK requires 4 qubits. The circuit construction is based on matrix (31), which is composed of the terms $Q_{i,i}$, $Q_{j,j}$ and $Q_{i,j}$, and vector (30), formed by summing contributions such as $L_{1,1}+L_{2,1}+L_{3,1}=L_1$, $L_{1,2}+L_{2,2}+L_{3,2}=L_2$, and so on for $L_3$ and $L_4$. The circuit setup mirrors the earlier 2 × 2 MIMO-NOMA example, starting with H gates to establish superposition across all qubits. Rzz gates represent the linear terms, parameterized by $\gamma$, while $ZZ$ gates account for the quadratic terms, also dependent on $\gamma$. The mixing Hamiltonian is then applied using $Rx$ gates, parameterized by $\beta$, just before measurement:

$$\mathbf{L}=\left[\begin{array}{c}{L}_1,L_2,L_3,L_4\end{array}\right]$$

(30)

$${\mathbf{Q}}_{\mathbf{4}\times \mathbf{4}}=\left[\begin{array}{cccc}{Q}_{1,1}-L_1& Q_{1,2}& Q_{1,3}& Q_{1,4}\\ 0& Q_{2,2}-L_2& Q_{2,3}& Q_{2,4}\\ 0& 0& Q_{3,3}-L_3& Q_{3,4}\\ 0& 0& 0& Q_{4,4}-L_4\end{array}\right]$$

(31)

Regarding quantum devices, they have limitations in the number of qubits and noise, which hinder the execution time, the scalability, and the accuracy of the results. More extensive scenarios, more users, and a higher order of modulation are challenging to develop on the current available quantum computers, and experiments could be run on IBM Quantum simulators to explore the behavior of larger quantum systems as alternative.

As an illustrative example, Figure 9 shows what could be the BER performance that would be calculated using the IBM Quantum’s system with 7 qubits implementing a MIMO $7\times 7$ detector, averaging the errors in 10,000 transmitted bits, again concerning the transmitted power, assuming distances for the 7 users of $d=[100,110,120,150,200,220,250]$ meters, respectively, and allocating power coefficient values according to their distances. This example highlights the usefulness of IBM Quantum’s simulators for evaluating the performance of small quantum systems, allowing researchers to study how quantum errors scale with system size and to optimize error correction strategies for real-world quantum devices. It is important to note that while the results obtained from the simulator are not exact representations of the behavior of real-world quantum systems, they can provide valuable insights into the factual correctness and adequate performance of quantum algorithms and circuits, especially when it comes to studying the effects of noise and other sources of errors.

Figure 10 summarizes our results, which are focused on the number of shots required for computing different values of BER at a 95% confidence level for different classical readout error probabilities. As shown, 1024 shots imply that IBM Quantum backend devices are very noisy (45% of the measures are affected by errors); however, it is also apparent that just by improving this value to the 30–40% range, it could cut the number of shots (and thus the computation time) to 64 (an improvement by a factor of 16 when compared to 1024). Also, as shown, in some instances, as few as 8 would suffice if measurement error probabilities within 20–30% were feasible.

6. Conclusions

The research community has increasingly turned its attention to the development of 6G technology, which promises unparalleled speed and connectivity, paving the way for a fully interconnected world. However, realizing the full potential of 6G requires computational capabilities that exceed those of current classical computers. QC, with its capacity to perform certain calculations exponentially faster than classical counterparts, has emerged as a potential enabler of 6G technology.

This paper has examined the potential of QC in the context of future 6G wireless technology, specifically focusing on improving the MLD of MIMO-NOMA uplink transmissions through the QAOA and its possible extension to massive MIMO, while adapting to the current limitations of QC. As the computational complexity of detecting a massive MIMO-NOMA signal increases disproportionately with the number of antennas or the modulation order, QC presents a viable approach to accelerating detection in the future.

However, it is important to recognize that the current NISQ era quantum processors, with only a few hundred qubits, are not yet advanced enough to achieve “quantum supremacy”. Thus, the continued development of quantum technology is crucial to unlocking its full potential. As this paper explores detection in MIMO-NOMA systems using existing QC capabilities, it is worth noting that more robust algorithms capable of achieving quantum supremacy may emerge. The forthcoming fault-tolerant era in QC is expected to introduce new use cases and significantly improve existing applications.

In conclusion, this work has provided insights into the potential impact of QC on the future of wireless technology. Despite the challenges that lie ahead, the findings of this study highlight the substantial promise of quantum computation within the domain of 6G technology. Consequently, it is imperative for the wireless research community to continue exploring quantum-based approaches, as doing so will be key to unlocking the full potential of 6G, leading to faster and more efficient communication in the years to come.