Abstract
Starting from the geometric description of quantum systems, we propose a novel approach to time-independent dissipative quantum processes according to which energy is dissipated but the coherence of the states is preserved. Our proposal consists of extending the standard symplectic picture of quantum mechanics to a contact manifold and then obtaining dissipation by using appropriate contact Hamiltonian dynamics. We work out the case of finite-level systems for which it is shown, by means of the corresponding contact master equation, that the resulting dynamics constitute a viable alternative candidate for the description of this subclass of dissipative quantum systems. As a concrete application, motivated by recent experimental observations, we describe quantum decays in a 2-level system as coherent and continuous processes.
1. Motivation and Previous Works
Dissipative quantum phenomena have been the subject of intense investigation since the early days of quantum mechanics [1]. The most widely adopted description of dissipative quantum processes is given by the Gorini–Kossakowski–Sudarshan–Lindblad (GKLS) equation [2,3,4]. This is because it has been proven that the GKLS equation describes the most general form of a non-unitary, linear, completely positive and trace-preserving dynamics; thus, one may ensure that the probabilistic character of quantum mechanics is preserved at all times. However, in the GKLS equation, in order to obtain a completely positive evolution, it is necessary to add the so-called jump term, which changes the rank of the state. As a consequence, the GKLS dynamics fundamentally couples energy dissipation and rank disipation.
On the other hand, it is possible to model energy dissipation without change in the rank of by means of a time-dependent Hamiltonian, where the time dependence describes, in an effective manner, the interaction of the system with the environment. In this case, the evolution is unitary; therefore, the rank of the state is preserved. For instance, recent impressive improvements in experimental settings have allowed the observation that the decays induced by a Rabi oscillator in a 2-level system are coherent and continuous processes [5] (see also [6] for theoretical analysis).
In this work, we propose an alternative method to describe a class of time-independent dissipative quantum phenomena by non-unitary evolution-preserving statistical mixing. This is based on the symplectic formulation of quantum mechanics and due to the analogy with the geometric description of classical dissipative systems: In classical mechanics, one can describe a wide class of dissipative systems by referring to the contactification of the symplectic phase space and then using contact Hamiltonian systems to define the dynamics. It has been shown that this approach, when applicable, provides several positive features, such as relying on canonical variables and producing a generalization of canonical transformations [7], enabling an extension of both Liouville and Noether’s theorems to the dissipative case [8,9,10,11,12,13], and providing a description in terms of variational principles [14,15,16,17,18,19,20] together with a natural route to field theories with dissipation [21].
Analogously, in the geometric description of n-level quantum systems, the pure states of the corresponding Hilbert space are points on the complex projective space , which is a symplectic manifold, and the Schrödinger dynamics on is projected onto Hamiltonian dynamics on such a manifold [22,23,24,25]. This is because pure quantum states in are actually rays, and the Schrödinger equation is invariant under dilations and multiplications by a global phase factor; that is, in the standard Schrödinger picture, one deals with redundant information in order to obtain a linear description. Interestingly, contact manifolds also appear naturally in this picture. In fact, by quotienting only over dilations, one obtains the manifold of normalized vectors in identified as the -dimensional unit sphere with the standard contact structure. An approach to describe dissipation in the quantum case by means of contact Hamiltonian flows on has been put forward already in [26].
Contrary to [26], we do not work on , but we proceed by analogy with the classical case, i.e., we perform a contactification of and investigate the dissipative dynamics by means of contact Hamiltonian systems defined on the extended space . We take a different route that is more directly connected with the procedure of contactification used in classical mechanics.
The structure of this work is as follows: after a brief review of the standard geometric description of n-level quantum systems in Section 2, we introduce our approach in Section 3, and we show that, by choosing the contact Hamiltonian appropriately, the dynamics on is projectable onto the proper dynamics on , thus preserving the purity of states while at the same time dissipating the expected value of the energy of the reference system. In this manner, we obtain a dissipative dynamics on the manifold of physical quantum states. Then, in Section 4, we consider the corresponding dynamics for the density operators, which we call the contact master equation, and we prove that the resulting map is both positive and trace preserving after a brief comparison with other approaches, thus agreeing with all the prescriptions of standard quantum mechanics. As a consequence, the proposed contact dynamics is a viable candidate for describing dissipative phenomena in quantum systems when the purity of the states is preserved. As an illustration of our formalism, we consider in Section 5 the important case of radiative decay in qubit systems, finding that our description can effectively model quantum decays (or excitations) as coherent and continuous processes. Finally, in Section 6, we summarize our results and highlight future directions.
2. Geometry and Dynamics of Conservative n-Level Quantum Systems
Let us start our study by recalling some aspects of the geometric description of finite-level quantum systems. For complete reviews, we refer to [22,23,25,27,28], while further results can be found in [24,26,29,30].
2.1. Kinematics: From to
It is well-known that, in the Hilbert space, there is a natural action of the Abelian group given by the following.
According to the statistical interpretation of the wave function, it turns out that pure states are better described by equivalence classes of vectors in with respect to this action, i.e., rays in the Hilbert space .
Let us show how, for finite-dimensional systems, the set of such equivalence classes can be given by the structure of a manifold: consider an n-level quantum system with Hilbert space and define . By selecting an orthonormal basis in , one may introduce a Cartesian coordinate system on such that for any element one has the following:
where Einstein’s summation convention over repeated indices is assumed here and in the following equations. The action defining the equivalence classes of pure quantum states may be described infinitesimally by means of two commuting linear vector fields given in Cartesian coordinates as follows:
where is the infinitesimal generator of dilations, while is the infinitesimal generator of the multiplication by a global phase factor. Now, dilations define a distribution in which the integral curves foliate the Hilbert space. Let denote such foliation, then the quotient space is the unit sphere.
In the following, an element of is denoted as , whereas is a vector in . Now, let be the foliation corresponding to the distribution generated by and . Then, the quotient space is identified with the complex projective space, defined as follows.
Furthermore, there is a one-to-one correspondence between elements of and rank-one projectors given by the following.
On , it is convenient to work with complex homogeneous coordinates. To introduce such coordinates, let denote the open subset where . Then, on , one may introduce the following coordinates.
The set of , with , constitutes an atlas for . In such coordinates, the projection from onto can be explicitly expressed as the following:
where we used the chart for the sake of simplicity, and we introduce the following notations.
To conclude the kinematical analysis of n-level systems, let us recall that is a Kähler manifold [25,28,31]; in fact, considering the homogeneous coordinates in Equation (8), one can introduce the 1-form of the following.
Then, the symplectic form on is given by the exterior derivative , which reads as follows.
Moreover, as proven by Wootters in [32], a natural notion of distance between quantum states is given by the Fubini–Study metric on , which has the following form [25,27,28,31]:
where . On the other hand, the -tensor of the following:
defines a complex structure on , such that the quadruple is a Kähler manifold [25,27,28,31].
2.2. Dynamics: Symplectic Hamiltonian Systems on
Having defined the canonical projection from to , one may project the dynamics of the system as follows: First, we recall that the Schrödinger dynamics may be viewed as a classical Hamiltonian system on with the symplectic structure given by the imaginary part of the Hermitian scalar product and the generating Hamiltonian function being the expectation value of the Hamiltonian operator . The corresponding Hamiltonian vector field then reads as follows:
where is the entry of [25]. Now, because , i.e., and are symmetries of the Schrödinger dynamics, it is possible to project onto the dynamics on [25,28,33]. It turns out that the projected dynamics is again a Hamiltonian vector field with respect to the symplectic structure , with generating Hamiltonian function , where here and in the following stands for the smooth functions on M for any smooth manifold M; that is, it satisfies the following.
In order to express Equation (15) in complex homogeneous coordinates on , we start by writing the expectation value of the observable in coordinates such as the following:
where is an –dimensional matrix, is an –dimensional column vector and a real quantity. Thus, by using Equations (11) and (15), we obtain the following:
where the component is the complex conjugate of , and the following is the case.
Therefore, the integral curves of this Hamiltonian vector field are solutions to the Hamiltonian equations of motion:
which is also called the matrix Riccati equation [34]. Hence, the matrix Riccati equation is simply the coordinate expression of the projection of the Schrödinger equation onto the complex projective space.
In addition, one may use the symplectic structure to introduce a Poisson bracket on [25,28]: given the expectation values and associated with the observables and , one defines the following.
In complex homogeneous coordinates this bracket reads as follows.
Furthermore, after some calculation, it is possible to prove that the Poisson bracket satisfies , where . Therefore, one has a clear connection between the Poisson bracket and the quantum commutator. In particular, considering the Hamiltonian of the system with expectation value , the evolution of the expectation value of an arbitrary observable is given by the following.
This result implies immediately that, in the time-independent case, is a first integral of the flow, i.e., the expectation value of the Hamiltonian is conserved. In addition, the expectation value of any observable commuting with is a first integral too.
Proceeding in parallel with the above construction of Hamiltonian vector fields and of the Poisson bracket by means of the symplectic structure, we are going to define now the gradient vector fields and the Jordan bracket by using the Fubini–Study metric.
Gradient vector fields are defined as follows:
and it is direct to verify that
with given in (13). Therefore, by employing Equations (17) and (18), one finds the explicit coordinate expression for the gradient vector field, which reads as follows.
On the other hand, the Jordan bracket between the expectation values and is defined as follows:
and in the coordinates, we have the following.
Finally, the Jordan bracket is connected with the dispersion and the correlation of the observables. That is, for every couple of observables and , their uncertainties and correlations are given by the following:
and
with being the anti-commutator. Thus, the Riemannian metric on takes into account part of the probabilistic character of quantum mechanics [35].
Example: The Conservative Qubit
As an example, let us consider a qubit in which is two-dimensional, and each point is given by . For this case, the complex projective space may be thought of as the unit sphere:
One may use the homogeneous coordinates on to induce coordinates on as follows: take each coordinate patch where , and introduce the homogeneous coordinates on (resp. ) as defined above. Thus, we have the following.
Then, by writing and using the stereographic projection from the north pole of the sphere, one obtains the corresponding point by the following.
For this example, let us consider the Hamiltonian operator as the matrix.
Thus, the expectation value of is given by the following:
and Hamilton’s Equation (19) reduces to the following.
To provide a qualitative description of the behavior of this nonlinear system, one first realizes that the critical points of the flow are located at the following.
They are both centers. The phase portrait in the complex plane is depicted in Figure 1a, while the corresponding vector field on obtained by means of (32) is displayed in Figure 1b.
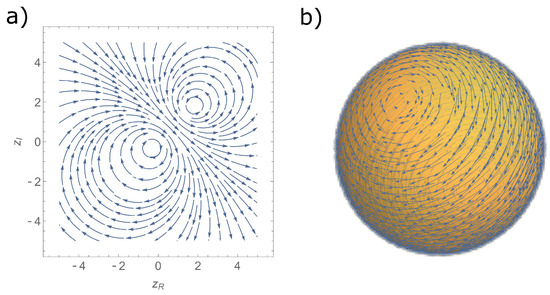
Another important quantity that may be easily calculated by means of Equation (28) is the uncertainty of the energy given by the following.
Clearly this is a positive quantity that only vanishes at the singular points .
3. Contact Geometry and Dynamics of Dissipative n-Level Quantum Systems
In this section, we consider a particular class of dissipative quantum systems, which are those that admit a contact Hamiltonian description (see also [7,11,12,21,26,36,37,38,39] for detailed discussions on the strengths and limitations of this approach both in the classical and quantum settings).
3.1. Kinematics: From to
In order to introduce dissipation, we will work on the contactification of . Therefore, let us first recall some basic facts of contact geometry [40,41].
A -dimensional manifold M is said to be an exact contact manifold if it is endowed with a global differentiable 1-form such that everywhere on Then, is called the contact form, and the contact structure on M is given by the (non-integrable) distribution of hyperplanes . In order to introduce a contact manifold for finite-dimensional quantum mechanical systems, we perform a contactification of the space of pure quantum states . Indeed, since is an exact symplectic manifold, one can consider the extended space , which carries a natural contact structure given as the kernel of the following contact form:
where S is the global coordinate function on the fiber , where S has unit of action, and we use a slight abuse of notation by indicating as the pullback of this 1-form on by means of the natural projection from onto the first argument. Let us observe that it is possible to define a Sasakian structure on starting from the Kähler structure on [40,42]. However, we do not need such structure in the following; therefore, we defer its analysis to a future contribution.
3.2. Dynamics: Contact Hamiltonian Systems on
The contact form allows one to associate a Hamiltonian vector field with every smooth function , defined by the following:
In this case, is called the contact Hamiltonian function. Now, we proceed to compute the coordinate expression of , which may be written as the following in general:
where the component is the complex conjugate of . Using Equations (38) and (39), one finds that the components of the contact Hamiltonian vector field in these coordinates are as follows:
which implies that the integral curves are solutions to the system of the differential equations.
From Equations (41) and (42), we can compute the evolution of any arbitrary real function to obtain the following:
where the bivector is given by the following.
Since we are interested in characterizing dissipative systems that dissipate the energy of some declared reference Hamiltonian system in this work, we shall henceforth assume that the contact Hamiltonian may be written as follows:
where the first term is the expectation value of the Hamiltonian operator of the conservative reference system given in Equation (16), while the second term is an instrumental perturbation which will be taken to be linear in order to result in projectable dynamics so that the projected dynamics can be observed as an effective description of some dissipative dynamics. Therefore, considering the expectation value of an arbitrary observable of the reference system, from Equation (44) we obtain the following:
where is the Poisson bracket given in Equation (21). Hence, it should be clear that the expectation value of the energy is not necessarily preserved along the trajectories of the contact Hamiltonian system.
Finally we remark that, from Equations (43), the contact dynamics is projectable onto a vector field if and only if the contact Hamiltonian function is linear in S. This is because the equations for the variables that characterize the state of the reference system defined on are decoupled from the equation for the additional variable S only in this case. It is for this reason that we will focus on this case only, leaving a detailed analysis of the general case to future investigations.
Example: The Dissipative Qubit
As an example, let us introduce dissipation in the qubit system described in the previous section. To perform this, we consider the following contact Hamiltonian:
where is the expectation value of the Hamiltonian of the conservative qubit (Equation (34)), and is a positive real constant that quantifies the strength of the coupling between the conservative system and the environment.
The Hamiltonian equations of motion (43) associated with the contact Hamiltonian (48) is read as follows.
We observe that, as expected, Equation (49) provides an effective equation of motion for the variable z, describing the state of the reference system, which is decoupled from the equation for the additional variable S.
As in the conservative case, we may now study the qualitative behavior of the dissipative qubit, focusing only on Equation (49). For the sake of simplicity, we consider here an example the particular case . The critical points satisfythe following.
To find solutions to this algebraic equation, first we assume that in order to obtain the reduced second-order equation of the following:
with the following solutions:
where . A direct computation shows that for if and only if ; therefore, these two critical points exist only in such case. When they exist, in the conservative limit , one recovers the analogous solutions in Equation (36) for the case . Additionally, in the dissipative qubit, one finds the following critical point:
which always exists.
To continue the qualitative study of the dynamics, we observe that the eigenvalues of the linearized system at the critical points and are always the same and they are given by the following.
While at the critical point , we have the following eigenvalues:
which are always real. From this linearization, it is possible to conclude that there is a bifurcation depending on the value of :
- (i)
- For such that , we have only the critical point , which is a stable node;
- (ii)
- For such that , we have two critical points and , and both are non-hyperbolic (eigenvalues );
- (iii)
- For such that , we have three different critical points with the following behavior: is always a saddle; the behavior of and depends on the term . If this is positive, then the critical points are stable foci. On the other hand, if this term is non-positive, then they are stable nodes.
Note that even in this simple example, we obtain very interesting dynamical behavior. Moreover, we remark that these types of critical points cannot be obtained in the case of a conservative (unitary) evolution.
By way of example, we have depicted the phase portrait for a choice of such that and in Figure 2. As observed in first panel in Figure 2, we have two stable foci and a saddle. However, recalling that this chart covers only the part of the Bloch sphere excluding the north pole, we also depict the corresponding vector field on in the second panel in Figure 2 from which it is clear that there is an additional critical point at the north pole, which is an unstable node.

Figure 2.
Phase portrait of the dissipative qubit with both in the complex plane and on . The parameters chosen for this representation are the following: and . One may observe the two stable foci and the saddle point both in the plane and in together with the unstable node at the north pole of the sphere, which cannot be observed in this chart on the plane. More details in the main text.
Finally, taking into account the definition of the uncertainty of the energy operator , one has the following.
We stress that, although the functional forms of (37) and (57) are the same, they are different functions of time since, in the two cases, evolves according to different dynamical equations.
.
4. The Contact Master Equation
So far we have considered dissipative quantum evolutions by using contact Hamiltonian systems defined on the manifold . However, the most common description of dissipative quantum systems is by means of density operators; therefore, we shall adapt our approach to pure states considered as rank-one projectors in this section.
Given a unital -algebra , a state on is a continuous linear function in the dual of such that for all observables , one has the following:
where is the identity, and an observable is a self-adjoint element. In particular, for finite-dimensional systems, we may restrict our attention to the -algebra of complex matrices, i.e., we may consider with . Thus, the space of states of is identified as the following:
where denotes the space of observables. The pairing map is the evaluation of the state on the self-adjoint element , and it is given explicitly by the following:
which corresponds to the mean value for the outcome of the measurement of the observable when the system is in the state . Furthermore, since there is a one-to-one correspondence between elements in and , it follows that the space may be decomposed as the following:
where . It is proven in References [30,43] that every is a homogeneous space for the Lie group ; thus, every admits the structure of a differential manifold.
Here, we are only interested in pure states, i.e., rank-one projectors in . Then, as we have already mentioned in Section 2, there is a one-to-one correspondence between states and rank-one projectors given by the relation (6). Thus, in homogeneous coordinates, we have the following.
Now, starting from the expression for the density matrix in the second equation in Equation (62) and taking into account the equations of motion (43), one may deduce the equation of motion for , which takes the following general form.
We first observe from the above equation that independently of the choice of the contact Hamiltonian. Therefore, the trace of is preserved along the evolution, which is a fundamental statistical condition for any admissible quantum evolution.
Remarkably, the evolution (63) can be written using two brackets, which is similar to the structure of the metriplectic and GENERIC formalisms [44,45,46,47,48] (although an approach to dissipative quantum systems directly based on the analogy with the GENERIC equation results in a different type of master equation; see [49,50]). Indeed, we have the following (see Appendix A for the proof):
where the dissipative bracket is the anti-commutator, and we have defined the dissipative potential to be the Hermitian operator given by the following:
where is an arbitrary -dimensional Hermitian matrix, and is the -dimensional column vector given by the following.
is the real quantity.
Let us remark that in Equation (64) there is a conservative part given by the standard von Neumann equation in addition to a contact perturbation introducing dissipation in conservative reference dynamics. Moreover, in general, Equation (64) is coupled to the equation of motion for the variable S given by the following.
They decouple if and only if the contact Hamiltonian is linear in S. In such case, one obtains from Equation (64) a Markovian equation for , which we call the contact master equation. Note that Markovianity in this case should be understood as satisfying the Chapman–Kolmogorov law for dynamical evolution. This is the case we will address in the following, leaving a detailed study of the general case for future investigations.
Let us now compare the contact master Equation (64) with the GKLS equation normally employed to describe dissipative phenomena in quantum systems. For the GKLS equation, we have the following:
where and are bounded operators. First of all, we note that, by comparing the GKLS evolution in Equation (69) with the contact evolution in Equation (64), it is clear that the absence in the latter of the “jump term” (also known as the Choi–Kraus term [2]). This is expected because this term is the one responsible for the change of rank of the density matrix, and the contact evolution considered here preserves the purity of the states. However, while in the GKLS equation the jump term is needed in order to enforce conservation of the trace and the complete-positivity of the map, we observe that it is no longer needed in the contact evolution, for these two properties are both automatically satisfied (at least for pure states). Hence, we observe that the contact master equation provides a (nonlinear) description of coherent dissipative phenomena.
Furthermore, one may also compare the contact master equation with other descriptions normally employed to describe dissipative systems. For instance, one may consider the description of an optical MASER (Microwave Amplification by Stimulated Emission of Radiation) [51,52]. Considering, for simplicity, the case of a 2-state system, one introduces the non-normalized density matrix:
in which the equation of motion reads as follows:
where is a time-dependent Hermitian operator, and is a diagonal operator with entries that describe phenomenologically the radiative decays of the eigenstates of to the ground state. Let us observe that the positivity of implies that ; therefore, the evolution is not trace-preserving. We conclude that the pathologies of Equation (71) can be removed with at least two methods: On the one side, one can introduce the jump term to obtain an equation of GKLS type, but this results in introducing dissipation of the rank; on the other side, the contact master equation provides an alternative option, one that fixes the pathologies of Equation (71) while preserving the coherence of the states. However, this comes at the price of introducing nonlinearities.
5. Application: Radiative Decay
The simplest dissipative quantum phenomenon that one can describe by the contact evolution is the radiative decay of a 2-level atom with levels and . To show this, let us consider as the conservative system the following Hamiltonian:
where and are the energies of the states, with . Then, the decay of the particle may be modelled by the contact Hamiltonian:
where represents the expectation value of the Hamiltonian (72), and the constant damping factor describes phenomenologically the radiative decay from the state to . The corresponding contact Hamiltonian equations of motion can be obtained from Equation (43) and read as follows.
In other words, we have a decoupled system of differential equations as expected; therefore, we can focus on the first equation only, for which its solution can be given explicitly by the following:
where the phase and the real constant are defined by the initial condition . Let us recall that because the homogeneous coordinates have been mapped to the sphere via the stereographic projection, in order to consider the state with energy as the initial condition, one has to consider as the “point at infinity” in the plane, corresponding to the north pole of the sphere. In Equation (76), this corresponds to taking .
As an illustration, we depict the behaviour of the solutions of Equation (76) in Figure 3. In Figure 3a, we show the phase portrait in homogeneous coordinates in the plane corresponding to the stereographic projection from the north pole of the sphere. Here, we have a stable focus at the origin; consequently, all nearby solutions evolve towards the origin. On the other hand, considering the coordinates obtained by stereographic projection from the south pole, one has an unstable focus at the origin, as shown in Figure 3b. Finally, both charts form an atlas for the Bloch sphere , and the behaviors of the vector field on such sphere are displayed in Figure 3c. All this is in agreement with our physical interpretation because the north pole corresponds to the excited state with energy and the south pole to the state with lower energy , i.e., we are dissipating energy until the system finally decays in the lower state.
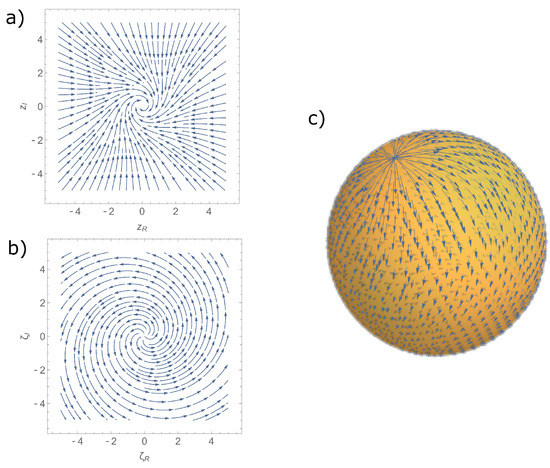
Figure 3.
Phase portrait of the vector field associated with the quantum decay from the higher energy to the lower energy with damping parameter . In (a) the vector field is plotted using the chart with coordinates defined in Equation (32). In (b) this vector field is plotted using the chart with coordinates defined in Equation (32). Finally in (c) the vector field is plotted in the Bloch sphere.
To observe clearly the continuous dissipation of the energy, one may compute the evolution of the expectation value of the conservative Hamiltonian operator (72) by using the solution (76) to obtain the following.
Then, it is not difficult to prove that for the initial condition we have and thus describing the radiative decay from the excited to the ground state. In Figure 4a, we display the continuous transition between these states, for which its speed depends on the value of . Furthermore, we remark that one may equivalently describe excitations within this model by simply exchanging and then having the transition from the lower state to the excited state .
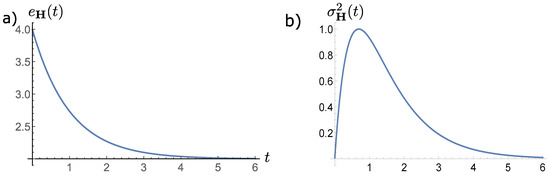
Figure 4.
(a) Continuous transition from the state with energy to the state with damping parameter . (b) Time evolution of the uncertainty of the energy operator with the same parameters.
One may also compute the uncertainty of the energy operator , namely the following:
Its evolution is plotted in Figure 4b. From this figure, one may observe that the uncertainty of the energy starts at zero, then increases up to the maximum value at . After this maximum, the curve decreases asymptotically to zero. Since is the statistical fluctuation around the expectation value, it follows that a measurement of with complete certainty is only possible in principle at the initial and final times.
Another relevant quantity is the probability of a transition between the states, denoted by and given by , where is the initial state and corresponds to the evolved normalized state at time t. Using (62), we obtain that is given by the following:
where we considered the initial condition in this expression. Moreover, by means of Equation (47), we can compute the rate of dissipation of this probability, which is , meaning that one has an exponential decay for the probability of a transition.
We remark again at this point that radiative decays are usually represented as sudden “jumps” and not as continuous transitions. However, recent experimental and theoretical investigations [5,6] have shown that it is possible to observe quantum jumps as continuous processes that preserve the coherence of the state. Here, we have observed in this example that the contact master equation yields another possibility to model quantum decays (or excitations) as coherent and continuous processes.
6. Conclusions and Perspectives
In this work, we have put forward a novel approach to the description of dissipative quantum systems based on the geometric approach to quantum mechanics and on the analogy with the description of classical dissipative systems based on contact Hamiltonian dynamics. Of special importance is the fact that the obtained evolution dissipates the expectation value of the energy of the reference system while preserving the purity of the states. In this manner, it yields a method to describe coherent dissipative dynamics, which inevitably escapes more standard approaches such as the GKSL equation. Among the possible applications, we have considered here, in particular, the important case of radiative decay for a 2-level system, both because of its theoretical importance in understanding quantum mechanics and because of recent experiments that point to an explanation in terms of the existence of coherent quantum trajectories for these systems [5,6].
At this point, there is a number of interesting questions open for future investigations. In particular, in this effort, we have considered the additional variable S as a “means to an end”, that is, as an effective tool that we have employed in order to produce a dissipative dynamics on the reference system in a geometric manner. However, the term as we have used it has the dimensions of an energy, and similar terms appear in the thermodynamic literature as the actual interchange of heat between the reference system and the environment [53,54]. Therefore, a deeper connection with an energy conservation principle may be responsible for our construction.
Still, concerning the variable S, in this work we have dealt only with contact Hamiltonian functions that are linear in S. This is because we can decouple the dynamics of S from that of the quantum states and obtain an evolution that is purely quantum in the sense that it does not depend on other variables.
However, we have remarked that the evolution corresponding to the most general contact Hamiltonian still preserves the trace of the density operator. This is interesting because, in such case, one expects to obtain a non-Markovian evolution mapping pure states into pure states.
Another interesting problem is the extension of the present approach to infinite dimensional quantum systems. Solving this problem in all its generality is not an easy task; however, one may be restricted to the problem of looking for the immersion of a contact manifold into the Hilbert space such that the evolution of the states is parametrized by the contact evolution.
Furthermore, given the importance of the Schrödinger dynamics in the description of quantum systems, one may wonder whether there is a Schrödinger-like equation associated with the contact evolution introduced here. Indeed, for some particular cases, it is possible to construct a Schrödinger equation; for instance, one may reproduce the contact evolution (49) by means of the projection (8) starting from the nonlinear Schrödinger equations:
or
It is not difficult to see that, in both equations, the normalization and the phase are not invariant, and they are involved in the evolution, which introduces nonlinearities in the equations.
Finally, a major motivation for our work and for further investigation is the applications of formalism and a deeper comparison with existing approaches. In the present work, we have deliberately only scratched the surface of some applications, but we expect that, as it happened in the classical case, further systems may be analyzed from this perspective, and new tantalizing results may possibly be found.
Author Contributions
Conceptualization and writing—original draft preparation, H.C.-P.; formal analysis, visualization, writing—review and editing H.C.-P., A.B. and A.G.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of the Contact Master Equation Form
In this appendix, we show that the contact master equation in Equation (63) can be written as in Equation (64). To perform this, let us assume that there exists an operator of the following form:
where is an arbitrary -dimensional Hermitian matrix, is an -dimensional column vector and is a real number. Our goal is to prove that the anticommutator of this operator and the density operator is given by the following:
where the density matrix is of the following form.
A direct computation of the anticommutator yields the following:
where represents the -dimensional identity matrix. Equating the right hand sides of Equations (A2) and (A4) provides the following system of equations.
Let us impose the following conditions:
which guarantee that (A7) is the conjugate transpose of (A6), i.e., Equation (A7) is no longer independent.
We now solve for from Equation (A6) and obtain the following:
where the inverse of the matrix is given by the following.
We then insert (A10) into (A8) and solve for and obtain the following.
So far, we have obtained expressions for and and Equations (A12) and (A13) respectively, for which Equations (A6)–(A8) are satisfied. The remaining Equation (A5) is trivially satisfied by using the following condition.
When the above is inserted into (A5), we yield the following.
As a result, Equation (A5) is trivially satisfied, without any further requirements on the Hermitian matrix . To summarize, we have the operator in (A1), with being any Hermitian matrix, and and given in (A12) and (A13), respectively, satisfies (A2), thus concluding the proof.
References
- Landau, L. Das dämpfungsproblem in der wellenmechanik. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- Chruściński, D.; Pascazio, S. A brief history of the GKLS equation. arXiv 2017, arXiv:1710.05993. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of n-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Minev, Z.K.; Mundhada, S.O.; Shankar, S.; Reinhold, P.; Gutiérrez-Jáuregui, R.; Schoelkopf, R.J.; Mirrahimi, M.; Carmichael, H.J.; Devoret, M.H. To catch and reverse a quantum jump mid-flight. Nature 2019, 570, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Snizhko, K.; Kumar, P.; Romito, A. Quantum Zeno effect appears in stages. Phys. Rev. Res. 2020, 2, 033512. [Google Scholar] [CrossRef]
- Bravetti, A.; Cruz, H.; Tapias, D. Contact Hamiltonian mechanics. Ann. Phys. 2017, 376, 17–39. [Google Scholar] [CrossRef]
- Bravetti, A.; Garcia-Chung, A. A geometric approach to the generalized Noether theorem. J. Phys. Math. Theor. 2021, 54, 095205. [Google Scholar] [CrossRef]
- Bravetti, A.; Tapias, D. Liouville’s theorem and the canonical measure for nonconservative systems from contact geometry. J. Phys. Math. Theor. 2015, 48, 245001. [Google Scholar] [CrossRef]
- Bravetti, A.; de León, M.; Marrero, J.C.; Padrón, E. Invariant measures for contact Hamiltonian systems: Symplectic sandwiches with contact bread. J. Phys. Math. Theor. 2020, 53, 455205. [Google Scholar] [CrossRef]
- De León, M.; Valcázar, M.L. Infinitesimal symmetries in contact Hamiltonian systems. J. Geom. Phys. 2020, 153, 103651. [Google Scholar] [CrossRef]
- Gaset, J.; Gràcia, X.; Muñoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050090. [Google Scholar] [CrossRef]
- Lazo, M.; Paiva, J.; Frederico, G. Noether theorem for action-dependent Lagrangian functions: Conservation laws for non-conservative systems. Nonlinear Dyn. 2019, 97, 1125–1136. [Google Scholar] [CrossRef]
- Cannarsa, P.; Cheng, W.; Wang, K.; Yan, J. Herglotz’ generalized variational principle and contact type Hamilton-Jacobi equations. In Trends in Control Theory and Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2019; pp. 39–67. [Google Scholar]
- Georgieva, B.; Guenther, R. First Noether-type theorem for the generalized variational principle of Herglotz. Topol. Methods Nonlinear Anal. 2002, 20, 261–273. [Google Scholar] [CrossRef]
- Georgieva, B.; Guenther, R.; Bodurov, T. Generalized variational principle of Herglotz for several independent variables. First Noether-type theorem. J. Math. Phys. 2003, 44, 3911–3927. [Google Scholar] [CrossRef]
- Liu, Q.; Torres, P.J.; Wang, C. Contact Hamiltonian dynamics: Variational principles, invariants, completeness and periodic behavior. Ann. Phys. 2018, 395, 26–44. [Google Scholar] [CrossRef]
- Vermeeren, M.; Bravetti, A.; Seri, M. Contact variational integrators. J. Phys. A Math. Theor. 2019, 52, 445206. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Yan, J. Implicit variational principle for contact Hamiltonian systems. Nonlinearity 2016, 30, 492. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Yan, J. Aubry–Mather theory for contact Hamiltonian systems. Commun. Math. Phys. 2019, 366, 981–1023. [Google Scholar] [CrossRef]
- Gaset, J.; Gràcia, X.; Muñoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. A contact geometry framework for field theories with dissipation. Ann. Phys. 2020, 414, 168092. [Google Scholar] [CrossRef]
- Ashtekar, A.; Schilling, T.A. Geometrical Formulation of Quantum Mechanics. In On Einstein’s Path; Springer: Berlin/Heidelberg, Germany, 1999; pp. 23–65. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef]
- Cruz-Prado, H.; Marmo, G.; Schuch, D. Nonlinear description of quantum dynamics. N-level quantum systems. J. Phys. Conf. Ser. 2020, 1612, 012010. [Google Scholar] [CrossRef]
- Ercolessi, E.; Marmo, G.; Mor, I.G. From the equations of motion to the canonical commutation relations. arXiv 2010, arXiv:1005.1164. [Google Scholar]
- Ciaglia, F.M.; Cruz, H.; Marmo, G. Contact manifolds and dissipation, classical and quantum. Ann. Phys. 2018, 398, 159–179. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Cariñena, J.F.; Ibort, A.; Marmo, G.; Morandi, G. Geometry from Dynamics, Classical and Quantum; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Cariñena, J.; Clemente-Gallardo, J.; Jover-Galtier, J.; Marmo, G. Tensorial dynamics on the space of quantum states. J. Phys. Math. Theor. 2017, 50, 365301. [Google Scholar] [CrossRef]
- Ciaglia, F.M.; Di Cosmo, F.; Ibort, A.; Laudato, M.; Marmo, G. Dynamical vector fields on the manifold of quantum states. Open Syst. Inf. Dyn. 2017, 24, 1740003. [Google Scholar] [CrossRef]
- McDuff, D.; Salamon, D. Introduction to Symplectic Topology; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Wootters, W.K. Statistical distance and Hilbert space. Phys. Rev. D 1980, 23, 357. [Google Scholar] [CrossRef]
- Marmo, G.; Saletan, E.J.; Simoni, A.; Vitale, B. Dynamical Systems: A Differential Geometric Approach to Symmetry and Reduction; John Wiley & Sons: Chichester, UK, 1985. [Google Scholar]
- Chaturvedi, S.; Ercolessi, E.; Marmo, G.; Mukunda, N.; Simon, R. Ray space ’riccati’ evolution and geometric phases for N-level quantum systems. Pramana 2007, 69, 317–327. [Google Scholar] [CrossRef][Green Version]
- Cirelli, R.; Mania, A.; Pizzocchero, L. Quantum mechanics as an infinite-dimensional Hamiltonian system with uncertainty structure: Part I. J. Math. Phys. 1990, 31, 2891–2897. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Guha, P. Nonstandard Hamiltonian structures of the liénard equation and contact geometry. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940001. [Google Scholar] [CrossRef]
- De León, M.; Lainz, M. A review on contact Hamiltonian and Lagrangian systems. arXiv 2020, arXiv:2011.05579. [Google Scholar]
- Guha, P.; Block, J.; Ghose-Choudhury, A. Generalized conformal Hamiltonian dynamics and the pattern formation equations. J. Geom. Phys. 2018, 134, 195–208. [Google Scholar] [CrossRef]
- Sloan, D. Dynamical similarity. Phys. Rev. D 2018, 97, 123541. [Google Scholar] [CrossRef]
- Blair, D.E. Riemannian Geometry of Contact and Symplectic Manifolds; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Geiges, H. An Introduction to Contact Topology; Volume 109 of Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2008; ISBN 978-0-521-86585-2. [Google Scholar]
- Boyer, C.; Galicki, K. Sasakian Geometry; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Chruściński, D.; Ciaglia, F.M.; Ibort, A.; Marmo, G.; Ventriglia, F. Stratified manifold of quantum states, actions of the complex special linear group. Ann. Phys. 2019, 400, 221–245. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620. [Google Scholar] [CrossRef]
- Guha, P. Metriplectic structure, leibniz dynamics and dissipative systems. J. Math. Anal. Appl. 2007, 326, 121–136. [Google Scholar] [CrossRef]
- Morrison, P. Thoughts on brackets and dissipation: Old and new. J. Phys. Conf. Ser. 2009, 169, 012006. [Google Scholar] [CrossRef]
- Morrison, P.J. Bracket formulation for irreversible classical fields. Phys. Lett. A 1984, 100, 423–427. [Google Scholar] [CrossRef]
- Pavelka, M.; Klika, V.; Grmela, M. Multiscale Thermo-Dynamics: Introduction to GENERIC; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2018. [Google Scholar]
- Öttinger, H.C. Nonlinear thermodynamic quantum master equation: Properties and examples. Phys. Rev. A 2010, 82, 052119. [Google Scholar] [CrossRef]
- Öttinger, H.C. The geometry and thermodynamics of dissipative quantum systems. EPL Europhys. Lett. 2011, 94, 10006. [Google Scholar] [CrossRef]
- Carmichael, H. An Open Systems Approach to Quantum Optics: Lectures Presented at the Université Libre de Bruxelles, October 28 to November 4, 1991; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lamb, W.E., Jr. Theory of an optical maser. Phys. Rev. 1964, 134, A1429. [Google Scholar] [CrossRef]
- Eberard, D.; Maschke, B.; Van Der Schaft, A. An extension of Hamiltonian systems to the thermodynamic phase space: Towards a geometry of nonreversible processes. Rep. Math. Phys. 2007, 60, 175–198. [Google Scholar] [CrossRef]
- Simoes, A.A.; De León, M.; Valcázar, M.L.; DeDiego, D.M. Contact geometry for simple thermodynamical systems with friction. Proc. R. Soc. A 2020, 476, 20200244. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).