1. Introduction
Quantum entanglement allows for the manifestation of surprising phenomena, when studying the coincidences between pairs of detection events. Famous examples include non-local interference, ghost imaging and quantum teleportation, while more recently this has become an essential ingredient of quantum communication technologies [
1,
2,
3,
4,
5]. Originally, quantum entanglement was seen as an affront to classical conceptions of space [
6] (think “spooky action at a distance”). Yet, Wigner’s delayed-choice experiment expanded this discussion to the dimension of time [
7,
8,
9,
10,
11,
12,
13,
14,
15]. If quanta can be forced to change distribution patterns long after being recorded, does it mean that measurement correlations transcend the boundaries of time? Quantum erasure appeared to give a positive answer to this question [
16,
17,
18,
19,
20]. If a signal beam is passed through an interferometer with distinguishable paths, the idler beam can be used to obtain path knowledge, making interference impossible. However, it is also possible to detect the idler in a way that “erases” path knowledge. This results in the display of interference fringes, even if the idler is detected long after the signal (and the signal event is irreversibly recorded).
While quantum erasure was compatible with novel interpretations, it did not fully close the door on traditional approaches. On the one hand, the data was not uniquely compatible with measurement-based changes in individual quantum properties. In other words, it was not clear whether switching the method of detection of the idler actually controlled the behavior of the signal quanta, rather than the rules of their post-selection [
20]. If two interference patterns are superimposed out of phase, fringe visibility is “washed out”, rather than “erased”. On the other hand, theoretical considerations did not seem decisive either. Alternative joint quantum measurements obey the superposition principle, which means that every observation corresponds to a component from a wide spectrum of possible outcomes. Therefore, it is not possible to conclude, on theoretical grounds alone [
8], that two alternative measurements target the same subset of quanta (after post-selection).
Notwithstanding, there is a way out of this conundrum, because the main concern in this debate is not whether quantum distributions agree with predictions, but whether clues about underlying mechanisms are available. What exactly is happening in the physical realm, when the predictions of quantum theory are confirmed? For the longest time, these questions belonged to the domain of pure speculation. However, two recent developments have changed the rules of the game. Firstly, technological advancements made it possible to conduct reliable experiments with four-quantum entanglement [
21,
22,
23]. Unlike two-quantum records, four quantum data-plots can answer “how” questions, because they make it possible to post-select two-event and four-event coincidences from one and the same record. Secondly, recent theoretical advancements have brought to light unexpected structural relationships between the observable aspects of a bipartite singlet state [
8,
24]. Many interpretations can explain the predictions of quantum theory, but not all of them can account for these subtle nuances, especially in the context of quantum monogamy [
25,
26,
27,
28]. In particular, changing the number of variables investigated with an
n-quantum system can change the expected rates of coincidence. This makes it possible to verify: does quantum monogamy happen simply because four quanta are detected (rather than two), or does it happen because a smaller subset of the data plot is post-selected? In other words, does the coefficient of correlation between two variables change because other parameters are also observed remotely, or does it merely change for a narrow slice of the data record? Accordingly, it is essential to carry out delayed choice monogamy erasure experiments, because they can finally elucidate the underlying principles for the analysis of quantum behavior, at least with regard to temporal non-locality. This could produce definitive answers to some of the questions that have been debated since the discovery of the Einstein-Podolsky-Rosen (EPR) paradox [
6].
2. Background Considerations
Delayed-choice quantum erasure involves a connection between two measurements separated in time, such that a “future” event appears to determine the profile of a “past” event. However, quantum theory is fundamentally non-signaling. Its predictions cannot be used to violate the arrow of time. So, what is going on? The simple answer is that quantum theory is only explicit about “well-defined” events, while EPR states are defined by their mutual relationships [
8]. Therefore, such relationships between quanta must be specified, before they can be revealed. In this case, one event is registered in “the past” and another in “the future”, but the relevant pattern can only be exposed when the two records are reconciled together, in a local frame of reference [
29]. In short, the predictions of quantum theory concern information, or patterns in our knowledge. They do not contain any explicit details about unobservable physical interactions between quanta. Therefore, any discussion about ontological aspects of quantum behavior, including the arrow of time, is meant to uncover facts that go beyond the scope of quantum theory. For example, we might want to know: given the known types of quantum information, what physical conclusions can be drawn with confidence? Granted, we cannot use quantum erasure to alter the past at will, but can we determine beyond reasonable doubt if quantum systems influence each other across time? What kind of experiments can lead to unequivocal answers to such questions?
The current state of the art on this topic is that quantum theory is interpretively overdetermined. In other words, too many competing interpretations are compatible with the same observations. If we look at quantum erasure from the point of view of an interpretation with collapse, the “clear” conclusion is that quantum behavior is non-local and retro-causal [
16,
17]. If we look at the same data from a Bohmian perspective, the equally “clear” conclusion is that quantum behavior is non-local and forward-causal [
30,
31]. Yet, an instrumentalist approach is also possible, in which the data has no temporal implications whatsoever. As shown in various demonstrations, quantum erasure can be explained as a mere “accounting” problem [
20], since a quantum state can be interpreted as a “catalogue of our knowledge” [
11]. The key to such arguments is that “future” events can be shown to generate prescriptions for sampling the “past” record, without altering it in any way. The proverbial fly in the ointment is that these prescriptions come from incompatible physical profiles that cannot be real at the same time. Therefore, it is still not clear: what exactly is happening, mechanically speaking, in a delayed-choice quantum erasure experiment?
In order to appreciate the challenge of interpreting this phenomenon without ambiguity, consider the following textbook example. A source of entangled quanta produces two beams (signal and idler), such that each detectable pair is in the Bell state:
The idler beam is detected with a significant delay, relative to the signal, one qubit at a time. Moreover, each qubit is measured after a random choice between the computational basis {
} or the diagonal basis {
}, such that:
Accordingly, the Bell state in Equation (1) can be rewritten as follows, in order to capture the difference between the two scenarios:
With this in mind, it is easy to envision what is going to be observed in the signal beam, conditional on either choice in the idler. Specifically, the signal detector always collects the same events, but the rules of coincidence change, with direct impact on the post-selected patterns. If the idler is measured in the computational basis , any of the two outcomes is expected with a likelihood of 50:50, both in the signal beam and the idler beam, but the two events are highly correlated. The signal and idler will always detect a or a at the same time. In the double-slit quantum eraser, this corresponds to the “path knowledge” scenario without interference fringes. However, if the idler beam is measured in the diagonal basis , then the expected outcome in the signal is a superposition between two components. Remarkably, the two outcomes have the same 50:50 distribution in the idler, but they generate two phase-shifted coincident patterns in the signal beam: and . The key detail is that the phase shift between these patterns cannot be removed. In the double-slit quantum eraser, they correspond to a set of fringes and a set of anti-fringes that become possible when path information is erased. Accordingly, it is tempting to conclude that nothing special is happening in the signal, even if the idler beam is detected in “the future”, because the so-called “path knowledge” measurement is always a mixture of two interference patterns that “wash out”. Unfortunately, this conclusion is not as solid as it seems, because there is more to this phenomenon than meets the eye.
According to quantum theory, it is possible to combine two quantum erasure experiments into one. This is known as the delayed-choice entanglement swapping protocol [
8,
11,
15]. Specifically, two pairs of entangled beams can be produced independently from each other. The signal beam from each pair is sent to a different observer (say, Alice or Bob), while the idler beams are measured together by a third party (say, Victor) in one of two possible ways. If “nothing special” was happening in the signal beams during quantum erasure, then the observations of Alice and Bob should remain uncorrelated with each other. Yet, shockingly, their beams can behave as if they are entangled (or not), even though none of the detected quanta were ever in contact with each other, directly or indirectly. This manifestation is entirely dependent on Victor’s choice whether to “swap” the input pattern of entanglement, or to preserve it. To clarify, the whole point of the preceding demonstration was that the same populations of quanta can be subdivided in two incompatible ways, without changing the actual record of events. However, here we notice that the same record of events can display the absence of correlation or the presence of Bell correlations, depending on a choice that is performed at a later time by Victor. How is it even possible for a fixed record of events to display Bell violations, when the whole point of Bell’s theorem [
32] is that such a reduction is impossible? Either we are dealing with interlaced quantum measurements that do not target the same populations, or the arrow of time is indeed violated. As a corollary, we can finally understand why quantum erasure experiments are so ambiguous, from an interpretive point of view. By design, quantum erasure works with symmetrical measurements. Therefore, it is not possible to state a priori if “the same exact” quanta are detectable in each measurement scenario. (Maybe they are, maybe they are not). Though, if it was possible to design a similar experiment in which the targeted population size was not equal, then this ambiguity would be diminished. Alternatively, if it was possible to reveal incompatible patterns of coincidence without actually repeating experiments, by merely processing the data differently at both ends of the experiment, then all the ambiguity would be gone. As a corollary, it might be possible to conduct a quantum erasure experiment in which the interpretive conclusions do not depend on arbitrary starting assumptions. If such an experiment can be identified, then quantum theory should be interpreted as non-signaling, both informationally and physically. In contrast, if such a phenomenon cannot be found, then this puzzle will continue to remain unsolved.
Mathematical arguments on topics of this level of complexity can be very precise. Unfortunately, they can also be misleading in the absence of a proper theoretical context. For example, Equations (1)–(4) above appear to describe a complete population. For any number of detected events, 100% are divided in two alternative ways, every time with a 50:50 distribution. Yet, such a conclusion would be incorrect. In an actual delayed choice quantum eraser experiment, these equations apply to a very small subset of all the detected quanta (less than 0.1%), because single detection events outnumber coincident detection events by three orders of magnitude [
18]. Notably, this is not just a technicality, and it has nothing to do with hypothetical loopholes that are sometimes invoked in debates about quantum entanglement. This is a natural aspect of quantum behavior. As it is known, undetected quanta are fundamentally undefined. Their wave-functions have the same levels of spectral complexity as macroscopic beams with chaotic light. For a helpful analogy, consider the fact that unfiltered sunlight cannot generate sharp fringes in a double-slit experiment. Indeed, Thomas Young was famously able to create the first “two-path” interferometer only after isolating a single spatial mode of sunlight with a pinhole [
20]. Likewise, sending a quantum signal beam through a double slit interferometer cannot produce observable interference fringes. Instead, the fringes are revealed in the coincidence regime between two entangled beams, provided that the idler beam (which is not passing through the two slits) is detected with a pinhole detector (rather than a bucket detector). In other words, a relevant spectral component has to be post-selected from a large number of overlapping modes, before the predictions of Equations (1)–(4) can be confirmed. Therefore, it is quite meaningful to ask whether alternative measurements in a quantum eraser target the same sub-ensemble, or not. In other words, do measured components, post-selected with incompatible procedures, correspond to one and the same slice of the input projection? Due to the underlying symmetries, alternative measurements expose sub-ensembles with the same size, but this only adds to the ambiguity, because conflicting interpretations are equally compatible with the record of observations.
A major source of confusion in this context is the radical difference between emitted quanta and detected quanta. An undetected system is governed by a quantum wave-function in all of its complexity. Conventionally speaking, it is “in all the states at the same time”. In contrast, detected quanta are governed by “collapsed” wave-functions. At most, they can reveal information about a single value from a large (and often continuous) distribution. Yet, the actual predictions of quantum theory concern these well-defined events, collected in large numbers, rather than the ideal single (undetected) quanta. Asher Peres, to cite just one example, was famous for his insistence that quantum theory contains no paradoxes, when understood correctly [
29]. In his proposal for a delayed-choice entanglement swapping experiment [
8], he made a point to clarify that quantum erasure describes relationships between sub-ensembles of detected events, rather than meaningful aspects of single systems. These insights were confirmed a few years later, when his predictions were confirmed [
11]. Yet, for the purpose of this discussion, we need to know more. Specifically, does quantum theory predict Bell violations for identical sub-ensembles, post-selected in alternative measurements, or does it predict them for different sub-ensembles? This is the missing piece of the puzzle in these perennial debates about the arrow of time in quantum mechanics. As will be shown below, the answer to this question will enable us to zero in on quantum monogamy as an adequate testbed for this project.
In order to interpret complex phenomena such as the delayed choice entanglement swapping, it helps to start with the basic underlying properties of Bell measurements. The most typical method for validating the presence of quantum entanglement is by testing for violations of Bell-type inequalities, such as the Clauser-Horne-Shimony-Holt (CHSH) inequality [
33]. For example, a pair of beams with entangled photons can be aimed at two detectors (Alice and Bob), each of them with a choice between two observables (
a or
a′ and
b or
b′). In the case of polarization-entangled photons, the highest violations are expected when the angle between the measured linear states of polarization is 22.5° [
34,
35,
36]. Accordingly, if
a corresponds to 0°, then
b must correspond to 22.5°, while
a′ and
b′ may correspond to 45° and 67.5°, respectively. To test for violations of the CHSH inequality, four joint measurements need to be performed, in order to determine four coefficients of quantum correlation (
CQ). Quantum entanglement is verified when the following inequality is violated:
As explained above, each coefficient of correlation is determined for a sub-ensemble of detectable photons. The four sub-ensembles are equal in size, but the big mystery is whether they are physically identical. Again, any quantum may be treated as a candidate for all the possible outcomes before detection, but it cannot “collapse” in all of them at the same time. Given that a set of quanta has generated a coincidence event for a and b, how likely are they to also generate coincidences for a′ and b? More importantly, does quantum theory provide a definitive answer to this question?
As it turns out, quantum theory can answer this question conclusively. In a recent article, Cetto and collaborators presented a rigorous analysis of the bi-partite quantum correlation function, with special emphasis on spin operators and their statistical implications [
24]. As they pointed out, the standard derivation of any Bell-type inequality is formulated for complete populations. Accordingly, in the case of the CHSH paradigm, the four coefficients of correlation are derived for one and the same probability space Λ, and the known inequality follows as a matter of course:
In contrast, this rule cannot work for spin ½ measurements in quantum mechanics, where the spin operator produces non-identical projections for each of the four measurements. Moreover, the magnitudes and orientations of the corresponding vectors in the Bloch sphere translate into different sub-ensembles of a detectable population, without spanning the full probability space. In the words of Cetto et al., incompatible measurements partition the probability space into incompatible subdivisions:
where {Λ
k}, {Λ
l}, {Λ
m}, {Λ
n} represent the four different partitionings of Λ corresponding to the four different pairs of vectors” [
24]. The full details of this demonstration can be found in the cited paper, but the relevant conclusion, for the purpose of this investigation, is that the four sub-ensembles of detected quanta, post-selected for each of the joint measurements in a CHSH test, cannot be physically identical. Accordingly, the Peres conjecture (mentioned above) has been rigorously proven, and we can see that—indeed—the strange predictions of quantum mechanics can be interpreted without paradox, even in the case of delayed-choice entanglement swapping. This insight provides a solid conceptual platform in the search for interpretively conclusive experiments regarding the arrow of time in quantum mechanics.
3. Experimental Implications
A major concern for the interpretation of quantum behavior is the risk of importing classical principles and concepts, without proper justification. In this case, the relevant issue is how to describe the act of measurement. What is the difference between a classical observation, and a quantum observation? Is it merely a difference of degree (large numbers of simultaneous events vs. one-at-a-time), or is there a qualitative difference? Additionally, if there is a qualitative difference, does it just happen spontaneously because one “enters the quantum realm”, or is the measurement scheme actually different in a substantial way? To get to the answer, consider the following. If it is possible to measure a classical system in many different ways, all of those potential outcomes are treated as alternatives to each other (we can have either outcome
A, or outcome
B, or any other outcome). In contrast, if several quantum measurements over non-commuting spin ½ variables are possible, then they are treated as superposed with each other (i.e., the system is in the vector sum of outcome
A and outcome
B, and any other possible outcome). In light of the correspondence principle, large numbers of quantum events should approximate classical behavior. Yet, there is no logical continuity between conjunction and disjunction. We cannot get one pattern from the other, merely by increasing the number of iterations. Therefore, the difference between classical and quantum measurements cannot be simply a matter of degree. There must be a qualitative difference between them, and this difference should be obvious in the corresponding scheme of detection. As shown above, quantum measurements and classical measurements provide answers to different types of questions. Even when classical observations are unconditional (and therefore complete), quantum measurements might be unavoidably conditional (and therefore partial), which is the main conclusion of Cetto et al. [
24].
In hindsight, the partial nature of spin ½ measurements could have been acknowledged from the inception of modern quantum theory. After all, it follows directly from the basic features of the superposition principle. If several measurement outcomes can be derived from the same wave-function in superposition with each other, then every individual outcome should be treated as a component of a wider spectrum (like the color “red” in the rainbow spectrum). By definition, to be in superposition is to be a part of something. Yet, this raises the question: how are the relevant components resolved in practice? For example, Bell experiments are typically performed by sending quanta of light (photons) through polarizing beam-splitters (PBS). This device is as simple as they come. In essence, it is just a pair of birefringent prisms glued together. So, how is it possible for one and the same PBS to behave differently at two levels of observation, in order to obey and to violate Bell-type inequalities in the same record of a delayed choice experiment? Indeed, the PBS cannot, but the measurement procedure is nonetheless different. The so-called classical measurements are supposed to be coarse, and they use “bucket” detectors (or something equivalent), while quantum measurements are intended to be fine, and therefore use “pinhole” detectors (or their equivalents). Though, it is not immediately clear: why would a pinhole be consequential when it comes to polarization? Does it not entail a fair sampling from an incoming projection, given that all the polarization components are superposed with each other? The key to this puzzle is that single quanta are governed by complex wave-functions. The probability distributions of single quanta are qualitatively similar to the distribution patterns of high intensity beams, as captured by the correspondence principle. This similarity facilitates the intuitive explanation (and even prediction) of single-quantum behavior in terms of Fresnel propagation [
3,
4].
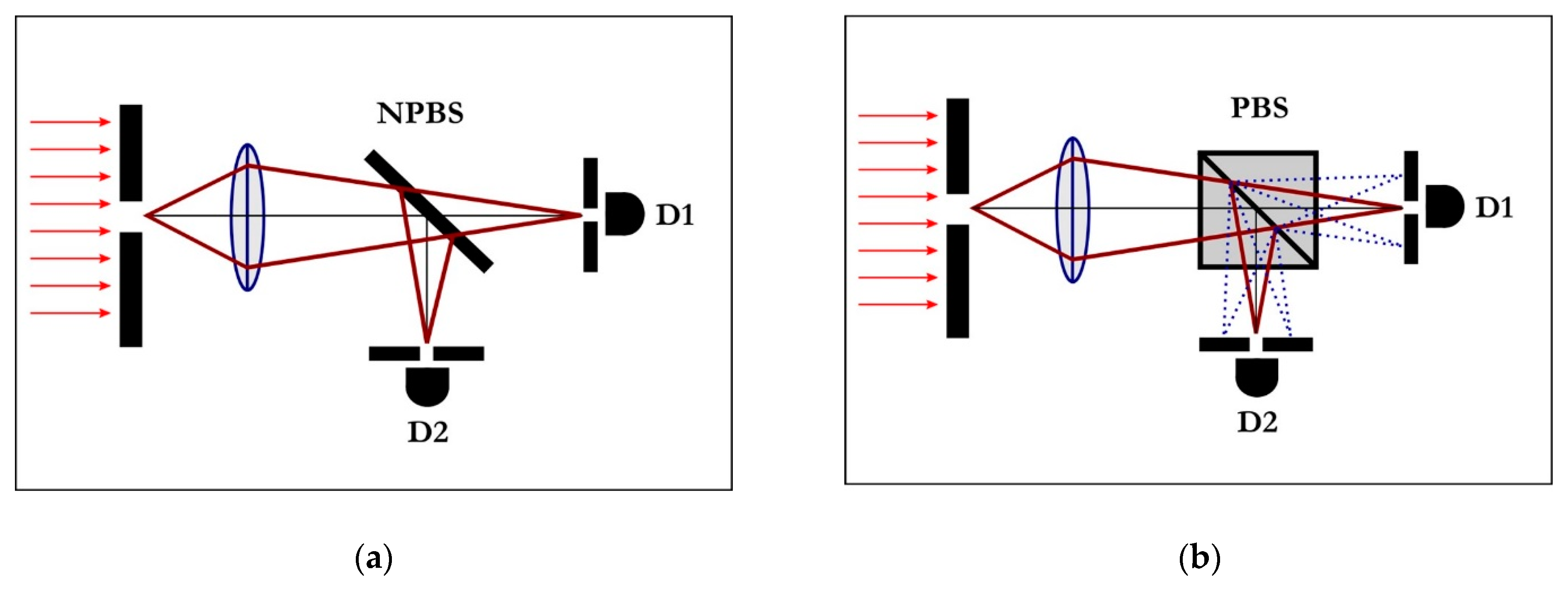
Let us consider a perfectly depolarized classical optical beam. In ideal conditions, the beam is likely to be split 50:50 by a PBS, with negligible losses. By design, there are numerous input states of polarization, but only two output states. As suggested above, this means that a classical measurement of this sort is very coarse. It erases all the information about input polarization components, and only reveals the output of a transformation: how are the input components redistributed between the chosen orthogonal modes of polarization (e.g., vertical and horizontal)? In contrast, quantum measurements are not meant to enforce transformations. They are designed to reveal information about the internal structure (i.e., the spectrum) of input beams, in the form of a distribution. Similar to spatial distributions, where different measurements expose the proportion of quanta arriving at different coordinates in the cross-section of a beam, polarization measurements determine the magnitude of individual components for any axis of interest. In practice, this is achieved by combining polarizing beam-splitters with spatial filters, as shown in
Figure 1. Birefringent crystals have only two kinds of internal paths (slow and fast), but there are numerous incident states of polarization. Therefore, different polarization modes suffer different phase-shifts during propagation through this medium. Some components are slowed down and still exit the fast output, others are slowed down less and still exit the slow output. As a result, a single optical mode (with sharp focal point after passing through a lens) is converted into a multi-mode projection (with numerous focal points), such that every output spatial mode is correlated with an input polarization mode. The basic physics behind this phenomenon can be found in textbook illustrations of Fresnel propagation [
3,
4,
37], wherein the focal point of every projection is determined by the distribution of phase differences between the superposed optical components. As a result, polarization information at the input is converted into spatial information at the output, in this case. This makes it possible to isolate relevant polarization vectors from the input beam, either with a pinhole or with the tip of a single-mode optical fiber.
In order to clarify the role of this mechanism, it is important to point out that all the successful Bell experiments with photons (older [
34,
35,
36] and newer [
38,
39,
40,
41]) combine spatial filters with polarizing analyzers. However, the stated purpose of these elements may differ from case to case. As explained above, in reference to the double-slit quantum eraser, pinhole detectors are the delayed-choice equivalent of classical pinholes. They post-select relevant components from complex projections. For example, entangled photons are often produced via parametric down-conversion in non-linear crystals with large surfaces of emission. In order to post-select consistent sub-ensembles, these surfaces need to be imaged with identical lenses, both in the signal and in the idler beams. This way, both detectors have a higher chance of detecting quantum pairs that emerged from a single source-point. Yet, the combination of lenses and pinholes results in a spatial filter that works in tandem with the PBS, as shown in
Figure 1. If the only function of this device was to post-select input spatial modes, then Bell violations would be impossible. Again, this discussion is not about the objective features of quantum entanglement that relate to undetected single entities. This is about the behavior of well-defined “collapsed” outcomes, whose distributions have to be extracted from fixed records of detection events without contradictions. Moreover, these distributions should be amenable to analysis with non-Kolmogorov probability models (including negative probability values [
42,
43]), which should be impossible in this regime, unless the demonstration of Cetto et al. [
24] is correct. Hence, spatial filters must indeed perform a double duty: they must post-select relevant spatial components and also isolate relevant sub-ensembles from the input polarization profile for each combination of joint measurements, as described above. In plain language, rotating the PBS changes the sub-ensemble of quantum pairs that are able to reach both quantum detectors through the corresponding pinholes, or (with even higher finesse) the receiving tips of single-mode optical fibers.
A direct consequence of this conclusion is that any given pair of entangled quanta has a variable probability of generating a coincidence, depending on the relative angles of polarization measurement. For example, if both quanta are measured in the same plane of polarization, the conditional (heralded) probability of detecting the signal, given that the idler was detected, is 100% in ideal conditions. However, a relative angle of 45° may only result in a conditional probability of 50%, if this process is assumed to conform to Malus’ law. All the other measurement combinations fall in-between these two extremes. Though, as shown above, this change in the rate of coincidence is due to an induced change in the associated spatial profile. Rotating the PBS changes the conditional probability of a quantum to land on the detector pinhole. Still, the input projection has numerous input modes in superposition. Due to the underlying symmetries, an equal proportion from different sub-ensembles drift in and out of the targeted coordinate of detection (more on this below). The end result is that any combination of measurements produces the same total number of coincidences for a fixed time interval, but—as predicted by quantum theory—it is always a slightly different sub-ensemble that ends up being post-selected. This conclusion has profound implications, because it can explain how different types of correlation can be post-selected from a fixed data record. Such a level of understanding is essential for designing a delayed-choice quantum eraser without interpretive ambiguities, as proposed in the next section.
Historically, most Bell experiments were performed with 2-quantum entanglement, usually with polarization entangled photons. However, modern quantum technology allows for experimental design with more than two entangled quanta [
21,
22,
23]. This means that it is possible to design a CHSH-type experiment, in which all the four necessary observables are measured in one shot, instead of making four independent joint measurements. What is the likely outcome of such an experiment? Will the CHSH inequality be violated, or not? For the purpose of the argument, let us consider an ideal source that is able to emit four photons at a time, with polarization parameters in the maximally entangled state:
What is the physical meaning of this description, assuming that all the photons in a set are subjected to independent polarization analysis, as it is done in a typical EPR experiment? The obvious answer is that all the detected sets are going to be perfectly correlated. If measured in the same plane, all the quanta will be detected as vertical, or all of them will be horizontal. More importantly, this state cannot produce correlations in violation of the CHSH inequality (or any other Bell-type inequality), because maximally entangled 4-quantum states are monogamous [
25,
26,
27,
28]. However, in a set with four maximally entangled photons, any two photons can also be treated as maximally entangled, as a pair. In other words, any two photons from such a set, randomly selected for pairwise analysis, will behave as if they are in the state:
Yet, in this regime of observation, we are no longer dealing with maximal entanglement, relative to the full 4-quantum set. Instead, we are dealing with distributive entanglement, which is polygamous [
44,
45,
46,
47]. In other words, if we change nothing in the scheme of detection, compared to the preceding description, we can detect the same set of four entangled photons and expect to obtain violations of the CHSH inequality, for any pair detected in isolation. How is it possible that one and the same record of detected events allows for the post-selection of pairwise coincidences that violate and do not violate a Bell-type inequality at the same time?
This mystery can be solved by taking into account that quantum states are not specified relative to the profile of emission, but rather to the profile of detection. Furthermore, the emergence of various observable patterns can be explained with the details presented above. Suppose that each of the four entangled beams is measured for a different observable, as needed for a typical CHSH test. Specifically,
a = 0°,
b = 22.5°,
a′ = 45° and
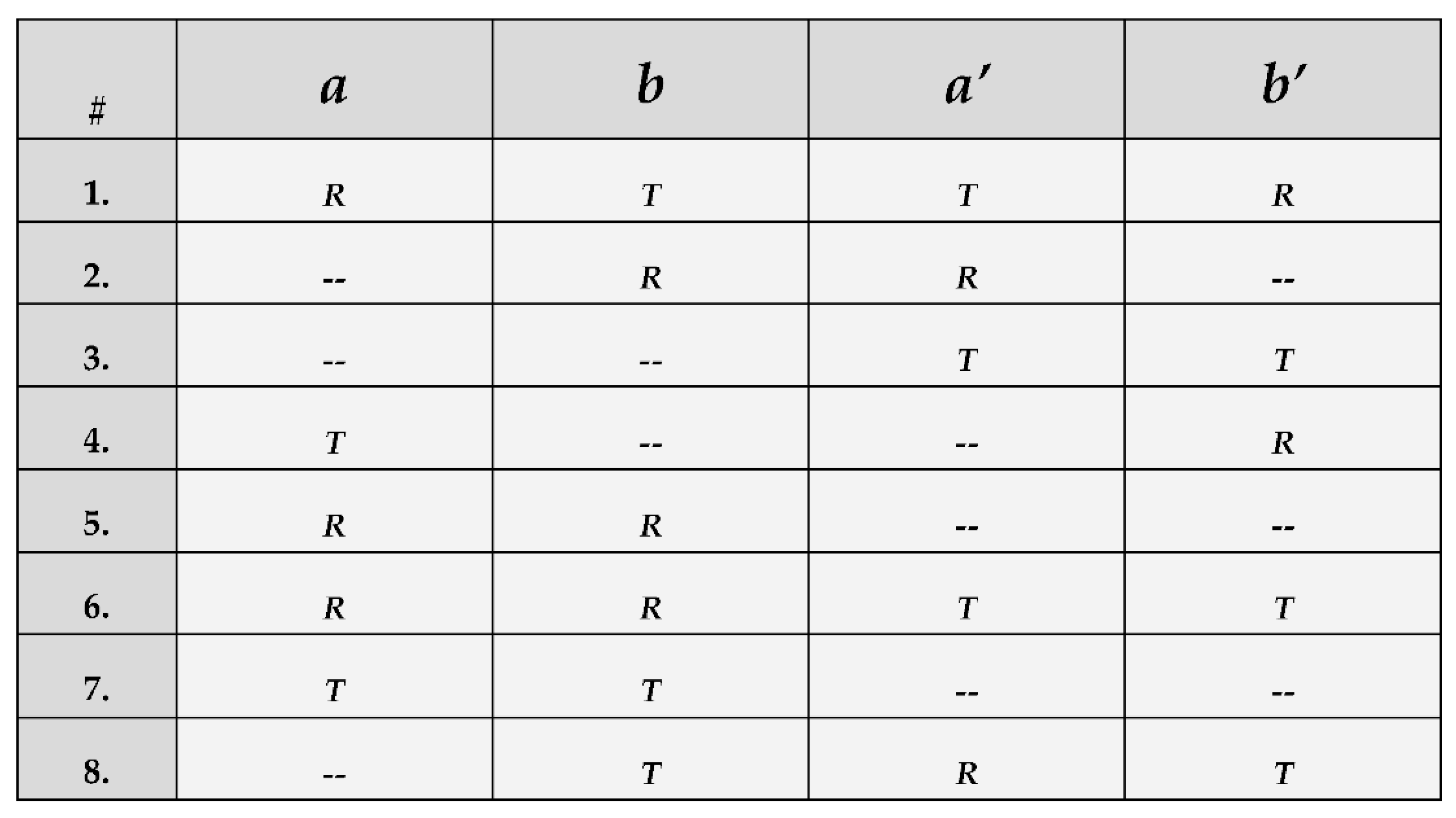
b′ = 67.5°. Just like in a two-quantum Bell test, single detection events are likely to outnumber coincident events by far. However, if we exclude from consideration all the experimental iterations with one detection event (or less) out of four, the remaining record of events is most likely to express a pattern that is shown in
Figure 2 below. In particular, adjacent pairs of events (such as
a and
b, or
b and
a′) have a significantly higher probability of coincidence than other combinations (such as
a with
a′, or
b with
b′). Therefore, in any representative section of the detection record (assuming fair sampling), double coincidences are expected to outnumber triple and quadruple coincidences. This is only natural, considering that quadruple events also include double events, but the reverse relationship does not hold. Hence,
Figure 2 contains coincidences for observables
a and
b only in iterations 1, 5, 6 and 7. Coincidences for observables
b and
a′, on the other hand, are present in iterations 1, 2, 6 and 8. Similarly, coincidences for
a′ and
b′ are found in iterations 1, 3, 6 and 8. As explained above, detectable events for observable
b are able to exhibit coincidences with both adjacent observables, but they are distributed in incompatible ways. A good estimate is that 50% or less of relevant events for observable
b can coincide jointly with observables
a and
a′. As a corollary, the raw data contains all the features of distributive entanglement. As long as the coincidences are post-selected in pairs, regardless of the presence or absence of events in the remaining channels, each combination will result in the selection of a different sub-ensemble from the input projection. Ergo, Bell violations are possible, because the four observables are not jointly distributed in the record of post-selected events. In contrast, observations of 4-quantum maximal entanglement require the physical presence of four coincident events in an iteration, before it can be counted. In
Figure 2, these clusters can only be found in lines 1 and 6. By default, these events are jointly distributed and Bell violations are impossible [
48]. Thus, post-selecting pairwise correlations from a record of 4-quantum coincidences will produce the appearance of monogamy. It is perfectly natural for quantum polygamy and quantum monogamy to coexist in a single data record, since the latter is a sub-ensemble of the former, in this case.
Given the goal of this discussion, it is important to understand why 4-quantum coincidences display classical correlations in the presented experiment. The proper conclusion is not that maximal entanglement can never violate Bell-type inequalities in 4-quantum protocols, but rather that it cannot do so for all four quanta at the same time. The physical reason for any change in the observable patterns of correlation is reducible to the ratio of detectable coincident events in each combination. The range of possible observations is bounded by two extremes. If all four photons are measured in the same way, then 100% of a targeted sub-ensemble is detectable by the four detectors, but one and the same group of collapsed quanta cannot produce equal amounts of information about incompatible variables. As a reminder, each detector collects a large number of single events, but only a small sub-ensemble is post-selected in the coincidence count regime—the one that can reveal information about the targeted components. Consequently, we measure four copies of the same sub-ensemble, and Bell violations are impossible. In the other extreme, if all the four quanta are measured in different ways (providing information about four variables), then four different sub-ensembles are targeted. However, post-selecting 4-photon coincidences results in the isolation of the small region of overlap between the four sub-ensembles. Again, the post-selected sub-ensembles are identical and necessarily produce a joint-distribution for the four measured variables. Therefore, Bell violations are impossible [
48]. However, measuring only two variables at a time avoids this process of truncation, revealing the statistical incompatibility between various pair-wise measurement combinations. For example, suppose that 75% of relevant events for observable
a have coinciding partners for observable
b. Likewise, 75% of the events for observable
b have coinciding partners for
a′, but only 50% of events for
a have matching partners for
a′. It follows that the two joint measurements (
a, b) and (
b,
a′) have equal size, but only 2/3 of the post-selected events are common in both combinations. It is the remaining 1/3 of the events that explain the violation of Bell-type inequalities, because they are statistically incompatible. Yet, making a triple post-selection for (
a,
b,
a′) leaves out this disjoint 1/3, preserving the common pool of events that are statistically compatible. Conversely, if the twins with triplets are subtracted from the longer list of double events, the remaining pairs for (
a,
b) and (
b,
a′) should be maximally incompatible with each other. In other words, they should be able to display super-quantum correlations, in violation of Tsirelson’s bound [
49,
50]. More importantly, the relevant parameter is not the number of detected quanta, but the number of detected variables. If four-quantum sets of entangled photons are used to measure only two variables redundantly, then 3-variable or 4-variable truncation is impossible during post-selection, and this makes it possible to obtain Bell violations in adequate combinations. Notably, by choosing which quanta to measure in non-identical ways and which quanta to measure in identical ways, it is possible to “swap” entanglement from any two quanta in a 4-quantum set to another pair.
With these details in mind, it is finally possible to address the source of ambiguity in the interpretation of delayed choice quantum phenomena. As a rule, these experiments require repeated measurements with quantitatively indistinguishable sub-ensembles. For instance, consider a two-photon experiment studying the correlations between various states of polarization. Suppose that every detector collects 1 million events, in a given time interval, but only 4000 coincidences are post-selected. As shown above, this is expected due to the multimode nature of quantum radiation. Ideally every one of the photons in channel #1 has a partner in channel #2, but only the targeted sub-ensemble is able to land consistently on all of the detection coordinates. For the purpose of the argument, let us assume that the explanation in
Figure 1 above is correct. Rotating the axis of any PBS results in spatial drift in the plane of detection. If the two polarization measurements are parallel, the detected sample is 4000 pairs, as stated. Though, as an exercise in counterfactual analysis, suppose that one detector was rotated by 22.5° instead, and 25% of the detectable single events drifted out. An equal number of quanta drifted in, with a proportional ability to find coincident partners in the other beam. Therefore, then new sample size of joint detection events is again 4000, but only 3000 pairs are common in both cases. Likewise, rotating the PBS by 45° would have resulted in a 50% drift, with the sample size fixed at 4000. Consequently, any pair-wise combination of measurements can result in the same ratio of coincident events. It is impossible to tell, just by looking at the data, if different coefficients of correlation apply to the same sub-ensemble of 4000 out of 1 million photon pairs, or not. The same ambiguity remains if the 2-quantum setting is replaced with a 4-quantum setting, measuring two observables at a time, such as (
a,
a,
b,
b), or (
a′,
b,
b,
a′). Still, this sort of invariance is impossible if the experiment is modified to detect 3 variables, or 4, rather than 2. As shown above, incompatible pairwise combinations result in partially incompatible sub-ensembles. This incompatibility is fundamental, and cannot be removed by any local mechanism for compensation. Therefore, a joint measurement for four variables, such as (
a,
b,
a′,
b′), must necessarily produce a dramatically smaller subset of coincident events. The obvious interpretive advantage is that a change in the observed pattern of coincident behavior is accompanied by a change in the relevant sample size. Moreover, it is even possible to post-select different patterns of coincidence from the same data plot without repeating experiments. As it is known, these are exactly the kinds of patterns that define the basic parameters of quantum monogamy. If such a setting is incorporated in an experiment that exhibits the features of delayed-choice quantum erasure, then age-old questions about the arrow of time in quantum mechanics can be answered conclusively.
4. Proposal
The best way to convey the mechanism of a quantum monogamy eraser is by describing four preliminary experiments that—in a real assay—would have to be performed as part of the calibration procedure. For instance, if the experiment is intended to measure photon polarization, step 1 is to confirm that the source is indeed capable of emitting high-quality 4-quantum entanglement. In other words, all the detectable sets of four photons must be highly correlated in polarization, as shown for example in one of the earliest demonstrations of this phenomenon [
21]. For the purpose of this discussion, let us consider a state with four identical quanta, as described in the preceding section. This makes it easier to visualize the relationship between entangled photons at the subsequent stages, when they are measured in non-identical ways. Case in point, step 2 is to conduct an experiment in which the four quanta are measured for 2 observables, rather than 1. For example, photons #1 and #4 might be passed through polarizing beam-splitters (PBS) with the fast axis oriented at 0°, while photons #2 and #3 are both measured at 22.5°. Even though fourfold coincidences are post-selected, the non-identical measurements are expected to display coefficients of correlation that can violate the CHSH inequality (if the experiment is repeated four times, to collect data about all the necessary measurement combinations). Again, this is a known phenomenon. This structure of observations is typical for entanglement swapping protocols [
8,
9,
10,
11,
13,
15]. Step 3 is to finally demonstrate the reality of quantum monogamy by measuring every photon in a different way. Since the goal is to work with settings that are relevant for the CHSH inequality, the four angles of polarization measurement should be 0°, 22.5°, 45° and 67.5° [
34,
35,
36]. In accordance with the rich literature on this topic [
28], the expected outcome is a non-violation. This is an obvious result, considering that a joint distribution for all the measured variables is going to be produced by default. Yet, step 4 is to complete the study of this state, by confirming the presence of distributive entanglement. The most relevant detail is achieved by measuring quanta #1 and #2, independently from any measurement of quanta #3 and #4, in order to prove that they can produce violations of the CHSH inequality.
A delayed choice monogamy eraser can be constructed by combining steps 2 and 3 in a single experiment. The trick is to detect photons #1 and #2 at time T1, while photons #3 and #4 are at time T2. The delay can be introduced by running the last two quanta through considerably longer optic fibers, before detection. In a nutshell, photons #1 and #2 must be detected in a fixed setting (e.g., 0° and 22.5°, respectively), while photons #3 and #4 can be measured in one of two ways: either for the same observables, as seen in step 2 (i.e., at 0° and 22.5°), or for different observables, as seen in step 3 (i.e., at 45° and 67.5°). As a result, the coefficients of correlation between photons #1 and #2, extracted from the record of 4-quantum coincidences, can be controlled at will by deciding how to measure photons #3 and #4. When fourfold coincidences reveal information about four observables, we have classical correlations and therefore a demonstration of quantum monogamy. When fourfold coincidences reveal information about two observables, we expect non-classical correlations, demonstrating the “erasure” of quantum monogamy. Yet, the choice between the two modes is done with a significant delay, long after recording the values of photons #1 and #2. Therefore, it seems undeniable that the present relationship between two quanta is influenced by the future observation of their entangled partners. Does it follow that the arrow of time is violated in this case?
The novelty of this proposal is not to show that monogamy erasure is possible. Granted, this is an interesting phenomenon, but it is “more of the same”, because it combines well-known features of 4-quantum entanglement with well-known features of already proven types of quantum erasure. The reason to carry out this experiment is the opportunity to settle perennial debates about quantum non-locality, given the details described in the previous section. As shown above, this can be achieved by designing experiments that target sub-ensembles with different size, or by achieving alternative incompatible observations in a single run of the experiment. Firstly, let us assume that photons #1 and #2 change their properties non-locally and collapse in different ways, depending on observer’s choices about photons #3 and #4. If this was true, then the underlying change would be fundamental and irreversible. Therefore, it should be impossible to post-select 2-quantum coincidences with non-classical coefficients from a monogamous data plot. In other words, the raw data of the experiment with 4 observables cannot contain any non-classical correlations, even if the coincidences between photons #1 and #2 are post-selected without regard for the behavior of photons #3 and #4. In contradiction with step 4, described above, two-quantum coincidences should not be able to violate any Bell-type inequality. Additionally, the same two-quantum coincidences should violate Bell-type inequalities, if photons #3 and #4 are detected for redundant observables, as in step 2. Secondly, let us assume that quantum erasure is an artifact of post-selection. In this case, the nature of 4-quantum coincidences should have no effect on the properties of raw 2-quantum events, and Bell violations should persist at the 2-quantum level even in monogamous data plots. Furthermore, if post-selection is the only reason for the observed change in behavior at the 4-quantum level, then the population of quantum pairs post-selected from streams #1 and #2 in step 2 cannot be identical to the population post-selected in step 3. Indeed, the analysis of Cetto et al., discussed above [
24], entails that the rate of 4-quantum coincidences should be smaller when four variables are observed, compared to the experiment in which two variables are detected. If the demonstrated effect of the delayed choice is to switch between two populations with different size at the 4-quantum level, then the hypothesis of temporal non-locality is automatically falsified. If we are dealing with two different populations by size, then we are not dealing with changes in one and the same population. Furthermore, coincidences for photons #1 and #2 can be post-selected in two alternative ways without repeating experiments: as isolated double events, or as members of quadruple events. If the data reveals that classical correlations emerge from a larger ensemble with non-classical correlations, then any concerns about possible violations of the arrow of time are going to be put to rest.
An interesting question to consider is whether a real experiment would support the hypothesis of temporal non-locality, of falsify it. For the purpose of the argument, let us feign ignorance about the discussed conclusions of Cetto et al. If delayed choice quantum erasure is produced by physical non-locality, then sample size should be irrelevant. Any change in behavior should be due to a change in the pattern of collapse. In other words, one and the same sub-ensemble of quantum pairs should display different coefficients of correlation, depending on future choices. If that was indeed the case, then photons #1 and #2 would have observable changes in behavior, even without reconciling the data with photons #3 and #4. After all, the record is already fixed, and the expected sample size is the same in both scenarios. Quadruple post-selection becomes redundant. Yet, this entails that quantum communication should be possible without quantum key distribution. The coefficient of correlation between photons #1 and #2 could be modulated by a choice from the future (or from another planet) regarding the pattern of observation for photons #3 and #4. In other words, quantum entanglement should allow for signaling non-locality, in direct contradiction with quantum theory and all the known quantum phenomena. Accordingly, the expected conclusion of the proposed experiment is that quantum theory is correct and that the arrow of time is indeed obeyed at the quantum level.