Measurement Uncertainty and Dense Coding in a Spin-Star Network

Abstract

Measurement uncertainty limits how precisely information can be extracted from quantum systems due to inherent quantum indeterminacy. On the other hand, dense coding capacity quantifies the amount of classical information that can be sent using shared entanglement, thereby enhancing communication efficiency beyond classical limits. In this paper, we investigate these two concepts for a spin-star network under an external magnetic field under a thermal regime, considering both homogeneous and inhomogeneous models. We reveal that under certain conditions, dense coding capacity not only becomes valid but is also optimized, implying that measurement uncertainty is significantly suppressed. Furthermore, we analyze the local quantum uncertainty of the thermal state under the influence of decoherence channels to assess the effectiveness of the approach studied.

1. Introduction

The uncertainty principle was introduced by Werner Heisenberg [1] (see English translation [2]) to distinguish between classical mechanics and quantum mechanics picture. This principle restricts two incompatible observables, constraining the capability of precisely predicting the desired outcomes of measurements. Earle Kennard [3] and Howard Robertson [4] formulated uncertainty for two observables according to the standard deviation. If there are two observables U and V, then

$$\Delta U\Delta V\ge {\displaystyle \frac{1}{2}}\left|\langle [U,V]\rangle \right|,$$

(1)

where $\Delta g=\sqrt{\langle g^2\rangle -{\langle g\rangle }^2}$ is the standard deviation, $\langle g\rangle$ is the expectation value of operator g, and $[U,V]=UV-VU$ is the commutator [5].

It should be noted that uncertainty relation (1) has some shortcomings, since its lower bound depends strongly on the state: when the system is in one of its eigenstates, the standard deviation is zero, which does not impose any limit on the observable’s standard deviation. Various attempts have been made to rectify and generalize the relationship (1) [6,7,8,9,10,11,12], the most essential of which was introduced by David Deutsch [13] and is known as the entropic uncertainty relation (EUR). Karl Kraus [14] and Hans Maassen and Jos Uffink [15] further developed Deutsch’s approach, proving the lower bound of the total entropy for two incompatible observables in a system, and they concluded that

$$H\left(U\right)+H\left(V\right)\ge -{log}_{2}c,$$

(2)

where $H\left(U\right)=-{\sum }_i{p}_i{log}_2{p}_i$ and $H\left(V\right)=-{\sum }_j{q}_j{log}_2{q}_j$ are the Shannon entropies, with $p_i=〈u_i\left|\rho \right|u_i〉$ and $q_j=〈v_j\left|\rho \right|v_j〉$ where $\left|u_i\right.〉$ and $\left|v_j\right.〉$ are the eigenvectors of U and V observables. $c={max}_{i,j}\left\{\right|\langle u_i|v_j\rangle {|}^2\}$ quantifies the complementarity between the two observables U and V. Indeed, c represents the maximum squared overlap between the eigenstates of the two measurements; the more incompatible the observables, the smaller the c, and the larger the entropic lower bound is.

In 2010, the entropic uncertainty relation in the presence of quantum memory (EUR-QM) was proposed in Ref. [16] as follows:

$$(U_L:=)S\left({\rho }_{U|B}\right)+S\left({\rho }_{V|B}\right)\ge (U_R:=)S\left({\rho }_{A|B}\right)-{log}_{2}c,$$

(3)

where $S\left({\rho }_{X|B}\right)=S\left({\rho }_{XB}\right)-S\left({\rho }_B\right)$ is conditional von Neumann entropy, and $S\left(\rho \right)=-{\sum }_i{\lambda }_i{log}_2{\lambda }_i$ with ${\lambda }_i$ denoting the eigenvalues of $\rho$. After measuring qubit A by Alice, the post-measurement states are

$${\rho }_{UB}=\sum _i({|u_i\rangle }_A\langle u_i|\otimes {\mathit{I}}_B){\rho }_{AB}({|u_i\rangle }_A\langle u_i|\otimes {\mathit{I}}_B),$$

(4)

and

$${\rho }_{VB}=\sum _j({|v_j\rangle }_A\langle v_j|\otimes {\mathit{I}}_B){\rho }_{AB}({|v_j\rangle }_A\langle v_j|\otimes {\mathit{I}}_B),$$

(5)

where ${\mathit{I}}_B$ is the identity operator in Bob’s Hilbert subspace. Note that numerous studies on quantum correlations, measurement uncertainty, and their connections have been carried out for various systems (see, e.g., [17,18,19,20,21,22,23,24] and references therein).

The EUR-QM (3) extends the fundamental Heisenberg uncertainty principle by incorporating correlations between measured systems and quantum memories. This refined relation plays a crucial role in the security analysis of quantum key distribution and other quantum communication protocols, where uncertainty bounds guarantee the confidentiality of transmitted information. Recent advances [25,26] have demonstrated the broad applicability of EUR-QM in designing and optimizing secure quantum communication schemes.

On the other hand, the dense coding protocol was originally introduced as a telecommunication protocol by Charles Bennett and Stephen Wiesner [27] and was first realized in optical systems in 1996 [28], which is considered one of the most significant secure processes of quantum communication. Since then, numerous studies have been conducted to explore dense coding, both in theory and in experiments [29,30,31,32,33,34,35,36,37].

In the dense coding protocol, entangled states and quantum channels are used to transmit classical information, during which one transmits two bits of information by sending one qubit. One of the key criteria of quantum density coding is the channel capacity, known as the dense coding capacity (DCC), measured by the Holevo quantity [38]:

$$\chi =S\left(\overline{\rho }\right)-S\left(\rho \right),$$

(6)

where $S\left(\rho \right)$ is von Neumann entropy, same as that in the inequality (3), and $\overline{\rho }$ denotes the signal ensemble average state.

For a two-qubit system, the ensemble average of individual states produced by the transformation unit is obtained from the following equation:

$$\overline{\rho }={\displaystyle \frac{1}{4}}\sum _{i=0}^3\left(U_i\otimes {\mathit{I}}_2\right)\rho (U_i^{†}\otimes {\mathit{I}}_2),$$

(7)

where the † symbol denotes the Hermitian conjugate, and $U_0={\mathit{I}}_2$, $U_1={\sigma }_x$, $U_2=i{\sigma }_y$, and $U_3={\sigma }_z$, with Pauli operators ${\sigma }_x$, ${\sigma }_y$, and ${\sigma }_z$. For $\chi >1$, the coding is valid; however, the optimal dense coding occurs for ${\chi }_{max}=2$.

Quantum correlations are crucial in quantum communication, and there are various ways to quantify them. One of the key measures of quantum correlations is the local quantum uncertainty (LQU) introduced in Ref. [39] for bipartite systems. This measure belongs to the class of quantum incompatibility measures and does not require complex optimization procedures, unlike some other measures.

For a bipartite system with density matrix ${\rho }_{AB}$, the LQU is computed as

$$\mathrm{LQU}\left({\rho }_{AB}\right)=\underset{k_A}{min}\mathcal{I}\left({\rho }_{AB},K_A\otimes I_B\right),$$

(8)

where $\mathcal{I}\left({\rho }_{AB},K_A\otimes I_B\right)$ is the skew information, introduced by Eugene Wigner and Mutsuo Yanase [40] and defined as

$$\mathcal{I}\left({\rho }_{AB},K_A\otimes I_B\right):=-{\displaystyle \frac{1}{2}}\mathrm{Tr}\left[{\left(\sqrt{{\rho }_{AB}},K_A\otimes I_B\right)}^2\right].$$

(9)

The comparably simple form of LQU for a qubit–qudit system reads

$$\mathrm{LQU}\left({\rho }_{AB}\right)=1-{\lambda }_{max}\left\{W_{AB}\right\},$$

(10)

where ${\lambda }_{max}$ represents the maximum eigenvalue of a $3\times 3$ matrix with the elements

$${\left(W_{AB}\right)}_{lk}\equiv \mathrm{Tr}\left[\sqrt{{\rho }_{AB}}\left({\sigma }_A^l\otimes I_B\right)\sqrt{{\rho }_{AB}}\left({\sigma }_A^k\otimes I_B\right)\right].$$

(11)

Note that for a general two-qubit X state, the LQU formula reads explicitly

$$\mathrm{LQU}\left({\rho }_{\mathrm{X}}\right)=min({\mathcal{U}}_0,{\mathcal{U}}_1),$$

(12)

where the branches ${\mathcal{U}}_0=1-W_{zz}$ and ${\mathcal{U}}_1=1-W_{xx}$ are defined in Ref. [41].

Spin-star networks represent an essential class of many-body quantum systems, appearing in practical platforms such as quantum dots, nitrogen–vacancy centers in diamond, and molecular nanomagnets. These systems naturally model a central qubit interacting with an environment of surrounding spins, providing a realistic testbed for investigating how thermal effects and environmental noise impact quantum correlations and information processing. It is also worth noting that spin-star networks share similarities with star-shaped quantum circuits studied in the context of coherent transport, such as multi-branch graphs for electron or excitation transfer [42], highlighting potential connections between our results on quantum correlations and broader phenomena in quantum transport and netwworked quantum systems. The motivation of this study is to explore how quantum correlations and measurement uncertainty behave in a spin-star network operating in a thermal regime. Specifically, this paper investigates the interplay between the EUR-QM and DCC for both homogeneous and inhomogeneous models. Additionally, the study reveals how thermal states evolve under the influence of noisy quantum channels, and how decoherence impacts the preservation of LQU and, consequently, the system’s quantum correlations.

The novelty of this study lies in demonstrating that the inhomogeneity parameter of the spin-star network plays a significant role in optimizing the DCC while suppressing measurement uncertainty. Moreover, the study systematically investigates the impact of decoherence channels on LQU, providing insight into how environmental noise degrades quantum correlations and directly affects DCC. This combined analysis of EUR-QM, DCC, and LQU under thermal and noisy conditions highlights so far unexplored aspects of quantum information processing in spin-star systems.

The paper is organized as follows. In Section 2, we investigate the physical scenario of a spin-star network system in both homogeneous and inhomogeneous models under a thermal regime. Section 3 is dedicated to the analysis of the relationship between EUR-QM and DCC for both models, Section 4 explores thermal LQU under decoherence effects and Section 5 discusses the physical interpretation of the results obtained. Finally, we conclude the paper with a summary in Section 6.

2. Physical Scenario: Spin-Star Network

In recent decades, various spin models have been introduced, and one of the most essential is the spin-star model [43]. In this model, a number of spins are considered, each of which interacts separately with a central spin, while the interaction between the spins themselves is insignificant [44]. The study of spin-star systems started in 2004 with the paper by Hutton and Bose [43]. Later on, a number of studies have been performed on spin-star systems [45,46,47,48,49,50,51,52].

The Hamiltonian of a spin-star network is introduced as follows (with the reduced Planck constant $\hslash =1$):

$$\mathcal{H}=\sum _{i=1}^{N-1}{j}_i\left({\sigma }_{+}^0{\sigma }_{-}^i+{\sigma }_{-}^0{\sigma }_{+}^i\right)+\Omega \sum _{i=1}^N{\sigma }_z^i,$$

(13)

where $j_i$ is the coupling parameter of the central spin with outer spins, ${\sigma }_i^{\pm }$ denote ladder operators (raising (+) and lowering (−) operators) for the ith spin, and ${\sigma }_0^{\pm }$ address the central spin. N is the number of spins [53,54] and $\Omega$ defines the magnitude of the external magnetic field.

The Gibbs density operator of the system in thermal equilibrium is given as

$$\rho \left(T\right)={\displaystyle \frac{1}{Z}}exp\left(-\beta \mathcal{H}\right),$$

(14)

where T is the temperature and $Z=\mathrm{Tr}\left[exp(-\beta \mathcal{H})\right]$ is a system partition function and $\beta =1/k_{B}T$, where $k_B$ is a Boltzmann constant, which for generalization set to $k_B=1$.

Here, we consider a three-spin-star system ($N=3$) with spin-$1/2$ particles (qubits), where the central spin interacts with two outer spins. Thus, two scenarios can be explored for the present spin-star network. For the first scenario, the condition $j_1=j_2=j$, known as the homogeneous Hamiltonian, is assumed. For the second scenario, conditions $j_1=xj$ and $j_2=j$ are assumed (called the inhomogeneous Hamiltonian), where x is a dimensionless parameter.

The eigenvalues and corresponding eigenstates of the Hamiltonian (13) with $N=3$ are reported in Appendix A. Using Equation (14), the thermal density matrix of the three-qubit system is obtained on the computational basis of the Hilbert space, as given in Appendix B.

For the homogeneous model, by taking partial traces over outer qubits of a three-qubit thermal state, the reduced density matrix ${\rho }_T={\rho }_{12}={\rho }_{13}$ can be expressed as

$${\rho }_T=\left(\begin{array}{cccc}a& 0& 0& 0\\ 0& b& f& 0\\ 0& f& c& 0\\ 0& 0& 0& d\end{array}\right),$$

(15)

where the reduced density matrices for the inhomogeneous model are:

$${\rho }_{12}=\left(\begin{array}{cccc}\alpha & 0& 0& 0\\ 0& \zeta & s& 0\\ 0& s& \tau & 0\\ 0& 0& 0& \xi \end{array}\right),$$

(16)

and

$${\rho }_{13}=\left(\begin{array}{cccc}\nu & 0& 0& 0\\ 0& \mu & \eta & 0\\ 0& \eta & \phi & 0\\ 0& 0& 0& \vartheta \end{array}\right).$$

(17)

All matrix elements are given in Appendix B.

3. Results

In this Section, we analyze and compare thermal EUR-QM and DCC concerning the temperature, coupling parameter, external magnetic field, and inhomogeneity parameter. Without loss of generality, let us take ${\sigma }_x$ and ${\sigma }_z$ as two incompatible observables for the evaluation of measurement uncertainty in the system considered.

Figure 1 illustrates the thermal evolution of the uncertainty and its bound and DCC for a homogeneous model (with the inhomogeneity parameter $x=1$) as functions of T, j, and $\Omega$. In Figure 1a, it is apparent that DCC and EUR-QM remain constant at considerably low temperatures, but with increasing temperature, DCC decreases and eventually disappears, while EUR-QM increases until its maximal value. One can also observe that there is an anti-correlated relationship between EUR-QM and DCC.

From Figure 1b, one can conclude that at a specific temperature of $T=0.5$ and fixed value of the external magnetic field, the measurement uncertainty (DCC) decreases (increases) with strengthening spin coupling and then stabilizes at a certain value. In Figure 1c, one finds that as the external magnetic field strength increases, DCC rises and ultimately stabilizes. However, for uncertainty and its bound, the opposite behavior occurs. That is, the spin coupling and external magnetic field play a constructive role in reducing measurement uncertainty while simultaneously increasing DCC.

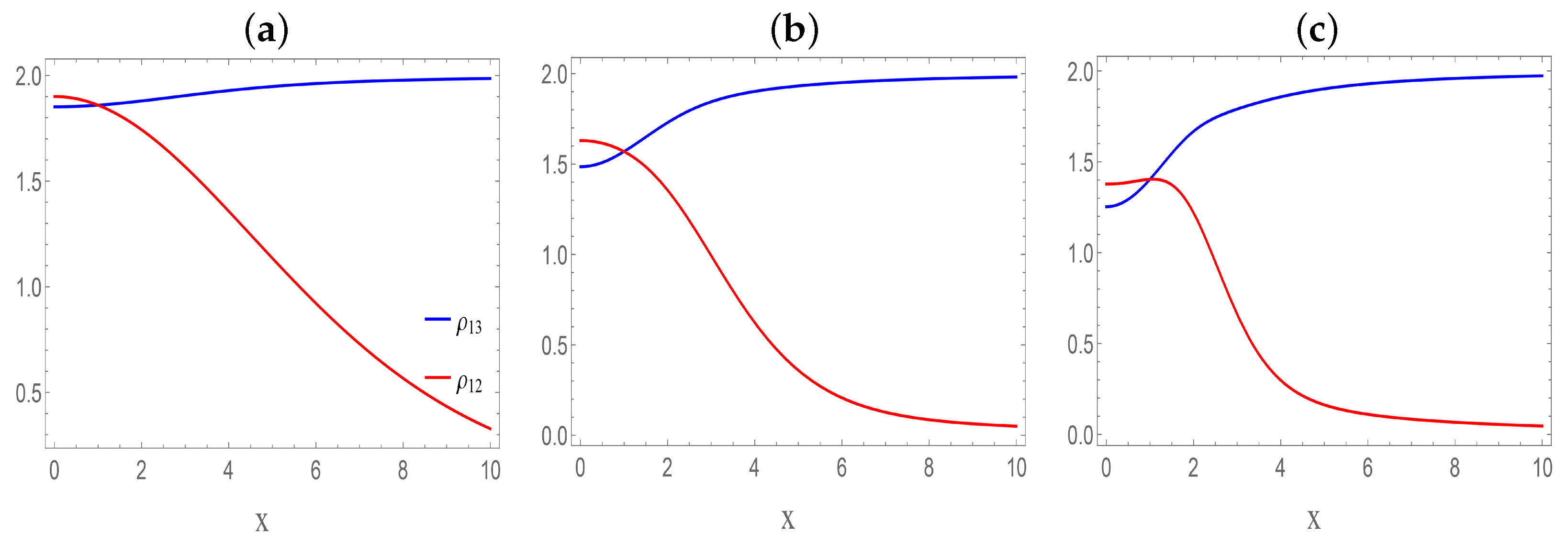
Figure 2 presents a comparison of $U_R\left({\rho }_{13}\right)$ and $U_R\left({\rho }_{12}\right)$ versus the inhomogeneity parameter x. A significant observation is that the quantities follow opposing trends: $U_R\left({\rho }_{12}\right)$ decreases and ultimately approaches zero, while $U_R\left({\rho }_{13}\right)$ increases and eventually stabilizes.

Figure 3 compares $\chi \left({\rho }_{12}\right)$ and $\chi \left({\rho }_{13}\right)$ as a function of the inhomogeneity parameter. As the inhomogeneity parameter increases, $\chi \left({\rho }_{13}\right)$ decreases and eventually vanishes, while $\chi \left({\rho }_{12}\right)$ not only increases but also becomes optimized.

4. Thermal LQU Under Decoherence

When quantum systems interact with the environment, the evolved state of the system can be described by the Born–Markov–Lindblad equations. This approach is justified when the environment acts as a memoryless reservoir and the system–bath coupling is sufficiently weak. The approach enables the use of completely positive trace-preserving (CPTP) maps to evolve the thermal state. This framework also allows us to analyze decoherence through established quantum channels, offering analytical tractability and physical insight into the robustness of quantum correlations in thermal spin-star networks.

Let the initial state of a system be $\rho$. Then, the resulting state after interaction with the environment is calculated as

$$\epsilon \left(\rho \right):=\sum _{i,j}{K}_{i,j}\rho {\mathit{K}}_{i,j}^{†},$$

(18)

where the Kraus operators $K_{i,j}$ referred to as $K_{i,j}=K_i\otimes K_j$ are related to the one-qubit quantum channels represented by $K_i$ and $K_j$. These Kraus operators must satisfy the condition ${\sum }_{i,j}{K}_{i,j}^{†}{K}_{i,j}=I$.

As mentioned in the Introduction, LQU is one measure of quantum correlations. Here, we specifically investigate the characteristics of thermal LQU and explore the effects of three types of decoherence channels [55], namely amplitude damping (AD), phase flip (PF), and phase damping (PD), on the thermal states (15)–(17).

4.1. Amplitude Damping Channel

The AD channel is a quantum operation that describes energy loss in the system. This channel leads to the loss of energy in quantum systems, which is represented by the following Kraus operators:

$$K_1=\left(\begin{array}{cc}1& 0\\ 0& \sqrt{1-\gamma }\end{array}\right)\mathrm{and}{K}_2=\left(\begin{array}{cc}0& \sqrt{\gamma }\\ 0& 0\end{array}\right),$$

(19)

where $\gamma =1-exp\left(-\kappa t\right)\in \left[0,1\right]$ denotes the decoherence parameter and $\kappa$ represents the decay rate.

4.2. Phase Damping Channel

The PD channel is a quantum channel that causes the loss of information in the system without energy loss. Kraus operators for this channel are

$$K_1=\left(\begin{array}{cc}1& 0\\ 0& \sqrt{1-\gamma }\end{array}\right)\mathrm{and}{K}_2=\left(\begin{array}{cc}0& 0\\ 0& \sqrt{\gamma }\end{array}\right).$$

(20)

4.3. Phase Flip Channel

In this channel, operator ${\sigma }_z$ can act on the qubit with probability $\gamma$. This dynamic leads to a unitary transformation characterized by ${\sigma }_z$, resulting in a phase flip. Consequently, the typical representation of the PF decoherence channel for a single qubit can be defined using the Kraus operators

$$K_1=\left(\begin{array}{cc}\sqrt{\gamma }& 0\\ 0& \sqrt{\gamma }\end{array}\right)\mathrm{and}{K}_2=\left(\begin{array}{cc}\sqrt{1-\gamma }& 0\\ 0& -\sqrt{1-\gamma }\end{array}\right).$$

(21)

Let us examine how the LQU varies with the decoherence parameter $\gamma$ in a thermal spin-star network under the PF, PD, and AD channels.

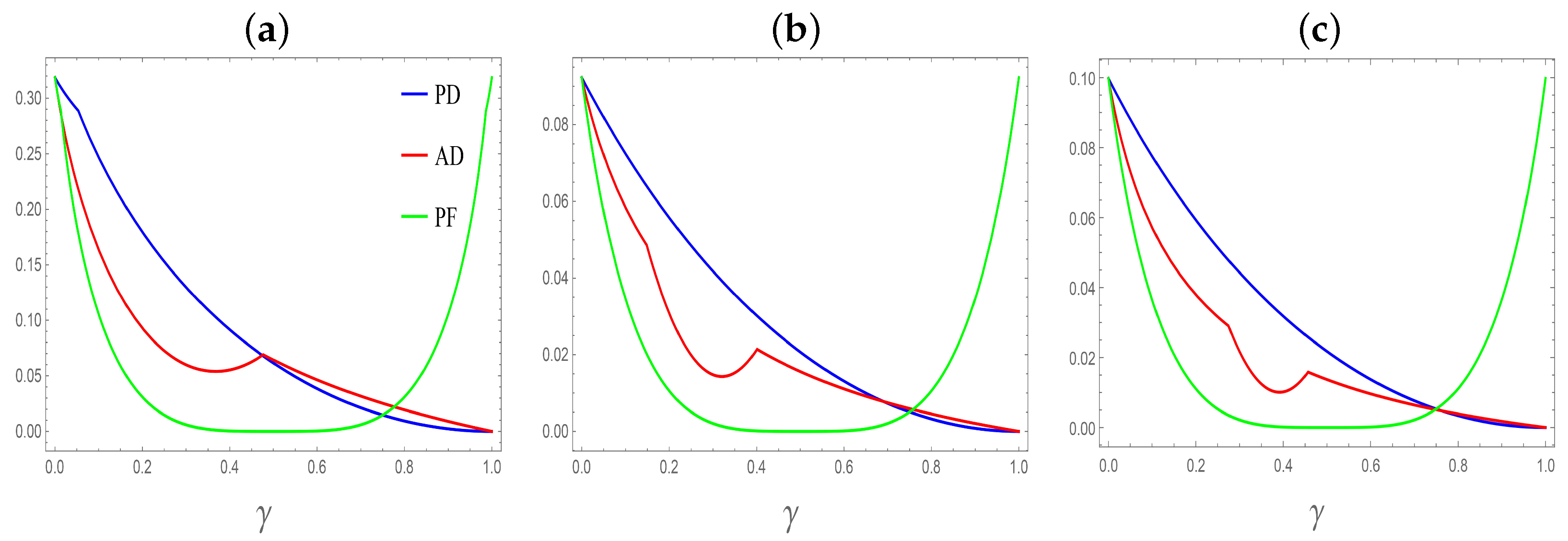
In Figure 4, thermal LQU (12) is plotted as a function of $\gamma$ with $T=j=\Omega =1$ for different types of decoherence channels and three reduced density matrices ${\rho }_T$, ${\rho }_{12}$ and ${\rho }_{13}$.

In Figure 4a, pertaining to the inhomogeneous model, it is observed that in the PD channel, LQU decreases with an increase of $\gamma$. In the AD channel, LQU decreases up to $\gamma$ around $0.3$, and then increases to a minimal value around $\gamma =0.5$ before returning to its trend, and (as there is a crossover point with the PD channel in this region) eventually and entirely vanishes. In the PF channel, LQU is observed to initially exhibiting a decreasing trend and then vanishes around $\gamma =0.5$, and then eventually returns to its maximum initial value. below.

Figure 4b shows the behavior of LQU for ${\rho }_{13}$ in different decohering channels. Similar to what is observed in Figure 4a, there are same trends in the channels, with the only difference that the effects of the channels on the state ${\rho }_{13}$ are better pronounced; that is, quantum correlation is initially observed to be lower.

Based on Figure 4c, the homogeneous model under the AD channel shows that the LQU undergoes quite a rapid and relatively short decrease around $\gamma =0.25$ to $0.35$, after which LQU returns to its regular trend. In the PD channel, as $\gamma$ increases, around $\gamma \approx 0.75$, there is a critical point where the LQU for both AD and PD channels becomes indistinguishable. This points that at this specific value of $\gamma$, the effects of both damping mechanisms on the LQU are essentially the same. Beyond that point, the LQU for both channels steadily diminishes and eventually vanishes. This signifies a complete loss of quantum correlations and dominance by the channel effects. In the PF channel, the LQU decreases with increasing $\gamma$ and assumes a symmetric shape around $\gamma =0.5$.

It is noteworthy that the reason for the sudden changes in the behavior of LQU is that there exists a crossover between two branches ${\mathcal{U}}_0$ and ${\mathcal{U}}_1$ of Equation (12), as also reported in Ref. [41].

In the AD channel, the environment induces energy dissipation from the system, leading to a decay in population in the excited state of the central spin. This results in a quite rapid degradation of quantum correlations, reflected in the steep decline in LQU. Interestingly, a temporary revival is observed in some cases of the reduced denstity matrices due to competition between the damping rate and thermal excitations. This non-monotonic behavior is associated with a crossover between different optimization branches in the LQU expression [41], reflecting sudden changes in the dominant source of quantum uncertainty.

The PD channel primarily affects the phase coherence of the system without altering the populations. As such, the reduction in LQU is rather gradual, highlighting the robustness of certain phase-based quantum correlations against pure dephasing noise.

Regarding the PF channel, LQU displays a symmetric behavior around the decoherence parameter $\gamma =0.5$, indicating that the maximum uncertainty occurs at this point. This symmetry arises from the nature of PF noise, where the effect of flipping with probability $\gamma$ is statistically equivalent to flipping with the probability ($1-\gamma$). Consequently, LQU decreases from its initial value, reaches a minimum around $\gamma =0.5$, and then mirrors the trend as $\gamma$ increases further.

5. Interpretation of Results and Discussion

The findings provide a rather detailed physical picture of how thermal effects, coupling parameters, external fields, inhomogeneity, and environmental noise influence measurement uncertainty and DCC in a spin-star network.

First, the analysis performed demonstrates that temperature plays a crucial role: at relativly low temperatures, both the EUR-QM and DCC remain constant. As temperature increases, DCC decreases and eventually vanishes due to thermal decoherence, while the measurement uncertainty grows and reaches its maximum bound. This anti-correlation illustrates the fundamental trade-off between accessible classical information and quantum uncertainty in thermal regimes. Indeed, as temperature increases, thermal noise destroys quantum coherence. This suppresses DCC, pointing that the system loses its capacity to transmit extra classical information using shared entanglement, while the measurement uncertainty bound increases. From physics point of view, this observation highlights how thermal energy disrupts the delicate quantum correlations needed for quantum communication tasks.

Second, the results reveal that stronger spin coupling and a higher external magnetic field can mitigate measurement uncertainty while enhancing DCC. This indicates that tuning these physical parameters may help preserving constructive quantum correlations and optimize dense coding protocols even in thermal environments.

Regarding the inhomogeneity parameter, the present study uncovers a remarkable competitive behavior: as the inhomogeneity increases, different parts of the spin-star network can either lose or gain quantum resources. Specifically, the uncertainty relation for the reduced density matrix ${\rho }_{12}$ decreases and vanishes, while that for the reduced density matrix ${\rho }_{13}$ increases and stabilizes, showing how local structural asymmetries can be leveraged to control where quantum correlations are concentrated. Likewise, the DCC reflects the following redistribution: $\chi \left({\rho }_{13}\right)$ decreases while $\chi \left({\rho }_{12}\right)$ increases and becomes optimized. By adjusting the inhomogeneity parameter x, quantum correlations can be concentrated in certain spin pairs while being suppressed in others. From physics point of view, this points that network inhomogeneity may be engineered to localize or redistribute constructive quantum resources where the latter are needed most, for example, to direct entanglement towards specific communication links.

Furthermore, by investigating the LQU under three fundamental decoherence channels, we clarify how different noise mechanisms deteriorate quantum correlations. The results indicate that LQU generally decreases as the decoherence parameter $\gamma$ increases, with notable crossover points and non-monotonic behavior in some channels. These sudden changes reflect the switching between different eigen-branches of the quantum state’s structure, consistent with the theoretical predictions in [41]. Importantly, we identify conditions under which certain channels affect LQU identically, revealing a critical parameter region where different types of decoherence become operationally indistinguishable.

Thus, these results obtained demonstrate that by suitably tuning thermal, coupling, and structural parameters (and understanding the influence of noise), one can manage quantum correlations, suppress measurement uncertainty, and optimize dense coding protocols in realistic thermal spin networks.

6. Conclusions and Outlook

In this paper, we investigated the interplay between measurement uncertainty, dense coding capacity, and local quantum uncertainty in a thermal spin-star network, by considering both homogeneous and inhomogeneous models and the effects of environmental decoherence channels. The results obtained provide us with significant physical insights.

We find that temperature plays a critical role in controlling quantum resources: while dense coding capacity remains stable at relatively low temperatures, the capacity degrades quite rapidly with increase of temperature due to thermal noise, whereas measurement uncertainty grows and reaches its maximum bound. This reveals a fundamental trade-off between thermal fluctuations and the preservation of quantum correlations required for quantum communication tasks.

The present analysis shows that stronger spin coupling and external magnetic fields may partially counteract thermal effects, aiding in suppression of the measurement uncertainty and enhance dense coding capacity. This implies that internal interactions and external controls can be tuned to stabilize quantum coherence and improve the performance of dense coding protocols under thermal conditions.

The inhomogeneity parameter provides an additional tool to redistribute quantum correlations within the network. By adjusting the inhomogeneity, quantum resources can be concentrated in specific spin pairs while being suppressed in others, allowing targeted optimization of dense coding capacity and uncertainty bounds. This highlights the potential of engineered asymmetry for controlling where quantum advantages are localized in a system.

Furthermore, the study of local quantum uncertainty under amplitude damping, phase flip, and phase damping channels demonstrates how different noise mechanisms erode quantum correlations. The observed non-monotonic behavior and crossover effects reveal that the impact of decoherence may vary significantly depending on the type of channel and system parameters, emphasizing the need to understand and mitigate specific environmental influences in practical implementations. While the Markovian assumption provides a simplified and extensively used description of environmental decoherence, this assumption excludes memory effects that are known to lead to non-Markovian behavior such as temporal revivals or information backflow. Although such phenomena could influence the dynamics of quantum correlations in our model, the qualitative behavior reported here—particularly the suppression of correlations and entropic uncertainty growth under noise—is expected to remain qualitatively valid. A detailed non-Markovian extension is left for future exploration.

Hence, the results obtained here demonstrate that by suitably tuning the thermal, interaction, and structural parameters and by characterizing the effects of decoherence channels, it is possible to manage measurement uncertainty and dense coding capacity in realistic noisy environments. The study provides valuable guidance for designing robust quantum information protocols and spin-based quantum devices operating at finite temperatures. Specifically, spin-star systems can be engineered in various physical platforms, such as solid-state spin qubits, quantum dots, and nitrogen–vacancy (NV) centers in diamond, where spin interactions and decoherence can be precisely controlled. The studied competition between quantum correlations and thermal or environmental noise is directly relevant to maintaining coherence and optimizing information protocols, such as dense coding, in these systems. This connection helps contextualize the theoretical findings within feasible experimental scenarios and may inform future investigations in quantum information processing.