Derivation of the Ray Equation from Snell’s Law

Abstract

The one-dimensional ray equation, the differential description of Fermat’s principle, is deduced directly from Snell’s law using two methods. In the first method, we obtain the ray equation from a differential equation relating the spatial coordinates derivative with the index of refraction field. In the second method, the ray equation is deduced from the proper generalization of Snell’s law for a refractive field, that is, a differential equation relating the index of refraction field and the refraction angle. Additionally, we used an intermediate expression of the first method to find a straightforward analytical solution of the ray path to an inferior mirage.

1. Introduction

The ray equation constitutes a fundamental approach to determine the path of a light ray (or a ray of any electromagnetic wave) given the local light speed [1] and reads

$$\nabla n={\displaystyle \frac{d}{ds}}\left(n{\displaystyle \frac{d\mathbf{r}}{ds}}\right),$$

(1)

where n is the index of refraction at any point in the propagating medium, $\mathbf{r}$ is the position vector of the light ray and s is the arc length along the ray trajectory. Solutions to the ray equation embody the answer to the problem in geometrical optics of calculating the trajectory of a light ray given the optical properties of the medium and the initial conditions. The equation has applications ranging from light paths through steady-state non-homogeneous atmosphere, like mirages, to the design of gradient-index materials [2]. The ray equation is analogous to the Euler–Lagrange equation. The former is deduced [3,4,5] from Fermat’s principle [6], a variational principle which plays in optics the role that the principle of least action plays in classical mechanics. Fermat’s principle states that the actual path travelled by a light ray between any two points is that for which the optical path length (and equivalently the transit time) between those points is an extremum, generally a minimum.

A former approach to describe the light trajectory in more restricted situations is Snell’s law, which relates the angles of incidence and transmittance (refraction) of a ray propagating across an infinitely sharp interface separating two media with different indices of refraction. Snell’s law was initially deduced by Ibn Sahl in 984 (see, e.g., [7]) but took its name after Willebrord Snellius who rediscovered it in 1621 [8].

This paper presents a pedagogically motivated derivation of the ray equation from Snell’s law. While it is well established that Snell’s law can be derived from the ray equation, as can be encountered in the literature [9,10], our approach reverses this path by deducing the continuous ray equation from Snell’s law in the discrete case. This reversed construction, to the best of our knowledge, has not been reported in the academic literature and can serve as an accessible conceptual bridge for students in pedagogical contexts. The derivation, though restricted to the one-dimensional form of the ray equation, is significant because Snell’s law is a less-general principle compared to the ray equation, which governs the trajectory of light in continuous media with varying refractive indices. The purpose of this paper is strictly educational: to provide an alternative approach that is accessible to undergraduate students with knowledge in geometric optics and circumvents the use of variational calculus. While standard treatments derive the ray equation via Fermat’s principle and variational methods [3], approaches that are elegant but often abstract, the consideration in this paper focuses on a concrete construction using layered media and limiting procedures.

The connection between Fermat’s principle and Snell’s law is classical: Snell’s law follows as a direct result when extremizing or minimizing the time taken by a light ray between two points in media with different refractive indices. Moreover, more general derivations of ray equations under smooth, non-linear boundaries and higher dimensions have been presented [9].

We present two methods to accomplish the task. In the first method, we obtain a differential equation relating the derivative of the Cartesian coordinates and the index of refraction field, an equation obtained earlier by Peter Dyson via a different approach [11]. Instead, we follow a detailed derivation considering a two-dimensional stratified medium composed of layers with different indices of refraction. By making infinitesimal the layer width, we develop a continuous description. From the equation obtained, called throughout the Dyson’s expression, we deduce the ray equation. In the second method, we generalize Snell’s law by means of a differential equation relating the refractive index field and the refraction angle with its derivative. The expression obtained is the differential analogous to Snell’s law so its integration brings back to Snell’s law. Then, from this expression, we get the ray equation.

Snell’s law predicts that the product $nsin\theta$, where $\theta$ is the refraction angle, remains constant when a light ray passes from one medium to another. In Ref. [12], it was demonstrated that, for the general case where the refractive properties of the medium are determined by a variable index field, this assertion only holds when the gradient of the refraction index is unidirectional. This is equivalent to the refractive index being a continuous function of a single spatial variable. The approach used here naturally reproduces the known result that $nsin\theta$ remains constant along the ray path when the gradient of the refractive index is unidirectional and is consistent with the findings of Ref. [12]. However, let us emphasize that the current study does not attempt to verify the results of Ref. [12] in the more general case of multidirectional gradients which are beyond the scope of the present study.

David Allwright obtained Fermat’s principle from Snell’s law when the propagation region is free from caustics [13]. This bears resemblance to the current study as the ray equation is commonly deduced from Fermat’s principle. With this in mind, let us emphasize key differences. Fermat’s principle connects a local refraction condition to a global variational principle governing light propagation but does not explicitly describe how rays evolve in a specific medium or situation. On the other hand, the ray equation offers a concrete mathematical tool aimed at providing a quantitative description of ray dynamics.

In the final part of this paper—in Section 3—we use Dyson’s expression to obtain an analytical solution to the path followed by a light ray in an inferior mirage. This problem is solved starting from the ray equation [14]. Although Dyson’s expression is less general than the ray equation, the Dyson’s expression can be applied more straightforwardly to the problem, this being the reason why the Dyson’s approach is chosen.

2. Derivation of the Ray Equation

2.1. Method 1

Consider an optical medium formed by a stack of k parallel layers immersed in a medium of index of refraction $n_0$, as shown in Figure 1. The ith layer has a width $\mathrm{\Delta }{x}_i$ and index of refraction $n_i$. A light ray impinges at the point $(x_0,y_0)$ on the left interface of the first layer, subtending an angle ${\theta }_0$ with respect to the interface normal. The transmitted ray forms a refracted angle ${\theta }_1$ with respect to the normal, which can be calculated from Snell’s law:

$$n_{0}sin{\theta }_0=n_{1}sin{\theta }_1.$$

(2)

An elementary calculation gives the height $y_1$ at which the ray meets the interface between layers 1 and 2 with an angle ${\theta }_1$:

$$y_1=y_0+tan{\theta }_1\mathrm{\Delta }{x}_1,$$

(3)

where $\mathrm{\Delta }{x}_1=x_1-x_0$. Repeating the procedure for ray height $y_k$, at the right interface of the kth layer, one has

$$y_k=y_0+\sum _{i=1}^{k}tan{\theta }_i\mathrm{\Delta }{x}_i,$$

(4)

where $\mathrm{\Delta }{x}_i=x_i-x_{i-1}$. One can express $tan{\theta }_i$ as

$$tan{\theta }_i={\displaystyle \frac{sin{\theta }_i}{\sqrt{1-{sin}^2{\theta }_i}}}.$$

(5)

Calculating the square root of $1-{sin}^2{\theta }_i$ in Equation (5) introduces a plus–minus sign not shown in Equation (5) and subsequent equations for simplicity. The transmission angle, ${\theta }_i$, of the ray exiting the interface at $x_{i-1}$ is equal to the incident angle with the interface at $x_i$ because the interfaces are parallel or equivalently, changes in the index of refraction only occur along the x-axis. Thus, $n_{i}sin{\theta }_i=n_{0}sin{\theta }_0$ is constant. Multiplying and dividing Equation (5) by $n_i$ and substituting the result into Equation (4) leads to

$$y_k=y_0+\sum _{i=1}^k{\displaystyle \frac{n_{0}sin{\theta }_0}{\sqrt{n_i^2-{(n_{0}sin{\theta }_0)}^2}}}\mathrm{\Delta }{x}_i.$$

(6)

Taking the limit when $\mathrm{\Delta }{x}_i$ tends to zero, $n_i\to n\left(x\right)$, one has

$$y\left(x\right)=y_0+{\int }_{x_0}^x{\displaystyle \frac{n_{0}sin{\theta }_0}{\sqrt{n^2-{(n_{0}sin{\theta }_0)}^2}}}dx.$$

(7)

Differentiating Equation (7) with respect to x, one obtains Dyson’s expression

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{n_{0}sin{\theta }_0}{\sqrt{n^2-{(n_{0}sin{\theta }_0)}^2}}}.$$

(8)

Let us emphasize that, in the transition to the continuous, $n_{i}sin{\theta }_i$ becomes $nsin\theta$, where $n=n\left(x\right)$ and $\theta =\theta \left(x\right)$ are smooth functions of x, and $\theta$ is the instantaneous angle between the ray direction and the x axis. While n and $sin\theta$ are variables, their product remains constant, so

$$nsin\theta =n_{0}sin{\theta }_0=a.$$

(9)

Thus, clearing for n in Equation (8) and differentiating (9) with respect to x, one has

$${\displaystyle \frac{dn}{dx}}=-{\displaystyle \frac{a{y}^{″}}{{\left(y^{\prime }\right)}^2\sqrt{1+{\left(y^{\prime }\right)}^2}}},$$

(10)

where the prime denotes x-derivative. Noting that

$${\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{1}{y^{\prime }}}\right)=-{\displaystyle \frac{y^{″}}{{\left(y^{\prime }\right)}^2}},$$

(11)

and

$${\displaystyle \frac{ds}{dx}}=\sqrt{1+{\left({\displaystyle \frac{dy}{dx}}\right)}^2},$$

(12)

where s is the arc length along the ray trajectory, one rearranges Equation (10) by substitution into it of Equations (11) and (12) to get

$${\displaystyle \frac{dn}{dx}}=a{\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{1}{y^{\prime }}}\right){\displaystyle \frac{dx}{ds}}.$$

(13)

With $y^{\prime }=tan\theta$ and inserting the constant $a=nsin\theta$ into the derivative, one finds

$${\displaystyle \frac{dn}{dx}}={\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{nsin\theta }{tan\theta }}\right){\displaystyle \frac{dx}{ds}}.$$

(14)

Let us emphasize that although we write the quantity a within the derivative in Equation (14), this does not imply that a varies with x in the case considered. Under the assumption of a unidirectional refractive index gradient, $a=nsin\theta =n_{0}sin{\theta }_0$ remains constant along the ray path. The inclusion of a into the derivative is a formal mathematical step, introduced to facilitate the algebraic manipulation leading to the final form of the ray equation. This symbolic treatment does not contradict the physical constancy of a, as dictated by Snell’s law. The differential element of arc length along the ray path $ds$ corresponds to the hypotenuse of an infinitesimal triangle with sides $dx$ and $dy$ and subtends an angle $\theta$ with the x axis (see inset of Figure 1), thus $cos\theta =dx/ds$. Making these substitutions, one has

$${\displaystyle \frac{dn}{dx}}={\displaystyle \frac{d}{dx}}\left(n{\displaystyle \frac{dx}{ds}}\right){\displaystyle \frac{dx}{ds}}.$$

(15)

Applying the chain rule to the right-hand-side of Equation (15), one gets

$${\displaystyle \frac{d}{ds}}\left(n{\displaystyle \frac{dx}{ds}}\right)={\displaystyle \frac{d}{dx}}\left(n{\displaystyle \frac{dx}{ds}}\right){\displaystyle \frac{dx}{ds}}.$$

(16)

and finally,

$${\displaystyle \frac{dn}{dx}}={\displaystyle \frac{d}{ds}}\left(n{\displaystyle \frac{dx}{ds}}\right).$$

(17)

which is the one-dimensional expression of the ray Equation (1).

2.2. Method 2

A different approach can start from Equation (18), the expression of Snell’s law for a refractive index field. This relates the refractive angle $\theta$, and the index of refraction n, at an arbitrary point in the light path, with the infinitesimal change in the refractive angle $d\theta$, when the light ray propagates an arc of differential length $ds$, through which the index of refraction changes an infinitesimal amount $dn$:

$$nsin\theta =(n+dn)sin(\theta +d\theta ).$$

(18)

Using the angle sum identity of the sine and given that $cosd\theta =1$, $sind\theta =d\theta$, and $dnd\theta cos\theta =0$, one finds

$${\displaystyle \frac{dn}{d\theta }}+ncot\theta =0.$$

(19)

Note that integration of Equation (19) gives Snell’s law (9), as it has to. Thus, differentiating Equation (9) constitutes a more straightforward way to obtain Equation (19); however, we choose the method shown to circumvent the explicit incorporation into the equations of the constant $a=n_{0}sin{\theta }_0$. Now, given that $dn/d\theta =(dn/ds)(ds/d\theta )$ and $cot\theta =dx/dy$, one has

$${\displaystyle \frac{dn}{ds}}=-{\displaystyle \frac{n}{y^{\prime }}}\kappa ,$$

(20)

where $\kappa =d\theta /ds$ is the curvature of the ray path. Using the chain rule for $dn/ds=(dn/dx)(dx/ds)$, the expression for curvature $\kappa =y^{″}/{[1+{\left(y^{\prime }\right)}^2]}^{3/2}$, and multiplying and dividing Equation (20) by $y^{\prime }$, one obtains

$${\displaystyle \frac{dn}{dx}}{\displaystyle \frac{dx}{ds}}=-{\displaystyle \frac{n{y}^{\prime }{y}^{″}}{{\left(y^{\prime }\right)}^2{[1+{\left(y^{\prime }\right)}^2]}^{3/2}}}.$$

(21)

Using Equations (11) and (12), one finds:

$${\displaystyle \frac{dn}{dx}}=n{\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{1}{y^{\prime }}}\right){\displaystyle \frac{dy}{dx}}{\displaystyle \frac{dx}{ds}}{\displaystyle \frac{dx}{ds}}.$$

(22)

By substituting $(dy/dx)(dx/ds)=dy/ds=sin\theta$ and $y^{\prime }=tan\theta$ into Equation (22), and inserting $nsin\theta$ into the derivative, one gets Equation (14) from which the ray Equation (17) was already obtained.

3. Analytical Solution of Mirage Ray-Path

Equation (8) is a differential equation of more natural interpretation and implementation than the one-dimensional ray Equation (17). Equation (8) allows the calculation of ray trajectory in a medium where the index of refraction is a continuous function of the spatial position. Despite its simplicity and elementary of deduction, Equation (8) is not taught in undergraduate courses and textbooks on optics (see, e.g., Refs. [1,15,16,17]). Let us apply Equation (8) to calculate the light path in an inferior mirage.

Inferior mirages form when light rays are refracted by a gradient of hot air which develops right above heating ground, typically sand or asphalt. As height increases, air becomes cooler and, in the absence of convection currents, denser, which produces an increasing index of refraction. An intuitive conclusion based on geometrical optics considerations leads to a belief that rays should remain horizontal when reaching the minimum and not bend; however, this has been discussed and solved [11,18,19,20].

According to Robert Fleagle, the air temperature profile decays exponentially with height [21], so the index of refraction can be exppressed as follows [14,22]:

$$n^2\left(x\right)=n_g^2+n_1^2[1-exp(-\alpha x)],$$

(23)

where $n_g$ is the air index of refraction at the ground surface, and $n_1$ and $\alpha$ are constants. Note that, in the description given here, the x-coordinate corresponds to the height over the ground and a refractive index is chosen increasing as x increases, opposed to what is depicted in Figure 1; see Figure 2 for reference. Substitution of Equation (23) into Equation (8) gives

$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{p}{\sqrt{1-qexp(-\alpha x)}}},$$

(24)

where $p=n_{0}sin{\theta }_0/\eta$, $q=n_1^2/{\eta }^2$, and ${\eta }^2=n_g^2+n_1^2-{(n_{0}sin{\theta }_0)}^2$. Equation (24) can be solved by basic integration methods; then, one gets

$$y=y_0\pm {\displaystyle \frac{p}{\alpha }}ln\left|{\displaystyle \frac{\sqrt{1-qexp(-\alpha x)}+1}{\sqrt{1-qexp(-\alpha x)}-1}}\right|,$$

(25)

where $y_0$ is the integration constant determined by the initial conditions. In Equation (25), we explicitly show the plus–minus sign that appears in the radical of Equation (5) to obtain both branches of the solution.

Given the construction of the frame of reference in the consideration here, the slope of the minimum in Equation (8) is vertical, that is, parallel to the y axis, so with the aim to determine the position of the minimum, we express Equation (8) as $dx/dy=0$. Hence, one finds out the condition that the index of refraction meets at the minimum of the ray path:

$${\displaystyle \frac{dx}{dy}}={\displaystyle \frac{\sqrt{n_m^2-{(n_{0}sin{\theta }_0)}^2}}{n_{0}sin{\theta }_0}}=0.$$

(26)

Here $n_m$ is the index of refraction at the minimum. Then,

$$n_m=n_{0}sin{\theta }_0.$$

(27)

Let us substitute $n_m$ (27) into Equation (23) to obtain the height $x_m$ over the ground of the minimum:

$$n_0^2{sin}^2{\theta }_0=n_g^2+n_1^2[1-exp(-\alpha x_m)],$$

(28)

and thus,

$$x_m=-{\displaystyle \frac{1}{\alpha }}ln\left|1+{\displaystyle \frac{n_g^2-n_0^{2}sin{\theta }_0^2}{n_1^2}}\right|.$$

(29)

Substitution of Equation (29) into Equation (25) gives the position $y_m$ of the minimum, which can be related to the distance from the observer.

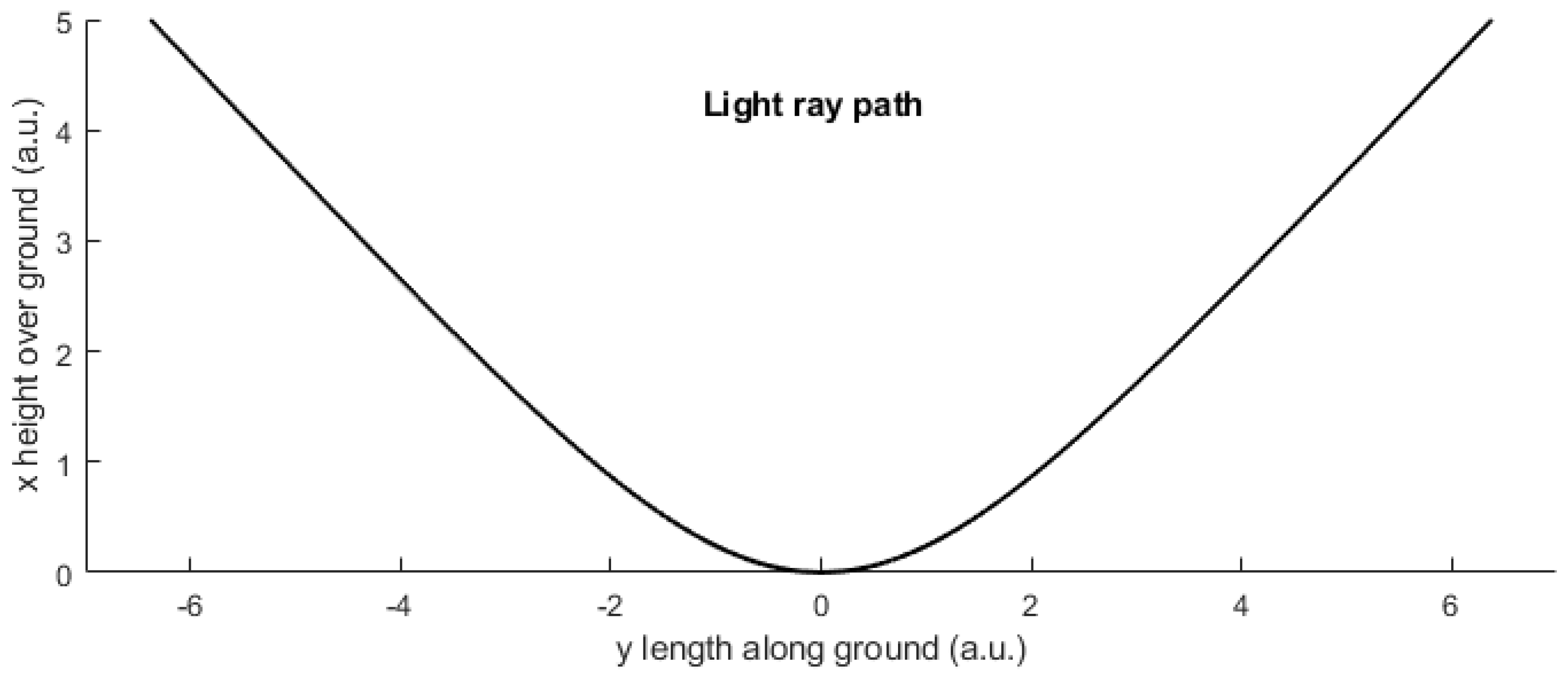
Figure 2 shows the light path of an inferior mirage, given by Equation (25) with $y_0=0$ and all other constants being set to 1. In this case, if the index of refraction at the ground meets the condition of Equation (27), the logarithm argument in Equation (29) is 1 and the height of the minimum is 0 what is represented in Figure 2.

4. Conclusions

Snell’s law constitutes a theoretical description aimed at addressing the change in direction of a light ray when passing through a sharp interface separating two media where light speed is different but constant at each side. Thus, it is not applicable to the calculation of the ray trajectory, when light velocity is a continuous function of position. The ray equation, derived from Fermat’s principle, stands as the appropriate framework for this general case. We deduce the ray equation in one dimension directly from Snell’s law using two methods: from a differential equation in terms of the Cartesian coordinates and the refractive index (Dyson’s expression) (method 1) and from the differential equivalent of Snell’s law (method 2), both obtained from Snell’s law.

In Section 3, we use Dyson’s expression to find an analytical solution for the light path in an inferior mirage. The application of Dyson’s expression to this problem is straightforward and provides a more natural approach compared to the ray equation. Throughout this study, we consider an index gradient along the x coordinate. When applied to the mirage problem, we get directly $y\left(x\right)$ and the curve rotated in contrast to Ref. [14].

Let us make two final remarks. This study is strictly limited to a one-dimensional derivation of the ray equation under the assumption of a unidirectional refractive index gradient; thus, the quantity $a=nsin\theta$ remains constant in accordance with Snell’s law. The goal here is pedagogical with the aim to show how Snell’s law, typically taught as a discrete boundary condition, can lead to the ray equation when applied in the continuous limit of a stratified medium, method 1, or in the differential version of Snell’s law, method 2.