Testing the Double-Logarithmic Asymptotic Gluon Density in Ultraperipheral Heavy-Ion Collisions at the Large Hadron Collider
Abstract
1. Introduction
2. Theoretical Framework and Phenomenological Models
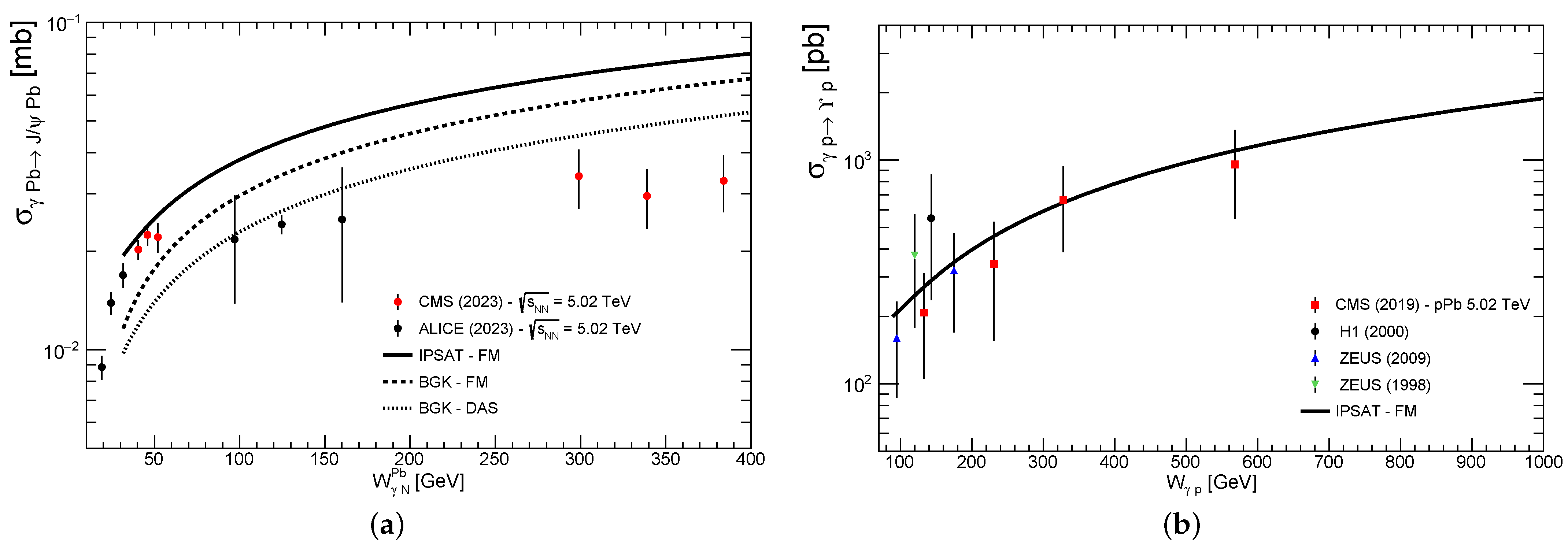
3. Results and Discussion
4. Conclusions and Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| nucleus–nucleus | |
| ALICE | A Large Ion Collider Experiment |
| BGK | Bartels–Golec-Biernat–Kowalski |
| c.m. | center-of-mass |
| CGC | color–glass condensate |
| DAS | double-asymptotic scaling |
| DDIS | diffractive DIS |
| DGLAP | Dokshitzer–Gribov–Lipatov–Altarelli–Parisi |
| DIS | deep-inelastic scattering |
| DVCS | deeply virtual Compton scattering |
| EIC | Electron–Ion Collider |
| EMD | electromagnetic dissociation |
| EPA | equivalent photon approximation |
| electron–nucleus | |
| electron–proton | |
| FM | Fagundes–Machado |
| HERA | Hadron–Electron Ring Accelerator |
| IPSAT | impact-parameter saturation model |
| LCG | light-cone Gaussian |
| LHeC | Large Hadron–Electron Collider |
| LHC | Large Hadron Collider |
| LHCb | LHC beauty (experiment) |
| LO | leading-order |
| NLO | next-to-LO |
| nucleon–nucleon | |
| parton density function | |
| proton–nucleus | |
| proton–proton | |
| pQCD | perturbative QCD |
| QCD | quantim chromodynamics |
| quark–anti-quark | |
| RHIC | Relativistic Heavy Ion Collider |
| STAR | Solenoidal Tracker at RHIC |
| UGD | unintegrated gluon distribution |
| UPC | ultraperipheral collision |
| V | vector meson |
| photon–nucleus/electron/nucleon/proton |
References
- Gribov, L.V.; Levin, E.M.; Ryskin, M.G. Semihard processes in QCD. Phys. Rep. 1983, 100, 1–150. [Google Scholar] [CrossRef]
- Mueller, A.H.; Qiu, J.W. Gluon recombination and shadowing at small values of x. Nucl. Phys. B 1986, 268, 427–452. [Google Scholar] [CrossRef]
- Mueller, A.H. Parton saturation: An overview. In Proceedings of the Cargese Summer School on QCD Perspectives on Hot and Dense Matter, Cargese, France, 6–18 August 2001; pp. 45–72. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 1994, 49, 2233–2241. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 1994, 49, 3352–3355. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Green’s functions in the color field of a large nucleus. Phys. Rev. D 1994, 50, 2225–2233. [Google Scholar] [CrossRef]
- Ayala, A.; Jalilian-Marian, J.; McLerran, L.D.; Venugopalan, R. The gluon propagator in non-Abelian Weizsäcker–Williams fields. Phys. Rev. D 1995, 52, 2935–2943. [Google Scholar] [CrossRef]
- Ayala, A.; Jalilian-Marian, J.; McLerran, L.D.; Venugopalan, R. Quantum corrections to the Weizsäcker–Williams gluon distribution function at small x. Phys. Rev. D 1996, 53, 458–475. [Google Scholar] [CrossRef]
- Iancu, E.; Venugopalan, R. The color glass condensate and high energy scattering in QCD. In Quark–Gluon Plasma 3; Hwa, R.C., Wang, X.-N., Eds.; World Scientific Co. Ltd.: Singapore, 2004; pp. 249–363. [Google Scholar] [CrossRef]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef]
- Morreale, A.; Salazar, F. Mining for Gluon Saturation at Colliders. Universe 2021, 7, 312. [Google Scholar] [CrossRef]
- Nikolaev, N.N.; Zakharov, B.G. Color transparency and scaling properties of nuclear shadowing in deep inelastic scattering. Z. Phys. C 1991, 49, 607–618. [Google Scholar] [CrossRef]
- Nikolaev, N.N.; Zakharov, B.G. Pomeron structure function and diffraction dissociation of virtual photons in perturbative QCD. Z. Phys. C 1992, 53, 331–346. [Google Scholar] [CrossRef]
- Mueller, A.H. Soft gluons in the infinite momentum wave function and the BFKL pomeron. Nucl. Phys. B 1994, 415, 373–385. [Google Scholar] [CrossRef]
- Mueller, A.H.; Patel, B. Single and double BFKL pomeron exchange and a dipole picture of high-energy hard processes. Nucl. Phys. B 1994, 425, 471–488. [Google Scholar] [CrossRef]
- Henkels, C.; de Oliveira, E.G.; Pasechnik, R.; Trebien, H. Exclusive photo- and electroproduction of excited light vector mesons via holographic model. Eur. Phys. J. C 2023, 83, 551. [Google Scholar] [CrossRef]
- Cisek, A.; Schäfer, W.; Szczurek, A. Exclusive production of ρ meson in gamma-proton collisions: dσ/dt and the role of helicity flip processes. Phys. Lett. B 2023, 836, 137595. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Salazar, F.; Schenke, B. Nuclear geometry at high energy from exclusive vector meson production. Phys. Rev. D 2022, 106, 074019. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Penttala, J. Complete calculation of exclusive heavy vector meson production at next-to-leading order in the dipole picture. J. High Energy Phys. 2022, 2022, 247. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Penttala, J. Exclusive production of light vector mesons at next-to-leading order in the dipole picture. Phys. Rev. D 2022, 105, 114038. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Penttala, J. Exclusive heavy vector meson production at next-to-leading order in the dipole picture. Phys. Lett. B 2021, 823, 136723. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Krelina, M.; Nemchik, J. Electroproduction of heavy quarkonia: Significance of dipole orientation. Phys. Rev. D 2021, 103, 094027. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Krelina, M.; Nemchik, J.; Potashnikova, I.K. Coherent photoproduction of heavy quarkonia on nuclei. Phys. Rev. D 2022, 105, 054023. [Google Scholar] [CrossRef]
- Cepila, J.; Contreras, J.G.; Vaculciak, M. Solutions to the Balitsky–Kovchegov equation including the dipole orientation. Phys. Lett. B 2024, 848, 138360. [Google Scholar] [CrossRef]
- Matousek, G.; Khachatryan, V.; Zhang, J. Scaling properties of exclusive vector meson production cross section from gluon saturation. Eur. Phys. J. Plus 2023, 138, 113. [Google Scholar] [CrossRef]
- Kumar, A.; Toll, T. Energy dependence of the proton geometry in exclusive vector meson production. Phys. Rev. D 2022, 105, 114011. [Google Scholar] [CrossRef]
- Anand, S.; Toll, T. Exclusive diffractive vector meson production: A comparison between the dipole model and the leading twist shadowing approach. Phys. Rev. C 2019, 100, 024901. [Google Scholar] [CrossRef]
- Xie, Y.P.; Goncalves, V.P. Exclusive processes in ep collisions at the EIC and LHeC: A closer look on the predictions of saturation models. Phys. Rev. D 2022, 105, 014033. [Google Scholar] [CrossRef]
- Henkels, C.; de Oliveira, E.G.; Pasechnik, R.; Trebien, H. Coherent photoproduction of light vector mesons off nuclear targets in the dipole picture. Nucl. Phys. A 2025, 1055, 123018. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Salazar, F.; Schenke, B. Energy dependent nuclear suppression from gluon saturation in exclusive vector meson production. Phys. Rev. D 2024, 109, L071504. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Salazar, F.; Schenke, B.; Shen, C.; Zhao, W. Effects of nuclear structure and quantum interference on diffractive vector meson production in ultraperipheral nuclear collisions. Phys. Rev. C 2024, 109, 024908. [Google Scholar] [CrossRef]
- Azevedo, C.N.; Goncalves, V.P.; Moreira, B.D. Associated vector-meson and bound-free electron-positron pair photoproduction in ultraperipheral PbPb collisions. Phys. Rev. C 2023, 108, 064907. [Google Scholar] [CrossRef]
- Goncalves, V.P.; Klasen, M.; Moreira, B.D. Exclusive J/Ψ plus jet associated production in ultraperipheral PbPb collisions. Eur. Phys. J. C 2023, 83, 895. [Google Scholar] [CrossRef]
- Boroun, G.R. A simple model for the charm structure function of nuclei. Phys. Lett. B 2024, 849, 138440. [Google Scholar] [CrossRef]
- Boroun, G.R. Heavy quark structure functions from unifying the color dipole picture and double asymptotic scaling approaches. Phys. Rev. D 2024, 109, 054012. [Google Scholar] [CrossRef]
- Bertulani, C.A.; Baur, G. Electromagnetic processes in relativistic heavy ion collisions. Phys. Rep. 1988, 163, 299–408. [Google Scholar] [CrossRef]
- Baur, G.; Hencken, K.; Trautmann, D.; Sadovsky, S.; Kharlov, Y. Coherent γγ and γA interactions in very peripheral collisions at relativistic ion colliders. Phys. Rep. 2002, 364, 359–450. [Google Scholar] [CrossRef]
- Bertulani, C.A.; Klein, S.R.; Nystrand, J. Physics of ultra-peripheral nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2005, 55, 271–310. [Google Scholar] [CrossRef]
- Baltz, A.J.; Baur, G.; d’Enterria, D.; Frankfurt, L.; Gelis, F.; Guzey, V.; Hencken, K.; Kharlov, Y.; Klasen, M.; Klein, S.R.; et al. The physics of ultraperipheral collisions at the LHC. Phys. Rep. 2008, 458, 1–171. [Google Scholar] [CrossRef]
- Klein, S.; Steinberg, P. Photonuclear and two-photon interactions at high-energy nuclear colliders. Ann. Rev. Nucl. Part. Sci. 2020, 70, 323–354. [Google Scholar] [CrossRef]
- Fagundes, D.A.; Machado, M.V.T. Asymptotic gluon density within the color dipole picture in light of HERA high-precision data. Phys. Rev. D 2023, 107, 014004. [Google Scholar] [CrossRef]
- Caola, F.; Forte, S. Geometric scaling from GLAP evolution. Phys. Rev. Lett. 2008, 101, 022001. [Google Scholar] [CrossRef]
- Ball, R.D.; Nocera, E.R.; Rojo, J. The asymptotic behaviour of parton distributions at small and large x. Eur. Phys. J. C 2016, 76, 383. [Google Scholar] [CrossRef]
- Rezaeian, A.H.; Schmidt, I. Impact-parameter dependent color glass condensate dipole model and new combined HERA data. Phys. Rev. D 2013, 88, 074016. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Zurita, P. In depth analysis of the combined HERA data in the dipole models with and without saturation. Phys. Rev. D 2018, 98, 036002. [Google Scholar] [CrossRef]
- Ball, R.D.; Forte, S. Double asymptotic scaling at HERA. Phys. Lett. B 1994, 335, 77–86. [Google Scholar] [CrossRef]
- Kowalski, H.; Teaney, D. An impact parameter dipole saturation model. Phys. Rev. D 2003, 68, 114005. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Schenke, B. Confronting impact parameter dependent JIMWLK evolution with HERA data. Phys. Rev. D 2018, 98, 034013. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation effects in deep inelastic scattering at low Q2 and its implications on diffraction. Phys. Rev. D 1998, 59, 014017. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation in diffractive deep inelastic scattering. Phys. Rev. D 1999, 60, 114023. [Google Scholar] [CrossRef]
- Bartels, J.; Golec-Biernat, K.J.; Kowalski, H. A modification of the saturation model: DGLAP evolution. Phys. Rev. D 2002, 66, 014001. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Sapeta, S. Heavy flavour production in DGLAP improved saturation model. Phys. Rev. D 2006, 74, 054032. [Google Scholar] [CrossRef]
- Golec-Biernat, K.; Sapeta, S. Saturation model of DIS: An update. J. High Energy Phys. 2018, 2018, 102. [Google Scholar] [CrossRef]
- Łuszczak, A.; Łuszczak, M.; Schäfer, W. Unintegrated gluon distributions from the color dipole cross section in the BGK saturation model. Phys. Lett. B 2022, 835, 137582. [Google Scholar] [CrossRef]
- Boroun, G.R. The unintegrated gluon distribution from the GBW and BGK models. Eur. Phys. J. A 2024, 60, 48. [Google Scholar] [CrossRef]
- Kovchegov, Y.V.; Levin, E. Quantum Chromodynamics at High Energy; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Kowalski, H.; Motyka, L.; Watt, G. Exclusive diffractive processes at HERA within the dipole picture. Phys. Rev. D 2006, 74, 074016. [Google Scholar] [CrossRef]
- Shuvaev, A.G.; Golec-Biernat, K.J.; Martin, A.D.; Ryskin, M.G. Off diagonal distributions fixed by diagonal partons at small x and ξ. Phys. Rev. D 1999, 60, 014015. [Google Scholar] [CrossRef]
- Harland-Lang, L.A. Simple form for the low-x generalized parton distributions in the skewed regime. Phys. Rev. D 2013, 88, 034029. [Google Scholar] [CrossRef]
- Favart, L.; Machado, M.V.T.; Schoeffel, L. Extraction of the skewing factor from the DIS/DVCS ratio. arXiv 2005, arXiv:hep-ph/0511069. [Google Scholar] [CrossRef]
- Favart, L.; Machado, M.V.T.; Schoeffel, L. An extraction of the skewing factor from DESY-HERA data. Braz. J. Phys. 2007, 37, 798–800. [Google Scholar] [CrossRef]
- Schoeffel, L. Deeply virtual compton scattering at HERA and perspectives at CERN. AIP Conf. Proc. 2008, 1056, 372–379. [Google Scholar] [CrossRef]
- Nemchik, J.; Nikolaev, N.N.; Zakharov, B.G. Scanning the BFKL pomeron in elastic production of vector mesons at HERA. Phys. Lett. B 1994, 341, 228–237. [Google Scholar] [CrossRef]
- Nemchik, J.; Nikolaev, N.N.; Predazzi, E.; Zakharov, B.G. Color dipole phenomenology of diffractive electroproduction of light vector mesons at HERA. Z. Phys. C 1997, 75, 71–87. [Google Scholar] [CrossRef]
- Cox, B.E.; Forshaw, J.R.; Sandapen, R. Diffractive Υ production at the Tevatron and LHC. J. High Energy Phys. 2009, 2009, 34. [Google Scholar] [CrossRef]
- Armesto, N.; Rezaeian, A.H. Exclusive vector meson production at high energies and gluon saturation. Phys. Rev. D 2014, 90, 054003. [Google Scholar] [CrossRef]
- Sampaio dos Santos, G.; Machado, M.V.T. On theoretical uncertainty of color dipole phenomenology in the J/ψ and Υphotoproduction in pA and AA collisions at the CERN Large Hadron Collider. J. Phys. G 2015, 42, 105001. [Google Scholar] [CrossRef]
- Sampaio dos Santos, G.; Machado, M.V.T. Light vector meson photoproduction in hadron–hadron and nucleus–nucleus collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2015, 91, 025203. [Google Scholar] [CrossRef]
- Gonçalves, V.P.; Machado, M.V.T.; Moreira, B.D.; Navarra, F.S.; Sampaio dos Santos, G. Color dipole predictions for the exclusive vector meson photoproduction in pp, pPb, and PbPb collisions at run 2 LHC energies. Phys. Rev. D 2017, 96, 094027. [Google Scholar] [CrossRef]
- Frankfurt, L.; Guzey, V.; Strikman, M. Cross section fluctuations of photon projectile in the generalized vector meson dominance model. Phys. Rev. D 1998, 58, 094039. [Google Scholar] [CrossRef]
- Forshaw, J.R.; Kerley, G.; Shaw, G. Extracting the dipole cross section from photo- and electroproduction total cross-section data. Phys. Rev. D 1999, 60, 074012. [Google Scholar] [CrossRef]
- Gonçalves, V.P.; Moreira, B.D. A phenomenological analysis of the nonperturbative QCD contributions for the photon wave function. Eur. Phys. J. C 2020, 80, 492. [Google Scholar] [CrossRef]
- Glauber, R.J. High-energy collision theory. In Lectures in Theoretical Physics. Volume 1; Brittin, W.E., Dunham, L.G., Eds.; Interscience Publishers, Inc.: New York, NY, USA; London, UK, 1959; pp. 315–414. Available online: https://archive.org/details/lecturesintheore0001unse/ (accessed on 31 March 2025).
- Gribov, V.N. Glauber corrections and the interaction between high-energy hadrons and nuclei. Sov. Phys. JETP 1969, 29, 483–487. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/29/3/p483?a=list (accessed on 31 March 2025).
- Gribov, V.N. Interaction of gamma quanta and electrons with nuclei at high energies. Sov. Phys. JETP. 1970, 30, 709–717. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/30/4/p709?a=list (accessed on 31 March 2025).
- Armesto, N. A Simple model for nuclear structure functions at small x in the dipole picture. Eur. Phys. J. C 2002, 26, 35–43. [Google Scholar] [CrossRef]
- Woods, R.D.; Saxon, D.S. Diffuse surface optical model for nucleon–nuclei scattering. Phys. Rev. 1954, 95, 577–578. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. Atom. Data Nucl. Data Tables 1987, 36, 495–536. [Google Scholar] [CrossRef]
- Roa, M.; Garrido, J.; Guevara, M. CGC and saturation approach: Impact-parameter dependent model of perturbative QCD and combined HERA data. Phys. Rev. D 2024, 110, 074006. [Google Scholar] [CrossRef]
- Drees, M.; Zeppenfeld, D. Production of supersymmetric particles in elastic ep collisions. Phys. Rev. D 1989, 39, 2536. [Google Scholar] [CrossRef]
- Aaij, R. et al. [The LHCb Collaboration] Central exclusive production of J/ψ and ψ(2S) mesons in pp collisions at = 13 TeV. J. High Energy Phys. 2018, 2018, 167. [Google Scholar] [CrossRef]
- Jones, S.P.; Martin, A.D.; Ryskin, M.G.; Teubner, T. Exclusive J/ψ production at the LHC in the kT factorization approach. J. Phys. G 2017, 44, 03LT01. [Google Scholar] [CrossRef]
- Abelev, B.B. et al. [ALICE Collaboration] Exclusive J/ψ photoproduction off protons in ultraperipheral p–Pb collisions at = 5.02 TeV. Phys. Rev. Lett. 2014, 113, 232504. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Energy dependence of exclusive J/ψ photoproduction off protons in ultra-peripheral p–Pb collisions at = 5.02 TeV. Eur. Phys. J. C 2019, 79, 402. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [CMS Collaboration] Measurement of exclusive Υ photoproduction from protons in pPb collisions at = 5.02 TeV. Eur. Phys. J. C 2019, 79, 277. [Google Scholar] [CrossRef]
- Flett, C.A.; Jones, S.P.; Martin, A.D.; Ryskin, M.G.; Teubner, T. Exclusive J/ψ and Υ production in high energy pp and p–Pb collisions. Phys. Rev. D 2022, 106, 074021. [Google Scholar] [CrossRef]
- Tumasyan, A. et al. [CMS Collaboration] Probing small Bjorken-x nuclear gluonic structure via coherent J/ψ photoproduction in ultraperipheral Pb–Pb collisions at = 5.02 TeV. Phys. Rev. Lett. 2023, 262301. [Google Scholar] [CrossRef]
- Adloff, C. et al. [H1 Collaboration] Elastic photoproduction of J/ψ and Υ mesons at HERA. Phys. Lett. B 2000, 483, 23–35. [Google Scholar] [CrossRef]
- Chekanov, S. et al. [ZEUS Collaboration] Exclusive photoproduction of Υ mesons at HERA. Phys. Lett. B 2009, 680, 4–12. [Google Scholar] [CrossRef]
- Breitweg, J. et al. [ZEUS Collaboration] Measurement of elastic Υ photoproduction at HERA. Phys. Lett. B 1998, 437, 432–444. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Coherent J/ψ photoproduction at forward rapidity in ultra-peripheral Pb–Pb collisions at = 5.02 TeV. Phys. Lett. B 2019, 798, 134926. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Coherent J/ψ and ψ′ photoproduction at midrapidity in ultra-peripheral Pb–Pb collisions at = 5.02 TeV. Eur. Phys. J. C 2021, 81, 712. [Google Scholar] [CrossRef]
- Bursche, A. (on behalf of the LHCb Collaboration). Study of coherent J/ψ production in lead–lead collisions at = 5 TeV with the LHCb experiment. Nucl. Phys. A 2019, 982, 247–250. [Google Scholar] [CrossRef]
- uszczak, A.; Schäfer, W. Coherent photoproduction of J/ψ in nucleus-nucleus collisions in the color dipole approach—An update. SciPost Phys. Proc. 2022, 8, 109. [Google Scholar] [CrossRef]
- Henkels, C.; de Oliveira, E.G.; Pasechnik, R.; Trebien, H. Momentum transfer squared dependence of exclusive quarkonia photoproduction in ultraperipheral collisions. Phys. Rev. D 2021, 104, 054008. [Google Scholar] [CrossRef]
- Henkels, C.; de Oliveira, E.G.; Pasechnik, R.; Trebien, H. Exclusive photoproduction of excited quarkonia in ultraperipheral collisions. Phys. Rev. D 2020, 102, 014024. [Google Scholar] [CrossRef]
- Ducati, M.B.G.; Griep, M.T.; Machado, M.V.T. Diffractive photoproduction of radially excited ψ(2S) mesons in photon–Pomeron reactions in PbPb collisions at the CERN Large Hadron Collider. Phys. Rev. C 2013, 88, 014910. [Google Scholar] [CrossRef]
- Kopeliovich, B.; Schäfer, A.; Tarasov, A. Nonperturbative effects in gluon radiation and photoproduction of quark pairs. Phys. Rev. D 2000, 62, 054022. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Krelina, M.; Nemchik, J.; Potashnikova, I.K. Ultraperipheral nuclear collisions as a source of heavy quarkonia. Phys. Rev. D 2023, 107, 054005. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE collaboration] Coherent photoproduction of ρ0 vector mesons in ultra-peripheral Pb–Pb collisions at = 5.02 TeV. J. High Energy Phys. 2020, 2020, 35. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] First measurement of coherent ρ0 photoproduction in ultra-peripheral Xe–Xe collisions at = 5.44 TeV. Phys. Lett. B 2021, 820, 136481. [Google Scholar] [CrossRef]
- Baltz, A.J.; Klein, S.R.; Nystrand, J. Coherent vector–meson photoproduction with nuclear breakup in relativistic heavy–ion collisions. Phys. Rev. Lett. 2002, 89, 012301. [Google Scholar] [CrossRef]
- Broz, M.; Contreras, J.G.; Tapia Takaki, J.D. A generator of forward neutrons for ultra-peripheral collisions: . Comput. Phys. Commun. 2020, 253, 107181. [Google Scholar] [CrossRef]
- Kryshen, E.; Strikman, M.; Zhalov, M. Photoproduction of J/ψ with neutron tagging in ultraperipheral collisions of nuclei at RHIC and at the LHC. Phys. Rev. C 2023, 108, 024904. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Energy dependence of coherent photonuclear production of J/ψ mesons in ultra-peripheral Pb–Pb collisions at = 5.02 TeV. J. High Energ. Phys. 2023, 2023, 119. [Google Scholar] [CrossRef]
- Abdulhamid, M.I. et al. [STAR Collaboration] Exclusive J/ψ, ψ(2s), and e+e- pair production in Au + Au ultraperipheral collisions at BNL Relativistic Heavy Ion Collider. Phys. Rev. C 2024, 110, 014911. [Google Scholar] [CrossRef]






| Model | [mb] | [GeV2] | /dof | p-Value | ||
|---|---|---|---|---|---|---|
| BGK | 1.0 (fixed) | 1.1 (fixed) | 0 | |||
| 0.1 (fixed) | 1.1 (fixed) | 0.213 | ||||
| 1.1 (fixed) | 0.244 | |||||
| 0.414 |
| Meson | [GeV] | [GeV] | [GeV−1] | [keV] | [keV] | Ref. | |||
|---|---|---|---|---|---|---|---|---|---|
| 0.7753 | 0.030 | 0.9942 | 0.8928 | 3.6388 | − | 7.04 | [41] | ||
| 3.097 | 1.3 | 0.5974 | 0.5940 | 1.5181 | − | 5.53 | [41] | ||
| 3.686 | 1.3 | 0.70 | 0.69 | 1.93 | −0.61 | 2.35 | [66] | ||
| 9.460 | 4.2 | 0.6866 | 0.6696 | 0.3354 | − | 1.29 | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fagundes, D.A.; Machado, M.V.T. Testing the Double-Logarithmic Asymptotic Gluon Density in Ultraperipheral Heavy-Ion Collisions at the Large Hadron Collider. Physics 2025, 7, 24. https://doi.org/10.3390/physics7030024
Fagundes DA, Machado MVT. Testing the Double-Logarithmic Asymptotic Gluon Density in Ultraperipheral Heavy-Ion Collisions at the Large Hadron Collider. Physics. 2025; 7(3):24. https://doi.org/10.3390/physics7030024
Chicago/Turabian StyleFagundes, Daniel Almeida, and Magno V. T. Machado. 2025. "Testing the Double-Logarithmic Asymptotic Gluon Density in Ultraperipheral Heavy-Ion Collisions at the Large Hadron Collider" Physics 7, no. 3: 24. https://doi.org/10.3390/physics7030024
APA StyleFagundes, D. A., & Machado, M. V. T. (2025). Testing the Double-Logarithmic Asymptotic Gluon Density in Ultraperipheral Heavy-Ion Collisions at the Large Hadron Collider. Physics, 7(3), 24. https://doi.org/10.3390/physics7030024






