Quantum Mechanical Numerical Model for Interaction of Dark Atom with Atomic Nucleus of Matter

Abstract

Within the framework of the XHe hypothesis, the positive results of the DAMA/NaI and DAMA/LIBRA experiments on the direct search for dark matter particles can be explained by the annual modulation of the radiative capture of dark atoms into low-energy bound states with sodium nuclei. Since this effect is not observed in other underground WIMP (weakly interacting massive particle) search experiments, it is necessary to explain these results by investigating the possibility of the existence of low-energy bound states between dark atoms and the nuclei of matter. Numerical modeling is used to solve this problem, since the study of the XHe–nucleus system is a three-body problem and leaves no possibility of an analytical solution. To understand the key properties and patterns underlying the interaction of dark atoms with the nuclei of baryonic matter, we develop the quantum mechanical description of such an interaction. In the numerical quantum mechanical model presented, takes into account the effects of quantum physics, self-consistent electromagnetic interaction, and nuclear attraction. This approach allows us to obtain a numerical model of the interaction between the dark atom and the nucleus of matter and interpret the results of direct experiments on the underground search for dark matter, within the framework of the dark atom hypothesis. Thus, in this paper, for the first time, steps are taken towards a consistent quantum mechanical description of the interaction of dark atoms, with unshielded nuclear attraction, with the nuclei of atoms of matter. The total effective interaction potential of the OHe–Na system has therefore been restored, the shape of which allows for the preservation of the integrity and stability of the dark atom, which is an essential requirement for confirming the validity of the OHe hypothesis.

1. Introduction

One of the most pressing unsolved mysteries of modern physics is that of the essence of dark matter. According to the modern standard cosmological model ΛCDM (Lambda-Cold Dark Matter), dark matter (DM) accounts for approximately 25% of the total energy density of the universe and is the dominant component of non-relativistic matter. Within the framework of cosmology and astrophysics, which are based on empirical data and evidence confirming the existence of dark matter, the latter is described as non-baryonic, since in order to explain its nature, dynamic characteristics, and theoretically possible observable manifestations, it is necessary to go beyond the Standard Model (SM) of elementary particles.

The non-baryonic nature of dark matter indicates the presence of new stable forms of non-relativistic matter in the universe, playing the role of stable dark matter particles. From the perspective of such particles, this stability implies that they possess new conserved quantum numbers (charges) that are absent from the particles of the SM which indicates the existence of a new symmetry extending that of the SM. Thus, in order for particles to claim the role of candidates for dark matter forming the large-scale structure of the universe, in addition to stability, the ability to match the measured density of dark matter and the ability to separate from plasma and radiation before the beginning of the stage of dominance of ordinary matter, all candidates for the role of dark matter particles must reflect the presence of some additional symmetry of the microcosm [1].

There are many models describing physics beyond the SM [1,2,3,4,5,6,7,8,9]. The lack of definitive experimental confirmation for weakly interacting massive particles (WIMPs) and the inability to detect supersymmetric (SUSY) particles at the energy scales probed by the Large Hadron Collider (LHC) suggest the need to explore alternative, non-supersymmetric explanations for the origin and nature of cosmological dark matter [10]. These observations also point to a potential resolution of the divergence problem associated with the Higgs boson mass, offering insights into the fundamental properties of dark matter. One promising avenue lies within composite Higgs boson models, which propose that stable, multicharged particles may exist. Such particles are predicted by certain extensions of the standard model, such as the minimal walking technicolor (WTC) framework [11,12,13,14,15].

The current paper considers a hypothetically possible connection between the composite nature of the Higgs boson and the existence of new, stable, multicharged, lepton-like particles. Moreover, the excess of hypothetical, stable, relict, negatively charged leptons of this type can be balanced with baryon asymmetry, due to sphaleron transitions in the early universe, which has made it possible to establish a connection between dark matter and the density of baryonic matter in the universe [16]. Such scenarios provide a novel perspective on dark matter suggesting that it possesses a composite structure [1]. Thus, within such a theoretical framework, the existence of additional heavy fermions is hypothesized, which interact through a new gauge force. Furthermore, the Higgs boson, in this context, is reinterpreted as a composite particle. This reinterpretation aligns the physics of the Higgs boson with the dynamics of these new gauge interactions, offering a unified understanding of its composite origin. It is assumed that the electric charge of the new, stable, multicharged particles is not fixed; however, there are exceptionally strict experimental restrictions that rigorously limit the possible charge value of these particles. Stable, negatively charged particles can only have a charge of $-2n$ [1], where n is a natural number; hereon, we indicate these particles as $\mathrm{X}$. In a special case, when the charge of a particle is $-2$, we denote it as ${\mathrm{O}}^{--}$.

These models also assume the presence of antiparticles with a charge of $+2n$, so the cosmological scenario should include a mechanism for their suppression. This can be realized under the conditions of charge asymmetry, in which particles with a charge of $-2n$ predominate [17]. As a result, antiparticles with a positive charge of $+2n$ can effectively annihilate in the early universe [18]. In the scenario under consideration, it is assumed that an excess of stable particles with a charge of $-2n$ compared to their antiparticles with a charge of $+2n$ occurs as a result of sphaleron transitions, which also lead to an excess of baryons [17,19,20,21]. The relationship between the excess of particles with a charge of $-2n$ and the baryonic asymmetry can explain the observed ratio of densities of baryonic and dark matter. There are various models predicting the appearance of such stable particles with a charge of $-2n$ [1].

This paper focuses on a scenario of composite dark matter in which hypothetical, stable, lepton-like (that is, without QCD (quantum chromodynamics) interaction or with strongly suppressed QCD interaction; according to the framework of the XHe hypothesis, a stable, charged X particle may exhibit lepton-like properties or represent a distinct combination of new heavy quark families, which are defined by their weak interactions with hadrons [1]) heavy particles ${\mathrm{X}}^{-2\mathrm{n}}$ bind using the usual electromagnetic Coulomb force with n nuclei of primary ${}^4\mathrm{He}$ into neutral atom-like states XHe, called dark atoms.

2. XHe Dark Atoms and Solving the Problem of Direct Search for Dark Matter Particles

Dark atom is atom of dark matter, which is a coupled quantum system of the X particle and the n nuclei of ${}^4\mathrm{He}$ (n–He nucleus).

Previous experimental evidence has indicated that the minimum mass for multicharged stable X particles is approximately $1\mathrm{TeV}$ [2,22]. At this mass scale for X particles, their cumulative contribution to the total density of non-relativistic matter aligns with the characteristics observed for dark matter. The mass of X particles with an even negative charge is actually equal to the mass of dark atoms thus providing a plausible explanation for the observed density of dark matter.

The structural properties of a dark atom system are characterized by the parameter $a\approx Z_{\alpha }{Z}_{\mathrm{X}}\alpha A_{\alpha }{m}_{\mathrm{p}}{R}_{n\mathrm{He}}$. Here, $\alpha$ represents the fine-structure constant, $Z_{\mathrm{X}}$ and $Z_{\alpha }$ denote the charge numbers of the X particle and the n–He nucleus, $m_{\mathrm{p}}$ is the proton mass, $A_{\alpha }$ corresponds to the mass number of the n–He nucleus, and $R_{n\mathrm{He}}$ represents the radius of n–He. The parameter a defines the ratio of the Bohr radius of the XHe atom to the radius of the n–He nucleus. If the Bohr radius of the dark atom is smaller than the size of the n–He nucleus, the dark atom adopts a Thomson-like structure; otherwise, it resembles a Bohr atom.

When the parameter a is within the range $0<a<1$, the bound state resembles a Bohr atom, with the negatively charged X particle at the center and the helium nucleus, treated as a point-like particle, orbiting around it, similar to Bohr’s atomic model. On the other hand, for a values in the range $1<a<\infty$, the system adopts characteristics of Thomson’s atomic model, where the not-point-like helium nucleus oscillates around the much heavier, negatively charged X particle. That is, in the case where the structure of the dark atom is akin that of a Thomson-like atom, the heavy point-like X particle is located inside the much lighter n–He nucleus of finite size (the radius of the n–He nucleus is greater than the Bohr radius), forming a connected quantum mechanical system of the XHe dark atom with this n–He nucleus. In Ref. [23], where it is determined that the XHe system constitutes three charged particles interacting via electromagnetic and nuclear forces, a step-by-step semiclassical numerical model was developed. This model allowed for a qualitative reconstruction of the effective interaction potential between the XHe atom and the target nucleus, employing the following two semiclassical methods: one based on reconstructing particle trajectories, including both the Bohr and Thomson atom models, and the other based on reconstructing the potential. In this paper, we consistently develop a completely quantum mechanical numerical model for the interaction of dark atoms with the nucleus of a substance in the XHe–nucleus system.

Dark atoms are considered the prospective candidates for composite dark matter, meeting all the necessary requirements to align with the cosmological data on which current cosmology is based [1]. Despite their nuclear interactions, the dark atom gas decouples from plasma and radiation before the era of matter domination, thereby contributing to the emergence and development of gravitational instability. This decoupling enables the amplification of small enough initial density fluctuations, leading to the large-scale structure formation of the universe, consistent with the observed anisotropy of the cosmic microwave background (CMB) radiation [1]. The unique properties of dark atoms introduce a “warmer-than-cold dark matter” scenario in structure formation, which, despite requiring further investigation, remains compatible with the data from precision cosmology [1]. This study presented, is relevant, among other points as soon as it is necessary to further study the nuclear physics of dark atoms and the active influence of XHe on nuclear transformations, as this is of a special importance when assessing the quantitative role of dark atoms in primary cosmological nucleosynthesis, the evolution of stars and various other physical, astrophysical, and cosmological manifestations of such an interaction in the early universe [1].

Despite the extensive efforts made to directly detect dark matter particles, the results have been contradictory. XHe atoms of composite dark matter could be key in addressing these inconsistencies. The properties of XHe atoms, which can be described by both the Thomson and Bohr models, contribute to significantly slowing the cosmic dark atom flux. This deceleration reduces their energy to thermal levels, causing them to diffuse slowly towards the Earth’s core. Such a deceleration mechanism makes it more challenging to detect dark matter particles through the conventional methods, which rely on recoil effects from WIMP–nucleus interactions [24].

The discrepancies in outcomes among experiments aiming to directly detect dark matter stem from the intricate nature of the interactions between dark matter particles and the detector materials used in underground setups. The framework of XHe posits that these complex interactions, combined with the potential formation of low-energy bound states in the XHe–nucleus system, may elucidate the positive results reported by the DAMA/NaI and DAMA/LIBRA experiments. These outcomes stand in contrast to the null results obtained by other experiments, such as XENON100, LUX, and CDMS [1,25].

The isoscalar and scalar characteristics of XHe dictate that quite low-energy bound states with ordinary nuclei can only be formed via an electric dipole ($E1$) transition. Such a transition necessitates a violation of isotopic symmetry, making it proportional to the square of the relative velocity between the interacting particles and thus sensitive to temperature. This dependence leads to the significant suppression of this mechanism in experiments operating at cryogenic temperatures [1].

This explanation accounts for why detection efforts other than those by DAMA/NaI and DAMA/LIBRA experiments have failed to produce positive results, as these experiments typically focus on observing nuclear recoil effects signals. Such signals might be misinterpreted as background noise due to their subtle nature [24]. Consequently, it becomes necessary to explore an alternative theoretical framework capable of explaining the outcomes of the DAMA experiments, which this study aims to develop and substantiate.

When quite low-velocity XHe dark atoms interact with ordinary nuclei, those atoms can form stable low-energy bound states. Within the uncertainties inherent to nuclear physics parameters, there exists a range where the binding energy of the XHe–Na system lies between 2 and 4 keV [1]. The transition of dark atoms into these bound states releases energy, which manifests as an ionization signal detectable by experimental setups like those in the DAMA study.

The concentration of XHe within underground detectors is governed by the equilibrium between the influx of cosmic dark matter atoms and their diffusion deeper into the Earth’s interior. The interaction between XHe and terrestrial material rapidly adjusts the dark atom presence in the Earth’s crust, shaped by variations in the cosmic flux of XHe. Consequently, the capture rate of these dark atoms is expected to exhibit seasonal fluctuations, producing a periodic annual modulation in the ionization signal arising from such interactions.

The unscreened nuclear charge of dark atoms raises the possibility that XHe atoms could engage in strong nuclear interactions with ordinary nuclei, potentially destabilizing the bound state of dark atoms. This process might result in the formation of anomalous isotopes, whose environmental concentrations are subject to stringent experimental constraints [1]. A notable implication of this model is the predicted appearance of anomalously heavy sodium isotopes in the DAMA detector material, with masses exceeding those of typical sodium isotopes by at least 1 TeV. These superheavy isotopes, if partially ionized, would exhibit mobility governed by atomic cross-sections significantly smaller—by several orders of magnitude—than those of OHe atoms [1]. As a result, such isotopes are expected to remain within the detector. Thus, performing mass spectrometry on the detector material could offer further evidence of the XHe component’s contribution to the DAMA signal. However, the techniques used must account for the delicate structure of XHe–Na bound states, as their binding energy is only a few keV [1].

3. The Effective Interaction Potential Between Dark Atoms and the Atomic Nucleus of Matter

To address the challenge of the formation of the overabundance of anomalous isotopes, the concentration of which is strictly limited in the environment, the XHe hypothesis introduces an effective interaction potential characterized by a shallow potential well coupled with a dipole Coulomb barrier. This structure serves to prevent the fusion of n–He and X particles with the nuclei of matter; see Figure 1. The presence of such features in the interaction potential is a critical requirement for the plausibility of the XHe dark matter model.

The form of effective potential (see Figure 1) is mainly due to the competition between the electromagnetic repulsion of n–He and the heavy nucleus of matter, as well as the nuclear attraction of the nuclear shell of a dark atom to the nucleus of matter.

The effective interaction potential of the XHe–nucleus system can be interpreted as the total potential energy of the nucleus of a substance when exposed to various forces from the dark atom, which is located at the beginning of the coordinate system, while the nucleus of matter slowly approaches the dark atom from the side of plus infinity. In the XHe–nucleus system, the following types of interactions operate between the dark atom and the nucleus of substance: the nuclear potential $U_{\mathrm{Nuc}}$ of interaction between n–He and the nucleus of a substance; the potential $U_{\mathrm{XHe}}^{\mathrm{e}}$ of the electrical interaction of unpolarized dark atoms with the nucleus of a substance taking into account the screening effect of the charge of the particle X by the n–He nucleus; the Stark potential $U_{\mathrm{St}}$ due to the Stark effect, leading to the polarization of XHe and the need for determining the electrical interaction of a polarized dark atom, that is, the dipole XHe, with the nucleus of matter; and finally, the centrifugal potential $U_{{\mathrm{rot}}_{\mathrm{XHe}-\mathrm{nuc}}}$ of the interaction of dark atoms with the nucleus of matter.

Considering all interaction types within the XHe–nucleus system, Figure 1 illustrates the theoretically expected qualitative behavior of a dark atom interacting with a nucleus of ordinary matter. In region IV, the nucleus remains distant from XHe, causing $U_{\mathrm{Nuc}}$ and $U_{\mathrm{XHe}}^{\mathrm{e}}$ to effectively vanish. These potentials only become significant at close proximity to the dark atom, as their magnitudes diminish rapidly with increasing separation. Consequently, the total interaction potential in this region is governed by $U_{\mathrm{St}}$ and $U_{{\mathrm{rot}}_{\mathrm{XHe}-\mathrm{nuc}}}$. Here, the dark atom undergoes negative polarization due to the external electric field generated by the matter nucleus. This causes the n–He component of XHe to shift leftward relative to particle X, which, in contrast, experiences attraction toward the nucleus.

As the nucleus approaches the dark atom, polarization intensifies, reaching its maximum in region III. At this point, the well depth, $-U_3$, is determined by the combined influence of the Stark and centrifugal potentials. The maximum negative value of the Stark potential corresponds to the largest negative dipole moment of XHe. Within this shallow well, a low-energy bound state between the dark atom and the nucleus of ordinary matter may form.

In region II, dipole Coulomb repulsion emerges between the nucleus and the dark atom. Here, the n–He particle begins to experience significant nuclear attraction from the matter nucleus, prompting it to shift rightward relative to particle X. This movement increases the likelihood of n–He tunneling into the matter nucleus, and the dipole moment of XHe shifts toward a positive value. The sum of $U_{\mathrm{St}}$ and $U_{{\mathrm{rot}}_{\mathrm{XHe}-\mathrm{nuc}}}$ determines the height of the dipole Coulomb barrier, $U_2$, which prevents the fusion of the matter nucleus with XHe, thereby preserving the integrity of the dark atom.

Finally, in region I, the nuclear potential, $U_{\mathrm{Nuc}}$, and the electric potential, $U_{\mathrm{XHe}}^{\mathrm{e}}$, dominate over $U_{\mathrm{St}}$ and $U_{{\mathrm{rot}}_{\mathrm{XHe}-\mathrm{nuc}}}$. This dominance results in the formation of a deep negative potential well of depth $-U_1$ in this region, reflecting the significant influence of these interactions at close distances.

Unlike ordinary atoms, dark atoms consist of a leptonic core and a nuclear shell, rendering standard atomic physics approximations ineffective. The challenge of describing the interaction between dark atoms and matter nuclei is three-body problem for which no exact analytical solution exists. Therefore, to assess the physical implications of the proposed scenario—characterized by a dipole Coulomb barrier and a shallow well within the effective interaction potential—a precise numerical quantum mechanical model of this three-body system is developed. This model must carefully account for the complex dynamics and non-trivial behavior intrinsic to such systems, enabling a rigorous validation of the proposed mechanism’s realization.

The subsequent sections of this paper outline the step-by-step development of a quantum mechanical numerical model for describing the interaction between a dark atom and the nucleus. The primary goal of this model is to reconstruct the effective interaction potential, offering a comprehensive analysis of the characteristics and subtleties involved in the interaction between dark atoms, as composite dark matter constituents, and the nuclei of ordinary matter.

4. The Isolated Dark Atom System

When subjected to the alternating electric field produced by an external nucleus, the XHe dark atom undergoes the Stark effect, which induces its polarization. This polarization gives rise to a dipole Coulomb repulsion between the XHe and the nucleus, facilitating the development of a bound state within this system. The presence of this bound state is attributed to the formation of a potential well located before the dipole Coulomb barrier in the total effective interaction potential.

To perform precise numerical modeling of the effective interaction potential in the XHe–nucleus system, an accurate computation of the Stark potential is essential. This potential governs the interaction between the polarized XHe dipole and the charged nucleus, playing a critical role in determining the following two key features: the depth of the potential well, which defines the conditions for forming a low-energy bound state between XHe and the nucleus of ordinary matter, and the height of the dipole Coulomb barrier, which serves as a repulsive force preventing the fusion of the dark atom with the nucleus. This calculation necessitates the quantum mechanical determination of the dipole moment $\overrightarrow{\delta }$ of the XHe. The Stark potential’s structure is directly influenced by the dipole moment $\overrightarrow{\delta }$, as characterized by the following relationship:

$$U_{\mathrm{St}}=e{Z}_{n\mathrm{He}}({\overrightarrow{E}}_{\mathrm{nuc}}·\overrightarrow{\delta }),$$

(1)

where e denotes the electron charge, ${\overrightarrow{E}}_{\mathrm{nuc}}$ represents the strength of the external electric field generated by the heavy charged nucleus, and $Z_{n\mathrm{He}}$ is the charge number of the n–He nucleus.

In this paper, we consider a special case of dark atoms when the charge of the X particle is −2, that is, when the X particle is a ${\mathrm{O}}^{--}$ particle bound to the ${}^4\mathrm{He}$ nucleus of primary helium with a neutral OHe dark atom of dark matter.

To perform precise quantum mechanical calculations of the dipole moment in a polarized dark atom, it is essential to determine the ground-state wave functions of helium within the OHe–nucleus system. Furthermore, obtaining the wave function of helium in its ground state for non-polarized OHe dark atom is equally meaningful. The procedure starts with the analysis of $\widehat{H_0}$, the Hamiltonian operator for the isolated OHe in the absence of any external perturbations.

Using a numerical difference scheme, $\widehat{H_0}$ is represented as a matrix, enabling the computation of its eigenvalues through numerical methods. These eigenvalues correspond to discrete energy states of helium, $E_{\mathrm{OHe}}$, in the isolated OHe. Simultaneously, the eigenvectors associated with these energy levels represent the helium wave functions, $\mathsf{\Psi }$, within the OHe system. Thus, the solution involves numerically resolving the following one-dimensional Schrödinger equation:

$$\widehat{H_0}\mathsf{\Psi }\left(\overrightarrow{r}\right)=E_{\mathrm{OHe}}\mathsf{\Psi }\left(\overrightarrow{r}\right),$$

(2)

or by presenting this expression in another form as follows:

$${\Delta }_r\mathsf{\Psi }\left(\overrightarrow{r}\right)+{\displaystyle \frac{2m_{\mathrm{He}}}{{\hslash }^2}}\left(E_{\mathrm{OHe}}+{\displaystyle \frac{4e^2}{r}}\right)\mathsf{\Psi }\left(\overrightarrow{r}\right)=0,$$

(3)

where $\overrightarrow{r}$ represents the position vector of the helium nucleus, $m_{\mathrm{He}}$ is the mass of the He nucleus, and ℏ is the reduced Planck constant. The origin of the coordinate system is located in the center of the particle ${\mathrm{O}}^{--}$.

Theoretical analysis indicates that the energy levels of helium, the mass and charge of which are concentrated at one point in the center of the particle, in the OHe dark atom, denoted as $E_{n_{\mathrm{OHe}}}$, follow a certain pattern analogous to the Bohr model of the hydrogen atom, as follows:

$$E_{n_{\mathrm{OHe}}}={\displaystyle \frac{-8m_{He}{\alpha }^2}{n^2}}\mathrm{MeV},$$

(4)

where n denotes a natural number, and $\alpha$ is the fine structure constant.

By numerically solving the one-dimensional Schrödinger Equation (2) using a numerical difference scheme for the helium radius vector $r=|2.5\times {10}^{-12}\mathrm{cm}|$ and setting the number of iterations to $N_{\mathrm{iter}}=2000$, the first three eigenvalues of the Hamiltonian operator, $\widehat{H_0}$, were determined as $E_{1,2,3_{\mathrm{num}}}=-1.585,-0.393,-0.042\mathrm{MeV}$, respectively. For comparison, a theoretical estimation of the initial three energy levels of helium in the OHe, derived using expression (4), results in the following: $E_{1,2,3_{\mathrm{OHe}}}=-1.589,-0.397,-0.177\mathrm{MeV}$, respectively. The numerical results for the first two energy levels are consistent with the theoretical values up to the second decimal place. For the purpose of calculating the dipole moment of polarized OHe in a quantum mechanical framework, it is sufficient to know the ground energy state wave function of helium in isolated OHe.

Once the wave functions for the specific energy states of helium in the dark atom are determined, a discrete spectrum of helium energy levels can be constructed. Additionally, the plots representing the squared modulus of the wave functions for these energy states in the dark atom potential can be built. Figure 2 illustrates the first three energy levels and the corresponding wave functions.

5. Three-Body OHe–Na System

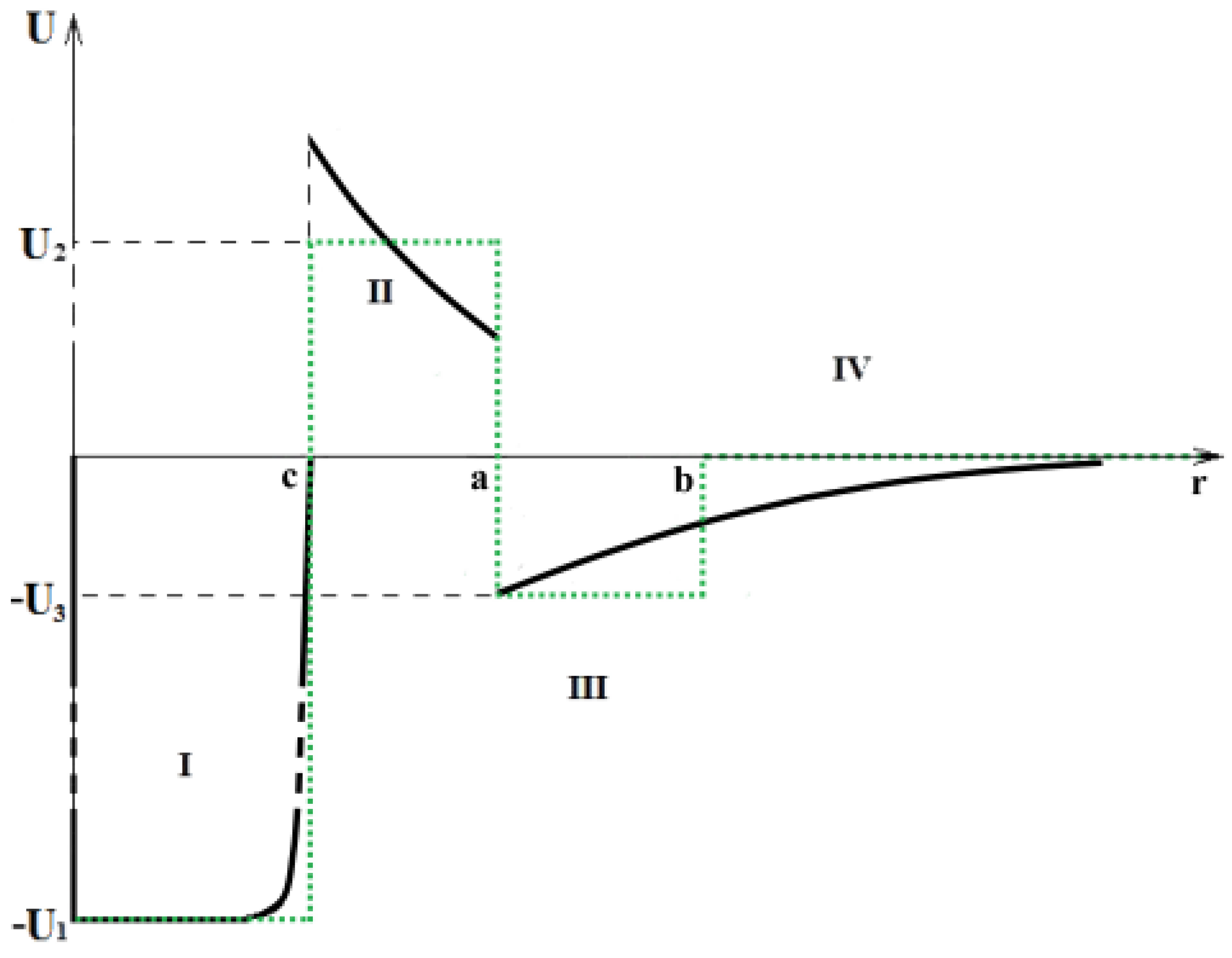
5.1. Potential of Interaction of Helium in the Three-Body OHe–Nucleus System

The three-body challenge under investigation is defined by the interaction within the XHe–nucleus system. Consider a particular instance where the XHe dark atom adopts the structure of a hydrogen-like Bohr atom, known as OHe. In this configuration, the coordinate system is anchored at the center of the ${\mathrm{O}}^{--}$ particle, which forms a bound dark matter atomic structure by interacting with the helium nucleus, treated as a point-like entity, through Coulomb forces. The OHe dark atom is influenced by an external, non-uniform electric field generated by a third particle, the nucleus, characterized by its charge number $Z_{\mathrm{nuc}}$, neutron count $N_{\mathrm{nuc}}$, and mass number A. This nucleus approaches the dark atom quite slowly, engaging in both the electromagnetic interactions and strong nuclear forces.

The Hamiltonian governing the dynamics of the point-like helium nucleus within the OHe–nucleus system can be expressed as follows:

$$\widehat{H}=\widehat{H_0}+\widehat{U},$$

(5)

where $\widehat{U}$ characterizes the interaction potential between helium and an external atomic nucleus.

To enhance the clarity of the description, the vectors $\overrightarrow{r}$, ${\overrightarrow{R}}_{\mathrm{OA}}$, and ${\overrightarrow{R}}_{\mathrm{HeA}}$ are defined as follows: $\overrightarrow{r}$ here represents the relative position vector connecting the ${\mathrm{O}}^{--}$ particle to the helium nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$ indicates the location of the external nucleus, and ${\overrightarrow{R}}_{\mathrm{HeA}}$ is the distance between the centers of helium and the nucleus of matter. These vectors are interconnected by the following relationship:

$${\overrightarrow{R}}_{\mathrm{HeA}}={\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}.$$

(6)

Consider the following equations for $\widehat{H_0}$ and $\widehat{U}$:

$$\widehat{H_0}=-{\displaystyle \frac{{\hslash }^2}{2m_{\mathrm{He}}}}\Delta -{\displaystyle \frac{4e^2}{r}},$$

(7)

$$\widehat{U}=U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)+U_{\mathrm{Nuc}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right),$$

(8)

where $U_{\mathrm{Nuc}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$ is expressed using the Woods–Saxon potential. Additionally, $U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$ represents the Coulomb potential characterizing the interaction between the point-like helium nucleus and the extended nucleus of ordinary matter.

The nuclear interaction potential is determined based on the distance between the neutron distribution surfaces of the nuclei involved. In particular, $U_{\mathrm{Nuc}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$ is expressed by the following equation:

$$U_{\mathrm{Nuc}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)=-{\displaystyle \frac{U_0}{1+exp\left(\frac{|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}|-R_{N_{\mathrm{nuc}}}-R_{N_{\mathrm{He}}}}{p}\right)}},$$

(9)

where $R_{N_{\mathrm{nuc}}}$ and $R_{N_{\mathrm{He}}}$ denote the root-mean-square radii associated with the neutron distributions in the heavy nucleus and the helium nucleus, respectively. The parameter $U_0$ represents the depth of the potential well, with a value of approximately of 43 MeV for the sodium nucleus, while p is the diffuseness parameter of about $0.55\mathrm{fm}$.

The radii $R_{N_{\mathrm{nuc}}}$ and $R_{N_{\mathrm{He}}}$ are determined according to the following equations [26]:

$$R_{N_{\mathrm{nuc},\mathrm{He}}}=\sqrt{{\displaystyle \frac{3}{5}}{R}_{0N_{\mathrm{nuc},\mathrm{He}}}^2+{\displaystyle \frac{7{\pi }^2}{5}}{a}_{N_{\mathrm{nuc},\mathrm{He}}}^2}\sqrt{1+{\displaystyle \frac{5b_{\mathrm{nuc},\mathrm{He}}^2}{4\pi }}}\mathrm{fm},$$

(10)

where $b_{\mathrm{nuc},\mathrm{He}}$ represents the deformation parameter for both the helium nucleus and the matter nucleus. Specifically, the sodium nucleus is assigned a deformation parameter value of $b_{\mathrm{Na}}=0.447$, while the helium nucleus is modeled as having a spherical symmetry, corresponding to a deformation parameter of zero. The parameter $R_{0N_{\mathrm{nuc},\mathrm{He}}}$ is the half-radius of the neutron distribution in the helium and matter nuclei and is determined by the number of neutrons N and protons Z in the nucleus and is calculated using the following expression:

$$R_{0N_{\mathrm{nuc},\mathrm{He}}}=0.953N_{\mathrm{nuc},\mathrm{He}}^{1/3}+0.015Z_{\mathrm{nuc},\mathrm{He}}+0.774\mathrm{fm},$$

(11)

where the parameter $a_{N_{\mathrm{nuc},\mathrm{He}}}$ is dimensional constant that depends on Z and N in the respective nucleus and is expressed by the following relation:

$$a_{N_{\mathrm{nuc},\mathrm{He}}}=0.446+0.072{\displaystyle \frac{N_{\mathrm{nuc},\mathrm{He}}}{Z_{\mathrm{nuc},\mathrm{He}}}}\mathrm{fm}.$$

(12)

For the Coulomb interaction potential $U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$ between the point-like helium nucleus and the nucleus of the heavy element, where the radius is taken as the root-mean-square radius of the proton distribution $R_{{\mathrm{p}}_{\mathrm{nuc}}}$, the potential is determined by the following equation:

$$U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)=\left\{\begin{array}{cc}{\displaystyle \frac{2e^2{Z}_{\mathrm{nuc}}}{|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}|}}\hfill & \mathrm{for}|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}|>R_{{\mathrm{p}}_{\mathrm{nuc}}},\hfill \\ {\displaystyle \frac{2e^2{Z}_{\mathrm{nuc}}}{2R_{{\mathrm{p}}_{\mathrm{nuc}}}}}\left(3-{\displaystyle \frac{|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}{|}^2}{R_{{\mathrm{p}}_{\mathrm{nuc}}}^2}}\right)\hfill & \mathrm{for}|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}|<=R_{{\mathrm{p}}_{\mathrm{nuc}}},\hfill \end{array}\right.$$

(13)

where $R_{{\mathrm{p}}_{\mathrm{nuc}}}$ is defined by the following expression [26]:

$$R_{{\mathrm{p}}_{\mathrm{nuc}}}=\sqrt{{\displaystyle \frac{3}{5}}{R}_{0{\mathrm{p}}_{\mathrm{nuc}}}^2+{\displaystyle \frac{7{\pi }^2}{5}}{a}_{{\mathrm{p}}_{\mathrm{nuc}}}^2}\sqrt{1+{\displaystyle \frac{5b_{\mathrm{nuc}}^2}{4\pi }}}\mathrm{fm},$$

(14)

where the parameter $R_{0{\mathrm{p}}_{\mathrm{nuc}}}$ represents the half-radius of the proton distribution in the nucleus and is calculated based on the charge number $Z_{\mathrm{nuc}}$ and the number of neutrons $N_{\mathrm{nuc}}$ in the heavy element nucleus as follows:

$$R_{0{\mathrm{p}}_{\mathrm{nuc}}}=1.322Z_{\mathrm{nuc}}^{1/3}+0.007N_{\mathrm{nuc}}+0.022\mathrm{fm},$$

(15)

whereas $a_{{\mathrm{p}}_{\mathrm{nuc}}}$ is dimensional constant, also dependent on the proton and neutron numbers of the nucleus, and is expressed by the following relation:

$$a_{{\mathrm{p}}_{\mathrm{nuc}}}=0.449+0.071{\displaystyle \frac{Z_{\mathrm{nuc}}}{N_{\mathrm{nuc}}}}\mathrm{fm}.$$

(16)

Thus, the Hamiltonian operator $\widehat{H}$ for the helium nucleus within the OHe–nucleus system is governed by the radius vectors $\overrightarrow{r}$ and ${\overrightarrow{R}}_{\mathrm{OA}}$. However, by fixing the position of ${\overrightarrow{R}}_{\mathrm{OA}}$ and altering the location of the substance’s nucleus, i.e., varying ${\overrightarrow{R}}_{\mathrm{OA}}$, one can derive a series of Schrödinger equations that depend exclusively on $\overrightarrow{r}$. Each of these equations corresponds to a specific configuration of the external nucleus relative to the dark atom.

Hence, the Schrödinger equation to be solved is expressed as follows:

$$\widehat{H}\mathsf{\Psi }\left(\overrightarrow{r}\right)=E\mathsf{\Psi }\left(\overrightarrow{r}\right),$$

(17)

which can be expressed as follows:

$$\Delta \mathsf{\Psi }\left(\overrightarrow{r}\right)+{\displaystyle \frac{2m_{\mathrm{He}}}{{\hslash }^2}}\left(E+{\displaystyle \frac{4e^2}{r}}-U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)-U_N\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)\right)\mathsf{\Psi }\left(\overrightarrow{r}\right)=0.$$

(18)

By approximating the Hamiltonian operator using the finite difference method in matrix form, it becomes feasible to numerically calculate the eigenvalues of the operator $\widehat{H}$, which correspond to the energy levels E of helium within the OHe–nucleus system for a given fixed position of the external nucleus ${\overrightarrow{R}}_{\mathrm{OA}}$. Additionally, the eigenvectors of the Hamiltonian, which describe the wave functions $\mathsf{\Psi }$ of the helium atom in this system, are determined.

To achieve this, it is necessary not only to represent the Laplace operator $\Delta$ in matrix form but also to construct the matrix representation of the interaction potential between the helium nucleus and the external nucleus in the OHe–nucleus system for each specified value of ${\overrightarrow{R}}_{\mathrm{OA}}$, as follows:

$$U_{\mathrm{He}}=-{\displaystyle \frac{4e^2}{r}}+U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)+U_N\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right).$$

(19)

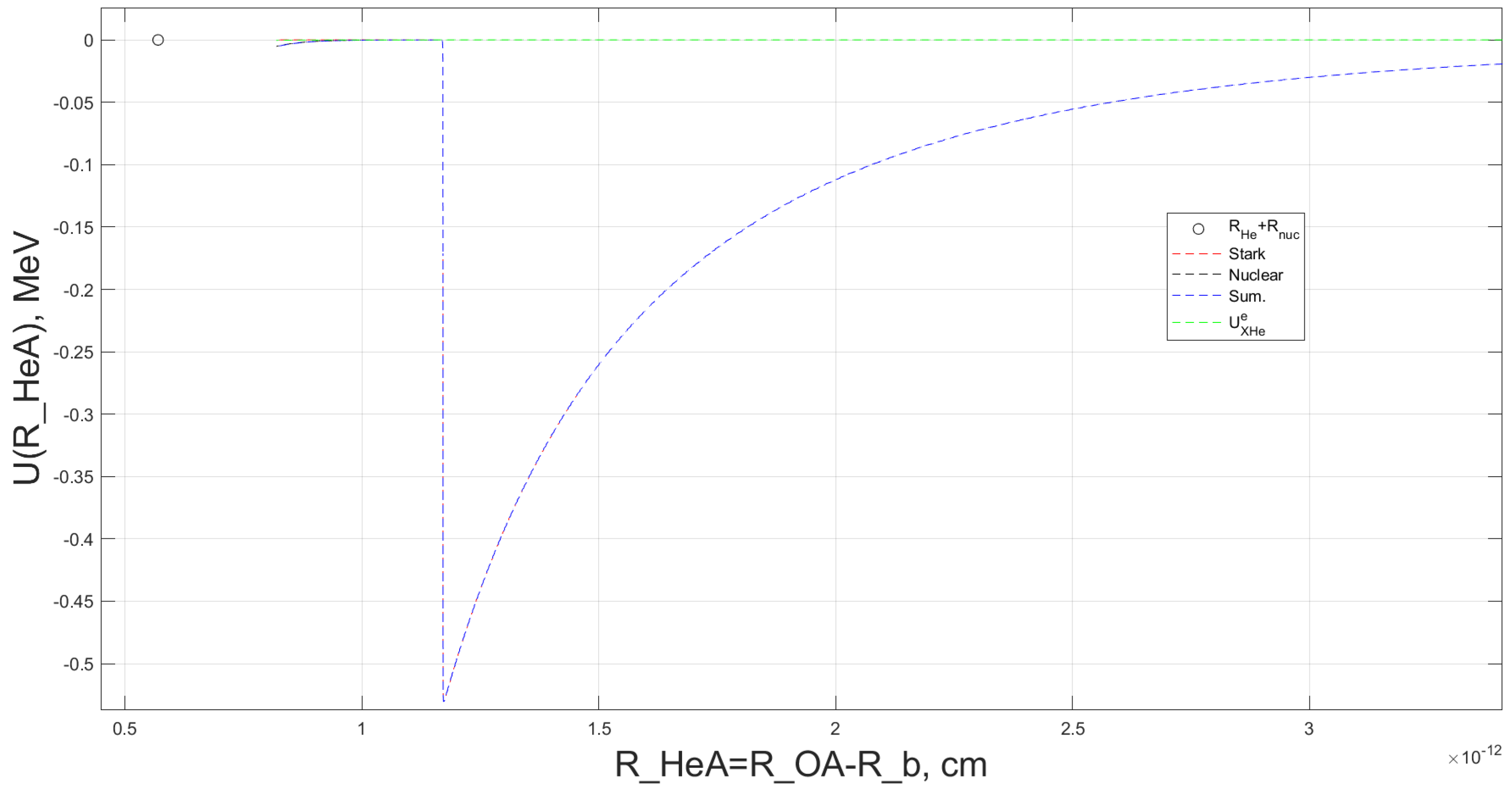
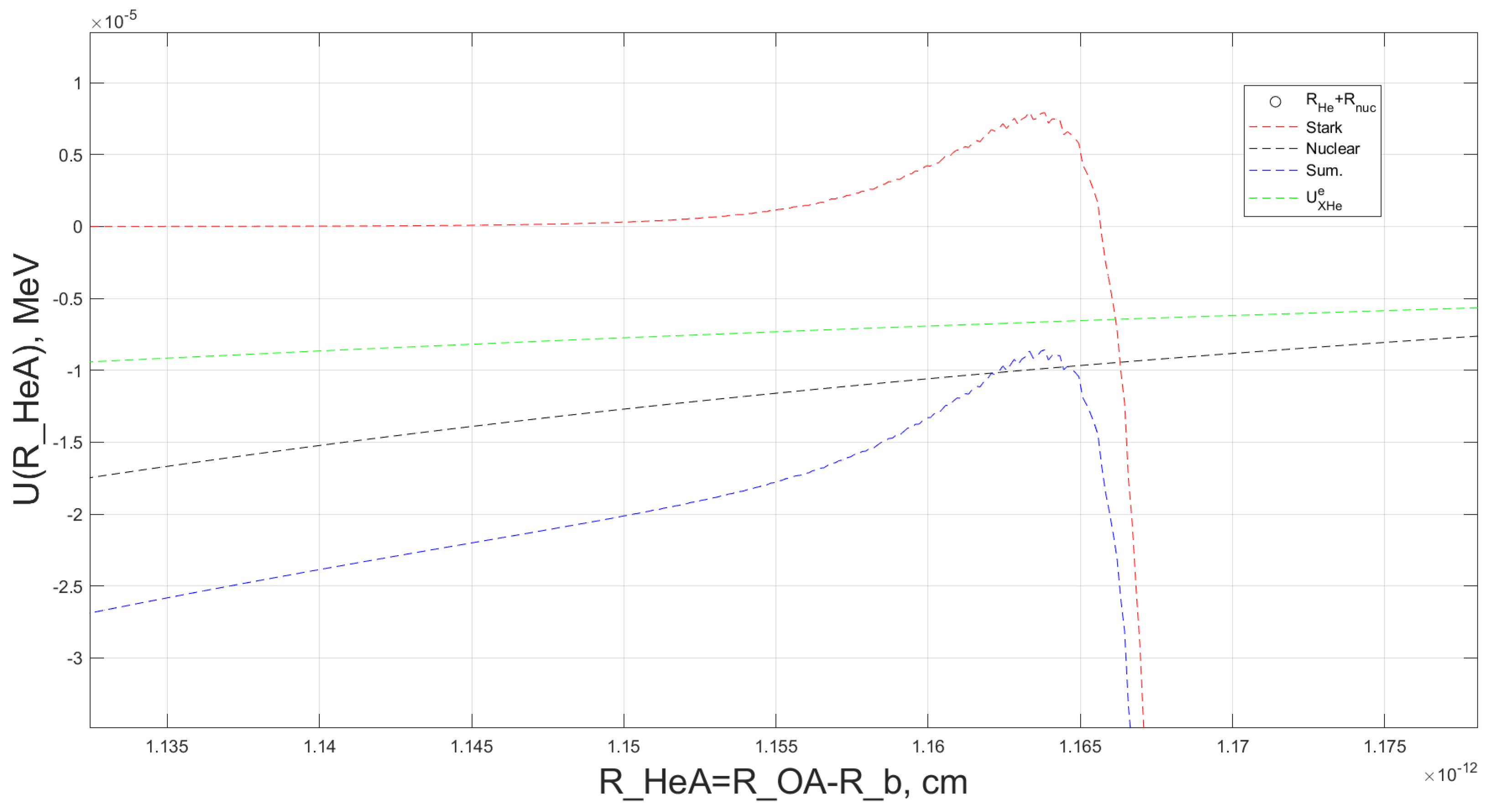
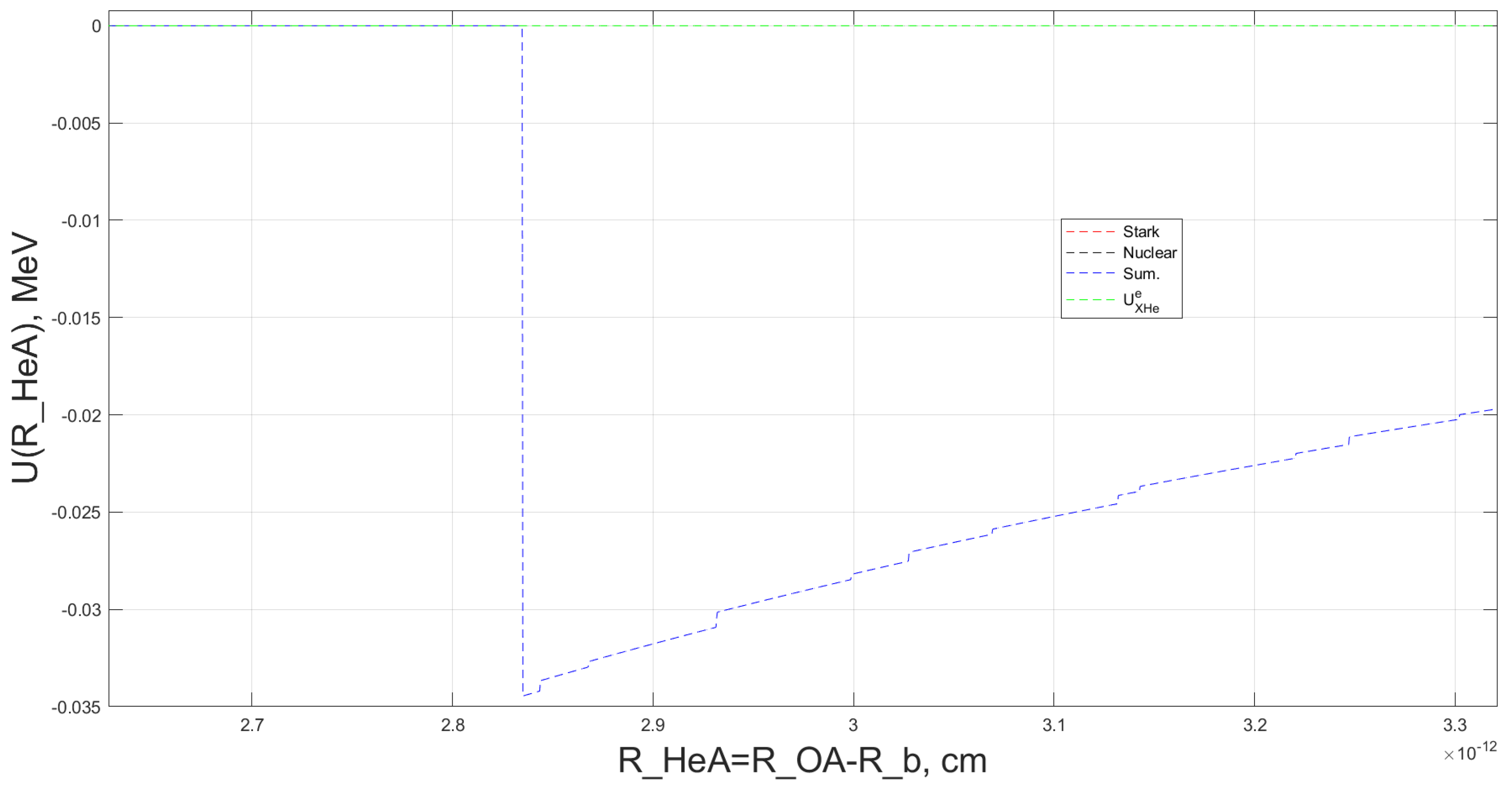
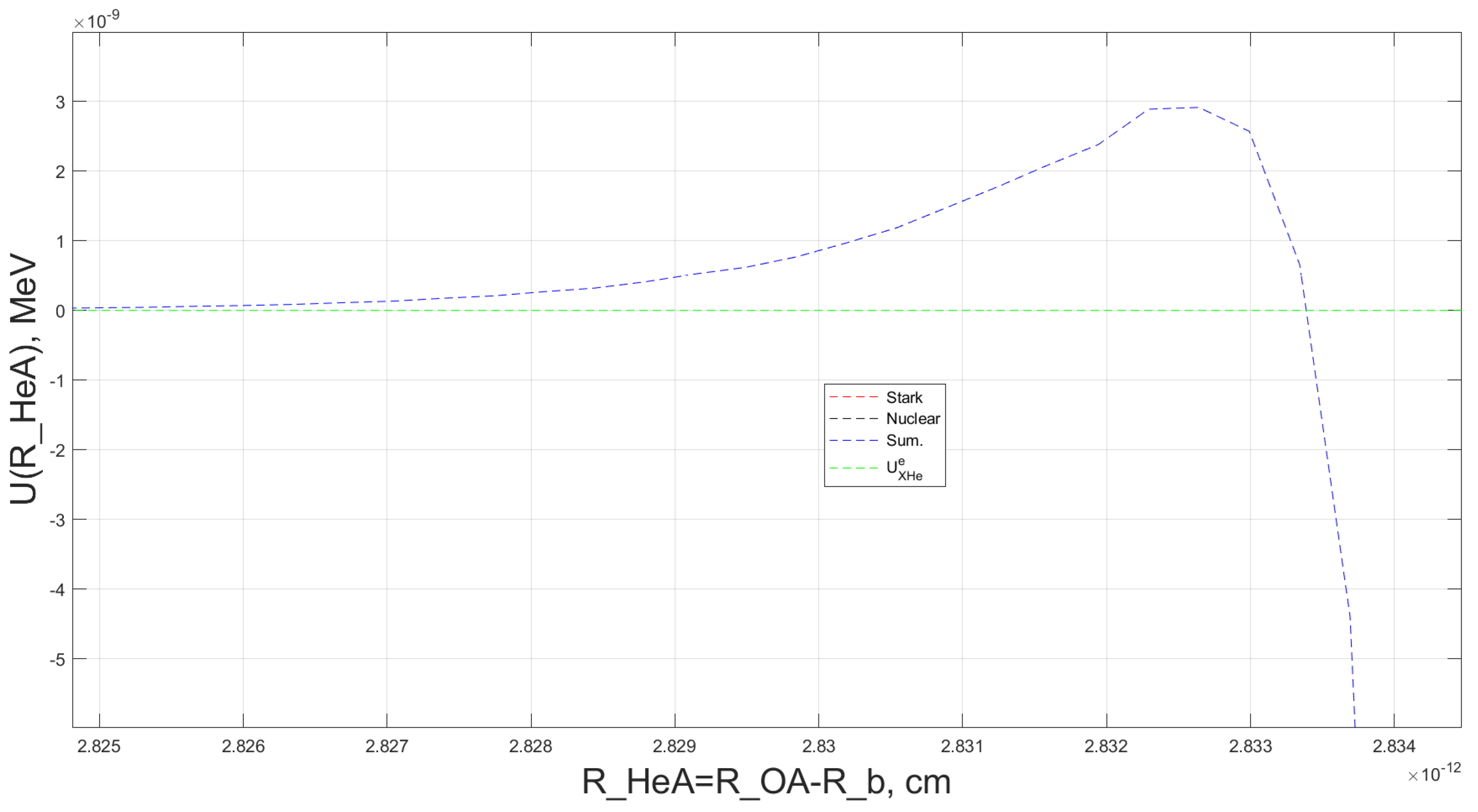
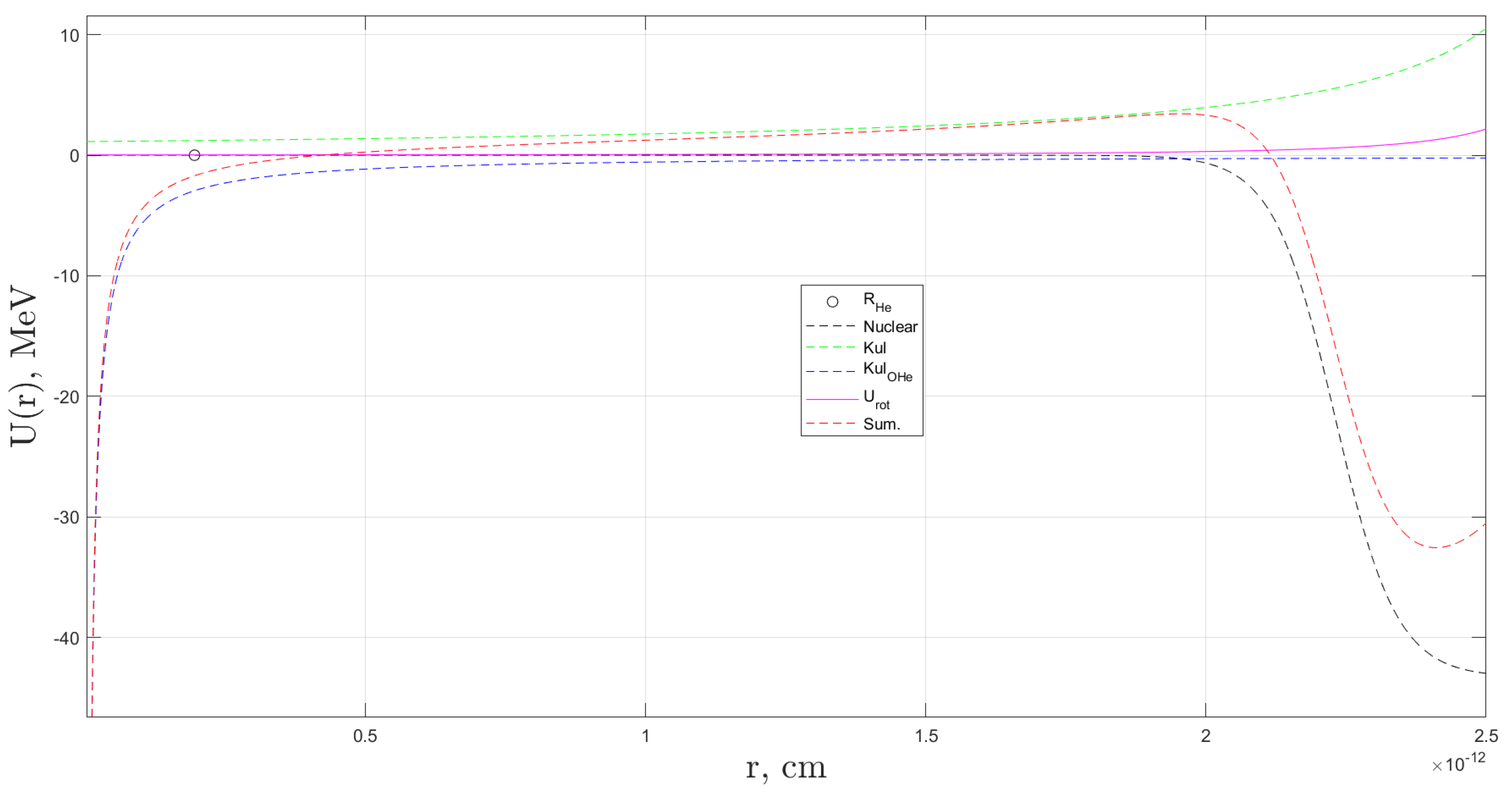
Figure 3 shows an example of the reconstructed total interaction potential, $U_{\mathrm{He}}$, for helium in the OHe–Na system. This potential is displayed as a function of the helium radius vector $\overrightarrow{r}$, while the radius vector ${\overrightarrow{R}}_{\mathrm{OA}}$ of the external sodium nucleus is kept fixed.

As shown in Figure 3, the interaction potentials highlight the contributions of the Coulomb and nuclear forces between the helium and sodium nuclei, alongside the Coulomb interaction between helium and the ${\mathrm{O}}^{--}$ particle. The total effective potential for helium within the OHe–Na system is also depicted.

To address the quantum mechanical three-body problem in the OHe–nucleus system, it is necessary to solve the Schrödinger equation for the helium nucleus under the assumption of a fixed position for the external nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$. This involves constructing the Hamiltonian of the helium nucleus in matrix form, enabling the numerical computation of its eigenvalues and eigenvectors. The eigenvalues represent the discrete energy states of helium, while the eigenvectors correspond to the helium $\mathsf{\Psi }$-functions within the OHe–nucleus system.

5.2. The Solving of the Schrödinger Equations for Helium Within the OHe–Nucleus System

In the absence of an external nucleus, the dark matter atom remains in an unpolarized state, with the ground-state energy level of helium in the OHe system being approximately $1.6\mathrm{MeV}$. When external nucleus approaches, the dark atom becomes polarized due to the electric field generated by the external heavy nucleus, leading to the onset of the Stark effect. As a result, OHe develops a non-zero dipole moment and begins to interact with the external nucleus as a dipole. This interaction is described by the Stark potential (see Equation (1)). In accordance with the dark atom model, the effective interaction potential between OHe and the external heavy nucleus is expected to give rise to a dipole barrier, which prevents dark matter particles from entering the nucleus. Furthermore, a low-energy bound state is anticipated to form between the dark atom and the external nucleus.

To solve the one-dimensional Schrödinger equation for the helium in the OHe–nucleus system, as expressed in Equation (18), it is crucial to establish the range of values for the helium radius vector, $\overrightarrow{r}$ while maintaining a fixed position for the external nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$. In this framework, $\overrightarrow{r}$ functions as an free variable influencing the total interaction potential experienced by the helium nucleus within the OHe–nucleus system for a specified position of the nucleus of matter.

The solution process entails addressing this set of equations, which involves the Schrödinger equation corresponding to each specific position of the external nucleus, which is considered to move slowly. Therefore, it is also essential to define the interval for the radius vector ${\overrightarrow{R}}_{\mathrm{OA}}$ of the external nucleus to comprehensively describe the interaction dynamics in this three-body system.

Setting $\overrightarrow{r}$ to fully overlap with ${\overrightarrow{R}}_{\mathrm{OA}}$ would quite probably place helium in the deep potential well generated by the heavy nucleus. Since the initial position of the helium nucleus is within the dark atom—where OHe exists as bound quantum mechanical system before interacting with the heavy nucleus—the intervals for $\overrightarrow{r}$ and ${\overrightarrow{R}}_{\mathrm{OA}}$ should be selected such that their boundaries are close but do not overlap. This approach allows the helium nucleus to initially remain within the dark atom, gradually sensing the influence of the approaching nucleus and, as it nears, to begin tunneling into the nucleus through the Coulomb barrier with increasing probability. Thus, for the given interval $\overrightarrow{r}$, with boundary points equal in magnitude but opposite in sign, the ${\overrightarrow{R}}_{\mathrm{OA}}$ interval is configured to begin at the maximal distance from the dark atom and to conclude near the right endpoint of the helium radius vector interval. That is, the radius vector of helium is given as $\overrightarrow{r}=[-d;d]$ and the radius vector of the outer nucleus of matter as ${\overrightarrow{R}}_{\mathrm{OA}}=[c;b]$, where $d,c,b>0$ and $d⩽b<c$. Thus, the fixed position of the nucleus of the substance, ${\overrightarrow{R}}_{\mathrm{OA}}$, consistently takes values from the interval $[c;b]$, starting from point c to point b. And for each point $q^{\ast }\in [c;b]$, the distance between the helium nucleus and the nucleus of matter, ${\overrightarrow{R}}_{\mathrm{HeA}}={\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}$, varies in the interval ${\overrightarrow{R}}_{\mathrm{HeA}}=[q^{\ast }+d;q^{\ast }-d]$. As the external nucleus approaches the dark matter atom, the polarization of OHe intensifies, responding to the proximity of the nucleus.

As the nucleus of the substance moves closer to the OHe system, the ground state of the helium nucleus in the dark atom undergoes the corresponding modifications. To evaluate the variation in the dipole moment of the polarized OHe, it is essential to compute the changes in both the ground-state energy and the wave functions of the polarized dark atom. By incrementally decreasing the distance between the external nucleus and OHe and solving the Schrödinger equation for helium at each fixed value of the radius vector ${\overrightarrow{R}}_{\mathrm{OA}}$ of the external nucleus, the complete energy spectrum of helium within the polarized OHe system was determined for each specific position of the outer nucleus. In these computations, the external nucleus was consistently assumed to be ${}^{11}\mathrm{Na}$.

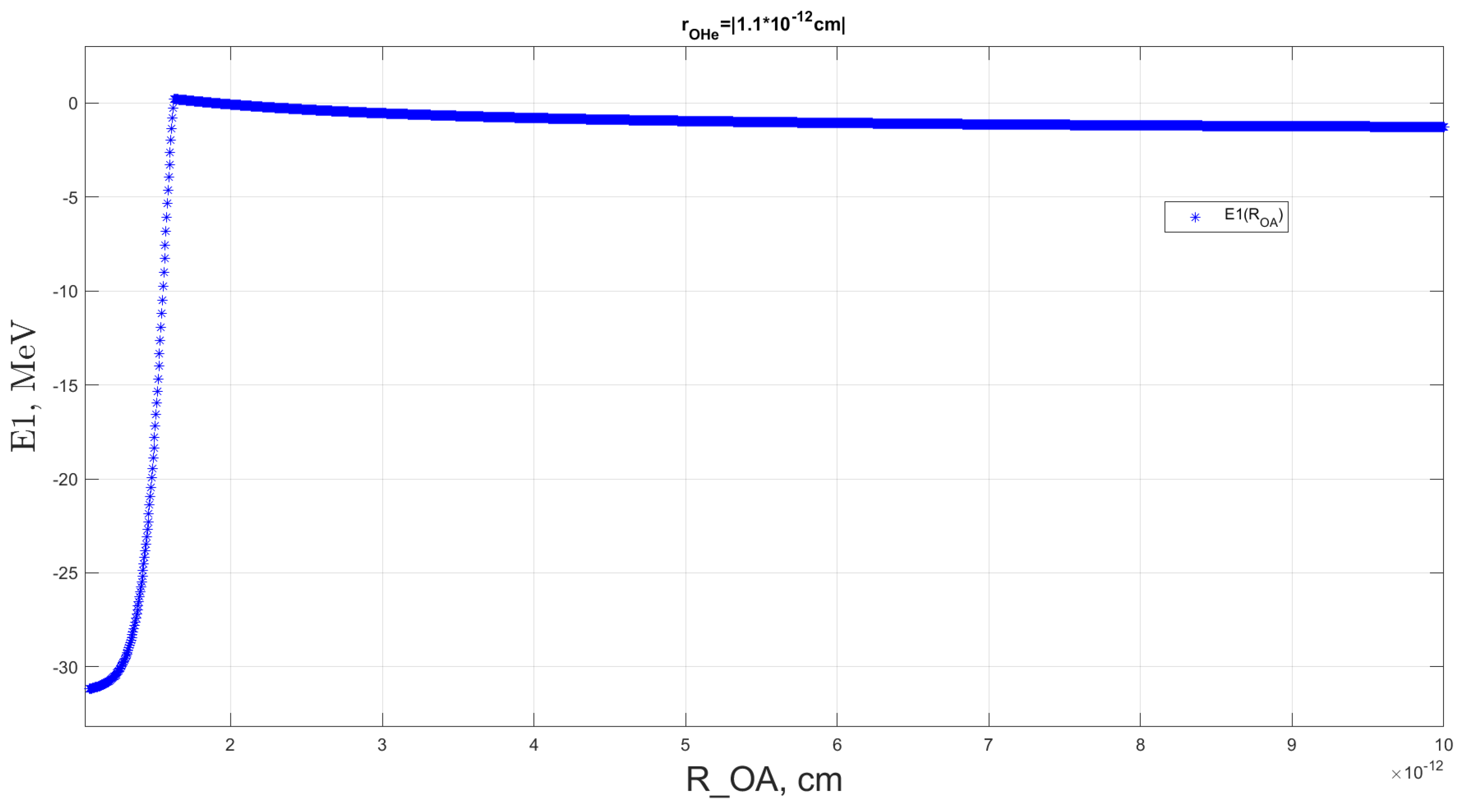
Figure 4 illustrates the dependence of the helium ground-state energy in the polarized dark atom on the radius vector of the sodium nucleus within a range where the helium radius vector is $r=|1.1\times {10}^{-12}\mathrm{cm}|$.

In Figure 4, the blue stars indicate the ground-state energy levels of helium within the polarized OHe, calculated for the various fixed values of the sodium nucleus’ radius vector, ${\overrightarrow{R}}_{\mathrm{OA}}$. The graph illustrates that when the external nucleus is positioned far from OHe, the dark atom exhibits behavior nearly identical to that of an isolated system. Under these conditions, the ground-state energy of helium stabilizes around $-1.6\mathrm{MeV}$, which corresponds to the binding energy of the OHe. However, as the sodium nucleus approaches, the polarization of OHe intensifies, leading to a shift in the helium ground-state energy toward positive values. At close enough separations, the probability of helium tunneling into the sodium increases significantly, with the energy levels converging to a value determined by the square of the modulus of the wave function at the point where helium is most probably in the middle of the sodium.

Consequently, by solving the Schrödinger equations for He in the OHe–Na system for the various fixed positions of the external nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$, the ground-state energy spectrum of helium in the polarized dark atom was determined, along with the corresponding wave functions associated with these energy states.

5.3. Calculation of the Values of the Dipole Moment of Polarized Dark Atom

Using the normalized ground-state wave function of helium in an unpolarized dark atom, ${\mathsf{\Psi }}_{\mathrm{OHe}}$, which was obtained by solving the Schrödinger equation for helium in an isolated OHe dark atom, along with the normalized wave functions of helium in a polarized dark atom corresponding to the various ground-state energy values, ${\mathsf{\Psi }}_{\mathrm{OHeNa}}$, we calculated the spectrum of dipole moment values $\delta$ for polarized OHe. The dipole moment $\delta$ for the given ${\mathsf{\Psi }}_{\mathrm{OHeNa}}$ was calculated by the following equation:

$$\delta ={\int }_r{\mathsf{\Psi }}_{\mathrm{OHe}}^{\ast }·r·{\mathsf{\Psi }}_{\mathrm{OHeNa}}·4\pi r^{2}dr.$$

(20)

To evaluate the integral in Equation (20), it is essential to precisely establish the integration limits. This requires considering the spatial probability distribution of helium within the polarized dark atom, as the goal is to calculate its dipole moments. The integration boundaries are determined by locating the points of intersection between the curve representing the squared modulus of the helium wave function and the curve depicting the total interaction potential for He in the OHe–Na system at the fixed position of ${\overrightarrow{R}}_{\mathrm{OA}}$.

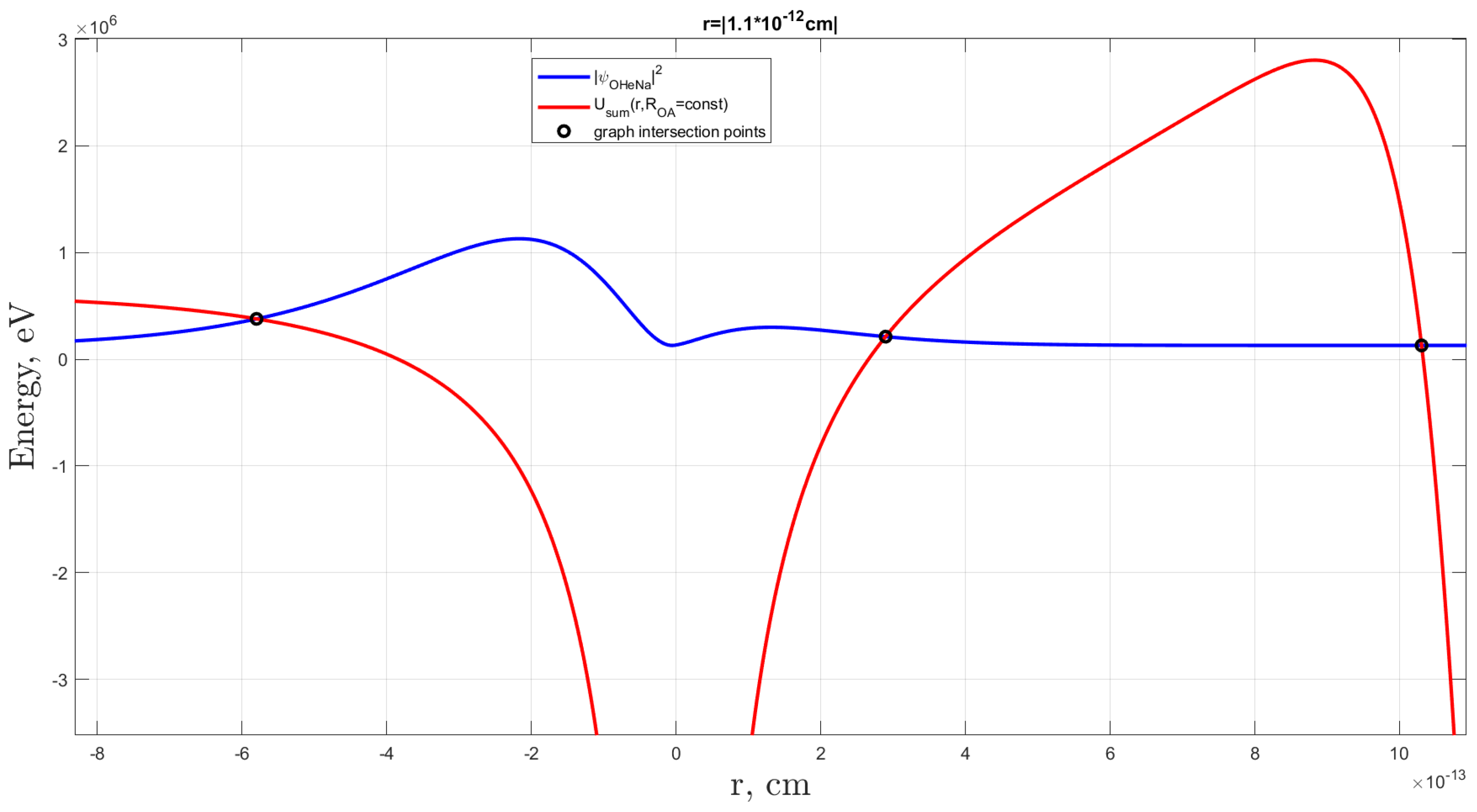
Figure 5 demonstrates the procedure of determining the integration boundaries needed for calculating the integral in Equation (20). In Figure 5, the red solid curve represents the total interaction potential of helium within the OHe–Na system for a specific fixed position of the sodium nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$. The blue solid curve illustrates the squared modulus of the helium ground-state wave function at the same fixed ${\overrightarrow{R}}_{\mathrm{OA}}$. The intersection points of these two graphs, marked by black circles, define the integration limits. Specifically, the first two intersections, moving from left to right, establish the bounds for Equation (20). In the example shown in Figure 5, the dark atom is in a state of negative polarization. This is indicated by the higher probability of finding helium on the left-hand side of the origin (the position of the ${\mathrm{O}}^{--}$ particle) compared to the right. The sodium nucleus is situated at a distance where helium begins to sense the nuclear potential, as evidenced by the formation of a potential well on the right-hand side of the Coulomb barrier. However, the nucleus remains far enough away to prevent significant tunneling of helium through the barrier.

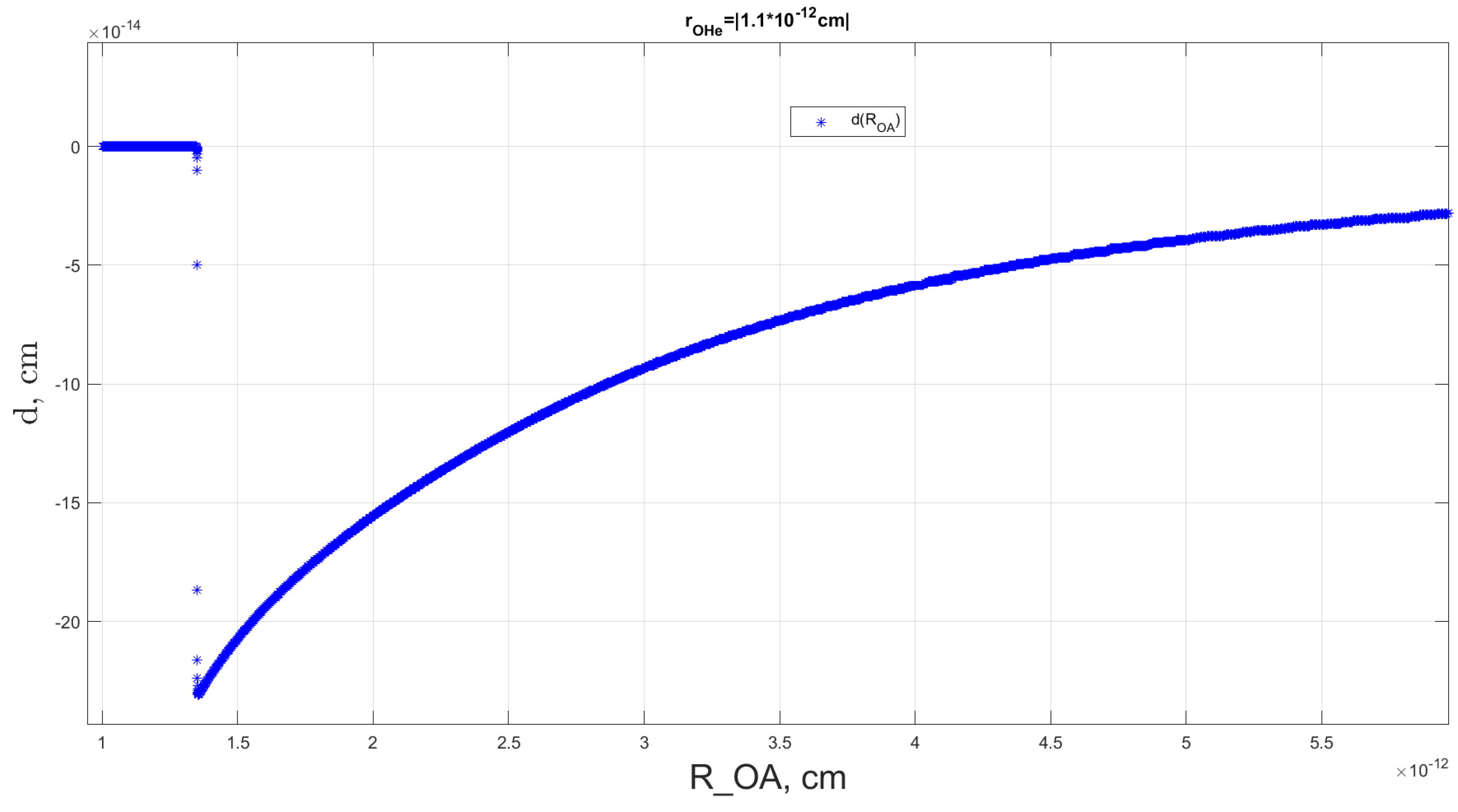
After determining the range of dipole moment values, $\delta$, for the polarized OHe dark atom at various fixed positions of the sodium nucleus, ${\overrightarrow{R}}_{\mathrm{OA}}$, one can represent the relationship between the dipole moment of the polarized dark atom and the radius vector ${\overrightarrow{R}}_{\mathrm{OA}}$ (see Figure 6).

In Figure 6, the blue stars depict the calculated dipole moment values for the polarized OHe, each corresponding to specific fixed positions of ${\overrightarrow{R}}_{\mathrm{OA}}$ within the interval where the helium radius vector is $r=|1.1\times {10}^{-12}\mathrm{cm}|$. Figure 6 shows that when the sodium nucleus is far from OHe, the dark atom behaves nearly as an isolated system, with its dipole moment approaching zero. However, as the sodium nucleus approaches the OHe, the polarization of OHe increases significantly, resulting in a progressively more negative dipole moment. This phenomenon occurs because the repulsive Coulomb force exerted by the sodium nucleus pushes helium preferentially to the left-hand side of the ${\mathrm{O}}^{--}$ particle. When the sodium nucleus is positioned quite close to the dark atom, such that ${\overrightarrow{R}}_{\mathrm{OA}}$ approaches the rightmost boundary of the helium radius vector interval $\overrightarrow{r}$, the nuclear interaction between helium and sodium dominates their Coulomb interaction, causing $\delta$ to trend back toward zero.

At a particular point, the likelihood of helium tunneling into the nucleus of the sodium increases significantly, resulting in a reversal of the dipole moment’s sign, making it positive (see Figure 7). Until this stage, the probability of helium remaining within the confines of the dark atom does not vanish, signifying that the OHe atom remains intact but undergoes a change in polarization. In this arrangement, the He nucleus is positioned between the ${\mathrm{O}}^{--}$ and the nucleus of the substance. Consequently, a dipole-induced Coulomb repulsion may develop between the helium and the sodium nucleus. This interaction, driven by the dipole coupling of the OHe atom with the external nucleus, can facilitate the emergence of a low-energy bound state in the OHe–Na system.

The reversal of the dipole moment’s sign aligns with the theoretical expectations. At large distances between the matter nucleus and the OHe, the repulsive Coulomb force acting on helium dominates over the nuclear attraction. In this scenario, helium is displaced further from the heavy nucleus, while the ${\mathrm{O}}^{--}$ is drawn toward the sodium by the Coulomb interaction. As the sodium nucleus approaches the OHe, the nuclear forces become increasingly prominent, positioning helium between the ${\mathrm{O}}^{--}$ and the sodium, as predicted. This shift is manifested as a change in the sign of the dipole moment.

Despite of this, the dipole Coulomb barrier introduces a repulsive force that prevents helium from fully merging with the sodium, thereby preserving the structural stability of the dark atom of the dark matter. As the vector ${\overrightarrow{R}}_{\mathrm{OA}}$ decreases further, bringing the sodium even closer to the OHe, the dipole moment progressively decreases, approaching zero (see Figure 7). This trend reflects helium’s deeper penetration into the sodium, which increases the possibility of quantum tunneling. Simultaneously, the probability of helium remaining confined in the OHe diminishes, causing the dipole moment to approach zero.

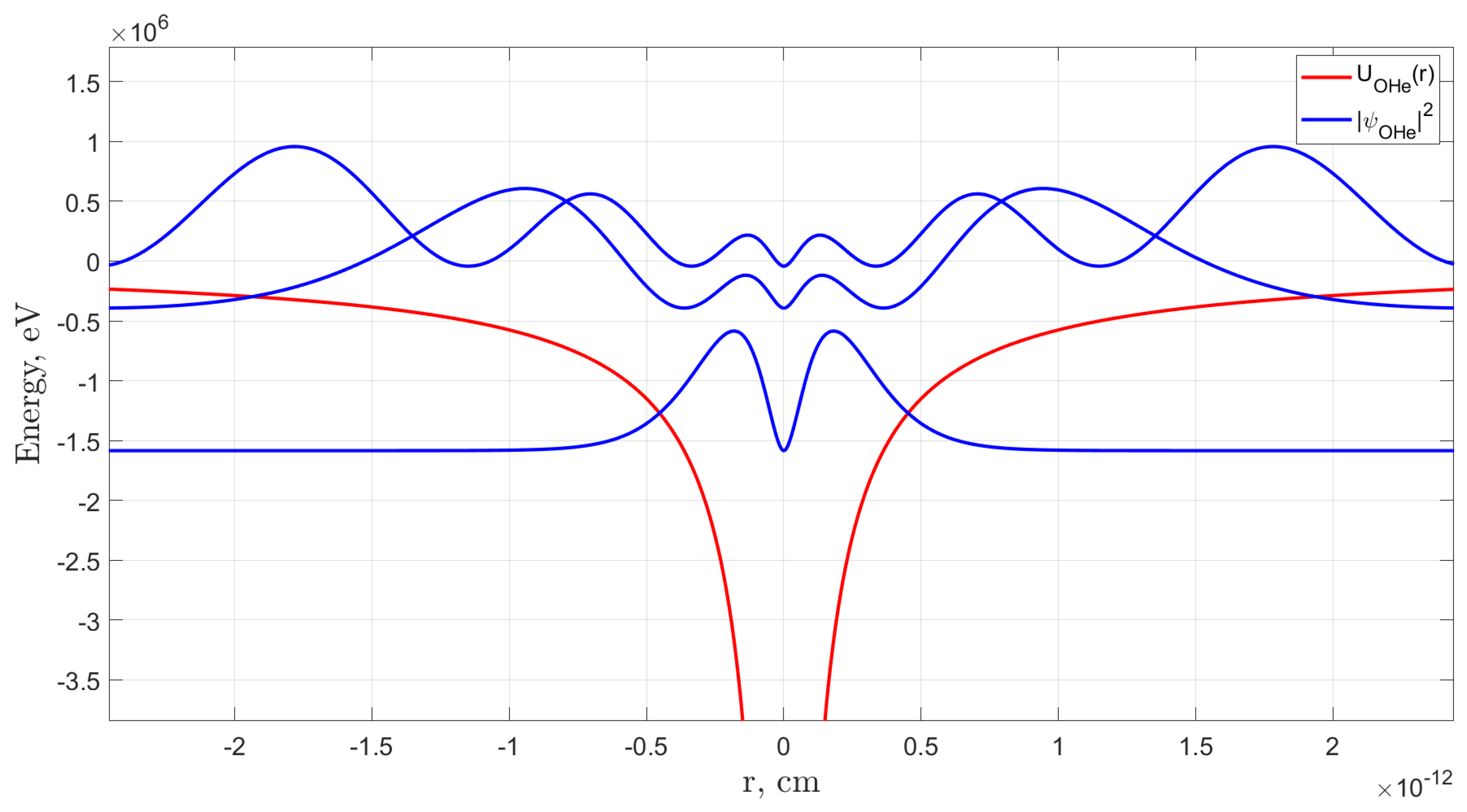
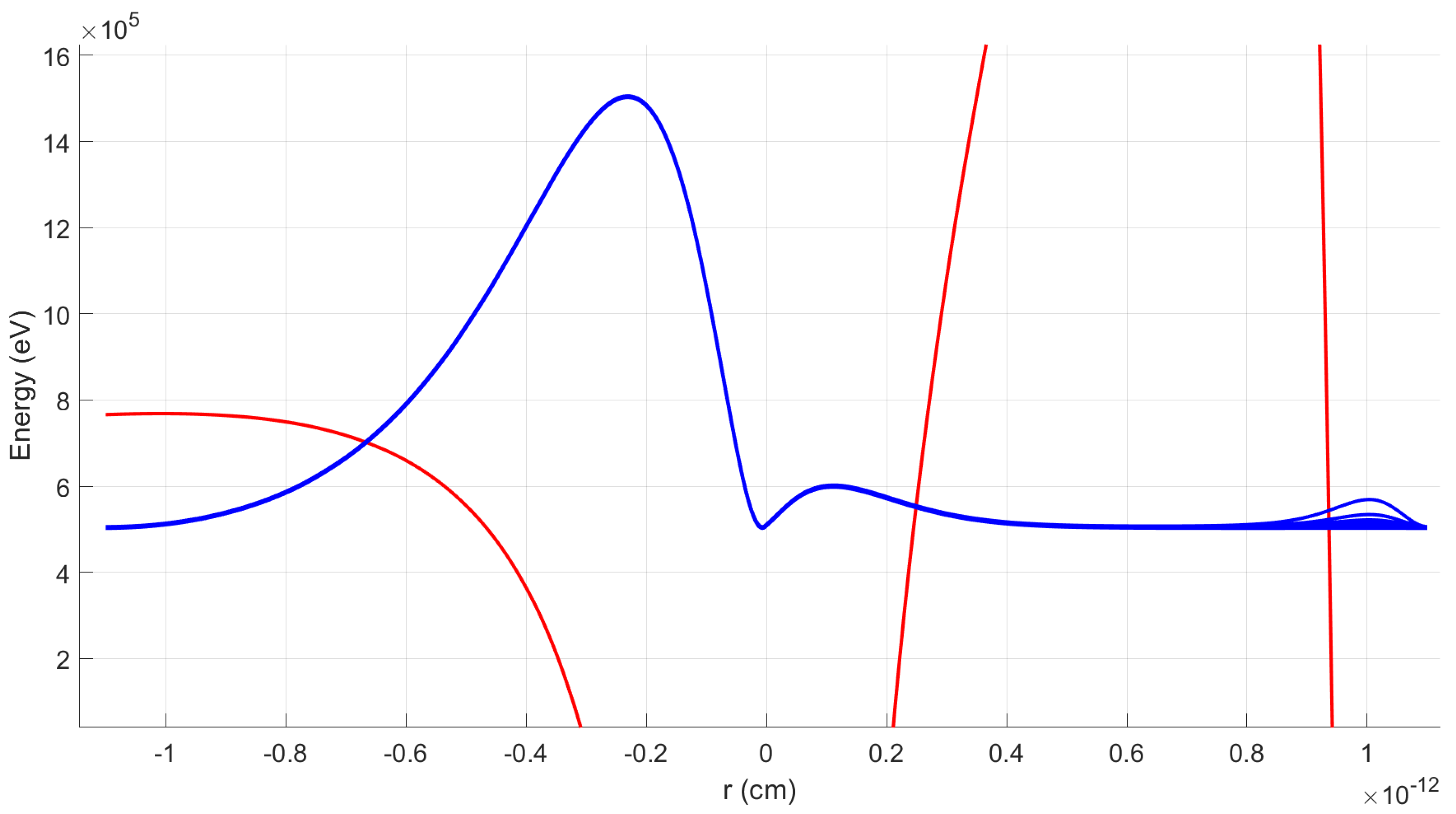
Figure 8 presents initial plots of the squared modulus of the helium $\mathsf{\Psi }$-functions (depicted by the blue solid line) corresponding to the ground-state energy levels within the total interaction potential of the OHe–Na system (indicated by the red solid line). These representations are associated with particular fixed positions of the sodium, marking the beginning of the OHe repolarization process. During this phase, the dipole moment begins to shift from its maximum negative value toward positive values, signaling an increased probability of helium tunneling into the sodium nucleus of matter by overcoming the Coulomb barrier. This progression ultimately results in the reversal of the dipole moment’s sign to positive, as evidenced by the dependence of the dipole moment on the sodium position shown in Figure 6 and Figure 7.

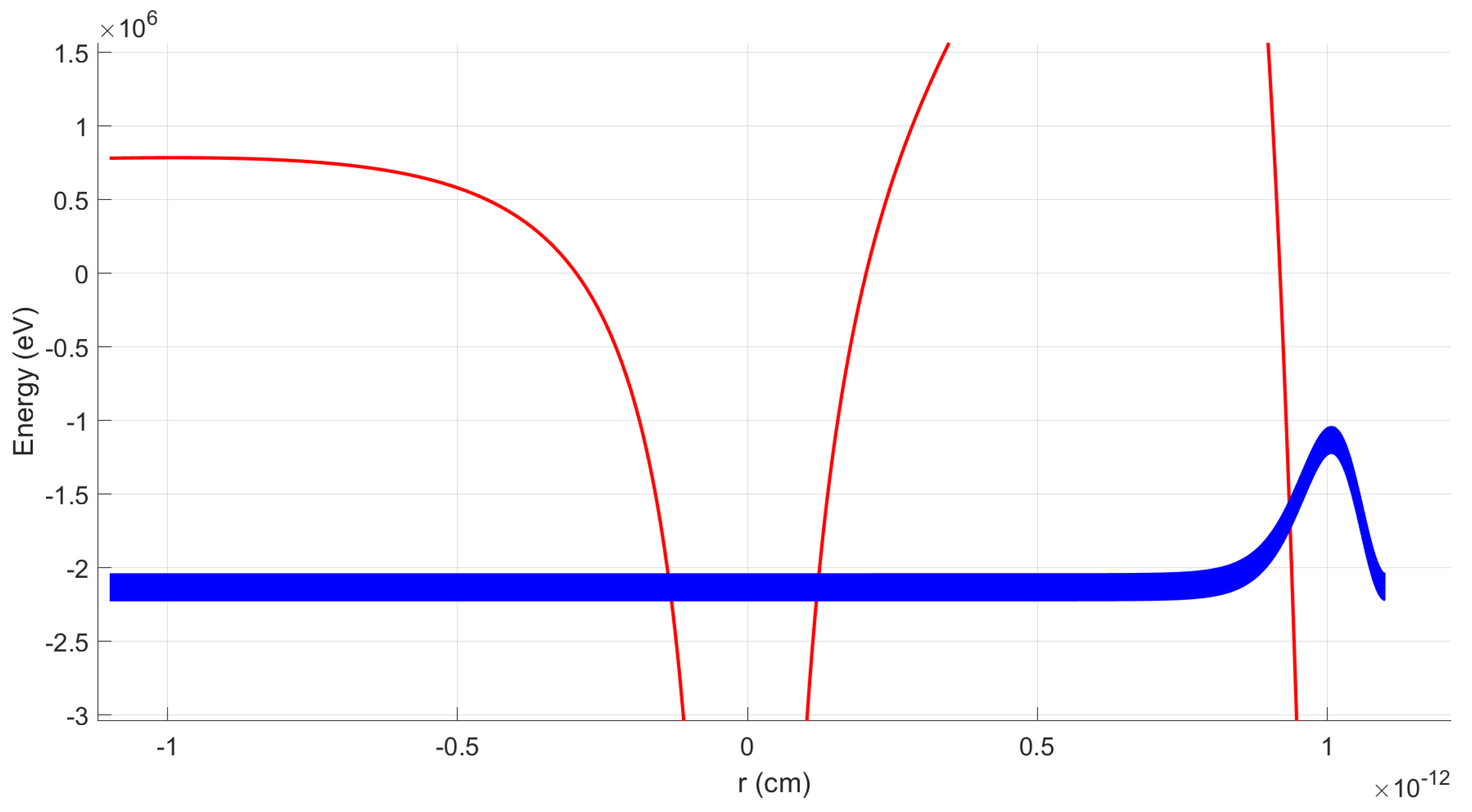
Figure 9 displays the additional plots of the squared modulus of the He $\mathsf{\Psi }$-functions (depicted by the blue solid line) corresponding to the ground-state energy levels in the helium total interaction potential (illustrated by the red solid line). These plots pertain to the specific configurations of sodium as helium transitions to a high-probability tunneling state from the repolarized OHe into sodium. At this stage, the dipole moment decreases from its peak positive value toward zero, coinciding with a significant reduction in the likelihood of helium remaining confined within the OHe. This phenomenon is further illustrated by the relationship between the dipole moment and the sodium position vector shown in Figure 7.

5.4. Reconstruction the Effective Interaction Potential of the OHe–Na System

To reconstruct the Stark potential (1), which represents the electric interaction between dipole of dark atom (polarized dark atom) and the nucleus of matter, we utilize the quantum mechanically computed dipole moment values. Additionally, to obtain the complete effective interaction potential for the OHe–Na system, that is, the total interaction potential of the sodium nucleus with the dark atom of OHe, one must also reconstruct the nuclear interaction potential, adopting Woods–Saxon model for the helium and sodium nuclei, along with the electrical interaction potential $U_{\mathrm{XHe}}^{\mathrm{e}}$ of the unpolarized OHe dark atom with the sodium nucleus.

In order to restore the shape of the interaction potential $U_{\mathrm{XHe}}^{\mathrm{e}}$, one needs to calculate the electric potential, $\varphi$, that creates unpolarized dark atoms as a whole in a general case, that is, for the XHe dark atom at distance r from the center of the X particle, in which we place the nucleus of the substance. To do this, one needs to solve the self-consistent Poisson equation for the test wave function $\psi ={\displaystyle \frac{e^{-r/r_0}}{\sqrt{\pi }{r}_0^{3/2}}}$, where $r_0$ is free parameter, as follows:

$${\displaystyle \frac{1}{r}}{\left(\varphi r\right)}^{″}=-4\pi e\left(n_{\mathrm{p}}+{\displaystyle \frac{Z_{\mathrm{X}}{e}^{-2r/r_0}}{\pi r_0^3}}\right),$$

(21)

where the prime denotes the derivative with respect to r, and $e{n}_{\mathrm{p}}$ is the charge density of n–He:

$$e{n}_{\mathrm{p}}=\left\{\begin{array}{cc}{\displaystyle \frac{e{Z}_{\alpha }}{\frac{4}{3}\pi R_{n\mathrm{He}}^3}}\hfill & \mathrm{for}r<R_{n\mathrm{He}},\hfill \\ 0\hfill & \mathrm{for}r>R_{n\mathrm{He}}.\hfill \end{array}\right.$$

(22)

As a result, by solving Equation (21), one obtains the electric potential created by the unpolarized dark atom XHe, consisting of the spherically symmetric uniformly charged nucleus n–He with radius $R_{n\mathrm{He}}$ and particle X, taking into account the screening effect of the nucleus n–He on the particle X, as follows:

$$\varphi =\left\{\begin{array}{cc}-e{Z}_{\mathrm{X}}{e}^{-2r/r_0}\left({\displaystyle \frac{1}{r_0}}+{\displaystyle \frac{1}{r}}\right)\hfill & \mathrm{for}r>R_{n\mathrm{He}},\hfill \\ -e{Z}_{\mathrm{X}}{e}^{-2r/r_0}\left({\displaystyle \frac{1}{r_0}}+{\displaystyle \frac{1}{r}}\right)+{\displaystyle \frac{e{Z}_{\mathrm{X}}}{r}}+\hfill \\ +{\displaystyle \frac{e{Z}_{\alpha }}{R_{n\mathrm{He}}}}\left({\displaystyle \frac{3}{2}}-{\displaystyle \frac{r^2}{2R_{n\mathrm{He}}^2}}\right)\hfill & \mathrm{for}r<R_{n\mathrm{He}}.\hfill \end{array}\right.$$

(23)

Therefore, the potential of the electrical interaction between the unpolarized XHe dark atom and the nucleus of substance is given by the following expression:

$$U_{\mathrm{XHe}}^{\mathrm{e}}=e{Z}_{\mathrm{A}}\varphi ,$$

(24)

where $Z_{\mathrm{A}}$ is the charge number of the nucleus of matter.

Thus, the $U_{\mathrm{XHe}}^{\mathrm{e}}$ potential is derived from solving the self-consistent Poisson equation while accounting for the screening effect of the ${\mathrm{O}}^{--}$ particle by the He nucleus, an effect that significantly diminishes with distance due to exponential decay.

Summing the nuclear interaction potential of the Woods–Saxon type, $U_{\mathrm{XHe}}^{\mathrm{e}}$ and $U_{\mathrm{St}}$ yields the total effective interaction potential form for the OHe dark atom’s interaction with the sodium nucleus (see Figure 10).

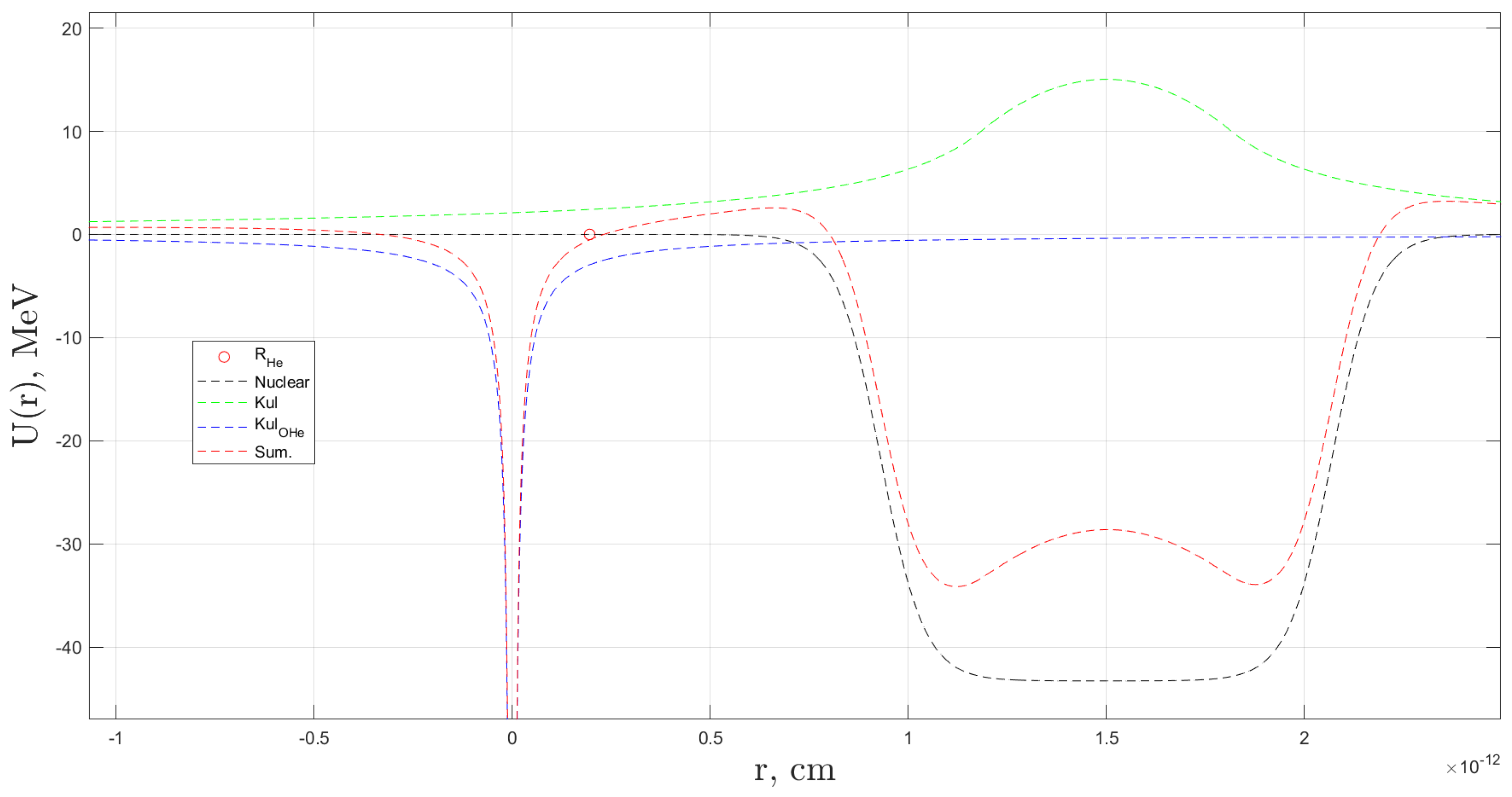
In Figure 10, the blue dotted curve represents the total effective interaction potential governing the interaction between OHe and the sodium. This potential describes the field in which the sodium nucleus is influenced by OHe. On the given scale, the individual contributions from the Woods–Saxon nuclear potential (depicted as a black dotted line) and $U_{\mathrm{XHe}}^{\mathrm{e}}$ (illustrated by a green dotted line) are minimal and can be considered negligible. As a result, the primary factors defining the depth of the potential well are the total effective potential (shown as a blue dotted line) and the Stark potential (shown as a red dotted line), determined by the negative dipole moment arising from the polarization of OHe. This well exhibits significant depth of approximately of $0.5\mathrm{MeV}$ indicating that a bound state between sodium and the dark atom in this potential—under the given intervals of $\overrightarrow{r}$ and ${\overrightarrow{R}}_{\mathrm{OA}}$—would possess relatively high energy, diverging from the lower energy states inferred from the DAMA experiment.

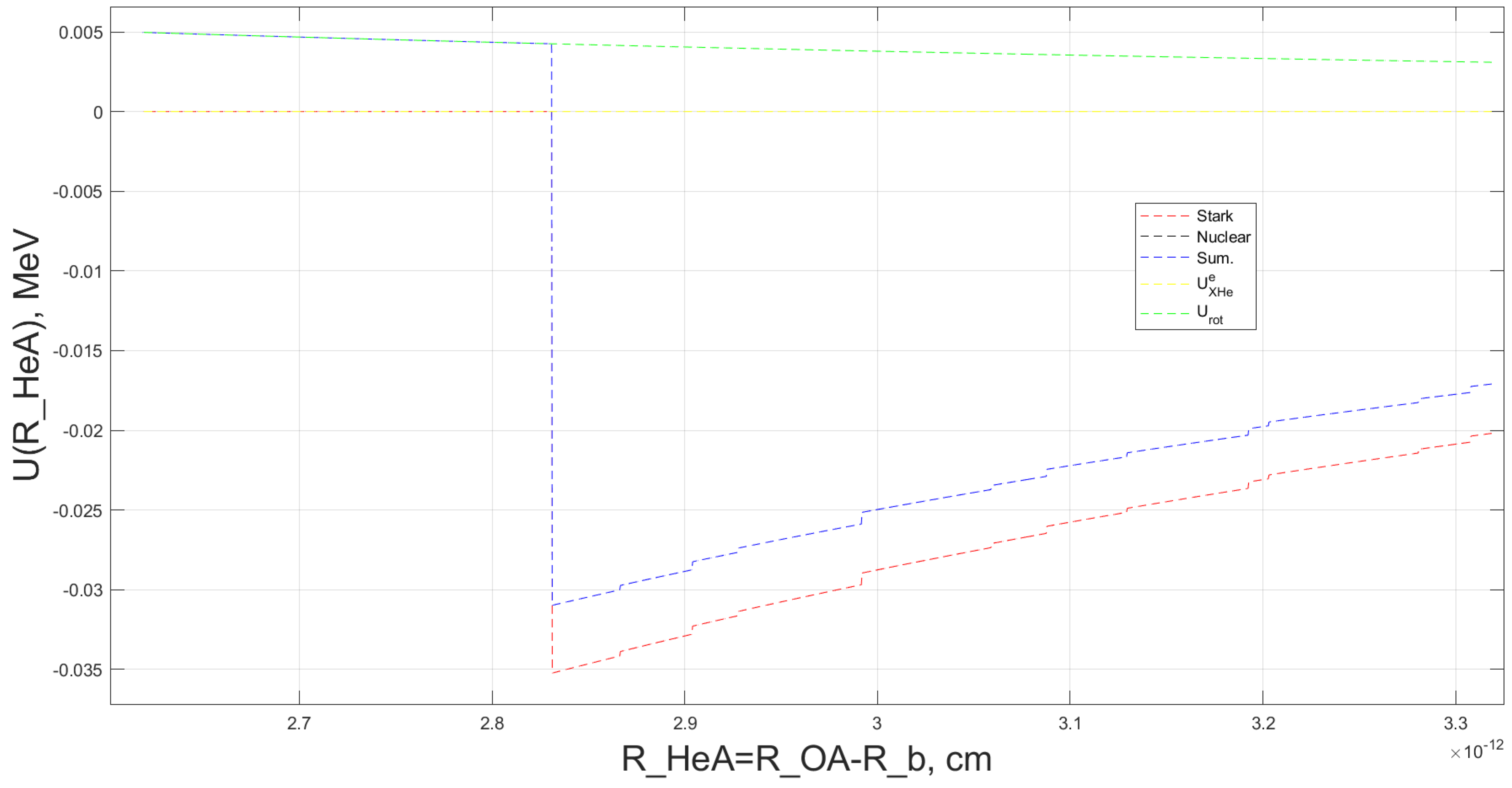
A more detailed representation of the effective interaction potential between OHe and the sodium nucleus can be constructed, especially around the region associated with dark atom repolarization, where the dipole moment shifts to positive values; see Figure 11.

Figure 11 analyzes the formation of a positive dipole Coulomb barrier within the total effective interaction potential in the OHe–Na system. This barrier emerges based on the ability of the Stark potential’s positive contribution (represented by the red dotted line), resulting from the positive dipole moment of the repolarized dark atom, to effectively oppose the combined negative effects of the nuclear interaction potential (illustrated by the black dotted line) and the electric interaction potential of unpolarized OHe with sodium, $U_{\mathrm{XHe}}^{\mathrm{e}}$ (depicted by the green dotted line).

As depicted in Figure 11, when the separation between helium and the sodium is approximately $11.6\mathrm{fm}$, the peak of the Stark potential remains insufficient to offset the combined negative contributions from the nuclear and the $U_{\mathrm{XHe}}^{\mathrm{e}}$ interaction potentials. This results in negative values for the total effective interaction potential. However, since the $\overrightarrow{r}$ is treated as a freely adjustable parameter in solving the Schrödinger equation for helium at fixed ${\overrightarrow{R}}_{\mathrm{OA}}$, this interval can be expanded. By simultaneously increasing the range of ${\overrightarrow{R}}_{\mathrm{OA}}$, the interaction distance at which He in the OHe begins to “feel” that the sodium can be extended.

Such adjustments would lead to a decrease in the maximum negative dipole moment of the polarized OHe. The negative dipole moment is primarily influenced by the Coulomb interaction between the helium and sodium nuclei, which diminishes as the separation between these nuclei occurs. Thus, the minimum of Stark potential, which determines the depth of the potential well in the effective interaction potential of the OHe–Na system, would become less.

Furthermore, extending the $\overrightarrow{r}$ and adjusting the ${\overrightarrow{R}}_{\mathrm{OA}}$ would result in a broader Coulomb barrier in the total effective interaction potential experienced by helium. This modification would alter the helium $\mathsf{\Psi }$-functions, thereby reducing the likelihood of helium tunneling into the sodium. Additionally, the positive dipole moment of the repolarized OHe, and the associated Stark potential barrier, would decrease. However, the increased distance between the nuclei would reduce the amplitudes of both the nuclear and the $U_{\mathrm{XHe}}^{\mathrm{e}}$ interaction potentials. Consequently, the total effective interaction potential in the OHe–Na system could exhibit the expected positive barrier values.

The OHe model suggests that the dipole Coulomb barrier in the total effective interaction potential of the OHe–Na system is sufficiently large to prevent a direct fusion between the nucleus of matter and the OHe. In the DAMA experiment conditions, the sodium exhibits thermal motion in the OHe–Na system, corresponding to the typical room temperature conditions of approximately $300\mathrm{K}$. This thermal movement results in a kinetic energy of about 2.6$\times {10}^{-2}\mathrm{eV}$ for the sodium. Consequently, the dipole Coulomb barrier in the effective interaction potential is expected to significantly exceed this energy level, ensuring the stability of the OHe system.

To analyze this phenomenon, the helium radius vector was extended from $r=|1.1\times {10}^{-12}\mathrm{cm}|$ to $r=|2.5\times {10}^{-12}\mathrm{cm}|$, while the sodium radius vector was set as $R_{\mathrm{OA}}=[3.5;2.8]\times {10}^{-12}\mathrm{cm}$. For each fixed value of ${\overrightarrow{R}}_{\mathrm{OA}}$, one-dimensional Schrödinger equations for helium were solved. The dipole moments corresponding to the ground-state energy levels of He in the polarized OHe were then determined. Based on these computed dipole moments, the effective interaction potential between OHe and sodium was subsequently reconstructed, see Figure 12 and Figure 13.

As illustrated in Figure 12, there is a noticeable reduction in the depth of the potential well for the effective interaction potential between the dark atom and the sodium nucleus (blue dotted line). A comparison of Figure 12 with Figure 10 reveals that, upon extending the interval $\overrightarrow{r}$ and increasing the sodium position ${\overrightarrow{R}}_{\mathrm{OA}}$, the depth of the potential well diminishes significantly, from approximately of 0.5 MeV to about 35 keV.

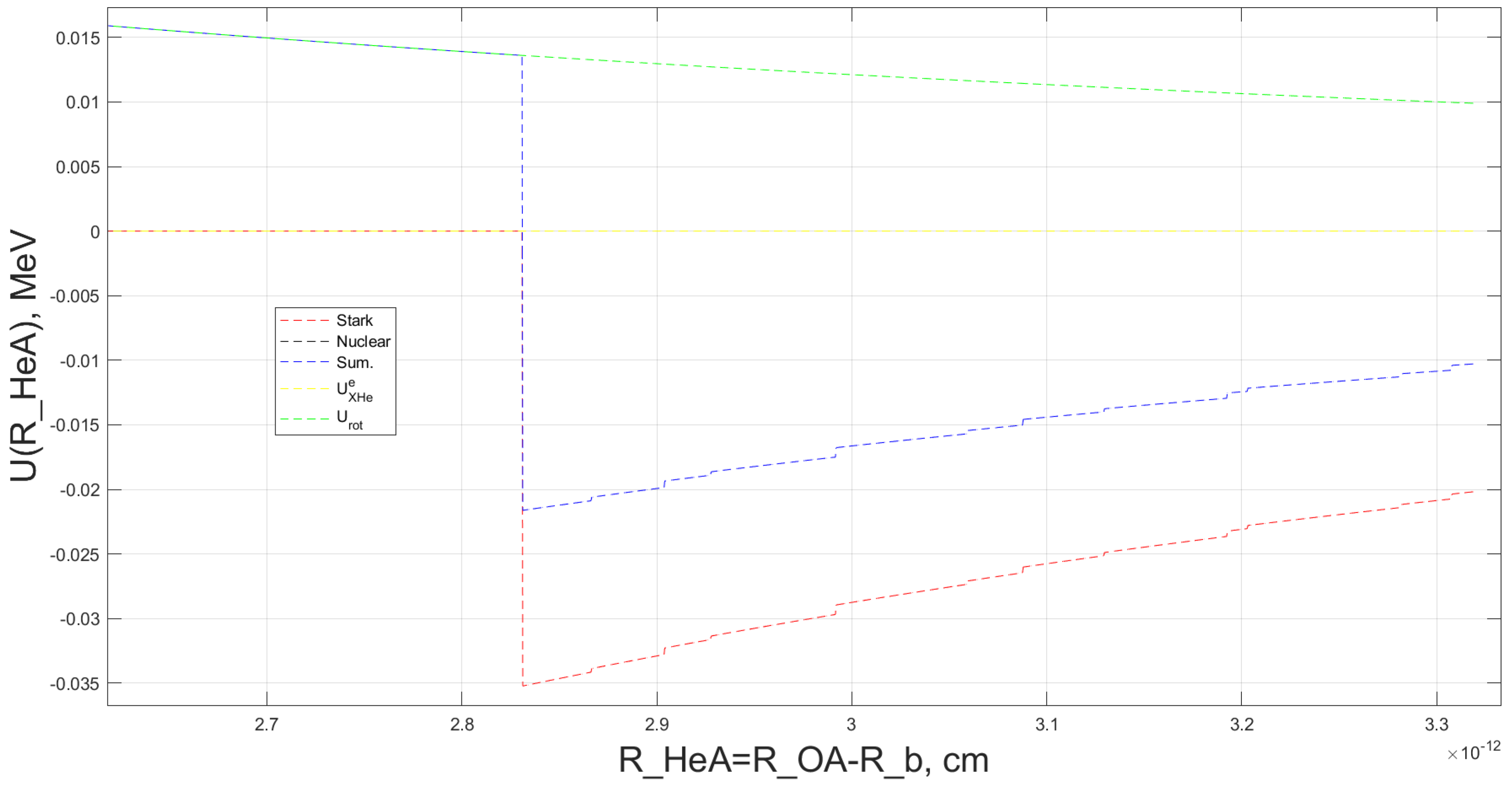
In Figure 13, the nuclear potential of Woods–Saxon (represented by the black dotted line) and $U_{\mathrm{XHe}}^{\mathrm{e}}$ (depicted as the green dotted line) diminish to negligible values at a separation approximately of 28.33 fm between the helium and sodium. As expected, the Stark potential emerges as the dominant contributor, establishing a positive potential barrier in the total effective interaction potential for the OHe–Na system. A comparison of Figure 11 and Figure 13 demonstrates that extending the interval $\overrightarrow{r}$ and increasing ${\overrightarrow{R}}_{\mathrm{OA}}$, representing the sodium nucleus’s position relative to the OHe, results in a reduction in the positive Stark potential barrier. This barrier diminishes from approximately 7.5 eV to about 0.3 $\times {10}^{-2}\mathrm{eV}$, with the change attributed to a decrease in the repolarized dark atom’s dipole moment.

In Figure 13, the dipole Coulomb barrier in the effective interaction potential is shown to be approximately ten times smaller than the kinetic energy of the sodium nucleus approaching the dark atom under the experimental conditions of the DAMA experiment (about $2.6\times {10}^{-2}\mathrm{eV}$). However, the depth of the potential well in this interaction remains nearly six times greater than the experimental findings reported by the DAMA experiment ($6\mathrm{keV}$) and significantly higher than the theoretically estimated binding energy of sodium in a low-energy state with the dark atom (about $4\mathrm{keV}$). To address these discrepancies, we extend the range of the helium radius vector $\overrightarrow{r}$, solve the Schrödinger equation for helium within the OHe–Na system, as well as increase ${\overrightarrow{R}}_{\mathrm{OA}}$, and thus further decrease the potential well depth and lower the dipole Coulomb barrier, which are already below the predicted values. Improving the accuracy of the numerical model is critical to refining these results, necessitating the consideration of additional effects that influence the interaction between the dark atom and the atomic nuclei. One such effect is the centrifugal interaction potential, $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$, which may play a role in characterizing the dynamics of the OHe–Na system.

5.5. Incorporating the Centrifugal Potential into the Quantum Mechanical Numerical Model

The centrifugal potential governing the interaction between the OHe and the sodium, $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$, depends on the total angular momentum of the interacting system, ${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}$, as well as the distance, R, between the two interacting particles. Neglecting the moments of inertia of the nuclei, it is expressed as follows (see Equation (27) in Ref. [27]):

$$U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}\left(R\right)={\displaystyle \frac{{\hslash }^2{c}^2{J}_{\mathrm{OHe}-\mathrm{Na}}(J_{\mathrm{OHe}-\mathrm{Na}}+1)}{2\mu c^2{R}^2}},$$

(25)

where $\mu$ denotes the reduced mass of the system and c denotes the speed of light.

Since the mass of the OHe is entirely determined by the ${\mathrm{O}}^{--}$, which is assumed to have a mass of $1\mathrm{TeV}$, and given that the sodium has a significantly smaller mass of approximately $m_{\mathrm{Na}}\approx 21.4\mathrm{GeV}$, the reduced mass of the OHe–Na system can be approximated as $\mu \approx m_{\mathrm{Na}}/c^2$.

The total angular momentum, ${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}$, for the interaction between OHe and the sodium nucleus is defined as follows:

$${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}\left(\rho \right)={\overrightarrow{l}}_{\mathrm{OHe}-\mathrm{Na}}\left(\rho \right)+{\overrightarrow{I}}_{\mathrm{Na}}+{\overrightarrow{I}}_{\mathrm{OHe}},$$

(26)

where ${\overrightarrow{l}}_{\mathrm{OHe}-\mathrm{Na}}\left(\rho \right)$ denotes the orbital angular momentum, which is a function of the impact parameter $\rho$, ${\overrightarrow{I}}_{\mathrm{Na}}$ is the sodium’s intrinsic angular momentum, and ${\overrightarrow{I}}_{\mathrm{OHe}}$ represents the spin of the $\mathrm{O}$ He. The ${\overrightarrow{I}}_{\mathrm{OHe}}$ is composed of the spin of the ${\mathrm{O}}^{--}$, ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}$, combined with the intrinsic angular momentum, ${\overrightarrow{I}}_{\mathrm{He}}$, of the He as follows:

$${\overrightarrow{I}}_{\mathrm{OHe}}={\overrightarrow{I}}_{\mathrm{He}}+{\overrightarrow{I}}_{{\mathrm{O}}^{--}}.$$

(27)

Let us consider the specific case of a direct collision between sodium and dark atom. In this head-on interaction, characterized by an impact parameter $\rho =0$, the orbital angular momentum of the system becomes zero, ${\overrightarrow{l}}_{\mathrm{OHe}-\mathrm{Na}}\left(0\right)=\overrightarrow{0}$. The sodium contributes intrinsic angular momentum which is defined as ${\overrightarrow{I}}_{\mathrm{Na}}=\overrightarrow{3/2}$.

The OHe spin is dictated by the spin of the ${\mathrm{O}}^{--}$, because the He intrinsic angular momentum is equal to ${\overrightarrow{I}}_{\mathrm{He}}=0$. The spin of ${\mathrm{O}}^{--}$ depends on the specific internal structure and properties of this particle. In particle models involving four or five fermion generations, a stable particle with a charge of −2, denoted as ${\Delta }_{\overline{\mathrm{U}}\overline{\mathrm{U}}\overline{\mathrm{U}}}^{--}$, is theoretically viable and consists of three antiquarks, such as fourth-generation $\overline{U}$ quarks, formulated as ${\Delta }_{\overline{\mathrm{U}}\overline{\mathrm{U}}\overline{\mathrm{U}}}^{--}=\left(\overline{U}\overline{U}\overline{U}\right)$ [1]. Consequently, if ${\mathrm{O}}^{--}$ takes the form of ${\Delta }_{\overline{\mathrm{U}}\overline{\mathrm{U}}\overline{\mathrm{U}}}^{--}$ and includes quarks from these extended families, then ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}=\overrightarrow{3/2}$. The walking technicolor (WTC) model, based on SU(2) symmetry, proposes a unique type of interaction that binds a novel type of quarks [11]. Within the framework of the walking technicolor theory, technibaryons are hypothesized to form from techniquarks that are bound by specific technicolor interaction and charge. If ${\mathrm{O}}^{--}$ is identified as a technibaryon, its spin, ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}$, may take on values of either $\overrightarrow{0}$ or $\overrightarrow{1}$. Additionally, WTC predicts the existence of a fourth generation of technileptons. If ${\mathrm{O}}^{--}$ is categorized as a member of the technilepton family, its spin would correspond to ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}=\overrightarrow{1/2}$.

In the scenario being analyzed, where the impact parameter satisfies $\rho =0$, the total angular momentum of interacting OHe and the sodium can be expressed as follows:

$${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}={\displaystyle \frac{\overrightarrow{3}}{2}}+{\overrightarrow{I}}_{{\mathrm{O}}^{--}}.$$

(28)

To account for the centrifugal potential $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$ within the total effective interaction potential of the OHe–Na system, it is necessary to include the centrifugal potential arising only due to the He and sodium interaction, denoted as $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$. Consequently, $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ must be added to the total potential affecting the He in the OHe–Na system (see Equation (19)) for each fixed position of sodium, ${\overrightarrow{R}}_{\mathrm{OA}}$, as follows:

$$U_{\mathrm{He}+\mathrm{rot}}=-{\displaystyle \frac{4e^2}{r}}+U_{\mathrm{Coulomb}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)+U_{oN}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)+U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right),$$

(29)

where $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$ is given by the following expression:

$$U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)={\displaystyle \frac{{\hslash }^2{c}^2{J}_{\mathrm{He}-\mathrm{Na}}(J_{\mathrm{He}-\mathrm{Na}}+1)}{2m_{\mathrm{He}}{c}^2{|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}|}^2}},$$

(30)

where ${\overrightarrow{J}}_{\mathrm{He}-\mathrm{Na}}$ denotes the total angular momentum associated with interaction of He and Na.

${\overrightarrow{J}}_{\mathrm{He}-\mathrm{Na}}$ is governed exclusively by the intrinsic angular momentum of Na. This arises from the feauture that $He$ possesses no intrinsic angular momentum, ${\overrightarrow{I}}_{\mathrm{He}}=\overrightarrow{0}$. Additionally, when Na approaches the helium with $\rho =0$, the orbital angular momentum between the two nuclei becomes negligible. Consequently, the total angular momentum for interaction particles simplifies to ${\overrightarrow{J}}_{\mathrm{He}-\mathrm{Na}}=\overrightarrow{3/2}$.

Figure 14 illustrates a representative case of the total interaction potential experienced by He within the OHe–Na system, $U_{\mathrm{He}+\mathrm{rot}}$. This potential accounts for the inclusion of the centrifugal interaction potential arising from the interaction between the He and Na. The plots are functions of the helium radius vector, $\overrightarrow{r}$, for a fixed value of ${\overrightarrow{R}}_{\mathrm{OA}}$.

Figure 14 illustrates the Coulomb and nuclear interaction potentials between He and Na, alongside the centrifugal potential, $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}\left(\right|{\overrightarrow{R}}_{\mathrm{OA}}-\overrightarrow{r}\left|\right)$, calculated for $\rho =0$. Additionally, the figure presents the Coulomb potential arising from the interaction between He and the ${\mathrm{O}}^{--}$ and, finally, the total effective potential acting on the He in the OHe–Na system.

Ultimately, we calculated the energy values of the ground state of He in polarized OHe through solutions for the Schrödinger equations for He in potentials $U_{\mathrm{He}+\mathrm{rot}}$. This analysis was conducted for the various fixed positions of the sodium in the range $R_{\mathrm{OA}}=[3.5;2.8]\times {10}^{-12}\mathrm{cm}$, as well as for $r=|2.5\times {10}^{-12}\mathrm{cm}|$. Corresponding wave functions associated with these energy values of the ground state were also calculated. Based on this information, dipole moments for each ground-state energy of He in the polarized OHe were evaluated. These dipole moments enabled the reconstruction of the total effective interaction potential in the OHe–Na system. This potential includes $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$ and is presented for two values of the total angular momentum ${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}$, $\overrightarrow{3/2}$ and $\overrightarrow{3}$; these total angular moments correspond to the following values of the spin of the ${\mathrm{O}}^{--}$ particle: ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}=\overrightarrow{0}$ and $\overrightarrow{3/2}$, respectively (see Figure 15 and Figure 16).

Increase in ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}$ and, therefore, the total angular momentum ${\overrightarrow{J}}_{\mathrm{OHe}-\mathrm{Na}}$ leads to a substantial amplification of the $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$ within the total effective interaction potential of the OHe–Na system, that, in turn, strongly affects the shape of this potential, as it can be seen in Figure 15 and Figure 16. An increase in ${\overrightarrow{I}}_{{\mathrm{O}}^{--}}$ quantitatively affects the effective potential by reducing the depth of the potential well and elevating the height of the dipole potential barrier. These changes play a crucial role in preventing both the uncontrolled fusion of the Na with the OHe and the subsequent disintegration of the latter.

The three-body dynamics inherent in the task we are considering necessitate a thorough consideration of the feedback mechanisms among the interacting components of the OHe–Na system, where the outcomes of their interactions directly influence the subsequent behavior of system. The analysis commenced by focusing on the He in the OHe–Na system. The forces acting upon He are systematically evaluated, and the total potential shaping its behavior in this system is reconstructed for each fixed position of sodium. By solving the Schrödinger equations for the total potentials of He, the dipole moments of the polarized OHe was calculated for each fixed ${\overrightarrow{R}}_{\mathrm{OA}}$. This methodology inherently captures the influence of the Na on the polarization of the OHe, characterized by the dark atom’s dipole moment.

Additionally, $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ is incorporated, which modifies the structure of the total interaction potential for He. The inclusion of $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ influences the dipole moment by changing the shape of the helium total interaction potential. Comparison of Figure 12 and Figure 16 reveals that the inclusion of $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ results in a deeper Stark potential well, what can be seen from Figure 16. Stark potential is closely aligned with the effective interaction potential depicted in Figure 12. These findings illustrate how $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ contributes to increasing the negative values of $\delta$.

Furthermore, adding $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ into $U_{\mathrm{He}+\mathrm{rot}}$ reduces the Stark potential’s dipole Coulomb barrier. This occurs because $U_{{\mathrm{rot}}_{\mathrm{He}-\mathrm{Na}}}$ promotes to increase in the positive value of the barrier in the total potential of helium, thereby reducing the probability of it tunneling into the Na. This highlights the role of Na in modifying the dark atom’s polarization. After that, OHe begins to interact with Na as dipole, and this interaction is expressed by the Stark potential. Beyond the Stark potential, Na interacts with OHe via additional contributions, including the $U_{{\mathrm{rot}}_{\mathrm{OHe}-\mathrm{Na}}}$, $U_{\mathrm{XHe}}^{\mathrm{e}}$, and the nuclear potential.

In conclusion, the total effective interaction potential of OHe–Na system, exemplified in Figure 16, is reconstructed. This potential depends on $I_{{\mathrm{O}}^{--}}$, yet its general structure aligns with theoretical predictions. The resulting total effective interaction potential makes it possible to expand the $\overrightarrow{r}$ interval, which facilitates a potential well depth of approximately of 6 keV and potential barrier height surpassing the sodium’s thermal kinetic energy, estimated at about 2.6 × 10⁻² eV. The presence of this positive dipole potential barrier is pivotal in averting the fusion of helium or ${\mathrm{O}}^{--}$ particle with the nucleus of a substance, thereby preserving the integrity and stability of the OHe. And it is a critical requirement for sustaining the validity of the OHe hypothesis.

6. Conclusions and Further Directions

This paper investigates the hypothesis of composite dark matter, consisting of XHe dark atoms. These dark atoms interact with the nuclei of ordinary substance through nuclear and electromagnetic forces. The distinctive properties of these interactions of XHe atoms with nuclei in underground dark matter detection experiments might explain the inconsistencies observed in various direct dark matter detection efforts [1].

To study the detailed interaction mechanisms between XHe and the ordinary nucleus, it is essential to determine the exact structure of their total effective interaction potential. Restoring this potential is essentially a three-body task, and therefore an exact analytical solution is unattainable. Consequently, the study employs numerical modeling to examine the behavior of XHe when interacting with the nucleus of a substance. This computational approach aims to reconstruct the precise effective potential and establish a framework for interpreting experimental results from direct dark matter detection efforts.

The quantum mechanical numerical model presented in this paper models a three-particle system interacting via electric, nuclear, and centrifugal interactions. The methodology involves solving the Schrödinger equation for helium in the OHe–Na system, with the sodium nucleus positioned at various fixed locations relative to the OHe atom. By incorporating both nuclear and electromagnetic interaction characteristics, this model enables the precise calculations of dark atom polarization by calculating the dipole moments of the polarized OHe atoms. These dipole moments, as functions of the distance between the sodium nucleus and the dark atom, facilitate an accurate reconstruction of the Stark potential, which plays a pivotal role in shaping the effective interaction potential of the OHe–Na system.

Finally, the total interaction potentials for He were comprehensively reconstructed for each fixed position of sodium ${\overrightarrow{R}}_{\mathrm{OA}}$. The Schrödinger equations were numerically solved for the following two scenarios: He in unpolarized OHe and in polarized OHe undergoing interaction with Na. From the computed $\mathsf{\Psi }$-functions of He, the $\delta$ of the polarized OHe were derived. These results facilitated the calculation of the Stark potential and the subsequent reconstruction of the total effective interaction potential of the OHe–Na system. This potential incorporated contributions from the Stark, nuclear, centrifugal, and $U_{\mathrm{XHe}}^{\mathrm{e}}$ potentials. Thus, in this paper, for the first time, steps have been taken towards a consistent quantum mechanical description of the interaction of dark atoms, with unshielded nuclear attraction, with the nucleus of atom of matter. The total effective interaction potential of the OHe–Na system has been restored, and its general form corresponds to theoretical predictions. This effective interaction potential contains a shallow potential well and a positive Coulomb dipole barrier exceeding the thermal kinetic energy of sodium. This allows us to preserve the integrity and stability of the dark atom, which is an essential requirement for confirming the validity of the OHe hypothesis.

In future studies, to further enhance the accuracy of the effective interaction potential reconstruction and achieve a physically meaningful description of dark atom interactions with heavy element nuclei, as well as to explain the results of direct dark matter detection experiments, the quantum mechanical approach to potential reconstruction will be refined. This refinement involves determining the nuclear and electromagnetic potentials for the XHe interactions with ordinary matter nuclei, incorporating the finite sizes of the interacting particles by considering the distributions of electric charge and nucleons within the nuclei. Additionally, the model accounts for nucleus of matter deformation. We solve the Schrodinger equation for the heavy element nucleus within this potential. Improvements in the numerical model presented here allows us to more accurately exploration of possible explanations for direct dark matter search paradoxes and provide a foundation for experimental tests regarding the dark atom hypothesis.