Towards Study of Two-Particle P_T Correlations in Hadronic Interactions at NICA

Abstract

A new method for studying two-particle transverse momentum ($P_T$) correlations in soft hadronic interactions is proposed. It is shown that Monte Carlo models: PYTHIA 6 and Geant4 FTF (FRITIOF), give different predictions for the correlations in proton–proton interactions. The correlations are connected with Schwinger’s mechanism of particle creation. These correlations can be studied in current and future experiments in high energy physics, in particular, at the Nuclotron-based Ion Collider fAcility (NICA).

1. Introduction

One of the most significant experimental results on soft hadronic interactions has been recently obtained by the NA61/SHINE Collaboration. In Ref. [1], the Collaboration presented the measurements of inclusive spectra and mean multiplicities of ${\pi }^{\pm }$, $K^{\pm }$, p and $\overline{p}$ produced in inelastic proton–proton interactions at incident projectile momenta, $P_{\mathrm{lab}}$, of 20, 31, 40, 80 and 158 GeV/c (where c denotes the speed of light), corresponding center-of-mass energies, $\sqrt{s}$ are 6.3, 7.7, 8.8, 12.3 and 17.3 GeV, respectively. The Collaboration compared their results with EPOS 1.99 [2] and UrQMD 3.4 [3,4] Monte Carlo models predictions. It has been concluded [1] that EPOS 1.99 model provided a good description of the measurements in the SPS (the Super Proton Synchrotron) energy range, while the predictions of the UrQMD 3.4 model significantly differed from the data.

Indeed, the UrQMD calculations for the rapidity distributions of ${\pi }^{\pm }$ mesons are close to the data only at $P_{\mathrm{lab}}=$ 158 GeV/c. The model underestimates the data at lower projectile momenta. As shown in Ref. [5], one reason for this is the underestimated probability of single diffraction dissociation at $\sqrt{s}<$ 15 GeV. Another reason is the enhanced production of mesons by fragmentation of di-quarks.

The EPOS model agrees well enough with the data at $P_{\mathrm{lab}}\ge$ 31 GeV/c.

Comparisons of the NA61/SHINE Collaboration data [1] with the Parton-Hadron-String-Dynamics (PHSD) and PYTHIA 8.2 Monte Carlo models predictions were presented in Ref. [6]. The description of the data provided by these two models is not excellent, especially for the proton spectra. The reasons mentioned above for the UrQMD model apply as well for the PHSD model. For the PYTHIA 8.2 model, the situation is more complicated. The PYTHIA model [7] does not consider the string junctions in baryons, using instead the so-called popcorn mechanism, but all attempts to tune the PYTHIA parameters were not successful, as we can see it.

The NA61/SHINE data were also analysed with the SMASH (Simulating Many Accelerated Strongly-interacting Hadrons) hadronic transport approach [8], based on the PYTHIA model. In addition to the difficulty to describing the spectra of protons, this approach fails to describe the event-averaged transverse momentum versus Feynman x-variable, $<P_T>$–$x_F$, correlations (see Figures 6, 12, and 20 in Ref. [8]), most probably due to the $P_T$ generation mechanism. Below, in Section 2, we show that these difficulties can be partially solved in the Geant4 FTF (FRITIOF) [9] and HIJING [10,11,12] Monte Carlo models. In Section 3, we propose a method for a detailed study of two-particle $P_T$ correlations. We hope that this method can be implemented at NICA—the Nuclotron-based Ion Collider fAcility [13], which is under construction at the Joint Institute for Nuclear Research (JINR), Dubna, Russia. Two experiments—the Multi Purpose Detector (MPD) and the Spin Physics Detector (SPD)—are foreseen at NICA. MPD experiment is aimed to the study of hot and dense baryonic matter in heavy ion collisions over the atomic mass range of A = 1 to 238 at a center-of-mass energy per nucleon pair, $\sqrt{s_{NN}}$, up to 9 GeV for ${}^{92}$U. The SPD Collaboration intends to study the spin structure of the proton and the deuteron, as well as other spin-related phenomena using polarized proton and deuteron beams at $\sqrt{s_{NN}}$ up to 27 GeV.

2. $<{\mathit{P}}_{\mathit{T}}^{\mathbf{2}}>$–${\mathit{x}}_{\mathit{F}}$ Correlations in Proton–Proton Interactions

The inclusive one-particle distribution, $E{d}^3\sigma /d^{3}P$, is a function of three variables: $P_x$, $P_y$ and $P_z$. Here, E and P are the produced particle energy and momentum, respectively, and $\sigma$ is the collision inelastic cross-section. The function must not depend on the azimuthal angle in the case of collisions of unpolarized particles. Thus, a pair of independent variables can be chosen such as $|{\overrightarrow{P}}_T|=\sqrt{P_x^2+P_y^2}$ and rapidity, $y=(1/2)log((E+P_z)/(E-P_z))$, or $|{\overrightarrow{P}}_T|$ and the Feynman variable, $x_F=2P_z/\sqrt{s}$. By integrating the distribution over $P_T$, one can obtain the particle multiplicity distribution on rapidity, $dn/dy=\int (E{d}^3\sigma /d^{3}P)d^2{P}_T/\sigma$. 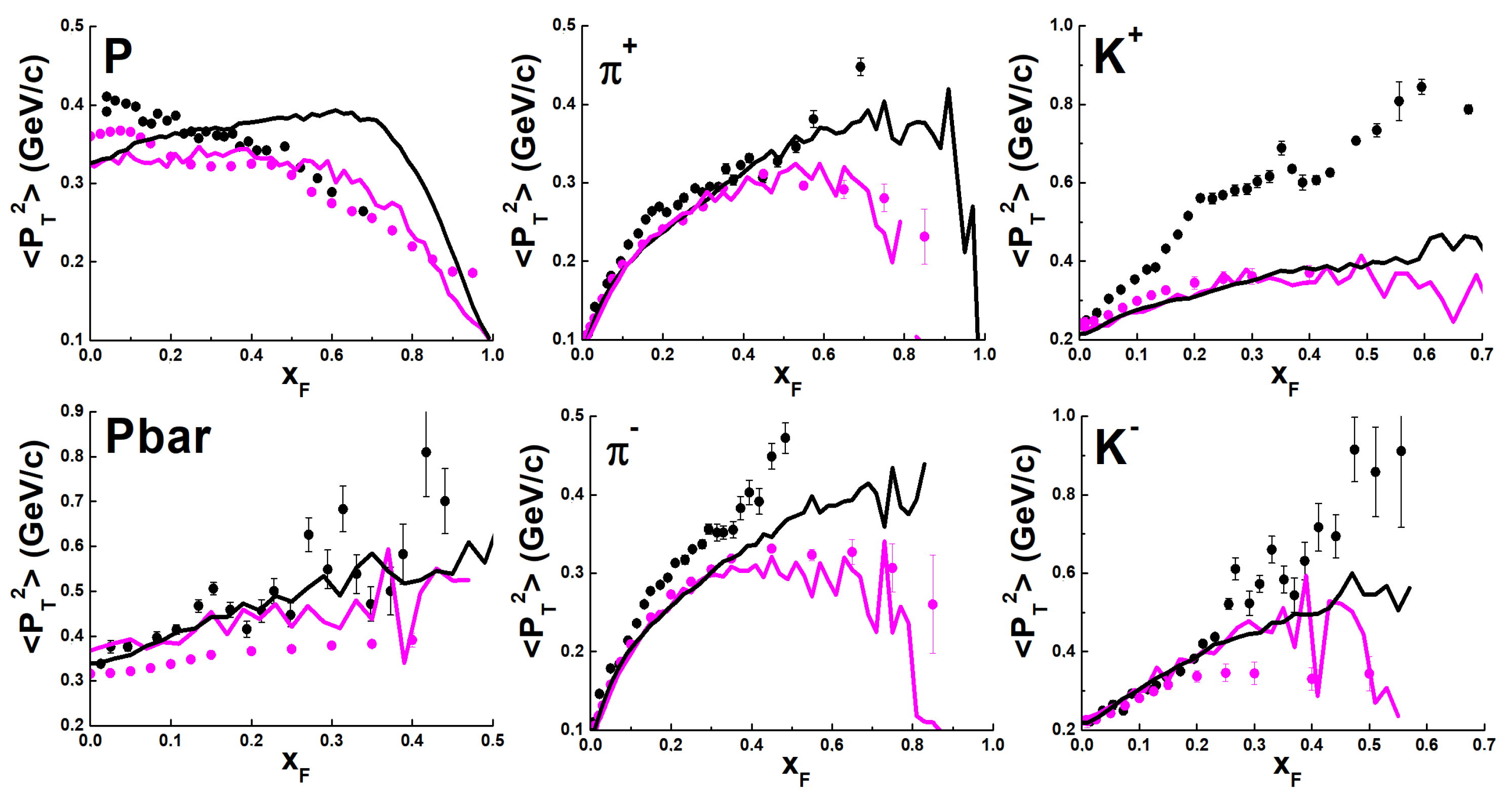A few experimental rapidity distributions are shown in Figure 1.

As Figure 1 shows, the models reproduce the general features of the distributions. The Geant4 FTF model describes well the ${\pi }^{-}$ meson distribution at $\sqrt{s}=17.3$ GeV. A successful FTF model description of the ${\pi }^{-}$ meson distributions in proton–proton interactions at other NA61/SHINE energies has been reported in Ref. [15]. As one can see in Figure 1, at higher energies, this model underestimates the ${\pi }^{+}$ and ${\pi }^{-}$ meson production, since it does not incluede hard interactions. The HIJING model, instead, takes into account hard interactions, and describes well the ${\pi }^{+}$ and ${\pi }^{-}$ distributions at $\sqrt{s}=27.5$ GeV. At $P_{\mathrm{lab}}=$ 158 GeV/c, it is rather challenging to comment on the calculations of the ${\pi }^{+}$ distributions, due to the effect of strong scattering present in the experimental data (see Figure 1).

The Geant4 FTF model has been developed by the authors of this paper, for some time, within the Geant4 Collaboration [16]. The presented results were obtained using the Geant4 version 11.1 (December 2022). We tuned the parameters of the HIJING model in Ref. [12], where various calculations for the NA61/SHINE data on proton–proton interactions are given. A comparison of the same data to the PYTHIA 6.4 [7] calculations is presented in Ref. [17]. The summary conclusion is that a good description of the $dn/dy$ distributions can be obtained for various models. The description of proton distributions requires particular efforts.

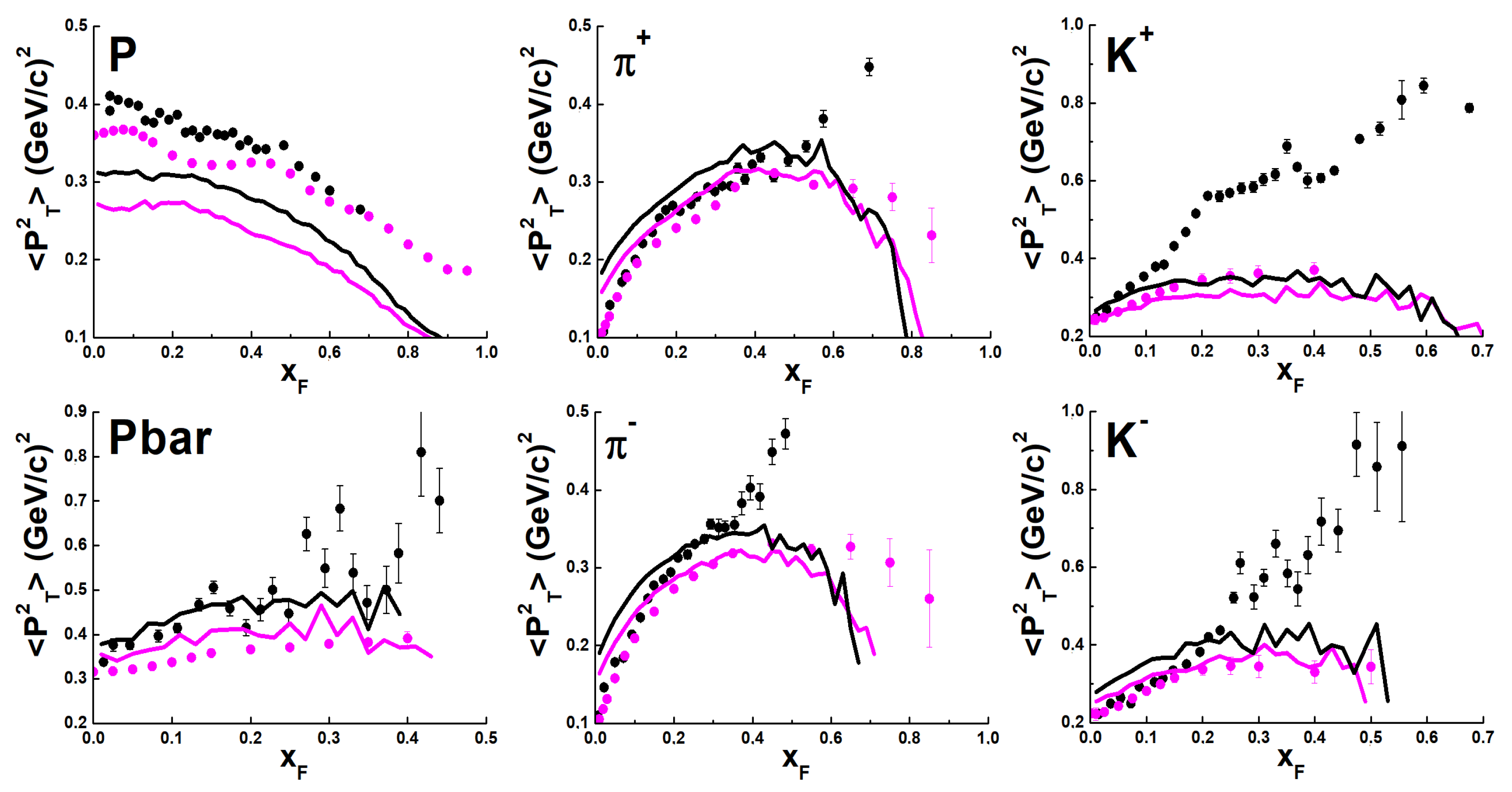
The NA61/SHINE Collaboration also presented $|{\overrightarrow{P}}_T|$ distributions of different-types of produced particles [1]. However, it is difficult to draw a firm conclusion from these data. Threfeore, we turn our attention to other experimental data [14,18,19,20], namely to $<P_T^2>$–$x_F$ correlations shown in Figure 2 and Figure 3.

The LEBC-EHS Collaboration [14] measured these correlations in proton–proton interactions at $\sqrt{s_{NN}}=$ 27.5 GeV. The NA49 Collaboration presented similar data [18,19,20] at $P_{\mathrm{lab}}=$ 158 GeV/c [21]. The two data sets show quite different behaviour:$<P_T^2>$ grows for $K^{\pm }$ and ${\pi }^{\pm }$ mesons with increasing $x_F$ in the LEBC-EHS data, whereas it decreases for $x_F>$ 0.5 in the NA49 data. It is not clear whether this contrasting behavior is because of the experimental methods used, or thanks to the turning on of new physical processes at 400 GeV/c.

The NA61/SHINE Collaboration did not provide the corresponding experimental data for the correlations in proton–proton interactions at $P_{\mathrm{lab}}=$ 158 GeV/c. Though, actually, the correlations can be extracted from the two-dimensional $d^{2}n/dyd{P}_T$ distributions measured by the NA61/SHINE Collaboration [1] (available at HEPDATA [22]) which can be re-calculated into $d^{2}n/d{P}_{T}d{x}_F$. The calculation of $<P_T>$ or $<P_T^2>$ correlations with $x_F$ requires all the data to be fitted, and numerical integration of the fitting functions. This would be a laborious exercise, in particular, for the calculation of errors and errors propagation. However, we consider this will not significantly influence our understanding. In addition, the NA61/SHINE Collaboration presented temperatures of the $P_T$ spectra (i.e., the inverse slope parameter) for different types of particles and various y-intervals (see Figure 39 in Ref. [1]). The temperatures are found to be smooth functions of y-intervals. The temperatures for different types of particles are close to each other for all NA61/SHINE energies. A significant difference between the experimental data and the EPOS calculations is observed only for proton temperatures. Thus, one expects that the $<P_T^2>$–$x_F$ correlation to be a smooth function, similar to the one at 158 GeV/c.

As seen in Figure 2, FTF model reproduces the general behavior of the data at $P_{\mathrm{lab}}$ = 158 GeV/c. At higher energies, FTF model does not describe the correlations for ${\pi }^{-}$, $K^{+}$ and protons. We consider that the strong discrepancy between the model calculations and the data for protons and $K^{+}$ mesons is due to the misidentification of $K^{+}$ mesons and protons at $P_{\mathrm{lab}}$ = 400 GeV/c. However, one cannot exclude other contributions. It is therefore helpful developing new methods for analizing experimental data.

The HIJING model calculations for the same data are shown in Figure 3. As can be seen, the predictions are close to the data at $P_{\mathrm{lab}}$ = 158 GeV/c. However, the model underestimates $<P_T^2>$ for protons. At higher energies, the significant growth of $<P_T^2>$ for ${\pi }^{+}$ and ${\pi }^{-}$ mesons at $x_F>$ 0.4 is not reproduced. The experimental behavior of $<P_T^2>$ for the K meson is rather complicated to understand.

The HIJING model considers hard processes in proton–proton interactions. Thus, a slow evolution of the correlations with the energy growth is observed. Such an evolution cannot be seen in FTF model calculations for ${\pi }^{+}$ and ${\pi }^{-}$ mesons at $x_F<$ 0.3.

Recapitulating, we conclude that the understanding and reproduction of the $<P_T^2>$–$x_F$ correlations for protons and K mesons is one of the main problems of the existing Monte Carlo hadronic models.

3. Study of Two-Particle Correlations

Studying the $P_T$ correlations in soft hadronic interactions it is possible to understand the disagreement between simulation and experimental data for $<P_T^2>$–$x_F$ correlations of protons and kaons, as described in Section 2. Different types of correlations were considered in the study of jets and associated particles in high energy physics experiments; see, e.g., [23,24]. Various methods of jet and particle reconstructions [25,26] and the analysis of their characteristics exist. However, at low energies, jets are not produced. We propose to apply some of the techniques used in analysis of high energy experiments also for lower energies, in particular, by replacing hard jets with triggered particles of a certain type.

Next, we consider two-particle $P_T$ correlations between the triggered particle and the other particles produced in the same event, so-called associated particles. The $P_T$ correlation function, C, of two particles is given by the equation:

$$C({\overrightarrow{P}}_T^{\mathrm{tr}},{\overrightarrow{P}}_T^{\mathrm{as}})=\frac{1}{N_{\mathrm{tr}}}\frac{dN\left(\mathrm{tr},\mathrm{as}\right)}{d^2{P}_T^{\mathrm{tr}}{d}^2{P}_T^{\mathrm{as}}},$$

(1)

where ${\overrightarrow{P}}_T^{\mathrm{tr}}$ and ${\overrightarrow{P}}_T^{\mathrm{as}}$ are the transverse momenta of the triggered particle and the associated particles, correspondingly. $N_{\mathrm{tr}}$ and $N\left(\mathrm{tr},\mathrm{as}\right)$ are, respectively, the number of triggered particles and the number of pairs of triggered and associated particles.

Since in many high energy experiments $\mathsf{\Lambda }$-hyperons are reconstructed well enough, we choose these particles as triggered ones in our investigation of $P_T$ correlations.

To decrease the number of independent variables of the correlation function, C, we consider the absolute value of the triggered particle’s transverse momentum ($|{\overrightarrow{P}}_T^{\mathrm{tr}}|$), and two projections of the associated particle transverse momentum, ${\overrightarrow{P}}_T^{\mathrm{as}}$, on ${\overrightarrow{P}}_T^{\mathrm{tr}}$ as independent variables. This is illustrated in Figure 4a, where the projections of ${\overrightarrow{P}}_T$’s of kaon and pion mesons as associated particles are given.

For each needed event, instead of calculating projections of an associated particle momentum on a momentum of a triggered particle using scalar and vector products of the momenta, one can perform the Euler rotation of the coordinate system and direct the new x-axis along the triggered particle momentum. In this case, the sought-for projections are $P_{T,x^{\prime }}^{\mathrm{as}}$ and $P_{T,y^{\prime }}^{\mathrm{as}}$. These projections are functions of the components of the associated particle momentum in the original coordinate system:

$$\begin{array}{c}\hfill P_{T,x^{\prime }}^{\mathrm{as}}=P_{T,x}^{\mathrm{as}}·cos\varphi +P_{T,y}^{\mathrm{as}}·sin\varphi ,\end{array}$$

(2)

$$\begin{array}{c}\hfill P_{T,y^{\prime }}^{\mathrm{as}}=-P_{T,x}^{\mathrm{as}}·sin\varphi +P_{T,y}^{\mathrm{as}}·cos\varphi ,\end{array}$$

(3)

where $\varphi$ is the azimuthal angle of the triggered particle, $\varphi =arctan{P}_{T,y}^{\mathrm{tr}}/P_{T,x}^{\mathrm{tr}}$ (see Figure 4a). These equations allow avoiding the Euler rotation of events.

We omit hereinafter the apostrophes of x and y for the new components of the transverse momenta of the associated particles.

Let us consider the connection of the correlation function with Schwinger’s mechanism of particle production (see Figure 4b).

A $\mathsf{\Lambda }$-hyperon consists of one $ud$ di-quark and one strange quark s. Correspondingly, the momentum of the hyperon, $P_{\mathsf{\Lambda }}$, is the sum of the di-quark momentum ($P_{qq}$) and the s-quark momentum ($P_s$). According to Schwinger’s mechanism [27], a strange quark and a strange anti-quark can be produced from the vacuum in a strong color field. The transverse momenta of s and $\overline{s}$ (anti-s) compensate each other. The $\overline{s}$-quark can combine with a quark (u or d) produced at the next fragmentation step and form a $K^0$ or $K^{+}$ meson. The transverse momentum of the strange quark enters into the $\mathsf{\Lambda }$-hyperon, and into the K-meson, but with opposite sign. Thus, the $P_T$ momentum of the $\mathsf{\Lambda }$-hyperon and the K-meson must be anti-correlated.

4. Calculations of Two-Particle Correlations

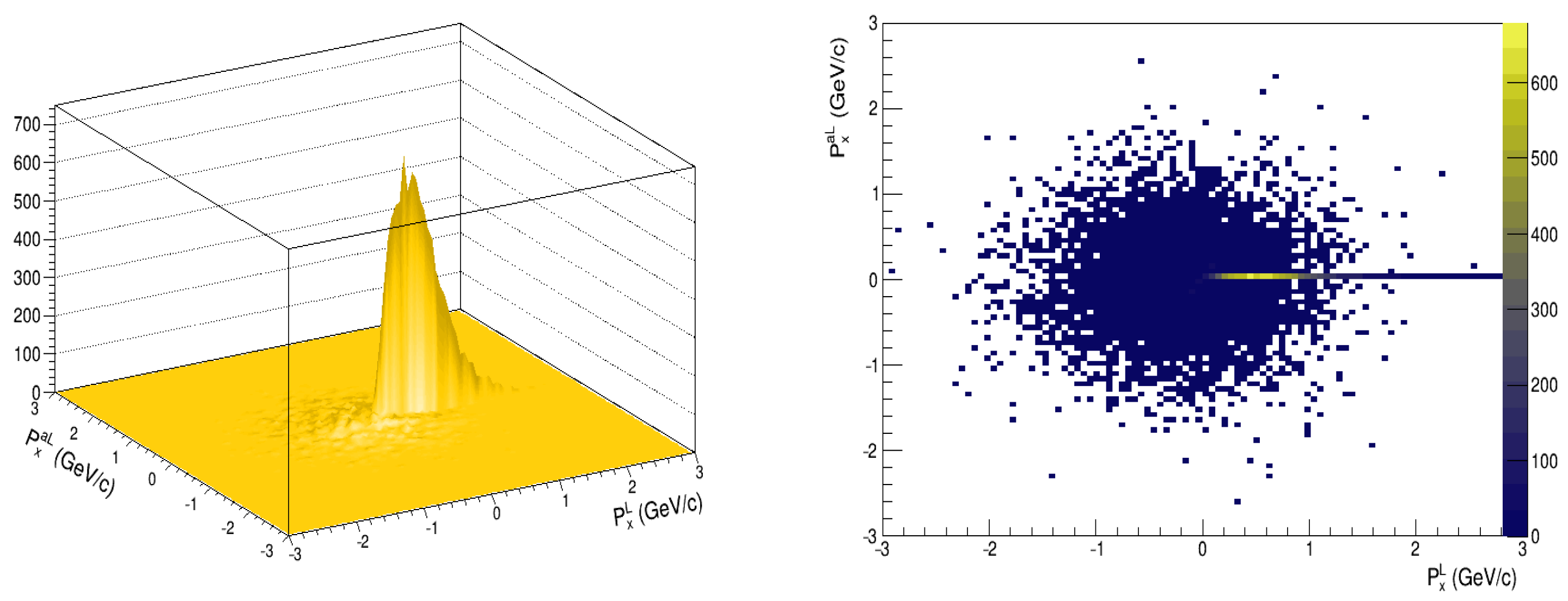
Let us demonstrate the method on events generated by the PYTHIA 6.4 and Geant4 FTF models at $\sqrt{s_{NN}}=$ 25 GeV (the highest possible energy at NICA; was chosen being close to the energy of 27.5 GeV of the LEBS-EHS experiment). The “traditional” 3-dimensional (3D) view of the $P_T$ correlations of $\mathsf{\Lambda }$ and anti-$\mathsf{\Lambda }$ ($\overline{\mathsf{\Lambda }}$) hyperons in the FTF model is presented in Figure 5, left. As seen, there is a peak at $P_x^{\mathsf{\Lambda }}\simeq 0$ and $P_x^{\overline{\mathsf{\Lambda }}}\simeq 0$ due to the dominant production of $\mathsf{\Lambda }$-hyperons. A significantly lower multiplicity of the $\overline{\mathsf{\Lambda }}$-hyperons is observed in the vicinity of the peak.

The 2D projection of the distribution on the $xy$ plane is shown in Figure 5, right. The horizontal line starting at $P_x^{\mathsf{\Lambda }}=0$ and $P_x^{\overline{\mathsf{\Lambda }}}=0$ corresponds to $\mathsf{\Lambda }$-hyperons; the points represent $\overline{\mathsf{\Lambda }}$. At first glance, the points are distributed evenly, and the overall shift of the points to the negative region of $P_x^{\mathsf{\Lambda }}$ is imperceptible.

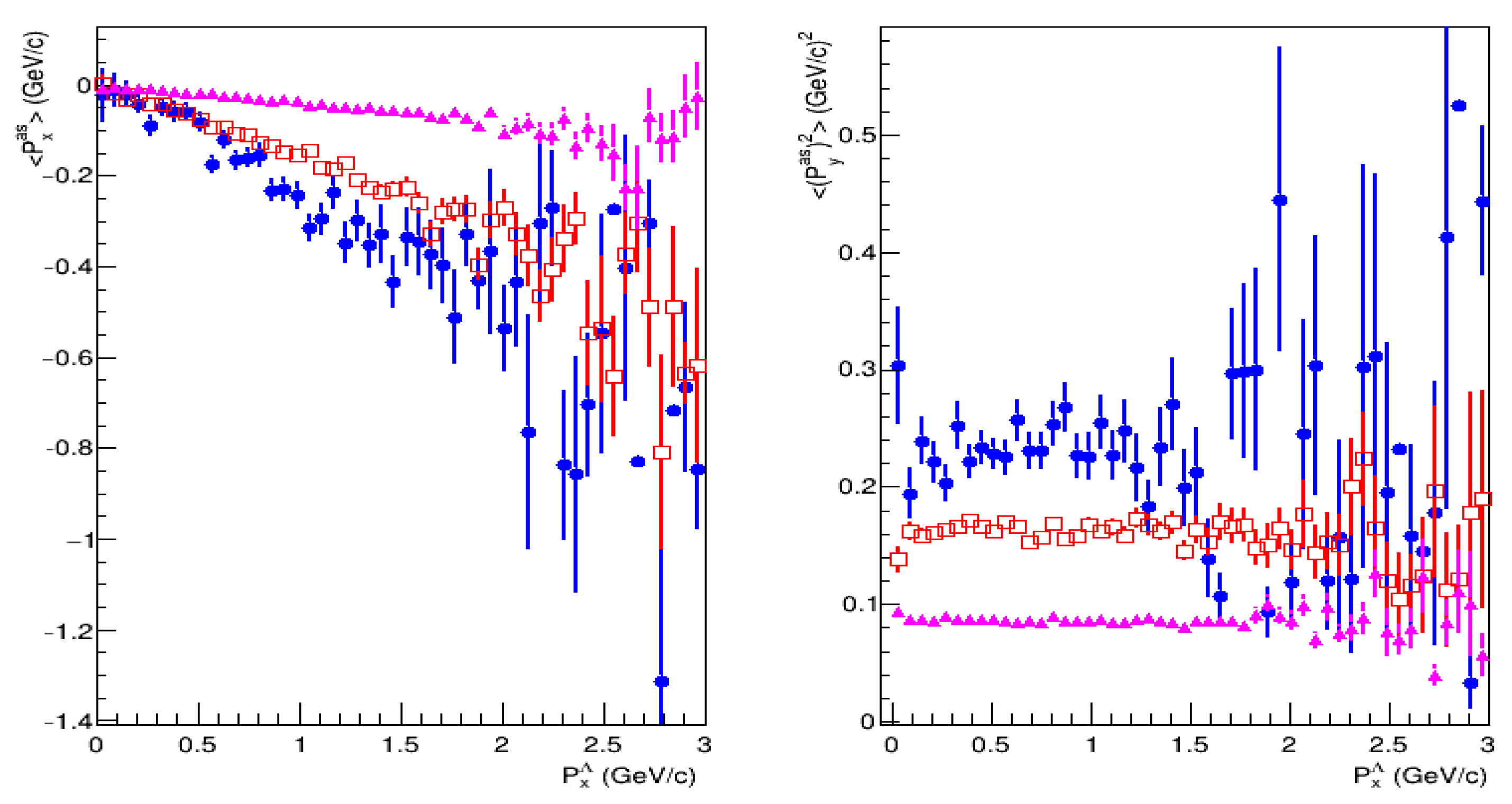
The shift can be more visible in Figure 6, where $<P_x^{\mathrm{as}}>$ and $<{\left(P_y^{\mathrm{as}}\right)}^2>$ are shown as a function of $P_x^{\mathsf{\Lambda }}$ for ${\pi }^0$-mesons, $K_S^0$-mesons, and $\overline{\mathsf{\Lambda }}$-hyperons in the FTF model. As one can see in Figure 6, left, the functions are approximately linear at small values of $P_x^{\mathsf{\Lambda }}$. The strongest correlation is observed between $\mathsf{\Lambda }$ and anti-$\mathsf{\Lambda }$ hyperons. A milder correlation takes place between $K_S^0$-mesons and $\mathsf{\Lambda }$-hyperons. The ${\pi }^0$–$\mathsf{\Lambda }$ correlation is weak. As also seen from Figure 6, right, $<{\left(P_y^{\mathrm{as}}\right)}^2>$ is almost constant. $<{\left(P_y^{\mathrm{as}}\right)}^2>$ grows with an increase of the associated particle mass.

The corresponding calculations for the PYTHIA 6.4 model are given in Figure 7. As one can see, the correlation between $<P_x^{\overline{\mathsf{\Lambda }}}>$ and $P_x^{\mathsf{\Lambda }}$ cannot be well observed. The PYTHIA model predicts the correlations between $<P_x^{K_S^0}>$ and $P_x^{\mathsf{\Lambda }}$, but weaker than the FTF model. Both models predict a weak correlation between $<P_x^{{\pi }^0}>$ of mesons and $P_x$ of $\mathsf{\Lambda }$-hyperons. In paper [17], it was shown that the correlations between $\mathsf{\Lambda }$-hyperons and $K^{+}$ and ${\pi }^{-}$ mesons differ strongly between the FTF and PYTHIA models; however, the correlations between $\mathsf{\Lambda }$-hyperons and $K^{-}$ and ${\pi }^{+}$ mesons are similar for both models. Summarizing, the FTF model predicts stronger correlations between $\mathsf{\Lambda }$-hyperons and strange particles than the PYTHIA model.

Baryon and anti-baryon production mechanisms are different in the two studied models. Pythi uses the so-called popcorn mechanism, which is well suited to explain the anti-baryon yield in $e^{+}{e}^{-}$ annihilations. In hadronic interactions, baryons can also be produced via the popcorn mechanism, but also as a result of beam remnant fragmentation. In the FTF model, it is assumed that di-quark–antidi-quark pairs can be produced from the vacuum, and di-quarks fragment as antiquarks, but with the fragmentation functions’ parameters different from the antiquark ones. Due to these assumptions, FTF model predicts a larger correlation between $\mathsf{\Lambda }$ and anti-$\mathsf{\Lambda }$ hyperons than that in the PYTHIA model. The correlation becomes weaker with increasing energy in the range $\sqrt{s_{NN}}=$ 10–25 GeV according to the calculations in the FTF model. This is connected with the decrease of the cross sections of reactions with quark exchange processes.

The correlation of $<{\left(P_y^{\mathrm{as}}\right)}^2>$ with $P^{\mathsf{\Lambda }}$ is shown in Figure 6, right, and Figure 7, right. As one can see, the correlation is almost constant in the main region of $P_x^{\mathsf{\Lambda }}$ variation within the statistical errors. However, the constants are different in the PYTHIA and FTF models. We consider these constants to be related to certain parameters of the models. Thus, we expect that the experimental study of the proposed correlations, in particular at the NICA/SPD experiment, will shed light on the fragmentation mechanism of the soft hadronic interactions.

5. Conclusions

The following conclusions are in order.

• It has been shown that there is a significant difference between the experimental data on $<P_T^2>$–$x_F$ correlations in proton–proton interactions from the NA49 and the LEBC-EHS Collaborations which has not been considered before in the literature. The nature of the difference is unknown.
• In order to clarify the nature of the difference in the measurements we proposed to study the two-particle $P_T$ correlations in soft interactions.
• The $P_T$ correlations are calculated between $\mathsf{\Lambda }$-hyperons and $\overline{\mathsf{\Lambda }}$-hyperons, K, $\pi$ mesons in the Geant4 FTF and PYTHIA 6.4 models.
• It is shown that the $P_T$ correlations of $\mathsf{\Lambda }$-hyperons with $\overline{\mathsf{\Lambda }}$-hyperons and K-mesons in the FTF model are larger than those in the PYTHIA model.
• The $P_T$ correlation of $\mathsf{\Lambda }$-hyperons with $\pi$-mesons is weak.
• The proposed correlations are rather sensitive to the mechanisms of particle production in the soft hadronic interactions implemented in various theoretical models.