Onset of Color Transparency in Holographic Light-Front QCD
Abstract
:1. Introduction
2. Physics of Color Transparency
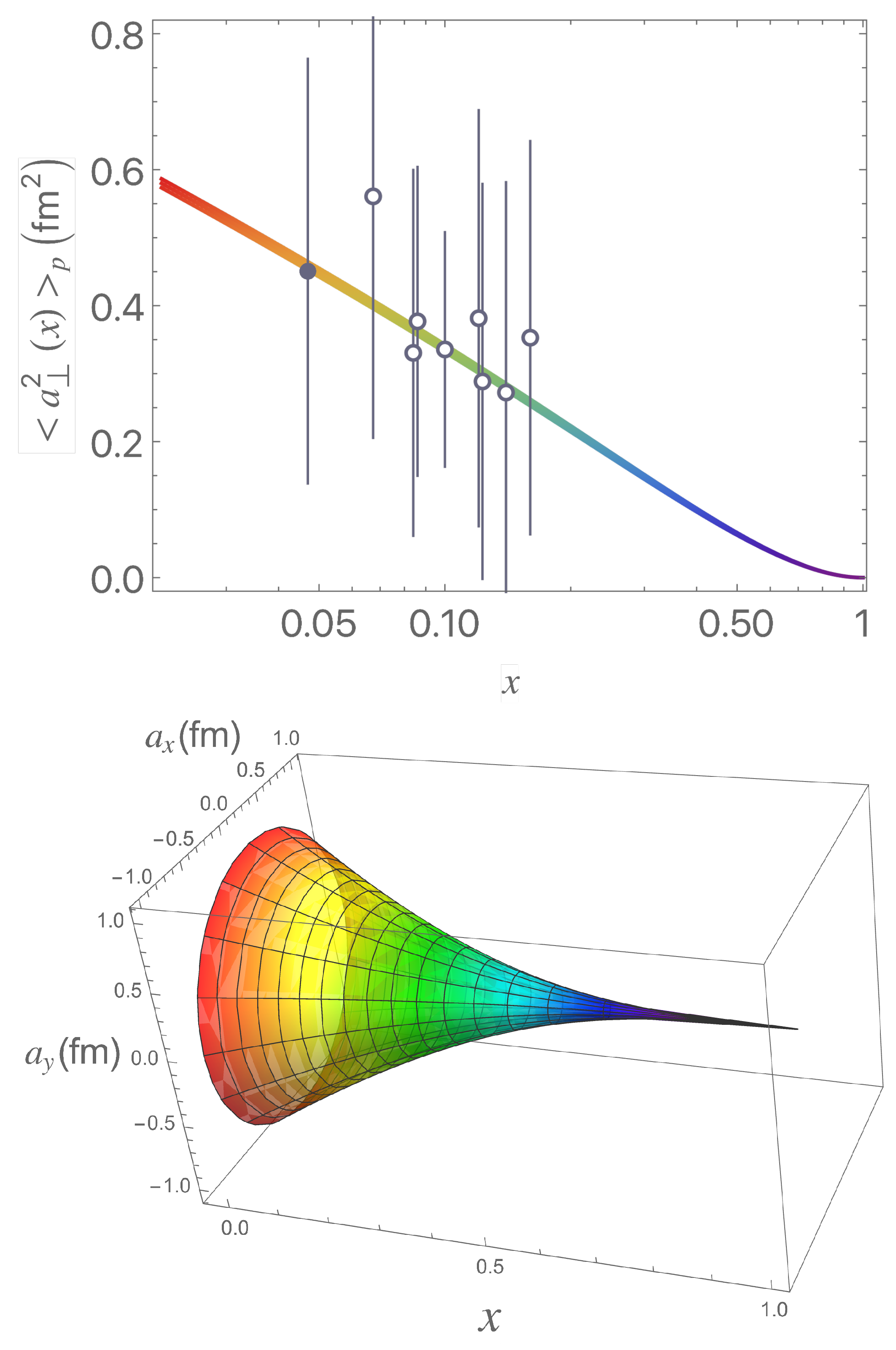
2.1. The Effective Transverse Size of a Hadron at Large Longitudinal Momentum Fraction x
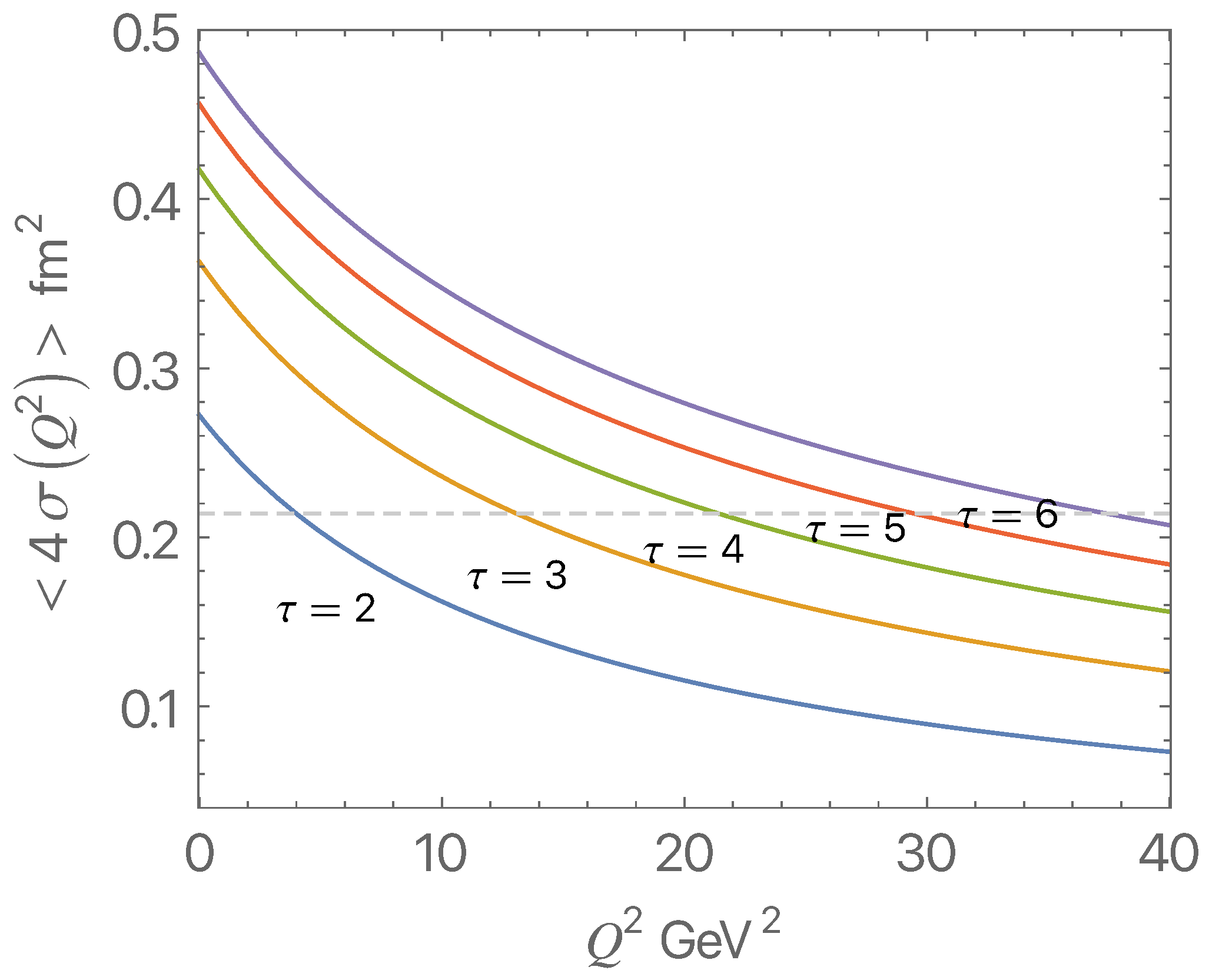
2.2. The Effective Transverse Size of a Hadron at Large Momentum Transfer t and the Onset of Color Transparency
2.3. Inelastic Corrections to the Onset of Color Transparency
2.4. The Feynman Mechanism
3. Discussion of the Results
3.1. Two-Stage Color Transparency in the Nucleon
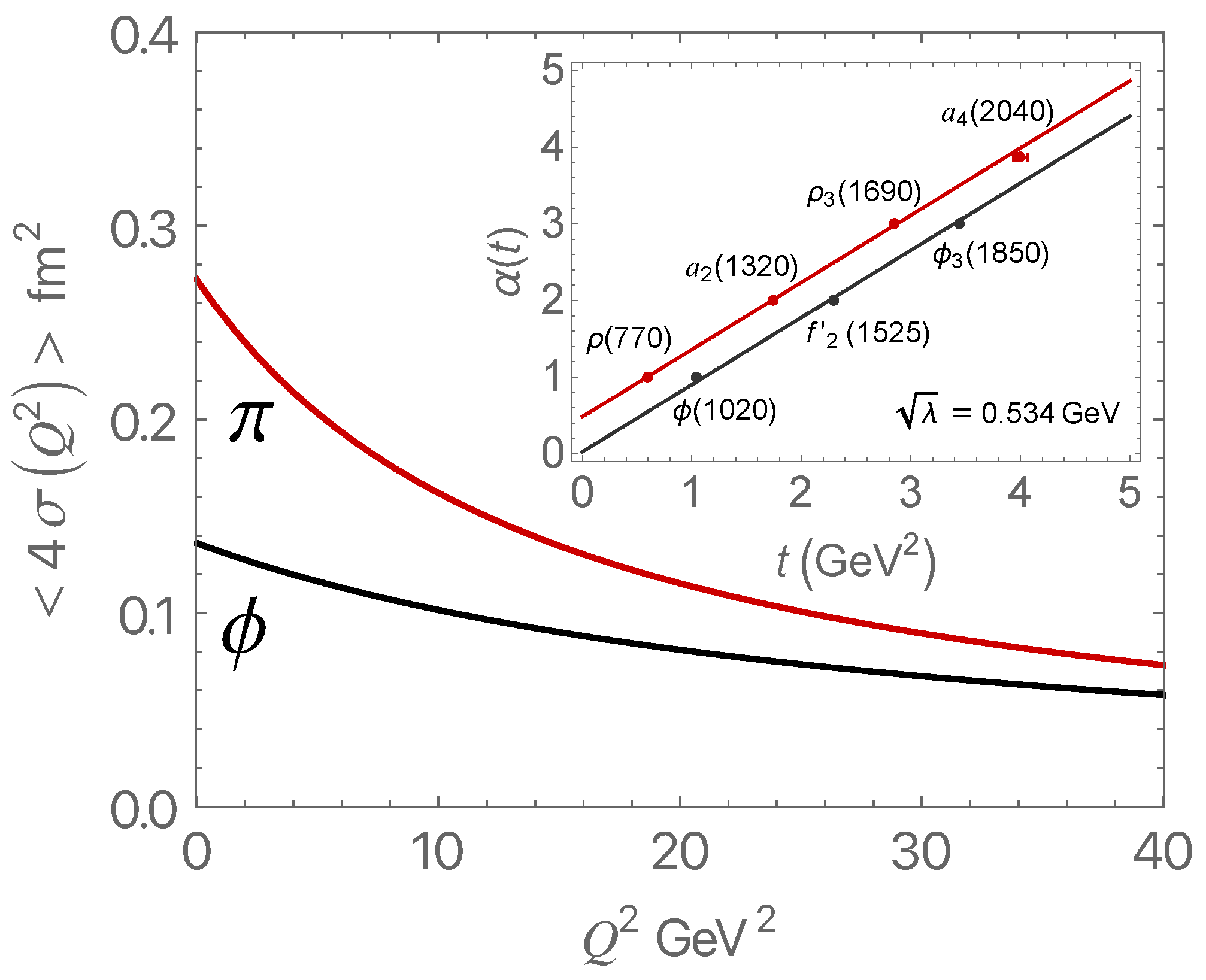
3.2. Effect of Quark Flavor on the Onset of Color Transparency
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Form Factors and Parton Distributions in Light-Front QCD
References
- Brodsky, S.J.; Mueller, A.H. Using nuclei to probe hadronization in QCD. Phys. Lett. B 1988, 206, 685–690. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Frankfurt, L.; Gunion, J.F.; Mueller, A.H.; Strikman, M. Diffractive leptoproduction of vector mesons in QCD. Phys. Rev. D 1994, 50, 3134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dutta, D.; Hafidi, K.; Strikman, M. Color transparency: Past, present and future. Prog. Part. Nucl. Phys. 2013, 69, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Jain, P.; Pire, B.; Ralston, J.P. Quantum color transparency and nuclear filtering. Phys. Rep. 1996, 271, 67–179. [Google Scholar] [CrossRef] [Green Version]
- Lepage, G.P.; Brodsky, S.J. Exclusive processes in perturbative quantum chromodynamics. Phys. Rev. D 1980, 22, 2157. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; Farrar, G.R. Scaling laws at large transverse momentum. Phys. Rev. Lett. 1973, 31, 1153–1156. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; Farrar, G.R. Scaling laws for large momentum transfer processes. Phys. Rev. D 1975, 11, 1309–1330. [Google Scholar] [CrossRef] [Green Version]
- Matveev, V.A.; Muradian, R.M.; Tavkhelidze, A.N. Automodellism in the large-angle elastic scattering and structure of hadrons. Lett. Nuovo Cim. 1973, 7, 719–723. [Google Scholar] [CrossRef]
- Fassi, L.E. et al. [CLAS Collaboration] Overview of color transparency measurements. AIP Conf. Proc. 2013, 1560, 475–479. [Google Scholar] [CrossRef]
- Bhetuwal, D. et al. [Hall C Collaboration] Ruling out color transparency in quasielastic 12C(e,e′p) up to Q2 of 14.2 (GeV/c)2. Phys. Rev. Lett. 2021, 126, 082301. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G.; Erlich, J. Light-front holographic QCD and emerging confinement. Phys. Rep. 2015, 584, 1–105. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G. Light-front holography and supersymmetric conformal algebra: A novel approach to hadron spectroscopy, structure, and dynamics. arXiv 2020, arXiv:2004.07756. [Google Scholar] [CrossRef]
- Maldacena, J.M. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef] [Green Version]
- Dirac, P.A.M. Forms of relativistic dynamics. Rev. Mod. Phys. 1949, 21, 392–399. [Google Scholar] [CrossRef] [Green Version]
- Fubini, S.; Rabinovici, E. Superconformal quantum mechanics. Nucl. Phys. B 1984, 245, 17–44. [Google Scholar] [CrossRef] [Green Version]
- De Téramond, G.F.; Dosch, H.G.; Brodsky, S.J. Baryon spectrum from superconformal quantum mechanics and its light-front holographic embedding. Phys. Rev. D 2015, 91, 045040. [Google Scholar] [CrossRef] [Green Version]
- Dosch, H.G.; de Téramond, G.F.; Brodsky, S.J. Superconformal baryon-meson symmetry and light-front holographic QCD. Phys. Rev. D 2015, 91, 085016. [Google Scholar] [CrossRef] [Green Version]
- Veneziano, G. Construction of a crossing-symmetric, Regge-behaved amplitude for linearly rising trajectories. Nuovo Cim. A 1968, 57, 190–197. [Google Scholar] [CrossRef] [Green Version]
- Ademollo, M.; Del Giudice, E. Nonstrong amplitudes in a Veneziano-type model. Nuovo Cim. A 1969, 63, 639–656. [Google Scholar] [CrossRef]
- Landshoff, P.V.; Polkinghorne, J.C. The scaling law for deep inelastic scattering in a new Veneziano-like amplitude. Nucl. Phys. B 1970, 19, 432–444. [Google Scholar] [CrossRef]
- De Téramond, G.F.; Liu, T.; Sufian, R.S.; Dosch, H.G.; Brodsky, S.J.; Deur, A. Universality of generalized parton distributions in light-front holographic QCD. Phys. Rev. Lett. 2018, 120, 182001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, T.; Sufian, R.S.; de Téramond, G.F.; Dosch, H.G.; Brodsky, S.J.; Deur, A. Unified description of polarized and unpolarized quark distributions in the proton. Phys. Rev. Lett. 2020, 124, 082003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Téramond, G.F.; Dosch, H.G.; Liu, T.; Sufian, R.S.; Brodsky, S.J.; Deur, A. Gluon matter distribution in the proton and pion from extended holographic light-front QCD. Phys. Rev. D 2021, 104, 114005. [Google Scholar] [CrossRef]
- Müller, D.; Robaschik, D.; Geyer, B.; Dittes, F.-M.; Hořejši, J. Wave functions, evolution equations and evolution kernels from light-ray operators of QCD. Fortsch. Phys. 1994, 42, 101–141. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.D. Gauge-invariant decomposition of nucleon spin. Phys. Rev. Lett. 1997, 78, 610–613. [Google Scholar] [CrossRef]
- Radyushkin, A.V. Scaling limit of deeply virtual Compton scattering. Phys. Lett. B 1996, 380, 417–425. [Google Scholar] [CrossRef] [Green Version]
- Carroll, A.S.; Barton, D.S.; Bunce, G.; Gushue, S.; Makdisi, Y.I.; Heppelmann, S.; Courant, H.; Fang, G.; Heller, K.J.; Marshak, M.L.; et al. Nuclear transparency to large angle pp elastic scattering. Phys. Rev. Lett. 1988, 61, 1698–1701. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F. Spin correlations, QCD color transparency and heavy quark thresholds in proton proton scattering. Phys. Rev. Lett. 1988, 60, 1924–1927. [Google Scholar] [CrossRef] [Green Version]
- Ralston, J.P.; Pire, B. Fluctuating proton size and oscillating nuclear transparency. Phys. Rev. Lett. 1988, 61, 1823–1826. [Google Scholar] [CrossRef]
- Lee, T.S.H.; Miller, G.A. Color transparency and high-energy (p,2p) nuclear reactions. Phys. Rev. C 1992, 45, 1863–1870. [Google Scholar] [CrossRef]
- Liuti, S.; Taneja, S.K. Generalized parton distributions and color transparency phenomena. Phys. Rev. D 2004, 70, 074019. [Google Scholar] [CrossRef] [Green Version]
- Burkardt, M.; Miller, G.A. Color transparent general parton distributions. Phys. Rev. D 2006, 74, 034015. [Google Scholar] [CrossRef] [Green Version]
- Soper, D.E. The parton model and the Bethe-Salpeter wave function. Phys. Rev. D 1977, 15, 1141–1149. [Google Scholar] [CrossRef]
- Burkardt, M. Impact parameter dependent parton distributions and off-forward parton distributions for ξ→0. Phys. Rev. D 2002, 62, 071503, Erratum in Phys. Rev. D 2002, 66, 119903. [Google Scholar] [CrossRef]
- Burkardt, M. Impact parameter space interpretation for generalized parton distributions. Int. J. Mod. Phys. A 2003, 18, 173–207. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Téramond, G.F. Hadronic spectra and light-front wave functions in holographic QCD. Phys. Rev. Lett. 2006, 96, 201601. [Google Scholar] [CrossRef] [Green Version]
- Drell, S.D.; Yan, T.M. Connection of elastic electromagnetic nucleon form-factors at large Q2 and deep inelastic structure functions near threshold. Phys. Rev. Lett. 1970, 24, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; Lepage, G.P. Exclusive Processes and the Exclusive-Inclusive Connection in Quantum Chromodynamics, SLAC-PUB-2294; Stanford Linear Accelerator Center: Menlo Park, CA, USA, 1977; Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/10/478/10478413.pdf (accessed on 7 May 2022).
- Dupre, R.; Guidal, M.; Vanderhaeghen, M. Tomographic image of the proton. Phys. Rev. D 2017, 95, 011501. [Google Scholar] [CrossRef] [Green Version]
- Sufian, R.S.; Liu, T.; de Téramond, G.F.; Dosch, H.G.; Brodsky, S.J.; Deur, A.; Islam, M.T.; Ma, B.Q. Nonperturbative strange-quark sea from lattice QCD, light-front holography, and meson-baryon fluctuation models. Phys. Rev. D 2018, 98, 114004. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G.; Lorcé, C. Universal effective hadron dynamics from superconformal algebra. Phys. Lett. B 2016, 759, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Xu, S. et al. [BLFQ Collaboration] Nucleon structure from basis light-front quantization. Phys. Rev. D 2021, 104, 094036. [Google Scholar] [CrossRef]
- Adhikari, L. et al. [BLFQ Collaboration] Generalized parton distributions and spin structures of light mesons from a light-front Hamiltonian approach. Phys. Rev. D 2021, 104, 114019. [Google Scholar] [CrossRef]
- Miller, G.A. Color transparency and light front holographic QCD. Physics 2022, 4, 590–596. [Google Scholar] [CrossRef]
- Farrar, G.R.; Liu, H.; Frankfurt, L.L.; Strikman, M.I. Transparency in nuclear quasiexclusive processes with large momentum transfer. Phys. Rev. Lett. 1988, 61, 686–689. [Google Scholar] [CrossRef]
- Caplow-Munro, O.; Miller, G.A. Color transparency and the proton form factor: Evidence for the Feynman mechanism. Phys. Rev. C 2021, 104, L012201. [Google Scholar] [CrossRef]
- Blaettel, B.; Baym, G.; Frankfurt, L.L.; Strikman, M. How transparent are hadrons to pions? Phys. Rev. Lett. 1993, 70, 896–899. [Google Scholar] [CrossRef]
- Frankfurt, L.; Miller, G.A.; Strikman, M. Coherent nuclear diffractive production of minijets: Illuminating color transparency. Phys. Lett. B 1993, 304, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Frankfurt, L.; Radyushkin, A.; Strikman, M. Interaction of small-size wave packet with hadron target. Phys. Rev. D 1997, 55, 98–104. [Google Scholar] [CrossRef] [Green Version]
- Sufian, R.S.; de Téramond, G.F.; Brodsky, S.J.; Deur, A.; Dosch, H.G. Analysis of nucleon electromagnetic form factors from light-front holographic QCD: The spacelike region. Phys. Rev. D 2017, 95, 014011. [Google Scholar] [CrossRef] [Green Version]
- Clasie, B.; Qian, X.; Arrington, J.; Asaturyan, R.; Benmokhtar, F.; Boeglin, W.; Bosted, P.; Bruell, A.; Christy, M.E.; Chudakov, E.; et al. Measurement of nuclear transparency for the A(e,e′π+) reaction. Phys. Rev. Lett. 2007, 99, 242502. [Google Scholar] [CrossRef] [Green Version]
- Qian, X.; Horn, T.; Clasie, B.; Arrington, J.; Asaturyan, R.; Benmokhtar, F.; Boeglin, W.; Bosted, P.; Bruell, A.; Christy, M.E.; et al. Experimental study of the A(e,e′π+) reaction on 1H, 2H, 12C, 27Al, 63Cu and 197Au. Phys. Rev. C 2010, 81, 055209. [Google Scholar] [CrossRef] [Green Version]
- West, G.B. Phenomenological model for the electromagnetic structure of the proton. Phys. Rev. Lett. 1970, 24, 1206–1209. [Google Scholar] [CrossRef]
- Miller, G.A. Charge density of the neutron. Phys. Rev. Lett. 2007, 99, 112001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, G.A.; Strikman, M.; Weiss, C. Pion transverse charge density from timelike form factor data. Phys. Rev. D 2011, 83, 013006. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brodsky, S.J.; de Téramond, G.F. Onset of Color Transparency in Holographic Light-Front QCD. Physics 2022, 4, 633-646. https://doi.org/10.3390/physics4020042
Brodsky SJ, de Téramond GF. Onset of Color Transparency in Holographic Light-Front QCD. Physics. 2022; 4(2):633-646. https://doi.org/10.3390/physics4020042
Chicago/Turabian StyleBrodsky, Stanley J., and Guy F. de Téramond. 2022. "Onset of Color Transparency in Holographic Light-Front QCD" Physics 4, no. 2: 633-646. https://doi.org/10.3390/physics4020042
APA StyleBrodsky, S. J., & de Téramond, G. F. (2022). Onset of Color Transparency in Holographic Light-Front QCD. Physics, 4(2), 633-646. https://doi.org/10.3390/physics4020042





