Enthusiasm and Skepticism: Two Pillars of Science—A Nonextensive Statistics Case
Abstract
1. Reminiscences Related to Jean Cleymans
2. Analysis of Joseph Kapusta’s Talk “A Primer on Tsallis Statistics for Nuclear and Particle Physics” (19 May 2021)
2.1. Preliminaries
2.2. On the Title of Kapusta’s Talk
- -
- A small book for teaching children to read;
- -
- A small introductory book on a subject;
- -
- A short informative piece of writing.
- -
- A small book containing basic facts about a subject, used especially when you are beginning to learn about that subject;
- -
- A basic text for teaching something.
2.3. Nonadditive Entropy : Where It Comes from
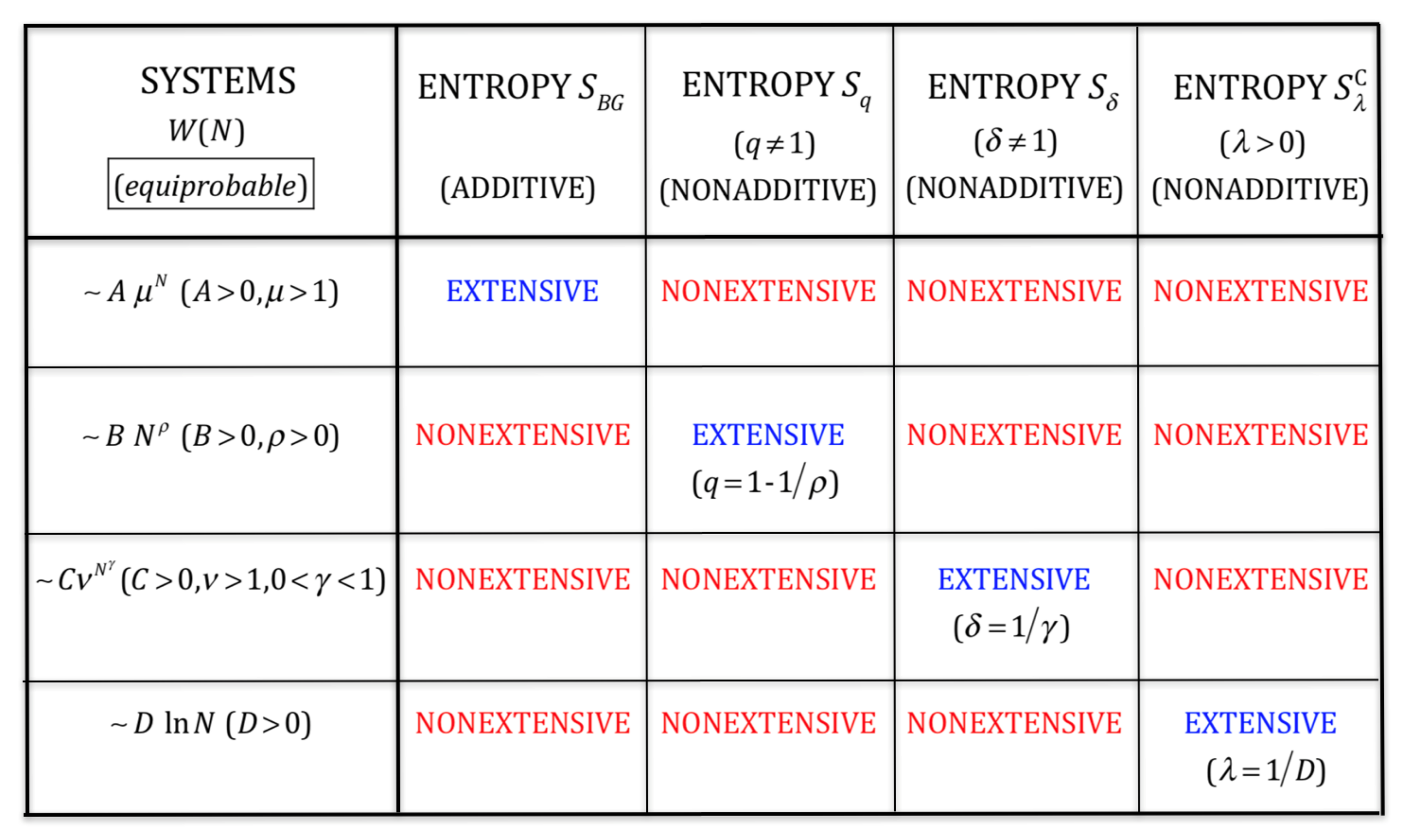
2.4. Additivity versus Extensivity
- Exponential class :This is the typical case within the Boltzmann–Gibbs theory. One gets: , therefore, is extensive, as thermodynamically required.
- Power-law class :One should not use since it implies , thus violating thermodynamics. One verifies instead that , as thermodynamically required.
- Stretched exponential class :In this case, no value of q exists which would yield an extensive entropy . One can instead use [50] with . Indeed, , as thermodynamically required.
- Logarithmic class :
2.5. On the Nature of the Constraints Used for Entropic Optimization
- The peculiar way the nonlinear constraint of type III was phrased by the speaker left floating in the audience (which even repeated this later on, with the tacit agreement of the speaker) that this assumption was violating the theory of probabilities. There is no such thing.Indeed, the above nonlinear constraint in is completely equivalent to a linear constraint expressed in terms of where (hence , with ) is the so-called “escort distribution,” defined in the theory of probabilities; see [87] and references therein.
- The requirement for system-independence for the adopted extremization procedure consists of having for both the norm constraint, expressed in terms of , and the energy constraint, expressed in terms of , one and the same upper admissible value for q. Let us illustrate this through an example. If the set of eigenvalues are nondegenerate, the extremizing q-exponential distribution with asymptotically behaves as . Therefore, its norm is well defined up to . The same happens with the constraint . Indeed, it asymptotically behaves as , hence it has the same upper bound admissibility, i.e., once again . In strong variance, if one were to use here the usual constraint, the asymptotic behavior would be given by , hence its upper admissible value would be , which differs from the norm admissibility value, . The general importance of this point is lengthily discussed in [88].
- All mean values must be mathematically defined for the fat-tailed distributions. This does happen with the appropriate escort averages but fails with the normal linear averages. A simple numerical example with q-Gaussians and its astonishing practical consequences are illustrated in [91].
2.6. On Ad Hoc Constraints for Optimizing the Entropy
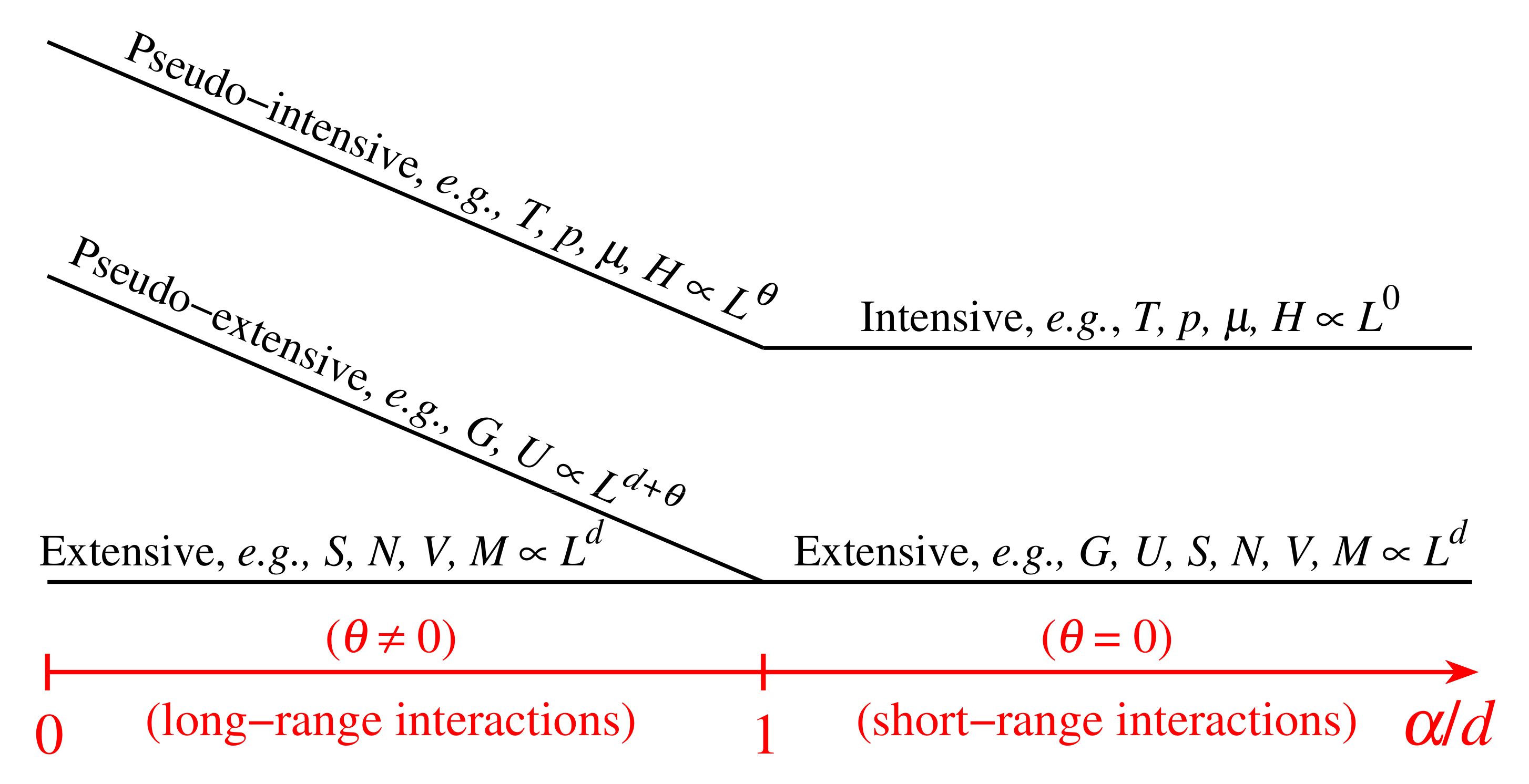
2.7. Thermodynamics and Legendre Transformations
- The ratio of any two pseudointensive variables (), e.g., , is intensive in all cases;
- The ratio of any pseudoextensive variable with any pseudointensive variable, e.g., , is extensive in all cases;
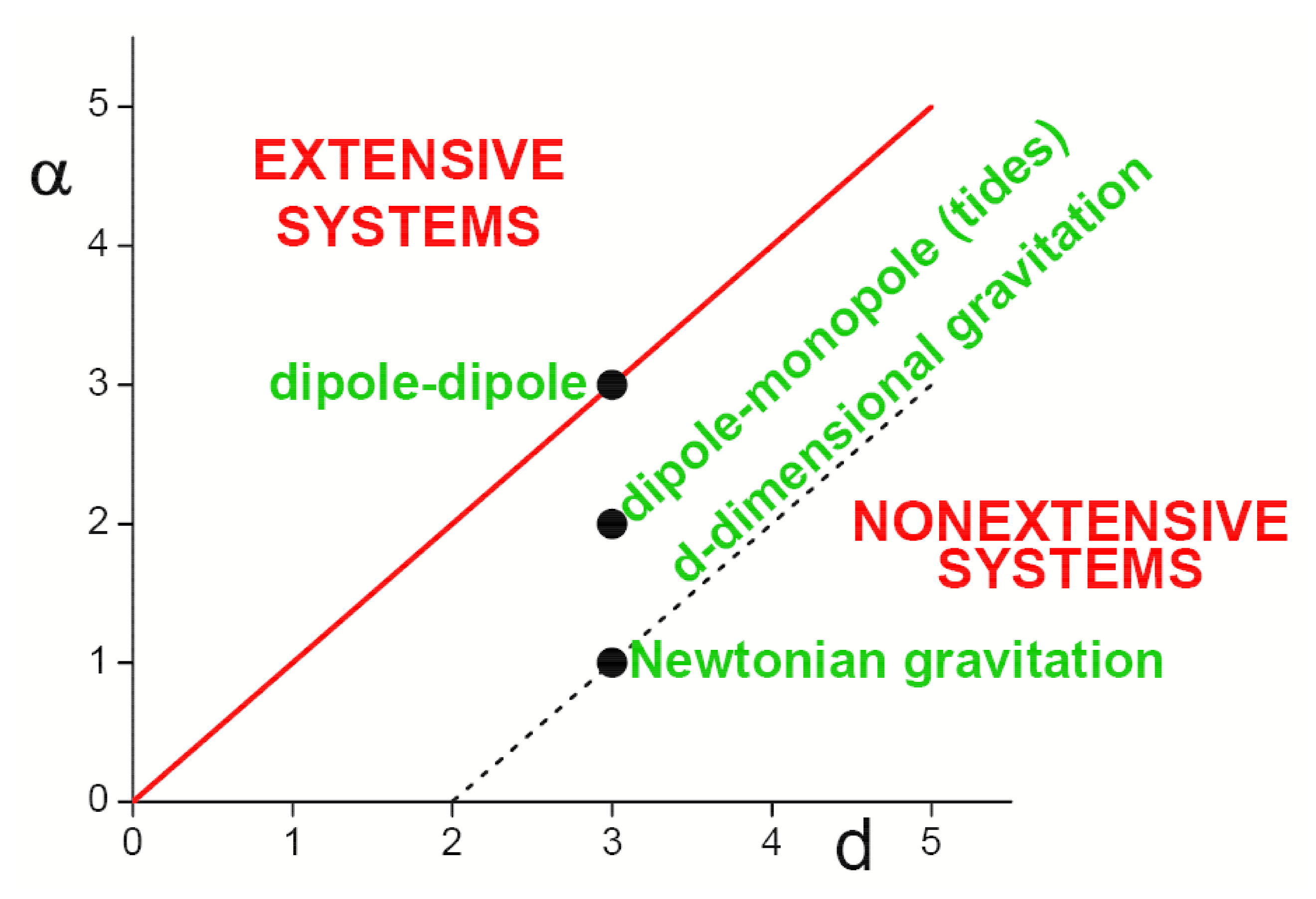
- A most important implication is that, in expressions such as where is an N-body Hamiltonian, the argument is extensive in all cases. This plays a crucial role in the possible q-generalization of what is currently referred to as the large deviation theory. Indeed, the extensivity of appears to mirror, in all cases, the extensivity of the total entropy involved in , being the ratio function (defined within the Large Deviation probability ), seemingly always related to some relative nonadditive entropy per particle [102,103,104,105,106].
2.8. Boltzmann Equation
- It recovers the standard product as the particular instance, i.e.,
- It is commutative for all values of q, i.e.,
- It is additive under q-logarithm for all values of q, i.e.,(referred to as “extensivity”), whereas let us remind that(referred to as “nonadditivity”).Consistently,whereas
- It is associative for all values of q, i.e.,
- It admits unity for all values of q, i.e.,
- It admits zero under certain conditions, namely
- It is distributive with regard to the generalized associative sum analyzed in [111], namely,
2.9. On the Second Principle of Thermodynamics
- It has been proved that a detailed balance implies the time irreversibility of [119].
- The celebrated Clausius inequality, , is consistent with the second principle. It has been shown [120] that it remains valid as it stands for as well.
- The time evolution of the entropy for low-dimensional maps, or, actually, the Pesin identities, do certainly not prove the validity of the second principle. However, the fact that the behavior is quite similar (see [123,124,125] and references therein) for, e.g., the logistic map at the most chaotic value of its external parameter (with ) and at the Feigenbaum point (with ) does provide a suggestive indication.
2.10. On the Zeroth Principle of Thermodynamics
2.11. Indices q: First-Principle Characterization of Universality Classes, or Merely Efficient Fitting Parameters?
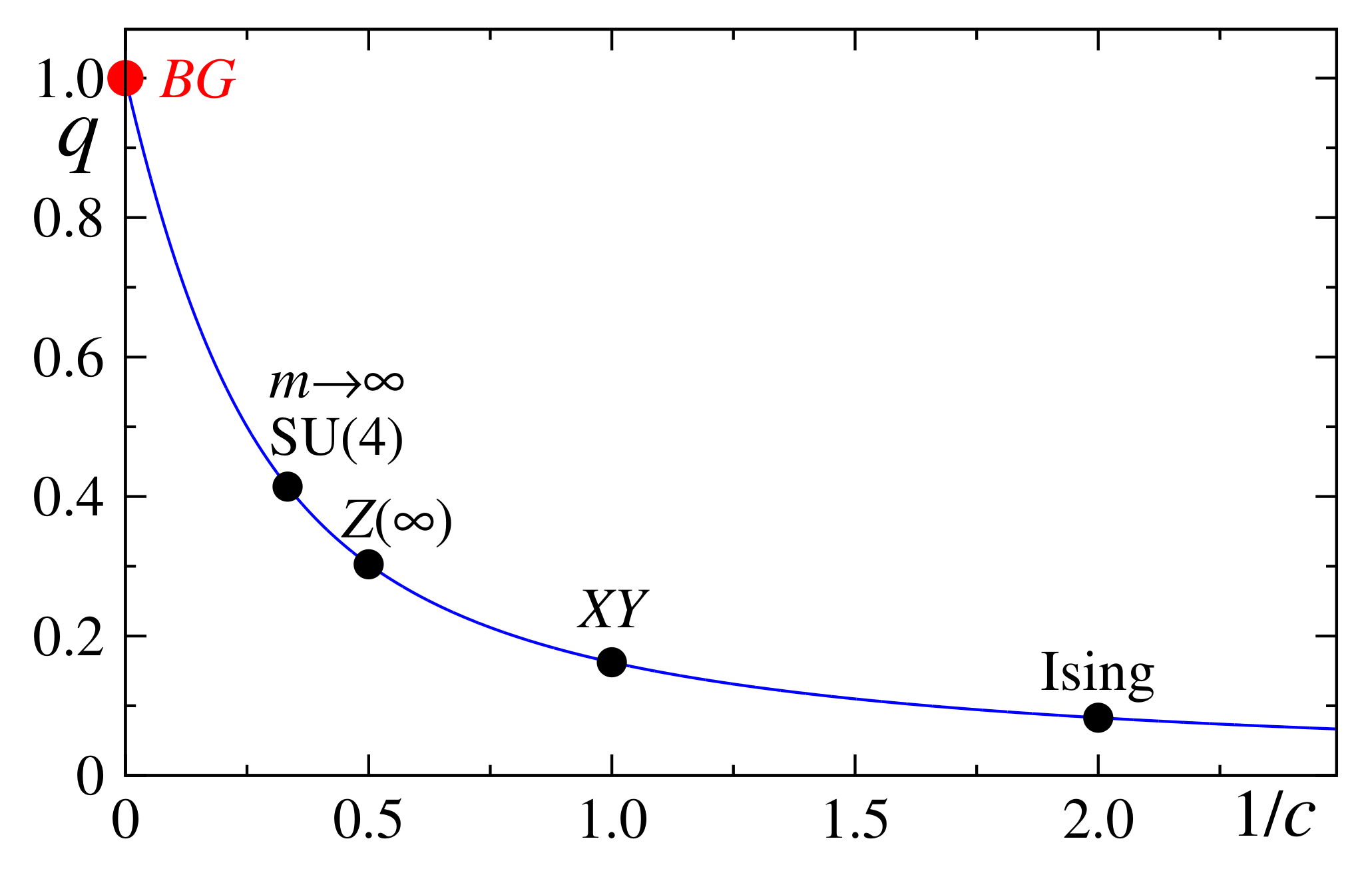
- First-principle quantum field theory calculation of q for a one-dimensional quantum many-body Hamiltonian system: One such example is the quantum phase transition at criticality for the first-neighbor Ising ferromagnet in the presence of a transverse magnetic field, and similar quantum systems characterized by a central charge, . A subsystem of large linear size L of an infinitely long such chain satisfies , which is nonextensive and therefore violates the Legendre structure of thermodynamics. It turns out, however, that a unique value of q exists such that , thus satisfying thermodynamics. Its value is given by [127]which is depicted in Figure 4. As one can see, q characterizes here the thermodynamically admissible entropies associated with the criticality universality classes of many-body systems, defined by the central charge c.
- Zero-Lebesgue occupancy of the probability space in the limit of a system with strongly correlated random binary variables [68]: it is verified that is extensive for a unique value of q, namely,where d is the width, , of the strip with nonvanishing probabilities.
- Overdamped d-dimensional many-body system with short-range repulsive interactions decaying as : The space attractor is a q-Gaussian with [82]The limit recovers the superconductor type-II space distribution, which has been proved to correspond to [73].
- Nonlinear dynamical systems exhibit various direct connections with the time evolution of the entropy and with its consequences. There are, in this respect, two important classes of chaotic behavior, namely: strong chaos, characterized by exponential sensitivity to the initial conditions (referred to, for classical systems, as having a positive maximal Lyapunov exponent); and weak chaos, characterized by subexponential (frequently, power-law) sensitivity to the initial conditions (referred to, for classical systems, as having a vanishing maximal Lyapunov exponent). Let us focus here on an important issue, namely, the time evolution of the entropy while exploring the system’s phase space. Let us illustrate this issue with a paradigmatic dissipative system, namely, the logistic map, . For , the system is strongly chaotic since the sensitivity to the initial conditions satisfies with a Lyapunov exponent . Consistently, if one starts at from a set of M initial conditions in an arbitrarily chosen single window with W of them equally partitioning the interval , one obtains the entropy production per unit time,thus verifying the Pesin identity. One consistently verifies that, for , vanishes, whereas, for , it diverges. In other words, is the unique value of the index for which asymptotically increases linearly with time.If the same operations are applied at the edge of chaos corresponding to the double-bifurcation accumulation point (weak chaos) of the z-logistic map ( with ) and its topologically equivalent one-dimensional dissipative maps, one verifies that with [125]. It follows that, for , diverges subexponentially, namely as the power-law . Moreover, it can be shown, through scaling arguments [128], thatwhere and refer to the (concave) multifractal function , defined in the interval with [87].If, for the standard logistic map (), one actually focuses on the Feigenbaum point (also referred to as the Feigenbaum–Coullet–Tresser point) , which corresponds to a vanishing Lyapunov exponent (i.e., weak chaos), one does verify that with [125], as well aswhere is the so called Feigenbaum universal constant. From this relation, it follows that(1018 exact digits are known [50]). Analogously to the Boltzmann–Gibbs case, a q-generalized Pesin identity is verified. Consistently, numerically appears to vanish for q above that special value and to diverge for q below that value. In other words, this is the unique value of the index q, for which asymptotically increases linearly with time, thus yielding a finite entropy production per unit time.
- Still in the area of nonlinear dynamical systems, now with degrees of freedom , scaling arguments [129] are consistent withwhere is the value of q for which the entropy production per unit time is finite, and characterize the -exponential sensitivity to the initial conditions, respectively, associated with the variable (). This quite general relation is verified in the following illustrative cases:(i) It suffices that one () of these q-indices equals unity and hence ;
- Another important issue is the central limit theorem attractor in the space of distributions when time-averaging a single coordinate of the system. Within this theorem, is defined. For example, for the logistic map with one has that, after proper scaling and centering, the distribution is given by a Gaussian, according to the classical central limit theorem, whereas, for , it is seemingly given by a q-Gaussian with .Let us further illustrate this issue with a paradigmatic conservative system, namely, the standard map, introduced by Chirikov in 1979. This area-preserving map turns out to be relevant within a variety of physical situations such as particle confinement in magnetic traps, particle dynamics in accelerators, comet dynamics, the ionization of Rydberg atoms, electron magnetotransport. It is defined as follows:Each point yields a Lyapunov exponent . Next, along the central limit theorem lines, let us define the following quantity:withwhere is the number of initial conditions and is the number of iterations for each of those M initial conditions. The limiting case (hence a linear map, though with a highly nontrivial set of stable orbits) exhibits zero Lyapunov exponent in the entire phase space. It has been studied [131] and the attractor is a q-Gaussian withThis is in notorious variance with the attractor corresponding to , where the Lyapunov exponents corresponding to almost all the points of the phase space are positive, Boltzmann’s molecular chaos hypothesis certainly is valid, and the corresponding attractor is a Gaussian, i.e., , in conformity with the standard central limit theorem.
- An interesting short-range-interacting d-dimensional ferromagnetic system is that whose symmetry is dictated by rotations in n dimensions, i.e., the so called symmetry ( corresponds to the model, corresponds to the Heisenberg model, and so on; corresponds to the spherical model). As soon as one focuses on the kinetics of point defects during a quenching from a high temperature to a zero temperature for the model, its theoretical description can be done in terms of a time-dependent Ginzburg–Landau equation [132,133]. The distribution of the vortex velocity turns out to be a q-Gaussian withThe index q decreases from two to one when d increases from zero to infinity. It is certainly intriguing, although yet unexplained, the fact that the value of q given in Equation (42) separates finite from infinite variance for d-dimensional q-Gaussians.
- Granular matter. The following scaling law was predicted in 1996 [84] (see also [83]):where q is the index of the q-Gaussian distribution of fluctuations and is the exponent associated with anomalous diffusion (i.e., the quadratic position scales like ; recovers the known scaling for Brownian motion normal diffusion, i.e., ). This scaling relation was experimentally verified in 2015 [139], within a precision along a wide experimental range, for vertically confined grains under horizontal shear.
- In some simple models, such as the so-called “inelastic Maxwell model,” analytic calculations can be performed; see, e.g., [140]). The velocity distribution that is obtained, from the microscopic dynamics of the system of cooling experiments for a spatially uniform gas whose temperature is monotonically decreasing with time, is given by (see [141] and references therein) a q-Gaussian with
- Lattice Boltzmann models for fluids. The incompressible Navier–Stokes equation has been considered [121] on a discretized D-dimensional Bravais lattice of coordination number b. It is further assumed that there is a single value for the particle mass, and also for speed. The basic requirement for the lattice Boltzmann model is to be Galilean invariant (i.e., invariant under a change of inertial reference frame) like the Navier–Stokes equation itself. It has been proved [121] that an H-theorem is satisfied for a trace-form entropy only if it is withTherefore, in all cases ( if , and if ), and approaches unity from below in the limit. This study has been generalized by allowing multiple masses and multiple speeds. Galilean invariance once again mandates [122] an entropy of the form , with a unique value of q determined by a transcendental equation involving the dimension and symmetry properties of the Bravais lattice as well as the multiple values of the masses and of the speeds. Of course, Equation (47) is recovered for the particular case of a single mass and a single speed. Finally, Equation (47) may be seen as one more verification of the structure reflected in Equation (37).
- In the area of high-energy collisions, a highly interesting development based on first-principle Yang–Mills/QCD grounds became available a couple of years ago [142]. It yieldedwhere is the number of colors and the number of flavors. If , one finds , hence , which is amazingly close to the LHC (Large Hadron Collider) values indicated in the figure of [143] exhibiting the fittings (along very many experimental decades; notice also that the fitting temperature GeV practically corresponds to the mass of pions, ubiquitous in proton–proton collisions) with which Kapusta begun his talk. Furthermore, if is used, is obtained which, interestingly enough, coincides with the value phenomenologically advanced in 2000 by Walton and Rafelski [144] in their approach of a heavy quark diffusing in a quark–gluon plasma.By the way, let me mention at this point that some years ago I briefly met in Brazil with the CERN researcher J. R. Ellis. I asked him whether he was aware that the q-exponential distribution ubiquitously emerged in high-energy collision data. He answered that he was aware. I then asked him whether he thought that this fact could be deduced from QCD. He answered that the value of q possibly yes, but the whole distribution probably not. The Deppman–Megias–Menezes relation (48) is by all means relevant along that line of thought; so are also the Wilk–Wlodarczyk, Beck and Beck–Cohen connections between q, fluctuations and degrees of freedom [145,146,147].
3. Final Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Group of Statistical Physics. Nonextensive Statistical Mechanics and Thermodynamics. Bibliography. Available online: http://tsallis.cat.cbpf.br/biblio.htm (accessed on 3 May 2022).
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Cleymans, J.; Hamar, G.; Levai, P.; Wheaton, S. Near-thermal equilibrium with Tsallis distributions in heavy ion collisions. J. Phys. G Nucl. Part. Phys. 2009, 36, 064018. [Google Scholar] [CrossRef]
- Cleymans, J. Is strangeness chemically equilibrated? arXiv 2010, arXiv:1001.3002. [Google Scholar] [CrossRef]
- Cleymans, J. Recent developments around chemical equilibrium. J. Phys. G Nucl. Part. Phys. 2010, 37, 094015. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution and transverse momentum distributions in high-energy physics. arXiv 2011, arXiv:1106.3405. [Google Scholar] [CrossRef]
- Cleymans, J. The thermal model at the Large Hadron Collider. Acta Phys. Pol. B 2012, 43, 563–570. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution in proton-proton collisions at √s = 0.9 TeV at the LHC. J. Phys. G Nucl. Part. Phys. 2012, 39, 025006. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic thermodynamics: Transverse momentum distributions in high-energy physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. Transverse momentum distributions at the LHC and Tsallis thermodynamics. arXiv 2013, arXiv:1310.0217. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. Transverse momentum distributions in p-Pb collisions and Tsallis thermodynamics. arXiv 2013, arXiv:1311.2909. [Google Scholar] [CrossRef]
- Cleymans, J. The Tsallis distribution at the LHC. arXiv 2012, arXiv:1210.7464. [Google Scholar] [CrossRef]
- Cleymans, J. The Tsallis distribution for p-p collisions at the LHC. J. Phys. Conf. Ser. 2013, 455, 012049. [Google Scholar] [CrossRef]
- Cleymans, J.; Lykasov, G.I.; Parvan, A.S.; Sorin, A.S.; Teryaev, O.V.; Worku, D. Systematic properties of the Tsallis distribution: Energy dependence of parameters in high energy p-p collisions. Phys. Lett. B 2013, 723, 351–354. [Google Scholar] [CrossRef]
- Cleymans, J. The Tsallis Distribution at the LHC. Talk at CERN Heavy Ion Forum, 1 February 2013, Geneva, Switzerland. Available online: https://indico.cern.ch/event/232225/ (accessed on 3 May 2022).
- Cleymans, J. The Tsallis Distribution. ALICE Matters 15 April 2013. Available online: https://alicematters.web.cern.ch/JeanCleyman (accessed on 3 May 2022).
- Cleymans, J. The Tsallis Distribution at the LHC. Talk at CERN Heavy Ion Forum, 13 January 2014, Geneva, Switzerland. Available online: https://indico.cern.ch/event/285968/ (accessed on 3 May 2022).
- Cleymans, J. The Tsallis distribution at the LHC: Phenomenology. AIP Conf. Proc. 2014, 1625, 31–37. [Google Scholar] [CrossRef]
- Cleymans, J. Systematic properties of the Tsallis distribution: Energy dependence of parameters. J. Phys. Conf. Ser. 2014, 509, 012099. [Google Scholar] [CrossRef]
- Cleymans, J. The Tsallis distribution at the LHC. EPJ Web Conf. 2014, 70, 00009. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. Transverse momentum distributions in proton-proton collisions at LHC energies and Tsallis thermodynamics. J. Phys. G Nucl. Part. Phys. 2014, 41, 065001. [Google Scholar] [CrossRef]
- Cleymans, J.; Azmi, M.D. Large transverse momenta and Tsallis thermodynamics. J. Phys. Conf. Ser. 2016, 668, 012050. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. The Tsallis distribution at large transverse momenta. Eur. Phys. J. C 2015, 75, 430. [Google Scholar] [CrossRef]
- Marques, L.; Cleymans, J.; Deppman, A. Description of high-energy pp collisions using Tsallis thermodynamics: Transverse momentum and rapidity distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar] [CrossRef]
- Deppman, A.; Marques, L.; Cleymans, J. Longitudinal properties of high energy collisions. J. Phys. Conf. Ser. 2015, 623, 012009. [Google Scholar] [CrossRef]
- Khuntia, A.; Sahoo, P.; Garg, P.; Sahoo, R.; Cleymans, J. Speed of sound in hadronic matter using non-extensive statistics. Proc. DAE–BRNS Symp. Nucl. Phys. 2015, 60, 744–745. Available online: http://sympnp.org/proceedings/60/ (accessed on 3 May 2022). [CrossRef]
- Thakur, D.; Tripathy, S.; Garg, P.; Sahoo, R.; Cleymans, J. Indication of a differential freeze-out in proton-proton and heavy-ion collisions at RHIC and LHC energies. Adv. High Energy Phys. 2016, 2016, 4149352. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Khuntia, A.; Pareek, P.; Sahoo, R. Radial flow in non-extensive thermodynamics and study of particle spectra at LHC in the limit of small (q−1). Eur. Phys. J. A 2016, 52, 30. [Google Scholar] [CrossRef]
- Khuntia, A.; Sahoo, P.; Garg, P.; Sahoo, R.; Cleymans, J. Speed of sound in hadronic matter using non-extensive Tsallis statistics. Eur. Phys. J. A 2016, 52, 292. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Mogliacci, S. Analytic results for the Tsallis thermodynamic variables. Phys. Rev. D 2016, 94, 094026. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Khuntia, A.; Pareek, P.; Sahoo, R. Small (q−1) expansion of the Tsallis distribution and study of particle spectra at LHC. In Proceedings of the 61st Annual Conference of the South African Institute of Physics (SAIP206), Johannesburg, South Africa, 4–8 July 2016; pp. 463–468. Available online: https://inspirehep.net/literature/1720205 (accessed on 3 May 2022).
- Cleymans, J.; Azmi, M.D.; Parvan, A.S.; Teryaev, O.V. The parameters of the Tsallis distribution at the LHC. EPJ Web Conf. 2017, 137, 11004. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Garg, P.; Kumar, P.; Mogliacci, S.; Sahoo, R.; Tripathy, S. Applications of the Tsallis statistics in high energy collisions. J. Phys. Conf. Ser. 2017, 878, 012016. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J. Non-extensive Fokker–Planck transport coefficients of heavy quarks. arXiv 2017, arXiv:1707.08425. [Google Scholar] [CrossRef]
- Khuntia, A.; Tripathy, S.; Sahoo, R.; Cleymans, J. Multiplicity dependence of non-extensive parameters for strange and multi-strange particles in proton-proton collisions at s = 7 TeV at the LHC. Eur. Phys. J. A 2017, 53, 103. [Google Scholar] [CrossRef]
- Parvan, A.S.; Teryaev, O.V.; Cleymans, J. Systematic comparison of Tsallis statistics for charged pions produced in pp collisions. Eur. Phys. J. A 2017, 53, 102. [Google Scholar] [CrossRef]
- Cleymans, J. On the use of the Tsallis distribution at LHC energies. J. Phys. Conf. Ser. 2017, 779, 012079. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Marques, L.; Mogliacci, S.; Paradza, M.W. On the precise determination of the Tsallis parameters in proton-proton collisions at LHC energies. J. Phys. G Nucl. Part. Phys. 2018, 45, 055001. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Cleymans, J.; Mogliacci, S.; Parvan, A.S.; Sorin, A.S.; Teryaev, O.V. Non extensivity of the QCD pT-spectra. Eur. Phys. J. A 2018, 54, 222. [Google Scholar] [CrossRef]
- Khuntia, A.; Sharma, H.; Tiwari, S.K.; Sahoo, R.; Cleymans, J. Radial flow and differential freeze-out in proton-proton collisions at √s = 7 TeV at the LHC. Eur. Phys. J. A 2019, 55, 3. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Determination of the chemical potential in the Tsallis distribution at LHC energies. arXiv 2020, arXiv:2010.05565. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Tsallis statistics in high energy physics: Chemical and thermal freeze-outs. Physics 2020, 2, 654–664. [Google Scholar] [CrossRef]
- Azmi, M.D.; Bhattacharyya, T.; Cleymans, J.; Paradza, M. Energy density at kinetic freeze-out in Pb-Pb collisions at the LHC using the Tsallis distribution. J. Phys. G Nucl. Part. Phys. 2020, 47, 045001. [Google Scholar] [CrossRef]
- Rath, R.; Khuntia, A.; Sahoo, R.; Cleymans, J. Event multiplicity, transverse momentum and energy dependence of charged particle production, and system thermodynamics in pp collisions at the Large Hadron Collider. J. Phys. G Nucl. Part. Phys. 2020, 47, 055111. [Google Scholar] [CrossRef]
- Kapusta, J.I. A Primer on Tsallis Statistics for Nuclear and Particle Physics. 19 May 2021. Available online: https://www.youtube.com/watch?v=CmyXk1Xkvcg (accessed on 3 May 2022).
- Maingueneau, D. Genèses du Discours; Mardaga: Bruxelles, Brussels, 1984. [Google Scholar]
- Pêcheux, M. Les Vérités de La Palice; Maspero: Paris, France, 1975. [Google Scholar]
- Foucault, M. L’ Ordre du Discours; Gallimard: Paris, France, 1971. [Google Scholar]
- Kapusta, J.I. Perspective on Tsallis statistics for nuclear and particle physics. Int. J. Mod. Phys. E 2021, 30, 2130006. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive Statistical Mechanics. Approaching a Complex World, 1st ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Watanabe, S. Knowing and Guessing; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Barlow, H. Conditions for versatile learning, Helmholtz’s unconscious inference, and the task of perception. Vision. Res. 1990, 30, 1561–1571. [Google Scholar] [CrossRef]
- Tsallis, C. Entropy. Encyclopedia 2022, 2, 264–300. [Google Scholar] [CrossRef]
- Enciso, A.; Tempesta, P. Uniqueness and characterization theorems for generalized entropies. J. Stat. Mech. 2017, 2017, 123101. [Google Scholar] [CrossRef]
- Tsallis, C.; Haubold, H.J. Boltzmann-Gibbs entropy is sufficient but not necessary for the likelihood factorization required by Einstein. EPL (Europhys. Lett.) 2015, 110, 30005. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical theory of communication. Part III. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Khinchin, A.I. The entropy concept of probability theory. Uspekhi Matem. Nauk 1953, 8, 3–20. (In Russian) [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Silverman, R.A.; Friedman, M.D., Translators; Dover: New York, NY, USA, 1957; pp. 1–28. [Google Scholar]
- dos Santos, R.J.V. Generalization of Shannon’ s theorem for Tsallis entropy. J. Math. Phys. 1997, 38, 4104–4107. [Google Scholar] [CrossRef]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar] [CrossRef]
- Topsøe, F. Factorization and escorting in the game-theoretical approach to non-extensive entropy measures. Phys. A Stat. Mech. Appl. 2006, 365, 91–95. [Google Scholar] [CrossRef]
- Amari, S.; Ohara, A.; Matsuzoe, H. Geometry of deformed exponential families: Invariant, dually-flat and conformal geometries. Phys. A Stat. Mech. Appl. 2012, 391, 4308–4319. [Google Scholar] [CrossRef]
- Biro, T.S.; Barnafoldi, G.G.; Van, P. New entropy formula with fluctuating reservoir. Phys. A Stat. Mech. Appl. 2015, 417, 215–220. [Google Scholar] [CrossRef]
- Penrose, O. Foundations of Statistical Mechanics: A Deductive Treatment; Pergamon: Oxford, UK, 1970; p. 167. [Google Scholar]
- Tsallis, C.; Cirto, L.J.L. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Einstein, A. Autobiographical Notes. In Albert Einstein: Historical and Cultural Perspectives; Holton, G., Elkana, Y., Eds.; Dover Publications: Mineola, NY, USA, 1997; p. 227. [Google Scholar]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Sci. USA 2005, 102, 15377. [Google Scholar] [CrossRef] [PubMed]
- Curado, E.M.F.; Tsallis, C. Generalized statistical mechanics: Connection with thermodynamics. J. Phys. A Math. Gen 1991, 24, L69–L72, Erratum in J. Phys. A Math. Gen. 1992, 25, 1019. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A Stat. Mech. Appl. 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Ferri, G.L.; Martínez, S.; Plastino, A. Equivalence of the four versions of Tsallis’s statistics. J. Stat. Mech. Theory Exp. 2005, 2005, P04009. [Google Scholar] [CrossRef]
- Ferri, G.L.; Martínez, S.; Plastino, A. The role of constraints in Tsallis’ nonextensive treatment revisited. Phys. A Stat. Mech. Appl. 2005, 347, 205–220. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Classes of N-Dimensional nonlinear Fokker–Planck equations associated to Tsallis entropy. Entropy 2011, 13, 1928–1944. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Time evolution of interacting vortices under overdamped motion. Phys. Rev. E 2012, 85, 021146. [Google Scholar] [CrossRef] [PubMed]
- Curado, E.M.F.; Souza, A.M.C.; Nobre, F.D.; Andrade, R.F.S. Carnot cycle for interacting particles in the absence of thermal noise. Phys. Rev. E 2014, 89, 022117. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.F.S.; Souza, A.M.C.; Curado, E.M.F.; Nobre, F.D. A thermodynamical formalism describing mechanical interactions. EPL (Europhys. Lett.) 2014, 108, 20001. [Google Scholar] [CrossRef]
- Nobre, F.D.; Curado, E.M.F.; Souza, A.M.C.; Andrade, R.F.S. Consistent thermodynamic framework for interacting particles by neglecting thermal noise. Phys. Rev. E 2015, 91, 022135. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Casas, G.A.; Nobre, F.D. Second law and entropy production in a nonextensive system. Phys. Rev. E 2015, 91, 012140. [Google Scholar] [CrossRef] [PubMed]
- Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Moreira, A.A. General continuum approach for dissipative systems of repulsive particles. Phys. Rev. E 2016, 93, 060103(R). [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D. Repulsive particles under a general external potential: Thermodynamics by neglecting thermal noise. Phys. Rev. E 2016, 94, 022120. [Google Scholar] [CrossRef]
- Moreira, A.A.; Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Tsallis, C. Overdamped dynamics of particles with repulsive power-law interactions. Phys. Rev. E 2018, 98, 032138. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker–Planck equation. Phys. A Stat. Mech. Appl. 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, R2197. [Google Scholar]
- Ribeiro, M.S.; Tsallis, C.; Nobre, F.D. Probability distributions extremizing the nonadditive entropy Sδ and stationary states of the corresponding nonlinear Fokker–Planck equation. Phys. Rev. E 2013, 88, 052107. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.S.; Nobre, F.D.; Tsallis, C. Probability distributions and associated nonlinear Fokker–Planck equation for the two-index entropic form Sq,δ. Phys. Rev. E 2014, 89, 052135. [Google Scholar] [CrossRef] [PubMed]
- Beck, C.; Schögl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Tsallis, C.; Plastino, A.R.; Alvarez-Estrada, R.F. Escort mean values and the characterization of power-law-decaying probability densities. J. Math. Phys. 2009, 50, 043303. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-central limit theorem consistent with nonextensive statistical mechanics. Milan J. Math. 2008, 76, 307–328. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Gell-Mann, M.; Steinberg, S. Generalization of symmetric α-stable Lévy distributions for q>1. J. Math. Phys. 2010, 51, 033502. [Google Scholar] [CrossRef] [PubMed]
- Thistleton, W.; Marsh, J.A.; Nelson, K.; Tsallis, C. Generalized Box-Muller method for generating q-Gaussian random deviates. IEEE Trans. Inf. Theory 2007, 53, 4805–4810. [Google Scholar] [CrossRef]
- Zanette, D.H.; Montemurro, M.A. A note on non-thermodynamical applications of non-extensive statistics. Phys. Lett. A 2004, 324, 383–387. [Google Scholar] [CrossRef]
- Montroll, E.W.; Shlesinger, M.F. Maximum entropy formalism, fractals, scaling phenomena, and 1/f noise: A tale of tails. J. Stat. Phys. 1983, 32, 209–230. [Google Scholar] [CrossRef]
- Englman, R. Maximum entropy principles in fragmentation data analysis. In High-Pressure Shock Compression of Solids II. Dynamic Fracture and Fragmentation; Davison, L., Grady, D.E., Shahinpoor, M., Eds.; Springer: New York, NY, USA, 1996; pp. 264–281. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A.; Soffer, B.H. Ambiguities in the forms of the entropic functional and constraints in the maximum entropy formalism. Phys. Lett. A 2007, 363, 48–52. [Google Scholar] [CrossRef]
- Tsallis, C. What should a statistical mechanics satisfy to reflect nature? Phys. D Nonlinear Phenom. 2004, 193, 3–34. [Google Scholar] [CrossRef]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Charles Scribner’s Sons: New York, NY, USA, 1902; Available online: https://www.gutenberg.org/files/50992/50992-pdf.pdf (accessed on 3 May 2022).
- Landsberg, P.T. Thermodynamics and Statistical Mechanics; Dover Publications: New York, NY, USA, 1990. [Google Scholar]
- Tsallis, C.; Cirto, L.J.L. Thermodynamics is more powerful than the role to it reserved by Boltzmann-Gibbs statistical mechanics. Eur. Phys. J. Spec. Top. 2014, 223, 2161–2175. [Google Scholar] [CrossRef][Green Version]
- Tsallis, C. Approach of complexity in nature: Entropic nonuniqueness. Axioms 2016, 5, 20. [Google Scholar] [CrossRef]
- Tsallis, C. Beyond Boltzmann-Gibbs-Shannon in physics and elsewhere. Entropy 2019, 21, 696. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, G.; Tsallis, C. Towards a large deviation theory for strongly correlated systems. Phys. Lett. A 2012, 376, 2451–2454. [Google Scholar] [CrossRef]
- Touchette, H. Comment on “Towards a large deviation theory for strongly correlated systems”. Phys. Lett. A 2013, 377, 436–438. [Google Scholar] [CrossRef]
- Ruiz, G.; Tsallis, C. Reply to Comment on “Towards a large deviation theory for strongly correlated systems”. Phys. Lett. A 2013, 377, 491–495. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Ay, N. Approaching a large deviation theory for complex systems. Nonlinear Dyn. 2021, 106, 2537–2546. [Google Scholar] [CrossRef]
- Tirnakli, U.; Marques, M.; Tsallis, C. Entropic extensivity and large deviations in the presence of strong correlations. Phys. D Nonlinear Phenom. 2022, 431, 133132. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Silva, R.; Plastino, A.R. Nonextensive thermostatistics and the H-theorem. Phys. Rev. Lett. 2001, 86, 2938–2941. [Google Scholar] [CrossRef]
- Lavagno, A. Relativistic nonextensive thermodynamics. Phys. Lett. A 2002, 301, 13–18. [Google Scholar] [CrossRef]
- Nivanen, L.; Le Méhauté, A.; Wang, Q.A. Generalized algebra within a nonextensive statistics. Rep. Math. Phys. 2003, 52, 437–444. [Google Scholar] [CrossRef]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Phys. A Stat. Mech. Appl. 2004, 340, 95–101, Corrigendum in Phys. A Stat. Mech. Appl. 2021, 581, 126206. [Google Scholar] [CrossRef]
- Borges, E.P.; da Costa, B.G. Deformed mathematical objects stemming from the q-logarithm function. Axioms 2022, 11, 138. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C. Mathematical Foundations of Nonextensive Statistical Mechanics; World Scientific: Singapore, 2022. [Google Scholar] [CrossRef]
- Megias, E.; Lima, J.A.S.; Deppman, A. Transport equation for small systems and the nonadditive entropy. Mathematics 2022, 10, 1625. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Tsallis, C. Möbius transforms, cycles and q-triplets in statistical mechanics. Entropy 2019, 21, 1155. [Google Scholar] [CrossRef]
- Tsallis, C.; Bemski, G.; Mendes, R.S. Is re-association in folded proteins a case of nonextensivity? Phys. Lett. A 1999, 257, 93–98. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Mendes, R.S.; Lenzi, E.K. Quantum statistical mechanics for nonextensive systems: Prediction for possible experimental tests. Phys. Rev. Lett. 1998, 80, 3907–3910. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Mendes, R.S.; Rajagopal, A.K. Quantum statistical mechanics for nonextensive systems. Phys. Rev. Lett. 1999, 59, 1398. [Google Scholar] [CrossRef]
- Chavanis, P.H. Hamiltonian and Brownian systems with long-range interactions: III. The BBGKY hierarchy for spatially inhomogeneous systems. Phys. A Stat. mech. Appl. 2008, 387, 787–805. [Google Scholar] [CrossRef]
- Mariz, A.M. On the irreversible nature of the Tsallis and Renyi entropies. Phys. Lett. A 1992, 165, 409–411. [Google Scholar] [CrossRef]
- Abe, S.; Rajagopal, A.K. Validity of the second law in nonextensive quantum thermodynamics. Phys. Rev. Lett. 2003, 91, 120601. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M.; Love, P.J.; Coveney, P.V.; Karlin, I.V.; Succi, S.; Yepez, J. Galilean-invariant lattice-Boltzmann models with H-theorem. Phys. Rev. E 2003, 68, 025103(R). [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M.; Love, P.; Yepez, J.; Coveney, P.V. Galilean-invariant multi-speed entropic lattice Boltzmann models. Phys. D Nonlinear Phenom. 2004, 193, 169–181. [Google Scholar] [CrossRef]
- Latora, V.; Baranger, M. Kolmogorov-Sinai entropy rate versus physical entropy. Phys. Rev. Lett. 1999, 82, 520–523. [Google Scholar] [CrossRef]
- Latora, V.; Baranger, M.; Rapisarda, A.; Tsallis, C. The rate of entropy increase at the edge of chaos. Phys. Lett. A 2000, 273, 97–103. [Google Scholar] [CrossRef]
- Baldovin, F.; Robledo, A. Nonextensive Pesin identity-Exact renormalization group analytical results for the dynamics at the edge of chaos of the logistic map. Phys. Rev. E 2004, 69, 045202(R). [Google Scholar] [CrossRef]
- Coniglio, A.; Fierro, A.; Herrmann, H.J.; Nicodemi, M. (Eds.) Unifying Concepts in Granular Media and Glasses; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Caruso, F.; Tsallis, C. Nonadditive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E 2008, 78, 021102. [Google Scholar] [CrossRef]
- Lyra, M.L.; Tsallis, C. Nonextensivity and multifractality in low-dimensional dissipative systems. Phys. Rev. Lett. 1998, 80, 53. [Google Scholar] [CrossRef]
- Ananos, G.F.J.; Baldovin, F.; Tsallis, C. Anomalous sensitivity to initial conditions and entropy production in standard maps: Nonextensive approach. Eur. Phys. J. B 2005, 46, 409. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Tsallis, C. Limit distributions of scale-invariant probabilistic models of correlated random variables with the q-Gaussian as an explicit example. Eur. Phys. J. B 2009, 72, 263–268. [Google Scholar] [CrossRef]
- Bountis, A.; Veerman, J.J.P.; Vivaldi, F. Cauchy distributions for the integrable standard map. Phys. Lett. A 2020, 384, 126659. [Google Scholar] [CrossRef]
- Mazenko, G.F. Vortex velocities in the O(n) symmetric time-dependent Ginzburg-Landau model. Phys. Rev. Lett. 1997, 78, 401–404. [Google Scholar] [CrossRef]
- Qian, H.; Mazenko, G.F. Vortex dynamics in a coarsening two-dimensional XY model. Phys. Rev. E 2003, 68, 021109. [Google Scholar] [CrossRef] [PubMed]
- Celikoglu, A.; Tirnakli, U.; Queiros, S.M.D. Analysis of return distributions in the coherent noise model. Phys. Rev. E 2010, 82, 021124. [Google Scholar] [CrossRef] [PubMed]
- Celikoglu, A.; Tirnakli, U. Earthquakes, model systems and connections to q-statistics. Acta Geophys. 2012, 60, 535–546. [Google Scholar] [CrossRef]
- Lutz, E. Anomalous diffusion and Tsallis statistics in an optical lattice. Phys. Rev. A 2003, 67, 051402(R). [Google Scholar] [CrossRef]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis distributions in dissipative optical lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar] [CrossRef]
- Lutz, E.; Renzoni, F. Beyond Boltzmann-Gibbs statistical mechanics in optical lattices. Nat. Phys. 2013, 9, 615–619. [Google Scholar] [CrossRef]
- Combe, G.; Richefeu, V.; Stasiak, M.; Atman, A.P.F. Experimental validation of nonextensive scaling law in confined granular media. Phys. Rev. Lett. 2015, 115, 238301. [Google Scholar] [CrossRef]
- Baldassari, A.; Marconi, U.M.B.; Puglisi, A. Influence of correlations on the velocity statistics of scalar granular gases. Europhys. Lett. (EPL) 2002, 58, 14–20. [Google Scholar] [CrossRef]
- Sattin, F. Derivation of Tsallis’ statistics from dynamical equations for a granular gas. J. Phys. A Math. Gen. 2003, 36, 1583–1591. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E.; Menezes, D.P. Fractals, nonextensive statistics, and QCD. Phys. Rev. D 2020, 101, 034019. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and pp¯ collisions. Phys. Rev. D 2015, 91, 114027. [Google Scholar] [CrossRef]
- Walton, D.B.; Rafelski, J. Equilibrium distribution of heavy quarks in Fokker–Planck dynamics. Phys. Rev. Lett. 2000, 84, 31. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the nonextensivity parameter q in some applications of Tsallis statistics and Lévy distributions. Phys. Rev. Lett. 2000, 84, 2770–2773. [Google Scholar] [CrossRef]
- Beck, C. Dynamical foundations of nonextensive statistical mechanics. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A Stat. Mech. Appl. 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Tsallis, C. Nonadditive Entropies and Statistical Mechanics at the Edge of Chaos: Cornerstones. The Santa Fe Institute YouTube. Available online: https://www.youtube.com/watch?v=uQGN2PThukk (accessed on 3 May 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsallis, C. Enthusiasm and Skepticism: Two Pillars of Science—A Nonextensive Statistics Case. Physics 2022, 4, 609-632. https://doi.org/10.3390/physics4020041
Tsallis C. Enthusiasm and Skepticism: Two Pillars of Science—A Nonextensive Statistics Case. Physics. 2022; 4(2):609-632. https://doi.org/10.3390/physics4020041
Chicago/Turabian StyleTsallis, Constantino. 2022. "Enthusiasm and Skepticism: Two Pillars of Science—A Nonextensive Statistics Case" Physics 4, no. 2: 609-632. https://doi.org/10.3390/physics4020041
APA StyleTsallis, C. (2022). Enthusiasm and Skepticism: Two Pillars of Science—A Nonextensive Statistics Case. Physics, 4(2), 609-632. https://doi.org/10.3390/physics4020041




