Color Transparency and Light-Front Holographic QCD
Abstract
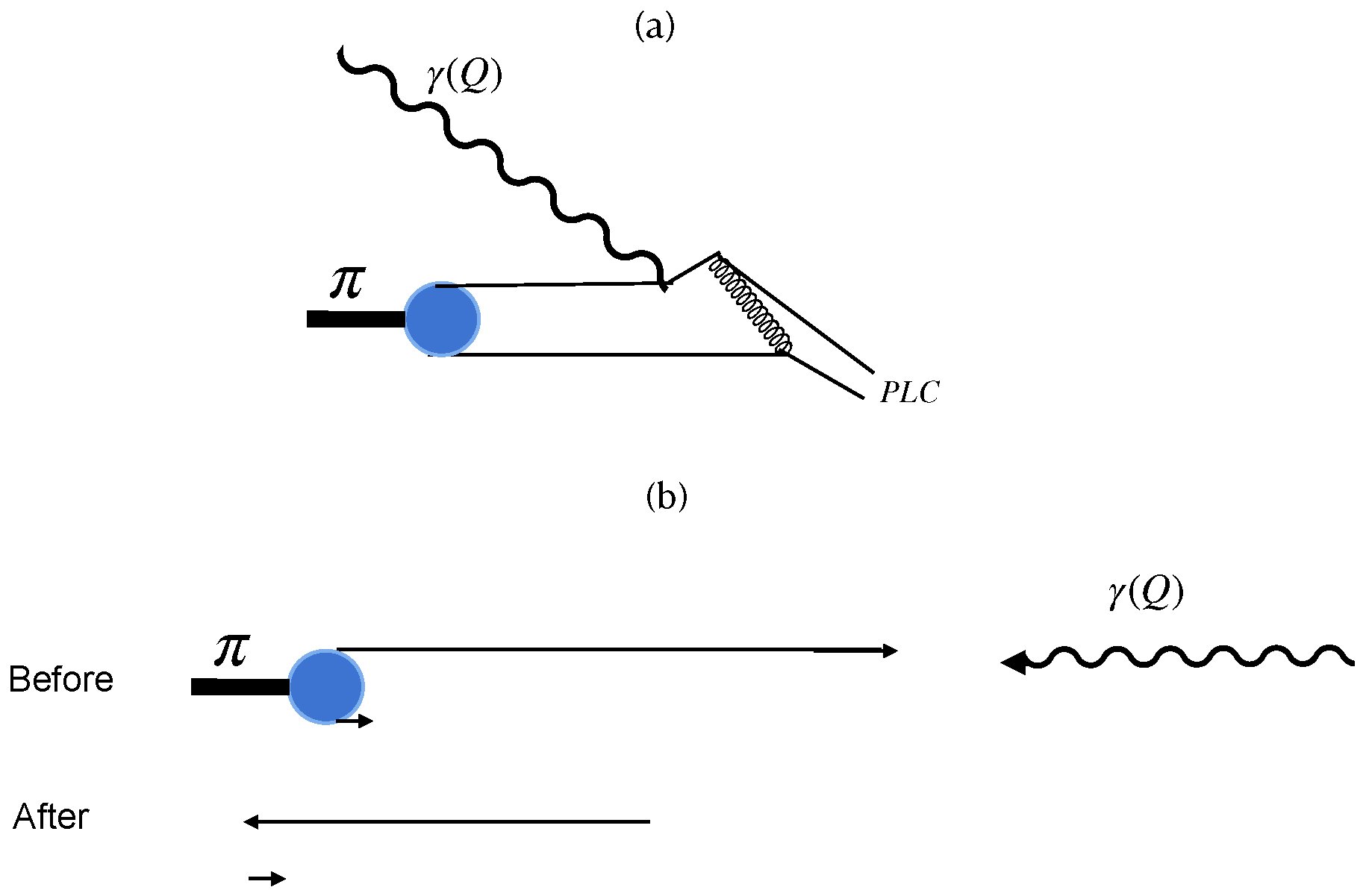
:- High-momentum transfer coherent reactions make point-like color-singlet objects, denoted as point-like configurations (PLCs). This statement was a prediction initially based on perturbative QCD (pQCD). For example, early pQCD calculations [5,6,7,8,9,10] of the pion elastic electromagnetic form factor were interpreted [11] to involve point-like configurations of quarks, meaning that the important regions of integration that contribute to the form factor are those in which the quark and anti-quark are very close together. The idea is that for the system to stay together when hit by a high-momentum virtual photon, the quark and anti-quark must be connected by the exchange of a high-momentum gluon, see Figure 1a. This idea is based on the ideas of perturbative QCD, but the validity of that version of QCD is not a necessary condition. Other strong interaction effects may also lead to the creation of a PLC.
- Small objects have small cross-sections. It has been widely reported that the imaginary part of the forward scattering amplitude, f, of a rapidly moving color singlet object is proportional to the square of the transverse separation b between positive and negative color charges. Two-gluon exchange [12,13,14] provides the lowest-order perturbative contribution to f. The remarkable feature is that, in the limit that b approaches 0, the cross-section vanishes because the color singlet point particles do not exchange colored gluons; concisely, This result is caused by interference between emission by quarks of different colors in coherent processes. Coherence means that one adds amplitudes to obtain the scattering amplitude, which is then squared to obtain the cross-section. The cancellation, known as color cancellation, is the basic ingredient behind QCD factorization proofs and is used elsewhere [15] and not questioned.
- A PLC, once created, will expand as it moves. This is because a PLC is not an eigenstate of the Hamiltonian. The expansion effect is diminished if the PLC moves with sufficiently high momentum.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frankfurt, L.L.; Miller, G.A.; Strikman, M. The Geometrical color optics of coherent high-energy processes. Ann. Rev. Nucl. Part. Sci. 1994, 44, 501–560. [Google Scholar] [CrossRef]
- Jain, P.; Pire, B.; Ralston, J.P. Quantum color transparency and nuclear filtering. Phys. Rep. 1996, 271, 67–179. [Google Scholar] [CrossRef] [Green Version]
- Ashery, D. High momentum diffractive processes and hadronic structure. Prog. Part. Nucl. Phys. 2006, 56, 279–339. [Google Scholar] [CrossRef]
- Dutta, D.; Hafidi, K.; Strikman, M. Color transparency: Past, present and future. Prog. Part. Nucl. Phys. 2013, 69, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Farrar, G.R.; Jackson, D.R. The pion form factor. Phys. Rev. Lett. 1979, 43, 246–250. [Google Scholar] [CrossRef]
- Efremov, A.V.; Radyushkin, A.V. Factorization and asymptotical behavior of pion form-factor in QCD. Phys. Lett. B 1980, 94, 245–250. [Google Scholar] [CrossRef]
- Lepage, G.P.; Brodsky, S.J. Exclusive processes in quantum chromodynamics: The form-factors of baryons at large momentum transfer. Phys. Rev. Lett. 1979, 43, 545–549, Erratum in Phys. Rev. Lett. 1979, 43, 1625–1626. [Google Scholar] [CrossRef] [Green Version]
- Lepage, G.P.; Brodsky, S.J. Exclusive processes in quantum chromodynamics: Evolution equations for hadronic wave functions and the form-factors of mesons. Phys. Lett. B 1979, 87, 359–365. [Google Scholar] [CrossRef]
- Duncan, A.; Mueller, A.H. Asymptotic behavior of composite-particle form factors and the renormalization group. Phys. Rev. D 1980, 21, 1636–1650. [Google Scholar] [CrossRef]
- Duncan, A.; Mueller, A. Asymptotic behavior of exclusive and almost exclusive processes. Phys. Lett. B 1980, 90, 159–163. [Google Scholar] [CrossRef]
- Mueller, A.H. Topics in high-energy perturbative QCD including interactions with nuclear matter. In Proceedings of the 17th Rencontres de Moriond on Elementary Particle Physics: I. Electroweak Interactions and Grand Unified Theories, Les Arcs, France, 14–20 March 1982; Tran Than Van, J., Ed.; Editions Frontieres: Gif-Sur-Yvette, France, 1988; pp. 13–43. [Google Scholar]
- Low, F.E. Model of the bare Pomeron. Phys. Rev. D 1975, 12, 163–173. [Google Scholar] [CrossRef]
- Nussinov, S. Colored quark version of some hadronic puzzles. Phys. Rev. Lett. 1975, 34, 1286–1289. [Google Scholar] [CrossRef]
- Gunion, J.F.; Soper, D.E. Quark counting and hadron size effects for total cross-sections. Phys. Rev. D 1977, 15, 2617–2621. [Google Scholar] [CrossRef]
- Donnachie, S.; Dosch, G.; Landshoff, P.; Nachtmann, O. Pomeron Physics and QCD; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Feynman, R.P. Photon-Hadron Interactions; W. A. Benjamin, Inc.: Reading, MA, USA, 1972. [Google Scholar] [CrossRef]
- Drell, S.; Yan, T.M. Connection of elastic electromagnetic nucleon form-factors at large Q2 and deep inelastic structure functions near threshold. Phys. Rev. Lett. 1970, 24, 181–185. [Google Scholar] [CrossRef] [Green Version]
- West, G.B. Phenomenological model for the electromagnetic structure of the proton. Phys. Rev. Lett. 1970, 24, 1206–1209. [Google Scholar] [CrossRef]
- Radyushkin, A.V. Nonforward parton densities and soft mechanism for form factors and wide-angle Compton scattering in QCD. Phys. Rev. D 1998, 58, 114008. [Google Scholar] [CrossRef] [Green Version]
- Ji, X. Generalized parton distributions. Ann. Rev. Nucl. Part. Sci. 2004, 54, 413–450. [Google Scholar] [CrossRef] [Green Version]
- Diehl, M. Generalized parton distributions. Phys. Rep. 2003, 388, 41–277. [Google Scholar] [CrossRef] [Green Version]
- de Teramond, G.F.; Liu, T.; Sufian, R.S.; Dosch, H.G.; Brodsky, S.J.; Deur, A. Universality of generalized parton distributions in light-front holographic QCD. Phys. Rev. Lett. 2018, 120, 182001. [Google Scholar] [CrossRef] [Green Version]
- Belitsky, A.V.; Radyushkin, A.V. Unraveling hadron structure with generalized parton distributions. Phys. Rep. 2005, 418, 1–387. [Google Scholar] [CrossRef] [Green Version]
- Frankfurt, L.; Miller, G.; Strikman, M. Precocious dominance of point-like configurations in hadronic form-factors. Nucl. Phys. A 1993, 555, 752–764. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Teramond, G.F.; Dosch, H.G.; Erlich, J. Light-front holographic QCD and emerging confinement. Phys. Rep. 2015, 584, 1–105. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; Pauli, H.C.; Pinsky, S.S. Quantum chromodynamics and other field theories on the light cone. Phys. Rep. 1998, 301, 299–486. [Google Scholar] [CrossRef] [Green Version]
- Dirac, P.A. Forms of relativistic dynamics. Rev. Mod. Phys. 1949, 21, 392–399. [Google Scholar] [CrossRef] [Green Version]
- de Teramond, G.F.; Brodsky, S.J. Light-front holography: A first approximation to QCD. Phys. Rev. Lett. 2009, 102, 081601. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Teramond, G.F. Hadronic spectra and light-front wavefunctions in holographic QCD. Phys. Rev. Lett. 2006, 96, 201601. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Teramond, G.F. Light-front dynamics and AdS/QCD correspondence: The pion form factor in the space- and time-like regions. Phys. Rev. D 2008, 77, 056007. [Google Scholar] [CrossRef] [Green Version]
- Polchinski, J.; Strassler, M.J. Deep inelastic scattering and gauge/string duality. J. High Energy Phys. 2003, 2003, 12. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Teramond, G.F. Light-front dynamics and AdS/QCD correspondence: Gravitational form factors of composite hadrons. Phys. Rev. D 2008, 78, 025032. [Google Scholar] [CrossRef] [Green Version]
- Abidin, Z.; Carlson, C.E. Gravitational form factors of vector mesons in an AdS/QCD model. Phys. Rev. D 2008, 77, 095007. [Google Scholar] [CrossRef] [Green Version]
- Brodsky, S.J.; de Teramond, G.F.; Dosch, H.G.; Lorce, C. Universal effective hadron dynamics from superconformal algebra. Phys. Lett. B 2016, 759, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Bhetuwal, D.; Matter, J.; Szumila-Vance, H.; Kabir, M.L.; Dutta, D.; Ent, R.; Abrams, D.; Ahmed, Z.; Aljawrneh, B.; Alsalmi, S.; et al. Ruling out color transparency in quasielastic 12C(e,e′p) up to Q2 of 14.2 (GeV/c)2. Phys. Rev. Lett. 2021, 126, 082301. [Google Scholar] [CrossRef] [PubMed]
- Caplow-Munro, O.; Miller, G.A. Color transparency and the proton form factor: Evidence for the Feynman mechanism. Phys. Rev. C 2021, 104, L012201. [Google Scholar] [CrossRef]
- Clasie, B.; Qian, X.; Arrington, J.; Asaturyan, R.; Benmokhtar, F.; Boeglin, W.; Bosted, P.; Bruell, A.; Christy, M.E.; Chudakov, E.; et al. Measurement of nuclear transparency for the A(e,e′π+) reaction. Phys. Rev. Lett. 2007, 99, 242502. [Google Scholar] [CrossRef] [Green Version]
- El Fassi, L.; Zana, L.; Hafidi, K.; Holtrop, M.; Mustapha, B.; Brooks, W.K.; Hakobyan, H.; Zhenga, X.; Adhikari, K.P.; Adikaram, D.; et al. [CLAS Collaboration]. Evidence for the onset of color transparency in ρ0 electroproduction off nuclei. Phys. Lett. B 2012, 712, 326–330. [Google Scholar] [CrossRef]
- Frankfurt, L.; Miller, G.A.; Strikman, M. Coherent nuclear diffractive production of mini-jets: Illuminating color transparency. Phys. Lett. B 1993, 304, 1–7. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, G.A. Color Transparency and Light-Front Holographic QCD. Physics 2022, 4, 590-596. https://doi.org/10.3390/physics4020039
Miller GA. Color Transparency and Light-Front Holographic QCD. Physics. 2022; 4(2):590-596. https://doi.org/10.3390/physics4020039
Chicago/Turabian StyleMiller, Gerald A. 2022. "Color Transparency and Light-Front Holographic QCD" Physics 4, no. 2: 590-596. https://doi.org/10.3390/physics4020039
APA StyleMiller, G. A. (2022). Color Transparency and Light-Front Holographic QCD. Physics, 4(2), 590-596. https://doi.org/10.3390/physics4020039




