u-Channel Color Transparency Observables
Abstract
1. Introduction
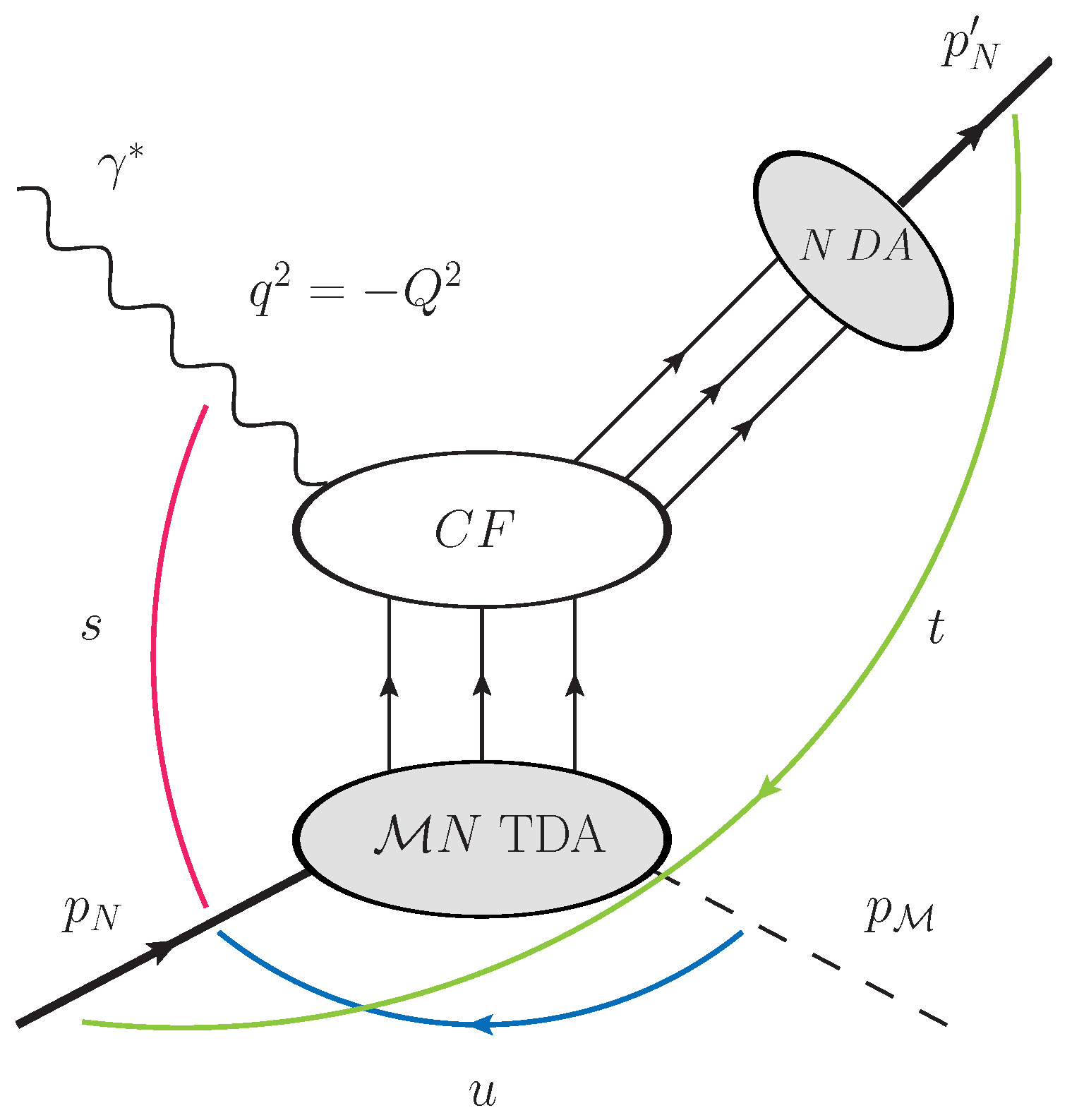
2. The Proposed Measurement
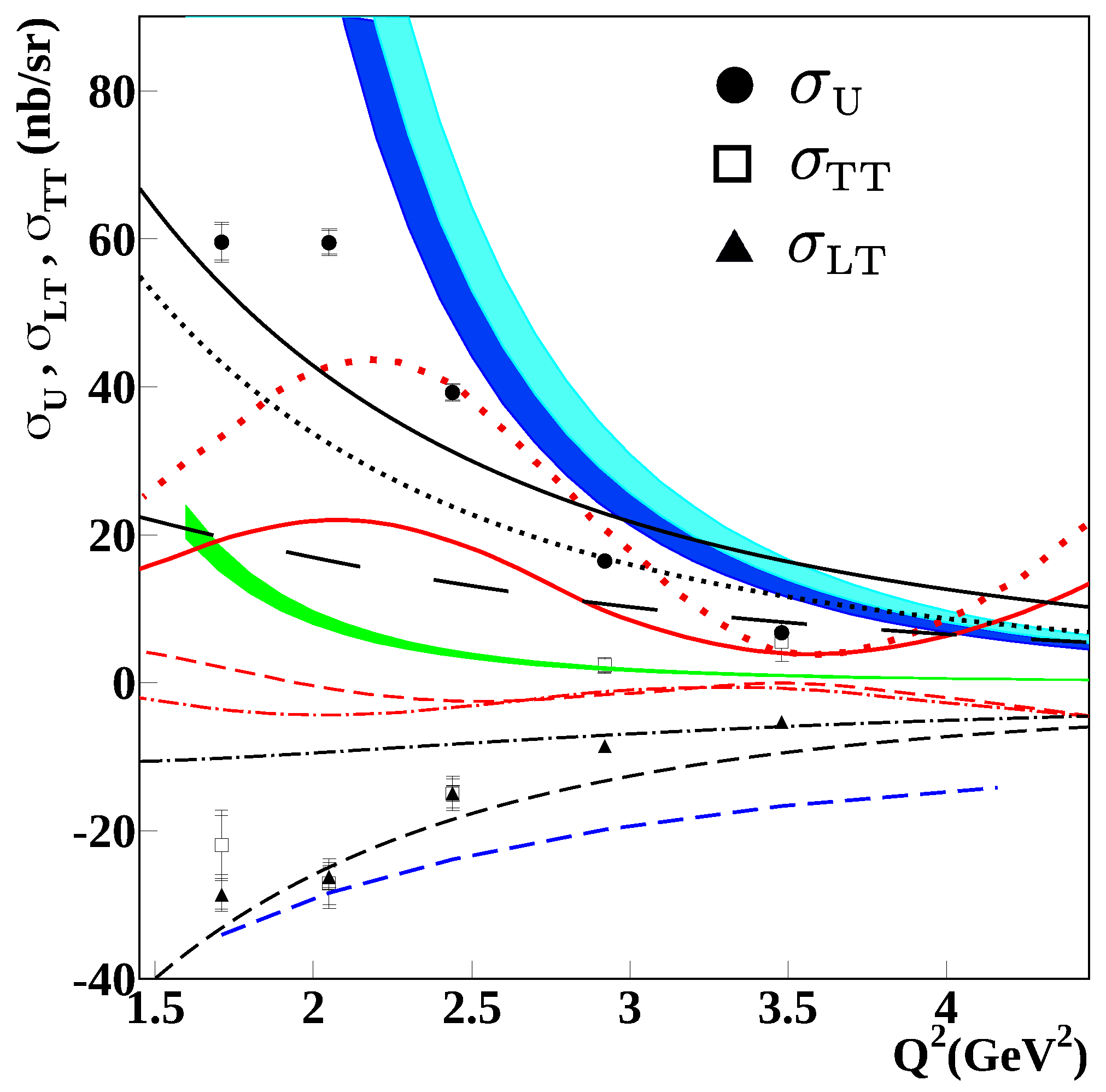
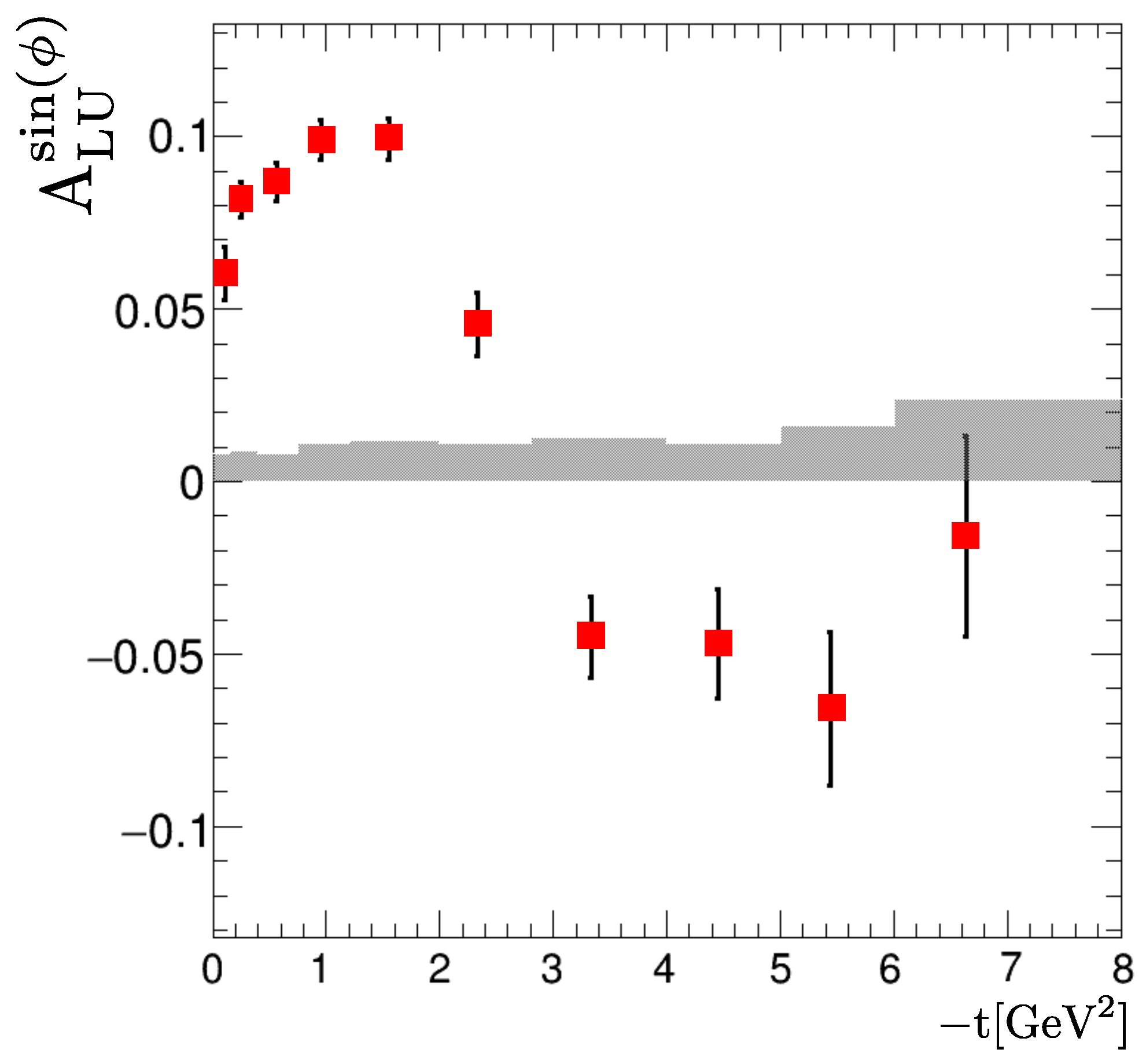
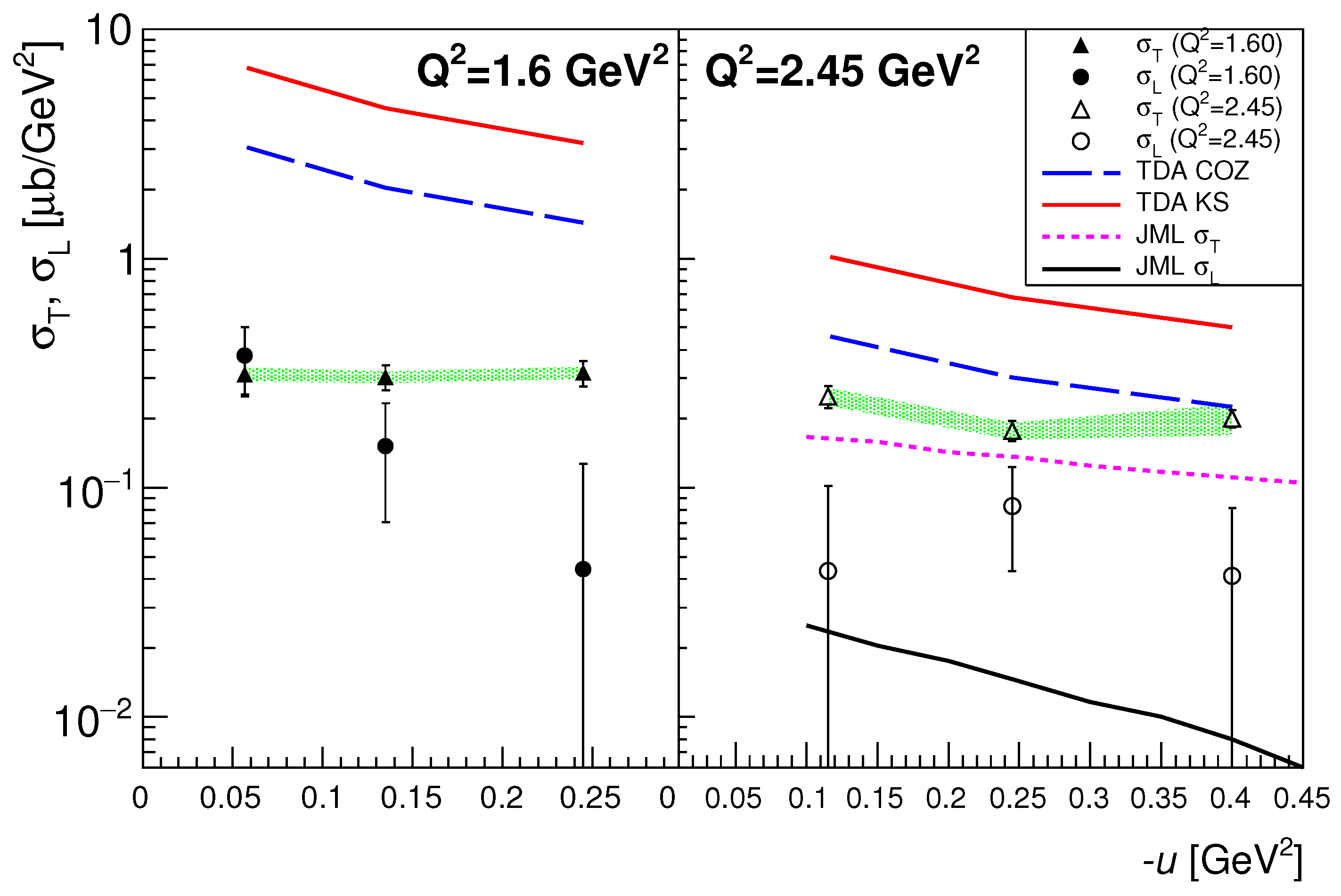
2.1. Previous Backward-Angle Data from Jefferson Laboratory (JLab)
2.2. Jefferson Lab Proposal E12-20-007
2.3. Nuclear Targets
2.4. Electron-Ion Collider (EIC) Perspective
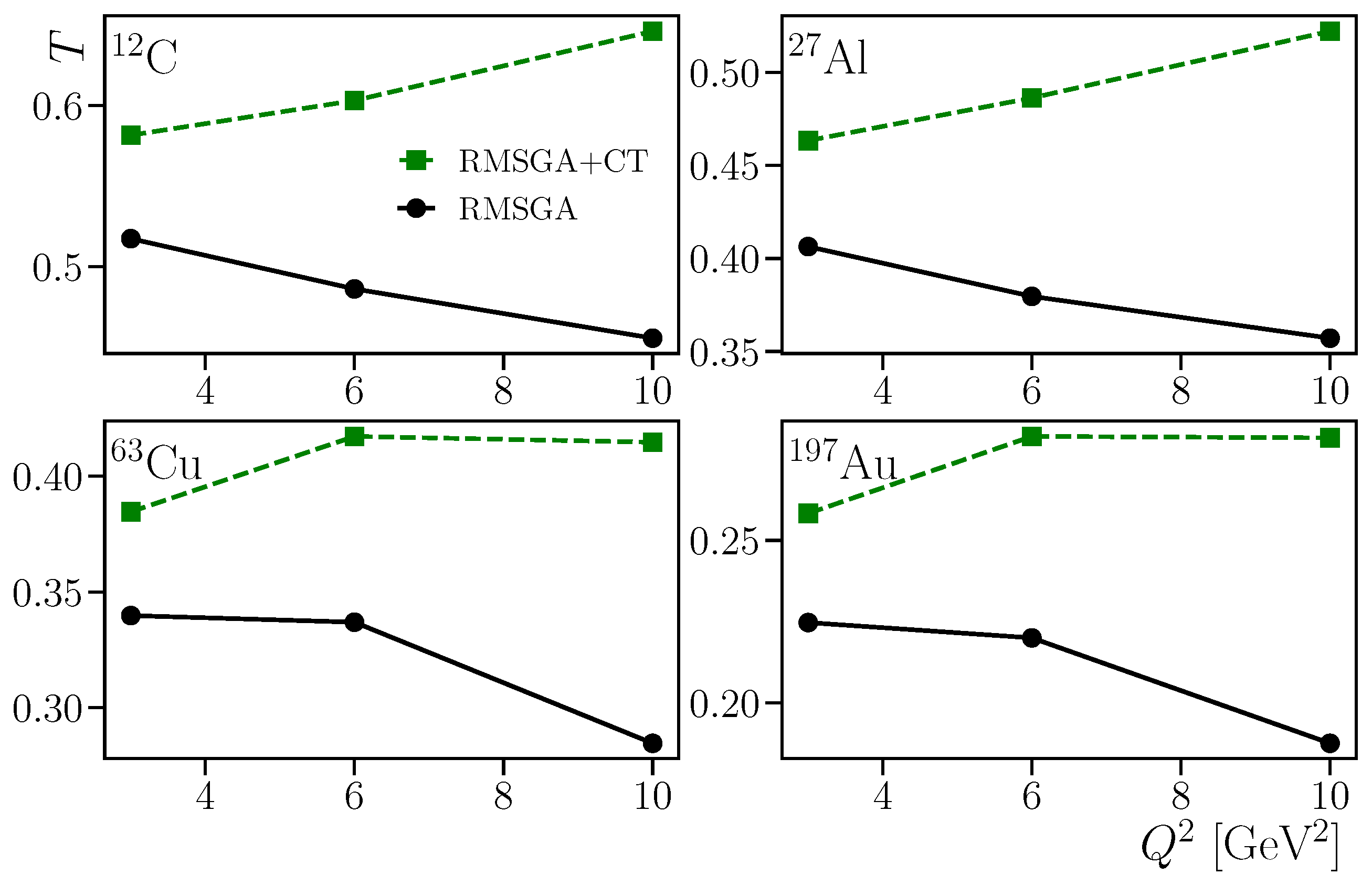
3. A Model Estimate of Nuclear Transparency
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mueller, A.H. Topics in high-energy perturbative QCD including interactions with nuclear matter. In Proceedings of the 17th Rencontres de Moriond on Elementary Particle Physics: I. Electroweak Interactions and Grand Unified Theories, Les Arcs, France, 14–20 March 1982; pp. 13–43. [Google Scholar]
- Brodsky, S.J. Testing quantum chromodynamics. In Proceedings of the XIII International Symposium on Multiparticle Dynamics, Volendam, The Netherlands, 6–11 June 1982; Kittel, W.E., Metzger, W.J., Stergiou, A., Eds.; World Scientific: Singapore, 1982; pp. 963–1002. [Google Scholar]
- Jain, P.; Pire, B.; Ralston, J.P. Quantum color transparency and nuclear filtering. Phys. Rep. 1996, 271, 67–179. [Google Scholar] [CrossRef]
- Diehl, M. Generalized parton distributions. Phys. Rept. 2003, 388, 41–277. [Google Scholar] [CrossRef]
- Kumericki, K.; Liuti, S.; Moutarde, H. GPD phenomenology and DVCS fitting: Entering the high-precision era. Eur. Phys. J. A 2016, 52, 157. [Google Scholar] [CrossRef]
- Clasie, B.; Qian, X.; Arrington, J.; Asaturyan, R.; Benmokhtar, F.; Boeglin, W.; Bosted, P.; Bruell, A.; Christy, M.E.; Chudakov, E.; et al. Measurement of nuclear transparency for the A(e,e′π+) reaction. Phys. Rev. Lett. 2007, 99, 242502. [Google Scholar] [CrossRef] [PubMed]
- El Fassi, L.; Zana, L.; Hafidi, K.; Holtrop, M.; Mustapha, B.; Brooks, W.; Hakobyan, H.; Zheng, X.; Adhikari, K.; Adikaram, D.; et al. Evidence for the onset of color transparency in ρ0 electroproduction off nuclei. Phys. Lett. B 2012, 712, 326–330. [Google Scholar] [CrossRef]
- Defurne, M.; Mazouz, M.; Ahmed, Z.; AlBataineh, H.; Allada, K.; Aniol, K.A.; Bellini, V.; Benali, M.; Boeglin, W.; Bertin, P.; et al. Rosenbluth separation of the π0 electroproduction cross section. Phys. Rev. Lett. 2016, 117, 262001. [Google Scholar] [CrossRef]
- Dlamini, M.; Karki, B.; Ali, S.F.; Lin, P.-J.; Georges, F.; Ko, H.-S.; Israel, N.; Rashad, M.N.H.; Stefanko, A.; Adikaram, D.; et al. Deep exclusive electroproduction of π0 at high Q2 in the quark valence regime. Phys. Rev. Lett. 2021, 127, 152301. [Google Scholar] [CrossRef]
- Kaskulov, M.M.; Mosel, U. Deep exclusive charged π electroproduction above the resonance region. Phys. Rev. C 2010, 81, 045202. [Google Scholar] [CrossRef]
- Ayerbe Gayoso, C.; Bibrzycki, Ł.; Diehl, S.; Heppelmann, S.; Higinbotham, D.W.; Huber, G.M.; Kay, S.J.D.; Klein, S.R.; Laget, J.M.; Li, W.B.; et al. Progress and opportunities in backward angle (u-channel) physics. Eur. Phys. J. A 2021, 57, 342. [Google Scholar] [CrossRef]
- Frankfurt, L.; Pobylitsa, P.; Polyakov, M.V.; Strikman, M. Hard exclusive pseudoscalar meson electroproduction and spin structure of a nucleon. Phys. Rev. D 1999, 60, 014010. [Google Scholar] [CrossRef]
- Pire, B.; Szymanowski, L. Hadron annihilation into two photons and backward VCS in the scaling regime of QCD. Phys. Rev. D 2005, 71, 111501. [Google Scholar] [CrossRef]
- Pire, B.; Szymanowski, L. QCD analysis of N → γ*π in the scaling limit. Phys. Lett. B 2005, 622, 83–92. [Google Scholar] [CrossRef]
- Pire, B.; Semenov-Tian-Shansky, K.; Szymanowski, L. Transition distribution amplitudes and hard exclusive reactions with baryon number transfer. Phys. Rept. 2021, 940, 2185. [Google Scholar] [CrossRef]
- Park, K.; Guidal, M.; Gothe, R.; Pire, B.; Semenov-Tian-Shansky, K.; Laget, J.-M.; Adhikari, K.; Adhikari, S.; Akbar, Z.; Avakian, H.; et al. Hard exclusive pion electroproduction at backward angles with CLAS. Phys. Lett. 2018, B780, 340–345. [Google Scholar] [CrossRef]
- Li, W.B.; Huber, G.M.; Blok, H.P.; Gaskell, D.; Horn, T.; Semenov-Tian-Shansky, K.; Pire, B.; Szymanowski, L.; Laget, J.-M.; Aniol, K.; et al. Unique access to u-channel physics: Exclusive backward-angle omega meson electroproduction. Phys. Rev. Lett. 2019, 123, 182501. [Google Scholar] [CrossRef] [PubMed]
- Diehl, S.; Joo, K.; Kim, A.; Avakian, H.; Kroll, P.; Park, K.; Riser, D.; Semenov-Tian-Shansky, K.; Tezgin, K.; Adhikari, K.P.; et al. Extraction of beam-spin asymmetries from the hard exclusive π+ channel off protons in a wide range of kinematics. Phys. Rev. Lett. 2020, 125, 182001. [Google Scholar] [CrossRef]
- Guidal, M.; Laget, J.M.; Vanderhaeghen, M. Pseudoscalar meson photoproduction at high energies: From the Regge regime to the hard scattering regime. Phys. Lett. B 1997, 400, 6–11. [Google Scholar] [CrossRef][Green Version]
- Laget, J.M. Exclusive meson photo- and electro-production, a aindow on the structure of hadronic matter. Prog. Part. Nucl. Phys. 2020, 111, 103737. [Google Scholar] [CrossRef]
- Laget, J.M. Unitarity constraints on meson electroproduction at backward angles. Phys. Rev. C 2021, 104, 025202. [Google Scholar] [CrossRef]
- Pire, B.; Semenov-Tian-Shansky, K.; Szymanowski, L. QCD description of backward vector meson hard electroproduction. Phys. Rev. D 2015, 91, 094006. [Google Scholar] [CrossRef]
- Chernyak, V.L.; Ogloblin, A.A.; Zhitnitsky, I.R. Calculation of exclusive processes with baryons. Z. Phys. C 1989, 42, 583–593. [Google Scholar] [CrossRef]
- King, I.; Sachrajda, C.T. Nucleon wave functions and QCD sum rules. Nucl. Phys. B 1987, 279, 785–803. [Google Scholar] [CrossRef]
- Li, W.B.; Huber, G.M.; Stevens, J.R.; Semenov-Tian-Shansky, K.; Szymanowski, L.; Pire, B.; Amaryan, M.; Androic, D.; Aniol, K.; Armstrong, D.; et al. Backward-angle exclusive π0 production above the resonance region. arXiv 2020, arXiv:2008.10768. [Google Scholar] [CrossRef]
- Lansberg, J.; Pire, B.; Semenov-Tian-Shansky, K.; Szymanowski, L. A consistent model for π N transition distribution amplitudes and backward pion electroproduction. Phys. Rev. D 2012, 85, 054021. [Google Scholar] [CrossRef]
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.-B.; et al. Electron-Ion Collider: The next QCD frontier—Understanding the glue that binds us all. Eur. Phys. J. 2016, A52, 268. [Google Scholar] [CrossRef]
- Aschenauer, E.; Kiselev, A.; Petti, R.; Ullrich, T.; Horn, T.; Furletova, Y.; Nadel-Turowski, P.; Gonella, P.; Jones, P.; Ilieva, Y.; et al. Electron-Ion Collider Detector Requirements and R&D Handbook; Brookhaven National Laboratory: Upton, NY, USA, 2020; Available online: http://www.eicug.org/web/ (accessed on 1 April 2020).
- Abdul Khalek, R.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science requirements and detector concepts for the Electron-Ion Collider. EIC Yellow Report. arXiv 2021, arXiv:2103.05419. [Google Scholar] [CrossRef]
- Willeke, F.; Beebe-Wang, J. Electron Ion Collider Conceptual Design Report 2021; Brookhaven National Lab. (BNL): Upton, NY, USA; Thomas Jefferson National Accelerator Facility (TJNAF): Newport News, VA, USA, 2021. [Google Scholar] [CrossRef]
- Hauenstein, F.; Jentsch, A.; Pybus, J.R.; Kiral, A.; Baker, M.D.; Furletova, Y.; Hen, O.; Higinbotham, D.W.; Hyde, C.; Morozov, V.; et al. Measuring recoiling nucleons from the nucleus with the Electron Ion Collider. arXiv 2021, arXiv:2109.09509. [Google Scholar] [CrossRef]
- Ryckebusch, J.; Debruyne, D.; Lava, P.; Janssen, S.; Van Overmeire, B.; Van Cauteren, T. Relativistic formulation of Glauber theory for A(e, e-prime p) reactions. Nucl. Phys. A 2003, 728, 226–250. [Google Scholar] [CrossRef][Green Version]
- Martinez, M.C.; Lava, P.; Jachowicz, N.; Ryckebusch, J.; Vantournhout, K.; Udias, J.M. Relativistic models for quasi-elastic neutrino scattering. Phys. Rev. C 2006, 73, 024607. [Google Scholar] [CrossRef]
- Cosyn, W.; Martinez, M.C.; Ryckebusch, J. Color transparency and short-range correlations in exclusive pion photo- and electroproduction from nuclei. Phys. Rev. C 2008, 77, 034602. [Google Scholar] [CrossRef]
- Cosyn, W.; Ryckebusch, J. Nuclear ρ meson transparency in a relativistic Glauber model. Phys. Rev. C 2013, 87, 064608. [Google Scholar] [CrossRef]
- Farrar, G.R.; Liu, H.; Frankfurt, L.L.; Strikman, M.I. Transparency in nuclear quasiexclusive processes with large momentum transfer. Phys. Rev. Lett. 1988, 61, 686–689. [Google Scholar] [CrossRef] [PubMed]
- Frankfurt, L.L.; Greenberg, W.R.; Miller, G.A.; Sargsian, M.M.; Strikman, M.I. Color transparency effects in electron deuteron interactions at intermediate Q2. Z. Phys. A 1995, 352, 97–113. [Google Scholar] [CrossRef]
- Carroll, A.S.; Barton, D.S.; Bunce, G.; Gushue, S.; Makdisi, Y.I.; Heppelmann, S.; Courant, H.; Fang, G.; Heller, K.J.; Marshak, M.L.; et al. Nuclear transparency to large angle pp elastic scattering. Phys. Rev. Lett. 1988, 61, 1698–1701. [Google Scholar] [CrossRef] [PubMed]
- Brodsky, S.J.; de Teramond, G.F. Spin correlations, QCD color transparency and heavy quark thresholds in proton-proton scattering. Phys. Rev. Lett. 1988, 60, 1924–1927. [Google Scholar] [CrossRef] [PubMed]
- Ralston, J.P.; Pire, B. Fluctuating proton size and oscillating nuclear transparency. Phys. Rev. Lett. 1988, 61, 1823–1826. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.S.H.; Miller, G.A. Color transparency and high-energy (p,2p) nuclear reactions. Phys. Rev. C 1992, 45, 1863–1870. [Google Scholar] [CrossRef]
- Bhetuwal, D.; Matter, J.; Szumila-Vance, H.; Kabir, M.L.; Dutta, D.; Ent, R.; Abrams, D.; Ahmed, Z.; Aljawrneh, B.; Alsalmi, S.; et al. Ruling out color transparency in quasielastic 12C(e,e′p) up to Q2 of 14.2 (GeV/c)2. Phys. Rev. Lett. 2021, 126, 082301. [Google Scholar] [CrossRef]
- Jain, P.; Pire, B.; Ralston, J.P. The status and future of color transparency and nuclear filtering. arXiv 2022, arXiv:2203.02579. [Google Scholar] [CrossRef]
- Pire, B.; Semenov-Tian-Shansky, K.M.; Shaikhutdinova, A.A.; Szymanowski, L. Backward timelike Compton scattering to decipher the photon content of the nucleon. arXiv 2022, arXiv:2201.12853. [Google Scholar] [CrossRef]
- Lansberg, J.; Pire, B.; Semenov-Tian-Shansky, K.; Szymanowski, L. Accessing baryon to meson transition distribution amplitudes in meson production in association with a high invariant mass lepton pair at GSI-FAIR with ANDA. Phys. Rev. D 2012, 86, 114033, Erratum in Phys. Rev. D 2013, 87, 059902. [Google Scholar] [CrossRef]
- Pire, B.; Semenov-Tian-Shansky, K.; Szymanowski, L. Backward charmonium production in πN collisions. Phys. Rev. D 2017, 95, 034021. [Google Scholar] [CrossRef]
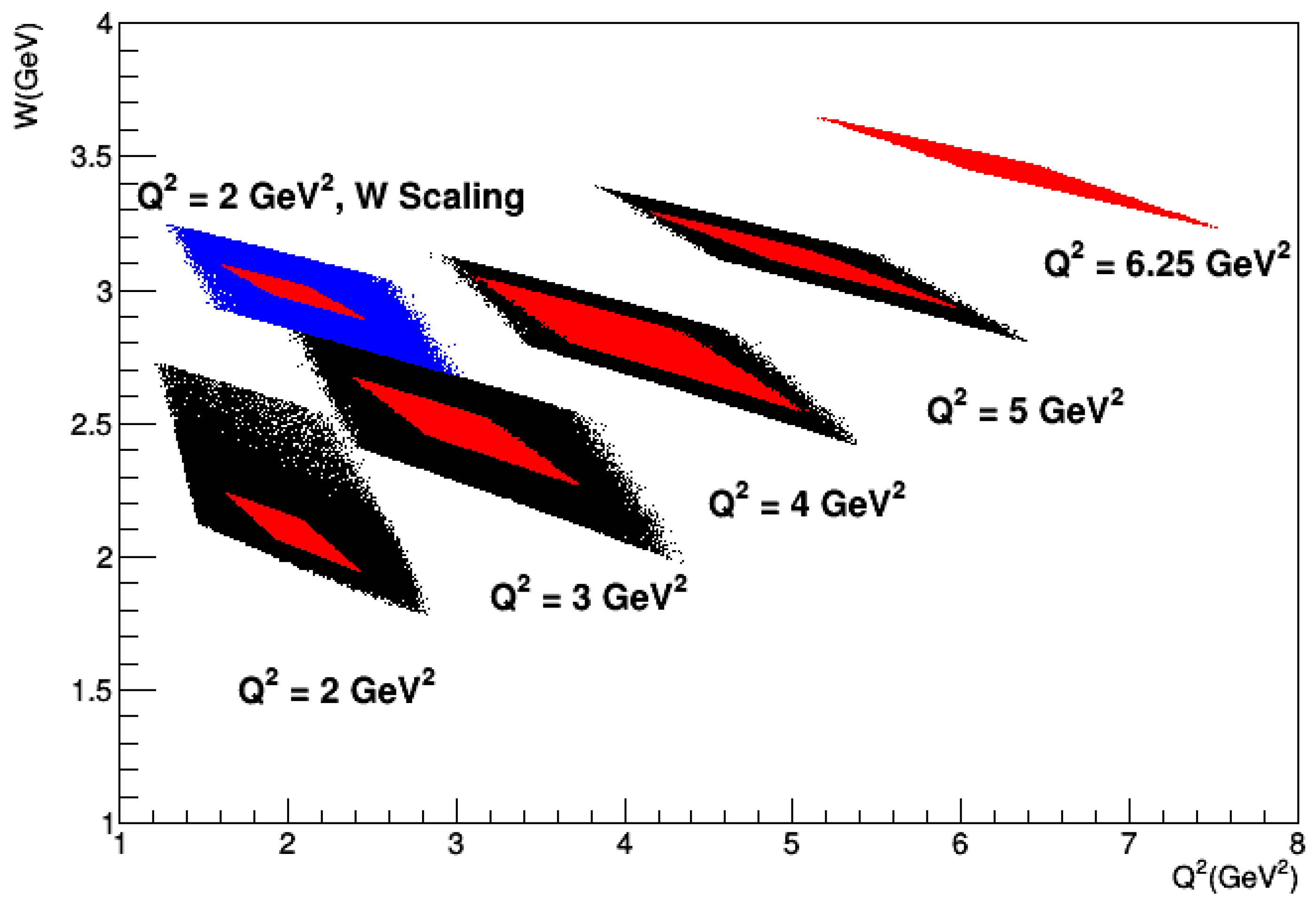

| Kinematics for GeV, GeV | |||||
|---|---|---|---|---|---|
| (GeV) | (GeV/c , deg) | (GeV/c, deg) | (GeV/c, deg) | (GeV) | (GeV) |
| 3 | 7.3, 11.3 | 3.9–3.6, 23–30 | 0.2–0.5, 202–95 | −5.7 to −5.2 | +0.5 to −0.1 |
| 6 | 5.7, 18.1 | 5.6–5.2, 19–24 | 0.1–0.5, 196–79 | −8.8 to −8.2 | +0.6 to 0.0 |
| 10 | 3.6, 29.7 | 7.7–7.3, 13–16 | 0.0–0.5, 193–61 | −12.8 to −12.1 | +0.6 to −0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, G.M.; Li, W.B.; Cosyn, W.; Pire, B. u-Channel Color Transparency Observables. Physics 2022, 4, 451-461. https://doi.org/10.3390/physics4020030
Huber GM, Li WB, Cosyn W, Pire B. u-Channel Color Transparency Observables. Physics. 2022; 4(2):451-461. https://doi.org/10.3390/physics4020030
Chicago/Turabian StyleHuber, Garth M., Wenliang B. Li, Wim Cosyn, and Bernard Pire. 2022. "u-Channel Color Transparency Observables" Physics 4, no. 2: 451-461. https://doi.org/10.3390/physics4020030
APA StyleHuber, G. M., Li, W. B., Cosyn, W., & Pire, B. (2022). u-Channel Color Transparency Observables. Physics, 4(2), 451-461. https://doi.org/10.3390/physics4020030





