1. Introduction
As one can understand, it is not an easy task to talk about breaking the light speed barrier, as it can raise various false rumors, especially after the sad story of the OPERA experiment [
1]. However, after having published a paper on the subject [
2], we decided to try to present it here in a rather entertaining manner.
2. Experimental Basis of Special Relativity
Experimental confirmations of special relativity are ubiquitous [
3]. One can say that special relativity is the most precisely tested theory. Let us provide some numbers to present the level of precision involved. Usually the breakdown of special relativity (Lorentz invariance) is characterized by introduction of Lorentz non-invariant terms in the interaction Lagrangian
L. One such term is
. As the separation of electromagnetic field into an electric
and a magnetic
fields depends on the observer, one should specify in which reference frame this square of the magnetic field is given. Usually the preferred frame is identified relative to the “rest frame of the Universe”,
S, in which cosmic microwave background is isotropic. In this frame
S, light velocity in vacuum, denoted by
c, will differ from the maximum attainable speed of a material body, taken to be unity, due to the additional term in the interaction Lagrangian. In another frame (for example, on Earth), which moves with respect to the frame
S with velocity
(for the solar system,
in dimensionfull units [
4]), the speed of light,
c, depends on the angle between its propagation direction and
. This light propagation anisotropy in the laboratory frame should lead to observable effects that are proportional to
if Lorentz invariance is violated [
5]. Nevertheless, no such anisotropy was found, and these null results provide the limit of applicability for special relativity. The modern limit on the velocity difference is as small as
[
5].
In addition to the square of the magnetic field, the only other renormalizable term that affects the propagation of light is
[
5], where
is a fixed 4-vector with a dimension of reciprocal length, the Greek letters take the values 0 (time) and 1, 2, and 3 (space coordinates), and
is a vector potential. This term in Lagrangian violates not only Lorentz symmetry but also charge (
C), parity (
P), and time (
T) reversal symmetry (
). Astronomical data and particle physics experiments severely constrain the magnitude of components of
. Namely, the constraint on the dimensionless parameter that might characterize
violation in particle physics is
(with
m the electron mass) [
5].
On the webpage [
3] one can find not only numerous experiments that confirm special relativity, but also several ones that contradict it. However, all experiments that refute special relativity have been wildly criticized, and none of these experiments came anywhere close to making a convincing statement [
3]. So, one can safely say that special relativity was thoroughly tested within the domain of its applicability and experimental evidence completely supports its validity.
3. Golden Shine of the Theory of Relativity
One could think that relativity belongs to the academic high-brow circles and has no relation to everyday life, but it would be not more than an unfortunate fallacy. For instance, every time one enjoys glitter of gold, one meets special relativity!
The fact is that for heavy atoms, relativistic corrections are significant and even necessary to explain chemical and physical behavior of these atoms [
6,
7]. The color of metals mainly results from the absorption of light when a
d electron “jumps” to an
s orbital. For silver, the absorption that corresponds to the
transition requires energy of 3.7 eV which belongs to the ultraviolet range. As a result, visible light is not absorbed by silver and all visible frequencies are reflected equally. This circumstance means that silver has no color of its own: it is silvery. If one was to do corresponding calculations for gold without including relativistic effects, one would have predicted the same result: that gold should be silvery. However, due to relativistic effects the
s and
p atomic orbitals, in gold are more “contracted” compared to non-relativistic predictions (the so-called “relativistic stabilization”), while
d and
f orbitals are on the contrary destabilized and become more diffuse. Consequently, for gold the gap between the
and
orbitals decreases and corresponds to the energy of 2.4 eV which leads to absorption of blue light and reflection of green and red. When combined, this spectrum results in the yellowish golden hue [
7,
8].
One also meets relativity, both special and general, every time GPS (Global Positioning System) is used for navigation, because without these theories GPS would not function properly [
9]. Finally, even in rather old cars, special relativity is under use! Indeed, calculations indicate that 10 out of 12 volts in a lead-acid car battery come from relativistic effects [
10].
4. Why Are We Interested in the Light Speed Barrier?
As one can see, relativity reigns even in everyday life. Why then are we interested in questioning light speed barrier? After all, we have experimentally tested whether it is possible to overcome it. One of the authors gave her best try in a leisure holiday experiment, but the results were overwhelmingly convincing: it is impossible to overcome light speed barrier on a horseback. One can see that the horse was somewhat embarrassed by this negative result (
Figure 1).
Quoting D.I. Blokhintsev [
11]: “The principal reason for concentrating our attention specifically on the theory of relativity is, of course, not any sympathy with ignorant attacks on this theory, but the circumstance that its basic postulates touch upon the deepest foundations of the physics—geometry of space-time”.
There are psychological reasons too. A human being cannot tolerate any limitations due to the rebellious nature of human mind. A Russian writer, Vasily Shukshin, in his short story
Stubborn fellow describes this peculiarity of human mind very eloquently [
12]: “Monya read the book which explained that a perpetuum mobile was impossible and that many had failed in an attempt to invent such a machine. He carefully studied the drawings of perpetual motion machines which had been proposed over the centuries. Then he started reflecting upon this problem, not troubling his head over friction or the laws of mechanics. He had his heart set on inventing a perpetuum mobile of a kind which had never been imagined before. For some reason, he refused to believe that it was impossible.”
For the very same reasons, we also refused to believe that the speed of light barrier was really impossible to overcome. And we set our hearts on inventing a way which had never been imagined before, a way into a dreamland without the speed limit.
5. Why the Light Speed Barrier?
The argument for the light speed barrier was given by Albert Einstein (
Figure 2) himself in his seminal first paper on special relativity [
13].
This argument is transparent enough: relativistic expression for the kinetic energy is
with
m being the mass and
V being the velocity of the object.
Then, following A. Einstein: “Thus, when
,
W becomes infinite. Velocities greater than that of light have, as in our previous results, no possibility of existence” [
13].
6. For Light Spots, There Is No Light Speed Barrier
Not every kind of superluminal motion is excluded by Einstein’s argument. One example of superluminal motion are light spots produced on a remote screen by a rotating source of light or particles. Such light spots are in many ways analogous to the subluminal radiation sources and in particular, they can generate Cerenkov radiation in “vacuum” [
15]. Aspects of the superluminal motion were considered previously by Heaviside (1888), Sommerfeld (1904), Wigner (1939), Tangherlini (1958) and Tanaka (1960), to name a few [
16].
Major difference between the superluminal and subluminal radiation sources is that according to the Einstein’s argument, the first ones cannot be represented by individual particles, but by patterns formed by aggregates of such particles in a coordinated motion. An interesting example of practical application of superluminal motion is a Gyrocon—a high-power microwave generator in which radiation is produced by conically moving relativistic beam of electrons [
16,
17]. The initial idea of a Gyrocon was suggested long ago independently by M.S. Neyman (1940), P.V. Hartley (1945) and J. W. McRae (1946) [
18]. However, the first realizations [
19,
20] were imperfect and yielded very low power output. It was G.I. Budker who realized the possibilities offered by relativistic energies of the electron beam in such a device. In a Gyrocon built by the Budker group, a harmonic used for the generation had phase velocity which was 1.84 times larger than the light velocity. Output power of the Gyrocon in the continuous mode reached 5 MW and produced radiation in the wavelength range from 30 cm to 1.1 m with the efficiency of the beam energy conversion into radiation of about 80% [
18].
Superluminal motion of this type has long found industrial applications. However, this is not the superluminal motion that interests us here.
7. Does Somebody Live to the North of the Himalayas?
In fact, Einstein’s argument given above is misleading. Following E.C.G. Sudarshan [
21]: “As analogy we may consider demographers studying the population patterns of the Indian Subcontinent. They would find that there are a lot of people in India but as you approached the Himalayas there are fewer and fewer people. Climbing the giddying heights is a difficult task and it is well-nigh impossible to climb it let alone live there. Suppose a demographer calmly asserts that there are no people north of the Himalayas since none could climb over the mountain ranges. That would be an absurd conclusion. People of Central Asia are born there and live there: they did not have to be born in India and cross the mountain ranges.”
8. Tachyons
In 1962 Sudarshan, Bilaniuk and Deshpande introduced a notion of faster-than-light particles that live “to the north of the Himalayas” in the sense that they always move with the velocity greater than the velocity of light [
22]. Later, such particles were named tachyons by Gerald Feinberg [
23].
One may wonder why it took so much time for the tachyon hypothesis to emerge. The answer lies partly in the sociopsychology of science. “In general, mathematicians tend to behave like “fermions” i.e., avoid working in areas which are too trendy whereas physicists behave a lot more like “bosons” which coalesce in large packs and are often “overselling” their doings, an attitude which mathematicians despise” [
24]. What is particularly worrisome is that “this “bosonisation” of crowds of theoretical physicists does not make them tolerant to new ideas that don’t fit with the common hopes of the “believers”” [
25].
In reality, the tachyon hypothesis can be traced back much earlier, to works by Lev Yakovlevich Shtrum in 1923 [
26,
27]. Shtrum was a head of Theoretical Physics Department at Kiev University from 1932 to 1936. Then, he was arrested and executed. His love for philosophy played a tragic role in his story, as it put him in touch with the philosopher Semyon Semkovsky, Lev Trotsky’s cousin. Shortly after Semkovsky was arrested as Trotsky’s relative, Shtrum was arrested too. He was tortured, forced to sign self-incriminations, and executed with a group of other Ukrainian scientists. The Stalinist government tried to annihilate him spiritually as well: his works were removed from Soviet libraries and destroyed. As a result, the tachyon hypothesis fell into oblivion for many years.
Risking his life, his friend and contemporary Vasily Grossman resurrected Shtrum’s name in a novel that later became the first part of his renowned novel
Life and Fate. The novel was first published in 1952 when Stalin was still alive. Fortunately, nobody among censors had suspected that the main hero of the novel, Victor Shtrum, had a real prototype in the face of the executed physicist. Nevertheless, on the grounds of official antisemitism of that time, censors demanded to remove the character from the novel. Grossman was steadfast with his answer: “I agree with everything but Shtrum” [
28].
Interestingly, Nathan Rosen, one of Einstein’s co-authors, replaced Shtrum as head of Theoretical Physics Department for two years. Rosen did not speak Russian and his lectures for students were translated from English. While working in the USSR, Rosen nevertheless learned to read a little Russian and fortunately, understood that he needed to flee the country when the events of 1937 began.
When an unemployed American scientist Nathan Rosen found work in the USSR, he was most apparently unaware of the tragic fate of his predecessor. In fact, Rosen was a very modest and positive person, as the following memories witness. A. Gordon recalls: [
29]: “I walked along the corridor seeing everywhere signs “Professor…”. At the very end of the corridor I noticed a door with a small copper plate with a name without the professor title. The office door opened and out of it came an old thin man politely greeting me. I saw him for the first time. Obviously, he was not a professor, maybe he was a manager, an engineer, or a technician. Professors, if they greeted you, they greeted conscious of their high position in the world of science, so that you feel their significance and importance. The owner of this office was too simple and friendly to be a professor. When he retired from the office, I approached the door to read the name on a small nameplate. It was written in a foreign language: N. Rosen.”
9. Tolman’s Antitelephone Paradox
The interval between emission and absorption of a superluminal tachyon is spacelike and this circumstance creates a real problem for the tachyon hypothesis: for events separated by a spacelike interval, their relative time order depends on choice of a reference frame, and in some inertial reference frames the tachyon will be absorbed before it is emitted. In 1917, Richard Tolman (shown with Einstein in
Figure 3) in his book
The Theory of Relativity of Motion showed that in this case one faces a paradox of causality, today called Tolman antitelephone paradox. Figuratively speaking, one can send a message into one’s own past using tachyons.
In fact, Tolman’s antitelephone paradox has already been invented in 1907 by Einstein himself [
31], who looks was aware of the weakness in the infinite kinetic energy argument. He concludes [
31]: “This result signifies that we would have to consider as possible a transfer mechanism whose use would produce an effect which precedes the cause (accompanied by an act of will, for example). Even though, in my opinion, this result does not contain a contradiction from a purely logical point of view, it conflicts so absolutely with the character of all our experience, that the impossibility of the assumption
is sufficiently proven by this result”.
The issue, raised by Tolman’s antitelephone paradox is, however, already present in quantum field theory that unifies the fundamental ideas of special relativity and quantum mechanics and is at the base of our modern theories of elementary particle physics.
10. Can Quantum Theory and Special Relativity Peacefully Coexist?
The second and most profound revolution in physics after special relativity was creation of quantum mechanics (
Figure 4 shows Bohr and Einstein discussing the point). Both theories are very successful. However, they are based on entirely different ideas, which are not easy to reconcile with each other.
Following F. Wilczek [
33]: “Imagine a particle moving on average at nearly the speed of light, but with an uncertainty in position, as required by quantum theory. Evidently, there will be some probability for observing this particle to move a little faster than average, and therefore, faster than light, which special relativity will not permit.”
11. Quantum Theory and the Problem of Superluminal Motion
In quantum field theory, the amplitude for a particle to propagate from a space-time point
x to a point
y is Lorentz invariant and is given by the Wightman propagator. When the difference
is purely in the spatial direction, and when the distance
r is much smaller than the particle’s reduced Compton wavelength
(natural units
are assumed, where
ћ is the reduced Planck constant), the Wightman function has the following asymptotics,
, and is not zero, despite zero time-interval between events at coordinates
x and
y. This means that the particle has a non-zero probability to propagate with infinite velocity in this frame. As one can see, it is not a trivial task to reconcile quantum mechanics with its notorious non-localities with special relativity. Quoting J. Butterfield [
34]: “Relativistic causality—formulate it as you like!—is a subtle matter in relativistic quantum theories.” Let us mention some other examples of the alleged superluminal effects which demonstrate a subtlety of coexistence of quantum mechanics with special relativity.
Hegerfeldt’s theorem states that the wave function of a quantum system, if initially localized in a finite region, immediately develops an infinite tail spreading over all space. As a result, transition probabilities in widely separated systems may instantaneously become nonzero [
35]. Maybe, then, it is not surprising that entanglement and mutual correlations can also be generated at space-like separated points [
36]. All of these are, of course, in spirit of old Einstein, Podolsky and Rosen paradox [
37].
However, it becomes even worse, as quantum mechanics predict that the transmission time across a potential barrier becomes independent of barrier thickness for very thick barriers, the so-called “Hartman effect” [
38]. Let us also mention the Scharnhorst and Drummond–Hathrell effects. The Scharnhorst effect predicts that light signals travel a bit faster than
c in the Casimir vacuum between two closely spaced conducting plates [
39]. In the Drummond–Hathrell effect, photons may propagate with superluminal velocity in certain gravitational backgrounds [
40,
41]. It is believed, however, that neither of these strange effects allows information to be transmitted faster than the light velocity, and thus, they are compatible with special relativity, although in a very subtle way [
42,
43].
12. Frustrated Total Internal Reflection
Frustrated total internal reflection [
44] is an optical analog of the quantum mechanical tunneling. It is known that, if an angle of incidence of a light beam at the boundary that separates optically denser medium, in which the light beam propagates, and the one of lower density, exceeds some critical angle, then it is totally reflected at this boundary. However, even in this case the electric field penetrates the adjacent medium, with the penetration depth of order of a wavelength, in a form of an evanescent wave. Evanescent modes are classical analogs of virtual photons [
45]. If a third optically dense medium is added at around a wavelength from the first medium, then because of the evanescent wave, the light beam penetrates to this medium much like the quantum tunneling of particles through potential barriers.
The Hartman effect was experimentally confirmed in frustrated total internal reflection [
46]. Günter Nimtz (
Figure 5) even states that he and his collaborators managed to transfer modulated Mozart’s 40th symphony at a superluminal speed of 4.7
c using this phenomenon for microwaves [
47]. Nevertheless, it seems that he is at error [
48,
49]. If you define the signal velocity as the velocity of the pulse maxima then indeed, an evanescent barrier can be crossed superluminally. However, even these superluminal wave packets still obey causality and the peaks of pulses in front and behind the evanescent barrier are not causally related [
50].
13. There Are No Paradoxes in Physics
“Of course, in physics there are never any real paradoxes because there is only one correct answer; at least we believe that nature will act in only one way (and that is the right way, naturally). So in physics a paradox is only a confusion in our own understanding,”, quoting R. Feynman (
Figure 6) [
52].
14. The Idea of Antiparticles
The above-given examples illustrate that there is some tension between quantum theory and special relativity in what concerns superluminality. Quoting F. Wiczek [
33]: “The only known way to resolve this tension involves introducing the idea of antiparticles.”
Quantum field theory offers a miraculously clever solution to the superluminal propagation dilemma [
54]. It is true that, for a particle propagating superluminally between space-time points separated by a spacelike interval, there is always a reference frame in which the particle propagates backwards in time, so that its absorption preceding its emission is in apparent violation of causality. Nevertheless, the particle’s energy in this frame is negative, and a negative energy particle propagating backward in time can be interpreted as a positive energy antiparticle propagating forward in time. This Stueckelberg-Feynman interpretation of antiparticles as negative energy particles moving backward in time provides quantum field theory’s resolution of superluminal propagation dilemma. Causality demands that any measurement performed at a space-time point
x cannot influence an outcome of another measurement at space-time point
y if the points are separated by a spacelike interval. Mathematically this means that two local observables commute if separated by a spacelike interval. The existence of antiparticles is crucial for a cancellation of all acausal terms in commutators of two local observables at spacelike separation. Therefore, quantum field theory does not allow information to be transmitted faster than the speed of light but at the expense of introducing antiparticles.
15. Stueckelberg—An Unconventional Hero
There was one central figure in the development of the idea of antiparticles as negative energy particles moving backwards in time. His full name was Johann Melchior Ernst Karl Gerlach Stueckelberg, Freiherr von Breidenbach zu Breidenstein und Melsbach.
Stueckelberg (
Figure 7) was from an aristocratic Swiss family. He made some deep and fundamental discoveries but remained a widely under-appreciated genius in the history of science [
55]. Maybe this is explained by the fact that apart from his relationship with Wolfgang Pauli, Stueckelberg had little contact with the scientific community partly due to his mental illness [
56]. While being in Princeton in 1932, Stueckelberg suffered from the first attack of bipolar disorder. Later during his life, the recurrent psychiatric conditions resulted in countless stays in mental hospitals and seriously handicapped Stueckelberg’s scientific career [
56].
Stueckelberg was not only the first person who introduced the aforementioned interpretation of antiparticles and illustrated the concept with graphs of space-time trajectories which today are called “Feynman diagrams”, he was also years ahead in the development of quantum electrodynamics (QED). Unfortunately, he did not promote his ideas, and published his articles mostly in French in a Swiss journal
Helevetica Physics Acta with a small international audience [
58].
After receiving the Nobel Prize for his work on QED, Richard Feynman gave a lecture in Geneva at which Stueckelberg was present. After the lecture, Feynman surrounded by his admirers noticed that Stueckelberg quietly left the lecture hall accompanied by his dog. Feynman was moved and remarked [
59,
60]: “He did the work and walks alone towards the sunset, and here I am, covered in all the glory, which rightfully should be his.”
Stueckelberg’s dog, Carlo III, was as legendary, as his master. Stueckelberg attended seminars and lectures always accompanied by his dog. Carlo III had even been granted right of access to CERN by the CERN Director General [
55]. At seminars, Carlo III had a reputation of a great expert in theoretical physics. Usually the dog was well behaved watching the lecture while Stueckelberg napped. Occasionally. Carlo III barked awaking his master who then always spotted a mistake on the blackboard [
55,
58]. The only reasonable explanation of how the dog spotted the errors (suggested by Valentine Telegdi [
55]) is that Carlo III was not an expert in theoretical physics but was a great expert in his master’s mood and he was reacting to his master unconscious uneasiness.
16. Reinterpretation Principle
Let us return to tachyons. One may think that the reinterpretation principle solves Tolman antitelephone and similar paradoxes [
61,
62].
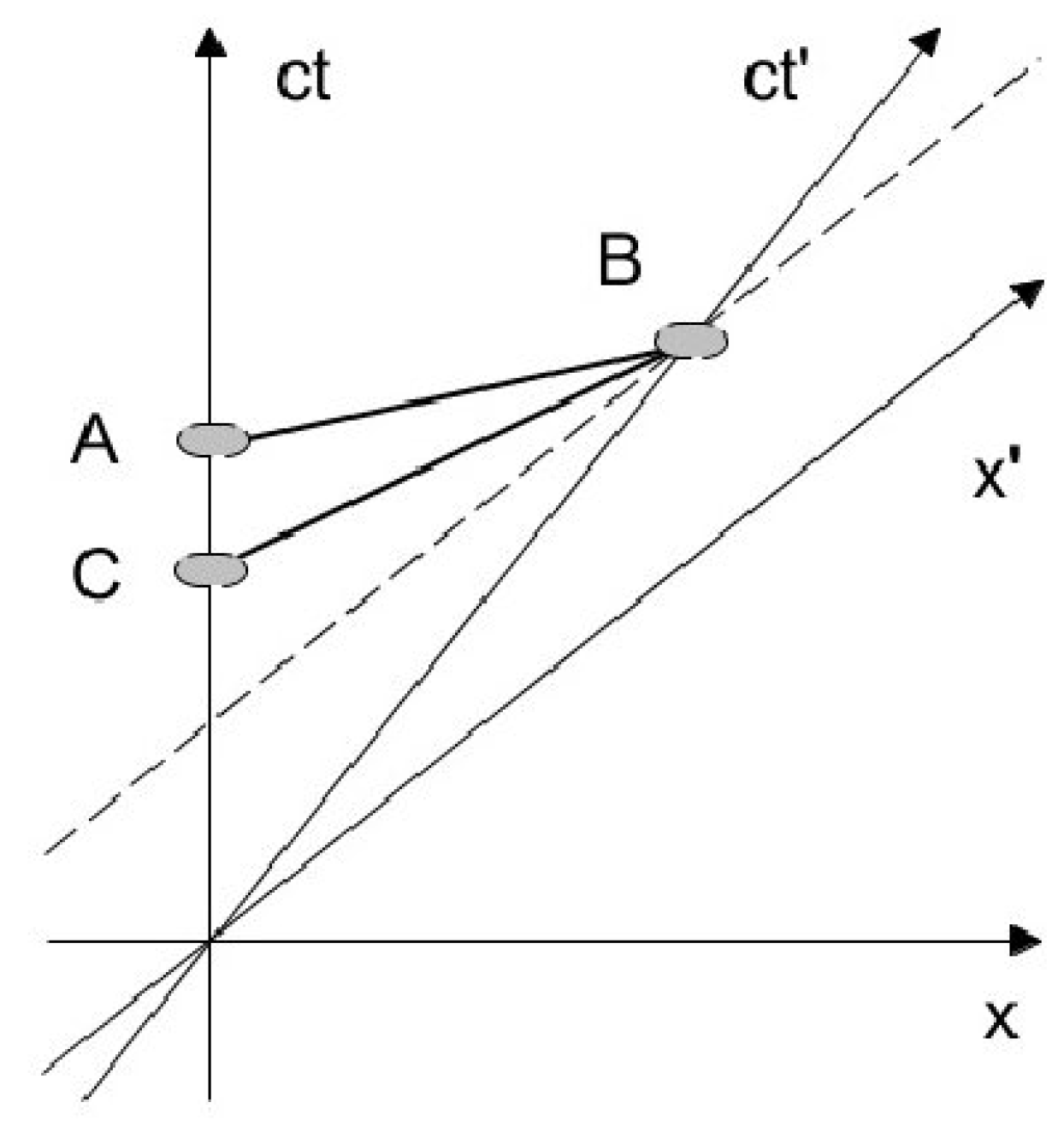
Let two observers
and
move with constant subluminal relative velocities,
t and
axes being the corresponding world-lines, see
Figure 8. Observer
sends a tachyon that follows
world-line (moves forward in time with respect to
) and is immediately reflected upon arrival at point
B. World-line
lies above the dashed line (the line of simultaneity for the event
B) which is parallel to the coordinate axis
. Therefore, with respect to
, the reflected tachyon moves forward in time. However, with respect to
, it moves backwards in time and arrives at point
C earlier than it was emitted.
The resolution of this paradox according to the reinterpretation principle is the following. It can be shown that while moving from B to C, the tachyon has a negative energy. Therefore, it can be reinterpreted as an antitachyon with a positive energy moving forward in time. So, from the point of view of the observer A the sequence of events looks like this: an antitachyon is emitted at point C and then a tachyon at point A. Both have positive energies and move forward in time. Then they annihilate at point B. There is thus no paradox in this sequence of events.
Not everyone agrees with such a solution to the Tolman’s antitelephone paradox (see, e.g., [
63]). Quoting Ref. [
64]: “Causality objections against superluminal particles are by far the most subtle, and much room for reflection remains in this regard.”
17. Gell-Mann’s Totalitarian Principle
Leaving aside subtleties related to the causality, one can invoke Gell-Mann’s totalitarian principle “everything not forbidden is compulsory” and ask: If tachyons are not forbidden by special relativity, why are they not observed? (In fact, the totalitarian principle first appeared in T.H. White’s Arthurian fantasy novel
The Once and Future King [
65]). Up to here, superluminality was emphasized a defining property of tachyons. This is no longer justified in quantum theory. Classical concept of propagation velocity is not well-defined for evanescent modes or virtual photons, as nothing well defined and localized propagates through the tunneling barrier in these cases.
The notion of particles, borrowed from the classical physics, is also not quite adequate in the quantum world. As a result, one can still speak about wave-particle duality, a concept as dubious as the devil’s pitchfork: a classic impossible figure (
Figure 9) [
66].
Left and right parts of this figure may be interpreted as two-dimensional projections of three-dimensional bodies, much like a part of properties of a quantum particle may be interpreted as particle-like while another part as wave-like. Then one tries to unify these interpretations through the concept of wave-particle duality, pretending that the figure above is a true three-dimensional figure. However, such interpretation is impossible, as the figure is, in reality, in two dimensions [
67].
So, it is better to call a quantum particle a quanton, which is neither a particle nor a waive, but a completely new object unknown to classical physics [
68]. The old tradition of describing the quantum world in classical concepts creates, of course, a serious logical tension when using two contradictory ideas for describing the same object, even if the so-called complementarity principle is evoked to soften conceptual conflicts. “It must be realized today that this view of the quantum world, adapted as it was to its first explorations, is totally outdated. In the past fifty years, we have accumulated sufficient familiarity, theoretical as well as experimental, with the quantum world to no longer look at it through classical glasses,” quoting J.-M. Lévy-Leblond [
68].
18. Classification of Quantons
The best-known way to classify free quantons propagating in Minkowski spacetime is through their symmetry properties, assuming that elementary quantons correspond to the unitary irreducible representations of the Poincaré group (inhomogeneous Lorentz group) found by Wigner. Depending on the four-momentum
p of a quanton, whose square is Lorentz invariant, and on the sign of its energy, one has six different classes of such representations [
69]:
- 1.
, ,
- 2.
, ,
- 3.
, ,
- 4.
, ,
- 5.
,
- 6.
.
Representations with negative energies (classes 2 and 4), as was already mentioned, should be reinterpreted as corresponding to antiparticles with positive energies belonging to classes 1 and 3. Class 1 corresponds to bradyons, massive quantons, which always move with velocities less than the speed of light in vacuum if described from classical perspective. Class 3 contains representations corresponding to luxons, quantons with zero mass like photons, which always move with maximum velocity c.
Representations in each group are further classified by considering the unitary irreducible representations of the so-called little group, a subgroup of the Poincaré group that leaves invariant a particular four-momentum characteristic for a given class. For class 1, a rest-frame momentum
can be chosen, and the little group is the three-dimensional rotation group SO(3). This group has finite dimensional unitary representations, characterized by one real number—the spin of the quanton. For class 3,
can be chosen, and the little group is the Euclidean group ISO(2) or transformations of the Euclidean plane which preserve the distance between points. ISO(2) is a semi-direct product of SO(2) and T(2), a group of translations in the plane. Correspondingly, the unitary irreducible representations, corresponding to the massless quantons, are of two types. If T(2) is represented by trivial representation, then unitary irreducible representations correspond to the representations of the two-dimensional rotation group SO(2) and are finite dimensional and characterized by the helicity of the quanton. If T(2) is represented by non-trivial representation, then the corresponding unitary irreducible representations of the Poincaré group are infinite dimensional and are characterized by a continuous parameter with the dimension of a mass even if they describe massless quantons. The second exotic property of such representations is that the corresponding quantons have infinite degrees of freedom (these representations contain all helicities from
to
∞ and are called infinite spin representations). Wigner has argued that the heat capacity of a gas of such quantons would be also infinite and rejected such representations as unphysical. For the modern perspective on the infinite spin representations, see, e.g., [
70].
Class 5 are representations of the symmetries of the vacuum. In this case, the little group is the entire Lorentz group, and all unitary representations are infinitely dimensional. These represantations are organized into the main and supplementary series. Some of them can correspond to pomerons, “without a doubt, one of the weirdest concepts of something particle-like that one could imagine,” quoting J. Swain [
69].
Finally, class 6 corresponds to tachyons. The little group is SO(2,1), the Lorentz group in a spacetime with one time-like and two spacelike dimensions. It is non-compact and has only infinite dimensional unitary representations except for a one-dimensional trivial representation. Thus, tachyons are quite different from the usual bradyons and luxons: either tachyon is a scalar particle with no spin, or it has an infinite number of polarization states. However, it was argued that, for tachyons, it is justified to resort to nonunitary representations, which are finite dimensional. This way integer and half-integer spins can be associated to tachyons too [
61] (although the finite-dimensional representations of the little group for tachyons are not unitary, a fully covariant theory for tachyons with any spin can be constructed with a helicity dependent invariant integral which cannot have the usual interpretation of probability or charge [
71]).
19. Tachyons and Instability
In quantum field theory, quantons are associated to relativistic fields [
72,
73,
74]. For the field
, the squared mass of the corresponding quanton equals the second derivative of the self-interaction potential
of this field at the origin
. If the squared mass is negative as for tachyons, the origin cannot be the minimum of the potential. In other words, the system with a tachyonic degree of freedom is unstable at
tachyonic vacuum state. As a result, the tachyonic field
will roll down towards the true vacuum, acquiring a non-zero vacuum expectation value (tachyon condensation).
For the true vacuum, the squared mass (the second derivative of the self-interaction potential) is positive, and small excitations of the field
around the true vacuum will appear as bradyons, not tachyons (for a pedagogical discussion of mass generation through spontaneous symmetry breaking, see [
75]).
If one considers spacelike four-momentum as a defining property of tachyons, then it becomes clear that tachyons play an important role in modern physics. The most notorious example of tachyon condensation is Higgs mechanism in the Standard Model of elementary particles physics. One can say that the Higgs boson is the most famous would-be tachyon. Tachyon condensation is important in string theory too [
76] and can play a role in early cosmology [
77].
Finally, every quanton can become tachyonic in a virtual state (the four-momentum of a virtual quanton can be spacelike).
20. Tachyons and the Light Speed Barrier
Initially, we were interested in tachyons as superluminal objects, but a disappointment awaits us here: tachyons cannot support the true superluminal propagation, even in a rolling state towards true vacuum. The argument goes as follows [
78,
79,
80].
Propagation of a free scalar tachyon in Minkowski spacetime is described by the usual wave equation for spin-zero particles, the Klein–Gordon equation, but with imaginary mass. The fundamental plane-wave solutions of the Klein–Gordon equation have the form , where E is the energy, for all relativistic quantons including tachyons for which with imaginary mass m. Because of the unusual negative sign of the squared mass term, the Klein-Gordon equation will have two kinds of solutions. For the first kind, and E is real. In this case, one has usual plane waves. For the second kind, , and then E becomes imaginary. The corresponding wave amplifies exponentially as time passes.
If the second type solutions are allowed, then a localized unstable wave-packet can be built. However, the Klein–Gordon equation, irrespective of the sign of the mass term, is a hyperbolic partial differential equation. Hyperbolic partial differential equations do not allow localized disturbances to spread with speeds faster than the maximum speed which is here the speed of light. If the second-type solutions are excluded, then it will be no longer possible to build localized wave-packets but only non-local disturbances of the tachyonic field that cannot be used to send information from one place to another faster than the speed of light.
Impossibility to construct a stable localized free-tachyon wave-packet implies that one cannot transmit information by tachyon field since the information would be destroyed by the inherent instability of these fields [
79]. Quoting G.W. Gibbons [
77]: “Contrary to popular prejudice: the tachyon is not a tachyon!”
21. The Frenkel–Kontorova Model
It is time to change the strategy in searching for superluminal objects. From what was said so far, it should be clear that there is virtually no chance if the Lorentz symmetry is indeed a fundamental property of Nature. On the other hand, one can consider situations where Lorentz symmetry emerges at low-energy limit but is not a fundamental property from the very beginning. The Frenkel–Kontorova model of crystal dislocations provides a good starting point [
78]. The Frenkel–Kontorova model describes a one-dimensional chain of atoms with harmonic interatomic interactions subjected to an external sinusoidal substrate potential.
The remarkable fact about the Frenkel–Kontorova model is that in the long wavelength approximation, when the lengths characterizing the chain discreteness are much smaller than the wavelength of chain excitation, its dynamics are described by the so-called sine-Gordon equation,
where
is the dimensionless field of displacements of the individual atoms from their equilibrium positions (see [
2] for details).
If the external potential is switched off, and the equation describes massless phonons traveling at the sound velocity, . For small oscillations, , and with non-zero external potential, the sine-Gordon equation turns into the Klein–Gordon equation describing massive phonons (bradyons) moving with subsonic velocities.
One can also consider small oscillations around the point of unstable equilibrium
. Setting
and assuming
, one obtains the equation
which has a minus sign before the mass term and describes supersonic phonons (tachyons). Despite the supersonic behavior, the field
does not allow information to be transmitted with the velocity
, as was explained above. One can repeat the basic arguments using this very example. The dispersion relation linking the frequency
to the wavenumber
k of tachyonic excitation has the form
. When
,
becomes imaginary, indicating the onset of instability. Any sharply localized source of perturbation will have such wave numbers in its Fourier spectrum and cause the instability. It can be then shown that the localized disturbance (information) will propagate with velocity
in accordance with the Cauchy–Kowalewska theorem of hyperbolic partial differential equations [
81].
22. Frenkel–Kontorova Solitons
The Frenkel–Kontorova model has a mechanical analog: a chain of pendula which can rotate around an elastic horizontal axis that couples them to each other by exerting a harmonic torque, see
Figure 10.
Some excitations of this chain of pendula have a form of traveling stable waves called solitons. Two particular cases of solitons are a kink (
) and anti-kink (
):
Here,
,
V is a kink velocity and
is a Compton wavelength (m
) of the Frenkel–Kontorova phonons. As one can see from the above expression, the width of the kink depends on its velocity the same way as for relativistic particles. Therefore, it always moves with subsonic velocities; see
Figure 11 for a mechanical model of the Frenkel–Kontorova kink.
On the other hand, there is a similar solution of the sine-Gordon equation, which can be called T-kink, and which always moves with supersonic velocity:
It is evident that T-kink is a mechanical model of a tachyon. In contrast to kinks, T-kinks are not stable. The reason for this difference can be understood as follows [
2]. One can visualize infinitely many minimums of the Frenkel-Kontorova external potential as depressions of a long slate. A kink corresponds to an infinite rope which begins in one depression of the slate and ends up in another neighboring depression. For an infinite rope, one needs an infinite energy to throw the rope from one depression to another one. For this reason, the kink is stable (can be annihilated only by a counter anti-kink). On the contrary, T-kink corresponds to a rope which lays on a slate ridge, then somewhere on the ridge it falls in the depression and raises again to the adjacent ridge. Of course, such configuration cannot be stable.
23. Emergent Relativity
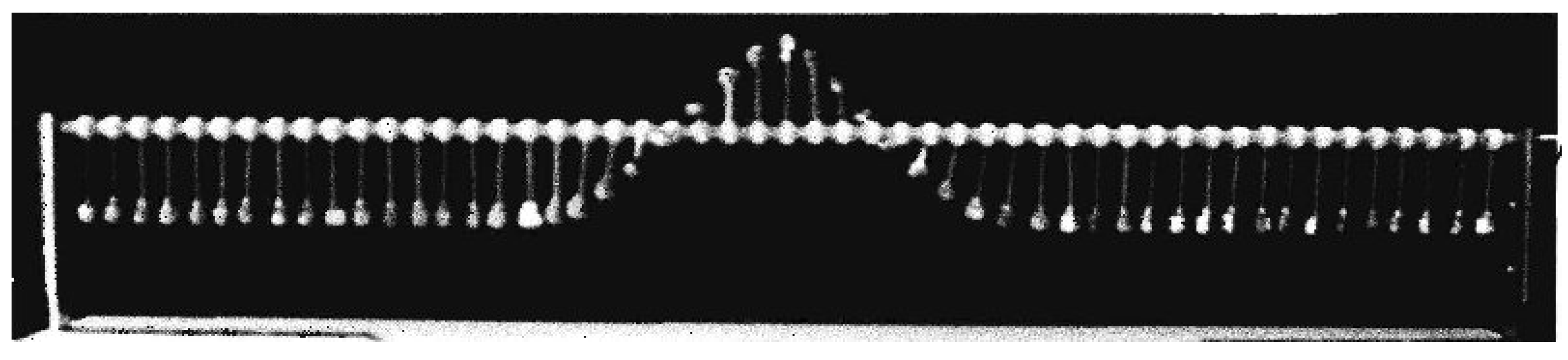
Frenkel–Kontorova solitons, remarkably, exhibit relativistic behavior. It was altready seen that the kink’s width is subject to Lorentz contraction. Interestingly, such length contraction can be observed by naked eyes on the strobe photography of a pendula realization of a kink traveling with some dissipation of energy due to friction effects [
82], see
Figure 12.
The kink moves from right to left and becomes wider as its velocity decreases. One can calculate the kink energy and discover that it is also given by the known relativistic expression,
, where
M is some constant (the kink mass) determined by parameters of the Frenkel–Kontorova model [
2].
This emergence of relativistic expressions is not surprising, as the sine-Gordon equation is in fact Lorentz invariant, provided the light velocity is replaced by the sound velocity
c. What is truly remarkable is that this relativistic invariance is an emergent phenomenon. It is absent at the fundamental level of the Frenkel–Kontorova chain, but appears in the long-wavelength limit. Apart from the Frenkel–Kontorova model, there are other examples when a relativistic behavior emerges in purely classical mechanical systems [
83].
Mexican artist Octavio Ocampo’s painting
Mouth of flower [
84] illustrates the idea of emergence wonderfully well. One can see the face of a lady on the painting. However, at a closer inspection one finds that at the fundamental level, there is no face but only some flowers and a butterfly.
24. Supersonic Solitons
Emergent relativity in the Frenkel–Kontorova model is approximate and holds only insofar as one can neglect discreteness effects. Even in the long-wavelength limit, not all interatomic interactions lead to the emergence of sound speed relativity in the atomic chains of the Frenkel–Kontorova type. Morikazu Toda managed to find exponential interatomic interactions that support supersonic solitons.
When the velocity of a Toda soliton approaches the sound velocity, its behavior is opposite to that of a tachyon: its energy approaches to zero and its width approaches to infinity. Despite this difference, the final result is the same: Toda solitons, like tachyons, cannot cross the sound barrier and become subsonic.
If one generalizes the Frenkel–Kontorova model by adding special kinds of anharmonicity in the interatomic potential, other types of solitons can be constructed that can cross sound barrier [
83]. In contrast to Frenkel–Kontorova and Toda solitons, Kosevich–Kovalev solitons can move with any velocity from zero to infinity [
85]. In some sense they interpolate between the subsonic Frenkel–Kontorova solitons and supersonic Toda solitons: for velocities much smaller than the sound velocity they resemble Frenkel–Kontorova solitons, and for velocities much greater than the sound velocity they resemble Toda solitons.
25. Elvisebrions
The above analyis of Kosevich–Kovalev and Toda solitons suggests a way how superluminal objects may be introduced in our world. Let us explain by a vivid analogy. One can classify creatures according to where they live with regard to the Himalayan range (light speed barrier).
There are creatures that live south to the Himalayas (bradyons), that hover over the range (luxons), and that live to the north (tachyons but they tend to condensate and move to southern regions). However, one cannot exclude that one day one meets an alien (though never met any of them so far) from a planet with no Himalayan range at all!
Such type of possibly superluminal objects, analogs of the Kosevich–Kovalev and Toda solitons, is conceptually different from the tachyons and deserves its own name. We name such objects elvisebrions (elvisebri means “swift as a lightning flash” in Georgian).
In more formal wording, we suggest a possibility that a hidden sector may exist which is either not Lorentz invariant or it is Lorentz invariant but with a different limiting speed. If the two sectors (hidden and visible) are connected very weakly, then it is expected that the Lorentz invariance may still be a very good approximation in the visible sector. Nevertheless, such a setup is no longer Lorentz invariant as a whole and, therefore, a possibility of hidden sector-induced superluminal phenomena does appear.
The two sectors could be connected through the Higgs portal as considered in [
86] and further analyzed in [
87]. It was shown that Lorentz invariance violation in the Higgs sector is communicated at one loop level to all other Standard Model particles. However, in the framework of the model, such effects are naturally small. Similar ideas have been formulated by Gonzalez–Mestres who calls this type of elvisebrions superbradyons [
88].
Finally, let us point to an interesting paper by Robert Geroch [
89] which actually provides a much more solid foundation for the elvisebrions hypothesis than we were able to give in this informal essay.
Quoting [
89]: “In short, the causal cones of special relativity, from this perspective, have no special place over and above the cones of any other system. This is democracy of causal cones with a vengeance. This, of course, is not the traditional view. That view—that the special relativity causal cones have a preferred role in physics—arises, I suspect, from the fact that a number of other systems—electromagnetism, the spin-s fields, etc.—employ precisely those same cones as their own. And, indeed, it may be the case that the physical world is organized around such a commonality of cones. On the other hand, it is entirely possible that there exist any number of other systems—not yet observed (or maybe they have been!)—that employ quite different sets of causal cones. And the cones of these <<other systems>> could very well lie outside the null cones of special relativity, i.e., these systems could very well manifest superluminal signals. None of this would contradict our fundamental ideas about how physics is structured: An initial value formulation, causal cones governing signals, etc.”
26. Final Words
As it is said in [
90]: “Science, particularly mathematics, though it seems less practical and less real than the news contained in the latest radio dispatches, appears to be building the one permanent and stable edifice in an age where all others are either crumbling or being blown to bits” We firmly believe that special relativity belongs to this permanent and stable edifice. Even if in the end it turns out that there are Lorentz non-invariant hidden sectors, special relativity will remain with us, as one of our most precious scientific theories. Alas, this does not mean it will last forever, as nothing lasts forever in the material world, especially such a fragile thing as intelligent life, and particularly in context of current climate change. To paraphrase English writer Virginia Woolf, it may happen that the very stone one kicks with one’s boot will outlast all our theories and achievements.