Abstract
In this paper, the validity of the shell-evolution picture is investigated on the basis of shell-model calculations for the atomic mass number neutron-rich nuclei. For this purpose, the so-called SDPF-MU interaction is used. Its central, two-body spin–orbit, and tensor forces are taken from a simple Gaussian force, the M3Y (Michigan 3-range Yukawa) interaction, and a meson exchange force, respectively. Carrying out almost a complete survey of the predicted effective single-particle energies, it is confirmed here that the present scheme is quite effective for describing shell evolution in exotic nuclei.
1. Introduction
One of the most important results obtained by investigating exotic nuclei (those from the stability) is the evolution of the shell structure, which is often called the shell evolution [1]. The evolution sometimes occurs in a more drastic way than as predicted by the standard Woods–Saxon potential model: some of the conventional neutron magic numbers, such as , 20, and 28, disappear, and new magic numbers, such as and 34, appear.
These phenomena indicate a mechanism of shell evolution beyond the potential models, and the role of effective interactions has recently received much attention. Historically, this idea was developed in the context of the shell model, dating back to 1960 when Talmi and Unna accounted for the inversion of single-particle levels in the p-shell nuclei [2]. Later, a similar expression was derived in Ref. [3], in which the effect of two-body interactions was formulated with what is now called the monopole interaction [4].
The impact of the monopole interaction on nuclear structure has been investigated with the development of large-scale shell-model calculations [4,5,6], in which -shell nuclei are very successfully described by using Kuo–Brown interactions with a few monopole matrix elements appropriately modified. The single-particle energy that includes the effect of the monopole interaction is often referred to as the effective single-particle energy [7,8].
One of the remaining issues concerning shell evolution is the general properties of the monopole interaction and their origin. One of the earliest attempts in this direction was carried out by Federman and Pittel [9], who indicated that the central force causes a sharp drop of the neutron orbital with the proton orbital occupied. With more data on exotic nuclei accumulated in the 1990s, the spin-isospin dependence of the effective interaction was highlighted in Ref. [10]. This property well accounts for the monopole interaction that was phenomenologically introduced in Ref. [11] to describe the shifting magic number from to 20. Finally, Otsuka et al. demonstrated [12] that the tensor force significantly increases or decreases spin–orbit splitting depending on the relative direction of the spin and orbital angular momenta that the last nucleons have.
For a unified description of the shell evolution, in [13], it was proposed that the central and tensor forces are the major sources of shell evolution, whereas the two-body spin–orbit force plays a unique role in the monopole matrix elements between specific orbitals [14]. The same conclusion was drawn from the spin-tensor decomposition of an effective interaction fitted to the experimental data [15]. In Ref. [13], shell evolution is described by an interaction that consists of a simple Gaussian central force and a meson exchange tensor force, whose choice is supported by “renormalization persistency” [16]. This interaction, named the monopole-based universal interaction, , and its variant were successfully applied to constructing effective interactions for shell-model calculations [17,18], whose focuses were placed on many-body properties, such as the onset of deformation due to the tensor force.
The aim of the present study is to quantitatively examine to what extent the shell evolution is described by such a simple scheme. To this end, the SDPF-MU interaction [18] is employed here whose cross-shell part is made of a variant of the interaction with the two-body spin–orbit force included, and the validity of its shell evolution is carefully examined by comparing with the relevant experimental data.
In this paper, neutron-rich nuclei with the atomic mass number are considered, where several doubly-closed-shell nuclei are known, including O, Si, S, Ca, Ca, Ca, and Ca. Hence, configuration mixing within the major shell is relatively suppressed along the atomic number, Z, and chains, for instance, which makes easier to identify the monopole matrix element most relevant to the shell evolution under debate. Here, a rather complete survey that covers both the proton and neutron shell evolution is conducted, thus, enabling to separate the unique roles of the central, spin–orbit, and tensor forces.
This paper is organized as follows. In Section 2, the interaction is introduced as used in the SDPF-MU interaction, and the different characteristics of the central, spin–orbit, and tensor forces are quantitatively presented with regard to the monopole matrix element. Section 3 dicusses how the shell evolution, caused by this interaction, can be validated by experimental data. Section 3.1 and Section 3.2 are devoted to proton shell evolution with varying neutron number and neutron shell evolution with varying proton numbers, respectively. Section 4 gives conclusions of the study.
2. Shell Evolution Caused by the SDPF-MU Interaction
2.1. Monopole Matrix Elements
The SDPF-MU interaction was constructed in Ref. [18] to describe the structure of neutron-rich nuclei around whose Fermi surface is located in the shell for protons and the shell for neutrons. Hence, the proton–neutron cross-shell interaction, i.e., the part of the interaction that is relevant to both the sd shell and the pf shell is responsible for the shell evolution occurring in this region.
The cross-shell part of the SDPF-MU interaction is provided by a minor modification of the interaction [13]. The interaction was proposed to give a universal behavior of shell evolution over the nuclear chart, consisting of a Gaussian central force and a meson exchange tensor force. In the SDPF-MU interaction, the following refinements to the original interaction are introduced:
- the central force includes density dependence;
- the two-body spin–orbit force is included in addition.
The central force of the shell-model effective interaction is subject to complicated renormalization and many-body effects. The basic strategy of is to determine the central force so that its monopole matrix elements are close to those of a reliable effective interaction. Here, the monopole matrix element between the orbitals and is defined by
where J runs over all the possible angular-momentum coupling that the Pauli principle allows, and T is the isospin coupling. In constructing the original interaction, the GXPF1A interaction [19] was used as a reference, and a reasonable but not perfect agreement was achieved. Namely, while most of the monopole matrix elements agree within 0.2 MeV, a few matrix elements differ by 0.5 MeV or more; see Figure 1 of Ref. [13]. To obtain a better result, the central force of the SDPF-MU interaction has the form of
where S and T denote the spin and isospin coupling, respectively, and is the projection operator onto a given (S, T). The and are the relative and center-of-mass coordinates, respectively: and . The is the density dependent part that was newly introduced in the refined , and its form was taken from the FPD6 interaction [20] as
with MeV and fm. The interaction, thus, has six free parameters, , , and . They were chosen to be MeV, , , , fm, and . The resulting agreement with the monopole matrix elements of the central force of GXPF1B is quite good, as illustrated in Figure 1 of Ref. [21].
The two-body spin–orbit force in the SDPF-MU interaction was taken from that of the M3Y (Michigan 3-range Yukawa) interaction [22]. The two-body spin-orbit force plays a minor role on shell evolution compared with the central and tensor forces, as far as a restricted region of the nuclear chart is considered: see Table 1 and discussion below. However, some specific evolutions of shell gaps are dominated by the two-body spin–orbit force, thus, included here for completeness.

Table 1.
Proton–neutron monopole matrix elements between the and orbitals obtained by the SDPF-MU interaction for the atomic mass number . The second to the fifth columns list the central (C), tensor (T), spin–orbit (LS), and the total values (in MeV), respectively. The sixth to ninth columns indicate the hierarchy of the C + T monopole matrix elements. The texts in red (blue) are to highlight the correspondence between the most attractive matrix elements of the central (tensor) force and (spin direction). See text for details.
The overall strength of the SDPF-MU interaction is scaled by a factor in the same way as the USD (Universal ) [23] and GXPF1 [24] interactions.
Table 1 presents the proton–neutron cross-shell monopole matrix elements, calculated with the SDPF-MU interaction, for central, tensor, and spin–orbit forces. The proton–neutron monopole matrix element for a pair with is given by
The second column of Table 1 indicates that the strengths of the central matrix elements can be grouped into two categories: one has MeV, and the other has much weaker strengths. As explained [1,13], this difference occurs because two orbitals with the difference of the number of nodes, , have a large spatial overlap, thus, gaining much attraction through short-range forces. Comparing the second and the sixth columns, one finds a good correspondence between and the strength of the central matrix elements.
The monopole matrix elements of the tensor force are characterized by the relative spin direction between the two orbitals considered, as pointed out in Ref. [12]. When the spins of two orbitals (with ) are parallel, i.e., - or - ( and stand for and , respectively), the tensor monopole matrix element is positive and otherwise negative. The third and the seventh columns of Table 1 exactly point to this property. This fact is accepted now, [1,12], and quantitative aspects of the tensor monopole matrix elements are as follows.
- Similar to the central force, the strengths for the orbitals are weaker than those of .
- Although the absolute values of the tensor matrix elements are much smaller than those of the central force, the difference between the largest matrix element and the smallest one reaches MeV, equivalent to that of the central force.
From the point 2, one concludes that the tensor force plays a role as important as the central force in shell evolution.
On the basis of the above arguments, let us label the orbital pairs to simply estimate the strengths of the monopole matrix elements due to the central and tensor forces without numerical calculations.
- The label consists of two characters: the first and the second ones are intended to grade the central and tensor monopole matrix elements, respectively. The net effect of these two characters stands for a rough estimate of the total monopole matrix element.
- Each part is evaluated on a scale of five levels defined by −, , 0, , and +, to indicate relative attraction within each type of force. The ”−” character is given to the most attractive (i.e., largest negative) pairs, and the ”+” character is given to the least attractive (or most repulsive) pairs among the whole monopole matrix elements of the central or tensor force.
- The first character gets ”−” for , or ”+” for .
- When the first character is ”−”, the second character gets either ”−”, 0 or ”+” depending on the relative spin direction mentioned above. When the first character is ”+”, the second character is replaced by , 0, or .
These labels are listed in the eighth column of Table 1. The actual sum of the central and tensor monopole matrix elements shown in the ninth column of Table 1 rather well follows this ordering, except for a few cases with in which the tensor force is less dominant.
Next, the two-body spin–orbit force is examined whose monopole matrix elements are presented in the fourth column of Table 1. The strengths of the elements are usually rather weak (see details in Supplemental Material in Ref. [1]), and the typical order of the monopole matrix elements is MeV ≈ MeV at . The signs of the elements are determined so that the inner nucleon (usually with lower orbital angular momentum, l) produces the normal spin–orbit splitting to the outer orbitals. Namely, when the inner and the outer orbitals are labeled i and j, respectively, their monopole matrix elements satisfy for and for .
More specifically, when monopole matrix elements between the and orbitals are considered, the orbitals are located closer to the center and thus can be regarded as the inner orbitals. Hence, this rule causes negative and positive monopole matrix elements for the and orbitals, respectively. One can also find that the monopole matrix elements between the and orbitals are much larger than the others. This is because this pair, having a relative orbital angular momentum alone, gains much energy due to the short-range nature of the two-body spin–orbit force.
2.2. Effective Single-Particle Energies
Once the cross-shell monopole matrix elements are determined the above-described way, one can obtain proton and neutron shell evolutions. The shell evolution is characterized by the effective-single-particle energy (ESPE), which includes the effects of valence nucleons on the single-particle energy. While the ESPEs can be defined for any wave function (see Ref. [1]), they are often estimated by filling configurations, so that one can directly connect monopole matrix elements to shell evolution. To simplify the discussion, a case of mass-independent two-body interactions is considered here. The ESPE of the neutron orbital, , changes by filling protons in the orbital as
When one defines the change of the ESPE of with filling as
the evolution of the shell gap between and with filling is expressed as
Figure 1 provides a schematic illustration of what is represented in Equation (7). One of the most important properties of is that this quantity does not depend on the choice of the core to define the ESPE. For example, the evolution of the shell gap can be probed not only by the systems with the core but also by those with the core or the core. This means that one can investigate a specific shell evolution for very neutron-rich isotones by using that of less neutron-rich ones, which will be utilized in some cases considered in Section 3.
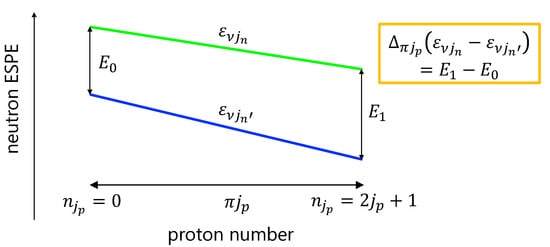
Figure 1.
Schematic illustration of what is investigated in this paper. The blue and green lines are, respectively, the effective single-particle energies (ESPEs) of the neutron orbital, and , that change with the proton orbital, , filled. The evolution of the shell gap, denoted as , is the main focus of this paper.
When one uses a mass-dependent interaction, Equation (7) is not exact but it is still useful for estimating shell evolution from monopole matrix elements.
3. Comparison to Experimental Data
The main objective of this paper is to examine how well the shell evolution described by Equation (7) is supported by experimental data. In Figure 2a,b, the proton shell evolution with neutrons occupying the shell, and the neutron shell evolution with protons occupying the shell are plotted, respectively. The former and the latter are examined in Section 3.1 and Section 3.2, respectively. In the following, for brevity, the quantum number n are omitted and only the other quantum numbers like are given.
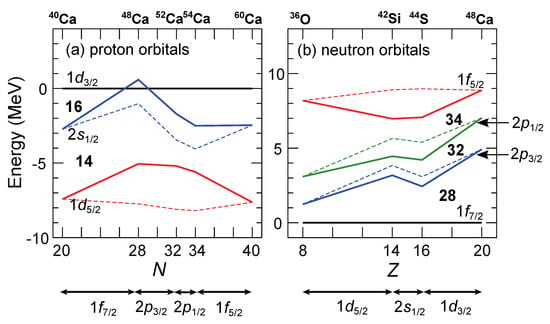
Figure 2.
Evolution of the ESPEs calculated with the SDPF-MU interaction with the tensor force included (solid lines) and not included (dashed lines). (a) Proton orbitals measured from for the atomic number isotopes and (b) neutron orbitals measured from for the neutron number isotones. The ESPEs are obtained by assuming filling configurations whose orders are indicated at the bottom of the figure.
In Figure 2, also the ESPE with the tensor force removed is plotted. One can immediately find that the proton orbital (Figure 2a) and the neutron orbital (Figure 2b) have the largest effect from the tensor force. Since the ESPEs shown are measured from the and orbitals, respectively, this result is a manifestation of a general property that the tensor force strongly affects the spin–orbit splitting (see Figure 1a of Ref. [12]).
To be more specific, when the proton orbital is filled, the evolution of the neutron spin–orbit splitting between and is expressed, by using Equation (7), as . The and values for the tensor force are always of the opposite sign due to the identity (valid for any isospin coupling T) [12], thus, magnifying the value.
In addition to evaluating the ESPE, we conducted large-scale shell-model calculations to more directly compare to the data. The procedure of the calculation was the same as that employed earlier [18,25]. The valence shell consists of the full and shells. The basis states considered are truncated to allow only (with ℏ being the reduced Planck constant and the angular frequency) excitations for natural-parity states and to allow excitations for unnatural-parity states. Note that, in the present case, excitation is equivalent to n-particle-n-hole excitation across the shell gap.
Let us stress that this truncation scheme (restricted to the lowest space) is introduced not only to make numerical computation possible but also to be in accordance with the way how the SDPF-MU interaction is constructed (see also Section 2.2 of Ref. [21]): (i) the central force of the cross-shell interaction in SDPF-MU is fitted to the GXPF1B interaction and (ii) the intra-shell interactions employed in the SDPF-MU interaction are based on USD for the shell and GXPF1B for the shell. The USD and the GXPF1B interactions are intended for the use of the model space. As shown in Ref. [18], the binding energies of neutron-rich nuclei in this region are well reproduced in this framework. The Hamiltonian matrices spanned by those basis states are numerically diagonalized by using the KSHELL code [26].
3.1. Proton Shell Evolution
3.1.1. From to
As shown in Figure 2a, the most distinct property by filling the orbital is that the shell gap sharply diminishes and that the order of and is finally inverted at the Ca core. The change of this shell gap is expressed as . Since the - and - pairs are labeled and , respectively, according to the rule, introduced in Section 2.1, this value is a large negative value. The actual number calculated with the SDPF-MU interaction is MeV. If the tensor force is omitted from the interaction, this value decreases to MeV, pointing to almost equal contributions of the central and tensor forces.
Experimentally, the evolution of the shell gap is well examined by the first excitation energies of K and K, which can be regarded as a proton hole in the Ca and Ca cores, respectively, from very large spectroscopic factors for the lowest two levels. The measured values of for K and K are 2.52 MeV and MeV, respectively.
Hence, if one assumes the pure single-hole states for the and states in K and K, the value estimated from these experimental data is MeV. The corresponding value obtained from large-scale shell-model calculations is MeV, which is somewhat overestimated; however, the sharp decrease of in going from K to K is well explained. Note that this number is very close to that evaluated from the ESPE ( MeV; see the first paragraph of this Subsection) because the first two levels of K are very close to single-proton-hole states.
Another important property in filling the orbital is that the proton spin–orbit splitting for the d orbitals sharply decreases. This is caused almost solely by the tensor force (Figure 2a) because the central force gives similar monopole matrix elements between the - and - pairs: those are and pairs, respectively. Hence, quantifying the spin–orbit splitting is the key to extracting the tensor-force driven shell evolution. By using the SDPF-MU interaction, the proton spin–orbit splittings for the d orbital are obtained to be 7.42 and 5.05 MeV for the Ca and Ca cores, respectively, indicating a more than 2 MeV reduction.
Unlike the cases of and , the proton hole does not appear as a nearly pure single-hole state because the excitation energy is much higher than other low-lying levels, making the hole state fragmented over many levels. For the present purpose, the distribution of spectroscopic factors provides crucial information. The one-proton removal spectroscopic factors from Ca and Ca were measured with reactions, such as (d, He) and . Although the reaction gives more reliable spectroscopic factors, those measured for Ca are concerning only a few low-lying states. Thus, the (d, He) data were used to estimate the spin–orbit splitting for Ca isotopes from the centroid of the measured spectroscopic factors, as discussed in Refs. [27,28].
The centroid of the spectroscopic factors, actually, provides the exact single-particle energy. However, there are many energy levels that cannot be detected by the actual experiment because their spectroscopic factors are too small to be measured. Although each of these undetected levels has a tiny contribution to the centroid, the total effect is not negligible because the number of such levels is very large. In this sense, the centroid of the spectroscopic factors that is obtained from experiment cannot be free from uncertainty associated with the limited experimental sensitivity. Hence, in order to validate theoretical single-particle energies, it is rather helpful to compare between experiment and theory regarding how major peaks are distributed. The results are shown in Figure 3, in which the spectroscopic factor for the orbital j is defined as
where and are the wave functions of the nuclei A and B, respectively (here, A and B correspond to Ca and K isotopes, respectively), and is the angular momentum of B.
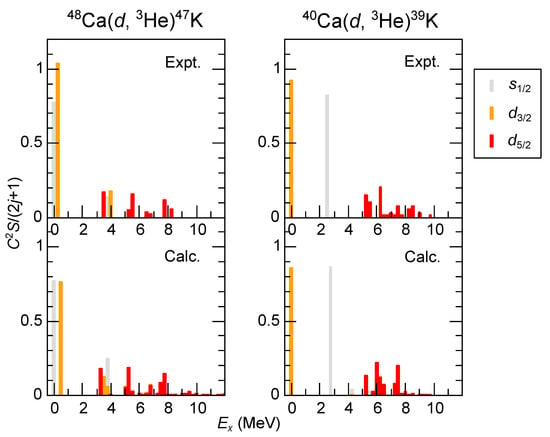
Figure 3.
Distribution of the one-proton removal spectroscopic strengths (see Equation (8)) from Ca (left) and Ca (right) comparing experimentalal results (”Expt.”) with shell-model calculations (”Calc.”). The spectroscopic factors shown are divided by to normalize to unity for fully occupied orbitals. The bin widths are 0.25 MeV. Data are from Refs. [29] (Ca) and [30] (Ca). See text for details.
For Ca, the calculations were carried out with the SDPF-MU interaction in the model space [18]. The present calculation successfully captures the characteristics of the measured distribution. For and , although the strengths are dominated by the lowest states, some strengths remain in the states slightly below 4 MeV due to the coupling to the state. Note that the sum of the experimental strengths for exceeds the sum-rule limit [29], indicating non-negligible uncertainties due to the reaction model employed. For , the calculation well reproduces three major peaks located at 3–4, 5–6, and 7–8 MeV, although the calculated peaks are located a few hundred keV lower than those of the experiment. If the tensor force is omitted, the calculated weight of the strengths is shifted higher and fails to reproduce the data as presented in [18].
For Ca, as seen in Figure 3, the strengths are highly fragmented as in Ca. This property is impossible to reproduce with the same setup as Ca, since only one state appears in the calculation. It is also found that the calculation was not sufficient to obtain enough fragmentation because of much smaller level densities compared with the data. To resolve this problem, the large-scale shell-model calculations were done to allow many-particle many-hole excitations across the core. Since it is still difficult to perform such calculations in the full - valence shell, the and orbitals are omitted from the valence shell, thus enabling calculations with the KSHELL code [26].
The effective interaction is taken from Ref. [31], a modified SDPF-M interaction whose single-particle energies are fine-tuned to reproduce the correct one-neutron separation energies of Ca. Note that the original SDPF-M interaction [11] was designed for the full model space. One expects that the truncation is sufficient to achieve convergent results. The resulting spin–orbit splitting of the d orbitals for the Ca core is close to that of SDPF-MU, 7.49 MeV, estimated from the ESPE.
Figure 3 presents the results of the calculations. Similar to Ca, the agreement with experiment is quite satisfactory. For and , the strengths near the level of Ca ( MeV) are much smaller than those for Ca, in good accordance with the measured distribution [30]. For , the calculated three major peaks at 5–6, , and 7–8 MeV well correspond to the measured peaks, although the highest peak is more fragmented in the experiment.
The above detailed comparisons of spectroscopic distributions confirm that a large reduction of the spin–orbit splitting, which amounts to MeV, occurs in reality as a meson exchange tensor force produces.
3.1.2. From to and Beyond
As the neutron number increases from , the Fermi surface moves to , which causes a different proton shell evolution from that for . Figure 2a indicates that the most prominent is that goes down relative to . This is caused by a positive because the - and - pairs are labeled ”” and ””. Although the tensor force causes attraction for the former pair, the central force that favors the latter surpasses this effect due to a larger spatial overlap. It is thus predicted that the orbital becomes the highest in the shell again at , leading to the reinversion of the - level ordering.
Similar to that of Section 3.1.1, K isotopes play a key role in probing this level ordering from experiment. The observed hyperfine structure ruled out a ground state for the isotope K [32], and its measured g-factor of [32] is very close to that of the single-proton hole in . From these data, it is concluded in Ref. [32] that the ground state of K must be a state that is dominated by the configuration. The predicted reinversion has thus been confirmed by experiment.
A deeper understanding of shell evolution can be obtained from excitation energies. In Figure 4, the energies of the levels, measured from the levels in neutron-rich K isotopes, are compared to theory. Very recently, the first excited levels in K () were measured to be 0.74 and 0.84 MeV, respectively [33]. These states are assigned to be from the observed parallel momentum distributions of the K residues after reactions.
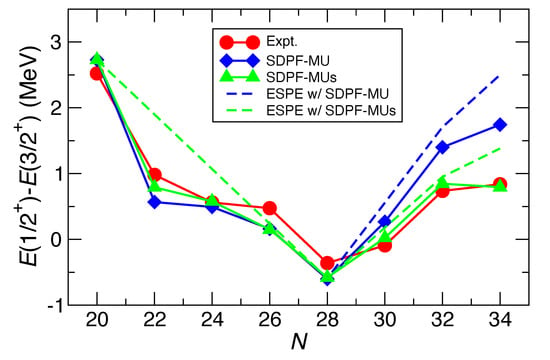
Figure 4.
Comparison of the evolution of the energy difference in neutron-rich K isotopes between experiment and theory. The red circles represent experimental data, and the blue diamonds and the green triangles stand for the results of large-scale shell-model calculations with the SDPF-MU and the SDPF-MUs interactions, respectively. The dashed lines in blue and green are the corresponding values evaluated from the ESPE (i.e., ) for the SDPF-MU and the SDPF-MUs interaction, respectively.
As shown in Figure 4, the measured values are lower than the shell-model results with the SDPF-MU interaction, 1.40 and 1.74 MeV, respectively. Although the calculated levels are located lower than those estimated from the ESPE, 1.71 and 2.50 MeV, respectively; the deviation from the experimental data may indicate the need of refining the monopole matrix elements, related to the shell evolution under discussion.
In Ref. [33], a modified SDPF-MU interaction was introduced (named SDPF-MUs) in which is shifted by MeV, equivalent to a MeV shift for the proton–neutron channel. The resulting levels in K are improved to be 0.85 and 0.79 MeV, respectively. These SDPF-MUs levels are also somewhat lower than those estimated from its ESPE, 0.95 and 1.38 MeV, respectively. This difference is caused by a many-body correlation, which makes single-hole strengths fragmented. Experimentally, three more levels are observed from the CaK reaction [33], which may indicate some deviation from the single-hole nature for or proton hole states fragmented.
As shown in Figure 4, the value evolves in a non-monotonic way; that is, it decreases until and then turns to increase. This evolution, following the ESPE, is caused by that of the ESPE of measured from . The reinversion of the - level ordering is a consequence of the non-monotonic evolution of single-particle level spacings.
Let us point out that such a non-monotonic evolution constitutes a strong evidence for the dominance of the effective interaction in shell evolution because simple one-body potential models like the Woods–Saxon ones always produce monotonic evolution of level spacings with changing mass number. Furthermore, in this particular case, the non-monotonic evolution is caused by the central force. To account for this, let us first remind one that the changes of for –28 and for –32 amounts, respectively, to and .
For the tensor force, holds, and only the first terms contribute to and . As shown in Table 1, both of them are negative, and the value keeps decreasing. On the other hand, the central-force contributions to and are negative and positive, respectively, thus producing a kink in and . Since this non-monotonic evolution is dominated by the central force, any microscopic model, with a reasonable two-body force, is able to describe that. In fact, both nonrelativistic and relativistic mean-field models produce similar effects [34,35].
Here, let us comment on the idea behind the empirical shift of monopole matrix elements employed in the SDPF-MUs interaction. As presented in Section 2.1, the cross-shell part of the SDPF-MU interaction consists of the central, two-body spin–orbit, and tensor terms. Among them, the tensor term is the most strongly supported by microscopic theories in terms of the “renormalization persistency”, named in Ref. [16]. On the other hand, the central term is constructed in a fully phenomenological way. The two-body spin–orbit term is too small to tune.
On the basis of this general consideration, it seems that the most reasonable method of monopole tuning is for the central term alone, with the other terms untouched. The SDPF-MUs interaction is made to follow this policy. With respect to the cross-shell interaction, the difference between SDPF-MU and SDPF-MUs is the shift of . The shift, MeV, is applied not only to the orbital but also to the orbital. The latter change is needed to keep the tensor term unchanged after carrying out the spin-tensor decomposition [36].
Finally, let us mention that the monopole matrix elements contain non-negligible contributions from the two-body spin–orbit force. This feature is discussed in Section 3.2.2.
3.2. Neutron Shell Evolution
In this Subsection, the neutron shells that change with the proton number are considered, as illustrated in Figure 2b. Let us start with the Ca core, since its neutron -shell energies are well established from the data. Next, the protons are removed from the , , and orbitals, and the relevant issues are discussed in Section 3.2.1, Section 3.2.2 and Section 3.2.3, respectively.
3.2.1. From to
As shown in Figure 2b, with protons removed from , the shell gap changes by . Note that the negative sign in is needed because the shell evolution is considered with decreasing Z. Since - and - are and pairs, respectively, this quantity should be negative. As discussed in Section 3.1.1, the strongly attractive monopole matrix element of causes the rapid decrease of the shell gap in going from to .
The decrease of the shell gap is difficult to evaluate from experimental data in the vicinity of isotones because the corresponding sulfur isotopes are deformed. As emphasized in Section 2.2, however, this decrease can be probed from another isotone chain. In this case, isotones provide useful information since both S and Ca are regarded as doubly-closed-shell nuclei with rather large first excitation energies (>3 MeV).
From the SS reaction data, the and strengths are concentrated in the ground state and the 0.646 MeV state, respectively, while some strengths remain in the state at 3.263 MeV with and in the state at 3.443 MeV with [37]. The measured spectroscopic strengths, thus, indicate a small shell gap that is less than 1 MeV on top of the S core. The shell-model calculation with the SDPF-MU interaction rather well reproduces this feature with at MeV, at MeV, at MeV, and at MeV. The calculated shell gap for the S core is MeV.
Similar data exist for the Ca core. The strengths are fragmented into the states at , , and MeV, which is impossible to reproduce with the calculations. The centroids of the spectroscopic factors measured with the CaCa reaction [38] suggest that the shell gap for Ca is 2.5 MeV. The SDPF-MU interaction produces the shell gap of 2.94 MeV, which is slightly larger than this value. Hence, a large decrease of the shell gap is confirmed, although the SDPF-MU interaction may overestimate this decrease by a few hundred keV.
The reduction of the shell gap should have a significant impact on the closed-shell structure. The breaking of the closure can be probed with one-neutron removal spectroscopic strengths from : if no strengths are observed, then no neutrons occupy the orbital, implying a complete closure. Although summing up all the strengths are desirable for a quantitative evaluation, excited states available in neutron-rich nuclei are limited. For this purpose, the strengths of the first levels between experiment and theory are compared and the results are shown in Figure 5.
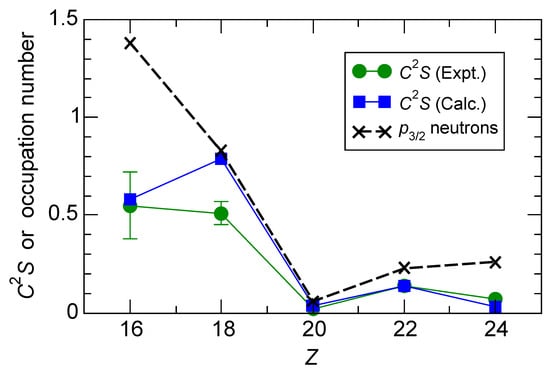
Figure 5.
One-neutron removal spectroscopic factors of the states from the ground states of isotones. The crosses denote the calculated neutron occupation numbers in the ground states of the isotones. Data are from Refs. [39] (, 22, and 24), [40] (), and [41] ().
It is natural that the strength for Ca is very small. As the proton number is away from , the strengths are naively expected to increase due to deformation caused by valence proton particles or holes. If deformation is controlled by the number of valence protons alone, those spectroscopic factors should be symmetric with respect to . However, the observed spectroscopic factors are rather large for the isotones, whereas they remain small for the isotones.
This behavior is well reproduced by the shell-model calculations with the SDPF-MU interaction. The same trend is seen in the occupation numbers, which are the upper limit of these spectroscopic factors. Hence, one concludes that the breaking of the closure is much greater for than for and that the reduction of the shell gap for lower Z works to enhance this property.
From Figure 5, it may look unexpected that the value for is only half the neutron occupation number of S unlike that for Ar. This is caused by a unique nuclear structure of S. As pointed out in Ref. [25], sulfur isotopes around S have two nearly degenerate deformed neutron orbitals on the Fermi surface with and , which make the and bands in S, respectively, by one-neutron occupation. Here, and K are, respectively, single-particle and total angular-momentum projection onto the symmetry axis, and is parity. The state in S is a member. Due to the near degeneracy of the and orbitals, the ground state of S has a strongly mixed configuration with two neutrons in and those in . As a result, about half the ground-state wave function of S, i.e., the part with two neutrons occupying the , is able to contribute to populating the band in S. The remaining fractions of should be distributed to the excited states, which was indeed observed [41].
Let us comment on other shell gaps. The discussions of the shell gap is given in Section 3.2.2, and here, just a brief remark to be made about the shell gap. A recent CaCa measurement clarified that the shell closure is rather good [42], while the shell gap for the Ca core was estimated to be MeV from the GXPF1Br interaction [43]. It was predicted that this shell gap enlarges with decreasing Z and that the fingerprint of the enlargement can be seen in the energies of the isotones with [44,45].
This prediction was confirmed later by measuring the level in Ar that is located at 1.656(18) MeV [46]. Interestingly, this level is even higher than that of the isotope, Ar. The change of the shell gap from to 16 is expressed as . The - and - are and pairs, respectively. Since the former pair is the most unfavored combination in energy in terms of both the central and tensor forces, this value is positive leading to the enlargement of the shell gap. Experimental evaluation of this enhancement is difficult for cores, but it is, however, possible for cores through spectroscopic strengths. Although the measured strengths are not complete for the S core, such an enlargement possibly occurs from the existing data (Figure 3 of [14]).
3.2.2. From to
Two protons are removed from the orbital as moving from to . Although the Si isotope, Si, is strongly deformed, the isotope, Si, can be regarded as a doubly closed-shell nucleus: its first excited state is (not ) and is located as high as 2.719(3) MeV [47]. In addition, a proton knockout experiment from Si [48] indicated small spectroscopic strengths of below MeV, thus, suggesting a good closure in Si. For this reason, it is a good approximation to substitute the yrast levels in Si for the neutron effective single-particle energies on top of the Si core.
As shown in Figure 2b, the shell gap changes by from to . The - and - pairs are and , respectively, since the tensor force does not contribute to the monopole matrix elements for . As discussed next, the spin–orbit force also adds a negative value for the -, and therefore the shell gap should enlarge. This enlargement is estimated from the yrast levels in Si and S to be MeV. The shell-model calculations with the SDPF-MU interaction lead to MeV, which is somewhat too large.
On the other hand, when one uses the SDPF-MUs interaction [33]—the one introduced in Section 3.1.2—to reproduce the levels in K, this value is modified to be MeV. Note that the values estimated from the ESPEs of SDPF-MU and SDPF-MUs are and MeV, respectively. These two independent experimental data—K isotopes and isotones—consistently require about a MeV modification of matrix elements for the SDPF-MU interaction. This looks like due to the uncertainty of the central force that is determined empirically with a simple potential.
Next, the evolution of the shell gap is discussed. The Si reaction experiment in inverse kinematics found two prominent peaks at 0.910 and 2.044 MeV, the former and the latter of which should be the and levels, respectively [14]. The interval of these two levels, 1.134 MeV, is much smaller than the corresponding value of S, 1.911 MeV. If these values are identical with the spin–orbit splitting between the p orbitals, the data point to a sharp reduction of 0.857 MeV. Since the matrix elements for the - and - pairs have no tensor contributions and the same central strengths (see Table 1), only the spin–orbit force can change this shell gap in terms of the shell model.
As pointed out in Section 2.1, the two-body spin orbit force produces particularly large monopole matrix elements between the s and p orbitals. The reduction of the p orbital splitting is evaluated from the ESPEs of the SDPF-MU interaction to be 0.54 MeV, while the actual shell-model calculation produces a 0.758 MeV reduction of the - level splitting in going from S to Si. Hence, although the two-body spin–orbit force is the dominant source of the observed reduction, correlation energy may account for the energy of a hundred keV order.
The origin of the observed reduction is still controversial. It is claimed [49] that Woods–Saxon potentials well account for the observed reduction of the spin–orbit splitting in going from the Ca to Si and that this occurs due to weak binding for lower Z isotopes. This effect causes a gradual reduction with decreasing Z, whereas the two-body spin–orbit force affects the p orbital splitting primarily with filled. Hence, one of the key issues to discriminate these effects is to establish how sharp this reduction occurs from the S to Si cores compared to that occurring from the Ca to S cores. Although one-neutron adding spectroscopic factors are measured for the S and Ca cores, the experimental uncertainty does not converge within the required accuracy (see the Supplemental Material of Ref. [1]).
3.2.3. From to
Finally, protons in are removed from to . As shown in Figure 2b, the shell gap sharply decreases again. Note that Figure 2b presents neutron ESPEs for the cores. When a similar figure is drawn for the cores, the ESPE of shifts downward by MeV, and the neutron and orbitals cross at around . In this Section, the evolution of the shell gap is examined; other gaps are difficult to access with the current experimental capability.
The change of the shell gap with Z decreasing from 14 to 8 is estimated to be . The - and - pairs are and , respectively. Although the tensor force produces a slightly larger positive value for the former pair, the central attraction overrides this effect, thus, causing a negative value in total.
For such proton deficient isotopes, one cannot obtain sufficient experimental information from the nuclei around . Moreover, isotones do not provide direct data for the present purpose because some isotopes in the “island of inversion” are strongly deformed. Hence, one relies on single-particle levels on top of the cores, although does not form a good closed shell except for with oxygen.
In Figure 6, the energy levels relative to are compared for experiment vs. theory. The data for Ne, Mg, and Si indicate a nearly linear change of these energies. Since the relevant one-neutron adding spectroscopic factors are not large, i.e., typically , as measured [50,51,52], these energy differences cannot be identified with the shell gap. However, the linear evolution reminds one of the famous “Talmi plot” [2], which successfully predicted the level in Be from the linearity. Thus, this behavior is worthy of particular attention.
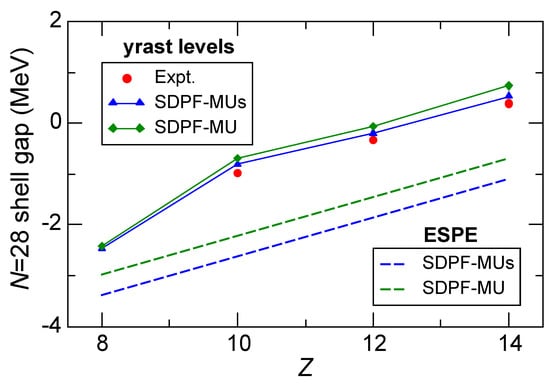
Figure 6.
Evolution of the shell gap in going from to 14 estimated from the values in the isotones (solid lines) and from the ESPE calculations (dashed lines). Data are from Refs. [50,51,52].
One can see from Figure 6 that the measurements are in a good agreement with the calculations based on the SDPF-MU and SDPF-MUs interactions. The SDPF-MUs interaction achieves better agreement because its shell gap on for the Si core is improved (see Section 3.2.2). These two interactions are quite successful in reproducing the slope of .
As one can also see from Figure 6, the slope is quite similar to what the ESPE predicts. Since the and values are kept unchanged in making the SDPF-MUs interaction based on SDPF-MU, the ESPEs are parallel. On the other hand, these ESPEs are shifted downward in parallel from by MeV. This difference arises from the assumption of the closure taken here to evaluate the ESPE.
However, in reality, a significant number of neutron excitations to occur in the Ne, Mg, and Si eigenstates. These neutron excitations attract a neutron in the orbital more than a one in because the monopole matrix element of - is more attractive than that of -, thus, shifting upward. Such significant neutron excitation to occurs similarly in the Ne, Mg, and Si isotopes. Hence, the evolution of is predominantly changed by the ESPE, providing evidence for the narrowing shell gap caused by the monopole matrix element .
It should be noted that the predicted at is closer to the ESPE estimate than those of other isotopes. This is due to the fact that the assumed closure works better at due to the occurrence of the magic number.
4. Conclusions
In this paper, an almost complete survey of proton and neutron shell evolution for atomic mass number neutron-rich nuclei is performed on the basis of shell-model calculations, in order to understand how well the observed evolution is explained with a simple monopole-based universal interaction, .
On the proton side, the observed one-proton removal spectroscopic distributions in Ca were very well reproduced with shell-model calculations, pointing to a MeV change of - spin–orbit splitting. Since this change is caused almost solely by the tensor force, this agreement quantitatively confirms the validity of a meson exchange tensor force in the interaction. The - level difference in K isotopes changes the sign twice, with filled and with filled.
As discussed, this change is caused by the “reinversion” of single-particle level ordering between and as a result of the non-monotonic evolution of these level spacings. Such a manner of evolution cannot be produced by one-body potential models, and therefore it is strong evidence for the dominant role of two-body forces in shell evolution. In this particular case, the non-monotonic evolution observed in K isotopes is driven by the central force.
On the neutron side, the neutron-number shell gap is reduced with protons removed from the and orbitals, dominated by the central force. The relevant single-particle-like levels are well reproduced by the shell-model calculation. In addition, the central force causes the enhancement of the shell gap for the atomic-number isotopes. This effect well accounts for the recently observed level in Ar.
In this way, the present scheme, based on , provides a successful description of the shell evolution. Neutron shell evolution in exotic nuclei is often argued in the context of weak binding. In the present study, we were successful in obtaining not only neutron shells but also proton shells that were free from weak binding. Thus, such a unified description strongly indicates the dominance of the effective interaction in shell evolution, as far as the region of the present study is concerned, including the narrowing shell gap toward a neutron-rich nuclei.
Funding
This work was supported in part by JSPS KAKENHI Grant Numbers 20K03981 and 15K05094.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks Takaharu Otsuka for valuable discussions on shell evolution and thank Noritaka Shimizu for his help with large-scale shell-model calculations.
Conflicts of Interest
The author declares no conflict of interest.
References
- Otsuka, T.; Gade, A.; Sorlin, O.; Suzuki, T.; Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 2020, 92, 015002. [Google Scholar] [CrossRef] [Green Version]
- Talmi, I.; Unna, I. Order of Levels in the Shell Model and Spin of Be11. Phys. Rev. Lett. 1960, 4, 469–470. [Google Scholar] [CrossRef]
- Bansal, R.; French, J. Even-parity-hole states in f7/2-shell nuclei. Phys. Lett. 1964, 11, 145–148. [Google Scholar] [CrossRef]
- Poves, A.; Zuker, A. Theoretical spectroscopy and the fp shell. Phys. Rep. 1981, 70, 235–314. [Google Scholar] [CrossRef]
- McGrory, J.B.; Wildenthal, B.H.; Halbert, E.C. Shell-Model Structure of 42−50Ca. Phys. Rev. C 1970, 2, 186–212. [Google Scholar] [CrossRef]
- Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef] [Green Version]
- Storm, M.H.; Watt, A.; Whitehead, R.R. Crossing of single-particle energy levels resulting from neutron excess in the sd shell. J. Phys. Nucl. Phys. 1983, 9, L165–L168. [Google Scholar] [CrossRef]
- Warburton, E.K.; Becker, J.A.; Brown, B.A. Mass systematics for A = 29–44 nuclei: The deformed A ~32 region. Phys. Rev. C 1990, 41, 1147–1166. [Google Scholar] [CrossRef] [Green Version]
- Federman, P.; Pittel, S. Towards a unified microscopic description of nuclear deformation. Phys. Lett. B 1977, 69, 385–388. [Google Scholar] [CrossRef]
- Otsuka, T.; Fujimoto, R.; Utsuno, Y.; Brown, B.A.; Honma, M.; Mizusaki, T. Magic numbers in exotic nuclei and spin-isospin properties of the NN interaction. Phys. Rev. Lett. 2001, 87, 082502. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Otsuka, T.; Mizusaki, T.; Honma, M. Varying shell gap and deformation in N ∼ 20 unstable nuclei studied by the Monte Carlo shell model. Phys. Rev. C 1999, 60, 054315. [Google Scholar] [CrossRef]
- Otsuka, T.; Suzuki, T.; Fujimoto, R.; Grawe, H.; Akaishi, Y. Evolution of nuclear shells due to the tensor force. Phys. Rev. Lett. 2005, 95, 232502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otsuka, T.; Suzuki, T.; Honma, M.; Utsuno, Y.; Tsunoda, N.; Tsukiyama, K.; Hjorth-Jensen, M. Novel features of nuclear forces and shell evolution in exotic nuclei. Phys. Rev. Lett. 2010, 104, 012501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burgunder, G.; Sorlin, O.; Nowacki, F.; Giron, S.; Hammache, F.; Moukaddam, M.; de Séréville, N.; Beaumel, D.; Càceres, L.; Clément, E.; et al. Experimental Study of the two-body spin-orbit force in nuclei. Phys. Rev. Lett. 2014, 112, 042502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smirnova, N.; Bally, B.; Heyde, K.; Nowacki, F.; Sieja, K. Shell evolution and nuclear forces. Phys. Lett. B 2010, 686, 109–113. [Google Scholar] [CrossRef] [Green Version]
- Tsunoda, N.; Otsuka, T.; Tsukiyama, K.; Hjorth-Jensen, M. Renormalization persistency of the tensor force in nuclei. Phys. Rev. C 2011, 84, 044322. [Google Scholar] [CrossRef]
- Yuan, C.; Suzuki, T.; Otsuka, T.; Xu, F.; Tsunoda, N. Shell-model study of boron, carbon, nitrogen, and oxygen isotopes with a monopole-based universal interaction. Phys. Rev. C 2012, 85, 064324. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Otsuka, T.; Brown, B.A.; Honma, M.; Mizusaki, T.; Shimizu, N. Shape transitions in exotic Si and S isotopes and tensor-force-driven Jahn-Teller effect. Phys. Rev. C 2012, 86, 051301. [Google Scholar] [CrossRef] [Green Version]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction GXPF1. Eur. Phys. J. Hadron. Nucl. 2005, 25, 499–502. [Google Scholar] [CrossRef]
- Richter, W.; Van Der Merwe, M.; Julies, R.; Brown, B. New effective interactions for the 0f1p shell. Nucl. Phys. A 1991, 523, 325–353. [Google Scholar] [CrossRef]
- Utsuno, Y.; Otsuka, T.; Shimizu, N.; Honma, M.; Mizusaki, T.; Tsunoda, Y.; Abe, T. Recent shell-model results for exotic nuclei. Epj Web Conf. 2014, 66, 02106. [Google Scholar] [CrossRef] [Green Version]
- Bertsch, G.; Borysowicz, J.; McManus, H.; Love, W. Interactions for inelastic scattering derived from realistic potentials. Nucl. Phys. A 1977, 284, 399–419. [Google Scholar] [CrossRef]
- Brown, B.A.; Wildenthal, B.H. Status of the nuclear shell model. Annu. Rev. Nucl. Part. Sci. 1988, 38, 29–66. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. Effective interaction for pf-shell nuclei. Phys. Rev. C 2002, 65, 061301. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Shimizu, N.; Otsuka, T.; Yoshida, T.; Tsunoda, Y. Nature of Isomerism in Exotic Sulfur Isotopes. Phys. Rev. Lett. 2015, 114, 032501. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, N.; Mizusaki, T.; Utsuno, Y.; Tsunoda, Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput. Phys. Commun. 2019, 244, 372–384. [Google Scholar] [CrossRef] [Green Version]
- Cottle, P.D.; Kemper, K.W. Persistence of the N = 28 shell closure in neutron-rich nuclei. Phys. Rev. C 1998, 58, 3761–3762. [Google Scholar] [CrossRef]
- Sorlin, O.; Porquet, M.G. Nuclear magic numbers: New features far from stability. Prog. Part. Nucl. Phys. 2008, 61, 602–673. [Google Scholar] [CrossRef] [Green Version]
- Banks, S.; Spicer, B.; Shute, G.; Officer, V.; Wagner, G.; Dollhopf, W.; Qingli, L.; Glover, C.; Devins, D.; Friesel, D. The 48Ca(, 3He)47K reaction at 80 MeV. Nucl. Phys. A 1985, 437, 381–396. [Google Scholar] [CrossRef]
- Doll, P.; Wagner, G.; Knöpfle, K.; Mairle, G. The quasihole aspect of hole strength distributions in odd potassium and calcium isotopes. Nucl. Phys. A 1976, 263, 210–236. [Google Scholar] [CrossRef]
- Go, S.; Ideguchi, E.; Yokoyama, R.; Aoi, N.; Azaiez, F.; Furutaka, K.; Hatsukawa, Y.; Kimura, A.; Kisamori, K.; Kobayashi, M.; et al. High-spin states in 35S. Phys. Rev. C 2021, 103, 034327. [Google Scholar] [CrossRef]
- Papuga, J.; Bissell, M.L.; Kreim, K.; Blaum, K.; Brown, B.A.; De Rydt, M.; Garcia Ruiz, R.F.; Heylen, H.; Kowalska, M.; Neugart, R.; et al. Spins and Magnetic Moments of 49K and 51K: Establishing the 1/2+ and 3/2+ Level Ordering Beyond N = 28. Phys. Rev. Lett. 2013, 110, 172503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Obertelli, A.; Doornenbal, P.; Barbieri, C.; Chazono, Y.; Duguet, T.; Liu, H.; Navrátil, P.; Nowacki, F.; Ogata, K.; et al. Restoration of the natural E(1/) − E(3/) energy splitting in odd-K isotopes towards N = 40. Phys. Lett. B 2020, 802, 135215. [Google Scholar] [CrossRef]
- Grasso, M.; Ma, Z.Y.; Khan, E.; Margueron, J.; Giai, N.V. Evolution of the proton sd states in neutron-rich Ca isotopes. Phys. Rev. C 2007, 76, 044319. [Google Scholar] [CrossRef] [Green Version]
- Nakada, H.; Sugiura, K.; Margueron, J. Tensor-force effects on single-particle levels and proton bubble structure around the Z or N = 20 magic number. Phys. Rev. C 2013, 87, 067305. [Google Scholar] [CrossRef] [Green Version]
- Kirson, M. Spin-tensor decomposition of nuclear effective interactions. Phys. Lett. B 1973, 47, 110–114. [Google Scholar] [CrossRef]
- Piskoř, Š.; Franc, P.; Křemének, J.; Schäferlingová, W. Spectroscopic information on 35S and 37S from the (d, p) reaction. Nucl. Phys. A 1984, 414, 219–239. [Google Scholar] [CrossRef]
- Uozumi, Y.; Kikuzawa, N.; Sakae, T.; Matoba, M.; Kinoshita, K.; Sajima, S.; Ijiri, H.; Koori, N.; Nakano, M.; Maki, T. Shell-model study of 40Ca with the 56-MeV (, p) reaction. Phys. Rev. C 1994, 50, 263–274. [Google Scholar] [CrossRef]
- Evaluated Nuclear Structure Data File (ENSDF). Available online: http://www.nndc.bnl.gov/ensdf/ (accessed on 1 January 2022).
- Lu, F.; Lee, J.; Tsang, M.B.; Bazin, D.; Coupland, D.; Henzl, V.; Henzlova, D.; Kilburn, M.; Lynch, W.G.; Rogers, A.M.; et al. Neutron-hole states in 45Ar from 1H(46Ar, d) 45Ar reactions. Phys. Rev. C 2013, 88, 017604. [Google Scholar] [CrossRef] [Green Version]
- Momiyama, S.; Wimmer, K.; Bazin, D.; Belarge, J.; Bender, P.; Elman, B.; Gade, A.; Kemper, K.W.; Kitamura, N.; Longfellow, B.; et al. Shell structure of 43S and collapse of the N = 28 shell closure. Phys. Rev. C 2020, 102, 034325. [Google Scholar] [CrossRef]
- Chen, S.; Lee, J.; Doornenbal, P.; Obertelli, A.; Barbieri, C.; Chazono, Y.; Navrátil, P.; Ogata, K.; Otsuka, T.; Raimondi, F.; et al. Quasifree neutron knockout from 54Ca corroborates arising N = 34 neutron magic number. Phys. Rev. Lett. 2019, 123, 142501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steppenbeck, D.; Takeuchi, S.; Aoi, N.; Doornenbal, P.; Matsushita, M.; Wang, H.; Baba, H.; Fukuda, N.; Go, S.; Honma, M.; et al. Evidence for a new nuclear ‘magic number’ from the level structure of 54Ca. Nature 2013, 502, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Utsuno, Y.; Otsuka, T.; Tsunoda, Y.; Shimizu, N.; Honma, M.; Togashi, T.; Mizusaki, T. Recent advances in shell evolution with shell-model calculations. JPS Conf. Proc. 2015, 6, 010007. [Google Scholar] [CrossRef] [Green Version]
- Steppenbeck, D.; Takeuchi, S.; Aoi, N.; Doornenbal, P.; Matsushita, M.; Wang, H.; Utsuno, Y.; Baba, H.; Go, S.; Lee, J.; et al. Low-Lying Structure of 50Ar and the N = 32 Subshell Closure. Phys. Rev. Lett. 2015, 114, 252501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.N.; Obertelli, A.; Doornenbal, P.; Bertulani, C.A.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Schwenk, A.; Stroberg, R.; et al. How robust is the N = 34 subshell closure? First spectroscopy of 52Ar. Phys. Rev. Lett. 2019, 122, 072502. [Google Scholar] [CrossRef] [Green Version]
- Rotaru, F.; Negoita, F.; Grévy, S.; Mrazek, J.; Lukyanov, S.; Nowacki, F.; Poves, A.; Sorlin, O.; Borcea, C.; Borcea, R.; et al. Unveiling the Intruder deformed state in 34Si. Phys. Rev. Lett. 2012, 109, 092503. [Google Scholar] [CrossRef] [Green Version]
- Mutschler, A.; Lemasson, A.; Sorlin, O.; Bazin, D.; Borcea, C.; Borcea, R.; Dombrádi, Z.; Ebran, J.P.; Gade, A.; Iwasaki, H.; et al. A proton density bubble in the doubly magic 34Si nucleus. Nat. Phys. 2017, 13, 152–156. [Google Scholar] [CrossRef] [Green Version]
- Kay, B.P.; Hoffman, C.R.; Macchiavelli, A.O. Effect of weak binding on the apparent spin-orbit splitting in nuclei. Phys. Rev. Lett. 2017, 119, 182502. [Google Scholar] [CrossRef] [Green Version]
- Brown, S.M.; Catford, W.N.; Thomas, J.S.; Fernández-Domínguez, B.; Orr, N.A.; Labiche, M.; Rejmund, M.; Achouri, N.L.; Al Falou, H.; Ashwood, N.I.; et al. Low-lying neutron f p-shell intruder states in 27Ne. Phys. Rev. C 2012, 85, 011302. [Google Scholar] [CrossRef] [Green Version]
- Matta, A.; Catford, W.N.; Orr, N.A.; Henderson, J.; Ruotsalainen, P.; Hackman, G.; Garnsworthy, A.B.; Delaunay, F.; Wilkinson, R.; Lotay, G.; et al. Shell evolution approaching the N = 20 island of inversion: Structure of 29Mg. Phys. Rev. C 2019, 99, 044320. [Google Scholar] [CrossRef]
- Piskoř, Š.; Novák, J.; Šimečková, E.; Cejpek, J.; Kroha, V.; Dobeš, J.; Navrátil, P. A study of the 30Si(d, p)31Si reaction. Nucl. Phys. A 2000, 662, 112–124. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).