Abstract
An acoustoelectric approach to neuron function is proposed that combines aspects of the widely accepted electrical-circuit-based Hodgkin–Huxley model for the generation and propagation of action potentials via electric polarization with mechanical models based on propagation via capillary waves. Explaining measured velocities of action potentials quantitatively, it also predicts the electrical tunability of highly anisotropic polarization packages that surf on the dynamic mechanical force field deforming the neuron membrane. It relies substantially on the local motion of dipoles formed by excess charges close to the inside surface of the neuron membrane, which in turn are anisotropically screened by water molecules in their hydration shell, thus modulating the strong electric field at the interface. As demonstrated on acoustic resonators of suspended nanowires fabricated out of amorphous dipolar silicon nitride, high electric fields combined with predominantly axial-strain modulation can cause transverse acoustoelectric polarization waves that propagate soliton-like with extremely low loss. In neurons, the modulation of electric polarization is confined in the nanometer-thin skin of a high electric field inside the neuron membrane and propagates phase-coherent along the axon as a lowest-order one-dimensional breathing mode, similar to transverse polarization pulses studied in nanowire resonators. Some experiments for the further manifestation of the model as well as topological protection of such breathing-mode polarization waves are discussed.
1. Introduction
The generation and propagation of action potentials in neurons are generally described by an electric model proposed by Hodgkin and Huxley [1] that has been very useful for explaining the generation of electric polarization confined close to the lipid membrane of a neuron via gated injection of excess charges through ion channels. To explain the slowdown of the polarization pulse signals along the neuron from close to the velocity of light of c = 3 × 108 m/s in usual electromagnetic wave guides to measured propagation velocities of action potentials, ranging between 1 and 100 m/s, it employs a rather dissipative RC-network of resistors R and capacitors C with RC time constants in the range of milliseconds. It ignores the mechanical motion of the confining elastic membrane of a neuron and the presence of dipolar screening of ionic charges through the omnipresent dipolar H2O molecules that tend to form a hydration shell around any local ionic charge. In contrast, there have been several mechanical models proposed starting with work by Helmholtz in 1850 [2], followed by Wilke (1912) [3], Tasaki et al. (1949) [4], Heimburg and Jackson (2005) [5], and Engelbrecht et al. [6]. All of these are discussed in conjunction with the Hodgkin–Huxley model in extensive recent reviews by Peyrard [7] and Holland et al. [8].
I became aware of the different mechanics-based approaches in 2018 through a talk by Matthias Schneider presented at the NIM conference “The Future of Nanoscience”, organized by the excellence initiative “Nanosystems Initiative Munich (NIM)” in September 2018 based on previous publications, e.g., [9,10] and an article by Douglas Fox on “The Brain Reimagined” published in April 2018 [11]. Both raised my curiosity and I started studying the relevant literature to better understand these mechanical concepts without getting fully convinced by the proposed models. With my own participation in collaborative experiments on ballistic transport of excitonic dipoles via surface acoustic waves (SAW) [12] and studies of acoustoelectric generated sound pulses propagating in high-quality nanostring resonators [13,14,15] I started to develop my own approach to a soliton-like propagation [16] of dielectric polarization [17]. Then, already retired for several years and without any student support and suitable laboratory, I got engaged in conceptional work combined with simple experimental studies to develop the model based on acoustoelectric generation and propagation of action potentials. I learned that individual soliton-like acoustic pulses can transport highly complex information content about their generating source and their propagation path and carry nearly undamped and phase-coherent energetic acoustoelectric wave packets that can be transformed into presumably phase-coherent electrochemical processes at synaptic transfer positions between neurons. Here, the term acoustoelectric should be understood rather generally, namely that propagating anisotropic deformations can cause propagating electric potentials with both longitudinal and transverse components of essentially a piezoelectric nature as in semiconducting [12] or insulating solid materials, e.g., [13,14,15] and, relying on ionic charge-density-dependent interactions in incompressible liquids, also mechanically caused transient changes of conductance involving partially diffusive charge propagation. Electrolytes near mechanically deformable interfaces can support both but, as discussed in detail below, the coherent propagation of interfacial polarization via rotation of water dipoles in neurons is likely to dominate the incoherent transport of ionic charges. Potentially, it, thus, can exchange information between our feet and our brain to perform analog computation and data storage with phase-coherent soliton-like hydro-acoustoelectric wave packets, somewhat similar to holography with light waves. At least, the concept of coherent information exchange via acoustoelectric waves that act as a conveyor belt for charge-neutral polarization signals, e.g., [12], is similar to the speech exchange in a tin-can telephone and is able to propagate complex information through a tensional prestressed, quasi-one-dimensional tubular system, filled with an incompressible water-based electrolyte.
Figure 1 displays schematically the structure of a neuron, consisting of the soma as the generator of acoustoelectric action potentials, the axon as a waveguide for the propagation of soliton-like action potentials as indicated by the yellow center and the synaptic terminals as transducers which coherently transduce action potentials via chemical and/or electromechanical processes to other neurons or cells acting as sensors. The acoustoelectric approach based on capillary interface waves directly explains the measured propagation velocities of action potentials and also gives reasonable estimates of the signal strength it generates and transports. It can explain the design of the soma and its dendritic arms filled with individual ion channels to generate specific pulse shapes that carry information about their sender. It can also explain the action of myelination [18] to modulate propagation velocities of action potentials and act as coupled acoustoelectric resonators that can focus energy onto the nodes of Ranvier to activate ion channels through force gradients. Possibly, it can explain why nature has chosen spiral molecules in the myelinated walls to control wave chirality and to act as acoustoelectric resonators filtering the wavelength and chirality of overtones. It also provides nonlinear enhancements of the tangential strain of the axon membrane and electric fields near the nodes of Ranvier to enable the electric-field-controlled opening of nearby ion channels. Possibly, the underlying physics can also explain long-established concepts in medical treatment such as acupuncture and osteopathic treatment since its main ingredients are based on water-based oscillating electrolytes in flexible tubing combined with electromechanical or chemical actuation.
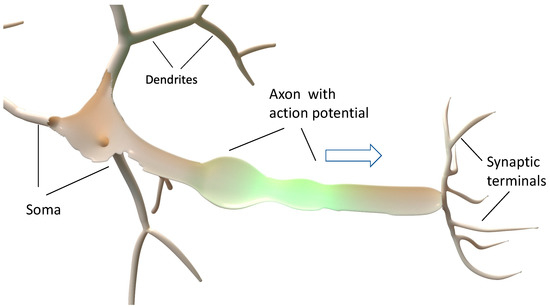
Figure 1.
Schematic sketch of a neuron. The action potential is generated in the soma and its dendrites, propagates soliton-like along the axon, and is transduced by the synaptic terminals to other neurons or sensor cells.
Of course, further experimental and theoretical work is needed to quantitatively confirm the concept introduced here. Experimentally, one needs to verify the phase-coherent and chiral propagation of action potentials as discussed below by optical monitoring the spatial and temporal behavior of propagating action potentials with high resolution, e.g., by employing fluorescent local optical emitters [18], interferometric detection [19,20], magnetooptic sensors [21], and electric-field-dependent optical phenomena such as the Franz–Keldysh effect [22]. Spectral analysis using optical, mechanical, and electromagnetic methods can also enable a wide-band Fourier-transform analysis of the frequency components of the shapes of individual action potentials without smoothing the pulses by external RC-time constants [23]. Optics can confirm the mechanical and electrical signatures of interfacial waves and detect the one-dimensional phase-coherent acoustoelectric propagation of confined electrical polarization by interface acoustic waves [12]. Theoretical work with finite-element calculations should help to quantitatively model the here-discussed propagation of a rather long wavelength and low amplitude interfacial waves with reasonable boundary conditions. A Monte Carlo-type calculation could improve insight into the dynamics of propagating polarization waves at the molecular scale.
2. Some Essentials of Acoustoelectric Communication
Whenever we communicate by speech or sounds, we rely on the fact that the material through which we wish to transmit analog-encoded information allows us to propagate acoustic waves phase coherently without frequency dispersion. This implies that the phase velocity is equal to the group velocity and is frequency independent for all relevant frequencies that transfer complex information. Single-frequency sinusoidal waves can be amplitude- and phase-modulated but contain little information with only those two independent parameters. In contrast, speech and sounds are usually composed of rather complex components of different amplitudes and frequencies such as overtones that need to propagate phase coherently in order to be recognizable by the receiver. This way, we can enjoy a concert only in an environment in which sounds of different frequencies propagate directed and phase coherent with the same velocity between the emitting instruments and the listener’s ears across a range of sufficiently small distances that do not yet cause serious dephasing via temporal delays caused by elastic scattering and, thus, avoiding echo phenomena. In addition, frequency-dependent damping on the direct route of transmission will not only weaken the signal but also distort the desired communication.
As an alternative to continuous wave acoustic communication employing amplitude and frequency modulation, one can utilize short click sounds as done by dolphins and whales [24,25]. Their short sound pulses can be encoded with a rather broad frequency spectrum and thus, again, rely on a medium in which a wide-frequency spectrum can be propagated phase coherently with essentially frequency-independent velocity and damping. This is the case for longitudinal sound waves in the air and other compressible isotropic media such as water but also for water–air interface waves propagating with wavelengths λ > 0.05 h in the shallow water of depth h. In this way, longitudinal shock waves pulses caused by an earthquake in Chile and originally propagating with the sound velocity of bulk water cs but propagate at the water–air interface with dispersion with the phase velocity for depths h > λ with g being the gravitational constant g and transforms again into nondispersive waves in shallow water of fixed depth h with and h < 0.05 that can pile up into a tsunami. Since water is nearly incompressible, volume pressure waves as well as surface waves preserve phase information rather well for each frequency component and, thus, are a little damped if they propagate in laminar flow without creating vortices. This is because internal friction is avoided by the strongly repulsive forces between the dipolar water molecules and bulk and interfacial waves are created by the rather small local motion of water molecules in elliptic orbits oriented along a plane spanned by the direction of wave propagation and its normal.
A quite different behavior was discovered in 1834 by John Scott Russell in a narrow water channel guiding a nonequilibrium pulse wave. There, he observed that a single gravitational surface wave pulse can propagate along the quasi-one-dimensional channel without shape change and very little damping, as exemplarily shown in Video 2 of Appendix A. The conditions to create such a solitary excitation were explained later by Korteweg and de Vries (KdV) by a nonlinear differential equation [16]. A similar solitonic behavior is observed in water-filled steel pipes as well as in train rails where sound pulses propagate with very little damping when confined to one-dimensional propagation. There, the frequency-filter effect that is provided for interfacial sound waves in a periodically clamped train rail may help train robbers detect early an approaching train.
The reduced damping of waves propagating at low frequency with a rather long wavelength in a spatially confined medium can also be understood through the absence of other excitations via which decay can occur under conservation of energy and linear and/or angular momentum by either direct decay or by inelastic scattering. This has already been recognized in studies of the damping of long-wavelength collective resonances of coupled magnetic dipoles such as ferromagnetic and antiferromagnetic resonance modes as well as standing spin-wave modes about 50 years ago. There, suitable sample preparation largely suppressed internal damping at low temperatures by a reduction of magnetic surface roughness scattering and enabled magnetic resonance quality factors Q = ν/Δν at microwave frequencies of order 100.000. This even allowed for the study of radiative broadening of such collectively oscillating magnetic dipole ensembles as limiting the resonance linewidth [26]. A related reduction of damping mechanisms of long-wavelength collective acoustic resonance modes was observed nearly two decades ago in discovering very high Q-values beyond Q > 100.000 in nanostring acoustic resonators fabricated out of insulating silicon nitride [27].
3. Learning the Magic of High-Quality Acoustic Resonators on Insulating Nanowires
This motivated me to study, with my junior collaborators, the damping of transverse acoustic resonances in nanowires of the dipolar-insulator silicon nitride in an effort to understand the damping mechanisms of such quasi-one-dimensional acoustic resonators suspended between two supports and studied in a vacuum at different temperatures. Rather soon we were able to largely understand the strong increase of Q to above 100.000 by the decoupling of highly elastic axial motion from a more lossy bending motion via tensional axial tensional prestress [13]. Furthermore, we were able to excite acoustic resonances efficiently through externally imposed electric gradient fields coupling to the field-effect-induced electrical polarization of silicon nitride as illustrated in Figure 2 [14].
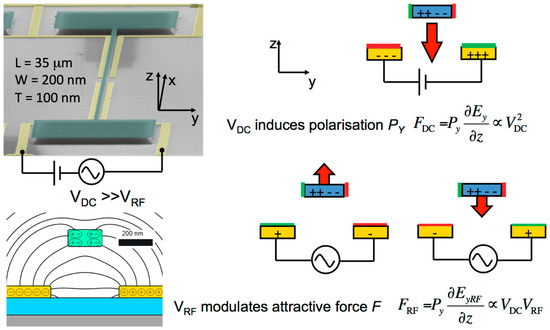
Figure 2.
An electron micrograph of a typical silicon nitride string resonator of length L, width W, and height T with its supports (green) is jointly displayed with a cross-sectional cut of the silicon substrate (grey), a SiO2 insulating layer (blue), and the supported electrodes (yellow). The right-side sketches how a static electric field Ey polarizes the string and an oscillating electric field EyRF initiates radio frequency mechanic resonance modes at MHz frequencies.
This way we could study the coherent coupling of the two lowest string modes exhibiting an energy gap reflecting the anticrossing of the two lowest radial modes [15]. Simulating the motion of the electric polarization vector in the energetic regime adjacent to the anticrossing, we discovered the chiral character of the coupled resonance modes as illustrated in Video 1 listed in Appendix A (also listed in the supplementary information of [15]. This enabled us to perform spin-echo-type resonance experiments with coherent polarization pulses between the two modes on a Bloch-like electrical polarization sphere, resulting in the observation of Rabi oscillations, Ramsey fringes, and Hahn echos of coherent classical polarization signals [15]. We could thus separate the inelastic energy decay rate 1/T1 from elastic phase decay processes governed by 1/T2 and discovered that the energy loss via the resonator supports was significantly larger than the phase decay rate by elastic processes in the studied strings with Q ≈ 200.000. The usually linearly polarized transverse vibrational modes can be decomposed into two circularly polarized chiral modes that propagate along a given string direction with opposite chirality, thus forming a transverse oscillating standing wave if excited by transverse forces alone. In pulsed experiments with suitably chosen pulse lengths, one axially directed chiral mode is preferred but will be reflected with opposite chirality in a node defined by the position of the support. The overlap with the incoming mode will again form a standing mode with equal reflection at both supports of the string. The abrupt impedance change at the support induces coupling to other higher order modes in the substrate and, thus, allows the more efficient transfer of energy from the long wavelength string modes into the mode mixtures occurring in the support. This explains at least qualitatively why energy relaxation becomes more efficient than elastic phase relaxation if long wavelength transverse resonator phonons of one chiral mode can decay into shorter wavelength phonons in the support by inelastic scattering removing energy from the oscillating nanoelectromechanical System (NEMS).
To reduce this decay process via the string support and to further increase the quality factor of such nanostring vibrations, the Lausanne team around T. Kippenberg modified the acoustic impedance along the string axis by a periodic axial strain modulation acting as a quasi-one-dimensional acoustic Bragg mirror [28]. This strain engineering resulted in extremely high Q-factors now exceeding 109 at room temperature. This demonstrates that mode mixing and decay of such quasi-one-dimensional resonator modes are drastically reduced by confining them axially in the central region of the acoustic string resonator, thus preserving the phase-coherent character of the chiral modes. Combined with the decoupling of bending motion from predominantly elastic axial motion via the tensile prestress of such nanostrings, this results in very low inelastic and elastic damping and high resonator Q-factors.
Since the motion of the chiral polarization modes is maximal close to the surface of the strings, the fundamental modes are donut-like and can be considered to be topologically protected through their quasi-one-dimensional, predominantly chiral character. The axial motion is driven by the coupling of the field-effect-induced dipolar polarization of the silicon nitride strings with the driving gradient potential which combines both an axial as well as a radial component to determine the chiral motion of the polarization vector around the string axis. Consequently, the gradient force excitation of the polarization vector couples the translational axial momentum with the radial torque in analogy to the spin-orbit interaction in coupled magnetic dipole chains. Most likely, this topological protection of the purity of the relevant chiral modes enables the extremely high Q-factors observed even at room temperature.
4. Capillary Waves as Carrier of Information in Neurons
Capillary waves are collective acoustical excitations that can propagate at interfaces between a liquid and another medium at which capillary forces act on the interfacial boundary. They are easily observed as short wave-length waves when a stone is thrown into the plane surface of a lake. At such a two-dimensional interface between an essentially incompressible liquid and, e.g., air, surface tension induced by deformation of the original plane interface causes a restoring force perpendicular to the interface acting opposite to the gravitational force. Capillary waves on a flat two-dimensional interfacial plane exhibit an abnormal dispersion and—in contrast to long-wavelength shallow water waves caused by gravity as restoring force—have an increase of the propagation velocity with decreasing wavelength. Therefore superposition of capillary waves with different frequencies washes out at large distances from their source of generation. This character changes if one confines such interface waves to one-dimensional propagation.
Capillary waves of an incompressible liquid confined in tubes of diameter D by a thin elastic membrane of thickness d << D were described independently by Moens and Korteweg in 1878 in an effort to understand the propagation of pulse waves in arteries (Moens) and sound waves in steel pipes (Korteweg) and are discussed in detail in a recent review [29]. Moens and Korteweg showed independently that such interfacial waves propagate as breathing-mode acoustic waves essentially without dispersion, i.e., with frequency-independent velocity given by the Moens–Korteweg equation:
For tubular elastic hoses confined by a lipid membrane with an isotropic two-dimensional elastic modulus κ = Ed ≈ 0.1 N/m (with Young modulus E) filled with a water-dominated electrolyte of density ρ ≈ 1 Kg/L and with diameter D ≈ 10 μm, one finds a propagation velocity of cC ≈ 3 m/s, comparable to the measured propagation velocities of action potentials in not-myelinated axons. With a period of T ≈ 1 ms, the wavelength of the fundamental breathing mode is . Since the elastic properties of lipid membranes contain nonlinear terms, it seems possible that they can exhibit solitary propagation following the Korteweg–de-Vries (KdV) equation mentioned above [16]. Actually, this was proposed and studied by Heimburg and Jackson [5] with a thermodynamic approach. This approach was not generally accepted because it ignored the role of ion injection in the generation of action potentials. Apparently, the authors also did not recognize the role of water dipoles for screening the ionic Coulomb potential and by mediating via their oscillatory motion with respect to the inside of the membrane long-range torsional forces between the excess charges fixed to positions on the membrane and the interfacial water dipoles in the liquid-crystal-like high-field Debye skin of thickness t~1 nm, as will be discussed below. Their model seems to assume thermodynamic equilibrium whereas the approach that is used here is based on solitary nonequilibrium collective capillary wave excitations that propagate particle-like ballistically because damping is considered to be negligible and transport electrical polarization by axially moving electro-mechanical potential gradients near the electrolyte-membrane interface.
5. Approaching the Mechanism of the Propagation of Action Potentials in Neurons
In principle, I want to demonstrate that a neuron can be considered as a complex acoustoelectric resonator system in which the local injection of ions triggers a quasi-ballistically propagating KdV-soliton-like action potential pulse that is phase-coherently transported by an axially propagating acoustoelectric interface excitation with an essentially constant group velocity [16]. Since a neuron, as displaced in Figure 1, consists of mostly tubular components, let us consider an axon-like tube, as displayed in Figure 3, of length L and diameter D with L >> D = 2R and λc >> D confined by a thin elastic bilipid membrane of thickness d ≈ 7 nm and closed at both ends with the soma and the synaptic terminal, respectively. The axon is filled with a water-based incompressible electrolyte and experiences a tensile prestress by an internal hydrostatic overpressure of typically 104 Pa, predominantly caused by hypertonic osmotic forces. Note that the length scales in Figure 3 are drastically distorted as for the example axon used here; we have L~1 m, λc = 3 mm, D = 10 μm, and d ≈ 7 nm, t ≈ 1 nm.
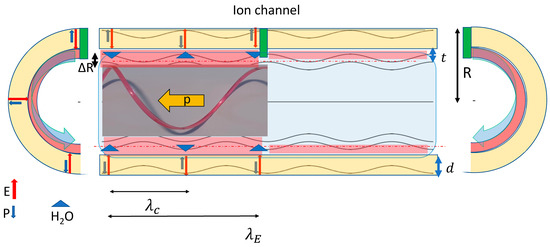
Figure 3.
Generation of chiral components of an action potential via injection of positively charged ions via an ion channel (green) which locally depolarizes and repolarizes the high field cylindrical Debye skin of thickness t (red) of a tubular axon of radius R. The local depolarization generates 4 chiral wave components propagating into opposing axial directions. For a given axial direction, two opposing chiral components create a breathing-mode capillary wave propagating near the electrolyte membrane interface along a spiral path (as indicated on the left of the ion channel for the right-hand polarized spiral. Here the red line visualizes the 3D nature of the spiral moving with momentum p, whereas the blue line presents a projection into the 2D axial plane) with the two opposing angular momenta MR and ML created by the ion-current pulse injected into the high electric-field region between the inside of the tubular lipid membrane of thickness d (yellow) and the Debye region in the electrolyte of thickness t (red). The capillary pulse wavelength λC is half the axial wave-length λE of the electric-field component E⊥ perpendicular to the membrane capacitor and the change of the local tube radius ΔR propagating with the capillary wave causes an enhanced axial polarization by the locally redistributed ionic charge and the anisotropic oscillating water dipoles as discussed in the main text.
Without electric bias across the neuron membrane, one would expect the polarization of water molecules near the lipid membrane to arrange antiferroelectrically in a predominantly laminar fashion to minimize their orientational polarization P⊥ oriented perpendicular to the membrane at any given temperature. Uniformly charging the membrane capacitor by providing excess ionic charges at the membrane interior through a bias voltage will induce a finite polarization of the membrane as well of the adjacent water molecules that form a hydration shell around the ions, at least partially screening the Coulomb potential of the locally bound ionic excess charges. With the outside potential of the neuron at potential V = 0, neurons at rest exhibit a typical inside bias voltage of V0 ≈ −70 mV. That generates a bare electric field of strength E0 ≈ 107 V/m. The resulting excess ionic charges attracted to the inside of the membrane form a dipolar polarization oriented perpendicular to the membrane–electrolyte interface opposing the bare electric field and are screened by the dipolar hydration shell toward the charge-neutral cylindrical bulk electrolyte within a Debye length of typically t ≈ 1 nm. The resulting voltage-dependent force acts perpendicular to the membrane and increases the tube radius at the rest voltage V0 by ΔR as shown by the colored sections on the right-hand side of Figure 3. If one would now apply in a quasi-stationary picture an inside bias oscillating in proportion to V0 cosz one would get a spatially oscillating membrane with amplitude ΔR~ΔF⊥, as shown in Figure 3.
From derivative δW/δR of the energy W of the cylindrical capacitor radius R and length L with W= ½ CV2 = (πRLε0/d)V2 and the fact that the membrane thickness d does not noticeably change with voltage V, the dipolar force per unit length that increases the radius of the tube is:
With the above values of V0, d, and one obtains with F⊥/L = κΔR/R an increase in tube radius of ΔR ≈ 2 nm as roughly indicated in Figure 3. This value compares reasonably well with typically observed radial deformations of axons caused by a transient action potential [5,19]. Correspondingly, one can estimate the shear angle Θ ≈ RΦ/(λc/4) with Φ = 90° by which the surface normal of the capillary wave is maximally tilted with respect to the normal of the membrane–electrolyte interface at rest. With the numbers above, one estimates Θ ≈ 1 degree. This seems too small to expect a sufficiently large axial polarization but note that the shear angle determines only the axis around which the polarization vector rotates. This will be discussed in detail below.
The left portion of Figure 3 tries to illustrate what happens when we use the injection of positive ions through the ion channel indicated in the center of the tube. Here, the dynamic deformation of the capacitor membrane is no longer the result of an imaginary quasistatic voltage but is induced as a traveling wave propagating from the stationary position of each ion channel toward both the left-hand side and the right-hand side with a wavelength λc. The total length of this wave packet is determined by the rate of injection of the positively charged ions, which defines the number of injected charges per unit length with respect to the number of polarizing charges per λc that are defined by the membrane voltage V0 at rest.
In the following, it is assumed that the charge density along the perimeter of any perpendicular cut through the axon tube is uniform whereas it changes axially according to the local radial and tangential electric-field components. This seems appropriate since the electric field changes on a length scale λc/D and, thus, is essentially independent in strength for a radial cut through the tubular axon. In addition, for a radially uniform membrane, the internal overpressure of the membrane assures that the cross section remains circular since the contained liquid is essentially incompressible. Of course, the lipid membrane will be axially stretched or compressed with respect to the rest position according to the local changes in axial and radial forces. Since the linear momentum of the injected ions along the radial direction is much smaller than the local radial and axial momentum created by the relocation of water dipoles between the axial minima and maxima driven by the axial and radial electrical field gradients, one can assume that the relatively slowly propagating potential spiral will be filled with ions with the goal to depolarize the membrane rather uniformly in both the radial and axial directions. Therefore, one can expect that the axial distribution of the injected charge will reflect the joint forces of the local electric field and the axial polarization gradients and will concentrate depolarizing charges more around the region of the highest absolute value of the electric field. It, thus, seems appropriate to approximate the axial variation of the perpendicularly acting force ΔF⊥ generated by the local electric field E⊥ acting on the membrane and propagating with constant velocity cc and a wavelength λE = 2λC corresponding wave vector kE = ½kc into one axial direction of an axon by:
The capacitance per length λC/2 is ≈ 1.2 × 10−10 As/V and the corresponding total charge needed to depolarize this capacitance is QT = C( when the effective bias voltage oscillates sinusoidally between V = V0 and V = 0 V. Providing this charge by singly charged ions requires N = CV0/(2e) ≈ 2 × 107 ions to achieve complete depolarization at the minimum of ΔR. The corresponding areal ion density N/πRλC yields an average ionic distance before depolarization of Δi ≈ 50 nm. Since action potentials measured on single ion channels exhibit depolarizing currents pulses of typically 3 pA in 0.5 ms [30] and thus deliver roughly N = 2 × 104 singly charged ions per depolarizing pulse, one needs, depending on axon radius, the depolarizing charge from up to 1000 simultaneously activated ion channels to generate an individual action potential pulse that fully depolarizes a λC/2-section of an axon while propagating with the constant group velocity. The position-dependent propagation delay between the charge packets injected at each participating ion channel thus determines the shape of the resulting action potential and provides a status report of the neuron and its environment typically lasting several milliseconds. Changes in the status are defined and transmitted by the generation of sequential action potential pulses with delay intervals of typically over 100 milliseconds. With 1/8CV02, one obtains a local energy reduction of such a depolarizing dipolar packet of ΔW~10−13 J. Since this is a collectively propagating mode similar to the acoustoelectric pulses discussed in Section 3, disorder and damping are most likely very small. All of this seems to be quite similar to what was observed in the propagation of transverse mode pulses as studied in suspended nanostrings, discussed in Section 2 and [15].
So far, we have not considered that an unpolarized breathing-mode wave propagating axially with a constant velocity can be described by two circular polarized waves with opposing chirality. If generated with a current pulse through an ion channel, one can expect to generate two polarization pulses of finite length propagating along the axis in opposite directions. It is illuminating to recognize that an individual right-hand circular polarized (RHCP-) wave packet confined to a tubular skin of water propagates from the ion channel to the left as indicated on the upper channel and in the section cut on the left of Figure 3a and an (LHCP-) wave propagates to the right. The superposition of both chiral modes in one propagation direction reflects a charge-neutral donut-like polarization ring surfing on the axially propagating potential gradient of the capillary wave. Basically, the motion of such a chiral wave packet is in analogy to a surfer surfing on the gradient potential of a spiral wave with wavelength λC, as indicated by the axial RHCP-spiral on the left section of Figure 3a. However, in the absence of gravity, the surfer would be pressed to the propagating spiral wave by centrifugal forces only. Considering the pulsed dipolar polarization excitation as charge-neutral quasiparticles surfing on a capillary breathing mode consisting of two oppositely rotating dipolar chiral modes, I named them dipolitons.
Avoiding mode mixing, such propagating polarization rings are likely to be topologically protected, thus propagating quasi-ballistically with little damping. This is indicated for the RHCP-mode propagation on the left of Figure 3. Note that for each chiral component, the total perpendicular polarization of the ring propagates on a spiral around the radius R, as indicated in the 3D RHCP spiral inserted on the left into Figure 3. Note that the inside of the membrane appears to be twisted by rotation with period λC for a given chirality. The superposition of two opposing chiral modes propagating in the same axial direction results in a propagating breathing mode and by locally opposing radial motion removes the twist of the membrane and from a stationary observer yields an oscillating polarization vector that rotates around the tilted axis normal to the membrane interface, as described above. The periodic stretching of the membrane with period T = λC/cc increases the amplitude of the axial and radial oscillations of the screening water dipoles, describing their motion around the axis tilted by Θ with respect to the normal of the axial propagation direction. Once such a propagating pulse is formed by the reorientation of water molecules by tangential and rotational movements; one can assume that it propagates with its impressed electrical polarization rather undamped as long as the flow within a wavelength section of the capillary wave is laminar. Typical values of the geometric dimensions of an axon and the propagation velocities of one have Reynolds numbers of order 100 and can assume laminar flow.
Since the water in the electrolyte is incompressible, the screening dipoles in the high-field Debye skin will be driven by an angular momentum initiated by the depolarizing pulse of ions. For symmetry reasons, the linear momentum p, characterizing the axial propagation of the capillary wave pulse, is accompanied by two angular momenta L = ½ Rxp of opposing chirality. Confining both the RHCP-wave packet and LHCP-wave packet to a narrow ring in the radial plane will generate a torque of T = 1/2 dL/dt along the +z and −z direction since motion along z is essentially confined to axial transport. Within the wavelength of λE = 2λc, the polarization will be opposing to the local electric field so that for a given chirality the polarization vector will move on a spiral of spatial period λE as indicated for the RHCP in the 3D picture inserted into Figure 3 carried by the cylindrical potential gradients at the same propagation velocity as the capillary wave. In that sense, the tilt of the polarization vector with respect to the axis of the axon will depend on the initiating impulse by the injected ions and, if that pulse transports a charge which corresponds to the initial depolarizing charge of a single ion channel, it will generate a single force impulse of length λc/4. From this point of view, the polarization pulse will propagate similarly to the pulse initiated by rotating a single pendulum by 180 degrees to initiate a pendulum soliton, as illustrated in Video 3 of Appendix A. Alternatively, one can describe the rotation of the polarization wave as propagating axially along the neuron with velocity cc and oscillating axially around the tilt axis in a coordinate system rotating with angular frequency Ω as an H2O-based dipolar polarization P. Note that the membrane polarization vector will oscillate with a smaller amplitude opposing the shear force of the locally stretched membrane whereas the H2O- based polarization oscillation moving with respect to the inner interface of the membrane will experience an additional Coriolis-like shear force which increases the forward amplitude and contributes to the solitonic character of the wave pulse.
The coupling between the electric polarization and the tilt vector is determined in part by the anisotropic dielectric susceptibility χ of confined water. As studied in nanometer narrow channels fabricated out of graphene-based heterostructures, the anisotropy of χ has been studied by the Manchester group around Andre Geim by spatially resolved capacitive studies with a scanning dielectric microscope [31]. They revealed the anisotropy of the dielectric tensor yielding χ// ≈ 70. This triggered the theoretically confirming work in the group around Roland Netz in Berlin that extended the studies also to bilayer interfaces confirming the experimental results [32]. With these, it is justified to use here values for the appropriate value for χ//~70 and increase the in-plane axial polarization P‖ of the screening water dipoles in the Debye layer to a value comparable to P⊥, thus, achieving a dynamic angle in the range around 45 degrees. Note this polarization results predominantly from the orientation of water dipoles which are able to follow the driving electric field up to radio frequencies without appreciable dissipation. Subsequent studies of the Manchester group also showed that sodium ions in a narrow channel adhere to the wall whereas protons continue to be mobile down to atomic-length scales [33], thus, justifying the here assumed little damping of oscillating water dipoles in their motion within the narrow high field region near the membrane–water interface.
Whereas the field-effect confined water is essentially incompressible, the membrane also carrying the excess ionic charge is highly compressible, thus, again justifying the relative motion of the water polarization with respect to the one of the membrane. For a more quantitative description of the relation between the amplitude and shape of polarization components parallel and perpendicular to the propagation direction, self-consistent numerical finite-element calculations of the charge-neutral polarization current are desirable. However, it should be clear that the polarization current is not carried by long-range mass and charge transport but propagates essentially charge neutral similar to waves through a chain of coupled pendula, as shown in Video 3 of Appendix A or La Ola waves in a fully packed soccer stadium.
So far, we have discussed the effect of a single charge package injected through an ion channel into any tubular part of a neuron, resulting in the generation of two oppositely propagating de- and repolarizing pulses as part of a hydrodynamic breathing-mode capillary wave propagating quasi-one-dimensionally in a tube filled with an incompressible electrolyte and confined by a thin flexible membrane. Now we focus on the soma and its dendrites as a generator of an action potential. As sketched in Figure 1, the soma is a compact resonator system reminiscent of bagpipes with several dendrites and the central soma containing on the order of 30–1000 simultaneously activated ion channels and opening to a single axon waveguide. Since the soma usually has dimensions that are smaller than a typical wavelength λc of a capillary wave in the axon, we can consider the individual polarization pulses generated within less than 1 ms to superimpose into a collective pulse that is broadened and distorted by phase delays related to the time delay of the propagation of pulse waves from the individual ion channels in the dendrites and the central Helmholtz-like resonator of the soma. In addition, polarization pulses generated in the direction opposite to the transition from the soma into the axon will be at least partially reflected and enter the axon with an additional delay [34]. Note that the elastic reflection of a chiral wave reverses its chirality and, thus, constructively interferes with the chiral wave component directly propagating toward the axon. Assuming that all generated pulses propagate phase-preserving with the same group velocity, one obtains at the entrance of the axon a pulses wave with a shape as illustrated in Figure 4 that is characteristic of most action potentials. As discussed above, the depolarization of an axon requires typically 107 ions/ms and, with 1000 ion channels contributing with 10.000 Na+ ions, each one can expect the rising flank of the action potential to last about 1 ms. During this time, the capillary wave propagates for typically 3 mm, significantly more than the dimensions of the soma and its dendrites. Once neutralized and repolarized by an exchange of positive- and negative-charged excess ions in the electrolyte it returns with some overshoot to the rest state and, thus, propagates with the originally imposed axial polarization through the axon.
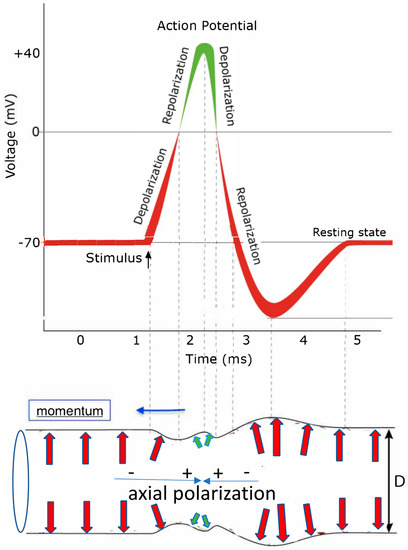
Figure 4.
This sketch tries to schematically display the correlation between a typical shape of an action potential (top) reflecting the temporal voltage change at the inside of the axon membrane, initiated by the transient opening of ion channels, injecting positively charged ions and deforming the axon diameter D (bottom) through an action potential moving to the left (blue arrow) as a capillary wave pulse as viewed from a stationary outside observer. The arrows indicate the orientation and size of polarization-induced forces onto the confining axon membrane. Red arrows mark polarization-caused forces by negatively charged excess ions and their hydration shell on the inside of the membrane and green arrows are forces caused by polarization induced by positively charged excess ions.
All ion channels contained in the dendrite and the soma cause wave packets in opposing directions, as discussed in Figure 3. The fact that the soma opens toward the axon breaks this axial symmetry and will force wave packets that originally propagate from the injecting ion channel in the direction away from the transition between the soma and the axon to be reflected at the closed end of each dendrite. This will change their chirality and direction to increase the net momentum towards the axon. These cause propagation delays that extend the pulse shape toward its end. Such reflections are illustrated in Figure A1 and the associated Video 4 of Appendix A where the soliton-like propagation through a mechanical spiral with reflecting ends is experimentally visualized. Shorter delay are caused by the fact that ion channels in the soma are placed at different positions along a length ≪ λc..
Hence, simultaneously started pulses moving towards the axon will experience a shorter distance-related delay without drastically changing the shape of the action potential. The steep rise at the beginning of the action potential and the extended back end can explain the shape change of the observed action potential [35] but its causes are rather likely propagation delays of phase-preserving charge-neutral polarization pulses and probably are not broadened significantly by damping through diffusive behavior of excess charges or viscous forces. Since the action potential contains strong axial potential gradients, it can synchronously activate ion channels on its path if an excess charge deficit occurs and fills up to the original potential level.
In my understanding, the pulse shape of action potentials should not change significantly with the distance from the soma because it contains the status message that the soma wants to distribute. Here, spatially and temporally resolved techniques with optical [18,19,20,21,22], magnetic [23], or capacitive probes [31] will help in studying the dynamics of propagating action potentials. Suitably designed to prevent the distortion of pulse shapes by externally imposed instrumental time constants, they could correlate the signal shape with the positions of the emitting ion channels and will be very helpful to obtain a more quantitative understanding. Correlation studies between locally measured gradient fields and the start of ion injection could profit from Franz–Keldysh effect tuning [22] of fluorescent emitters inserted in the membrane under triggered excitation.
The model presented so far also helps to understand why nature has chosen myelination to improve the axial transport of action potentials, as illustrated in Figure 5. Myelination has a twofold effect [17,36,37,38]. One is that the myelinated sections have stiffer walls, increasing the propagation velocity, and possess no ion channels in the center region. As acoustic resonators, the myelinated section can increase local fields and concentrate axial field gradients near their end close to the nodes of Ranvier. Ion channels located there can utilize the increased gradient fields to lower the activation threshold for ion injection and coherently preserve the ionic density by synchronously filling up the excess ion reservoir. In addition, the chiral network of the myelinated membranes may support filtering by preferring one chirality for sending signals in a preferred direction. This would allow the use of chirality as a tool for separating forward transport from the soma along the axon from backward transport towards the soma. Allowing efficient two-way communication opposing solitonic signals will not destroy each other by destructive interference, as illustrated in Video 2 of Appendix A. Myelination may also be utilized for frequency-component filtering and for the reduction of noise caused by the irregular motion of the axon in its environment.
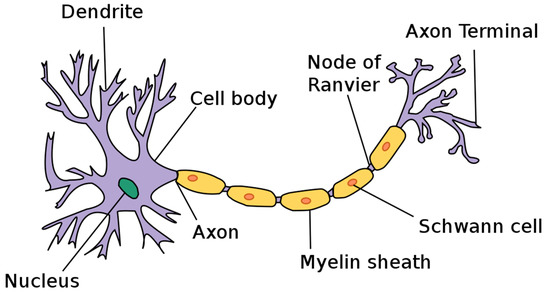
Figure 5.
Components of a myelinated axon, from Wikipedia, File Neuron.svg, User: Dhp1080 “Anatomy and Physiology” by the US National Cancer Institute’s Surveillance, Epidemiology and End Results Program, created: 17 March 2019 http://creativecommons.org/licenses/by-sa/3.0/ (accessed on 23 January 2023).
Finally, myelination, combined with chiral propagation, has the potential to avoid reflection from the synaptic terminations since, similar to phase matching between electromagnetic waveguides and cavities, nature could use it to concentrate the energy of action potentials into the synaptic terminations to activate other coherently transducing processes such as chemical transduction or acoustoelectric isolators or signal splitters. In a more general context, the importance of propagation of information in biological systems via coherent waves beyond quasistatic reaction–diffusion concepts have been already addressed by Robert Laughlin nearly a decade ago [39] but seems to be still neglected in conventional approaches to biological functions. Here, further experimental studies with an improved temporal and spatial resolution of propagating action potentials based on local electric, magnetic, and optical probes and correlated detection methods would, in conjunction with accompanying theoretical investigations, certainly improve our understanding of the character and sound of action potentials and more generally of information processing in living systems.
6. Some Conclusions
The proposed model rather simply explains the signal generation of electric polarization components through local charge injection through individual ion channels that, in turn, causes rotation of water molecules in the hydration shell around the injected excess ions. This local motion of water molecules initiates capillary wave packets at each participating ion channel that superimpose, coming from different parts of the soma with its dendrites, with different small time delays of order or smaller than milliseconds to generate an individual characteristic action potential at the entrance to the axon with temporal shapes that function analogously to the click sounds in marine animal communication and contain a characteristic spectrum of higher frequency components that all propagate with the same group velocity, essentially defined by geometric and elastic parameters, as defined by Equation (1). The electromechanical coupling defining the propagating axial polarization is dominated by the strong anisotropy of the dielectric function of the nanometer-thin water skin in the high-electric-field Debye regime adjacent to the interior of the confining lipid membrane which is responsible for the relatively strong axial polarization caused by a relatively small tilt angle of the membrane interface. Both the effect of the elasticity of the lipid membrane and the anisotropic response of the water dipoles surrounding the excess ion charges are not addressed by the Hodgkin–Huxley model and are not known to be reported elsewhere by the author.
Another important feature is the fact that capillary waves in a tensionally prestressed tube are likely to propagate soliton-like with little dissipation in analogy to acoustoelectric sound waves in prestressed insulating nanostrings, as discussed above. This reflects the concept of tensional integrity, abbreviated to tensegrity and introduced in the 1960s by architect Buckminster Fuller and now, under the name of biotensegrity, getting increasingly popular in the biophysics of cells and bodies. By tensional prestress and imprinting information into resilient temporal shapes, action potentials can be preserved in low-loss propagation thus efficiently transporting analog sound-like information by individual shape-preserving acoustoelectric capillary wave pulses. Frequency [23] and shape [35] analysis in the recent literature support this concept but do not provide the acoustoelectric description discussed here. This concept differs substantially from other Morse-code-based and essentially digital models that encode information in zero-signal temporal intervals of typically 100 ms between individual action potentials. This needs more time to transfer more specific information via on–off signals, making it hard to explain the short reaction times to nervous signals observed in nature. The model proposed here should not only help to increase our understanding of neural communication but hopefully should also contribute to increasing conservative methods of healing neural ailments.
In any case, a deeper understanding of the function of neurons beyond the Hodgkin–Huxley model based on a detailed understanding of the coupling of electrodynamic and hydrodynamic interactions is certainly highly desirable and needed for a better understanding of our nervous systems. I personally find the route via coherent interaction of propagating acoustoelectric wave pulses containing characteristic high-frequency components a more promising approach than thinking of digital communications as a Morse code. However, a combination of both using phase-preserving pulse shapes in combination with discrete time intervals may also be an option. In any case, I consider it also as another example that nature has utilized rather intricate physical concepts long before physicists became aware of them.
As an individual approaching the age of eighty, I happened to be able to use my own body as a case study for parts of the proposed model of neuron function. When I pulled too heavy a load nearly three years ago, I injured my lumbar spine. Apparently, it also squeezed a neuron on its route through my hip to my left leg which got numb and partially paralyzed. I tried to fight this conservatively with medical gymnastics and acupuncture which both helped. Being introduced to massage of my fasciae, I discovered that by using this on my left leg along the routing of the affected nerve, I was able to remove the neural blockade and interpreted it as removing an acoustoelectric impedance mismatch of the nerve. During the same period, I also experienced numbness in my left arm and hand, diagnosed as polyneuropathy, and, again, by massage of the relevant fasciae, I was able to remove this defect so far permanently. The combination of fasciae massage and Pilates training, both techniques that may be associated with the restoration of biotensegrity, made me convinced that the above-proposed model helped me substantially to get rid of some age-related defects so that I can now again walk, bicycle, row, and, occasionally, lift a heavy beer mug again without pain. Of course, this individual case study is not the basis for this manuscript but perhaps it will help others to treat nerve-related ailments conservatively.
Funding
Financial support by the excellence cluster “Nanosystems Initiative Munich” (NIM) and the Center for NanoScience (CeNS) for supporting me as a senior member to travel to meetings and discussions with colleagues is gratefully acknowledged.
Data Availability Statement
The data used here have been derived from equations and reports of literature cited in the text. In addition, I have reminded myself of general textbook knowledge of elastic properties of tubular systems filled with incompressible liquids by relying on The Feyman Lectures of Physics, by R. P. Feynman; R. B. Leigton And M. Sands, Volume II, Chapters 38–40 in the 1964 edition, published by Adisson-Wesley Publishing Company, Reading, MA, USA.
Acknowledgments
In the process of trying to better understand the mechanisms that enable the generation, propagation, and processing of information in the neuron network of living systems, I profited enormously from discussions with colleagues and friends, by learning from their responses, constructive criticism, their questions that I was unable to answer promptly, and their guidance to existing literature that I was not yet aware of. Without their input, I would not have been able to develop a hopefully somewhat coherent picture. I wish to thank all of them and, in particular, Matthias Schneider for making me aware of the controversial discussions and literature about how nerves are thought to operate, Achim Wixforth and Christoph Westerhausen for enthusiastically supporting my attempts to develop a reasonably consistent coupled acoustoelectric wave-based model and pointing me to literature that I had not be aware of, Roland Netz and his team for stimulating calculations and discussions about potential experiments concerning the microscopic behavior at interfaces between lipid membranes and electrolytes, Thomas Heimburg for commenting on my efforts from his more thermodynamic point of view, Jan Behrends, Robert Blick, Andrea Brueggemann, Klaus Dransfeld, Niels Fertig, Thomas Faust, Peter Fratzl, Erwin Frey, Hermann Gaub, Sasha Govorov, Alex Hoegele, Khaled Karrai, Klaus von Klitzing, Bob Laughlin, Bert Lorenz, Stefan Manus, Florian Marquardt, Michel Orrit, Michel Peyrard, Eva Weig, and Wilhelm Zwerger for stimulating discussions and hints, Chris Hohmann for supporting me in transforming my model into understandable graphics, and last but not least my wife Sabine for her patience and understanding when I started experiments with more or less confined water waves in our basement and was periodically absent from the real world with my thoughts about capillary wave transport of information as well as my Pilates friends, who often had to listen to and question my thoughts in our weekly pub visit after our exhaustive physical exercise.
Conflicts of Interest
The author declares no conflict of interest in the results.
Appendix A
Here the links to four videos are given that illustrate the dynamics of solitonic acoustoelectric excitations, as discussed in the main text.
Video 1 illustrates the rotation of the coupled mode polarization of a nanostring resonator on a Bloch-like sphere, as discussed in [15] and originally published in the Supplementary information of this publication https://cast.itunes.uni-muenchen.de/clips/ZsCwnoYTvF/vod/raw.mp4 (accessed on 31 January 2023).
Video 2 shows a channel-guided solitonic water wave and the nondestructive collision of two opposing waves as predicted by the Korteweg–de-Vries equation, posted on youtube: https://www.youtube.com/watch?v=wEbYELtGZwI (accessed on 28 January 2023).
Video 3 shows three examples of how solitons can be visualized: https://www.youtube.com/watch?v=Ud7STKWNmQw (accessed on 28 January 2023).

Figure A1.
This photo and Video 4 show my own experiments on how a solitonic excitation can propagate through a soft chiral spring, prestressed by gravity with a weight, in an effort to imitate the propagation of a chiral action potential pulse through an axon. The spiral spring is fabricated out of a rectangular plastic wire which has a radial width of 3 mm and an axial width of 2 mm and is wound into a spiral of 9 cm diameter with right-hand turn chirality—a toy named “Slinky”. Shocking the spring locally with short radial compression, one initiates a solitonic pulse moving with low damping axially through the spring with a propagation velocity faster than the harmonic oscillation of the spring. https://cast.itunes.uni-muenchen.de/clips/3zte0uDMZo/vod/online.html, (accessed on 23 January 2023).
Soliton Propagation on a Prestressed Spiral Spring. Available online: https://cast.itunes.uni-muenchen.de/clips/3zte0uDMZo/vod/online.html (accessed on 31 January 2023).
References
- Hodgkin, A.I.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Von Helmholtz, H. Note sur la vitesse de propagation de l’agent nerveux dans les nerfs rachidiens. In Hermann von Helmholtz. Klassische Texte der Wissenschaft; Schmidgen, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 55–56. Available online: https://link.springer.com/chapter/10.1007/978-3-662-63833-0_3 (accessed on 23 January 2023).
- Wilke, E. Das Problem der Reizleitung im Nerven vom Standpunkte der Wellenlehre aus betrachtet. In Pflüger’s Archivgesamte Physiologie des Menschen und der Tiere; Springer: New York, NY, USA, 1912; Volume 144, pp. 35–38. Available online: https://scholar.archive.org/work/5azemvvcd5fpfdzuee2jorajni/access/ia_file/crossref-pre-1923-scholarly-works/10.1007%252Fbf01679971.zip/10.1007%252Fbf01681175.pdf (accessed on 23 January 2023).
- Tasaki, I. The excitatory and recovery processes in the nerve fibre as modified by temperature changes. Biochim. Biophys. Acta 1949, 3, 498–509. [Google Scholar] [CrossRef]
- Heimburg, T.; Jackson, A.D. On Soliton propagation in biomembranes and nerves. Proc. Natl. Acad. Sci. USA 2005, 102, 9790–9795. [Google Scholar] [CrossRef] [PubMed]
- Engelbrecht, J.; Peets, T.; Tamm, K. Electromechanical coupling of waves in nerve fibers. Biomech. Model. Mechanobiol. 2018, 17, 1771–1783. [Google Scholar] [CrossRef] [PubMed]
- Peyrard, M. How is information transmitted in a nerve? J. Biol. Phys. 2020, 46, 327–341. [Google Scholar] [CrossRef]
- Holland, L.; de Regt, H.W.; Drukarch, B. Thinking About the Nerve Impulse: The Prospects for the Development of a Comprehensive Account of Nerve Impulse Propagation. Front. Cell. Neurosci. 2019, 13, 208. [Google Scholar] [CrossRef]
- Griesbauer, J.; Bössinger, S.; Wixforth, A.; Schneider, M.F. Propagation of 2D Pressure Pulses in Lipid Monolayers and Its Possible Implications for Biology. Phys. Rev. Lett. 2012, 108, 198103. [Google Scholar] [CrossRef]
- Fichtl, B.; Shrivastava, S.; Schneider, M.F. Protons at the speed of sound: Predicting specific biological signaling from physics. Sci. Rep. 2016, 6, 22874. [Google Scholar] [CrossRef]
- Fox, D. The brain, reimagined. Sci. Am. 2018, 318, 60–67. Available online: https://www.jstor.org/stable/27173430 (accessed on 23 January 2023). [CrossRef]
- Rocke, C.; Zimmermann, S.; Wixforth, A.; Kotthaus, J.P.; Böhm, G.; Weimann, G. Acoustically Driven Storage of Light in a Quantum Well. Phys. Rev. Lett. 1997, 78, 4099–4102. [Google Scholar] [CrossRef]
- Unterreithmeier, Q.P.; Faust, T.; Kotthaus, J.P. Damping of Nanomechanical Resonators. Phys. Rev. Lett. 2010, 105, 027205. [Google Scholar] [CrossRef] [PubMed]
- Unterreithmeier, Q.P.; Weig, E.M.; Kotthaus, J.P. Universal transduction scheme for nanomechanical systems based on dielectric forces. Nature 2009, 458, 1001–1004. Available online: https://www.nature.com/articles/nature07932 (accessed on 23 January 2023). [CrossRef] [PubMed]
- Faust, T.; Rieger, J.; Seitner, M.J.; Kotthaus, J.P.; Weig, E.M. Coherent control of a classical nanomechanical two-level system. Nat. Phys. 2013, 9, 485–488. [Google Scholar] [CrossRef]
- Miles, J. The Korteweg-de Vries equation: A historical essay. J. Fluid Mech. 1981, 106, 131–147. [Google Scholar] [CrossRef]
- Kotthaus, J.P. A Nano-Electro-Mechanical Hydrodynamic Approach to Neuron Function, Colloquium Presented at the Center for NanoScience (CeNS), LMU Munich on 19 June 2020. Available online: https://cast.itunes.uni-muenchen.de/clips/15EwHp9wo0/vod/online.html (accessed on 23 January 2023).
- Salzer, J.L. Schwann Cell Myelination. Cold Spring Harb. Perspect. Biol. 2015, 7, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Hill, B.C.; Schubert, E.D.; Nokes, M.A.; Michelson, R.P. Interferometer Measurement of Changes in Crayfish Axon Diameter Concurrent with Action Potential. Science 1977, 196, 426–428. [Google Scholar] [CrossRef]
- Mader, M.; Julia Benedikter, J.; Lukas Husel, L.; Hänsch, T.W.; Hunger, D. Quantitative Determination of the Complex Polarizability of Individual Nanoparticles by Scanning Cavity Microscopy. ACS Photon. 2022, 9, 466–473. [Google Scholar] [CrossRef]
- Song, Y.; Lukin, M.D.; Park, H.; Walsworth, R.L. Optical magnetic detection of single-neuron action potential using quantum defects in diamond. Proc. Natl. Acad. Sci. USA 2016, 113, 14133–14138. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S. Relation between electroabsorption in bulk semiconductors and in quantum wells: The quantum confined Franz-Keldysh Effect. Phys. Rev. B 1986, 33, 6976. [Google Scholar] [CrossRef]
- Waterstraat, G.; Körber, R.; Storm, J.H.; Curio, G. Noninvasive neuromagnetic single-trial analysis of human neocortical population spikes. Proc. Natl. Acad. Sci. USA 2021, 118, e2017401118. [Google Scholar] [CrossRef]
- Zahn, M.J.; Rankin, S.; McCullough, J.L.K.; Koblitz, J.C.; Archer, F.; Rasmussen, M.H.; Laidre, K.L. Acoustic differentiation and classification of wild belugas and narwhals using echolocation clicks. Sci. Rep. 2021, 11, 22141. [Google Scholar] [CrossRef]
- Jones, J.M.; Frasier, K.E.; Westdal, K.H.; Ootoowak, A.J.; Wiggins, S.M.; Hildebrand, J.A. Beluga and narwhal echolocation click detection and differentiation from long-term Arctic acoustic recordings. Polar Biol. 2022, 45, 449–463. [Google Scholar] [CrossRef]
- Sanders, R.W.; Paquette, D.; Jaccarino, V.; Rezende, S.M. Radiation Damping in magnetic resonance II: Continuous-Wave antiferromagnetic-resonance experiments. Phys. Rev. B 1974, 10, 32–138. [Google Scholar] [CrossRef]
- Verbridge, S.S.; Parpia, J.M.; Reichenbach, R.B.; Bellan, L.M.; Craighead, H.G. High quality factor resonance at room temperature with nanostrings under high tensile stress. J. Appl. Phys. 2006, 99, 124304. [Google Scholar] [CrossRef]
- Ghadimi, A.H.; Fedorov, S.A.; Engelsen, N.J.; Bereyhi, M.J.; Schilling, R.; Wilson, D.J.; Kippenberg, T.J. Elastic strain engineering for ultralow mechanical dissipation. Science 2018, 360, 764–768. [Google Scholar] [CrossRef]
- Hodis, S.; Zamir, M. Mechanical events within the arterial wall under the forces of pulsatile flow: A review. J. Mech. Behav. Biomed. Mater. 2011, 4, 1595. [Google Scholar] [CrossRef]
- Fertig, N.; Klau, M.; George, M.; Blick, R.H.; Behrends, J.C. Activity of single ion channel proteins detected with a planar microstructure. Appl. Phys. Lett. 2002, 81, 4865–4867. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Hu, S.; Ares, P.; Janardanan, A.; Yang, Q.; Radha, B.; Taniguchi, T.; Watanabe, K.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339–1342. [Google Scholar] [CrossRef]
- Loche, P.; Ayaz, C.; Wolde-Kidan, A.; Schlaich, A.; Netz, R.R. Universal and Nonuniversal Aspects of Electrostatics in Aqueous Nanoconfinement. J. Phys. Chem. 2020, 8, 4365–4371. [Google Scholar] [CrossRef]
- Gopinadhan, K.; Hu, S.; Esfandiar, A.; Lozada-Hidalgo, M.; Wang, F.C.; Yang, Q.; Tyurnina, A.V.; Keerthi, A.; Radha, B.; Geim, A.K. Complete steric exclusion of ions and proton transport through confined monolayer water. Science 2019, 363, 145–148. [Google Scholar] [CrossRef]
- Golding, N.L.; Kath, W.L.; Spruston, N. Dichotomy of Action-Potential Backpropagation in CA1 Pyramidal Neuron Dendrites. J. Neurophysiol. 2001, 86, 2998–3010. [Google Scholar] [CrossRef] [PubMed]
- Naundorf, B.; Wolf, F.; Volgushev, M. Unique features of action potential initiation in cortical neurons. Nature 2006, 440, 1060–1063. [Google Scholar] [CrossRef] [PubMed]
- Sherman, D.L.; Brophy, P.J. Mechanisms of axon ensheathment and myelin growth. Nat. Rev. Neurosci. 2005, 6, 683–690. [Google Scholar] [CrossRef] [PubMed]
- Fields, R. A new mechanism of nervous system plasticity: Activity-dependent myelination. Nat. Rev. Neurosci. 2015, 16, 756–767. [Google Scholar] [CrossRef]
- Chang, K.J.; Redmond, S.; Chan, J. Remodeling myelination: Implications for mechanisms of neural plasticity. Nat. Neurosci. 2016, 19, 190–197. [Google Scholar] [CrossRef]
- Laughlin, R.B. Critical waves and the length problem of biology. Proc. Natl. Acad. Sci. USA 2015, 112, 10371–10376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).