Abstract
The generation of a virtual, personal, auditory space to obtain a high-quality sound experience when using headphones is of great significance. Normally this experience is improved using personalized head-related transfer functions (HRTFs) that depend on a large degree of personal anthropometric information on pinnae. Most of the studies focus their personal auditory optimization analysis on the study of amplitude versus frequency on HRTFs, mainly in the search for significant elevation cues of frequency maps. Therefore, knowing the HRTFs of each individual is of considerable help to improve sound quality. The following work proposes a methodology to model HRTFs according to the individual structure of pinnae using multilayer perceptron and linear regression techniques. It is proposed to generate several models that allow knowing HRTFs amplitude for each frequency based on the personal anthropometric data on pinnae, the azimuth angle, and the elevation of the sound source, thus predicting frequency magnitudes. Experiments show that the prediction of new personal HRTF generates low errors, thus this model can be applied to new heads with different pinnae characteristics with high confidence. Improving the results obtained with the standard KEMAR pinna, usually used in cases where there is a lack of information.
1. Introduction
The head-related transfer function (HRTF) is a personal function that describes the propagation of the sound from a source to the auditory system of a human subject [1]. This function is particular to each individual because it largely depends on the anatomical structure of each person and the location of the transmitting and receiving elements [2]. Thus, the use of generic HRTFs, which have not been adapted to each particular individual, has been demonstrated to inhibit a high quality sound experience, and, in many cases, generate disorientation and confusion [3]. This has led to a multitude of studies regarding the generation of near-field HRTFs based on the binaural sound measurement in the free field [4,5,6,7,8].
The head-related impulse response (HRIR) in the time domain or HRTF in the frequency domain is defined by some authors such as Blauert [2] as an acoustic filter from a sound source to the entrance of the ear canal. These functions define the relation between the location of the source, the particular form of the listener’s auditory system, and the final effect on the sound. For this reason, each individual’s HRIR must be measured in order to improve the individual’s sound experience. The acoustic waves received by each individual are reflected and refracted by the pinnae, generating notches and peaks in the acoustic spectrum. Due to the variation of individuals’ pinnae, the HRIR and HRTF are unique to each individual [9,10,11,12].
Previous works to characterize individual HRTFs have been mainly categorized into two different approaches [13]. The first is the most precise method to obtain individual HRTFs. Acoustic signals are measured in an anechoic chamber by placing microphones in the ear canals to perform the necessary measurements to characterize each individual [14,15]. The second approach is less precise but it is faster and uses fewer resources. Acoustic signals are generated by predictive models, obtaining a good approximation of the characteristics of each user [16,17,18].
The problem is that obtaining these functions for each individual requires the use of special equipment and the cost of working time of experts. Machine learning methods are a very useful tool to solve this problem, as they can generalize new information based on historical data that defines the problem. Several studies in this field have used machine learning techniques in relation to HRTFs [19,20,21,22,23,24,25,26], although they used different methodologies and had different objectives in comparison to the current study. These works demonstrated how these techniques can be used to optimize and customize HRTFs with accurate results [11,27,28,29].
This work introduces a new approach to personalize HRTFs using machine learning techniques. The process is explained in the flow chart shown in Figure 1. Here, several models generalize the relation between HRTFs, source location, and individual ear shape. Two models were developed: a linear model, based on linear regression, and a nonlinear model, based on multilayer perceptron artificial neural network [30]. The applied prediction methodology was based on a training and testing process which optimized and generalized the model’s predictions while avoiding any possible overfitting. Initially, a multivariate analysis was performed to analyze the available dataset with two goals: build a more accurate model and have a better understanding of the problem. Later, a repeated cross-validation training was conducted. During this process, the most significant parameters of each algorithm were adjusted to improve the accuracy of the obtained models [31]. During this step, some robustness criteria were applied as help along the optimization of the training process, with the goal of selecting the most accurate models. Finally, the models with the best predictive behavior were selected and tested with information not previously used during the training. Obtaining in this way the real regression capacity of the model, preventing overfitting [32,33].
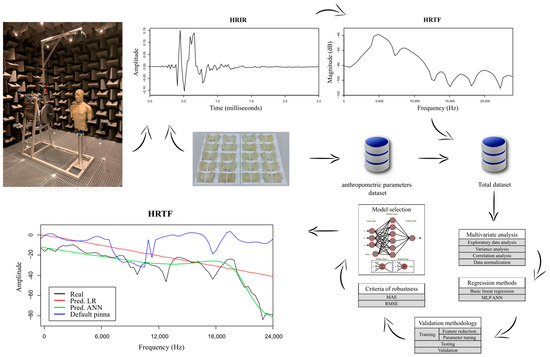
Figure 1.
Flow diagram of the process performed in this work.
Finally, an analysis of the results was performed to know the reliability of the prediction and the efficiency of the applied models. Additionally, in this analysis, the obtained results were compared with the HRTFs measured using standard pinnae in order to verify if the models had a more accurate behavior than the standard HRTFs and thus could be used to improve the quality sound experience.
The remainder of this paper is as follows. Section 2 describes the Viking2 dataset which was used for the study and the new features under analyses. In addition, Section 2 describes the analyses that were performed, the results of which are presented in Section 3. Finally, Section 4 contains some concluding remarks.
2. Materials and Methods
This work was performed based on the Viking2 dataset [34], which contains both acoustic and anthropometric data for 20 individuals. Section 2.1 describes the acoustic measurements and Section 2.2 describes the anthropometric features used in this study.
Then, in Section 2.4, Section 2.5, Section 2.6, Section 2.7 and Section 2.8, the followed methodology is explained. How two techniques, one linear and one nonlinear, were applied to the problem under consideration, obtaining the prediction of HRTF based on personal anthropometric data of the pinnae and the position of the sound source. For this purpose, a multivariate analysis and a training/testing methodology were used, with the aim of developing a better understanding of the problem and predicting the amplitude of each frequency in the HRTF.
2.1. Acoustic Measurements
The acoustic data in the Viking2 dataset consists of a series of HRIR measurements for each of the individuals. Each HRIR signal is measured on a KEMAR mannequin equipped with a replica of the corresponding individual’s left pinna. The mannequin is mounted on a 360° rotating cylindrical stand and a Genelec 8020CPM-6 loudspeaker mounted on an L-shaped rotating arm. These signals were gathered at the University of Iceland in an anechoic environment with a focus on extra median plane measurements. The dataset includes full-sphere HRIRs measured on a dense spatial grid (1513 positions). These 1513 positions mark the location of the sound source, which is defined by the azimuth angle and elevation angle in vertical-polar coordinates. Elevations are uniformly sampled in 5° steps from −45° to 90°. Azimuths are sampled based on Table 1 in order to obtain a uniform density of the sphere. An overview of the methods and procedures of how HRIR signals were measured can be found in Spagnol et al. [4] and Onofrei et al. [35].

Table 1.
Parameters that define the position of the source in each HRIR measurement.
Starting from these measured HRIR signals, the corresponding HRTFs were obtained, from which the amplitude in dB was generated to be added to the final dataset. Sixty-five instances per ear type and per position were calculated, covering the frequency range from 0 to 24 kHz (Figure 2).
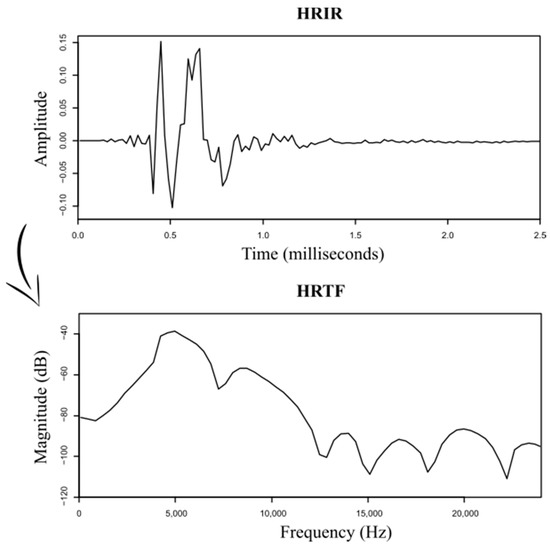
Figure 2.
Relation between HRIR and HRTF. Example: ‘A’ pinna, , .
2.2. Anthropometric Data
A second source of information, based on these same 20 artificial pinnae, was also used. Measurements of 15 pinna anthropometric parameters, including 11 linear and 4 angular parameters (Table 2) were gathered for this work. There is currently no standard definition for these parameters; the parameters selected for this study are focused on obtaining a relatively integral representation of pinna features, following previous works found in the literature [8,36,37,38]. The anthropometric parameters of each pinna were measured from the 3D models used to manufacture silicone replicas of the pinnae (Figure 3). Table 3 summarizes the distribution of these anthropometric parameters, which indicates the parameter space covered by the final model.

Table 2.
Parameters measured in the pinnae.
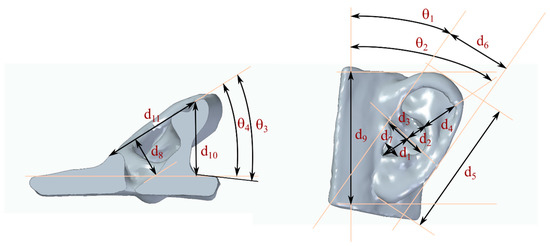
Figure 3.
Definition of the anthropometric parameters measured in the pinna.

Table 3.
Statistics of the anthropometric parameters measured for this study.
2.3. Final Dataset
The final dataset was formed by a total of 21 features, of which 20 were independent variables that defined the only output variable, which was the amplitude of each of the frequencies that defined the HRTF. This study only considered the left pinna, and with this premise, the total number of instances that form the dataset was 1966900.
2.4. Multivariate Analysis
Initially, a general multivariate analysis was performed to obtain a better understanding of the problem and about the available data in order to make the most accurate prediction. For this purpose and to improve the precision of the built models, a study of the possible outliers, a correlation analysis, variance and covariance analysis, as well as a multivariate graphical analysis were performed [39].
2.5. Simple Linear Regression
The linear regression technique (LR) is applied to predict numerical variables using a model that statistically relates a dependent feature with several independent features through a linear relationship such as that shown in Equation (1).
where are the independent features, is the dependent feature, are the weight coefficients of each independent feature obtained in based at the least squares method, is the number of features, and is the bias of this relationship.
2.6. Artificial Neural Networks
A multilayer perceptron artificial neural network (MLP ANN) is a feedforward single-hidden-layer neural network (given by Equation (2)); it has the ability to accurately predict complex nonlinear mappings inspired by the behavior of the biological neural system [40,41].
where , is the number of neurons, is the number of features, is the weight assigned to each neuron, is the bias assigned to each neuron, is the weight assigned to each variable that defines the network, and express the activation function. In this case, the activation function is a sigmoid function for the hidden layer,, and a linear function for the output layer. Finally, the method uses the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm to optimize the network and to find the internal weight constants, and also the decay parameter to avoid overfitting.
2.7. Validation Method
A validation process was necessary to analyze the precision with which the models define the problem. Several candidate models were built and trained based on different techniques and this evaluation must determine which one was the most accurate to solve the problem under study; the remaining models were discarded. In order to have the same weight for all the variables within the built models when making the prediction of the dependent variable, the first step in this process was to normalize the features that define the problem, in this case between 0 and 1. Subsequently, the dataset was divided into three blocks, the training dataset, the testing dataset, and the validation dataset.
The training dataset consisted of 17 pinnae (1,671,865 instances) and it was used to build and train the models. Two of the remaining three pinnae (196,690 instances) made up the testing dataset and were not otherwise used during training, with what they served to evaluate the real prediction capacity of the models. The last pinna was the standard KEMAR pinna (98,345 instances), which was used to validate the selected models. This validation was focused on analyzing how the predicted HRTFs improved the sound experience that can be obtained using the information of the standard pinna.
During the training stage, in order to avoid overtraining, a 50 repeated 10-fold cross-validation process was applied, where the parameters that defined the algorithms were tuned to optimize the precision of the models (Table 4). The process was repeated several times, since the MLP ANN algorithm uses randomly initialized weights that define their structure and the accuracy assigned to the models can vary depending on the values selected in each initialization.

Table 4.
Tuned parameters during the training stage for each of the regression techniques applied in the analysis: brief definition and applied range.
Finally, the most accurate models, when predicting the amplitude of each of the frequencies obtained for each technique, were selected from among the built models: one based on LR as a linear model, and one based on MLP ANN as a non-linear model. Using the selected two models, the behavior of how the prediction generalizes the problem was studied, along with the accuracy of the obtained results.
The whole process defined by this methodology was performed using an R statistical software environment v4.1.1 [42].
2.8. Robustness Criteria
To compare the different candidate models, an accuracy measure must be defined. In this work, the mean absolute error (MAE) and the root mean square error (RMSE) (Equations (3) and (4)) were used for this purpose, two of the most applied computational validation errors in supervised machine learning.
where are the measured values, are the predicted values, and is the number of instances applied into the validation process.
3. Results and Discussion
A multivariate analysis was performed to have a better understanding of the problem and to detect possible useless variables or instances in the final dataset for the problem under study. Within this analysis, the dependent variable was studied, and in this case it was the amplitude of each of the measured frequencies (Figure 4). It was found that the distribution was not completely Gaussian since it has a skewness of −1.56, and therefore the original dataset is slightly unbalanced. That means that the low amplitude values are more complex to predict.
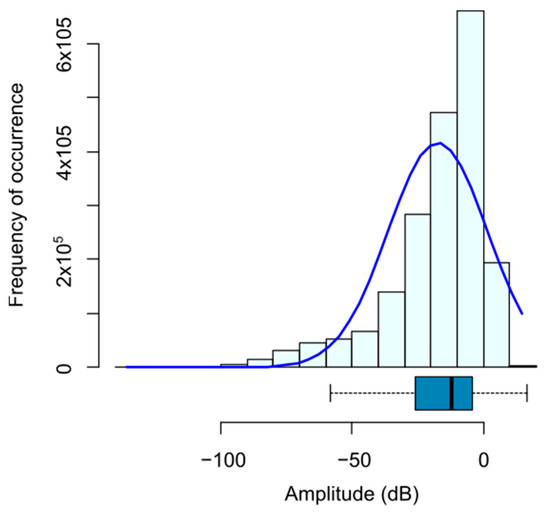
Figure 4.
Frequency distribution of the dependent variable. Amplitude in dB.
Then, an analysis of variance (ANOVA) was performed to assess the uncertainty in the experimental measurements performed on the anechoic environment chamber. The amplitude of each of the studied frequencies were analyzed against the independent variables. The p-values obtained show low values for the most of the variables, indicating that the observed relationships are statistically significant (Table 5). Thus, when the p-value is lower than 0.1, it is considered, with a low level of uncertainty, that the null hypothesis can be confidently rejected, and the independent variables give significant information to predict the independent variables. A low residual standard error of 0.08768 on 1671846 degrees of freedom is obtained. Finally, a correlation analysis was performed to identify and measure the relation among pairs of variables. For example, in Figure 5, the correlation found between the elevation angle, azimuth angle, frequency, and amplitude is shown. This correlation analysis confirmed what it could be observed with the analysis of variance, that the most influential variable for knowing the amplitude was the value of its frequency.

Table 5.
Results obtained from the ANOVA analysis for the predicted feature. Significant codes according to p-value: ‘***’ 0.001, ‘*’ 0.05, ‘ ’ 0.1.
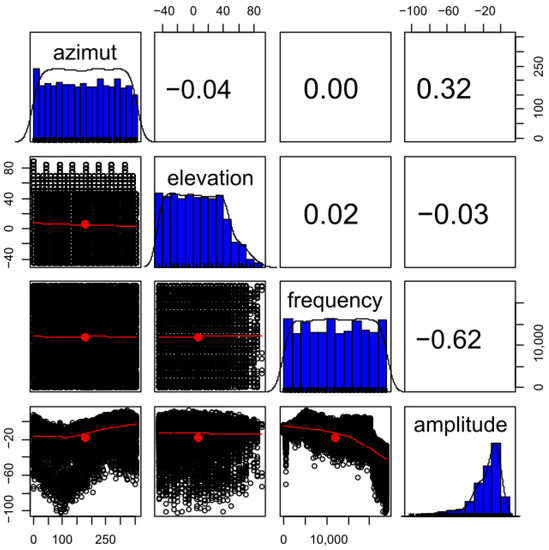
Figure 5.
Graphical correlation analysis between elevation angle, azimuth angle and frequency with the output, in this case, the amplitude of each frequency.
Once the multivariate analysis was completed and based on its results, it was observed that the independent variables adequately defined the dependent variable, and consequently with the available dataset it was possible to build and train accurate models based on the proposed methodology. However, attention should especially be focused on the residuals obtained by the models at low amplitude values, since the dataset was not totally balanced.
The first analyzed prediction method was a linear regression. The obtained results were promising since the calculated errors were low (Table 6 and Table 7) and the predictions fit quite well with the trends of the original curves (Figure 6). This linear method also allowed knowing the relationship between the independent variables and the dependent variable (Equation (5)), giving a clear idea of the influence of each variable in the prediction of the amplitude at each frequency.

Table 6.
Obtained results during the training and testing stage for the total dataset.

Table 7.
Obtained results during the testing stage for the pinnae ‘R’ and ‘S’, pinnae that form the test dataset. Additionally, it is shown the error committed in the case of using the standard KEMAR pinnae (Pinna ‘T’) instead of the models.
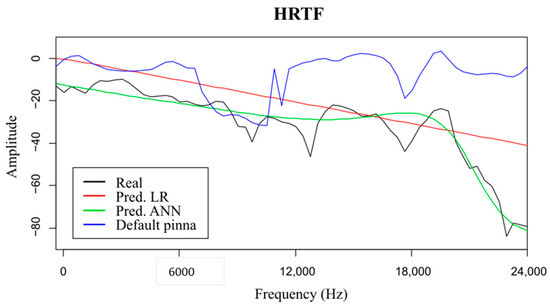
Figure 6.
Graphic representation of one random selected HRTF of the used to test the models (Pinna ‘S’, , ). Comparison between the real HRTF of the selected case, the predicted HRFT using LR, the predicted HRFT using MLP ANN, and the real HRTF measured with the standard pinna (Pinna ‘T’).
Although with the use of the LR technique, it was also observed that the model predicts with greater error the amplitudes that have lower values, and especially when there were abrupt variations in amplitude values between nearby frequencies (Figure 6 and Figure 7). As can be seen in Figure 7, the study of the residuals obtained supported this conclusion, obtaining a minimum value of −103.13, in the 1Q of −6.35, a median value of 0.03, a 3Q equal to 8.39 and a maximum value of 42.76. In addition, based on this analysis and focused on the Q-Q plot, it was observed that the samples within the quantile that defined the lowest amplitude values did differ significantly from the line that compares the real distribution with the predicted distribution.
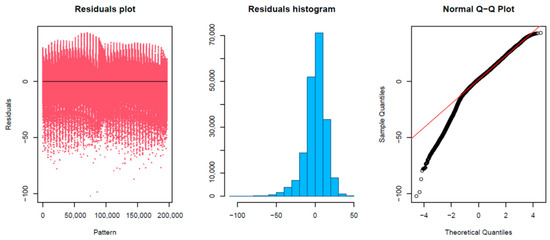
Figure 7.
Graphic analysis of the residuals obtained in the prediction of the testing dataset using the model built based on the LR algorithm.
The study of LR results led to conduct another analysis using a non-linear model, in this case one model built based on MLP ANN. This new task was focused on improving the weaknesses of the linear model. To do this, during the training, a tuning of the most significant variables of the algorithm was performed at the same time as 50 times repeated cross validation (Figure 8). For this algorithm, it was concluded that the chosen neural network structure was formed by 20 neurons in its hidden layer and a weight decay value of 0.005, values that provided a model with accurate prediction results.
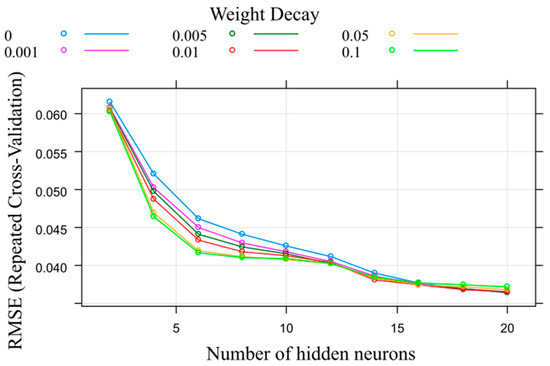
Figure 8.
RMSE obtained during the training stage for the nonlinear model. Number of neurons and weight decay were tuned.
The use of this nonlinear model led to observe a more accurate prediction at low amplitudes and also, a better adjustment when there is an abrupt amplitude variation of nearby frequencies (Figure 6 and Figure 9). Additionally, in Figure 9, the study of the residuals obtained showed a minimum value of −87.05, in the 1Q of −8.23, a median value of 4.71, a 3Q equal to 12.83, and a maximum value of 54.14. In this last case, the residual plots showed a fairly random pattern with positive and negative residuals, indicating that the model provided accurate fit to the data. Furthermore, the residual histogram had a symmetric bell shape, and the normal probability plot followed the straight line in a more accurate way, mainly at the extremes of the graph where the linear model failed. It was also observed in Figure 9, a more marked difference in the residuals generated depending on each of the testing pinnae.
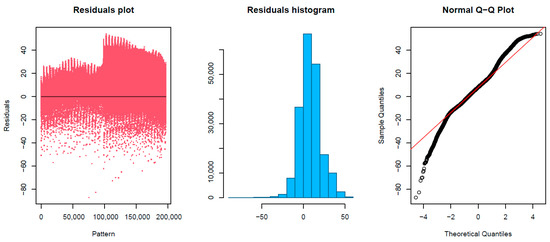
Figure 9.
Analysis of the residuals obtained in the prediction of the testing dataset using the model built based on the multilayer perceptron artificial neural network algorithm.
Finally, to check the methodology and the progress it provides in the field, the error obtained by the predictions was compared with the error that would be obtained in the case of using the HRTFs measured on the standard KEMAR pinna (Table 7). In this case, it was verified that both model predictions improved the results obtained with the standard pinna, but especially when the ANN-based model was applied. Although these models still did not very accurately predict possible frequency notches, they showed accurate results predicting the HRTFs trend and showed especially important improvements in comparison with the results obtained using the standard pinna. It can be concluded that these models supply useful information to obtain a higher quality sound experience, improving the information given by the standard pinna.
4. Conclusions
Based on the study performed on this work, two major problems have been observed when working with virtual personal auditory space. The first HRTFs that define the space change considerably with the morphological features of each individual. Additionally, the second HRTFs that perform all the measurements to obtain these functions for a new individual is a complex and expensive task. Faced with these problems, it has been observed that the use of multivariate analysis techniques can help considerably when studying how these functions vary, and also to understand their relationship with the morphological attributes of different individuals. It has also been proven that the use of supervised machine learning techniques applied to datasets adapted to the problem under study, allows predicting HRTFs with relatively low errors of new individuals with its personal morphological features, even if these differ from the individuals studied in the dataset used to train the models. It was also observed that to model a complex problem as HRTFs, linear techniques get greater errors despite generating important information related to the problem, for example an easy-to-understand-and-interpret mathematical equation that relates the features to each other. Furthermore, non-linear techniques better fit and generalize the problem in order to predict these functions. In addition, when the results obtained with these models and the results generated based on a standard pinna are compared, it is observed that the adjustment of HRTFs based on the morphological attributes of each individual is significantly improved. Application of more advanced algorithms in future enhancement could generate more accurate predictions and even detect frequency notches more clearly.
Author Contributions
Conceptualization, R.F.M. and R.U.; methodology, R.F.M.; software, R.F.M.; validation, R.F.M., M.R. and R.U.; formal analysis, R.F.M. and R.U.; investigation, R.F.M.; resources, R.U.; data curation, E.M.S., P.J. and R.U.; writing—original draft preparation, R.F.M.; writing—review and editing, R.F.M., P.J., E.M.S. and R.U.; visualization, R.F.M. and P.J.; supervision, M.R. and R.U.; project administration, R.U.; funding acquisition, R.F.M. and R.U. All authors have read and agreed to the published version of the manuscript.
Funding
The authors wish to thank to the Basque Government for its support through the KK-2019-00033 METALCR2, and the University of the Basque Country UPV/EHU for its support through the MOV21/03.
Data Availability Statement
The raw data of the experiments can be requested from the authors.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Moller, H.; Sorensen, M.F.; Hammershoi, D.; Jensen, C.B. Head related transfer functions of human subjects. J. Audio Eng. Soc. 1995, 43, 300–321. [Google Scholar]
- Blauert, J.P. Spatial Hearing; Revised Edition; MIT: Cambridge, MA, USA, 1997. [Google Scholar]
- Wenzel, E.M.; Arruda, M.; Kistler, D.J.; Wightman, F.L. Localization using non-individualized head-related transfer functions. J. Acoust. Soc. Am. 1993, 94, 111–123. [Google Scholar] [CrossRef]
- Spagnol, S.; Purkhús, K.B.; Björnsson, S.K.; Unnthórsson, R. The Viking HRTF dataset. In Proceedings of the 16th Sound & Music Computing Conference (SMC 2019), Málaga, Spain, 28–31 May 2019; pp. 55–60. [Google Scholar]
- Yu, G.; Wu, R.; Liu, Y.; Xie, B. Near-field head-related transfer-function measurement and database of human subjects. J. Acoust. Soc. Am. 2018, 143, EL194–EL198. [Google Scholar] [CrossRef]
- Gupta, N.; Barreto, A.; Joshi, M.; Agudelo, J.C. HRTF database at FIU DSP Lab. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 169–172. [Google Scholar]
- Xie, B.; Zhong, X.; Rao, D.; Liang, Z. Head-related transfer function database and its analyses. Sci. China Physics Mech. Astron. 2007, 50, 267–280. [Google Scholar] [CrossRef]
- Algazi, V.R.; Duda, R.O.; Thompson, D.M.; Avendano, C. The CIPIC HRTF database. In Proceedings of the IEEE ASSP Workshop on Applications of Signal Processing to Audio and Acoustics, New Platz, NY, USA, 21–24 October 2001; pp. 99–102. [Google Scholar]
- Stitt, P.; Katz, B.F.G. Sensitivity analysis of pinna morphology on head-related transfer functions simulated via a parametric pinna model. J. Acoust. Soc. Am. 2021, 149, 2559–2572. [Google Scholar] [CrossRef]
- Spagnol, S.; Geronazzo, M.; Avanzini, F. On the Relation Between Pinna Reflection Patterns and Head-Related Transfer Function Features. IEEE Trans. Audio, Speech, Lang. Process. 2012, 21, 508–519. [Google Scholar] [CrossRef]
- Zotkin, D.Y.N.; Hwang, J.; Duraiswaini, R.; Davis, L.S. HRTF personalization using anthropometric measurements. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19–22 October 2003; pp. 157–160. [Google Scholar]
- Lopez-Poveda, E.A.; Meddis, R. A physical model of sound diffraction and reflections in the human concha. J. Acoust. Soc. Am. 1996, 100, 3248–3259. [Google Scholar] [CrossRef]
- Pollack, W.B.K.; Kreuzer, W.; Majdak, P. Perspective Chapter: Modern Acquisition of Personalised Head-Related Transfer Functions—An Overview. In Advances in Fundamental and Applied Research on Spatial Audio; IntechOpen: Rijeka, Croatia, 2022. [Google Scholar]
- Bomhardt, R. Anthropometric Individualization of Head-Related Transfer Functions. Analysis and Modeling. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2017. [Google Scholar]
- Brinkmann, F.; Dinakaran, M.; Pelzer, R.; Grosche, P.; Voss, D.; Weinzierl, S. A Cross-Evaluated Database of Measured and Simulated HRTFs Including 3D Head Meshes, Anthropometric Features, and Headphone Impulse Responses. J. Audio Eng. Soc. 2019, 67, 705–718. [Google Scholar] [CrossRef]
- Jiang, Z.; Sang, J.; Zheng, C.; Li, A.; Li, X. Modeling individual head-related transfer functions from sparse measurements using a convolutional neural network. J. Acoust. Soc. Am. 2023, 153, 248–259. [Google Scholar] [CrossRef]
- Gutierrez-Parera, P.; Lopez, J.J.; Mora-Merchan, J.M.; Larios, D.F. Interaural time difference individualization in HRTF by scaling through anthropometric parameters. EURASIP J. Audio Speech Music Process. 2022, 2022, 1–19. [Google Scholar] [CrossRef]
- Yao, D.; Zhao, J.; Cheng, L.; Li, J.; Li, X.; Guo, X.; Yan, Y. An individualization approach for head-related transfer function in arbitrary directions based on deep learning. JASA Express Lett. 2022, 2, 064401. [Google Scholar] [CrossRef] [PubMed]
- Grijalva, F.; Martini, L.; Florencio, D.; Goldenstein, S. A Manifold Learning Approach for Personalizing HRTFs from Anthropometric Features. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 559–570. [Google Scholar] [CrossRef]
- Xie, B.; Zhong, X.; He, N. Typical data and cluster analysis on head-related transfer functions from Chinese subjects. Appl. Acoust. 2015, 94, 1–13. [Google Scholar] [CrossRef]
- Li, L.; Huang, Q. HRTF personalization modeling based on RBF neural network. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3707–3710. [Google Scholar] [CrossRef]
- Chan, C.F.; Wang, Z. Hrir Customization Using Common Factor Decomposition and Joint Support Vector Regression. In Proceedings of the 21st European Signal Processing Conference, Marrakech, Morocco, 9–13 September 2013. [Google Scholar] [CrossRef]
- Kistler, D.J.; Wightman, F.L. A model of head-related transfer functions based on principal components analysis and minimum-phase reconstruction. J. Acoust. Soc. Am. 1992, 91, 1637–1647. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Zhuang, Q. HRIR personalisation using support vector regression in independent feature space. Electron. Lett. 2009, 45, 1002–1003. [Google Scholar] [CrossRef]
- Huang, Q.-H.; Fang, Y. Modeling personalized head-related impulse response using support vector regression. J. Shanghai Univ. 2009, 13, 428–432. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, L.; Ma, H.; Wu, Z. HRTF personalization based on artificial neural network in individual virtual auditory space. Appl. Acoust. 2008, 69, 163–172. [Google Scholar] [CrossRef]
- Lee, G.W.; Kim, H.K. Personalized HRTF Modeling Based on Deep Neural Network Using Anthropometric Measurements and Images of the Ear. Appl. Sci. 2018, 8, 2180. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Kuo, T.-H.; Chi, T.-S. Autoencoding HRTFS for DNN Based HRTF Personalization Using Anthropometric Features. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 271–275. [Google Scholar] [CrossRef]
- Zhang, M.; Ge, Z.; Liu, T.; Wu, X.; Qu, T. Modeling of Individual HRTFs Based on Spatial Principal Component Analysis. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2020, 28, 785–797. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Martinez, R.F.; Lorza, R.L.; Delgado, A.A.S.; Piedra, N. Use of classification trees and rule-based models to optimize the funding assignment to research projects: A case study of UTPL. J. Inf. 2021, 15, 101107. [Google Scholar] [CrossRef]
- Lostado-Lorza, R.; Escribano-Garcia, R.; Fernandez-Martinez, R.; Illera-Cueva, M.; Mac Donald, B.J. Using the finite element method and data mining techniques as an alternative method to determine the maximum load capacity in tapered roller bearings. J. Appl. Log. 2017, 24, 4–14. [Google Scholar] [CrossRef]
- Martinez, R.F.; Iturrondobeitia, M.; Ibarretxe, J.; Guraya, T. Methodology to classify the shape of reinforcement fillers: Optimization, evaluation, comparison, and selection of models. J. Mater. Sci. 2016, 52, 569–580. [Google Scholar] [CrossRef]
- Spagnol, S.; Miccini, R.; Unnthórsson, R. The Viking HRTF Dataset v2. Zenodo. 2020. Available online: https://doi.org/10.5281/zenodo.4160401 (accessed on 1 January 2023).
- Onofrei, M.G.; Miccini, R.; Unnthórsson, R.; Serafin, S.; Spagnol, S. 3D ear shape as an estimator of HRTF notch frequency. In Proceedings of the 17th Sound & Music Computing Conference (SMC 2020), Torino, Italy, 24–26 June 2020; pp. 131–137. [Google Scholar]
- Guo, Z.; Lu, Y.; Zhou, H.; Li, Z.; Fan, Y.; Yu, G. Anthropometric-based clustering of pinnae and its application in personalizing HRTFs. Int. J. Ind. Ergon. 2021, 81, 103076. [Google Scholar] [CrossRef]
- Spagnol, S. HRTF Selection by Anthropometric Regression for Improving Horizontal Localization Accuracy. IEEE Signal Process. Lett. 2020, 27, 590–594. [Google Scholar] [CrossRef]
- Nishino, T.; Inoue, N.; Takeda, K.; Itakura, F. Estimation of HRTFs on the horizontal plane using physical features. Appl. Acoust. 2007, 68, 897–908. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 8th ed.; Pearson: Andover, UK, 2019. [Google Scholar]
- Ripley, B. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Funahashi, K.-I. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 1 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).